基于机器学习的分形导数 Maxwell 混凝土徐变模型

doi:10.3785/j.issn.1008-973X.2026.03.004

基于机器学习的分形导数 Maxwell 混凝土徐变模型

梅生启^,, 李旭峰, 王兴举^,, 刘晓东, 吴黎明, 李星艳, 刘哲

1. 石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043

2. 石家庄铁道大学交通运输学院，河北石家庄 050043

3. 山西交通物流集团有限公司，山西太原 030011

4. 石家庄铁道大学土木工程学院，河北石家庄 050043

5. 四川轻化工大学土木工程学院，四川自贡 643000

Machine-learning based fractal derivative Maxwell concrete creep model

MEI Shengqi^,, LI Xufeng, WANG Xingju^,, LIU Xiaodong, WU Liming, LI Xingyan, LIU Zhe

1. State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures, Shijiazhuang Tiedao University, Shijiazhuang 050043, China

2. School of Traffic and Transportation, Shijiazhuang Tiedao University, Shijiazhuang 050043, China

3. Shanxi Transportation Logistics Group Limited Company, Taiyuan 030011, China

4. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China

5. School of Civil Engineering, Sichuan University of Science and Engineering, Zigong 643000, China

通讯作者: 王兴举，男，教授. orcid.org/0000-0003-0556-5943. E-mail: wangxingju@stdu.edu.cn

收稿日期: 2025-03-9

基金资助:

国家自然科学基金资助项目（52108161）；河北省高等学校科学研究资助项目（BJK2024127）；石家庄铁道大学土木工程学院自主科研课题（TMXN2201）；石家庄铁道大学研究生创新资助项目（YC202407, YC202426）.

Received: 2025-03-9

Fund supported:

作者简介 About authors

梅生启（1990—），男，副教授，从事结构长期性能的研究.orcid.org/0000-0001-5049-393X.E-mail：cshqmei@stdu.edu.cn , E-mail：cshqmei@stdu.edu.cn

摘要

为了解决现有混凝土徐变模型计算复杂且对多源分散数据预测精度有限的问题，通过物理模型与数据驱动融合的方式，结合具有物理意义的分形导数理论与XGBoost机器学习算法，提出可预测的分形导数 Maxwell混凝土徐变模型. 基于从NU混凝土徐变数据库中筛选出的746组试验数据，建立混凝土材料特性、环境条件与分形导数Maxwell模型关键参数（分形阶数和黏性系数）之间的映射关系，采用贝叶斯优化方法确定模型的最优超参数. 研究结果表明，所构建模型在测试集上对分形阶数和黏性系数的预测决定系数分别达到0.919和0.908，在独立的验证集上，预测决定系数的评分为0.909，展现出良好的拟合性能和泛化能力. 与既有模型相比，提出的物理-数据融合模型在保留理论解释性的同时，有效提高了整体的预测精度.

关键词： 混凝土徐变 ; 分形导数理论 ; Maxwell模型 ; 机器学习算法 ; 预测模型

Abstract

A predictable fractal derivative Maxwell concrete creep model was proposed to address the problems of complex calculations and limited prediction accuracy for multi-source dispersed data in existing concrete creep models. The fractal derivative theory was combined with the XGBoost machine learning algorithm through a physics-data fusion approach. A mapping relationship between concrete material characteristics, environmental conditions, and the key parameters of the fractal derivative Maxwell model (fractal order and viscosity coefficient) was established based on 746 sets of experimental data selected from the NU concrete creep database. Bayesian optimization was adopted to determine the optimal hyperparameters. The constructed model achieved coefficients of determination (R²) of 0.919 and 0.908 for the prediction of the fractal order and the viscosity coefficient on the test set, respectively. An R² score of 0.909 was obtained on an independent validation set. These results demonstrate that the model has good fitting performance and generalization capability. The proposed physics-data fusion model improves overall prediction accuracy while retaining theoretical interpretability compared with existing models.

Keywords： concrete creep ; fractal derivative theory ; Maxwell model ; machine-learning algorithm ; prediction model

PDF (1274KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

梅生启, 李旭峰, 王兴举, 刘晓东, 吴黎明, 李星艳, 刘哲. 基于机器学习的分形导数 Maxwell 混凝土徐变模型. 浙江大学学报(工学版)[J], 2026, 60(3): 487-494 doi:10.3785/j.issn.1008-973X.2026.03.004

MEI Shengqi, LI Xufeng, WANG Xingju, LIU Xiaodong, WU Liming, LI Xingyan, LIU Zhe. Machine-learning based fractal derivative Maxwell concrete creep model. Journal of Zhejiang University(Engineering Science)[J], 2026, 60(3): 487-494 doi:10.3785/j.issn.1008-973X.2026.03.004

混凝土在持续荷载作用下的变形增长形象，即徐变的科学发现，可以追溯至1907年. 百年来的研究表明，混凝土徐变可以达到瞬时弹性变形的数倍. 徐变效应可能引起预应力损失、结构挠度累积和内力重分布等系列问题^[1]，是预应力结构、超高层建筑、核电工程安全壳结构设计控制的重要因素之一. 以美国为例，每年用于因混凝土徐变、耐久性问题引发的公路损伤维护费用从2009年的788亿美元^[2]攀升至2019年的1230亿美元^[3]. 精确可靠的徐变预测对于优化结构设计、合理评估长期性能以及降低全寿命周期维护成本变得尤为关键.

徐变预测的有效性和准确性取决于徐变模型的选择. 既有的ACI 209R-92^[4]、MC2010^[5]、B4^[6]和GL2000^[7]等模型多为半理论半经验型模型^[8]. 近年来，随着试验数据的不断积累，Feng等^[9-10]采用机器学习算法对混凝土徐变进行建模分析. 机器学习的可解释性及过程透明化是仍需关注的.

基于分数阶导数理论的分数阶黏弹性模型可以用较少的元件实现更高的精度^[11-12]. 分数阶导数的卷积积分开发全局运算符，需要更高的计算成本和内存需求^[13]. 为了提高分数阶模型的计算效率，没有卷积积分的分形导数理论^[14]逐渐被推广应用于蠕变计算^[15]、扩散分析^[16]领域.

本文提出可预测的分形导数Maxwell徐变计算模型. 融合具有明确物理意义的分形导数Maxwell理论模型与数据驱动的XGBoost机器学习算法，既保留了物理模型的理论解释性，又利用了机器学习算法在参数预测方面的优势. 基于混凝土徐变数据库，建立材料特性、环境条件与分形导数Maxwell模型参数间的映射关系. 通过贝叶斯优化方法，确定最优模型超参数. 构建既具备物理基础，又拥有精准预测能力的混凝土徐变模型. 算例验证表明，提出的模型不仅可以在训练集和测试集上展现出优异的拟合性能，而且在独立验证集上表现出良好的泛化能力.

1. 分形导数Maxwell模型

1.1. 分数阶黏弹性模型

作为材料黏弹性能的典型力学特征之一，混凝土、金属、岩石等多种材料均会发生徐变^[17]. Vandamme等^[2,18]通过水泥浆体纳米压痕试验证实了水化硅酸钙的徐变特性，为黏弹性研究提供了试验验证. 经典的黏弹性模型基于弹性元件和黏性元件的组合，描述黏弹性行为. 为了获得更好的拟合精度，经典的黏弹性模型须结合更多的弹性元件或黏性元件. Neville等^[19]总结了19种黏弹性模型用于混凝土徐变计算，认为当单元数过多时，会带来一些不适定性问题，导致模型参数的物理意义不明确.

将黏性元件换成分数阶导数的形式^{[11, 20]}，形成分数阶黏性元件^[21]. 将分数阶黏性元件全部或部分替换经典模型中的黏性元件，形成分数阶黏弹性模型. 已有研究表明，与经典的黏弹性模型相比，分数阶黏弹性模型可以更加精准地描述混凝土的徐变行为^[22-23],

分数阶微积分的定义包含卷积算子，从而产生了分数阶微积分的全局性质. 以Caputo定义^[24]为例，可以表述为

(1)$ \frac{{{{\text{d}}^a}u(t)}}{{{\text{d}}{t^a}}} = \frac{1}{{\varGamma (1 - \alpha )}}\int_0^t {{{(t - \tau )}^{ - \alpha }}} u'(\tau ){\mkern 1mu} {\text{d}}\tau . $

式中：$\alpha $为分数阶阶数，$\alpha $= 0~1.0. 由于分数阶的这种非局部性质，一般来说，分数阶导数模型的数值求解计算量很大.

1.2. 分形导数的定义

通过将标准整数时空变换为分形时空结构，分形导数的定义可以表述为

(2)$ \frac{{{\text{d}}u(t)}}{{{\text{d}}{t^p}}} = \mathop {\lim }\limits_{t' \to t} \frac{{u(t) - u(t')}}{{{t^p} - {{t'}^p}}}. $

式中：p为时间上的分形及分形导数的阶数. 从式（2）可以看出，分形导数是没有卷积积分的局部算子. 在分形不变性和分形等价的假设下^[25]，分形导数可以通过标度变换$\hat t = {t^p}$简化为普通导数.

该方法已成功应用于获得分形扩散方程的基本解，扩散方程的基本解形式为拉伸高斯分布^[26]. 类似地，分形理查德方程很好地描述了多孔介质中水传输的非玻尔兹曼标度现象^[27].

1.3. 分形导数Maxwell模型

采用分形黏性元件来表征黏弹性材料的流变特性的分形导数黏弹性模型^[13]，如表1所示.

表 1 分形导数黏弹性模型的示意图及应力-应变关系

Tab.1 Schematic diagram and stress-strain relationship of fractal derivative viscoelastic model

分形黏弹性模型	示意图	表达式
分形黏性元件		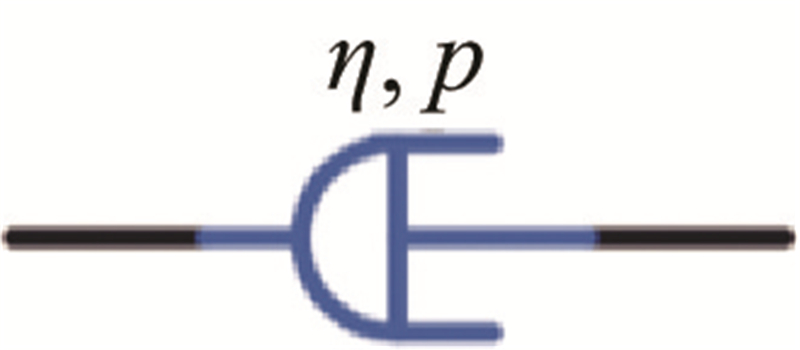$\sigma = {\text{ }}\eta \dfrac{{{\text{d}}\varepsilon }}{{{\text{d}}{t^p}}}$
分形Maxwell模型		$\dfrac{{{\text{d}}\varepsilon }}{{{\text{d}}{t^p}}} = \dfrac{1}{E}\dfrac{{{\text{d}}\sigma }}{{{\text{d}}{t^p}}}+\dfrac{\sigma }{\eta }$
分形Kelvin模型		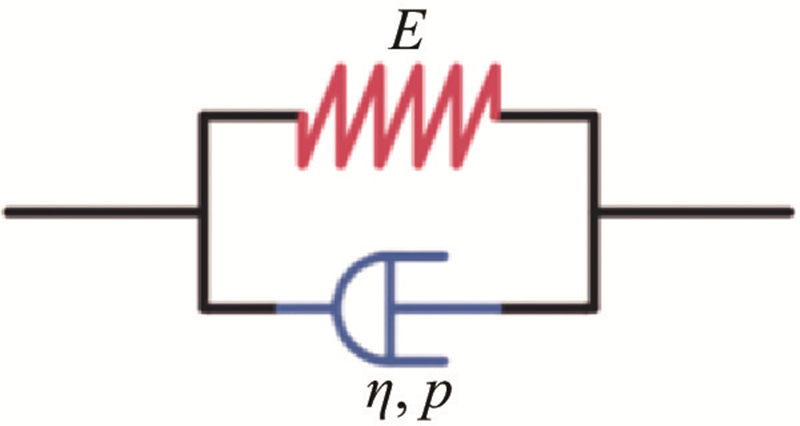$\dfrac{{{\text{d}}\varepsilon }}{{{\text{d}}{t^p}}}+\dfrac{E}{\eta }\varepsilon = \dfrac{\sigma }{\eta }$

新窗口打开| 下载CSV

推导得到分形导数Maxwell模型的混凝土徐变柔量及徐变度的表达式如下：

(3)$ C(t) = \frac{{{t^p}}}{\eta }, $

(4)$ J(t) = \frac{1}{E}+\frac{{{t^p}}}{\eta }. $

2. 机器学习算法及数据集

2.1. XGBoost

XGBoost（extreme gradient boosting）是基于梯度提升决策树（gradient boosting decision tree，GBDT）的高效算法实现，由Chen等^[28]提出. 作为GBDT算法的改进版本，XGBoost在数学形式上采用加法模型. 对于包含n个样本和m个特征的数据集$D = \left( {{x_i},{y_i}} \right)$，数据集的预测模型可以表示为K个基本模型的组合：

(5)$ {\hat y_i} = \sum\limits_{k = 1}^K {{f_k}} ({x_i});\;{f_k} \in \varphi . $

式中：$\hat {{y_i}}$为预测标签，${f_k}\left( {{x_i}} \right)$为第k个模型对样本${x_i}$的预测分数，$\varphi $为回归树的集合.

2.2. 贝叶斯优化

贝叶斯优化（Bayesian optimization, BO）是基于概率分布的高效优化算法. 该方法通过构建先验函数和采集函数2个关键组件，在较少的迭代次数内找到接近最优的解决方案^[29].

贝叶斯优化算法主要包含2个相互作用的关键组件. 第1个组件是统计模型，用于基于已观察到的函数评估（或样本）来表示未知的目标函数，通常采用高斯过程作为统计模型. 第2个组件是采集算法，它利用构建的统计模型来决定在目标函数的哪个位置进行查询，以构建更好的统计模型供未来使用. 这种基于概率模型的搜索策略使得算法能够在较少的评估次数内找到较好的解决方案.

在工程设计的黑箱优化问题中，贝叶斯优化已被证明是有效的. 虽然针对约束优化问题的扩展在低维相对简单的优化问题中表现良好，但这些约束贝叶斯优化方法在找到好的设计时可能需要大量函数的评估，特别是当可行设计空间受到高度约束时. 在实际应用中，需要权衡优化效果和计算成本.

2.3. 评价标准

为了全面评估机器学习模型的预测性能，采用3个统计指标：决定系数R²、平均绝对误差MAE和均方根误差RMSE.

R²反映了模型对数据变异性的解释程度：

(6)$ {R^2} = 1 - {{\displaystyle \sum\limits_{i = 1}^n ( {y_{i,{\text{pre}}}} - {{\bar y}_{{\text{pre}}}}{)^2}}}\left/{{\displaystyle \sum\limits_{i = 1}^n {{{({y_{i,{\text{exp}}}} - {{\bar y}_{{\text{exp}}}})}^2}} }}\right.. $

式中：${y_{i,\mathrm{{pre}}}}$ 为模型的第i次预测值，${y_{\mathrm{{exp}}}}$ 为第i次试验观测值，$\overline y $为相应数据的平均值. R²的取值为0~1.0，R²越接近1表示模型的预测效果越好.

MAE直接度量了预测值与实际值之间的平均偏差，

(7)$ {\text{MAE}} = {n^{-1}}{{\displaystyle \sum\limits_{i = 1}^n | {y_{i,{\text{exp}}}} - {y_{i,{\text{pre}}}}|}}. $

MAE直接以实际单位衡量误差，具有直观的物理意义，便于工程实践中的误差评估.

均方根误差RMSE通过平方项加重了较大误差的影响：

(8)$ {\text{RMSE}} = \sqrt {{n^{-1}}{{\displaystyle \sum\limits_{i = 1}^n {{{({y_{i,{\text{exp}}}} - {y_{i,{\text{pre}}}})}^2}} }}} . $

RMSE保持了原始数据的单位，与MAE相比，对异常值更加敏感，能够更好地反映模型预测的稳定性.

这3个评价指标共同构成全面的模型评估体系：R²反映了模型的总体拟合优度，MAE提供了误差的直观度量，RMSE强调了预测的稳定性和可靠性.

2.4. 数据集

2.4.1. 混凝土徐变数据集

采用由美国西北大学建立的NU混凝土徐变数据库. 该数据库收录了1809条收缩试验数据和1403条徐变试验数据，详细记录了试验数据来源、混凝土配合比、环境条件及试件尺寸等关键信息.

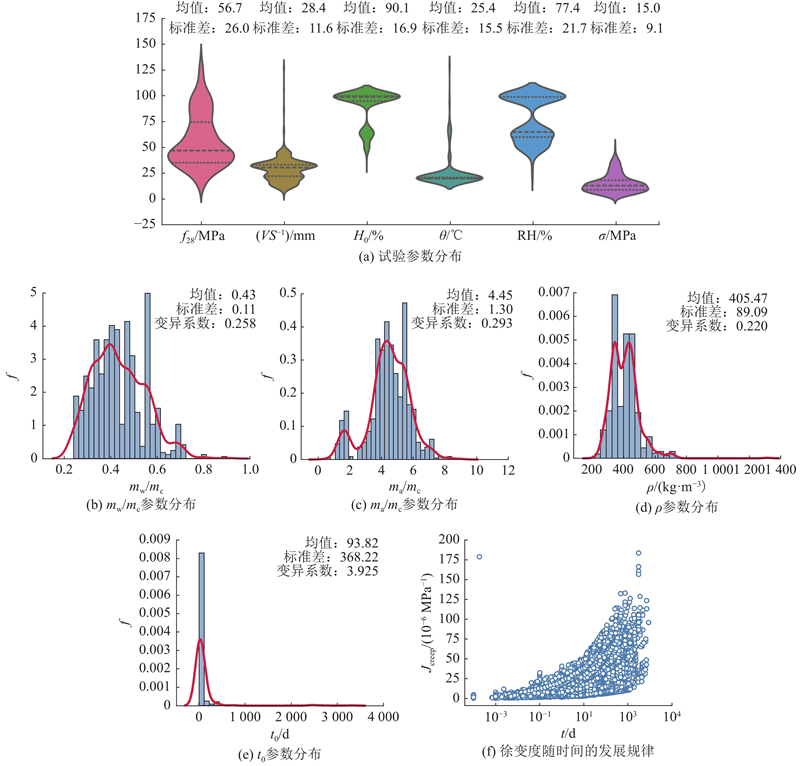
为了确保机器学习模型训练的数据质量，根据数据库数据的完整程度以及与相关研究的对比分析，对NU数据库进行系统筛选，最终获得746组基本徐变试验数据，包含14 565个数据点. 每组数据包含11个特征变量：水泥质量密度ρ(单位立方米体积混凝土所需水泥质量)、水灰比m_w/m_c(以质量比表示)、骨料水泥比m_a/m_c(以质量比表示)、28 d抗压强度f₂₈、试验温度$ \theta $、相对湿度RH、体表比V/S、养护相对湿度H₀、持荷应力σ、加载龄期t₀和持续荷载作用时间dt、输出变量混凝土徐变度J_creep. 该数据库各特征以及输出变量的统计信息如图1所示. 其中，f为概率密度.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 混凝土徐变数据库的参数分布

Fig.1 Parameter distribution of concrete creep database

从图1的统计结果可知，筛选后的数据集涵盖了广泛的混凝土设计参数与试验条件. 具体而言，28 d抗压强度为20~130 MPa，体现了从普通强度到高强度混凝土的全面覆盖. 体表比为12~60 mm，反映了不同构件尺寸的影响. 加载龄期为7~90 d，能够反映早期至标准龄期的加载效应. 试验温度和相对湿度分别为5~30 ℃和40%~100%，代表了不同环境条件下的徐变特性. 在配合比设计方面，m_w/m_c主要分布在0.3~0.6，m_a/m_c集中在3~6，这些参数的分布特征与工程实践中常用的混凝土配合比设计相符. 这种全面的参数覆盖为后续建立可靠的徐变预测模型提供了坚实的数据基础. 筛选后的数据集对于不同强度等级的混凝土、不同试验环境和加载龄期都有较宽的变化范围.

2.4.2. 独立验证数据集

为了确保模型评估的客观性和可靠性，选取文献[30]的3组混凝土徐变数据作为独立验证集. 这3组试验中的机制砂母岩类型为花岗岩，属于二区中砂. 3组试验采用不同的石粉质量分数(机制砂中石粉质量与机制砂质量的比值)为3.5%、7.0%和10.4%.

这些数据完全独立于模型开发过程，未参与任何模型的训练或测试阶段. 通过使用这样的独立验证集，可以更准确地评估提出模型的泛化性能，避免过拟合带来的评估偏差.

3. 可预测模型的构建

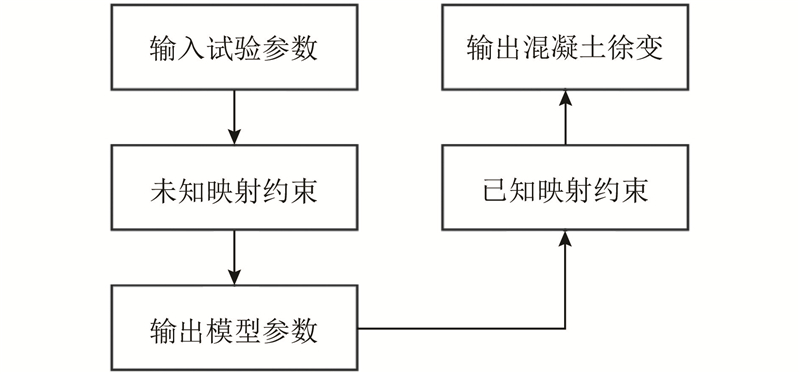
模型的构建思路如图2所示，在这种混合建模方法中，物理模型和机器学习模型通过参数映射实现了有机结合. 物理模型提供了可靠的理论框架，机器学习模型通过数据驱动的方式优化了模型参数. 该方法将具有明确物理意义的分形导数Maxwell模型与具有强大数据处理能力的机器学习算法相结合，以期在保持模型物理解释性的同时，提高预测精度. 在这种混合建模框架下，分形导数Maxwell模型提供了描述混凝土徐变行为的理论基础. 与传统的整数阶Maxwell模型相比，分形导数Maxwell模型通过引入分形导数，能够更准确地描述混凝土在持续荷载作用下的非线性变形特性. 模型中的关键参数（如分形阶数和黏性系数）难以通过简单的试验方法直接确定. 为了解决该问题，引入XGBoost算法对参数进行建模. XGBoost作为集成学习算法，具有优秀的特征学习能力和较强的泛化性能. 通过建立混凝土材料特征、环境条件与模型参数之间的映射关系，该算法能够根据实际的工程条件，自动调整模型参数. 这种结合不仅提高了预测精度，而且保持了模型结果的物理可解释性.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 融合建模方法的示意图

Fig.2 Schematic diagram of integrated modeling method

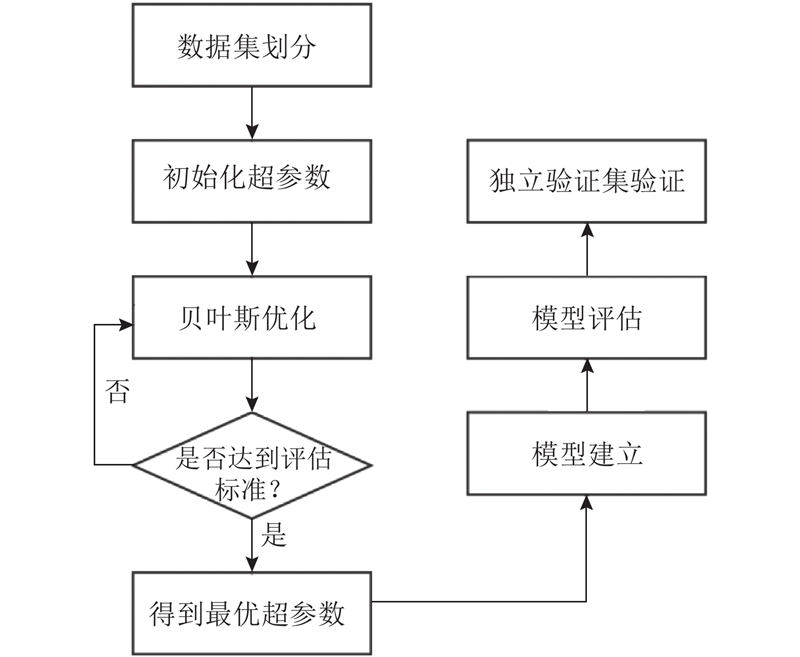
构建的物理-数据融合模型包含2个关键组成部分：基于分形导数Maxwell模型的物理模型框架和基于XGBoost的参数优化模块. 该模型通过XGBoost算法建立试验参数与模型参数间的映射关系，实现了物理模型与数据驱动方法的有机结合. 模型的构建过程主要包括数据预处理、特征选择和参数设置等环节. 每个环节的设计都致力于在保持物理意义的同时提高预测精度. 模型的构建过程如图3所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 可预测模型的构建过程

Fig.3 Construction process of predictive model

3.1. 数据预处理

在数据预处理阶段，需要采取系统的步骤来准备模型训练所需的数据集. 将NU数据库中筛选得到的基本徐变数据与机制砂混凝土的徐变数据进行整合. 这一合并过程为后续的参数优化提供了充足的数据基础.

由于XGBoost模型的目标是预测分形Maxwell模型的分形阶数p和黏性系数η，需要通过非线性拟合预先获取每组试验数据对应的参数值. 具体而言，采用Levenberg-Marquardt（LM）算法，基于每组试验数据的徐变度和持荷时间，拟合得到对应的p和η，拟合结果如图4所示. 其中，F为频数. 依据参数的拟合结果进行相关性分析，结果如图5所示. 其中，IC为相关系数.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 徐变度分形参数的拟合结果

Fig.4 Fitting result of fractal parameter for specific creep

在拟合过程中，未对参数范围进行限制. 从图4可以看出，2个参数均为0~1.0，这符合该模型的理论，也符合参数的实际意义. 从图5的相关性分析结果可以看出，参数p主要受混凝土本身性质的影响，参数η更多地受到试验参数的影响.

对参数拟合结果的评估如图6所示. 其中，残差J_res为拟合得到参数计算的徐变度与真实徐变度的差值. 从图6可以看出，即使对于跨度达数年的长期徐变数据，该方法也能实现优秀的拟合效果.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 分形参数拟合的相关性分析

Fig.5 Correlation analysis of fitted fractal parameter

图 6

新窗口打开| 下载原图ZIP| 生成PPT

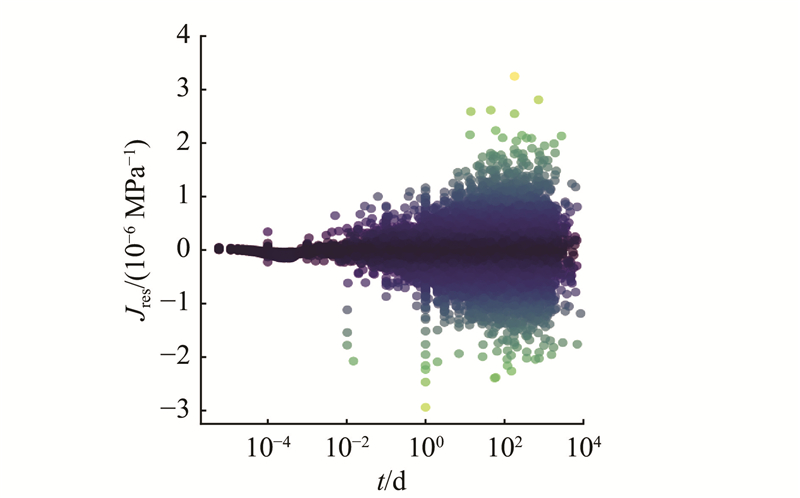
图 6 拟合徐变度与真实徐变度残差

Fig.6 Residual between fitted specific creep and measured specific creep

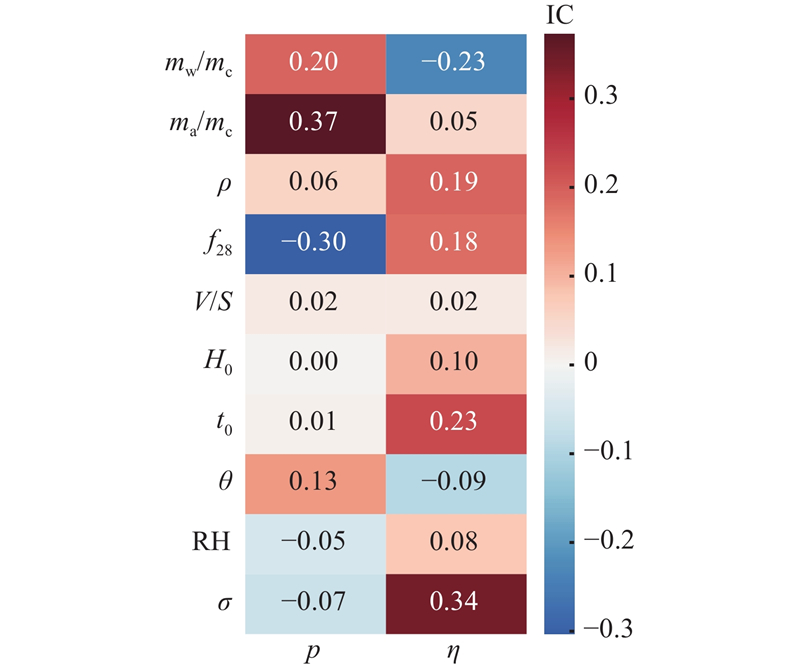
3.2. 特征选择

在特征工程方面，选取10个基本特征作为模型输入. 这些特征可以分为3类：材料特征、环境特征和荷载特征. 材料特征包括ρ、m_w/m_c、m_a/m_c和f₂₈，环境特征包括$ \theta $、RH、V/S和H₀，荷载特征包括σ和t₀.

为了消除量纲影响并提高模型的训练效率，对所有特征进行标准化处理. 标准化处理方法为Z-score法，标准化公式为

(9)$ z = \frac{{x - \mu }}{\sigma }. $

式中：$\mu $为特征数据的均值，$\sigma $为特征数据的标准差. 标准化过程会将特征数据转换为均值为0、方差为1的标准正态分布.

将数据集划分为75%的训练集和25%的测试集，设置随机种子数为42，以确保结果的可重复性. 数据集的划分方式以及模型输入输出的定义已完全确定，下一步将构建机器学习模型.

3.3. 参数设置

为了提高模型的预测精度和泛化能力，采用贝叶斯优化方法，对XGBoost模型的超参数进行系统优化. 优化过程采用5折交叉验证，搜索范围的设置如表2所示.

表 2 贝叶斯优化的超参数搜索范围

Tab.2 Hyperparameter search range for Bayesian optimization

超参数	搜索范围
树的最大深度 d_max	[3, 20]
学习率 $ \mathit{\alpha } $	[0.001, 0.3]
树的数量 M	[10, 500]
子节点最小权重 W_min	[1, 7]
分裂阈值 $ \mathit{\gamma } $	[0, 1]
样本采样比例 r_s	[0.6, 1.0]
特征采样比例 r_f	[0.6, 1.0]

新窗口打开| 下载CSV

在优化过程中，设置初始随机采样点数量n₀ = 5，最大迭代次数N_max = 50，并通过设置随机种子数s = 42，确保结果的可重复性. 优化目标是最大化模型在交叉验证过程中的R²评分.

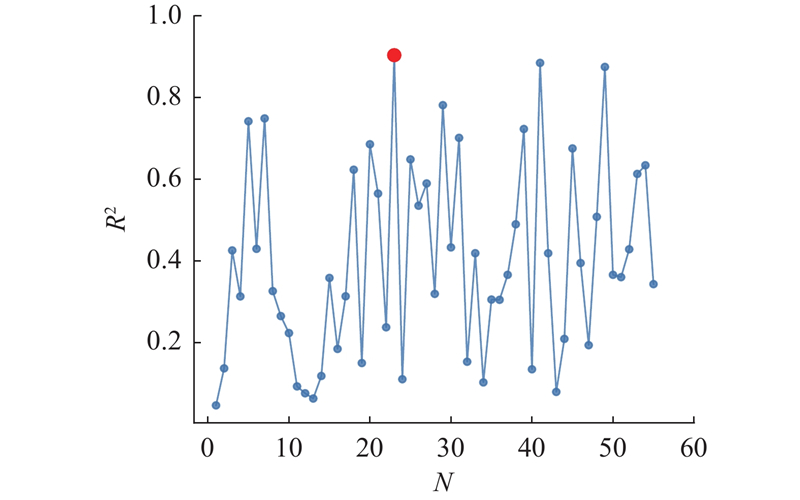
如图7所示为XGBoost模型的R²评分与迭代次数之间的对应关系.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 R²评分迭代图

Fig.7 R² score iteration diagram

3.4. 模型评估

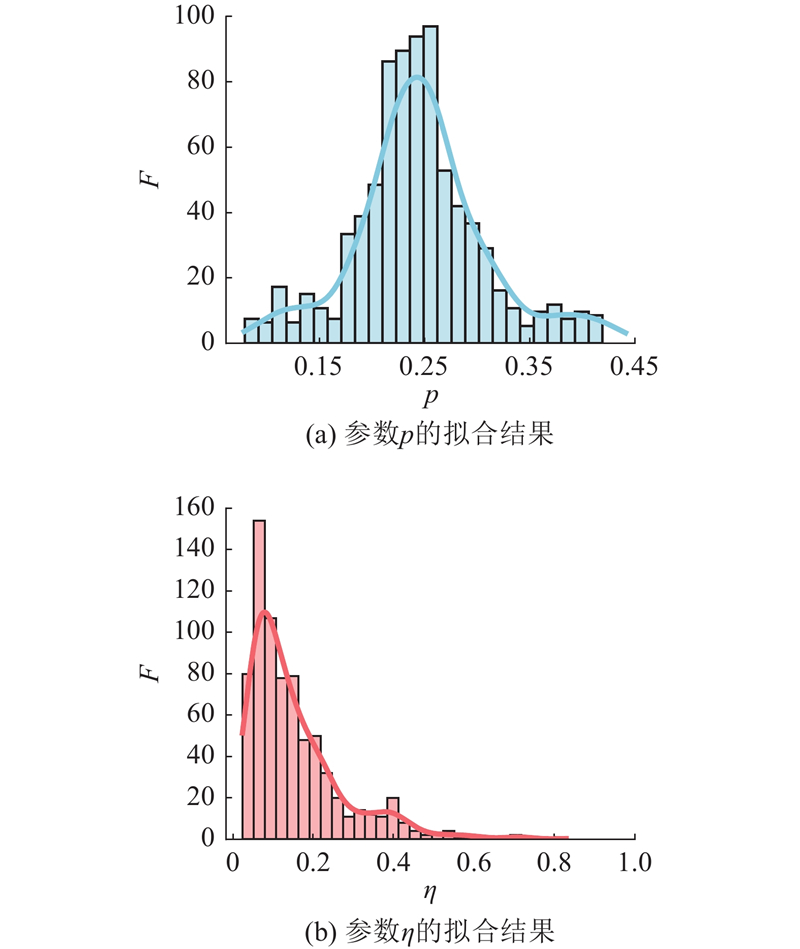
通过反复优化和测试，最终确定的最优参数组合如下：r_f = 1.0，$ \gamma $ = 0.37，$ \alpha $ = 0.1431，d_max = 5，W_min = 1.9171，N_max=475，r_s=1.0. 这组参数在保证模型预测精度的同时，维持了较好的泛化性能. 模型在25%的测试集上参数p的R²评分为0.919，RMSE仅为0.017 9；参数η的R²评分为0.908 0，RMSE为0.037 8. 利用训练好的XGBoost模型预测所有样本的p和η参数，如图8所示为计算得到的徐变度预测值J_pred与实测值J_true的对比散点图.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

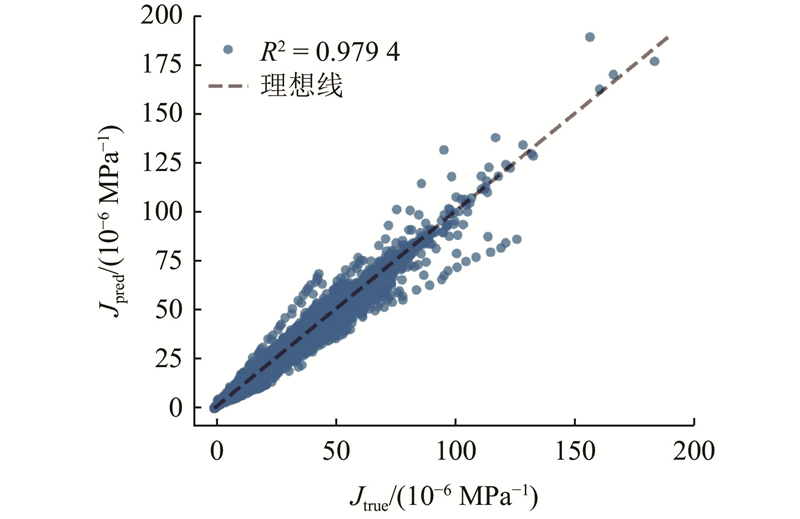
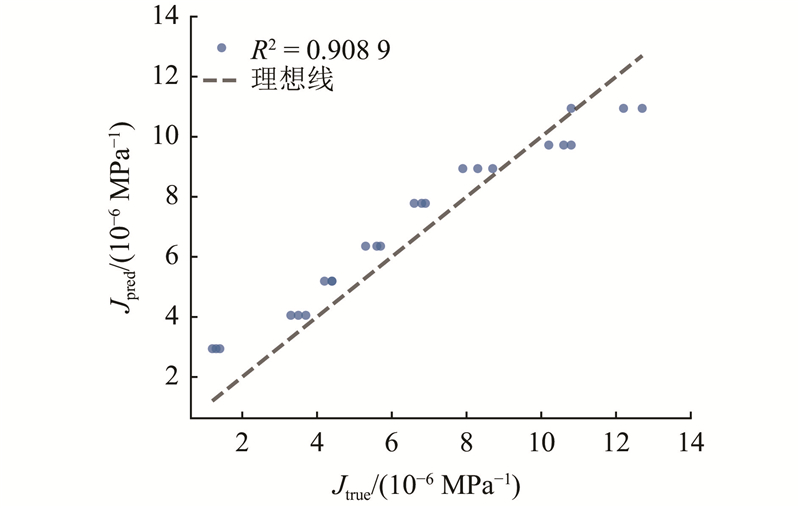
图 8 预测值与实测值的散点分布图

Fig.8 Scatter distribution plot of predicted value versus measured value

4. 可预测模型验证

为了验证训练得到的XGBoost模型对新的试验数据的预测能力，使用验证数据集来对模型的泛化能力进行评估.

如图9所示为物理-数据融合模型在验证集上的预测效果. 从图9的散点分布可以看出，预测值与实测值之间呈现出良好的线性相关性，大部分数据点都分布在理想线（虚线）附近. 该模型在验证集上获得了0.908 9的R²评分，表明该模型对混凝土的徐变行为具有较强的预测能力.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9 融合模型的评估

Fig.9 Evaluation of integrated model

在预测结果中可以观察到一些特征：当徐变度较大时，预测值略微低于实测值，这表明模型在预测较大的徐变变形时可能存在一定程度的低估. 这种现象可能与建模过程中未考虑单独的骨料参数有关. 骨料特性对混凝土徐变行为有重要的影响，特别是在大变形阶段，这为未来模型的进一步优化指明了方向.

提出的物理-数据融合模型兼具物理模型的理论解释性和数据驱动方法的预测精度. 与分数阶Maxwell模型相比，分形导数Maxwell模型仅需极少元件即可实现高精度拟合，且局部算子性质避免了分数阶导数计算中耗时的卷积积分，大幅提升了计算效率. 利用XGBoost算法，构建混凝土材料特性与分形模型参数间的映射关系，验证集性能稳定（R²=0.909），显著优于既有的徐变计算模型^[10]. 相较于纯数据驱动方法，本文模型保留了物理参数的明确意义，同时借助机器学习提高预测精度和可靠性，在计算复杂度和工程实用性之间进行了一些平衡调整.

本文模型适用于强度为20~130 MPa、不同环境条件（温度为5~30 ℃，相对湿度为40%~100%）下的混凝土徐变预测，能够覆盖不同的构件尺寸和加载龄期. 该模型在较大徐变度处存在轻微的低估趋势，这可能与未单独考虑骨料参数有关.

5. 结　论

（1）提出基于机器学习的可预测分形导数Maxwell混凝土徐变模型. 该模型通过将具有明确物理意义的分形导数Maxwell理论与XGBoost机器学习算法相融合，实现了物理模型与数据驱动方法的有效结合.

（2）基于NU混凝土徐变数据库的746组试验数据和14 565个数据点，利用建立的XGBoost模型，实现了混凝土材料特性、环境条件与分形导数Maxwell模型关键参数之间的映射关系. 在测试集上，模型对分形阶数p和黏性系数η的预测R²评分分别达到0.919和0.908，RMSE分别为0.017 9和0.037 8.

（3）在独立的机制砂混凝土徐变验证数据集上，提出的模型获得了0.909的R²评分，验证了该模型在新数据上的泛化能力. 在较大徐变度的区域，提出的模型存在轻微低估的趋势，这可能与未单独考虑骨料参数有关.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

VOYIADJIS G Z. Handbook of damage mechanics: nano to macro scale for materials and structures [M]. New York: Springer, 2022.