基于机器学习的分形导数 Maxwell 混凝土徐变模型
Machine-learning based fractal derivative Maxwell concrete creep model
| 分形黏弹性模型 | 示意图 | 表达式 |
| 分形黏性元件 | 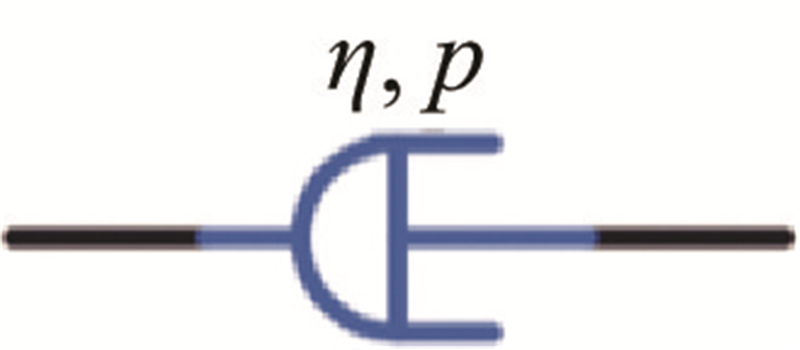 | |
| 分形Maxwell模型 |  | |
| 分形Kelvin模型 | 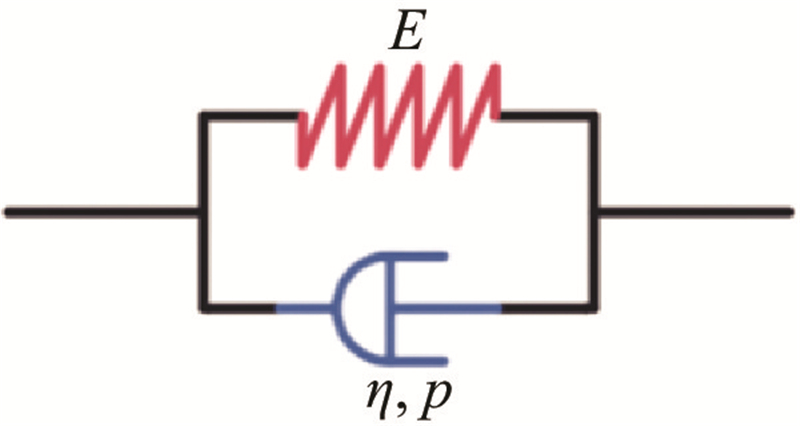 |
基于机器学习的分形导数 Maxwell 混凝土徐变模型 |
||||||||||||
| 梅生启,李旭峰,王兴举,刘晓东,吴黎明,李星艳,刘哲 | ||||||||||||
|
Machine-learning based fractal derivative Maxwell concrete creep model |
||||||||||||
| Shengqi MEI,Xufeng LI,Xingju WANG,Xiaodong LIU,Liming WU,Xingyan LI,Zhe LIU | ||||||||||||
| 表 1 分形导数黏弹性模型的示意图及应力-应变关系 | ||||||||||||
| Tab.1 Schematic diagram and stress-strain relationship of fractal derivative viscoelastic model | ||||||||||||
|
||||||||||||