浙江大学学报(工学版)

浙江大学学报(工学版), 2026, 60(2): 445-454 doi: 10.3785/j.issn.1008-973X.2026.02.023

交通工程、土木工程

考虑桩-筒变形协调的钢护筒-碎石复合桩水平承载力计算理论

徐瑞麟,, 易恩泽, 吴君涛,, 王奎华, 张智卿, 汤旅军

1. 浙江大学 建筑工程学院，浙江 杭州 310058

2. 浙江大学 平衡建筑研究中心，浙江 杭州 310063

3. 温州理工学院 建筑与能源工程学院，浙江 温州 325035

4. 浙江水利水电学院 建筑工程学院，浙江 杭州 310018

Analytical method for evaluating lateral bearing capacity of gravel-filled canister-monopile considering pile-canister deformation coordination

XU Ruilin,, YI Enze, WU Juntao,, WANG Kuihua, ZHANG Zhiqing, TANG Lüjun

1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

2. Center for Balance Architecture, Zhejiang University, Hangzhou 310063, China

3. College of Architecture and Energy Engineering, Wenzhou University of Technology, Wenzhou 325035, China

4. College of Civil Engineering and Architecture, Zhejiang University of Water Resources and Electric Power, Hangzhou 310018, China

通讯作者: 吴君涛，男，博导，研究员. orcid.org/0000-0001-9092-401X. E-mail：wujuntao31@126.com

收稿日期: 2025-02-7  

基金资助: 中国工程院战略研究与咨询项目（2025-XZ-75）；国家自然科学基金资助项目（52178358, 52108349, 52178367）；浙江省自然科学基金重点资助项目（LTGG24E080001）.

Received: 2025-02-7  

Fund supported: 中国工程院战略研究与咨询项目（2025-XZ-75）；国家自然科学基金资助项目（52178358,52108349,52178367）；浙江省自然科学基金重点资助项目（LTGG24E080001）.

作者简介 About authors

徐瑞麟（2001—），男，硕士生，从事桩基承载力研究.orcid.org/0009-0008-2088-3783.E-mail：ruilinxu@zju.edu.cn , E-mail：ruilinxu@zju.edu.cn

摘要

为了解决深远海海上风机基础成本较高的问题，提出由大直径单桩、钢护筒与桩筒间填充碎石3个部分组成的新型钢护筒-碎石复合桩. 在服役期间，碎石能够填充桩-土因长期循环作用产生的间隙，有效抑制桩周土体弱化，提升单桩的水平承载力. 针对水平受荷状态下的钢护筒-碎石复合桩进行承载力分析，考虑桩筒间填充碎石对桩身侧向支承刚度的提升作用以及护筒受荷后的水平位移发展，提出考虑桩-筒变形协调的应变楔耦合计算模型. 通过将筒径缩小至桩径，筒高缩减至零，填充碎石设置为桩周土体，使所提计算模型退化至单桩水平承载力计算模型，并与已有解析理论进行对比验证. 将所提模型计算结果与有限元计算结果对比，进一步验证模型的合理性及可靠性. 基于验证后的计算模型对钢护筒-碎石复合桩的主要设计参数进行分析，结果表明，钢护筒直径、高度与筒内碎石弹性模量均与钢护筒-碎石复合桩水平承载力呈正相关关系，护筒埋深存在最优设计值.

关键词： 复合桩 ; 海上风电 ; 修正应变楔方法 ; 水平承载力 ; 参数分析 ; 砂土

Abstract

To address the high cost of foundations for offshore wind turbines in deep and far-sea environments, a novel gravel-filled canister-monopile (GCM) was proposed, which consists of three components: a large-diameter monopile, a steel canister, and gravel filled between the pile and the canister. During service, the gravel was able to fill gaps generated in the pile–soil interface due to long-term cyclic loading, effectively mitigating the weakening of the surrounding soil and thereby enhancing the lateral bearing capacity of the monopile. To analyze the lateral bearing behavior of the gravel-filled canister-monopile, a strain wedge coupled model considering pile–canister deformation coordination was developed, taking into account the increase in lateral support stiffness provided by the filled gravel and the horizontal displacement development of the canister under load. By reducing the canister diameter to that of the pile, setting the canister height to zero, and treating the filled gravel as surrounding soil, the proposed model degenerated into a conventional monopile lateral bearing model, which was validated through comparison with existing analytical theories. Further comparisons with finite element analysis results confirmed the reasonableness and reliability of the proposed model. Based on the validated model, a parametric analysis of the main design parameters of the gravel-filled canister-monopile was conducted. The results indicated that the steel canister diameter, height, and the elastic modulus of the gravel were all positively correlated with the lateral bearing capacity, while the canister embedment depth exhibited an optimal design value.

Keywords： composite pile ; offshore wind turbine ; modified strain wedge method ; lateral bearing capacity ; parameter analysis ; sand

PDF (1842KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

徐瑞麟, 易恩泽, 吴君涛, 王奎华, 张智卿, 汤旅军. 考虑桩-筒变形协调的钢护筒-碎石复合桩水平承载力计算理论. 浙江大学学报(工学版)[J], 2026, 60(2): 445-454 doi:10.3785/j.issn.1008-973X.2026.02.023

XU Ruilin, YI Enze, WU Juntao, WANG Kuihua, ZHANG Zhiqing, TANG Lüjun. Analytical method for evaluating lateral bearing capacity of gravel-filled canister-monopile considering pile-canister deformation coordination. Journal of Zhejiang University(Engineering Science)[J], 2026, 60(2): 445-454 doi:10.3785/j.issn.1008-973X.2026.02.023

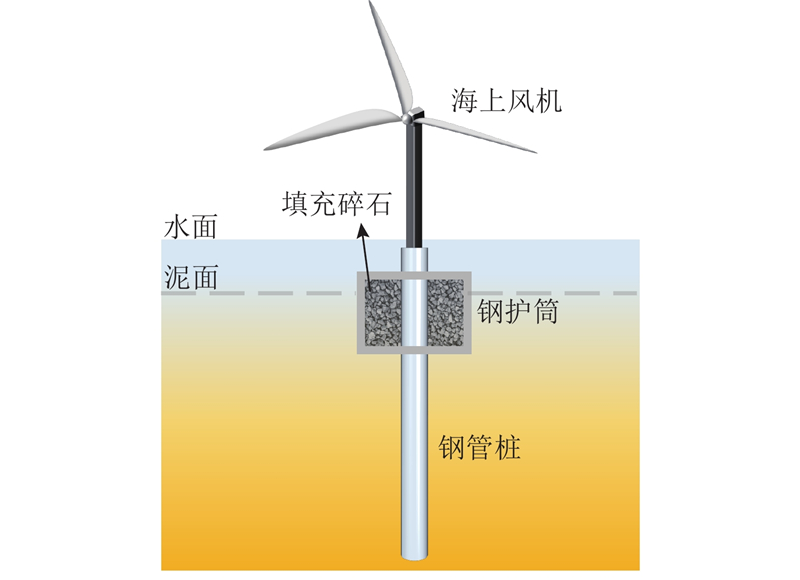
海上风电作为可再生能源的重要组成部分，受到越来越广泛的关注. 海上风电基础作为海上风机的支承结构，是风机安全稳定运行的重要保障. 当前，海上风电基础形式各异，其中单桩基础凭借其良好的沉降控制与优异的承载性能，在海洋风机基础的建设中占据主导地位. 相较于陆上风机，海上风机承受的环境载荷更复杂，在服役期间受到波浪、水流和风载荷的激励，对基础的水平承载力有更高的要求[1]. 工程上通常采用增加桩基的桩径与灌入深度来提高单桩基础水平承载力，促使工程成本急剧上升与施工难度显著增大. 对此众多学者开发出新型桩基础[2-4]，其中Qiu等[5]提出的钢护筒-碎石复合桩型（在单桩周围添置用碎石填充的钢护筒），通过模型试验与有限元模拟证明了该体系可以提升桩基的水平承载力，改善筒体下的土体强度. 该桩型在受到水平荷载时涉及桩、碎石、筒与场地土四者间的相互作用，普通单桩的水平承载力计算理论无法对其进行计算分析，须考虑钢护筒-碎石复合桩水平受荷特性的计算理论与分析方法.

针对水平受荷桩的计算理论和分析方法较多，但有各自的适用条件和局限性[6]. 其中p-y曲线法适用于静载和动载分析，能考虑桩-土非线性作用与土体塑性屈服，因而运用广泛[7-8]. Norris等[9-10]提出应变楔模型法，将一维Winkler地基梁的p-y参数与三维土体应变楔关联. 该方法不受p-y曲线函数形式的局限，明确土体基本参数和本构关系便可以计算桩基在任意土层的水平受荷响应. 徐令宇[11]通过在应变楔模型中引入邓肯-张与摩尔-库伦模型，分别改进了砂土与黏土的应力-应变关系，给出应变楔高度的计算方法，并明确应变楔高度以下的地基反力模量计算方法，使得模型得以反映桩基尺寸效应对地基反力模量的影响. 杨晓峰等[12]假设三维被动土楔后桩身的水平位移呈沿深度非线性变化，分别引入双曲线型的土体水平应力-应变关系和桩-土界面处桩侧剪应力-位移关系，修正了原有应变楔模型，改善了原应变楔模型计算的水平承载力偏高的问题. Ashour等[13]将应变楔模型法引入砂土中水平受荷斜桩的计算，研究了倾斜角度对桩基响应的影响. 周德泉等[14]基于传统应变楔理论，引入Boussinesq解，构建斜桩挠曲微分方程，提出基于应变楔模型的堆载下被动斜桩受力变形分析模型. 罗丽娟等[15]基于应变楔模型构建改进分析模型，提出以被动土拱破坏为判据，修正群桩计算宽度并引入静止土压力影响, 揭示了邻桩相互作用下土抗力变化规律.

综上所述，水平受荷桩应变楔模型分析法已被证明能够较好地分析计算桩基的水平承载力，并且得到广泛运用. 本研究基于已有应变楔理论研究成果，针对水平受荷状态下的钢护筒-碎石复合桩进行承载力分析，考虑桩筒间填充碎石对桩身侧向支承刚度的提升作用以及护筒受荷后的水平位移发展，提出基于桩-筒变形协调的桩-碎石-筒-场地土应变楔耦合计算模型，并验证计算模型的正确性；讨论复合桩主要设计参数（护筒直径、护筒高度、护筒埋深以及碎石弹性模量）对桩身承载力的影响.

1. 钢护筒-碎石复合桩水平承载力计算理论

1.1. 基本假设

本复合桩型由钢管桩、护筒与碎石3个部分组成，如图1所示. 在桩身受到水平荷载时，桩身的部分荷载传给碎石，再由护筒传递给周围土体，同时桶内碎石会下落填充桩土间的空隙，以此来提升桩基的承载力. 在本研究中，基本假定包括：1）研究对象为砂土，桩-土作用后间隙较小，碎石下落对土体强度的提升有限[5]，暂不考虑碎石下落对桩土空隙的填充；2）砂土对桩、筒的作用等效为非线性弹簧，使用应变楔理论求解；3）护筒形状为均匀圆形桶，在受荷过程中，将筒体运动视为平动，不考虑桶体的转动.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   钢护筒-碎石复合桩示意图

Fig.1   Schematic diagram of gravel-filled canister-monopile


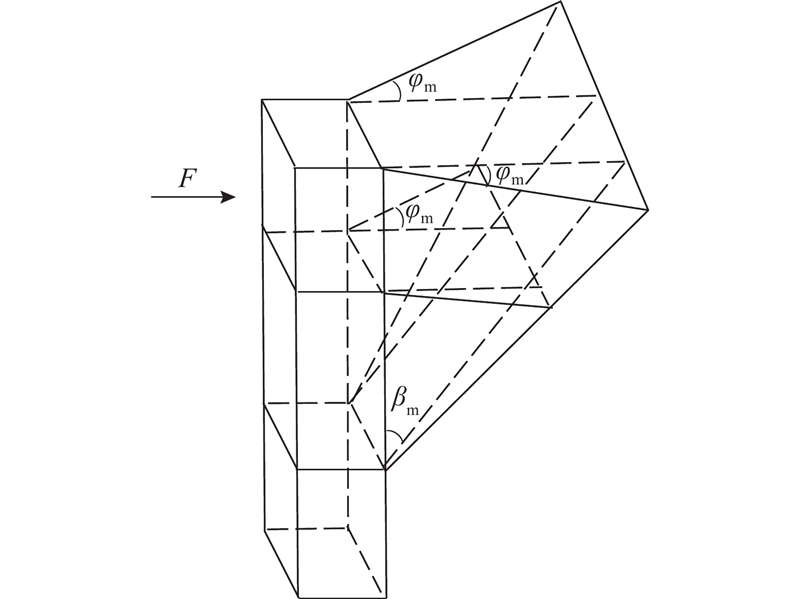
1.2. 桩-土侧向作用应变楔模型

当桩顶承受水平荷载时，桩周土体对桩身产生反作用力，可将其等效为winker弹性地基梁上的非线性弹簧，桩-土系统的控制方程为

$ EI\frac{{{\partial ^4}y}}{{{\partial ^4}z}} + ky = 0. $

式中：EI 为桩身抗弯刚度；y 为桩身水平位移；z 为地表以下深度；地基反力模量k = p/y，其中p为单位桩长提供的土体抗力. 为了得到k 的具体表达式，Norris等[9-10]将水平受荷桩前处于被动受压状态的土体简化成三维楔形体，即应变楔模型，如图2所示. 楔形体由扇形角$ {\varphi }_{\text{m}} $、底角$ {\beta }_{\text{m}} $和楔形体深度H 加以描述，同时$ {\varphi }_{m} $又是土体的发挥内摩擦角，与$ {\beta }_{\text{m}} $的关系为

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   应变楔模型示意图

Fig.2   Schematic diagram of strain wedge model


$ {\beta _{\rm{m}}} = {\rm{4}}{{\rm{5}}^ \circ } + \frac{{{\varphi _{\rm{m}}}}}{2}. $

原始应变楔模型因假设桩身位移呈线性变化，不能较好地描述实际情况，因此杨晓峰等[12]将土体分层计算，使得桩身水平向变形沿深度为非线性变化，修正了原始应变楔模型，如图3所示. 在该模型中桩和应变楔均沿深度均匀分层，每层深度为h，第i层土的应变为$ {\varepsilon }_{i} $，单桩在i层的上、下界面处位移分别为$ {y}_{i - 1} $和$ {y}_{i} $，则第i层单桩偏移角$ {\delta }_{i} $与桩身位移的关系、第i层的土体应变分别为

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   应变楔模型分层计算示意图[12]

Fig.3   Schematic diagram of layered calculation of strain wedge model[12]


$ \tan {\delta _i} = \frac{{{y_{i - 1}} - {y_i}}}{h}, $

$ {\varepsilon _i} = \frac{{{y_{i - 1}} + {y_i}}}{{2\overline {E{F_i}} }}. $

式中：$ \overline{E{F}_{i}} $为楔形体内过i层中心的楔形体长度. 通过应变摩尔圆进一步得到$ {\delta }_{i} $、$ {\varepsilon }_{i} $以及土体发挥内的摩擦角$ {\varphi }_{\text{m}i} $的关系[10]：

$ {\delta _i} = \frac{{\left( {1 + \upsilon } \right){\varepsilon _i}}}{2}\cos {\varphi _{{\rm{m}}i}}. $

式中：$ \upsilon $为土体泊松比. 本文研究对象为砂土，土体的应力应变关系本构采用双曲线模型进行描述[16-17]，表达式为

$ { {\Delta {\sigma _{{\rm{h}},i}}} } = \dfrac{{{\varepsilon _i}}}{{\dfrac{1}{{{K_{\rm{E}}}{{p}_{0}}{{\left( {{{{\sigma _{{v_{0,i}}}}}}/{{{p_0}}}} \right)}^n}}} + \dfrac{{{\varepsilon _i}{R_{\rm{f}}}}}{{{{ {{\sigma _{{\rm{hf}},i}}} }}}}}}, $

$ { {{\sigma _{{\rm{hf}},i}}} } = {\sigma _{{v_{0,i}}}}\left[ {{{\tan }^2}\left( {\frac{{{\text{π}}}}{4} + \frac{\varphi }{2}} \right) - 1} \right]. $

式中：$ \Delta {\sigma }_{\text{h},i} $为应变楔模型中第i层土体水平向应力增量[10]；$ {\sigma }_{{{v}_{0,i}}} $为第i层土体的竖向有效应力；$ {{\sigma }_{\text{hf},{i}}} $为土体破坏时的应力差，p0为标准大气压；$ {K}_{\text{E}} $为弹性模量数，与相对密实度有关，n 为弹性模量指数，$ {R}_{\text{f}} $为破坏比，三者的取值参考文献[17]. 通过应力水平SL建立水平向应力增量$ \Delta {\sigma }_{\text{h}} $与土体发挥摩擦角$ {\varphi }_{\text{m}i} $的关系[10]为

$ {\mathrm{SL}}_{i}=\frac{{\Delta {\sigma }_{\text{h},{i}}}}{{\Delta {\sigma }_{\text{hf},{i}}}}=\frac{{\text{tan}}^{2}\left(\text{π}/4+{\varphi }_{\text{m}i}/2\right) - 1}{{\text{tan}}^{2}\left(\text{π}/4+\varphi /2\right) - 1}. $

桩侧剪应力$ {\tau }_{i} $与桩身位移$ {y}_{i} $的关系同样使用双曲线形式的荷载传递模型[18-19]描述，表达式为

$ \tau =\frac{\varDelta }{\dfrac{1}{2{\tau }_{\text{ult}}}+\dfrac{\varDelta }{{\tau }_{\text{ult}}}}, $

$ {\tau _{{\rm{ult}}}} = {K_0}{\sigma _{{\rm{v}}0}}\tan {\varphi _{\rm{s}}}. $

式中：Δ为桩-土界面相对位移，本研究对应桩身水平位移y；$ {\tau }_{\text{ult}} $为极限剪应力；侧向土压力系数$ {K}_{0} $=1.0；$ {\varphi }_{s} $为桩-土界面摩擦角，与材料属性有关，取值参考文献[20]. 计算得到水平向应力增量$ \Delta {\sigma }_{\text{h},i} $与桩侧剪应力$ {\tau }_{i} $后，即可由力平衡关系[10]得到单位桩长土体抗力，表达式为

$ {p_i} = \Delta {\sigma _{{\rm{h}},i}}\left( {D + 2\overline {EF} \tan {\varphi _{{\rm{m}}i}}} \right){S_1} + 2{\tau _i}D{S_2}. $

式中：D为桩径或桩身宽度；$ {S}_{1} $、$ {S}_{2} $分别为桩型系数，圆桩时$ {S}_{1} $=0.75、$ {S}_{2} $=0.50，方桩时$ {S}_{1}={S}_{2}=1.00 $[21].

1.3. 筒-土侧向作用修正应变楔模型

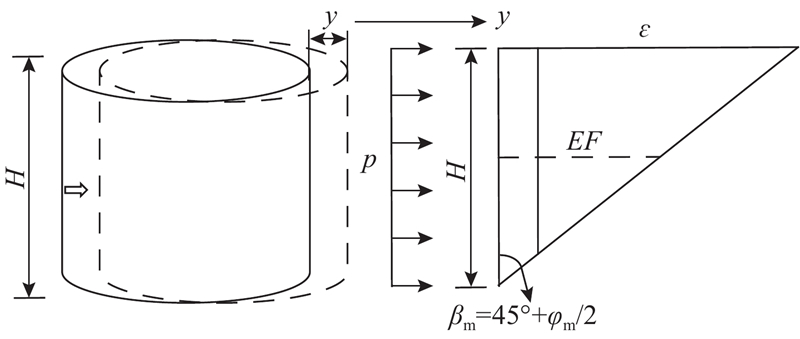
桩体在水平荷载作用下主要表现为弯曲变形，但在钢护筒-碎石复合桩中护筒的高度远小于桩长，筒径约为桩径的3倍[5]，桩身在护筒范围内的变形可近似视为平动，进而桩体通过碎石传递给筒体的荷载可近似为均布荷载，因此护筒在受荷后的运动状态可近似等效为平动. 本研究针对护筒的运动状态提出筒-土侧向作用修正应变楔模型. 假定护筒受荷后仅发生平动，忽略其转动，与桩体受力类似，筒体前土体处于被动受压状态，将其简化为如图2所示的楔形体，由扇形角$ {\varphi }_{\text{m}} $、$ {\beta }_{\text{m}} $和H加以描述，这里的H为护筒的埋深. 不同于桩体，筒体水平位移沿深度不变，因此修正应变楔模型中不需要分层考虑土体，由如图4所示的几何关系可以得到土体发挥内的摩擦角$ {\varphi }_{\text{m}} $与土体水平向应变$ \varepsilon $的关系为

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   筒体运动及修正应变楔竖向剖面示意图

Fig.4   Schematic diagram of vertical section of cylinder motion and modified strain wedge


$ \varepsilon = \frac{y}{{\overline {EF} }} = \dfrac{{2y}}{{H\tan \left( {{\rm{4}}{{\rm{5}}^ \circ } + \dfrac{{{\varphi _{\rm{m}}}}}{2}} \right)}}. $

土体水平向应力增量$ \Delta {\sigma }_{\text{h}} $与桩侧剪应力$ \tau $的计算同样使用双曲线模型，由此得到单位筒高的筒体受到的土体抗力，表达式为

${p_{\rm{t}}} = \Delta {\sigma _{\rm{h}}}\left( {W + \tan \left({\rm{4}}{{\rm{5}}^ \circ } + \frac{{{\varphi _{\rm{m}}}}}{2}\right)\tan {\varphi _{\rm{m}}}} \right){S_1} + 2\tau W{S_2}. $

式中：$ W $为护筒的直径. 筒体受到的土体抗力合力为

$ {F_1}({y_{\rm{t}}}) = {p_{\rm{t}}}H. $

1.4. 计算流程

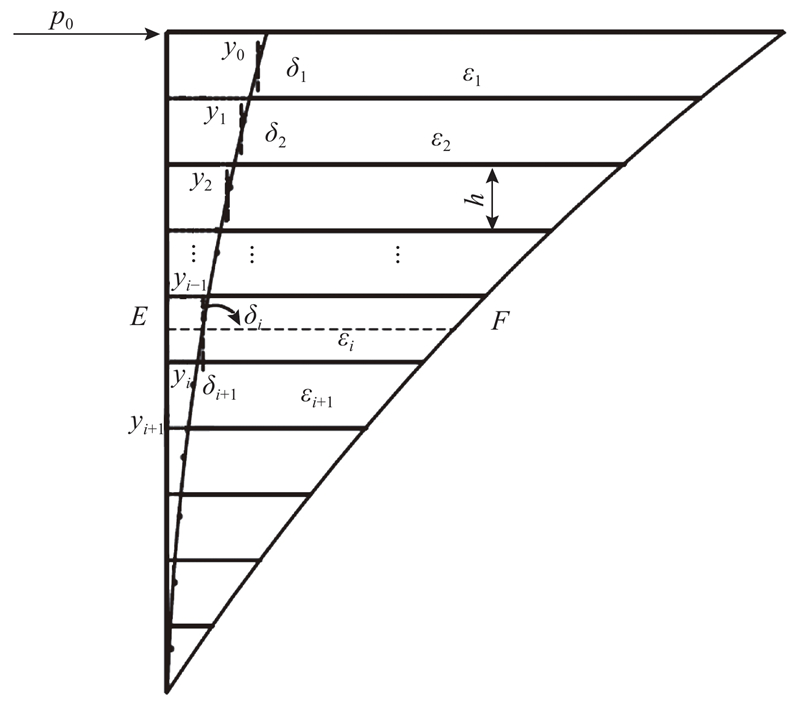
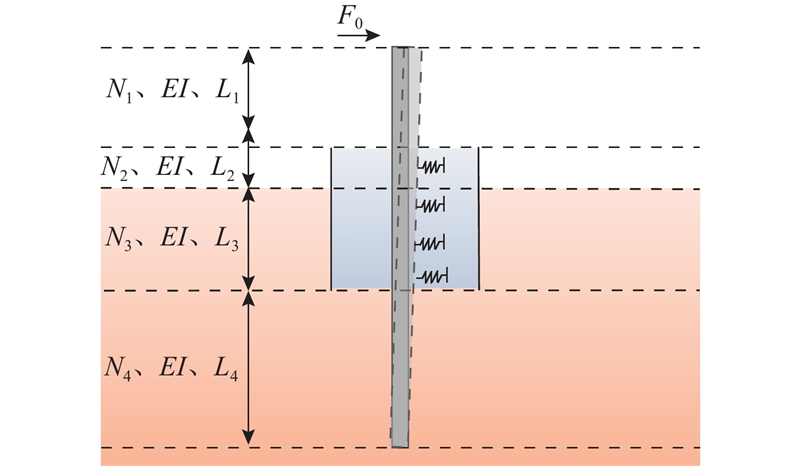
在计算过程中，将系统分为4段，如图5所示，每段的长度记作$ {L}_{n}(n=1,2,3,4) $，将整个体系均匀地分成N个单元，每个单元的高度记作$ \Delta L $，得到

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   钢护筒-碎石复合桩水平承载力计算模型示意图

Fig.5   Schematic diagram of calculation model for lateral bearing capacity of gravel-filled canister-monopile


$ N = \sum\limits_{n = 1}^4 {{N_n} = } \sum\limits_{n = 1}^4 {\frac{{{L_n}}}{{\Delta L}}} . $

式中：$ {N}_{n} $分别为每段体系的单元数. 第一段桩体不受抗力，显然反力模量k=0；第二、第三段桩体的反力由碎石提供，护筒的存在导致桩基发生的水平位移与碎石发生的水平压缩形变不相等，须分开考虑. 本研究在考虑碎石抗力时，将碎石等效为弹簧，其反力模量由碎石弹性模量确定[22]，表达式为

$ {k_{\rm{s}}} = \alpha {E_s}. $

式中：ks为碎石反力模量，物理意义为单位桩长在碎石发生单位形变下受到的反力；Es为碎石的弹性模量；$ \alpha $为经验系数，当研究对象为水平受荷桩时，取$ \alpha =1.2 $[23-24]. 再由力的平衡关系与地基反力模量的定义得到第二、第三段桩体的反力模量：

$ k = \frac{{{k_{\rm{s}}}({y_i} - {y_{\rm{t}}})}}{{{y_i}}};\quad {N_1} \leqslant i \leqslant {N_1} + {N_2} + {N_3}. $

式中：$ {y}_{\text{t}} $为筒体水平位移. 将$ {k}_{\text{s}}({y}_{i} - {y}_{\text{t}}) $理解为单位桩长桩基受到的碎石反力大小. 在求解过程中依据力的平衡关系确定筒体的位移$ {y}_{\text{t}} $. 护筒所受的推力来自碎石，土体提供抗力，土体抗力的表达式见式（14），可视为关于筒体位移$ {y}_{\text{t}} $的函数；在计算碎石给予护筒推力时，碎石受到桩基传递的力集中在护筒的空间内，其三维效应不显著，因此将碎石简化为连接桩与筒的一维弹簧，表达式为

$ {F_2}({y_{\rm{t}}}) = \sum\limits_{i = {N_1}}^{{N_1} + {N_2} + {N_3}} {{k_{\rm{s}}}\Delta L({y_i} - {y_{\rm{t}}})} . $

由式（18）可知，碎石提供的推力也可以视为关于筒体位移$ {y}_{\text{t}} $的函数，将式（14）与式（18）联合迭代求解即可确定护筒发生的位移. 第四段应变楔发展深度范围内桩体的反力由土体提供，表达式为

$ {k_i} = \frac{{{p_i}}}{{\left( {{y_{i - 1}} + {y_i}} \right)/2}};\quad N - {N_4} \leqslant i \leqslant N. $

确定反力系数后，即可采用差分法求解式（1），结合桩顶和桩端的水平和弯矩约束情况，其差分求解方程组为

$ {\boldsymbol{KY}} = {\boldsymbol{F}}. $

式中：$ \boldsymbol{K} $为(N +1)× (N +1)阶刚度矩阵；$ \boldsymbol{Y} $和$ \boldsymbol{F} $分别为(N +1)阶桩身位移向量和水平荷载向量，具体求解方法参考文献[25]. 在应变楔以下区域，地基反力模量随深度线性变化，Zhang[26]建议，此时地基反力模量$ k={n}_{{\mathrm{h}}}z $，其中$ {n}_{{\mathrm{h}}} $为地基反力常数，取值与砂土相对密实度Dr相关，具体取值可参考文献[26].

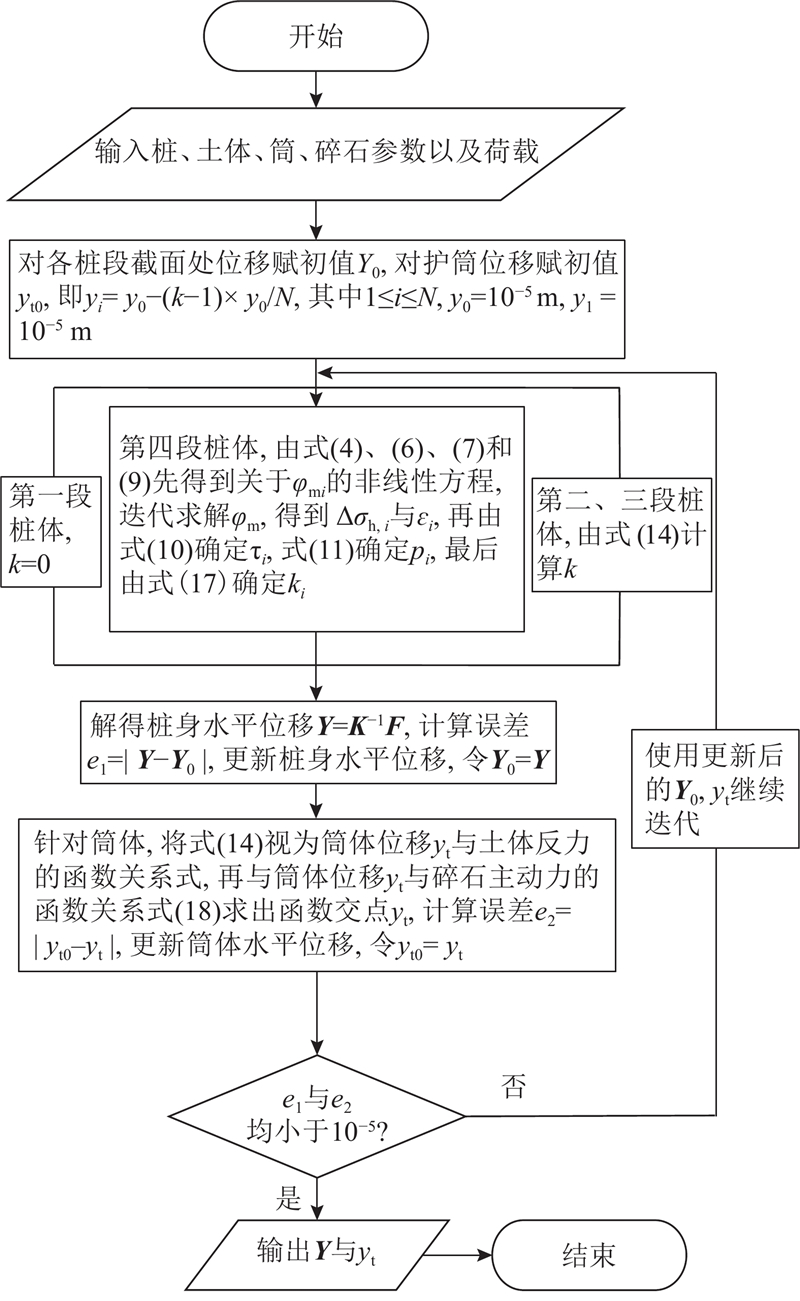
本研究提出的考虑桩-筒变形协调的钢护筒-碎石复合桩水平承载力理论计算流程如图6所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   钢护筒-碎石复合桩水平承载力理论计算流程图

Fig.6   Flowchart of theoretical calculation for lateral bearing capacity of gravel-filled canister-monopile


2. 模型验证

2.1. 所提模型与已有解析理论的对比

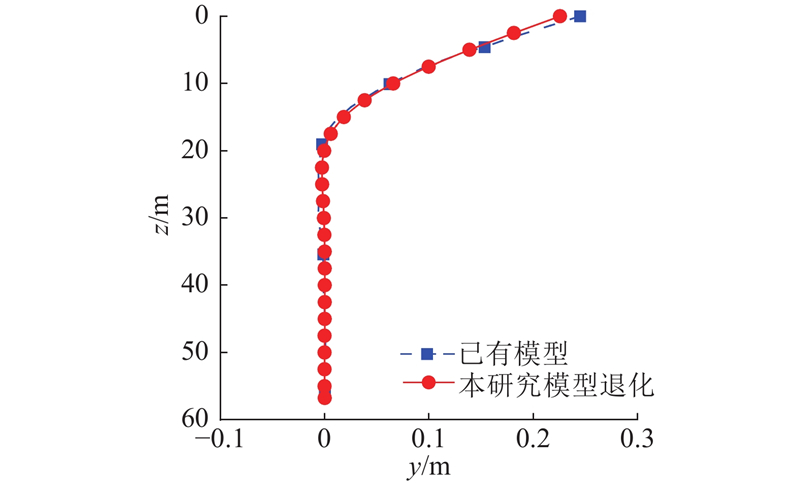
为了验证本研究提出的考虑桩-筒变形协调的钢护筒-碎石复合桩水平承载力计算理论的正确性，将所提计算模型退化至单桩应变楔计算模型，并与杨晓峰等[12]提出的单桩应变楔计算模型进行对比. 解的退化思路：将护筒直径逼近于桩径，护筒高度逼近于0，桶内碎石弹性模量设置为桩周土体弹性模量. 对比工况中土体有效重度为14.935 kN/m3，土体内摩擦角为39°，相对密实度为65%；桩基埋深、桩径分别为50.0、2.5 m，抗弯刚度为56.66 GN·m2，单桩加载位置位于地表以上2.7D处，荷载大小为6.202 MN. 如图7所示为本研究计算理论的退化解与已有应变楔模型计算得到的桩身位移沿桩深度的分布情况. 结果表明，所提模型退化后的解与已有解的计算结果基本一致，初步验证了所提模型的合理性.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   不同应变楔计算模型的计算结果对比

Fig.7   Comparison of results between two strain-wedge calculation models


2.2. 所提模型与有限元的对比

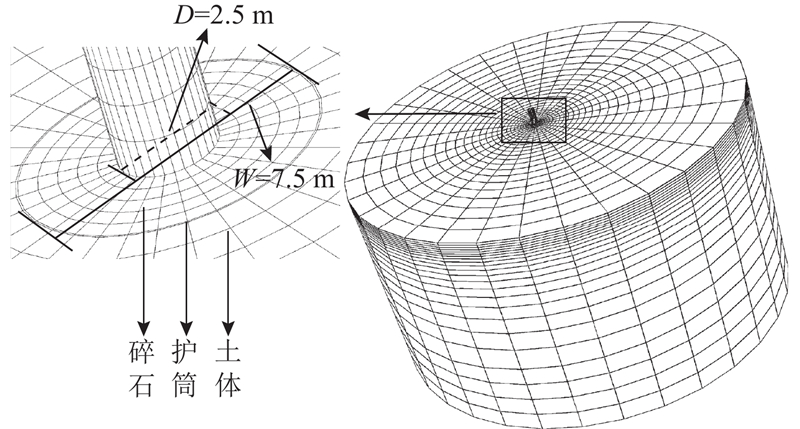
为了进一步验证计算模型的正确性及适用性，采用Abaqus有限元软件进行建模，将模型计算结果与应变楔计算结果进行对比. 有限元模型为钢管桩与套筒形式，埋置于均质砂土中，套筒内填置碎石，如图8所示. 模型网格数共28864个，已完成收敛性分析. 为了避免边界效应的影响，设置模型半径为15倍筒径，模型底部至桩底的距离为5倍筒径. 模型中将钢管桩等效为抗弯刚度一致的实心桩，土体采用摩尔-库伦本构模型，碎石仅考虑弹性变形，套筒定义为刚体；依据实际情况针对桩、筒、碎石、土共设置7项接触，竖向接触均采用硬接触，切向接触均设置为“罚”，摩擦系数计算公式为$ \tan \;(0.67\varphi ) $[27-28]. 模型中各部件参数如表1所示.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   钢护筒-碎石复合桩的建模示意图

Fig.8   Model schematic of gravel-filled canister-monopile


表 1   有限元模型各部件参数

Tab.1  Component parameters of finite element model

部件参数数值
土体有效重度/(kN·m−3)14.935
摩擦角/(°)39
膨胀角/(°)9
黏聚力/kPa0.10
弹性模量/MPa40
泊松比0.25
桩体埋入桩长L/m50
桩径D/m2.50
抗弯刚度EI/(GN·m2)56.66
等效弹性模量/GPa29.55
泊松比0.20
护筒筒高H/m5
筒径/m7.5
壁厚/m0.05
埋深/m5

新窗口打开| 下载CSV


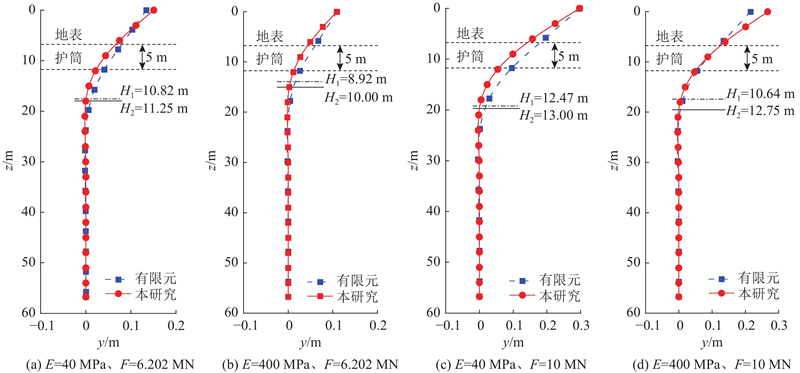
验证计算考虑碎石弹性模量分别为40 MPa与400 MPa，荷载大小分别为6.202 MN与10 MN共计4种计算工况，单桩加载位置位于地表以上2.7D处. 如图9所示为采用所提计算模型与有限元计算得到的桩身位移沿桩深度的分布情况. 可以看出，所提模型计算结果与有限元数值计算结果较为吻合，所提模型计算结果的桩身上部位移略小于有限元计算结果，原因是所提模型假设套筒的运动为平动，不考虑转动. 在有限元计算结果中，选取桩土接触表面上土体水平位移第一零点处的深度作为应变楔发展深度H1，对比所提模型计算的应变楔深度H2，二者接近，进一步验证了所提模型的正确性.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   不同工况下桩身位移沿深度的分布

Fig.9   Distribution of pile displacement at various depths under different working conditions


朱斌等[29]进行了砂土中大直径单桩水平静载离心模型试验，本研究选取其中1组试验结果进行对比分析，试验用的砂土和原型桩的参数如表2所示，考虑到较密实砂土的剪胀性，选取峰值摩擦角为39°. 在原型桩的基础上添置碎石筒，参数见表1，使用所提模型计算钢护筒-碎石复合桩的位移-荷载曲线，与文献[29]中的试验结果、该工况对应退化解计算结果进行对比，单桩加载位置位于地表以上2.7D 处. 如图10所示，所提模型退化解与试验结果接近，进一步验证了模型的正确性，同时由位移-荷载曲线可知复合桩的静力承载性能优于传统单桩.

表 2   桩体性能试验用参数

Tab.2  Parameters for pile performance tests

名称参数数值
试验干砂有效重度/(kN·m−3)14.935
峰值摩擦角/(°)39
残余摩擦角/(°)35
黏聚力/kPa0.00
相对密实度Dr/%65
泊松比0.25
原型钢管桩埋入桩长L/m50
桩径D/m2.50
抗弯刚度EI/(GN·m2)56.66
壁厚/m0.045
泊松比0.20

新窗口打开| 下载CSV


图 10

新窗口打开| 下载原图ZIP| 生成PPT

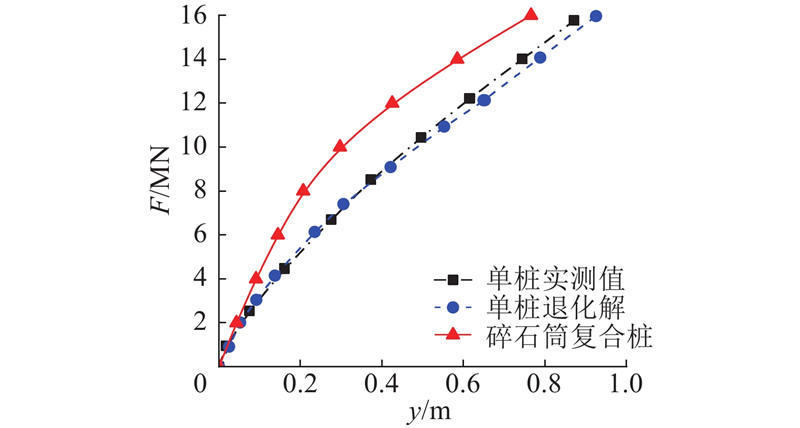
图 10   钢护筒-碎石复合桩与单桩位移-荷载曲线对比

Fig.10   Comparison of displacement-load curves for gravel-filled canister-monopile and single pile


3. 参数分析

为了探究复合桩中主要设计参数对桩基础承载性能的影响，以2.2节中的桩、土参数为例，针对护筒直径、护筒高度、护筒埋深与筒内碎石弹性模量4个变量开展参数分析. 除了针对护筒埋深的参数分析外，在针对1个变量进行分析时，其余3个变量均与2.2节一致，4个变量的取值如表3所示. 单桩加载位置位于地表以上2.7D处.

表 3   钢护筒-碎石复合桩主要设计参数的取值

Tab.3  Selected values of main design parameters for gravel-filled conister-monopile

参数数值
筒径Dc/m2D、3D、4D、5D
筒高H/m0.10L、0.15L、0.20L、0.25L
护筒埋深hc/m0.5H、0.6H、0.7H、0.8H、0.9H、1.0H
碎石弹性模量Es/MPa40、400、4000、40000

新窗口打开| 下载CSV


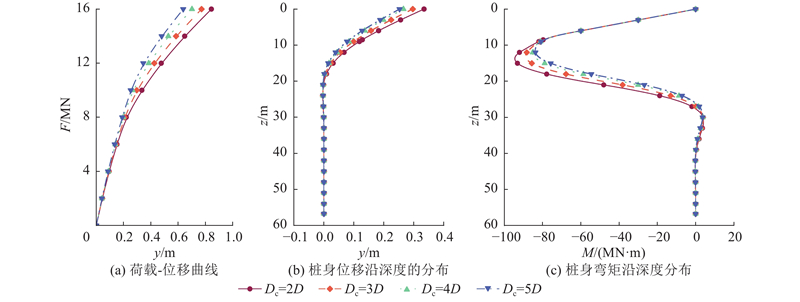
如图11所示为在不同筒径下桩顶的荷载-位移曲线，荷载大小为10 MN时桩身位移与弯矩沿深度分布的计算结果. 随着筒径增加，土体给予护筒反力的范围提升，桩身位移与弯矩下降，桩身承载性能提升. 当护筒直径较大时，提升护筒直径带来的桩身承载力提升不明显. 如本算例中护筒直径为4D与5D时，2种工况下的荷载-位移曲线与桩身弯矩沿深度分布情况几乎一致，因此在实际工程中可考虑通过增加护筒直径来提升桩基承载力.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   不同筒径下的钢护筒-碎石复合桩性能参数对比

Fig.11   Comparison of performance parameters for gravel-filled canister-monopile under different canister diameters


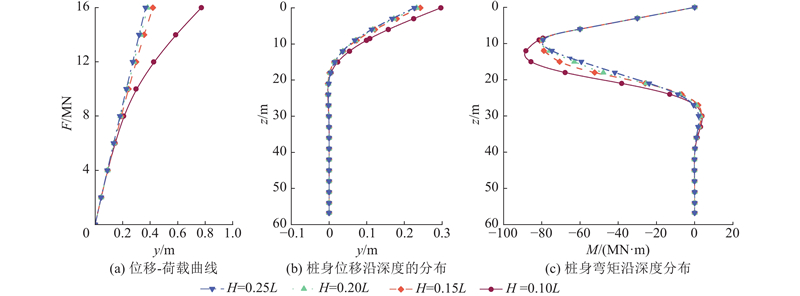
如图12所示为在不同护筒高度大小下桩顶的荷载-位移曲线，荷载大小为10 MN时桩身位移与弯矩沿深度分布的计算结果. 随着筒高增加，碎石与护筒能提供反力的深度增加，桩身位移与弯矩下降，桩身承载性能提升. 但护筒高度不易过大，一是过度提升护筒高度带来的桩身承载力提升不明显，二是筒高的提升会相应增加施工难度. 如本算例中当护筒深度超过0.10L，不同筒高对应工况下的荷载-位移曲线与桩身位移、弯矩沿深度分布情况几乎一致，因此在实际工程中护筒高度须控制在合理范围内.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   不同筒高下的钢护筒-碎石复合桩性能参数对比

Fig.12   Comparison of performance parameters for gravel-filled canister-monopile under different canister heights


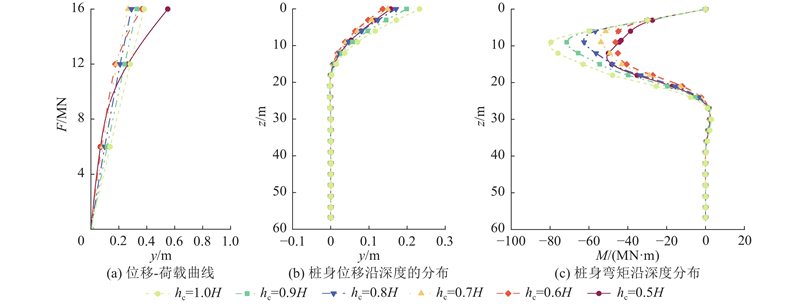
为了直观表现护筒不同埋深对桩基承载能的影响，选取筒高为0.2L、筒径为3D的护筒进行分析. 如图13所示为在不同护筒埋深下桩顶的荷载-位移曲线，荷载大小为10 MN时桩身位移与弯矩沿深度的分布的计算结果. 由图13（a）可知，在荷载大小于13 MN时，护筒埋深为0.6H的桩基础承载性能最好；大于13 MN时，护筒埋深为0.7H的桩基础承载性能最好. 由图13（b）与图13（c）可知，在10 MN的荷载下，护筒埋深为0.6H的桩基础桩身位移最小，与之对应的桩身最大弯矩也最小. 原因是土面以上的筒和碎石在一定程度上能限制桩基的位移，若土面以上的护筒高度较高、埋深较小，筒周土体与护筒的作用区域变小，进而影响护筒的稳定，随之影响桩基的承载性能，因此在单工况下，理论上存在最优的护筒埋深. 由此可知，在实际工程中，可依据桩基的受力情况确定最优的护筒埋深.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   不同护筒埋深下的钢护筒-碎石复合桩性能参数对比

Fig.13   Comparison of performance parameters for gravel-filled canister-monopile under different embedded depths of canister


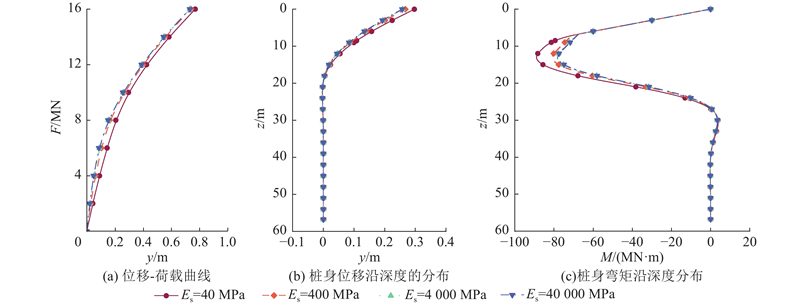
如图14所示为在不同碎石弹性模量下桩顶的荷载-位移曲线，荷载大小为10 MN时桩身位移与弯矩沿深度分布的计算结果. 可以看出，碎石弹性模量的提升对桩基的承载性能的提升有限. 在本算例中，当碎石弹性模量超过桩周土体弹性模量10倍后，不同碎石弹性模量对应工况下的荷载-位移曲线与桩身位移、弯矩沿深度分布情况几乎一致. 因此在实际工程考虑成本的情况下，碎石弹性模量仅需略大于土体弹性模量.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   不同碎石弹性模量下的钢护筒-碎石复合桩性能参数对比

Fig.14   Comparison of performance parameters for gravel-filled canister-monopile under different elastic moduli of gravel


4. 结　语

本研究针对水平受荷状态下的钢护筒-碎石复合桩进行承载力分析，考虑桩筒间填充碎石对桩身侧向支承刚度的提升作用以及护筒受荷后的水平位移发展，提出基于桩-筒变形协调的桩-碎石-筒-场地土应变楔耦合计算理论；分别进行所提理论的退化解与已有理论对比，所提理论与有限元计算结果对比，验证理论的合理性及可靠性. 研究结果表明，1）护筒直径、护筒高度与护筒内碎石弹性模量均与钢护筒-碎石复合桩的承载力呈正相关关系；2）在工程实际中，须依据实际情况在合理范围内提高护筒直径、护筒高度与护筒内碎石弹性模量；3）护筒埋入土体深度对钢护筒-碎石复合桩的承载力有重要影响，存在护筒最佳埋深，在实际工程中可依据桩基参数、受力情况确定最优的护筒埋深. 本文理论仅适用于静力条件下钢护筒-碎石复合桩水平承载力的计算，未针对其循环受荷载工况下的承载力进行分析. 后续将通过试验明确钢护筒-碎石复合桩循环荷载后筒内碎石下落迁移情况，结合试验结果提出适用于循环荷载条件下钢护筒-碎石复合桩水平承载力的计算理论.

参考文献

范小雪, 李原, 吴文兵, 等

饱和土中大直径缺陷桩水平振动响应研究

[J]. 岩石力学与工程学报, 2020, 39 (2): 413- 423

[本文引用: 1]

FAN Xiaoxue, LI Yuan, WU Wenbing, et al

Horizontal vibration response of defective large-diameter piles embedded in saturated soils

[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39 (2): 413- 423

[本文引用: 1]

ARSHI H S, STONE K, GUNZEL F. Cost efficient design of monopile foundations for offshore wind turbines [C]// Proceedings of the 16th European Conference on Soil Mechanics and Geotechnical Engineering: Geotechnical Engineering for Infrastructure Development. London: [s.n.], 2015: 1237–1242.

[本文引用: 1]

高鲁超, 戴国亮, 姚中原, 等

水泥土大直径单桩水平承载性能试验研究

[J]. 东南大学学报: 自然科学版, 2024, 54 (1): 142- 148

DOI:10.3969/j.issn.1001-0505.2024.01.018     

GAO Luchao, DAI Guoliang, YAO Zhongyuan, et al

Experimental study on lateral bearing behaviors of large-diameter monopiles in cement-soil

[J]. Journal of Southeast University: Natural Science Edition, 2024, 54 (1): 142- 148

DOI:10.3969/j.issn.1001-0505.2024.01.018     

王安辉, 章定文, 谢京臣

软黏土中劲性复合桩水平承载特性p-y曲线研究

[J]. 岩土工程学报, 2020, 42 (2): 381- 389

DOI:10.11779/CJGE202002020      [本文引用: 1]

WANG Anhui, ZHANG Dingwen, XIE Jingchen

p-y curves for lateral bearing behavior of strength composite piles in soft clay

[J]. Chinese Journal of Geotechnical Engineering, 2020, 42 (2): 381- 389

DOI:10.11779/CJGE202002020      [本文引用: 1]

QIU X, M

HESHAM EI NAGGAR M, WANG K. Experimental and numerical studies on lateral bearing characteristics of innovative gravel-filled canister-monopile (GCM) hybrid foundation

[J]. Marine Georesources and Geotechnology, 2024, 42 (12): 1824- 1843

DOI:10.1080/1064119X.2024.2304049      [本文引用: 3]

常林越, 王金昌, 朱向荣, 等

水平受荷长桩弹塑性计算解析解

[J]. 岩土力学, 2010, 31 (10): 3173- 3178

[本文引用: 1]

CHANG Linyue, WANG Jinchang, ZHU Xiangrong, et al

Analytical elastoplastic solutions of laterally loaded long piles

[J]. Rock and Soil Mechanics, 2010, 31 (10): 3173- 3178

[本文引用: 1]

苏静波, 邵国建, 刘宁

基于P-Y曲线法的水平受荷桩非线性有限元分析

[J]. 岩土力学, 2006, 27 (10): 1781- 1785

DOI:10.3969/j.issn.1000-7598.2006.10.028      [本文引用: 1]

SU Jingbo, SHAO Guojian, LIU Ning

Nonlinear finite element analysis of piles under lateral load based on P-Y curves

[J]. Rock and Soil Mechanics, 2006, 27 (10): 1781- 1785

DOI:10.3969/j.issn.1000-7598.2006.10.028      [本文引用: 1]

陈祥, 孙进忠, 蔡新滨

基桩水平静载试验及内力和变形分析

[J]. 岩土力学, 2010, 31 (3): 753- 759

[本文引用: 1]

CHEN Xiang, SUN Jinzhong, CAI Xinbin

Horizontal static loading test and analyses of internal force and distortion on single pile

[J]. Rock and Soil Mechanics, 2010, 31 (3): 753- 759

[本文引用: 1]

NORRIS G M. Theoretically based BEF laterally loaded pile analysis [C]// Proceedings of the 3rd International Conference on Numerical Methods in Offshore Piling. Paris: Technip, 1986: 361–386.

[本文引用: 2]

ASHOUR M, NORRIS G, PILLING P

Lateral loading of a pile in layered soil using the strain wedge model

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124 (4): 303- 315

DOI:10.1061/(ASCE)1090-0241(1998)124:4(303)      [本文引用: 6]

徐令宇. 桩基础水平响应计算方法及其抗液化性能研究 [D]. 大连: 大连理工大学, 2013: 1−156.

[本文引用: 1]

XU Lingyu. Computation method for response of laterally loaded piles and liquefaction-mitigation performance of piled foundation [D]. Dalian: Dalian University of Technology, 2013: 1−156.

[本文引用: 1]

杨晓峰, 张陈蓉, 黄茂松, 等

砂土中桩土侧向相互作用的应变楔模型修正

[J]. 岩土力学, 2016, 37 (10): 2877- 2884

DOI:10.16285/j.rsm.2016.10.019      [本文引用: 5]

YANG Xiaofeng, ZHANG Chenrong, HUANG Maosong, et al

Modification of strain wedge method for lateral soil-pile interaction in sand

[J]. Rock and Soil Mechanics, 2016, 37 (10): 2877- 2884

DOI:10.16285/j.rsm.2016.10.019      [本文引用: 5]

ASHOUR M, ALAAELDIN A, ARAB M G

Laterally loaded battered piles in sandy soils

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146: 06019017

DOI:10.1061/(ASCE)GT.1943-5606.0002186      [本文引用: 1]

周德泉, 朱沁, 王创业, 等

基于应变楔模型的堆载下被动斜桩受力变形分析

[J]. 湖南大学学报: 自然科学版, 2024, 51 (5): 46- 55

[本文引用: 1]

ZHOU Dequan, ZHU Qin, WANG Chuangye, et al

Analysis on stress and deformation of passive battered piles under surcharge based on SW model

[J]. Journal of Hunan University: Natural Sciences, 2024, 51 (5): 46- 55

[本文引用: 1]

罗丽娟, 任翔, 李晟, 等. 基于土拱效应和黄土改进应变楔模型的抗滑桩水平承载力计算[EB/OL]. (2024−03−30)[2025−02−07]. https://doi.org/10.16183/j.cnki.jsjtu.2023.650.

[本文引用: 1]

DUNCAN J M, CHANG C Y

Nonlinear analysis of stress and strain in soils

[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96 (5): 1629- 1653

DOI:10.1061/JSFEAQ.0001458      [本文引用: 1]

BYRNE P M, CHEUNG H, YAN L

Soil parameters for deformation analysis of sand masses

[J]. Canadian Geotechnical Journal, 1987, 24 (3): 366- 376

DOI:10.1139/t87-047      [本文引用: 2]

WONG K S, TEH C I

Negative skin friction on piles in layered soil deposits

[J]. Journal of Geotechnical Engineering, 1995, 121 (6): 457- 465

DOI:10.1061/(ASCE)0733-9410(1995)121:6(457)      [本文引用: 1]

陈仁朋, 周万欢, 曹卫平, 等

改进的桩土界面荷载传递双曲线模型及其在单桩负摩阻力时间效应研究中的应用

[J]. 岩土工程学报, 2007, 29 (6): 824- 830

DOI:10.3321/j.issn:1000-4548.2007.06.006      [本文引用: 1]

CHEN Renpeng, ZHOU Wanhuan, CAO Weiping, et al

Improved hyperbolic model of load-transfer for pile-soil interface and its application in study of negative friction of single piles considering time effect

[J]. Chinese Journal of Geotechnical Engineering, 2007, 29 (6): 824- 830

DOI:10.3321/j.issn:1000-4548.2007.06.006      [本文引用: 1]

KULHAWY F H. Limiting tip and side resistance: fact or fallacy? [C]// Proceedings of Symposium on Analysis and Design of Pile Foundations. New York: ASCE, 1984: 80–98.

[本文引用: 1]

BRIAUD J L, SMITH T, MEYER B. Laterally loaded piles and the pressuremeter: comparison of existing methods [M]// LANGER J A, MOSLEY E T, THOMPSON C D. Laterally loaded deep foundations: analysis and performance. [S.l.]: ASTM, 1984: 97–111.

[本文引用: 1]

DOBRY R, VICENTI E, O’ROURKE M J, et al

Horizontal stiffness and damping of single piles

[J]. Journal of the Geotechnical Engineering Division, 1982, 108 (3): 439- 459

DOI:10.1061/AJGEB6.0001259      [本文引用: 1]

MAKRIS N, GAZETAS G

Displacement phase differences in a harmonically oscillating pile

[J]. Géotechnique, 1993, 43 (1): 135- 150

[本文引用: 1]

WU J, EL NAGGAR M H, WANG K

Analytical model for laterally loaded soil-extended pile shaft applied to verifying the applicability of lateral PS method

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2021, 147 (10): 04021103

DOI:10.1061/(ASCE)GT.1943-5606.0002636      [本文引用: 1]

刘汉龙, 朱春鹏, 沈杨

酸碱污染土工程性质研究

[J]. 湖南大学学报: 自然科学版, 2008, 35 (11): 39- 44

[本文引用: 1]

LIU Hanlong, ZHU Chunpeng, SHEN Yang

Study on fundamental engineering properties of polluted soil by acid and alkali

[J]. Journal of Hunan University: Natural Sciences, 2008, 35 (11): 39- 44

[本文引用: 1]

ZHANG L

Nonlinear analysis of laterally loaded rigid piles in cohesionless soil

[J]. Computers and Geotechnics, 2009, 36 (5): 718- 724

DOI:10.1016/j.compgeo.2008.12.001      [本文引用: 2]

ACHMUS M, ABDEL-RAHMAN K. Finite element modelling of horizontally loaded monopile foundations for offshore wind energy converters in Germany [C]// Proceedings of the International Sympodium on Frontiers in Offshore Geotechnics. London: [s.n.], 2005: 391–396.

[本文引用: 1]

WU J, EL NAGGAR M H, WANG K

Dynamic response of poroelastic soil adjacent to an axially vibrating pile

[J]. Journal of Engineering Mechanics, 2024, 150 (11): 04024084

DOI:10.1061/JENMDT.EMENG-7930      [本文引用: 1]

朱斌, 熊根, 刘晋超, 等

砂土中大直径单桩水平受荷离心模型试验

[J]. 岩土工程学报, 2013, 35 (10): 1807- 1815

[本文引用: 2]

ZHU Bin, XIONG Gen, LIU Jinchao, et al

Centrifuge modelling of a large-diameter single pile under lateral loads in sand

[J]. Chinese Journal of Geotechnical Engineering, 2013, 35 (10): 1807- 1815

[本文引用: 2]

/

〈 〉