机器学习方法被广泛用于土体沉降预测中,对盾构施工引发的地表最大沉降的预测研究日渐成熟[7]. 仅预测沉降的最终值无法反应施工中盾构机与地层间复杂的联系[8],且无法实现对土体沉降的动态监测. 深度学习方法被用来预测盾构施工中土体沉降的发展过程. 例如,Yan等[8]以Adaboost.RT为基础融合反向传播模型、极端学习机和支持向量回归建立集成模型,该模型的预测效果显著优于单一模型及其组合模型;Ye等[9]使用时序土体沉降的实时监测值和下一时刻的预测值共同作为反向传播模型的输入,发现考虑时序效应的模型对不同测点的沉降值均表现出较高的预测精度. 长短期记忆(long short term memory,LSTM)模型的时序沉降预测性能优异[10-11]. Cao等[12]开发出基于自适应噪声和经验模态分解法的LSTM模型,该模型在不同沉降监测点处均表现出较高的预测精度和较小的绝对误差;Ma等[13]采用最大化信息系数法简化LSTM模型的输入特征,发现优化后的模型在测试集中对隧道拱顶的沉降预测结果接近真实值;Li等[14]对比相同输入特征下LSTM和门控循环单元(gated recurrent unit, GRU)模型对地表沉降的预测结果,发现2种模型在训练集中的准确率分别为92.9%和91.4%,继而采用LSTM模型预测不同地层中的地表沉降,发现平均准确率为77.4%. 现场采样点间通常存在时空关联性[15-16],一些研究通过卷积神经网络(CNN)来提取数据的空间特征[17-18],再结合LSTM模型共同实现对数据时空特性的捕捉[19-20]. 例如,吴伟强[19]对比CNN-LSTM、循环神经网络(recurrent neural network, RNN)和LSTM模型对金川铜镍矿西二采区的面状地表沉降的预测结果,发现CNN-LSTM模型的平均绝对百分比误差和平均绝对误差最小分别为0.461和5.23 mm;洪宇超等[20]采用CNN-LSTM和LSTM模型对上海云岭超深基坑的变形进行预测,发现CNN-LSTM模型的平均预测相对误差为2.00%,优于LSTM模型.
双向循环神经网络(bidirectional recurrent neural network,Bi-RNN)能够有效捕获数据间的时空特性,这不仅降低了计算复杂度,也简化了模型设计[21-22]. Vaswani等[23]开发出注意力机制算法,通过关注序列数据中的重要信息来加强对数据时空特性的捕捉,包括自注意力(self-attention,SA)机制和多头自注意力(multi-head self-attention,MHSA)机制. Zhang等[24]引入SA机制使生成对抗插补网络生成与真实数据集相近的伪数据集;Fan等[25]认为结合SA机制的生成对抗网络能够准确地重构出台风激励下结构的动态响应;高墨通等[26]构建CNN-SA-LSTM模型对龙首矿西二采区的地表沉降进行预测,平均平均绝对误差和均方根误差较CNN-LSTM模型分别降低了81.2%和73.9%. 双向循环网络结构尚未被成熟应用于岩土工程领域以提高对时序数据的预测精度;此外,相较于SA机制,MHSA机制能从不同子空间中获取数据的多层次特征,尚未见与现有模型结合应用于土体沉降预测中. 本研究提出结合MHSA机制和双向循环长短期记忆(Bi-LSTM)的土体沉降预测模型. 1)将多通道沉降数据联合输入模型,通过双向架构来捕捉数据的时空特性;利用MHSA机制从多角度获取数据的不同特征,加强对数据关键信息的提取. 2)基于同一案例确定模型的架构,对比结合MHSA和SA机制前后Bi-LSTM模型的沉降预测效果. 3)结合不同案例测试所提模型在不同工程应用中的预测精度并分析注意力机制对模型预测效果的影响.
1. 土体沉降预测模型
本研究以预测土体沉降的动态变化趋势为切入点,基于MHSA-Bi-LSTM模型,利用实际工程中的前期土体沉降监测数据实现对盾构施工引发的下一阶段土体沉降变化趋势进行预测. 结合不同工程案例分析并验证模型应用在不同水文地质工程中的泛化能力.
1.1. 双向长短期记忆模型
式中:Γf、Γi和Γo分别为遗忘门、输入门和输出门,xt, ht−1和ct−1为单元的输入向量,ht和ct为单元的输出向量,b和W分别为权重和偏置向量,-ct、ct和ct−1分别为记忆细胞单元的候选值、当前时刻的记忆细胞单元和前一时刻的记忆细胞单元,
1.2. 注意力机制
1.2.1. 自注意力机制
SA机制是模拟人脑关注机制的算法,通过赋予序列数据不同的权重值来捕捉数据的关键信息并准确地把握数据的全局特征. 自注意力机制的计算步骤[23]如下:根据给定的输入序列通过相应的权重矩阵分别计算出查询变量Q、键变量K和值变量V,再根据Q和K间的相似性计算出V的权重,最后通过加权求和线性连接层获得自注意力层的输出O.
式中:X为输入序列;dk为键变量的维度,用于缩放点积;Wq、Wk和Wv分别为Q、K和V变量相应的权重矩阵;Soft为逻辑回归函数;W0和b0分别为权重和偏置向量;Att表示注意力运算.
1.2.2. 多头自注意力机制
MHSA机制是SA机制的变体,通过多次不同的线性变换获得多个自注意力头,每个头都能独立学习序列数据在不同子空间中的特征,最终将多个头的结果进行合并以从不同的角度关注序列数据的层次化特征,丰富数据的表达能力[23].
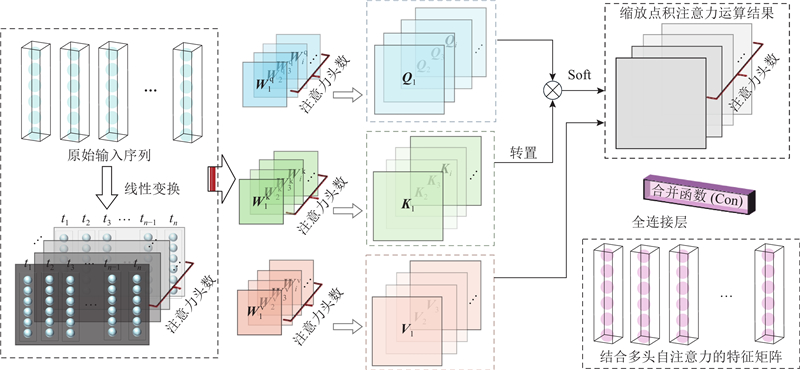
式中:i为第i个头,Wiq、Wik和Wiv分别为Q、K和V在第i个头中的权重矩阵,m为多头自注意力机制的头数,hm为第m个头的数据矩阵,Con为合并函数. MHSA的计算步骤如图1所示.
图 1
图 1 多头自注意力机制的计算步骤
Fig.1 Calculation procedure of multi-head self-attention mechanism
1.3. 预测模型搭建
1.3.1. 模型构建
图 2
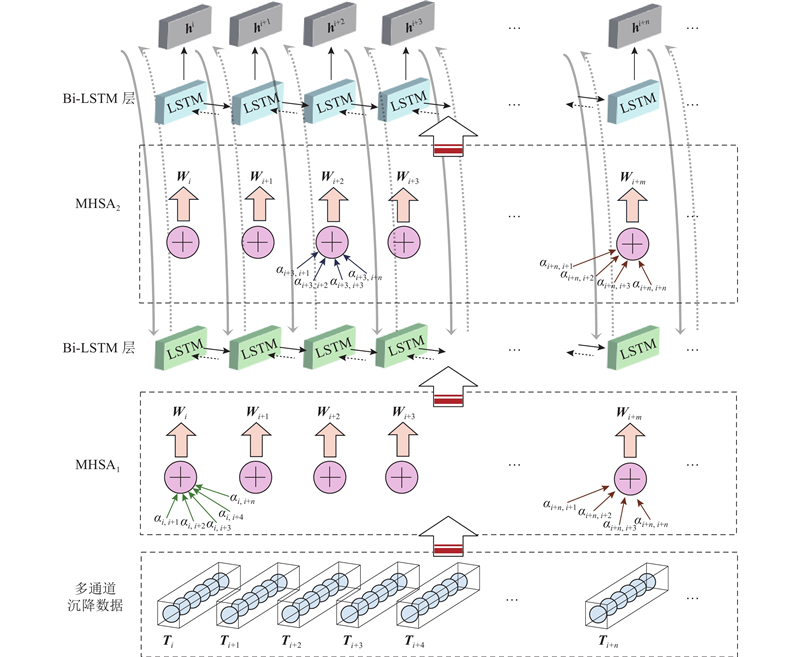
图 2 多头自注意力-Bi-LSTM模型架构
Fig.2 Architecture of multi-head self-attention-Bi-LSTM model
1)输入数据源于现场实测的n个土体沉降监测点,若使用n个同类型传感器采集0~t时刻的沉降数据,则模型的输入是大小为t×n的二维数据矩阵,其中t为时间,n为传感器个数.
2)在数据输入第一层Bi-LSTM前,通过第一层多头自注意力MHSA1对数据的重要特征进行提取. 此后,每个时刻的数据输出表示为[W1(k), W2(k), W3(k),···,Wt(k)],
式中:
3)使用滑动窗口技术将输入序列依次输入第一层Bi-LSTM,使模型能够提取多个时间尺度上的数据变化趋势并充分利用历史数据信息. 通过交叉验证确定较优滑动窗口大小为50,使用前50个数据来预测第51个数据值.
4)数据经第一层Bi-LSTM处理后被输入第二层多头自注意力MHSA2进行多维度的特征提取. 处理后数据被传递至第二层Bi-LSTM,最终通过全连接层产生时序沉降的预测结果.
1.3.2. 参数配置
将总数据的80%作为训练集采用10倍交叉验证方法训练模型,即将训练样本分为10组,取训练结果的均值作为模型最终的训练误差,比较不同超参数配置下模型的预测误差,确定超参数的较优值,使用训练好的模型在测试集中进行效果评估. 在MHSA-Bi-LSTM模型中,对比当注意力头数分别设置为2、4和8时模型的预测精度,发现无论是否重调超参数,模型的精度始终在注意力头数为4时表现最优,因此,本研究设置注意力头数为4以从不同的子空间中捕捉数据特征.
本研究确定的模型参数主要包括:隐藏单元和注意力单元个数、滑动窗口大小、学习率、迭代次数、批大小和Dropout. 参考文献[28]~[30],将模型参数范围设置如下:隐藏单元数NH或注意力单元数Nu为[32, 64, 128, 256, 512]、学习率为[
表 1 不同深度学习模型的超参数配置
Tab.1
| 参数 | 数值 | ||
| MHSA-Bi-LSTM | SA-Bi-LSTM | Bi-LSTM | |
| L1-Nu | 32 (MHSA1) | 64 (SA1) | — |
| L1-NH | 64 | 64 | 128 |
| L2-Nu | 64 (MHSA2) | 128 (SA2) | — |
| L2-NH | 128 | 128 | 128 |
| 学习率 | 0.01 | 0.01 | 0.01 |
| Dropout | 0.5 | 0.4 | 0.5 |
| 批大小 | 128 | 128 | 64 |
| 迭代次数 | 200 | 175 | 150 |
| 计算时间/s | 618 | 536 | 447 |
2. 案例分析与模型验证
2.1. 工程概况
2.1.1. 研究案例1
将某隧道项目中的土体沉降实测数据分为训练和测试2个部分,使用训练样本调优并确定模型超参数,验证模型在测试样本中的预测效果. 该项目采用盾构法同时开挖南向和北向2条隧道,北线隧道上方地表附近有古塔,因而土体沉降监测装置布置在北线隧道上方,共计6个沉降监测点(Y1~Y6). 施工现场采用光纤布拉格光栅液位传感器对土体沉降数据进行采集,采集时间为2019年3—9月直至沉降值趋于稳定,具体施工信息见文献[9]. 2条隧道沿东西向长度为879.0 m,净距为9.0 m,隧道的内径和外径分别为11.3和10.3 m,盾构机直径为11.67 m. 如表2所示,现场地层条件由上至下依次为杂填土(1号)、粉土(2号)、泥质黏土(3号)、淤泥质粉土(4号)和粉质黏土层(5号),隧道施工主要穿越4号和5号土层. 表2中,E为土体弹性模量,ν为土体的泊松比,γ为土体重度,c为土体黏聚力,ψ为土体内摩擦角,h为土层厚度.
表 2 盾构隧道项目的地层性质(案例1)
Tab.2
| 土层编号 | E/(N∙mm−2) | ν | γ/(kN∙m−3) | c/kPa | ψ/(°) | h/m |
| 1 | 4.38 | 0.29 | 18.4 | 15 | 8 | 2.40 |
| 2 | 4.08 | 0.25 | 18.2 | 26 | 13 | 2.40 |
| 3 | 2.0 | 0.33 | 17.3 | 12 | 10 | 3.85 |
| 4 | 3.5 | 0.35 | 17.7 | 13 | 13 | 12.00 |
| 5 | 8.0 | 0.30 | 18.3 | 24 | 21 | 7.20 |
2.1.2. 研究案例2
基于案例1中已训练好的模型,采用某地铁项目中的土体沉降实测值分析该模型在不同工程地质条件下预测效果. 该工程采用盾构法同方向开挖2条隧道,开挖直径均为6.45 m,净距为7.80 m. 隧道开挖区段于DK6+992.00和DK7+537.05间且穿越复杂的土-岩复合地层. 现场的稳定孔隙水在地表下埋深为1.60~4.45 m,粉砂层中稳定的微孔承压水位于地表下埋深为3.55 m处. 该场地地下水水位较高,这会增加盾构施工中地层失稳的风险. 隧道中相同位置的管片对应的地层性质如表3所示[31],其中A为全风化花岗岩层,B为中风化花岗岩层,C为粉质黏土层Ⅰ,D为砾状粉质黏土,E为粉质黏土层Ⅱ. 沉降监测点位于左和右线隧道中心正上方地表处,本研究选择2条隧道对应的第225环和365环管片上方的沉降数据用于模型测试.
表 3 盾构隧道项目的地层性质(案例2)
Tab.3
| 管片 | 地层 | ν | γ | c | ψ | h |
| 225左线(A&C) | C | — | 18.5 | 27.3 | 13.2 | −10~−20 |
| 225右线(B&D) | B | 0.16 | — | 7.5 | 49.2 | −10~−20 |
| 365左线(C&B&E) | E | — | 19.1 | 35.3 | 16.7 | −10~−25 |
| 365右线(B&C) | — | — | — | — | — | −10~−25 |
2.2. 数据划分与模型训练
2.2.1. 数据归一化
采用Max-Min归一化方法将实测土体沉降数据缩放至[0,1]区间. 在案例1中,联合Y3、Y4和Y5监测点的沉降数据共同作为模型的输入,这3个监测点分别位于北线隧道中心处Y4、左(Y3)和右(Y5)边界正上方处,通过模型捕捉不同位置和不同时刻传感器数据的时空特性进行沉降预测,输出分别对应3个传感器的沉降数据. 在案例2中,联合相同管片位置处两点的时序沉降数据作为模型的输入,选用案例1中预测效果较优的模型直接进行测试. 共计2组测试集分别对应225环和365环的管片.
2.2.2. 时序交叉验证
采用时序交叉验证方法通过训练样本确定模型的最优架构. 与传统交叉验证方法不同,时序交叉验证方法避免使用未来数据训练模型,即每次使用0~t时刻的数据训练模型,使用t~t+m时刻用于验证,依次扩大训练集(0~t+n时刻),验证集大小不变(t+n~t+n+m时刻),直至训练结束. 取预测结果的均值作为模型的训练总误差,该过程确保模型具备良好的泛化性.
2.2.3. 评估指标
选用3种指标对模型的预测性能进行评估:平均绝对误差MAE、均方误差MSE和平均绝对百分比误差MAPE. 采用泰勒图分析3种模型的预测结果,泰勒图综合相关系数R、标准差SD和中心均方根差异CRMSD这3个指标,R和SD用于量化预测值与真实值间的可比性,CRMSD用于描述预测值与真实值的差异.
式中:
2.2.4. 消融实验
为了探明模型中的重要模块(如多头自注意力机制、自注意力机制、滑动窗口、双向架构和Dropout技术)对预测效果的影响,以案例2中模型的预测结果为基准,分析模型性能在消除不同模块后的变化情况. 采用平均相对准确率ACC评估消融后模型对土体沉降的预测效果,
2.3. 预测结果分析
2.3.1. 案例1分析
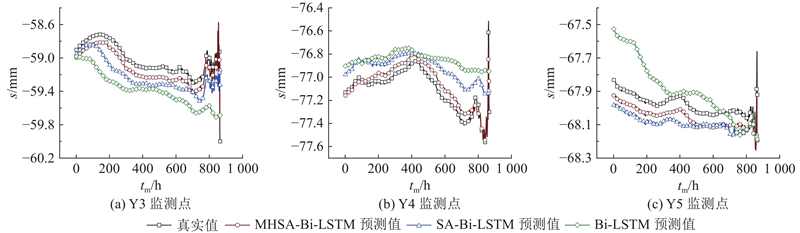
采用较优参数配置下的模型对土体沉降s进行预测,优化器均为Adam,结果如图3所示,其中tm为监测时间. 不同模型对土体沉降数据的预测趋势与真实数据趋势总体相近,表明模型的超参数配置较合理. 对于不同的沉降监测点,Bi-LSTM模型对真实土体沉降趋势的预测显著不足且预测值与实际值间存在较大差异;引入注意力机制后的模型对数据变化趋势的预测接近真实数据;相比于SA-Bi-LSTM模型,MHSA-Bi-LSTM模型的预测值与真实值间的差异更小.
图 3
图 3 不同深度学习模型的土体沉降预测结果对比(案例1)
Fig.3 Comparison of soil settlement predictions across different deep learning models (case 1)
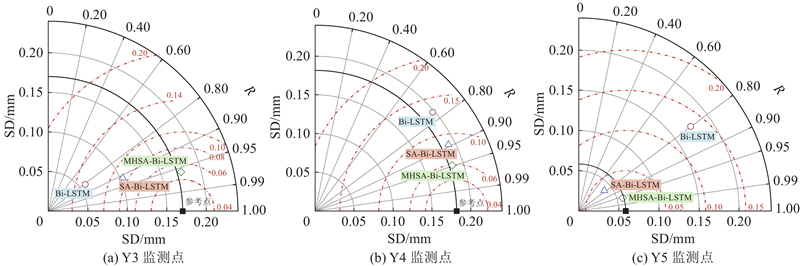
3种模型对不同监测点处土体沉降预测结果的泰勒图解如图4所示,泰勒图指标如如表4所示,其中模型1为MHSA-Bi-LSTM,模型2为SA-Bi-LSTM,模型3为Bi-LSTM. 对于Y3监测点,3种模型于泰勒图中的位置均接近于恒定标准差弧线,表明模型预测值的标准差与真实值的标准差相近,与模型2和模型3相比,模型1预测值的标准差与真实值标准差的差异最小;相对参考点的位置而言,模型1与之距离最近,模型2次之,模型3最远,表明模型1的R最大且CRMSD最小;相反,模型3的R最小且CRMSD最大. 对于Y4监测点,模型1在泰勒图中的位置相较于其他2种模型更接近恒定标准差弧线,因此其预测值的标准差接近真实值的标准差,模型3几乎偏离了恒定标准差弧线,表明其预测值标准差与真实值标准差的差异较大;比较模型点与参考点的相对位置发现,模型1与参考点的距离最近且R最大,模型3与参考点的距离最远且R最小. 对于Y5监测点,模型1和模型2在泰勒图中的位置与恒定标准差弧线更接近,模型3基本偏离恒定标准差弧线;模型1与参考点的距离最近,CRMSD最小且R最大,模型2和模型3大致位于同一条恒定相关系数直线上,二者R相近,但模型2的CRMSD比模型3的更低.
图 4
图 4 不同深度学习模型的土体沉降预测结果的泰勒图解(案例1)
Fig.4 Taylor diagram graphical presentation of soil settlement predictions produced by different deep learning models (case 1)
表 4 不同深度学习模型在不同监测点的土体沉降预测泰勒图参数值(案例1)
Tab.4
| 监测点 | 模型 | SD/mm | R | CRMSD/mm | |
| 预测 | 真实 | ||||
| Y3 | 1 | ||||
| 2 | |||||
| 3 | |||||
| Y4 | 1 | ||||
| 2 | |||||
| 3 | |||||
| Y5 | 1 | ||||
| 2 | |||||
| 3 | |||||
采用MAE、MSE和MAPE来评价模型在不同监测点处对土体沉降的综合预测效果,结果如表5所示. 可以看出,模型3的平均预测性能显著低于模型1和模型2,其平均MSE、MAE和MAPE值分别为0.085 5 mm、0.249 1 mm和3.77%. 结果表明,SA和MHSA机制可以提升模型的预测效果. 具体来说,与模型3相比,对于引入SA机制后的模型2,平均MSE和MAE分别降低了47.07%~67.87%和11.43%~43.72%;对于引入MHSA机制后的模型1,平均MSE和MAE降低了75.70%~94.37%和38.25%~76.35%. 与模型2相比,模型1的平均MSE、MAE和MAPE分别降低了54.09%~89.17%、30.28%~68.15%和31.25%~68.0%,表明模型1在3种模型中的预测效果最优,其平均MSE、MAE和MAPE分别为0.008 3 mm、0.083 0 mm和1.27%.
表 5 不同深度学习模型的土体沉降预测性能指标对比(案例1)
Tab.5
| 监测点 | 模型 | MSE/mm | MAE/mm | MAPE/% |
| Y3 | 1 | 1.9 | ||
| 2 | 3.5 | |||
| 3 | 6.2 | |||
| Y4 | 1 | 0.8 | ||
| 2 | 2.5 | |||
| 3 | 3.3 | |||
| Y5 | 1 | 1.1 | ||
| 2 | 1.6 | |||
| 3 | 1.8 |
综上, MHSA-Bi-LSTM和SA-Bi-LSTM模型对盾构引发的土体沉降的预测效果相较Bi-LSTM模型更优,其中MHSA-Bi-LSTM模型的预测效果最优.
2.3.2. 案例2分析
选用案例1中预测效果较优的模型1和模型2,测试二者在案例2中的预测效果以评估模型的泛化性能. 如表6所示为3种模型预测结果的平均性能指标. 可以看出,模型1和2在案例2中同样表现出较模型3更好的预测效果. 对于同一监测点而言,模型1比模型2的预测更准确. 与模型2相比,模型1的平均MSE、MAE和MAPE值分别降低了11.9%、17.6%和38.9%,这一结论与案例1中的结果一致. 此外,模型1的总平均相对误差RE=0.38 mm,模型2的总平均RE=0.55 mm. 可见,MHSA机制较SA机制对模型预测性能的提升效果更优.
表 6 不同深度学习模型的土体沉降预测性能指标对比(案例2)
Tab.6
| 监测点 | 模型 | MSE/mm | MAE/mm | MAPE/% | RE/mm |
| 225-左 | 1 | 0.122 | 0.295 | 9.72 | 0.38 |
| 2 | 0.141 | 0.357 | 15.55 | 0.59 | |
| 225-右 | 1 | 0.115 | 0.276 | 8.25 | 0.39 |
| 2 | 0.138 | 0.334 | 14.12 | 0.41 | |
| 365-左 | 1 | 0.167 | 0.378 | 9.28 | 0.37 |
| 2 | 0.181 | 0.415 | 14.23 | 0.61 | |
| 365-右 | 1 | 0.157 | 0.285 | 8.98 | 0.38 |
| 2 | 0.174 | 0.392 | 15.36 | 0.57 | |
| 均值 | 1 | 0.140 | 0.309 | 9.06 | 0.38 |
| 2 | 0.159 | 0.375 | 14.82 | 0.55 |
对比2.3.1节中模型在案例1中的预测结果发现,采用已训练好的模型对案例2的沉降数据集直接预测,平均预测性能指标比案例1中的更高. 具体来说,模型1在案例1中的总平均MAPE为1.27%,在案例2中为9.06%;模型2在案例1中的总平均MAPE为2.53%,在案例2中为14.82%. 由此可见,模型在案例2中的预测效果相比于案例1中有所降低,主要原因是训练好的模型未经调试直接用于测试,由于模型在搭建过程中采用交叉验证方法和正则化技术,使得模型在案例2中仍表现出较好的预测效果. 分析结果表明,本研究所提模型在不同工程地质条件下的泛化性能较强.
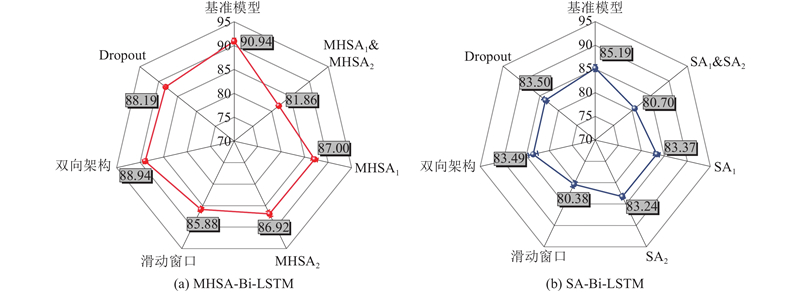
以225环和365环管片位置处土体沉降预测结果的平均准确率为评价指标,如图5所示为案例2中模型在消除不同模块后ACC的变化情况. 可以看出,当同时消除模型中的2层SA或MHSA层时,模型的ACC会显著降低. 最终MHSA-Bi-LSTM和SA-Bi-LSTM模型经消融后的ACC相近分别为81.86%和80.70%,证实了MHSA机制相较于SA机制对模型预测准确性的提升效果更优. 当分别消除MHSA-Bi-LSTM模型中的MHSA1或MHSA2时,ACC分别降低至87.00%和83.37%,但模型预测准确率累计损失值仍低于同时消除2层MHSA时模型的预测准确率,SA-Bi-LSTM模型表现出相同的规律. 这表明同一模型的不同注意力层间不是相互独立的,相邻注意力层间存在潜在的相互依赖关系与相关性. 模型中的双向架构模块和Dropout技术对模型预测效果的影响不明显. 相反,滑动窗口对预测准确性的影响较显著,消除滑动窗口后MHSA-Bi-LSTM和SA-Bi-LSTM模型的预测准确度分别降低至85.88%和80.38%. 可见,对于时序数据预测研究,采用数据滑动窗口技术可有效提升模型的预测准确性.
图 5
图 5 不同深度学习模型的模块消融实验结果(案例2)
Fig.5 Ablation experiment results for different deep learning models (case 2)
2.3.3. 结果讨论与分析
在案例1中,融合MHSA和SA机制后Bi-LSTM模型优于原始的Bi-LSTM模型,其中MHSA-Bi-LSTM模型具有最优的沉降预测效果. 原因是注意力机制能够进一步提取数据的主要特征并加强模型对重要信息的关注程度,捕获时序数据微小的变化趋势,使模型展现出较优的预测效果. MHSA机制通过设置多个自注意力层在不同的子投影空间中并行计算自注意力,合并结果以提取数据的多层次特征,增强表达能力,使模型展现出比使用SA机制更优的预测效果. 消融实验证实,MHSA机制对模型预测性能的提升优于SA机制. 在案例2中,尽管MHSA-Bi-LSTM和SA-Bi-LSTM模型的预测效果不及在案例1中优异,但二者仍表现出较低的预测误差和较高的预测准确度. 原因是模型在案例1中使用交叉验证、滑动窗口和Dropout技术进行训练后,降低了对原数据的依赖性,表现出良好的泛化性能. 在案例2中,模型参数未经调优导致预测效果有所下降,因此在工程应用中,建议根据现场的实际需求进行模型超参数微调以满足精度需要.
3. 结 语
本研究基于Bi-LSTM模型,设计2层循环结构使模型能够捕捉到不同监测点数据间的时空特性以及同一监测点不同时刻数据间的长距离依赖关系. 将2种注意力机制分别融入Bi-LSTM模型中以提升模型对土体沉降的预测效果. 依托2个实际工程案例确定模型的最优架构,验证所提模型在不同工况下沉降预测效果的泛化性能. 1)在案例1中,Bi-LSTM模型的平均预测效果最差,但引入注意力机制后模型的预测效果显著提升. 在案例2中,MHSA-Bi-LSTM和SA-Bi-LSTM模型的预测效果良好,但不及在案例1中的优异,MHSA-Bi-LSTM模型的预测效果最佳. 2)消融实验发现,同时消除多个注意力层对预测效果的影响高于单独消除注意力层的累计影响,说明模型相邻的注意力层间具有较强的相关性和依赖性;此外,合适的数据滑动窗口设置对于时序数据至关重要. 3)MHSA-Bi-LSTM模型可用于预测盾构引发的土体沉降. 联合多个沉降监测点的前期数据作为模型的输入进行下一阶段土体沉降预测. 实际应用中须根据现场实测数据对模型进行微调和训练,以便增强模型对新数据集的适应性. 4)本研究所提模型适用于地层条件相对稳定的场地土体沉降预测. 在地质条件突变时,预测精度可能受限,须结合实时监测数据进行动态校正. 未来计划探索数据融合、多源信息整合及自适应学习等方法,提升模型对复杂地质环境的适应能力.
参考文献
基于深度学习的盾构机土舱压力场预测方法
[J].
Deep learning-based prediction method for chamber pressure field in shield machines
[J].
软岩地层盾构隧道施工引起的地层沉降预测
[J].DOI:10.13722/j.cnki.jrme.2019.1192 [本文引用: 1]
Prediction of ground settlement caused by shield construction in soft rock ground
[J].DOI:10.13722/j.cnki.jrme.2019.1192 [本文引用: 1]
基于GA-Bi-LSTM的盾构隧道下穿既有隧道沉降预测模型
[J].
Settlement prediction model of shield tunnel under-crossing existing tunnel based on GA-Bi-LSTM
[J].
隧道开挖地表沉降动态预测及影响因素分析
[J].DOI:10.16285/j.rsm.2021.1201 [本文引用: 1]
Dynamic prediction and influence factors analysis of ground surface settlement during tunnel excavation
[J].DOI:10.16285/j.rsm.2021.1201 [本文引用: 1]
基于多域物理信息神经网络的复合地层隧道掘进地表沉降预测
[J].
Prediction of tunneling-induced ground surface settlement within composite strata using multi-physics-informed neural network
[J].
机器学习方法在盾构隧道工程中的应用研究现状与展望
[J].DOI:10.11835/j.issn.2096-6717.2022.069 [本文引用: 1]
Review and prospect of machine learning method in shield tunnel construction
[J].DOI:10.11835/j.issn.2096-6717.2022.069 [本文引用: 1]
Tunnel surface settlement forecasting with ensemble learning
[J].DOI:10.3390/su12010232 [本文引用: 2]
Machine learning-based forecasting of soil settlement induced by shield tunneling construction
[J].DOI:10.1016/j.tust.2022.104452 [本文引用: 2]
Artificial intelligence driven tunneling-induced surface settlement prediction
[J].DOI:10.1016/j.autcon.2024.105819 [本文引用: 1]
基于循环神经网络的盾构隧道引发地面最大沉降预测
[J].
Prediction of maximum ground settlement induced by shield tunneling based on recurrent neural network
[J].
Deep learning neural network model for tunnel ground surface settlement prediction based on sensor data
[J].DOI:10.1155/2021/9488892 [本文引用: 1]
Machine learning in conventional tunnel deformation in high in situ stress regions
[J].DOI:10.3390/sym14030513 [本文引用: 1]
Prediction of surface settlement induced by large-diameter shield tunneling based on machine-learning algorithms
[J].DOI:10.1155/2022/4174768 [本文引用: 1]
Prediction of shield tunneling-induced ground settlement using LSTM architecture enhanced by multi-head self-attention mechanism
[J].DOI:10.1016/j.tust.2025.106536 [本文引用: 4]
Prediction of surface settlement around subway foundation pits based on spatiotemporal characteristics and deep learning models
[J].DOI:10.1016/j.compgeo.2024.106149 [本文引用: 1]
Convolutional neural network-based safety evaluation method for structures with dynamic responses
[J].DOI:10.1016/j.eswa.2020.113634 [本文引用: 1]
Reconstruction of long-term strain data for structural health monitoring with a hybrid deep-learning and autoregressive model considering thermal effects
[J].DOI:10.1016/j.engstruct.2023.116063 [本文引用: 1]
基于时空关联特征的CNN-LSTM模型在基坑工程变形预测中的应用
[J].
Application of CNN-LSTM model based on spatiotemporal correlation characteristics in deformation prediction of excavation engineering
[J].
Reconstruction of structural long-term acceleration response based on BiLSTM networks
[J].DOI:10.1016/j.engstruct.2023.116000 [本文引用: 1]
Sensor data reconstruction using bidirectional recurrent neural network with application to bridge monitoring
[J].DOI:10.1016/j.aei.2019.100991 [本文引用: 1]
Missing data repairs for traffic flow with self-attention generative adversarial imputation net
[J].DOI:10.1109/TITS.2021.3074564 [本文引用: 1]
Structural dynamic response reconstruction using self-attention enhanced generative adversarial networks
[J].DOI:10.1016/j.engstruct.2022.115334 [本文引用: 1]
结合卷积神经网络和注意力机制的LSTM采空区地表沉降预测方法
[J].DOI:10.13474/j.cnki.11-2246.2024.0610 [本文引用: 1]
LSTM goaf surface subsidence prediction method combining convolutional neural network and attention mechanism
[J].DOI:10.13474/j.cnki.11-2246.2024.0610 [本文引用: 1]
Long short-term memory
[J].DOI:10.1162/neco.1997.9.8.1735 [本文引用: 3]
Forecasting maximum surface settlement caused by urban tunneling
[J].DOI:10.1016/j.autcon.2020.103375 [本文引用: 2]
Single layer & multi-layer long short-term memory (LSTM) model with intermediate variables for weather forecasting
[J].DOI:10.1016/j.procs.2018.08.153
A data-driven structural damage identification approach using deep convolutional-attention-recurrent neural architecture under temperature variations
[J].DOI:10.1016/j.engstruct.2022.115311 [本文引用: 2]
Forecasting and early warning of shield tunnelling-induced ground collapse in rock-soil interface mixed ground using multivariate data fusion and catastrophe theory
[J].DOI:10.1016/j.enggeo.2024.107548 [本文引用: 1]