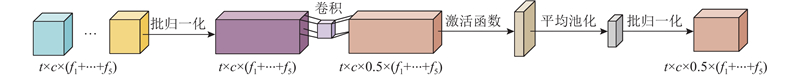据世界卫生组织统计，每年约有119万人死于道路交通事故^[1]. 驾驶员的不当驾驶行为是引发交通事故的重要原因^[2]，这常与疲劳^[3]、情绪、分心等因素有关. 驾驶员遇到紧急情况时没有立即采取制动措施也是引发交通事故的原因之一. 脑电信号（electroencephalography, EEG）能够反映大脑活动的变化，具有时间分辨率高、无创性和便携性等优点，其在驾驶员状态和行为^[4]监测领域的应用因此备受关注. 基于EEG进行紧急制动分类识别在驾驶员行为实时监测和智能驾驶辅助系统开发领域展现出良好的应用前景. 智能驾驶辅助系统通过实时采集驾驶员的EEG，分析大脑在紧急制动情境下的神经活动状态，预测驾驶员的制动意图，从而为紧急制动行为提供智能辅助和预警，减少事故发生，提升驾驶安全性.

紧急制动对时间要求极高，如何预判并进行制动仍是研究人员致力解决的难题. Haufe等^[5]提出利用驾驶模拟器进行紧急制动和正常驾驶2种驾驶场景的数据采集，通过事件相关电位（event related potential, ERP）特征使用正则化线性判别分析（regularized linear discriminant analysis, RLDA）分类器对紧急制动意图与正常驾驶进行分类，发现使用EEG和肌电（electromyogram, EMG）模拟辅助系统比仅依赖于踏板响应的系统早130 ms检测到紧急制动. 该研究团队随后在真实汽车上的验证结果与模拟驾驶相似^[6]. Kim等^[7]丰富了驾驶场景，增加非紧急（软）制动情况，EEG特征除了ERP特征外，还包括准备电位（readiness potential, RP）和事件相关去同步化（event-related desynchronization, ERD）特征，其紧急制动意图与正常驾驶分类结果优于仅使用ERP特征. 既有研究成果表明，基于电生理学进行紧急制动意图检测是可行的. 随着机器学习和深度学习的发展，一些学者采用机器学习和简单的深度学习算法对紧急制动行为进行分类识别研究，Lee等^[8]采用RCNN研究紧急情况下视觉感觉过程诱发的早期ERP曲线，发现RCNN方法比制动踏板早380 ms检测到制动意图. Hernández等^[9]提出在驾驶员压力、工作量和疲劳的状态下检测紧急制动意图，采用CNN和SVM对EEG进行分类，平均识别率均超过70%. Teng等^[10]设计脑控汽车的仿真实验，功率谱密度（power spectral density, PSD）检测率超过94%. Wang等^[11]采用3种制动场景，开发基于SVM的二进制分类器，识别驾驶意图；结果表明，3类的平均识别准确率均超过74%. Nguyen等^[12]提出自回归（auto-regressive, AR）特征提取与人工神经网络（ANN）相结合的新方法，该方法可以在检测到紧急制动意图约600 ms前开始执行制动事件，准确率达到91%. Zhang等^[13]从检查EEG是否提供有用的驾驶员表现测量的方面出发，发现被试采取紧急制动行为的重要反应时间是制动前的第2秒. Nacpil等^[14]从电极的脑电图中提取PSD，以此来训练和评估SVM，该模型仅使用1个电极，与先前研究者使用的模型对比，SVM的AUC更高. Liang等^[15]在模拟驾驶平台上进行3种不同的场景实验，对比分析了2种制动模式的EEG特征图，采用传统方法、基于黎曼几何的方法和基于深度学习的方法进行紧急制动意图预测，结果表明，基于黎曼几何的方法和基于深度学习的方法都优于传统方法.

综上，现有针对紧急制动意图的特征提取主要基于时域和频域特征，且多为传统提取方法. 对于制动过程中脑活动的空间域特征缺乏研究，对大脑在紧急制动时的激活模式尚未形成完整的认识. 本研究1）采用多尺度卷积层（multi-scale convolution，MSC）直接对原始EEG进行特征提取. 这种端对端^[16]的方法能够从EEG中提取更多丰富的特征^[17]，同时计算每个通道之间的脑功能测量矩阵，构建脑功能网络，得到空间图结构信息；脑功能网络图结构是非欧几里得数据，图卷积神经网络（graph convolutional network，GCN）模型能够充分学习其特征. 2）对实验结果进行分析讨论，进一步挖掘神经生理原因，为辅助驾驶设备在紧急情况发生时检测驾驶员的制动意图提供科学依据.

实验采用Haufe等^[5]发布的公开数据集. 该数据共包含18名被试，使用脑电帽从59个头皮电位和2个眼电电极采集EEG数据，采样率为200 Hz，实验范式如图1所示. 参与者通过方向盘和油门/刹车踏板控制虚拟赛车，以100 km/h的速度跟随前方领头车辆. 当2辆车制动距离不超过20 m时，领头车会突然减速至60~80 km/h并闪烁刹车灯作为刺激. 参与者立即进行紧急制动，以避免碰撞. 领头车在减速3 s后恢复到100 km/h，并在车距离超过100 m时等待跟随车辆靠近.

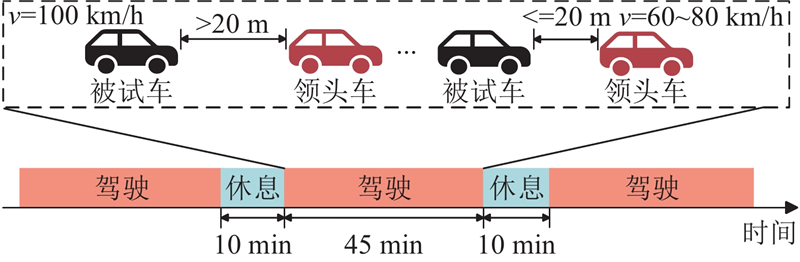
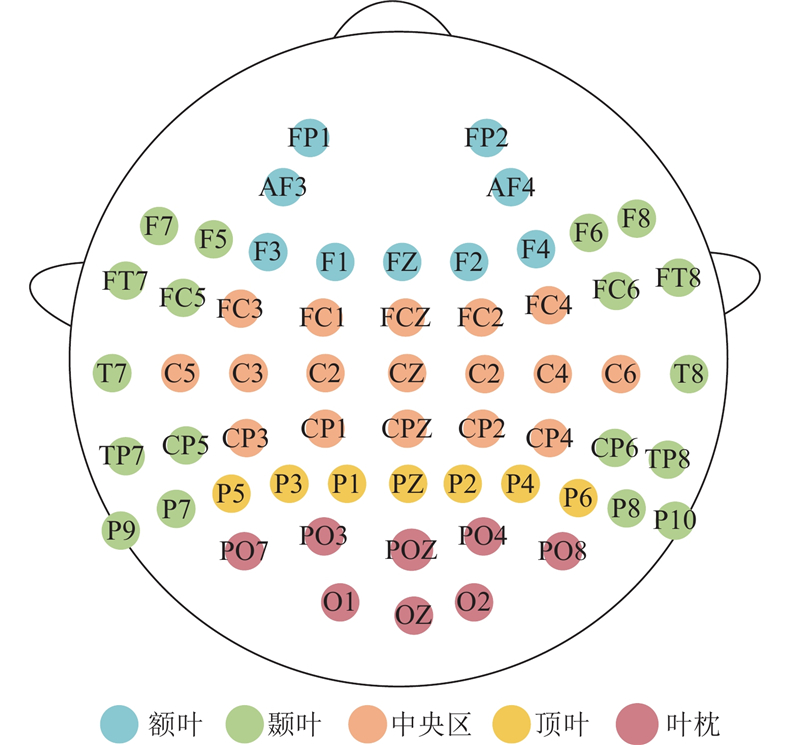
使用EEGLAB工具包对数据进行预处理. 先将原始EEG数据转换为EEGLAB支持的数据格式；再进行皮层电极定位，选择59个电极通道，电极通道如图2所示. 接着进行数据分段（epoch）.Wang等^[18]为了完整捕捉紧急制动前后的神经动态变化，采用8 s时间窗，针对紧急制动和正常驾驶2种行为，一方面考虑能够将制动动作前后的动态过程和信号特征变化表现出来，另一方面避免采取过长的时间窗而引入太多无关信息的问题；选择每个动作的前7 s和后3 s，形成10 s的分段. 为了提升数据质量，先去除眼电电极带来的伪迹，在独立成分分析（independent component analysis, ICA）之前，进行数据平均参考预处理，之后使用ICA去除脑电数据中的伪迹干扰，完成后，手动检查并删除残留的坏段. 由于领头车辆减速行为是随机的，每位被试获得的分段数量不同，分别为457、452、474、338、412、476、479、466、467、473、382、414、430、443、470、441、417、465，总共获得7 956个分段数据.

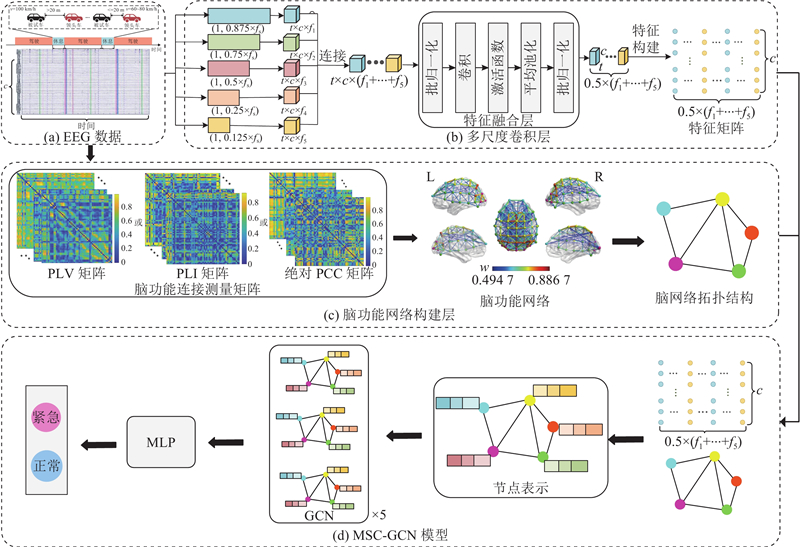
如图3所示为融合多尺度卷积、脑功能网络和图卷积神经网络的紧急制动行为识别模型的技术路线. 将经过预处理后的EEG数据输入多尺度卷积层进行特征提取；采用逐一卷积进行特征融合，同时求取脑功能测量连接矩阵，构建功能性脑网络，得到空间图结构信息；将融合到的节点特征和空间图结构信息放入图卷积神经网络中进行分类识别.

采用不同的脑功能连接测量矩阵，能够全面地捕捉大脑的多样化特征. 不同的连接矩阵从不同的角度描述脑区间的交互方式和特性，能够全面刻画脑网络的复杂性与多样性. 本研究将相位锁值（phase locking value，PLV）^[19]、相位滞后指数（phase lag index，PLI）^[20]作为评估相位同步的指标，评估2个电极之间的相位关系，使用相位同步方法分析大脑内的功能连接；将皮尔逊相关系数（pearson correlation coefficient，PCC）^[21]的绝对值作为评估大脑功能连接的指标，通过量化脑区间的线性依赖关系来刻画大脑内的功能连接.

1）PLV是任意2个信号之间平均相位差的绝对值，直接计算观测值之间相对相位的矢量平均值，数值介于0~1.0. 该指标通过比较2个信号的相位差来评估它们的同步性，计算式为

(1)$ {V}_{\text{PL}}=\left| \frac{1}{N}\sum\limits_{{t}=1}^{N}{\text{e}}^{\text{j}\left({\phi }_{X}\left(t\right)- {\phi }_{Y}(t)\right)}\right| . $

式中：N为信号的个数，$ {\phi }_{X}(t) $和$ {\phi }_{Y}(t) $为X和Y在时间点t的瞬时相位，j为虚数单位. 相位锁值为0，表示2个通道之间的相位差随时间变化，观察到的信号的区域之间没有连接；相位锁值为1，代表2个EEG通道之间的相位差大多是恒定的，是完美连接.

2）PLI用于测量2个信号之间的相位差分布的不对称性. 该指标反映2个信号之间的相位超限或滞后的一致性，是相位同步的有用的度量，计算式为

(2)$ {I}_{\text{PL}}=\left| \frac{1}{N}\sum \limits_{n=1}^{N}\text{sign} \;({\phi }_{X}(t)- {\phi }_{Y}(t))\right| . $

式中：sign(·)为符号函数，即判断相位差是正的，还是负的. 如果相位差为正，sign(·)返回1；如果相位差为负，sign(·)返回−1；如果相位差为0，则返回0.

3）绝对PCC用于评估2个变量之间的线性关系，计算式为

(3)$ {C}_{\text{PC}} =\left| \frac{\displaystyle\sum\limits_{i=1}^{N}({X}_{i}- \overline{X})({Y}_{i}- \overline{Y}）}{\sqrt{\displaystyle\sum\limits_{i=1}^{N}{({{X}_{i}}- \overline{X})}^{2}}\sqrt{\displaystyle\sum\limits_{i=1}^{N}{({{Y}_{i}}- \overline{Y})}^{2}}}\right| . $

式中：$ \overline{X} $和$ \overline{Y} $分别为信号X和Y的平均值. PCC的取值范围为[−1,1]，能够测量2个信号是正相关还是负相关. 绝对PCC为PCC的绝对值，绝对值越大，相关性越强.

脑功能网络构建的关键是对节点和边的定义以及阈值的选取. 将节点定义为EEG的电极位置，即59个节点，边定义为节点之间在功能连接层面的关系，即脑功能连接测量矩阵PLV、PLI和绝对PCC. 对EEG预处理后，求取每个被试的每个分段的功能性连接矩阵；选取最大值会忽略掉更多的重要信息，因此选择对每个被试的每个分段计算的矩阵取均值，得到最终的功能连接性矩阵. 脑网络比较复杂且存在大量的弱连接，它们可能是噪声引起的，并不能代表脑区之间的连接关系，有必要选择合适的阈值来构建功能性脑网络. 分别将PLV矩阵、PLI矩阵和绝对PCC矩阵中的连接权值组成权值向量，如图4所示为该向量的频率直方图，w为权值，f为出现频次. 以上四分位点作为最终的阈值^[22]，依据上述方法，得到不同矩阵下的阈值分别为0.480 71、0.254 30和0.494 73. 将大于阈值的连接边权值保留，小于阈值的连接边权值设置为0，并将自连接的权值设置为0，得到节点之间连边的关系，构建功能性脑网络^[23]，如图3(c)所示为根据测量矩阵构建的脑功能网络，其中w为节点之间连边的权值. 通过所构建的脑功能网络，获取大脑不同电极之间的功能连接关系，并基于这些连接关系提取空间图结构信息.

对于脑功能网络，通过计算不同的复杂性度量，对紧急制动和正常驾驶2种驾驶行为下的度量进行T检验，分析不同驾驶行为的大脑网络差异. 选择复杂网络中常用的网络特征参数对不同脑区下的EEG进行分析，即介数中心性BC、聚类系数C、同配系数ASS、传递性系数TRA、全局效率Ge. 1）介数中心性是指节点所有最短路径中经过该节点的路径数占总最短路径数的比例，计算式为

(4)$ \text{B}{\text{C}}_{i}=\sum \limits_{i\ne s\ne t}^{}\frac{d_{st}^{i}}{{d}_{st}} . $

式中：$ d_{st}^{i} $为经过节点i，且为最短路径的路径数量，d_st为连接起点s和终点t的最短路径数量. 2）聚类系数用来衡量节点之间连接的紧密程度，值越高表示节点之间越容易形成团簇，计算式为

(5)$ {C}_{i}=\frac{2{E}_{i}}{{k}_{i}({k}_{i}- 1)}, $

(6)$ C=\frac{1}{N}\sum \limits_{i=1}^{N}{C}_{i} . $

式中：N为节点，k_i为节点i的相邻节点数，E_i为节点i的k_i个邻节点之间实际存在的边数. 3）同配系数是指网络中度值相似的节点之间连接的趋势，用于评估网络中节点度的相关性，计算式为

(7)$ \text{ASS}=\frac{\displaystyle\sum_{j k} j k\left(e_{j k}-q_j q_k\right)}{\sigma^2} . $

式中：j、k为网络中某条边两端节点的度值，e_jk为边两端节点的度分别为j和k的联合概率，q_j为边一端节点的度为j的概率，$ {\sigma }^{2} $为节点度的方差. 4）传递性系数是指网络中三角形与三元组的比率，三角形意味着三条边互相连接，计算式为

(8)$ \text{TRA}=\frac{2 \displaystyle\sum_{j, k}\left(w_{i, j} w_{j, k} w_{k, i}\right)^{1 / 3}}{k_i\left(k_i-1\right)} . $

式中：$ \displaystyle\sum_{j, k}\left(w_{i, j} w_{j, k} w_{k, i}\right)^{1 / 3}$闭合三角形的数量. 5）全局效率是指平均所有节点对之间的效率之和，其中效率是指2个节点之间最短路径长度的倒数.

(9)$ \text{Ge}=\frac{1}{N(N- 1)}\sum \limits_{i\ne j}\frac{1}{{d}_{ij}} . $

式中：d_ij为两点之间的最短路径.

多尺度卷积层共2个模块，分别是时间卷积层和特征融合层. 时间卷积层通过不同尺度卷积核提取特征，特征融合层对学习到的特征进行融合.

多尺度时间卷积层利用并行多尺度一维时间核（temporal kernel, T核）对脑电信号进行特征提取. 为了动态学习EEG的频率表示，将时间核的长度设置为采样率f_s的不同比率^[17]，分别采用（1，0.875×f_s）、（1，0.75×f_s）、（1，0.5×f_s）、（1，0.25×f_s）和（1，0.125×f_s）的卷积核对EEG进行卷积. 卷积核表示为$ S_\text{T}^{k}=(1,{\alpha }^{k}\times {f}_{{\mathrm{s}}}) $，其中$ \alpha $为比率系数. 预处理后的脑电信号$ {\boldsymbol{x}}\in {{R}}^{c \times l} $，其中c为EEG通道数量，l为时间维度的样本长度. 并行应用5个多尺度时间核来动态学习时间/频率表示. 之后使用特征的平均合并平方的对数^[24]来学习功率特征. 一维卷积层用作数字过滤器，可以输出不同频段的过滤信号. 通过对滤波后的信号进行平方，可以得到它们的功率. 平均池化层作为窗口函数，计算短时间内的平均功率，应用对数激活函数，提升特征提取的性能. $ {\boldsymbol{x}}_{\text{T}}^{k}\in {{R}}^{t \times c \times{{f}_{k}}} $为时间核的输出，其中t为T核的数量.

(10)$ {\boldsymbol{x}}_{\text{T}}^{k}={\phi }_{\log }({F}_{\text{AP}}({\phi }_{\text{s}}({F}_{\text{C}}({\boldsymbol{x}},S_\text{T}^{k})))) . $

式中：$ {F}_{\text{C}}({\boldsymbol{x}},{S}_\text{T}) $为x上使用T核的卷积运算，$ {\phi }_{\text{s}}(\cdot ) $为平方函数，$ {F}_{\text{AP}}(\cdot ) $为平均池化，$ {\phi }_{\log }(\cdot ) $为对数函数. 将卷积得到的输出沿着特征维度进行拼接，多尺度时间卷积层的输出$ \tilde{{\boldsymbol{x}}}\in {\bf{R}}^{t\times c\times \sum_{k=1}^{4}{f}_{k}} $，表示为

(11)$ \tilde{{\boldsymbol{x}}}={H }({\boldsymbol{x}}_{\text{T}}^{1}, \cdots,{\boldsymbol{x}}_{\text{T}}^{k}) . $

式中：H(·)为沿着特征维度进行拼接操作.

如图5所示，特征融合过程将不同层次的T核的输出结果进行拼接后，采用逐一卷积层融合不同尺度的卷积核学习到的特征. 为了减少内部协变量偏移效应，在卷积之前之后使用批量归一化，引入Leaky ReLU激活函数，使用平均池化对学习到的特征进行下采样. 在批量归一化之后，将融合特征展平为图卷积神经网络层的节点特征矩阵. 提取的特征矩阵$ \boldsymbol{X}\in {{R}}^{c\times \left(t\times \left(\sum\nolimits_{k=1}^{4}{f}_{k}/2\right)\right)} $表示为

(12)$ \boldsymbol{X}={F}_{\text{re}}({F}_{\text{bn}}({F}_{\text{AP}}({\phi }_{\text{L}}({F}_{\text{con}}({F}_{\text{bn}}(\tilde{{\boldsymbol{x}}})))))) . $

式中：$ {F}_{\text{bn}}(\cdot ) $为批处理归一化函数，$ {F}_{\text{con}}(\cdot ) $为一对一卷积函数，$ {\phi }_{\text{L}}(\cdot ) $为Leaky ReLU函数.

本研究设计的GCN模型主要由5个卷积层组成，基于EEG的脑功能连接矩阵，建立表征脑电电极拓扑关系的图拉普拉斯算子以及多尺度卷积层提取的特征矩阵，作为GCN的前期输入，图卷积层学习融合脑电特征与电极拓扑的广义特征；接入多层感知机（multilayer perceptron，MLP）分类头，输出分类结果，通常采用反向传播算法，使模型对输入数据的预测结果更加准确.

无向加权图表示为G={V,E,A}，其中V为节点，E为连接节点的边的集合，$ \boldsymbol{A}\in {{R}}^{N\times N} $为2个节点之间的相关性加权邻接矩阵. 使用3种脑功能连接测量矩阵PLV、PLI和绝对PCC分别构建脑网络，将构建的脑网络作为图的邻接矩阵A. 定义L=D–A为拉普拉斯矩阵，其中D为度矩阵，$ {\boldsymbol{D}}_{ii}=\displaystyle\sum \nolimits_{j=1}^{N}{\boldsymbol{A}}_{ij} $. 为了确保数值稳定性和正则化效果，使用对称归一化拉普拉斯矩阵：

(13)$ {\tilde{\boldsymbol{L}}}=\boldsymbol{I}- {\boldsymbol{D}}^{- \frac{1}{2}}\boldsymbol{A}{\boldsymbol{D}}^{- \frac{1}{2}} . $

式中：I为单位矩阵.

脑电数据通常表现为非欧几里得结构，为此使用基于谱图的图卷积. 谱图卷积利用拉普拉斯矩阵在频域上执行滤波操作，依赖于图结构中的连接关系. 图的频域是基于图结构的频谱表示，它通过图拉普拉斯矩阵的特征分解来实现，特征分解表示为

(14)$ {\tilde{\boldsymbol{L}}}=\boldsymbol{U}\boldsymbol{\mathit{\Lambda }}{\boldsymbol{U}}^\text{T} . $

式中：$ \boldsymbol{U}=[\boldsymbol{u}_{0}, \cdots,\boldsymbol{u}_{N- 1}]\in {{R}}^{N\times N} $为特征向量矩阵，$ {\boldsymbol{\varLambda }}=\text{diag }({\lambda }_{0}, \cdots,{\lambda }_{N- 1})\in {{R}}^{N\times N} $为对角矩阵. 对于经过卷积提取的脑电信号$ \boldsymbol{X}\in {{R}}^{c\times \left(t\times \left(\sum \nolimits_{k=1}^{4}{f}_{k}/2\right)\right)} $，图傅里叶变换（graph fourier transform, GFT）^[25]使用$ {\tilde{\boldsymbol{L}}} $的特征向量基U在频域上的表示为

(15)$ {\hat{\boldsymbol{X}}}={\boldsymbol{U}}^\text{T}\boldsymbol{X} . $

则逆图傅里叶变换表示为

(16)$ \boldsymbol{X}=\boldsymbol{U}{\boldsymbol{U}}^\text{T}\boldsymbol{X}=\boldsymbol{U}\hat{\boldsymbol{X}} . $

图卷积$ G $的定义为

(17)$ \boldsymbol{X}*G{\boldsymbol{g}}=\boldsymbol{U}(({\boldsymbol{U}}^\text{T}\boldsymbol{X})\odot ({\boldsymbol{U}}^\text{T}{\boldsymbol{g}})) . $

式中：$ \odot $为Hadamard乘积，滤波器$ {\boldsymbol{g}}\in {{R}}^{N} $. 将滤波器定义为$ {g}_{\theta }({\boldsymbol{\varLambda }})=\text{diag }(\boldsymbol{\theta }) $，$ \boldsymbol{\theta }\in {{R}}^{N} $为傅里叶系数的向量，则图卷积可简化为

(18)$ \boldsymbol{X}*G{g}_{\theta }=\boldsymbol{U}{g}_{\theta }(\boldsymbol{\mathit{\Lambda }}){\boldsymbol{U}}^\text{T}\boldsymbol{X} . $

谱图卷积相较于空间卷积的不同之处在于滤波器$ {g}_{\theta } $的选择. 由于非参数滤波器在空间上不是局部化的，计算复杂度太高，采用切比雪夫多项式逼近的方法来解决这个问题. $ {g}_{\theta }({\boldsymbol{\varLambda }}) $可以通过切比雪夫多项式的截断展开式很好地近似，直到K阶：

(19)$ {g}_{\theta }({\boldsymbol{\varLambda }})=\sum \limits_{k=0}^{K- 1}{\boldsymbol{\theta }}_{k}{T}_{k}(\mathbf{\tilde{{\boldsymbol{\varLambda }}}}) . $

式中：$ {\tilde{{\boldsymbol{\varLambda }}}}=2\,{\boldsymbol{\varLambda }}/{\lambda }_{\max }- \boldsymbol{I} $；切比雪夫多项式的递归定义为T_k(x)=2xT_k-1(x)–T_k-2(x)，其中T₀(x)=1且T₁(x)=x.图卷积操作可以重新表述为

(20)$ \boldsymbol{X}*G{g}_{\theta }=\boldsymbol{U}\sum \limits_{k=0}^{K- 1}{\boldsymbol{\theta }}_{k}{T}_{k}(\mathbf{\tilde{\boldsymbol{\varLambda }}}){\boldsymbol{U}}^\text{T}\boldsymbol{X}=\sum \limits_{k=0}^{K- 1}{\boldsymbol{\theta }}_{k}{T}_{k}({\tilde{\boldsymbol{L}}})\boldsymbol{X} . $

式中：缩放拉普拉斯算子$ {\tilde{\boldsymbol{L}}}=2\boldsymbol{L}/{\lambda }_{\max }- \boldsymbol{I} $.

分别选取任意被试的正常驾驶和紧急制动的分段数据，分别求PLV、PLI和绝对PCC矩阵，按照流程构建脑功能网络. 如图6所示为根据不同的脑功能连接测量矩阵构建正常驾驶（左）和紧急制动（右）的脑功能网络拓扑连接图，脑功能网络图中不同颜色的节点代表不同的大脑区域，连接线的粗细和颜色变化表明大脑网络中连接的强度，连接性越粗、颜色越红表示连接强度强，反之，则连接强度弱. 在2种驾驶行为过程中，脑区间的交互都涉及全脑区，这与驾驶过程中涉及空间感知、视觉注意、听觉注意、判断决策等多个方面^[26]，需要大脑各个区域之间的协调和配合来共同完成相一致. 右脚刹车由左脑控制，因此在脑功能网络图中可以明显看到左脑的连接强度高于右脑. 对比来看，紧急制动状态下，节点之间的连线更接近橙色和红色，脑区间的功能连接强度更高，原因是在紧急制动状态下被试需要快速感知、判断和执行动作，导致脑功能网络强度更高. 在正常驾驶状态下，节点之间的高强度连接明显减少，原因是此时脑功能活动更趋于基础状态，主要处理简单的感知和运动信息.

为了进一步探讨紧急制动行为背后的神经生理原因，针对大脑中不同脑区，即额叶、颞叶、中央区、顶叶和枕叶，以PLV为脑功能连接测量矩阵，分别构建紧急制动和正常驾驶下的脑功能网络，对2种不同的驾驶行为进行差异性分析，结果如表1所示，其中—表示没有显著性差异，*表示p< 0.05，**表示p< 0.01. 差异性的结果表明，紧急制动行为涉及全脑的协调工作，但不同脑区的贡献存在差异. 额叶、中央区和颞叶在多个网络特征上表现出高度显著性，在紧急制动行为中协同作用，共同完成从认知决策到运动执行的全过程. 这是因为额叶主要负责执行控制和抑制控制，中央区主要负责直接控制运动执行，颞叶主要负责感知处理和高级认知，整合听觉、视觉信息以辅助决策，3个脑区相互配合，实现紧急制动行为的高效响应. 顶叶和枕叶在部分特征上显示显著性，但整体差异性较弱，主要为信息辅助作用. 这是因为顶叶主要通过空间认知和注意力调节发挥作用，枕叶的主要作用是视觉信息处理，特别是运动目标的检测和轨迹预测，共同为决策提供信息支持.

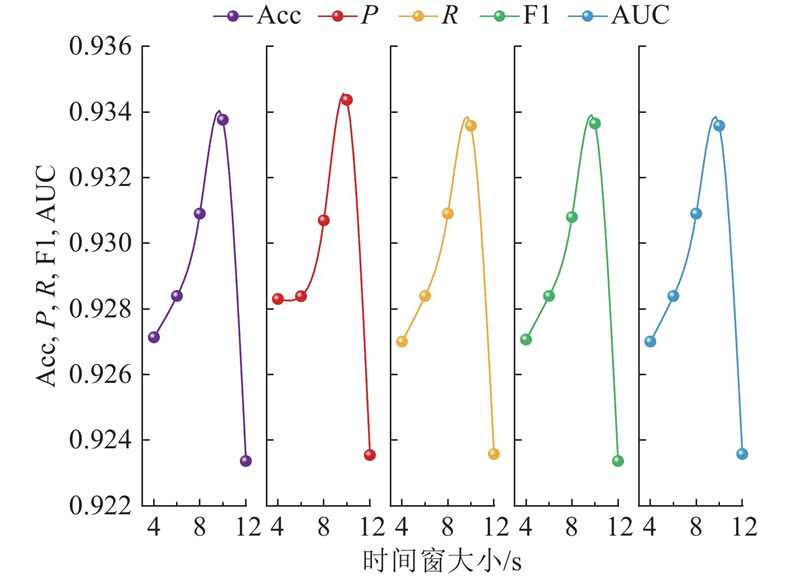
为了验证截取的10 s时间窗对提取脑电信号特征的有效性，分别截取4、6、8、10和12 s时间窗，使用PLV矩阵作为脑功能连接测量矩阵开展对比实验. 衡量模型综合性能的评价指标包括模型分类的准确率Acc、精确度P、召回率R、F₁分数和ROC曲线下面积AUC. 如图7所示，随着时间窗长度的增加，分类性能逐渐提升，当时间窗为10 s时，分类性能达到最优，这说明10 s的时间长度能够较为全面地提取紧急制动过程中EEG的关键特征，有效提升模型对目标模式的识别能力. 时间窗增至12 s后，虽然EEG信息增加，但也将较多与紧急制动无关的冗余信号引入，影响了分类器对关键特征的识别能力，导致分类性能下降.

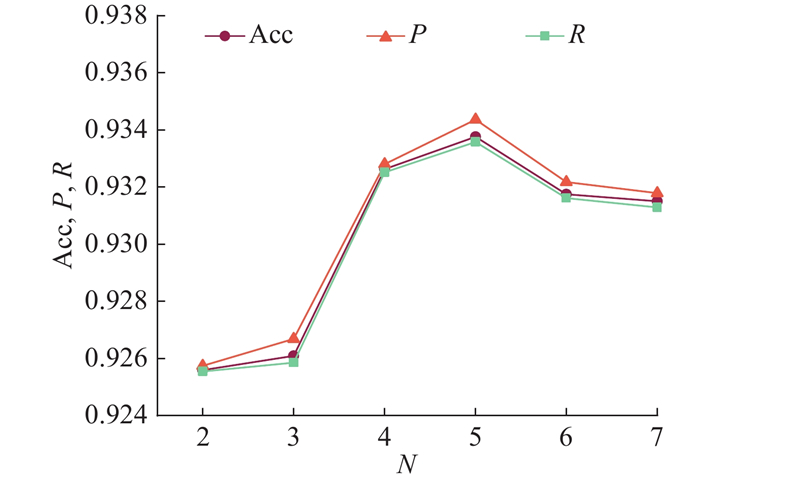
为了验证本研究提出的多尺度卷积对提取脑电信号特征的有效性，设计不同尺度数量的卷积核进行实验验证，使用PLV矩阵作为脑功能连接测量矩阵，结果如图8所示. 可以看到，只有2个尺度的并行卷积核提取的特征得到的分类准确率、F1分数以及召回率最低，模型的分类准确率随卷积核的尺度数量增加而增加，当卷积核的尺度数量到达5时，准确率最高，再次增加卷积核的尺度数量，准确率、F1分数以及召回率都随之降低. 因此，选取5个尺度的卷积核能够充分有效地提取脑电信号特征.

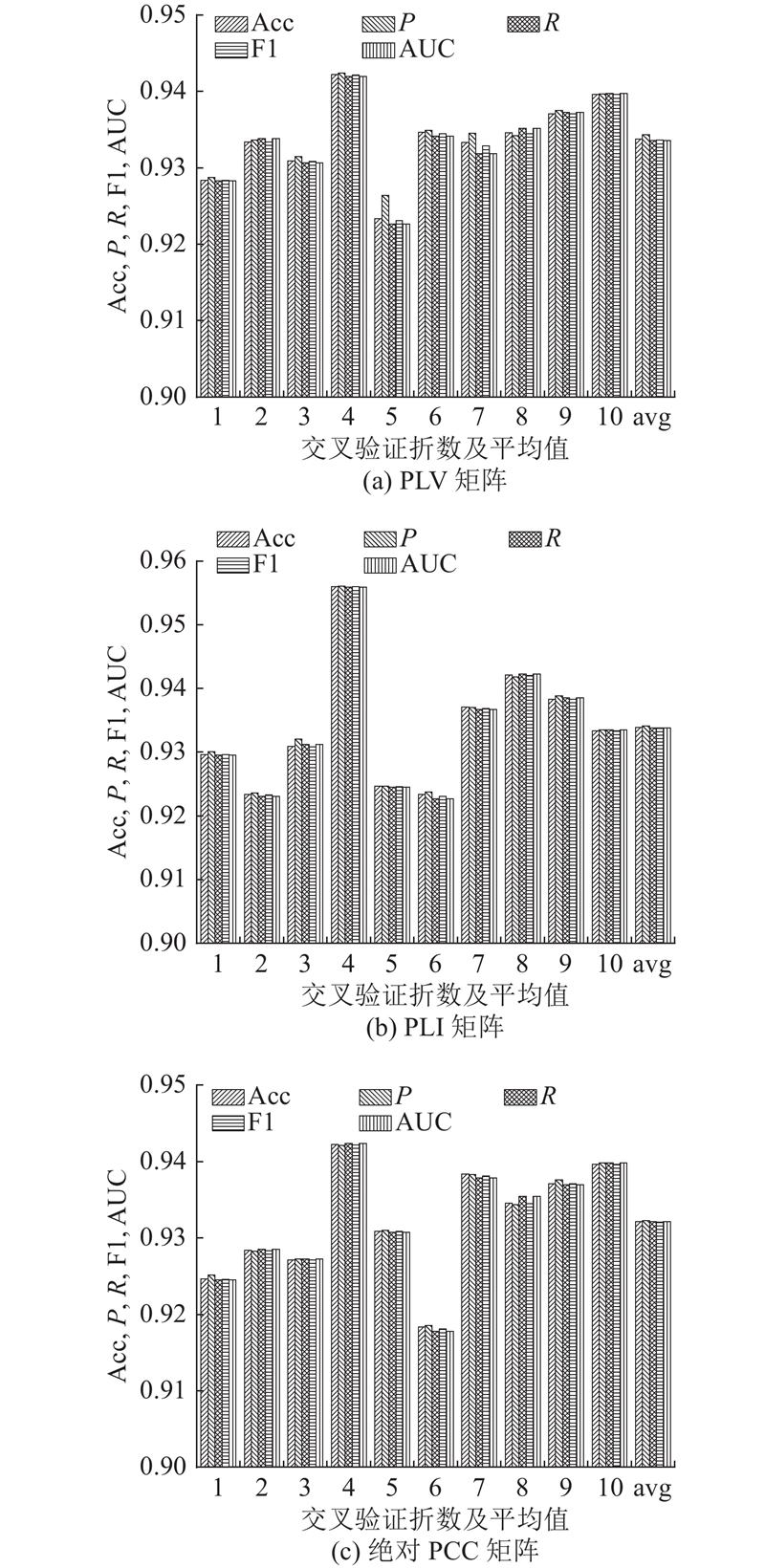
十折交叉验证法将数据集分为10份，为了降低数据划分偶然性，提高模型泛化能力，依次用每份作为验证集训练模型来平均损失评估超参数. 如图9所示为不同矩阵下多被试十折交叉验证结果，平均准确率都超过93.00%，其中PLV的最高准确率为94.22%，最低准确率为92.34%；PLI最高准确率可达95.60%，最低准确率为92.34%；绝对PCC的最高准确率为94.22%，最低准确率为91.83%，不同矩阵准确率波动起伏较小，证明该模型稳定且可靠.

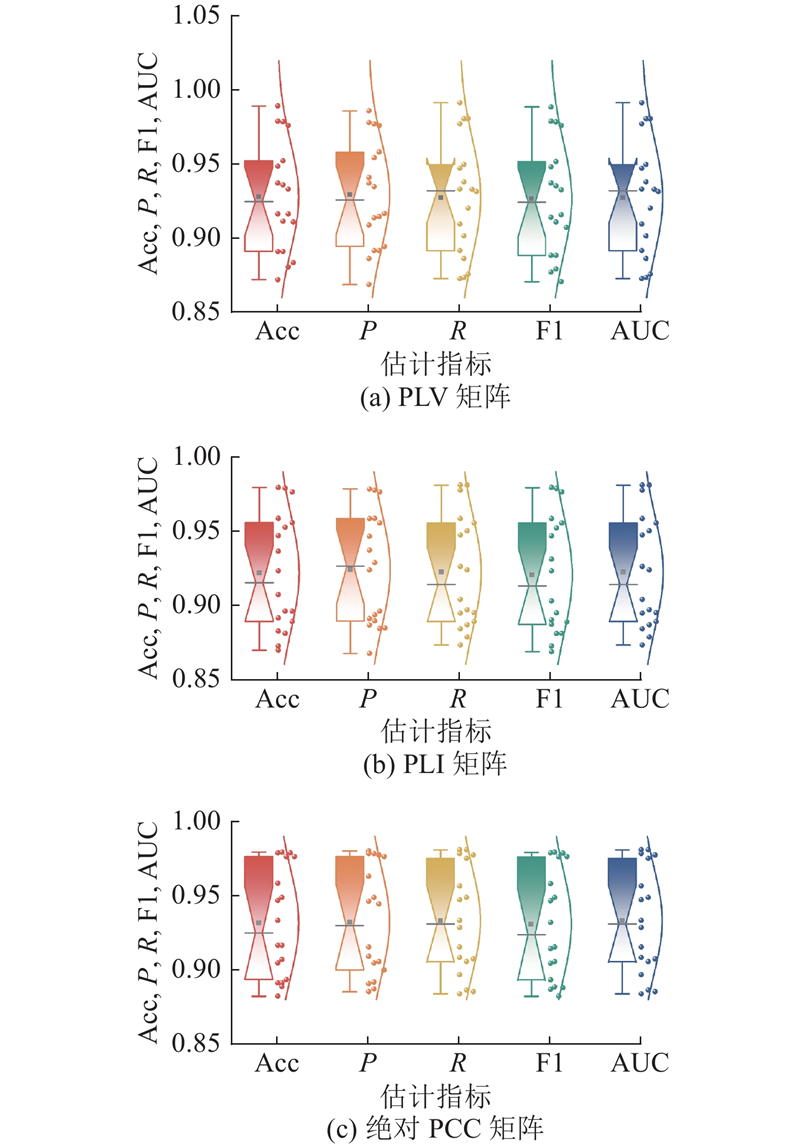
为了进一步验证模型性能，分别对18名被试进行单被试分. 如图10所示为不同矩阵下单被试分类结果，PLV矩阵下的单被试平均准确率为92.82%，其中最高准确率为98.94%、最低准确率为87.23%；PLI矩阵下的单被试平均准确率为92.17%，其中最高准确率为97.92%、最低准确率为86.96%；绝对PCC矩阵下的单被试平均准确率为93.16%，其中最高准确率为97.92%、最低准确率为88.24%. 可以看出，PLV和PLI矩阵下的单被试分类结果差异性较大，绝对PCC矩阵下的单被试分类结果差异性较小，分布比较集中. 原因是PLV和PLI强调的是信号之间的相位同步性，它们在被试间的差异较大，导致更大的分类结果差异，PCC更注重信号的幅度相关性，在不同被试间具有较小的差异性，分类结果的差异性较小.

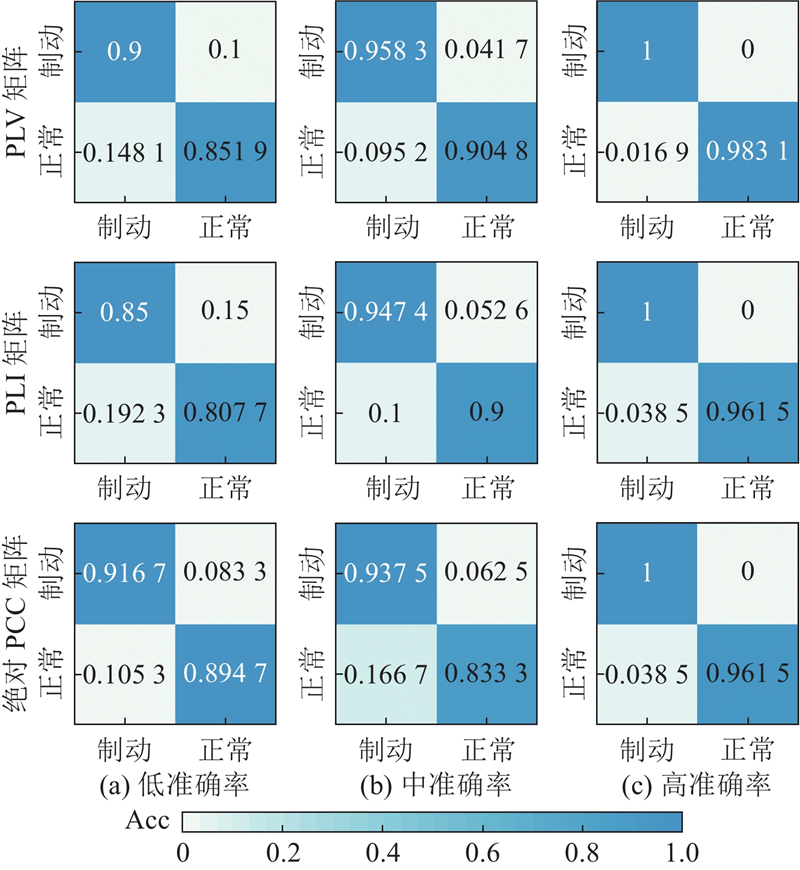
EEG质量受多种因素影响，被试的生理状态如注意力、疲劳程度以及肌肉动作（如咬牙）都会使EEG质量出现差异. 如图11所示，分别挑选准确率最高、最低和中等的被试绘制混淆矩阵. 可以看到，PLV和PLI的结果差异性更大、绝对PCC的更为集中，虽然单被试分类结果有差异，但整体上结果较好，模型具有良好的性能.

为了更好地理解多尺度卷积层以及图卷积神经网络层的单独贡献，通过删除这些模块来进行消融研究，结果如表2所示. 为了研究GCN的贡献，从模型中移除该模块，时间卷积层的输出被按特征重新整形为节点，并传递到MLP进行分类. 为了研究MSC的贡献，从模型中移除该模块，预处理后的脑电数据被直接用作GCN的输入，后传递到MLP. 去除GCN后，准确率下降了0.36个百分点，该结果验证了图卷积神经网络层的有效性；去除MSC后，准确率下降了0.42个百分点，该结果验证了多尺度卷积层的有效性，且多尺度卷积层的贡献大于图卷积神经网络层的贡献.

将所提模型分别与基于CNN、RNN和GNN的脑电信号分类算法进行性能和运行时间t_t对比，结果如表3所示. 其中基于CNN的算法包括EEGNet^[27]和DeepConvNet^[24]，基于RNN的算法为BiRNN^[28]，基于GNN的算法为DGCNN^[29]. 所用数据集均为统一预处理后的脑电数据，为了公平比较，所用参数都为算法提出者建议的最佳参数. 从性能方面看，所提模型分类结果的准确率为93.38%，均优于其他算法，该结果肯定了利用多尺度卷积层能够更加全面地提取脑电信号特征，将其输入图卷积神经网络层也能更好提升分类精度. 虽然所提模型在运行效率上仍有优化空间，但表现比DeepConvNet和BiRNN算法好. 模型较高的复杂度在一定程度上增加了计算成本，从而影响运行效率，但也是提升模型表达能力和分类性能所需付出的代价. 整体来看，所提模型更具优势，未来将进一步优化模型结构，以在保证性能的同时提升运行效率.

为了系统验证模型性能，在Haufe团队发布的驾驶脑电数据集上开展对比研究. Haufe等^[5]提取脑电信号的ERP特征，与线性判别分析相结合，在制动前130 ms实现制动意图检测，但未披露具体分类准确率指标. 袁月婷等^[23]提取EEG的空域特征，分类算法为SVM，分类识别准确率为84%. 本研究所提模型通过多尺度卷积提取EEG不同尺度的特征，并与图卷积神经网络相结合，分类准确率为93.38%，优于对比算法的分类结果.

本研究针对紧急制动和正常驾驶行为提出融合多尺度卷积、脑功能网络和图卷积神经网络的分类模型. 1）利用多尺度卷积对脑电信号进行特征提取，充分挖掘信号的时频特性；2）采用脑功能网络，充分整合脑区间的连接特征，增强模型对空间和时间依赖的学习能力；3）将脑电特征、脑功能网络拓扑结构与图卷积神经网络相结合，利用非欧几里得结构的建模能力，显著提高分类性能. 所提模型多被试分类准确率最高为95.60%，单被试下的最高准确率为98.94%；消融实验结果表明，多尺度卷积模块和图卷积神经网络模块都有突出贡献，多尺度卷积的贡献高于图卷积神经网络. 研究结果不仅证明了所提模型对紧急制动行为脑电信号分类识别的有效性，也对基于脑电信号的智能辅助驾驶紧急制动意图预测模型的开发提供了参考. 尽管该模型在实验室环境下的数据集上的分类效果良好，但未考虑真实驾驶环境下的数据集. 对于真实环境下数据质量低、易受环境干扰问题，未来计划采用关键脑区的电极，提高可穿戴性，引入多模态数据，将刹车信号、油门/刹车力度、眼动追踪等数据相结合，增强模型对复杂驾驶环境的适应能力.