在船舶工程领域,由金属材料制造的螺旋桨重量较大,导致轴系负荷较重,且容易引发轴系及船体振动. 螺旋桨的轻量化设计一直是船舶推进技术的重点发展方向. 近年来,鉴于聚甲醛、碳纤维等轻质材料具有轻量化、高强度、抗腐蚀等性能优势,逐步被用作船舶螺旋桨的加工材料. 由此类材料制造的螺旋桨常在流体载荷作用下发生不可忽略的弹性形变,对螺旋桨的水动力性能、振动噪声性能均产生了较大影响. 因此,在弹性螺旋桨的设计过程中必须考虑形变作用,提前明确桨变形模式、幅度与叶片动态载荷的关系.
国内外学者针对弹性螺旋桨的结构变形规律已经开展了大量研究,在优化设计方面取得了一定进展. 李子如等[1]研究发现在非均匀来流中,正交各向异性的碳纤维桨叶在高伴流区域、叶梢和导边区域的结构变形较大. Young[2]基于边界元(boundary element method, BEM)/有限元(finite element method, FEM)流固耦合方法研究复合材料螺旋桨的水动力性能,结果表明在设计工况下变形后的螺旋桨效率高于未产生变形的螺旋桨. 何朋朋[3]采用计算流体力学(computational fluid dynamics, CFD)/有限元流固耦合方法研究发现,相比于刚性桨,树脂桨在低进速系数、重负荷条件下的桨叶螺距、推力系数和扭矩系数有一定增加. 李雪芹等[4]根据叶片厚度和载荷分布将螺旋桨叶片划分为4个区域,按照不同铺层角度铺设碳纤维,从而增加叶片结构刚度,有效减小了结构变形. 洪毅等[5]采用预变形策略使树脂基纤维桨叶的水动力性能提升至与金属螺旋桨的设计值基本一致,证明了预变形策略的可行性. Zhang等[6]分析发现增大弹性模量或剪切模量会提高推进效率,减小桨叶变形,并总结了用于选择DTNSRDC
当前有关弹性螺旋桨非定常力特性的研究相对较少,仍然需要深入揭示桨变形模式、幅度与叶片动态载荷的关系. 王玮等[7]对比发现材料的弹性模量和刚度阻尼的增大会引起一阶叶频处轴向非定常力脉动幅值降低,而对质量阻尼并无明显影响. 武兴伟等[8]研究发现当激励频率接近于弹性螺旋桨的一阶固有频率时,弹性效应会显著放大纵向激励力. 丁永乐等[9]分析得出均匀来流下弹性螺旋桨的桨叶振动频率主要受前二阶湿模态频率的影响,非定常流场负载频率的影响次之. Zou等[10]建立流体-螺旋桨-轴系-轴承系统的动力学模型,发现螺旋桨和轴系的弹性效应改变了水母模态的频率,而对非水母模态的影响较小. 姜宜辰等[11]研究发现螺旋桨的弹性效应对不同方向上的噪声影响不同,并且会带来整体噪声的指向性变化.
由于桨叶动态载荷与非定常激励力是引发船舶轴系与壳体振动的重要激励因素,面向弹性螺旋桨的深入应用,亟需对弹性螺旋桨变形特性及其与激励力的关联进行进一步的研究. 采用CFD/FEM流固耦合方法,研究弹性螺旋桨在不同伴流场下的结构变形规律;通过对比刚性和弹性螺旋桨激励力特性,分析稳态变形和动态变形对激励力的时均值和脉动值的影响,从而揭示弹性螺旋桨结构变形对激励力的调控机制. 本研究旨在为船舶推进系统的振动噪声控制提供理论依据,期望对弹性螺旋桨的工程应用形成支撑.
1. 基本模型说明
1.1. 流固耦合控制方程
弹性螺旋桨在旋转过程中受到流体载荷的作用,会产生几何非线性的结构变形,因此采用流固耦合(fluid-structure interaction, FSI)计算方法模拟流体域与固体域的相互作用,以准确求解弹性桨叶的结构变形以及激励力特性.
流固耦合计算区域分为流体域和固体域,固体域在外力作用下会发生结构变形,动力学控制方程为
式中:u(t)为t时刻结构体的节点位移,Ms为结构体的质量矩阵,Cs为结构体的阻尼矩阵,Ks为结构体的刚度矩阵,Fext(t)为t时刻系统所受的外载荷向量.
在进行水弹性分析时,为了简化问题,不考虑轴系力、重力等外力,将弹性螺旋桨整体看作1个完整系统,其所受外力可以分为3部分:
式中:Ff为流体作用力,Fcent为离心力,Fcori为科氏力.
当流体黏性不可忽略时,流体作用力可以进一步分解为正压力和剪切力的积分:
式中:S为物体表面积;p为流体作用在物体表面的压力,τ为剪切力,在后续数值模拟中可以求解两者并传递至固体域,进行流固耦合交界面的数据交换;n和t分别为流固耦合表面的法向和切向向量.
在流固耦合理论中,为了体现流体对结构运动的影响,以便于分析弹性螺旋桨的非稳态响应,式(1)通常表示为
式中:Mf为附加质量矩阵,Cf为附加阻尼矩阵.
上述动力学方程描述了弹性螺旋桨在流体载荷作用下的结构变形特性,为后续采用数值模拟方法对弹性螺旋桨进行流固耦合求解奠定了理论基础.
1.2. 计算模型与参数设置
1.2.1. 几何模型
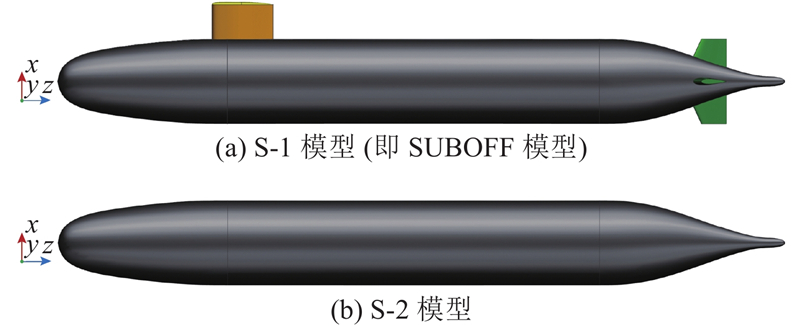
螺旋桨在船尾的非均匀伴流条件下会产生显著的非定常激励力. 以标准模型SUBOFF为船体对象,其总长L =
图 1
图 1 不同附体的航行体几何模型
Fig.1 Submarine vehicle geometric models with different appendages
图 2
为了研究复合材料螺旋桨的弹性变形特征,采用各向同性的聚甲醛(polyoxymethylene, POM)材料作为螺旋桨材料,以研究螺旋桨变形模式、变形特征对激励力的影响规律. 相比于传统金属材料镍铝青铜(nickel aluminium bronze, NAB),其密度明显降低. 2种材料的属性如表1所示,其中ρ为密度,E为弹性模量,μ为泊松比.
1.2.2. 数值模型
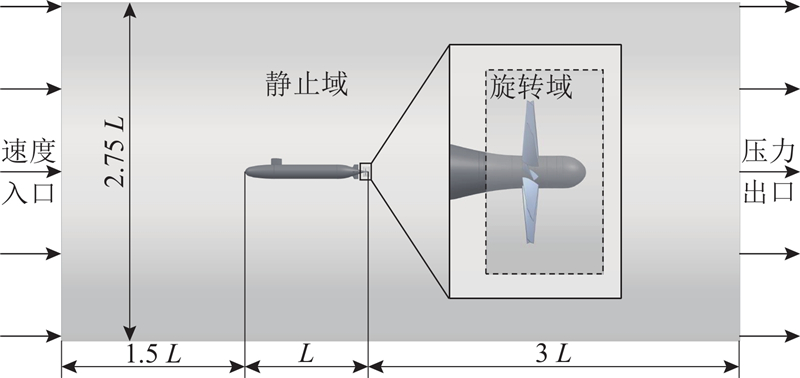
基于前述几何模型,通过建立包含流体域和固体域的数值模型,结合计算流体力学和有限元法实现流固耦合求解,旨在研究不同伴流条件下弹性螺旋桨的激励力和结构变形. 基于STAR CCM+计算平台对航行体-螺旋桨一体化组合模型进行数值模拟,建立如图3所示的圆柱体计算域. 其中,L为SUBOFF模型的长度,入口与航行体头部的距离为1.5L,出口与航行体尾部的距离为3L,计算域的直径为2.75L. 在边界条件设置方面,将来流入口设置为速度入口,出口设置为压力出口.
图 3
图 3 航行体-螺旋桨组合模型的计算域
Fig.3 Computational domain of vehicle-propeller combined model
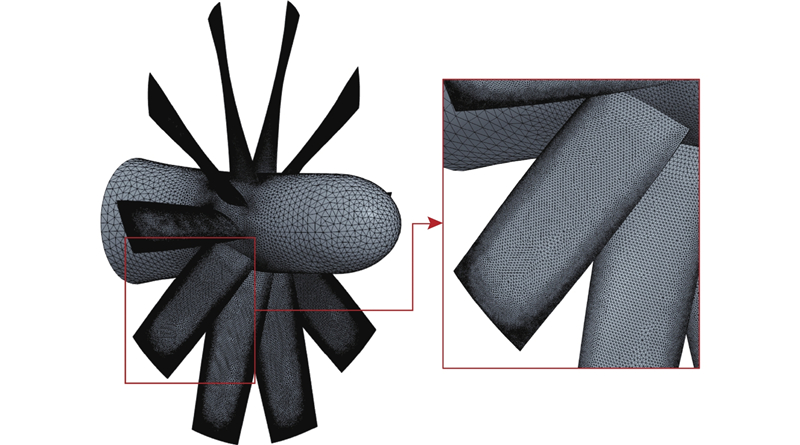
流体域分为静止域和旋转域2个部分,静止域采用切割体网格,而旋转域的网格形式为多面体网格. 为了精细模拟航行体表面的流动特征,使用棱柱层网格划分航行体和螺旋桨表面的边界层网格,保证大部分壁面y+在30~60内. 同时对航行体的围壳区域和螺旋桨的尾流区域进行逐级局部加密,以兼顾计算精度与网格量需求. 流体域网格数合计6.64×106,包括静止域5.34×106,旋转域1.30×106. 流体域网格划分示意图如图4所示.
图 4
固体域采用四面体网格,该网格形式适用于复杂几何结构,能够有效避免网格畸变,并提升计算稳定性. 此外,在螺旋桨叶片边缘区域进一步加密网格,以提高结构响应的计算精度. 固体域网格数为1.50×106,表面网格如图5所示.
图 5
基于上述网格划分方式,对流体域和固体域的求解方法、求解器等进行合理设置. 对于流体域,使用RANS(Reynolds-averaged Navier-Stokes)方法并结合SST k-ω湍流模型对航行体流场及螺旋桨激励力进行数值模拟计算;对于固体域,采用有限元方法计算弹性螺旋桨在流体载荷作用下的结构变形. 流体域与固体域之间的数据传递通过流体结构耦合求解器实现. 在流固耦合交界面上,流体域的载荷即压力p和壁面剪切应力τ通过积分传递至固体域的表面节点,固体域的位移u通过径向基函数(radial basis function, RBF)插值传递回流场,驱动流体域网格变形. 为了准确捕捉螺旋桨的非定常特性,采用隐式非稳态的求解器并结合滑移网格技术进行瞬态计算,以提取螺旋桨的非定常力.
2. 数值模拟方法验证
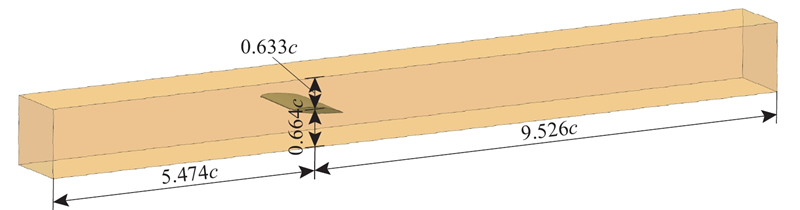
在非均匀伴流条件下,弹性螺旋桨的试验数据难以获取且公开试验数据匮乏,导致直接验证其流固耦合数值模拟结果的可靠性存在困难. 因此,基于弹性水翼的公开试验展开流固耦合数值模拟方法的验证,通过对比弹性水翼的试验数据与模拟结果,验证本研究所采用的流固耦合计算方法的有效性. 尽管水翼与螺旋桨的几何特征和流场特征存在差异,但是两者在流体载荷传递、结构变形计算等核心物理过程上具有一致性,可以为螺旋桨的数值模拟提供可信度支撑.
图 6
图 7
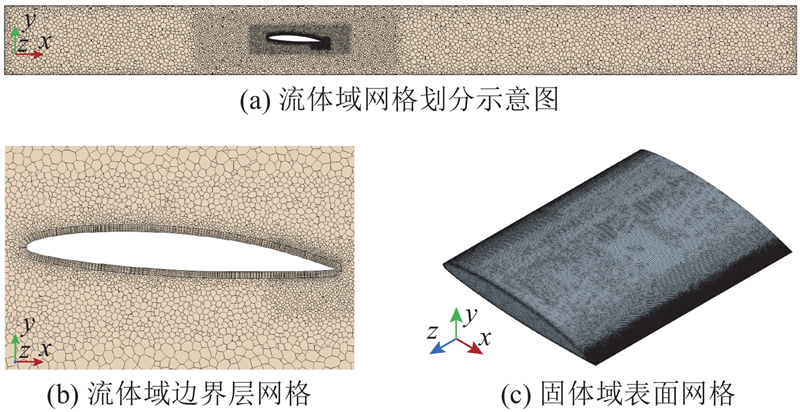
图 7 水翼计算域网格划分示意图
Fig.7 Schematic diagram of hydrofoil computational domain meshing
表 2 水翼升力系数的计算值与试验值
Tab.2
| 数据来源 | CL | θ/(°) | |
| 刚性水翼 | 弹性水翼 | ||
| 试验测量 | 1.065 | 1.18 | −0.39 |
| 数值模拟 | 1.078 | 1.13 | −0.37 |
| 误差/% | 1.22 | 4.24 | 5.13 |
式中:L为水翼升力,
图 8
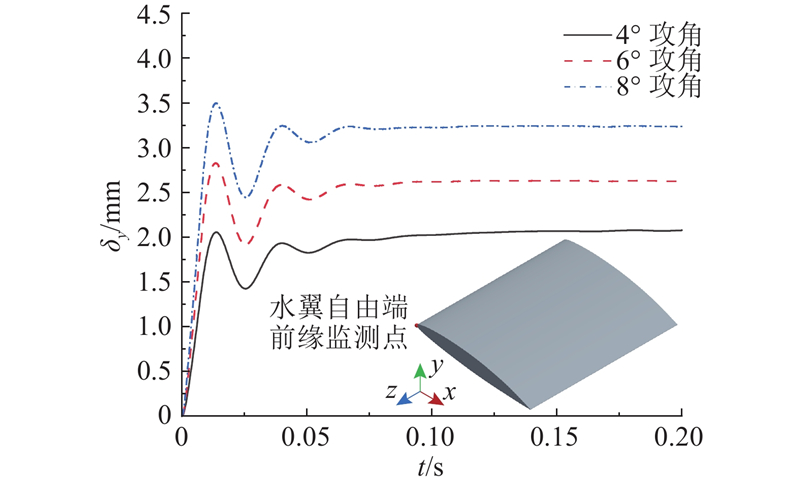
图 8 弹性水翼垂向位移时域图
Fig.8 Time-domain diagram of vertical displacement of elastic hydrofoil
图 9
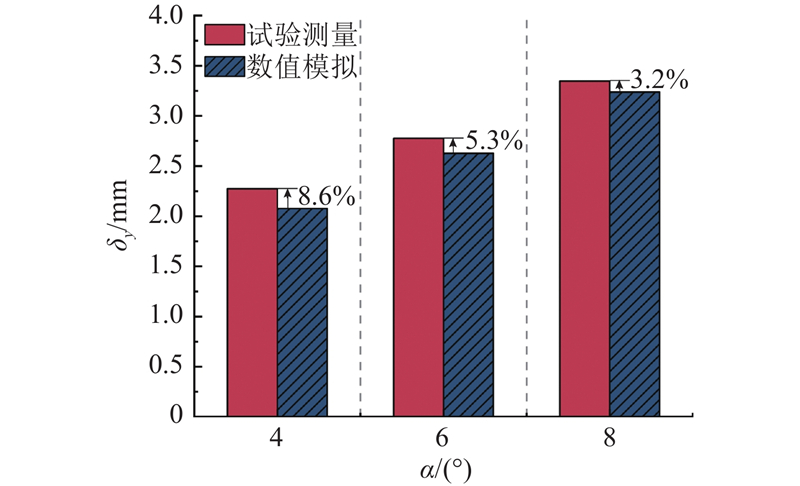
图 9 弹性水翼垂向位移计算值与试验值
Fig.9 Calculated and experimental values of vertical displacement of elastic hydrofoil
3. 数值结果分析
采用已建立的数值模型和数值模拟方法,通过对航行体尾流中的弹性螺旋桨开展流固耦合计算,量化均匀与非均匀伴流场下周期性激励差异,分离并总结稳态、动态变形的时空特征,明确两者对轴向激励力的影响.
3.1. 伴流场特性
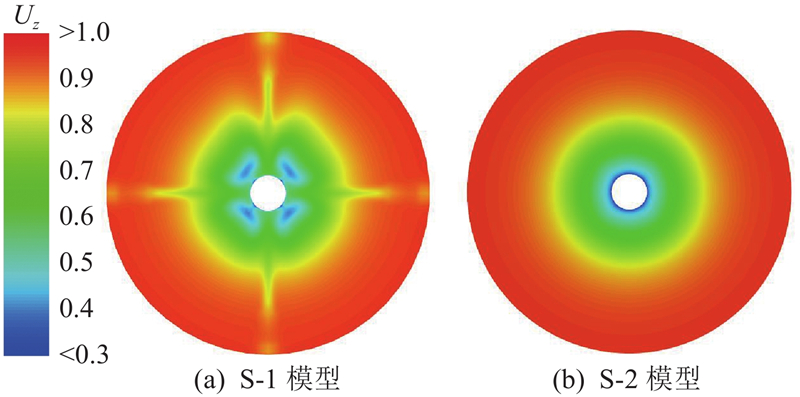
由于螺旋桨单叶片受力波动与变形波动主要由不均匀来流激励引起,而附体结构及边界层是引起航行体尾部伴流不均匀性的主要原因,为了便于后续螺旋桨结构变形和激励力研究,对S-1和S-2模型的伴流场进行谐调分析. 参照1.2.2节,设置来流速度为6.096 m/s,对2个航行体模型进行定常计算. 在桨盘面处以直径为D的截面提取速度值,如图10所示,其中Uz为归一化轴向速度. S-1模型的伴流场呈现明显的不均匀分布,存在4个速度亏损区域;由于垂向方向上同时存在围壳和艉舵,该方向上的速度亏损最为明显. S-2模型的伴流场周向分布均匀. 此外,S-1模型截面处的平均轴向速度为5.16 m/s,S-2模型的平均轴向速度更高,为5.31 m/s. 结果表明,航行体附体对后方伴流场的不均匀分布有着明显影响,且会导致伴流场速度减小.
图 10
图 10 桨盘面处无量纲轴向速度云图
Fig.10 Non-dimensional axial velocity contour at propeller disk plane
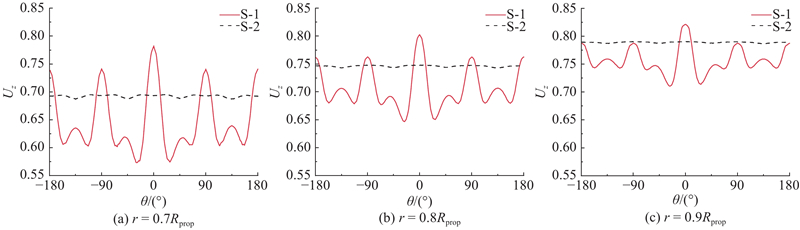
为了更好地分析螺旋桨的来流特性,提取桨盘面处半径r = 0.7Rprop、0.8Rprop、0.9Rprop的圆周上不同航行体无量纲轴向速度的周向分布,如图11所示,其中θ为所在位置的周向角度. 可以看出,桨盘面不同半径处的速度分布相似. 对于S-1模型,在不同半径的圆周上,4个舵的后方均存在4个明显的波峰,其中位于0°围壳后方的波峰最为显著. 对于S-2模型,由于周向网格差异速度存在微小局部波动,无明显的波峰与波谷,周向不均匀度较小.
图 11
图 11 桨盘面处无量纲轴向速度的周向分布图
Fig.11 Circumferential distribution diagram of non-dimensional axial velocity at propeller disk plane
为了定量表征航行体尾流伴流的周期成分及幅值,对桨盘面的轴向速度进行谐调分析. 在r = 0.7Rprop、0.8Rprop、0.9Rprop处各取360个均匀分布的点,假设不同半径的圆周上的速度分布由不同阶次的谐调分量叠加而成:
式中:v(r, θ)为螺旋桨盘面处任意位置的速度,r和θ分别为径向位置和周向角度,
对比不同伴流场的各阶谐调分量A,如图12所示. S-1模型的谐调分量集中在4、8等阶数,S-2模型的谐调分量无明显规律,且各阶分量均明显小于S-1模型.
图 12
综上所述,S-1模型的伴流场存在明显的周期性流体载荷波动,而S-2模型伴流场的流体载荷波动微小.
3.2. 不同伴流场下弹性螺旋桨的结构变形
采用流固耦合计算方法对比不同伴流场下弹性螺旋桨的结构变形特性,并分别探讨稳态变形与动态变形的规律.
3.2.1. 弹性螺旋桨的动态变形特性
为了研究弹性螺旋桨运行过程中的结构变形特性,对弹性螺旋桨的位移进行监测与分析. 将S-1、S-2航行体模型与POM材料的弹性螺旋桨进行匹配,由此构建的航行体-螺旋桨一体化组合模型被分别命名为S-1-elastic模型和S-2-elastic模型.
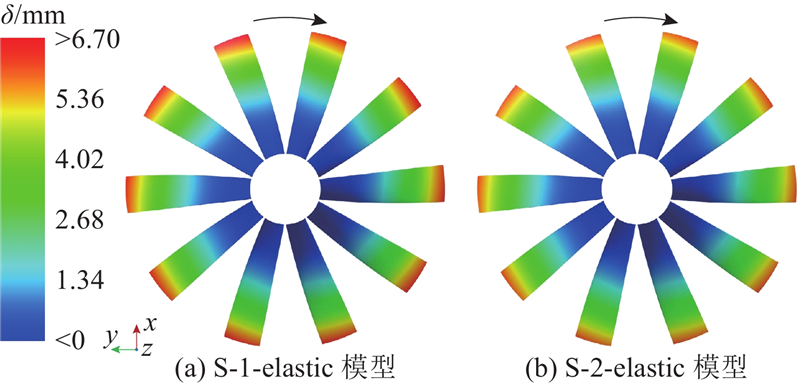
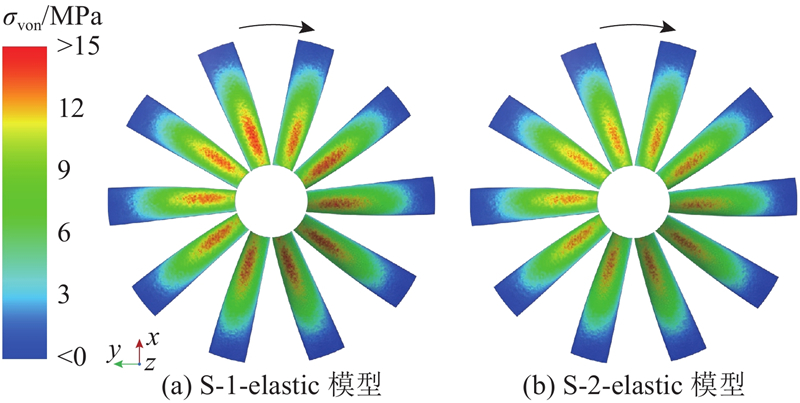
为了直观呈现弹性螺旋桨结构变形的分布情况,绘制第150圈时计算收敛后弹性螺旋桨的总位移云图,如图13所示. S-1-elastic和S-2-elastic模型的弹性螺旋桨的形变分布特征基本一致;随着半径的增加,弹性螺旋桨位移δ增大,在叶梢处达到最大值,且前缘位移更大. S-1-elastic模型的最大位移量为6.70 mm,为螺旋桨直径的2.65%;S-2-elastic模型最大位移量为6.15 mm,为螺旋桨直径的2.43%. 对比不同伴流场下弹性螺旋桨的位移情况,S-1-elastic模型的位移值比S-2-elastic模型大8.9%,表明伴流场对螺旋桨结构变形的大小有一定影响. 由于S-1模型中附体的存在导致螺旋桨作用区域的轴向平均速度相对较小,S-1-elastic模型的螺旋桨最大位移略大于S-2-elastic模型. 从图14的应力云图可以看出,弹性螺旋桨等效应力σvon在叶片中低半径处的中间位置达到最大,从中间逐渐向四周递减,在叶梢处达到最小值. S-1-elastic模型的最大等效应力为15.94 MPa,S-2-elastic模型的最大等效应力为14.95 MPa,两者的最大等效应力值接近.
图 13
图 14
图 14 弹性螺旋桨等效应力云图
Fig.14 Equivalent stress contour diagram of elastic propeller
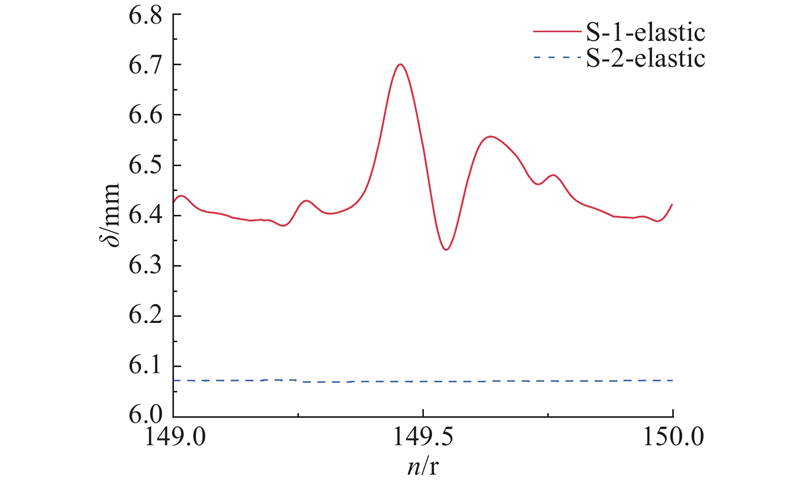
为了详细分析弹性螺旋桨结构变形的时域特性,对弹性螺旋桨单叶片的最大位移进行监测,选取计算稳定时旋转圈数n=149~150的结果呈现,如图15所示. 结果显示,在不均匀伴流场下的弹性螺旋桨叶片位移呈现明显的周期性波动,而周向均匀伴流场下的螺旋桨位移呈均匀分布,表明不均匀伴流场是弹性螺旋桨动态变形的主要激励源.
图 15
图 15 149~150圈螺旋桨位移时域图
Fig.15 Time-domain diagram of propeller displacement from 149 to 150 revolutions
根据上述叶片结构变形规律分析,结合3.1节中S-1和S-2模型的伴流场分布特性,将弹性螺旋桨的结构变形视为稳态变形和动态变形共同叠加的结果. 其中,稳态变形是螺旋桨在时均流体载荷作用下产生的,表现为螺旋桨的平均变形状态;动态变形由非定常脉动载荷诱发,表现为围绕稳态变形的周期性波动变形状态.
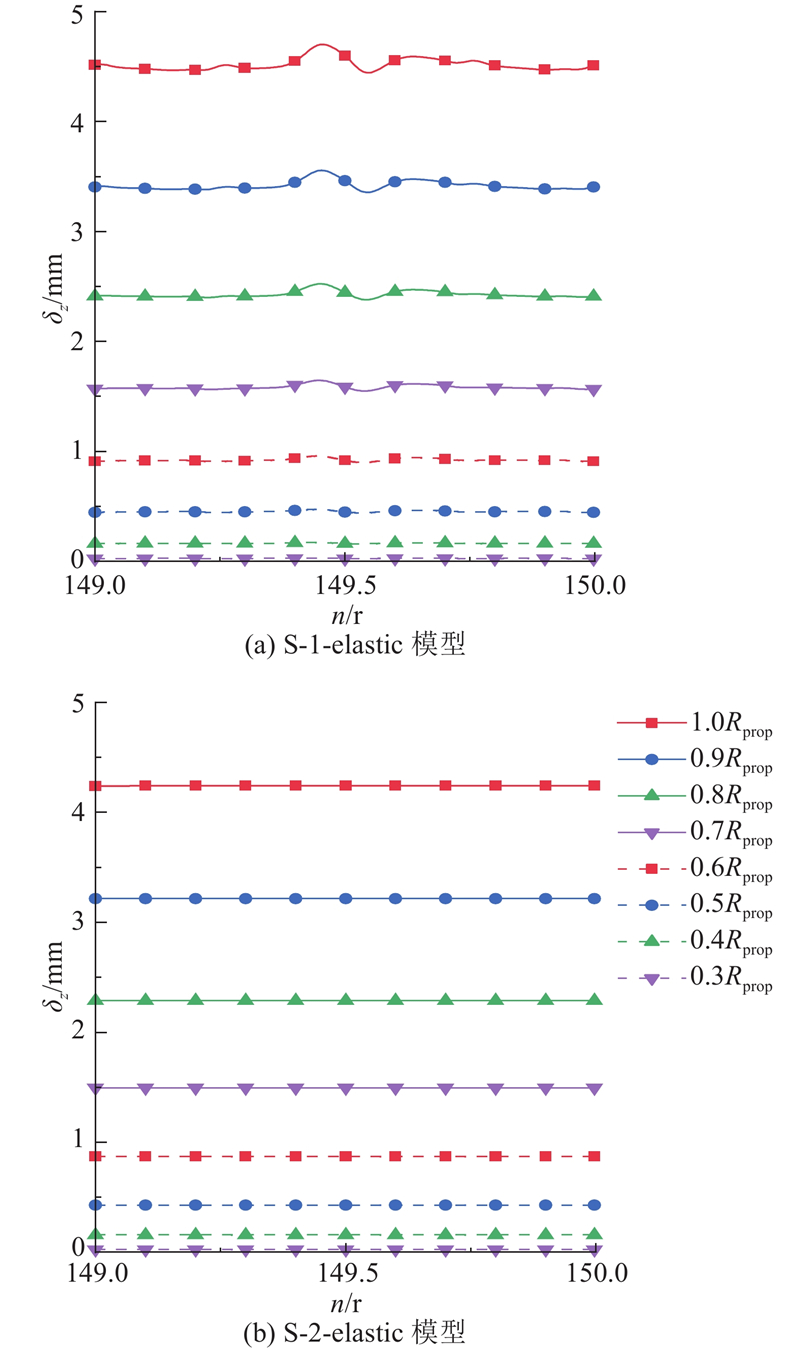
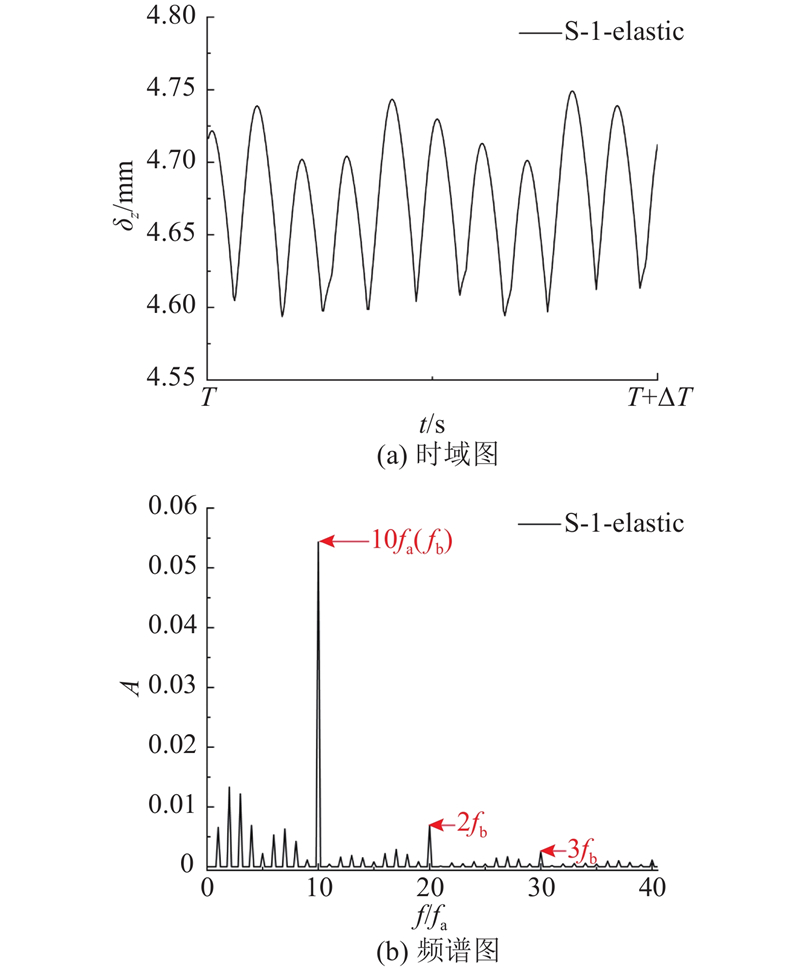
为了进一步研究弹性螺旋桨的动态变形情况,在叶片的0.25Rprop~1.00Rprop半径处的前缘和后缘布置监测点并获取位移数据,结构变形监测点位置如图16所示. 对螺旋桨旋转1圈的过程中不同半径处前缘监测点的轴向位移δz数据进行分析,如图17所示. 对于S-1-elastic模型,不同半径处的轴向位移均表现出周期性波动,尤其在高半径区域的波动更加明显. 其中叶梢部位(r = 1.0Rprop)前缘轴向位移的波峰值为4.70 mm,占螺旋桨直径的1.86%,波谷值为4.44 mm;经计算得到轴向位移波动幅值为0.26 mm,占螺旋桨直径的0.10%. 波动特征呈现1个大波峰和3个小波峰,这是由于围壳和艉舵的存在使伴流场呈现周向不均匀性,从而诱发了弹性螺旋桨叶片位移的周期性波动. 对于S-2-elastic模型,叶片不同半径处的轴向位移均无明显波动,表现为水平线,这是因为伴流场分布均匀,使螺旋桨叶片的位移波动微小,动态变形可以忽略不计. 上述分析表明弹性螺旋桨的动态变形受伴流场脉动载荷的影响.
图 16
图 16 结构变形监测点位置示意图
Fig.16 Schematic of structural deformation monitoring point locations
图 17
图 17 149~150圈前缘监测点位移时域图
Fig.17 Time-domain diagram of displacement at leading-edge monitoring points from 149 to 150 revolutions
3.2.2. 弹性螺旋桨的稳态变形特性
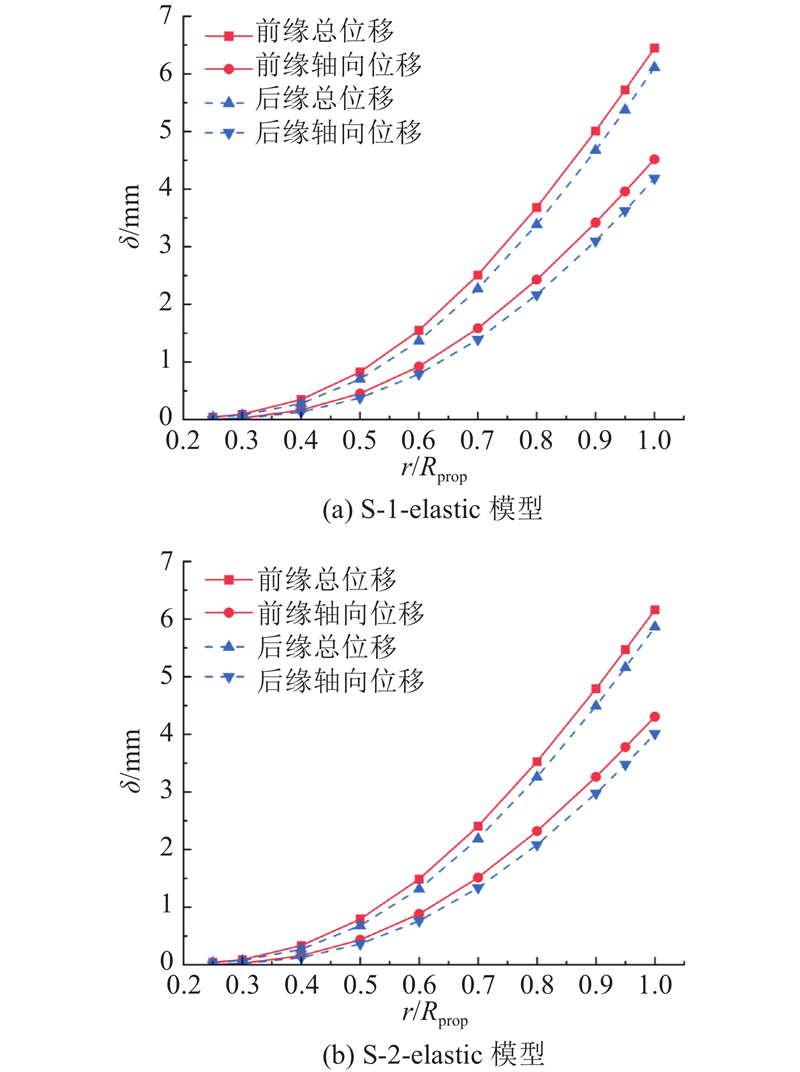
为了研究弹性螺旋桨的稳态变形,对位移数据进行时均处理,获得不同半径处螺旋桨叶片的稳态变形数据,如图18所示. 根据计算结果,S-1-elastic模型的叶梢部位前缘轴向位移为4.52 mm,占螺旋桨直径的1.79%. 分析发现叶片总位移和轴向位移均随半径的增大呈上升趋势,且增长速率逐渐加快. 总位移由x、y、z轴的位移共同组成,其中z轴方向的位移即轴向位移. S-1-elastic和S-2-elastic模型的弹性螺旋桨叶梢部位前缘轴向位移分别占总位移的70.07%和69.88%,其他半径处也呈现轴向位移占总位移较大比例的特征,因此轴向变形是螺旋桨稳态变形的主要表现形式. 此外,在S-1-elastic和S-2-elastic模型中,同一半径处叶片前缘位移均大于后缘位移,形成叶片的扭转,从而引起螺距角的变化. 鉴于螺距角对螺旋桨水动力性能的重要作用,后续对叶片各半径位置的螺距角展开分析.
图 18
图 18 弹性螺旋桨叶片前缘与后缘的时均位移分布
Fig.18 Time-averaged displacement distribution at leading and trailing edges of elastic propeller blade
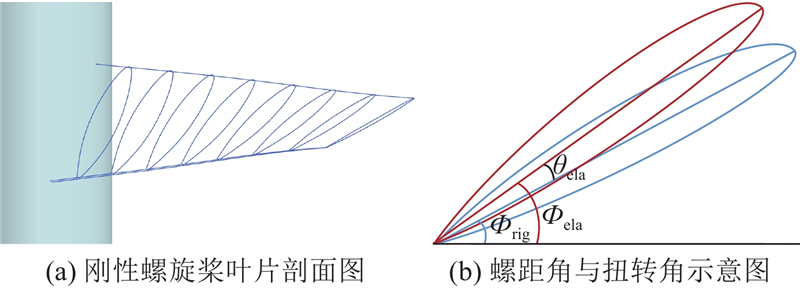
图 19
图 19 螺旋桨螺距角与扭转角的关系示意图
Fig.19 Schematic of relationship between pitch angle and twist angle of propeller
表 3 不同半径处螺旋桨的螺距角及扭转角
Tab.3
| r/Rprop | Φrig/(°) | θS-1/(°) | θS-2/(°) |
| 0.3 | 55.855 | 0.039 | 0.037 |
| 0.4 | 50.086 | 0.119 | 0.111 |
| 0.5 | 44.699 | 0.212 | 0.197 |
| 0.6 | 39.274 | 0.318 | 0.294 |
| 0.7 | 33.881 | 0.530 | 0.482 |
| 0.8 | 28.881 | 0.867 | 0.831 |
| 0.9 | 24.699 | 0.614 | 0.552 |
| 1.0 | 21.654 | 0.620 | 0.548 |
综上所述,研究了不同伴流场条件下弹性螺旋桨的结构变形特性. 结果表明,伴流场通过时均载荷与脉动载荷的作用,分别驱动弹性螺旋桨发生稳态与动态变形. 这一结论为后续分析弹性螺旋桨的流致激励力形成机理提供了关键依据.
3.3. 弹性螺旋桨结构变形对激励力的影响
基于不同伴流场中弹性螺旋桨的结构变形特征分析,通过对刚性和弹性螺旋桨激励力特性的对比,阐明稳态变形与动态变形分别对轴向激励力时均值与脉动值的影响,从而揭示弹性螺旋桨结构变形对激励力的调控机制.
3.3.1. 稳态变形对激励力时均值的影响
基于3.2.2节,进一步研究由时均载荷引发的稳态变形对流致激励力时均值的影响. 将S-1、S-2航行体与刚性螺旋桨进行匹配,并将航行体-螺旋桨一体化组合模型分别命名为S-1-rigid模型和S-2-rigid模型.
为了探讨螺旋桨稳态变形对激励力时均值的影响,对比分析同一伴流场条件下刚性和弹性螺旋桨的激励力,如表4所示. 其中Fx为横向力,Fy为垂向力,Fz为轴向力,T为转矩. S-1模型中弹性螺旋桨的轴向力时均值比刚性螺旋桨增大了9.5%,转矩增大了10.8%;S-2模型中的弹性螺旋桨也具备相似特征. 结果表明,弹性螺旋桨的轴向力和转矩均比刚性螺旋桨大.
表 4 不同模型中螺旋桨激励力时均值
Tab.4
| 模型 | Fx/N | Fy/N | Fz/N | T/(N·m) |
| S-1-elastic | 0.166 | 0.557 | 507.3 | 29.7 |
| S-1-rigid | 0.160 | 0.420 | 463.3 | 26.8 |
| S-2-elastic | − | 486.5 | 28.8 | |
| S-2-rigid | − | 459.6 | 26.6 |
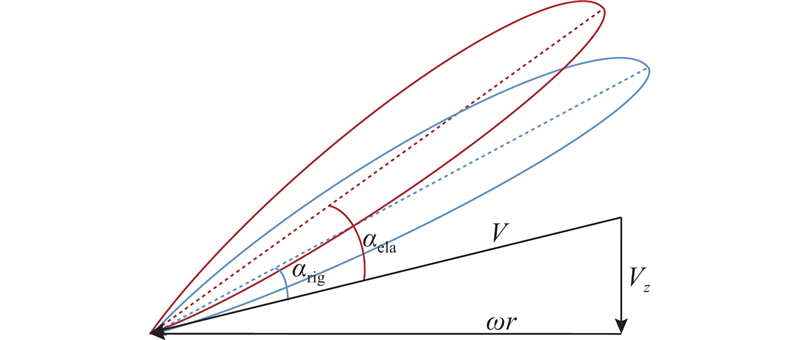
根据叶片速度三角形原理,当切向速度ωr(ω为角速度)和轴向速度Vz相同时,若螺距角增大,则合速度与叶片的攻角α增大,叶片受力也就越大,如图20所示. 结合3.2节中的分析,弹性螺旋桨稳态变形中存在螺距角增大的现象,由此可以得出弹性螺旋桨稳态变形会增大激励力时均值的结论.
图 20
综上所述,研究了稳态变形对弹性螺旋桨激励力时均值的影响. 结果表明,弹性螺旋桨稳态变形中螺距角的增大引起攻角增大,从而使轴向力时均值上升.
3.3.2. 动态变形对激励力脉动值的影响
进一步研究由脉动载荷引发的动态变形对流致激励力脉动值的影响. 由于S-2伴流场中流体载荷波动微小,S-2模型中弹性螺旋桨的动态变形可以被忽略,因此仅对S-1伴流场中弹性螺旋桨动态变形对激励力非定常特性的影响展开研究.
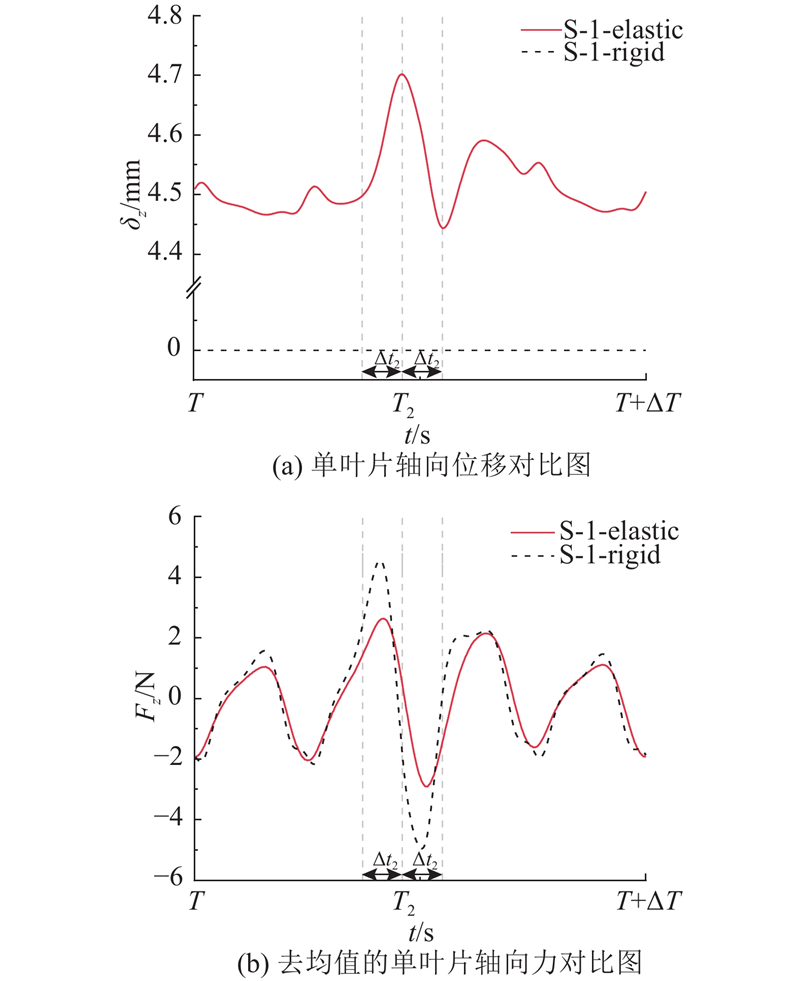
为了分析弹性螺旋桨动态变形对激励力脉动值的影响,首先对单叶片的轴向位移及轴向力的关系进行研究. 图21(a)展示了螺旋桨旋转1圈的时间内叶片轴向位移随时间的变化,其中T2为弹性螺旋桨单叶片的轴向位移到达最大值的时刻,T2+Δt2为轴向位移达到最小值的时刻,ΔT为螺旋桨旋转1圈的时长. 为了便于比较同一时间区间内刚性和弹性螺旋桨单叶片轴向力的波动幅值,分别对两者进行去均值处理,结果如图21(b)所示. 观察到弹性螺旋桨的单叶片轴向力波动幅值更小,针对最大波峰和波谷处的单叶片轴向力的区别展开分析并揭示原因. 在(T2−Δt2)~T2内,弹性螺旋桨叶片变形增大,其吸收部分流体载荷能量并储存为弹性势能,抑制轴向力的增长趋势,因此弹性螺旋桨的轴向力峰值低于刚性螺旋桨. 在T2~(T2+Δt2),弹性螺旋桨叶片变形减小,之前储存的弹性势能逐步释放,从而减缓了轴向力的降低速度,使得弹性螺旋桨轴向力谷值高于刚性螺旋桨. 上述分析表明,弹性螺旋桨的动态变形通过吸收伴流激励能量或释放储存的弹性势能实现缓冲,能够降低轴向力波动幅值. 而刚性螺旋桨来流激励能量直接作用在叶片上,呈现出更强的轴向力脉动.
图 21
图 21 动态变形对单叶片轴向力波动幅度的影响
Fig.21 Effect of dynamic deformation on fluctuation amplitude of single-blade axial force
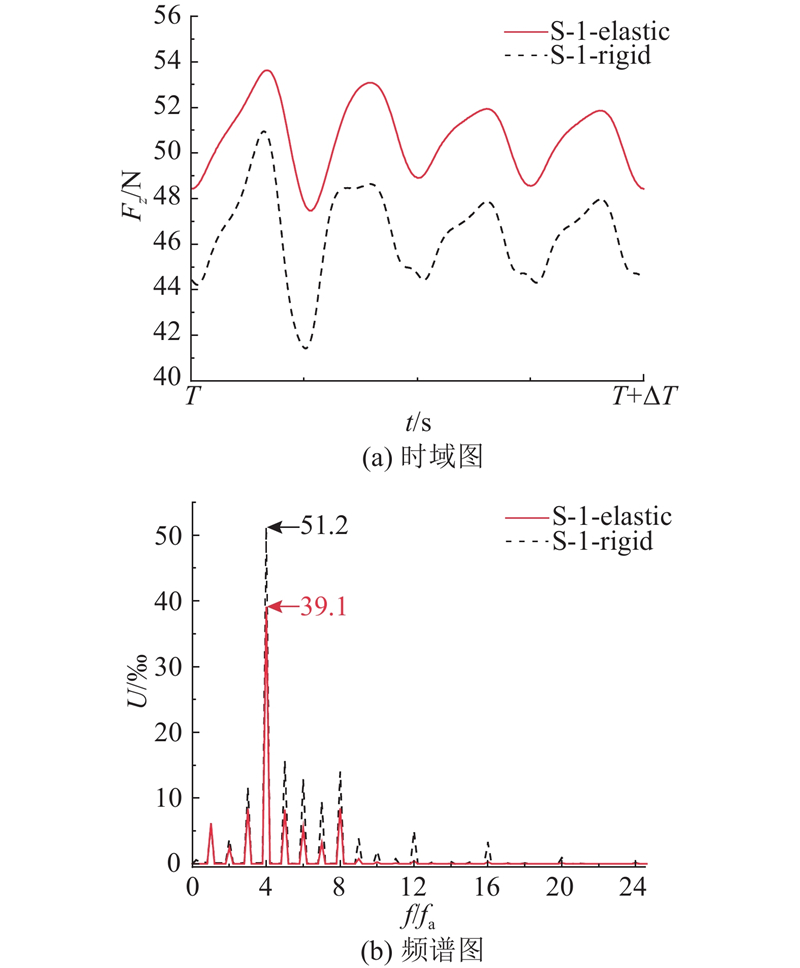
基于对时域曲线的初步分析,进一步量化分析刚性和弹性螺旋桨的激励力频率特性及其主导成分. 采用快速傅里叶变换(fast Fourier transform, FFT)对单叶片轴向激励力进行频谱分析. 图22(a)展示了刚性和弹性螺旋桨单叶片轴向力的时域曲线. 图22(b)为单叶片轴向力频谱图,其中U为FFT结果除以各模型单叶片轴向激励力的时均值而得到的相对幅值;轴频fa为螺旋桨旋转轴的旋转频率,fa = 19.35 Hz;叶频fb为轴频乘以叶片数,即fb = 10fa = 193.50 Hz. 由图可知,S-1模型的螺旋桨单叶片轴向力的相对幅值在4fa处明显较大. 这是因为S-1航行体中艉舵和围壳的存在导致伴流场轴向速度分布不均匀,使伴流场的四阶谐调分量突出,所以螺旋桨单叶片轴向力在4倍轴频处呈现明显的脉动. 对比刚性和弹性螺旋桨的相对幅值,发现弹性螺旋桨在主频处的幅值比刚性螺旋桨减小了23.6%,表明弹性螺旋桨的单叶片动态变形能够缓冲伴流场的周期性来流激励,从而抑制单叶片轴向激励力.
图 22
图 22 刚性和弹性螺旋桨单叶片轴向激励力特性
Fig.22 Axial excitation force characteristics of single blade of rigid and elastic propellers
图 23
图 23 十叶片弹性螺旋桨的整体动态变形特性
Fig.23 Overall dynamic deformation characteristics of ten-blade elastic propeller
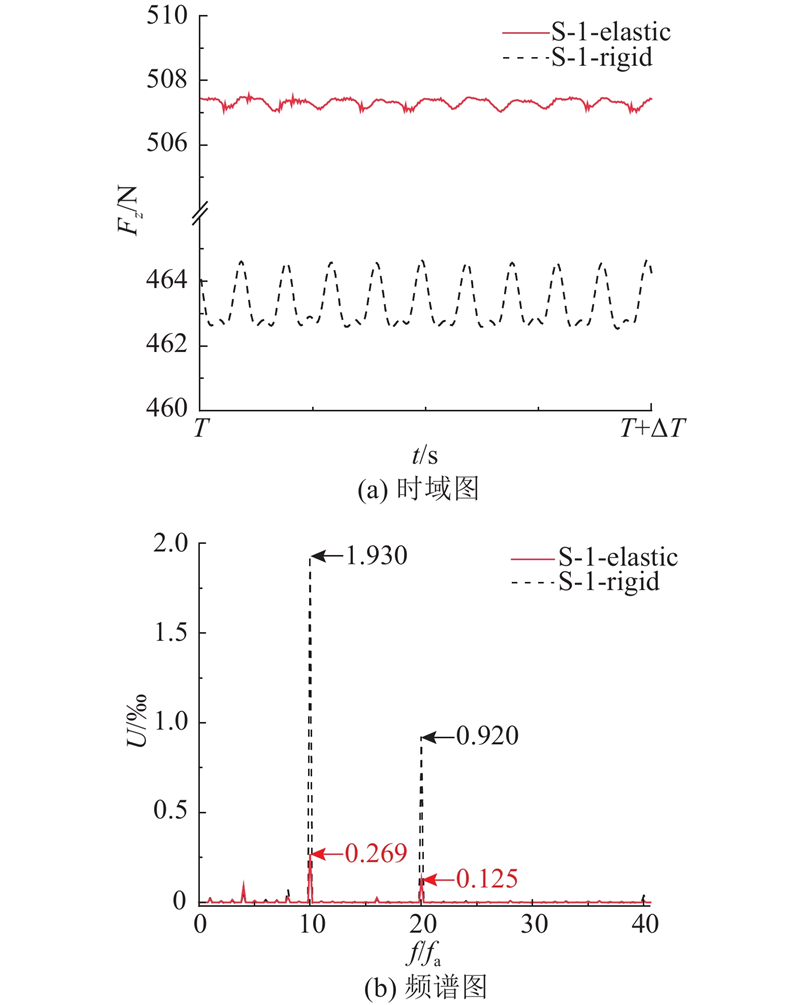
关于螺旋桨整体的激励力,刚性和弹性螺旋桨轴向力在旋转1圈的时间内均呈现10个周期性波峰和波谷,如图24(a)所示. 弹性螺旋桨的波动幅值明显小于刚性螺旋桨. 对轴向力数据进行FFT处理,如图24(b)所示,其中U为FFT结果除以各模型十叶片轴向激励力的时均值而得到的相对幅值. 可以发现刚性螺旋桨在主频fb处的轴向力峰值远高于弹性螺旋桨,在2fb、3fb和4fb处也存在更为明显的脉动,表明刚性螺旋桨在叶频及其倍频处的激励响应更强. 这是由于弹性螺旋桨的轴向位移与轴向力按照相同频率脉动,其动态变形能够适应外部激励,具备自适应调节能力,从而抑制了螺旋桨轴向激励力. 相比于刚性螺旋桨,弹性螺旋桨轴向力在叶频处的激励力幅值降低了86.1%.
图 24
图 24 十叶片刚性和弹性螺旋桨的整体轴向激励力特性
Fig.24 Overall axial excitation force characteristics of ten-blade rigid and elastic propellers
综上所述,研究了弹性螺旋桨的动态变形对激励力特性的影响. 结果表明,弹性螺旋桨的动态变形通过吸收伴流激励能量或释放储存的弹性势能,降低了单叶片轴向力的波动幅值与4倍轴频处的脉动幅值. 同时,动态变形的频率响应与激励力振动频率一致,这种自适应调节能够有效抑制螺旋桨激励力在叶频及其倍频处的相对幅值.
4. 结 论
采用流固耦合数值模拟方法研究弹性螺旋桨在不同伴流场条件下的结构变形特性及其对激励力的影响机理,揭示了弹性螺旋桨结构变形对激励力的调控机制,主要结论如下.
(1)弹性螺旋桨的结构变形受到伴流场的来流激励驱动,可以解耦为保持不变的稳态变形和波动变化的动态变形. 其中,动态变形由脉动载荷主导,呈现与伴流场周向速度相似的波动特点,且随着半径增大,叶片位移波动幅值变大;稳态变形由时均流体载荷主导,主要表现为螺旋桨叶片的轴向位移,且随着半径增长,叶片位移变大.
(2)在弹性螺旋桨的稳态变形过程中,由于叶片不同半径处的螺距角均呈现增大的特征,导致攻角增大,叶片受力变大,从而使轴向力时均值上升. S-1模型的弹性螺旋桨轴向力时均值较刚性螺旋桨增大了9.5%.
(3)弹性螺旋桨的动态变形通过吸收伴流激励能量或释放储存的弹性势能形成缓冲作用,能够有效降低单叶片轴向力的波动幅值,从而抑制激励力脉动;单叶片轴向力在主频(4倍轴频)处的激励力幅值降低了23.6%. 而且,弹性螺旋桨整体动态变形的响应频率与轴向激励力的脉动频率相匹配,具备自适应调节能力,从而抑制了激励力脉动;螺旋桨轴向力在叶频(10倍轴频)处的激励力幅值降低了86.1%.
(4)以各向同性的POM材料为例,研究弹性螺旋桨变形模式、变形特征对叶片动态载荷、激励力的影响规律. 相比之下,各向异性的复合材料具备独特的可设计性,但是由于其力学构型设计、流固耦合计算方法更为复杂,未在本研究中体现. 后续将进一步探索碳纤维、玻璃纤维等各向异性材料的材料性能、铺层设计对结构变形与激励力特性的影响,为弹性螺旋桨的设计与应用提供更丰富的理论依据和可行的方案.
参考文献
复合材料螺旋桨非定常流固耦合特性数值分析
[J].
Numerical analysis of unsteady fluid-structure interaction of composite marine propellers
[J].
Fluid-structure interaction analysis of flexible composite marine propellers
[J].DOI:10.1016/j.jfluidstructs.2007.12.010 [本文引用: 1]
基于铺覆模拟的复合材料螺旋桨叶片分区域铺层优化
[J].DOI:10.12044/j.issn.1007-2330.2022.01.006 [本文引用: 1]
Regional stacking sequence optimization of composite propeller blade based on draping simulation
[J].DOI:10.12044/j.issn.1007-2330.2022.01.006 [本文引用: 1]
复合材料船用螺旋桨设计与CFD/FEM计算
[J].DOI:10.11918/j.issn.0367-6234.2010.03.016 [本文引用: 1]
Design of composite marine propeller and the calculation of CFD/FEM
[J].DOI:10.11918/j.issn.0367-6234.2010.03.016 [本文引用: 1]
Improving the propulsion performance of composite propellers under off-design conditions
[J].DOI:10.1016/j.apor.2020.102164 [本文引用: 1]
弹性螺旋桨的轴向非定常力分析
[J].
Axial unsteady force analysis of flexible propeller
[J].
弹性螺旋桨纵向激励力特性研究
[J].DOI:10.3969/j.issn.1006-1355.2023.01.002 [本文引用: 1]
Study on the longitudinal excitation force characteristics of elastic propellers
[J].DOI:10.3969/j.issn.1006-1355.2023.01.002 [本文引用: 1]
柔性螺旋桨非定常流场及结构动态响应数值计算
[J].DOI:10.11990/jheu.201712053 [本文引用: 1]
Numerical investigation of the unsteady flow and structural dynamics of a flexible propeller
[J].DOI:10.11990/jheu.201712053 [本文引用: 1]
Theoretical study on the axial excitation force transmission characteristics of marine propellers
[J].DOI:10.1016/j.oceaneng.2019.106364 [本文引用: 1]
弹性对螺旋桨激励力和噪声特性影响分析
[J].DOI:10.11990/jheu.202302020 [本文引用: 1]
Influence of elasticity on propeller excitation force and noise characteristics
[J].DOI:10.11990/jheu.202302020 [本文引用: 1]
潜艇伴流场对螺旋桨激励力的影响
[J].
Influence of wake field on propeller exciting force of submarine
[J].
An experimental analysis of fluid structure interaction on a flexible hydrofoil in various flow regimes including cavitating flow
[J].DOI:10.1016/j.euromechflu.2012.03.009 [本文引用: 1]
Hydroelastic response and stability of a hydrofoil in viscous flow
[J].DOI:10.1016/j.jfluidstructs.2012.12.011 [本文引用: 1]
An experimental study of boundary-layer transition induced vibrations on a hydrofoil
[J].DOI:10.1016/j.jfluidstructs.2011.04.002 [本文引用: 2]
Cavity induced vibration of flexible hydrofoils
[J].DOI:10.1016/j.jfluidstructs.2014.05.007 [本文引用: 1]