滑梁式空气箔片轴承是一种具有发展潜力的轴承结构. 与波箔型空气箔片轴承相比,其制作工艺简单,成本较低. 鉴于现阶段对其力学及润滑性能的理论研究尚不够深入,研究结构参数对滑梁式空气箔片轴承润滑性能的影响规律十分必要.
目前对空气箔片轴承的研究主要集中于波箔型结构. Walowit等 [1]首次构建箔片弹性变形模型并求得弹性系数,结合一维Reynolds方程研究轴承的静特性. Heshmat等[2]提出波箔的线性弹簧等效模型,利用有限差分法计算轴承在不同尺寸和运行参数下的静特性. Carpino等[3-4]在考虑箔片弯曲、润滑膜和弹性支承共同作用的基础上,求解Reynolds方程,得到气膜压力分布情况,利用有限元法预测箔片结构变形量. 许怀锦等[5-6]通过数值方法求解压力控制方程和气膜厚度方程,对比研究波箔型轴承和刚性轴承的润滑性能. Kim等[7]借助直接隐式积分法求解箔片轴承的非线性动力模型,研究轴承在不同设计参数和运行条件下对质量不平衡激励的响应. Ku等[8]用光学跟踪系统测量箔片轴承在各种运行条件下的波箔二维变形量,发现设计参数会影响波箔结构特性. Radil等[9]试验研究半径间隙对波箔型轴承气膜承载力的影响及结构参数对承载能力和热学性能的影响. Li等[10]通过试验研究非均匀波箔型轴承支承的空压机轴颈的动力学特性,发现减小半径间隙可以抑制轴颈振动. 许浩杰等[11]综合考虑箔片结构变形、可压缩气体Reynolds方程、能量方程和表面粗糙度,研究空气箔片径向轴承的静动特性,同时分析箔片结构尺寸参数如何影响波箔轴承静动特性.
波箔的加工生产对模具的依赖度高,而轴承性能对波箔尺寸变化敏感,这使得模具加工的精度要求很高,导致生产成本居高不下. 随着激光切割技术的发展,滑梁式箔片轴承的优势逐渐显现. 由于滑梁箔片只需通过激光切割即可满足高精度加工要求,与常见的波箔型轴承相比,滑梁式箔片轴承具有显著的经济性优势. 然而,目前公开文献中对其性能的研究仍处于探索阶段. 冯凯等[12]研究三瓣式弹性箔片轴承,用数值研究证明该结构可以提高轴承稳定性和承载力. 李长林等[13-15]对三瓣结构的滑梁式轴承进行研究,计算滑梁形变并对该轴承的静动特性及其支撑的转子系统的性能进行分析. 吴洋等[16]采用非线性薄板单元建立滑梁箔片力学模型,并对该轴承静态特性进行精确计算. 但这些研究均针对三瓣结构的滑梁式空气箔片轴承. 顾晨昀等[17]对整周结构的滑梁式空气轴承的疲劳寿命进行理论研究,但未进一步对其承载能力和润滑性能进行分析.
在前人研究的基础上,以梯形滑梁结构的空气箔片轴承为研究对象,应用力学和流体润滑理论,构建流固耦合计算模型. 通过数值计算的方法,深入研究结构参数对其润滑性能的影响规律.
1. 计算模型构建
1.1. 滑梁式箔片轴承结构及工作原理
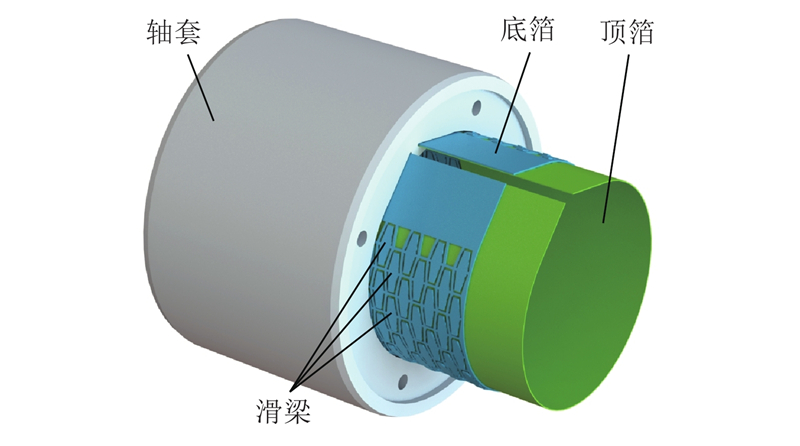
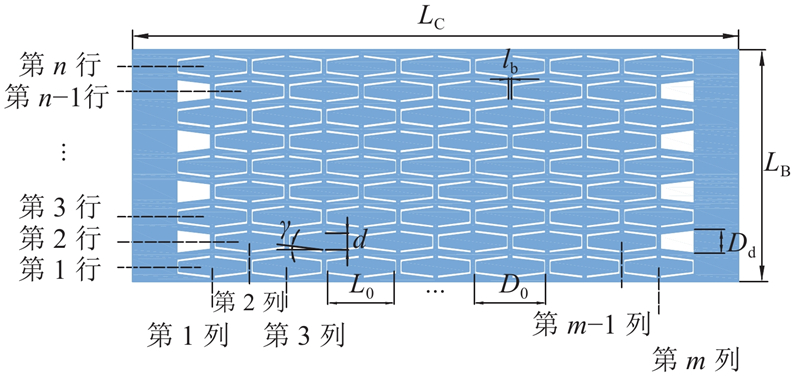
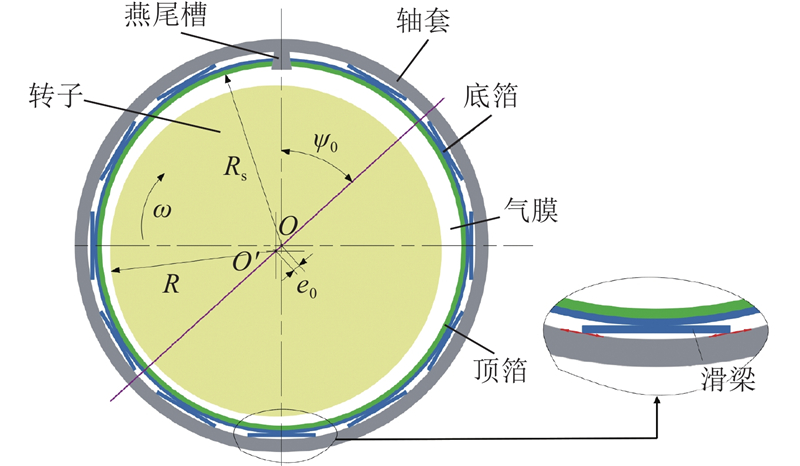
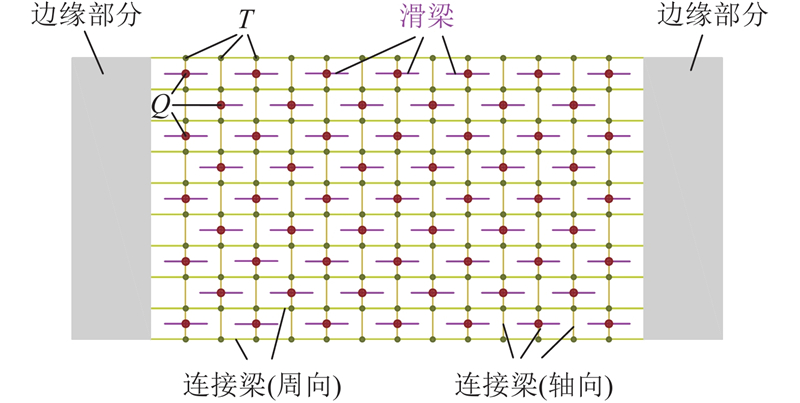
图1为滑梁式空气箔片轴承的基本结构. 其中,轴承的顶箔和底箔均为一片式的完整箔片,为整周结构. 底箔为滑梁箔片,其主要参数如图2所示.滑梁在底箔片上按照一定的规律排列,其形状由长度L0、宽度d和梯形斜率γ决定;LC为箔片周向长度,LB为箔片轴向长度,m和n分别为周向和轴向滑梁个数. 当滑梁箔片弯曲时,箔片上的滑梁将保持直线形状,并在安装后与轴套内表面接触,起到支撑顶箔的作用,如图3所示.其中,R为轴颈半径,Rs为顶箔安装后的圆弧半径,O和O'分别为轴套和转子的中心,e0为转子的偏心距,ψ0为偏位角,ω为转子旋转的角速度. 由于收敛间隙的存在,轴颈在高速转动时产生气膜动压,此时,底箔上的滑梁弯曲,滑梁的两端会在轴套上滑动.
图 1
图 2
图 3
1.2. 箔片的力学模型
1.2.1. 顶箔的力学分析
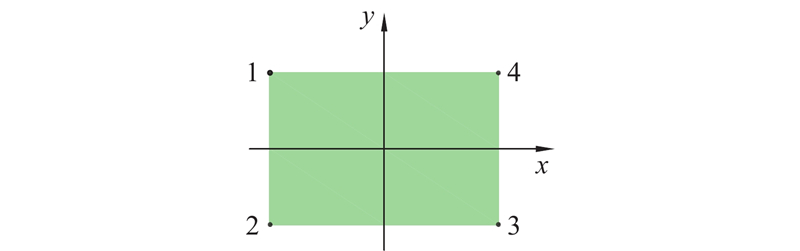
由于箔片的厚度通常不超过0.3 mm,可以采用Kirchhoff理论,使用薄板单元对箔片进行力学建模. 顶箔为规则的矩形结构,故采用图4中的矩形单元建立力学模型. 图中,x和y为单元内的局部坐标.
图 4
基于薄板理论,挠度w与转角θx、θy满足
设单元e内节点i的挠度及x和y向弯角分别为
式中:
单元e内的弯曲应变κe可以表示为
式中:Be为单元应变矩阵. 单元的总位能
式中: Pe为对应的单元载荷阵列;D为弹性矩形,且
其中E、μ和t分别为箔片的弹性模量、泊松比和厚度. 基于最小位能原理,式(4)的变分为0,化简后得到单元e的平衡方程:
式中:Ke为单元e的刚度矩阵.
计算顶箔中所有单元的
1.2.2. 滑梁箔片的力学分析
考虑到滑梁箔片复杂的几何结构,在进行力学分析时需要进行适当的简化. 如图5所示,将滑梁箔片划分为3个部分,分别为滑梁、连接梁和边缘部分. 其中,边缘部分为规则的矩形结构,可以通过式(5)建立其单元刚度矩阵,并在集成后得到边缘部分的结构刚度矩阵Kb. 连接梁又分为周向部分和轴向部分,两者存在交点T. 滑梁和轴向连接梁相交于Q点.
图 5
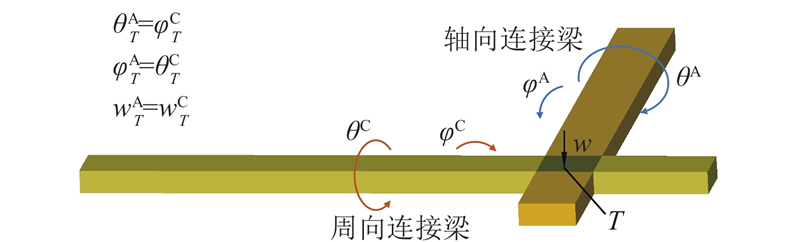
如图6所示,在交点T处,周向梁与轴向梁有相同的挠度w. 此外,两者的扭角与弯角应当是耦合的,即周向梁扭角
图 6
式中:
式中:
式中:广义弹性矩阵
式中:
建立所有连接梁单元的
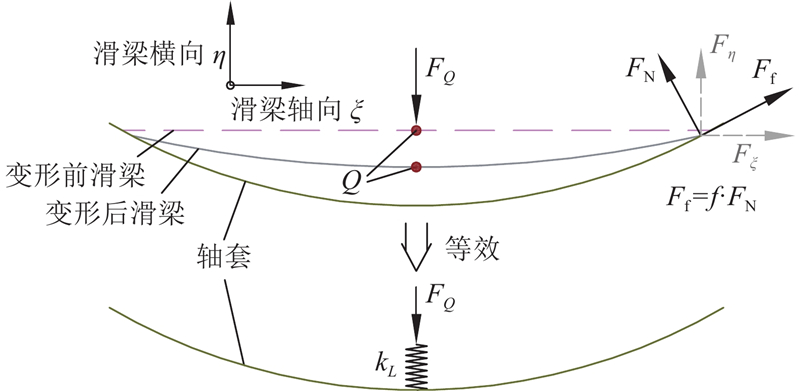
滑梁在结构中起到支撑的作用,其两端与轴套接触,如图7所示. 图中,Q点为滑梁与轴向连接梁的连接点,也是滑梁对顶箔的支撑点. 因此,可以通过分析滑梁在Q点的挠度与载荷关系,将序号为L的滑梁等效为刚度为kL的支撑弹簧.当滑梁弯曲时,其两端与轴套接触,滑梁与轴套间存在法向接触力FN和摩擦力Ff,滑动摩擦系数为f,取f=0.3. 经过坐标转换后,滑梁的端部受到轴向力Fξ和横向力Fη的作用,并且滑梁的水平位移u和竖直挠度w是耦合的.
图 7
图 7 滑梁与轴套的接触示意图
Fig.7 Schematic of contact between sliding beam and shaft sleeve
若采用线形梁单元进行力学分析,则无法考虑Fξ和u对挠度w的影响,这显然是不合理的. 因此,结合梁的大变形特点对滑梁的挠度进行数值研究,并对滑梁形变做以下假设:
1)在弹性范围内;
2)为纯弯曲,忽略切应力和拉伸或压缩导致的形变.
根据几何关系和本构关系,滑梁的曲率半径ρ与弯曲内力M满足
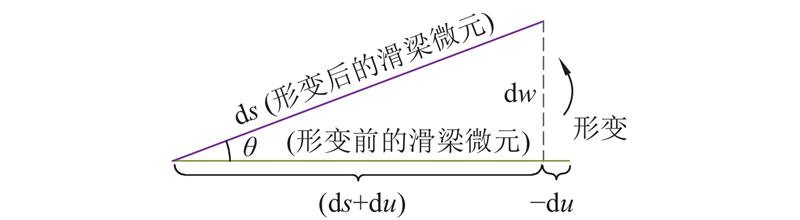
式中:s为滑梁的长度. 如图8所示,形变后滑梁的位移u、w、θ与s之间满足几何关系:
图 8
由式(12)得到:
将滑梁离散为两点形式的梁单元,结合式(7),以节点位移
式中:
由于滑梁为变截面梁,式(15)中Iz可以采用线性插值形式. 滑梁单元的总位能
式中:
并且满足
式中:
将式(18)和式(19)代入式(17),根据最小位能原理,梁单元总位能的变分为0,化简后得到:
式中:
对式(20)求微分得到:
式中:
对每根滑梁中所有的
在
滑梁L在Q点处的支撑刚度kL为
计算所有滑梁对Q点的支撑刚度并进行集成,得到滑梁的支撑刚度矩阵
对Kb、Kl与Kh进行集成,得到底箔的刚度矩阵KB. KB与所有滑梁在Q点的挠度阵列W有关. 需要先设定滑梁在Q点的初始挠度阵列W0,再结合图7中轴套对滑梁端部的接触约束,采用直接迭代法对式(22)确定滑梁端部载荷Fξ,然后由式(23)和式(25)确定每个滑梁中Q点的支撑刚度kL,并计算
式中:t为迭代层数,
1.3. 流固耦合计算
1.3.1. 气膜压力分布的计算
对于稳定运转的滑梁式空气轴承,可以看作等温状态,采用雷诺润滑方程:
式中:ψ和λ分别为轴承的周向角度和轴向坐标,h和p分别为气膜的厚度和压力分布函数,ηA为空气的动力黏度.
当已知顶箔的挠度分布函数w时,气膜厚度的表达式为
式中:取燕尾槽中心处的ψ=0;h0为标准气膜厚度,即e0=0时的半径间隙.
式(27)为椭圆方程,采用有限差分法求解. 在圆周方向上采用连续性条件;在轴向端面处,气膜压力满足边界条件:
1.3.2. 流固耦合计算方法构建
设定转子偏心距e0和偏位角
式中:r为迭代层数,
迭代收敛后,得到给定
式中:Mf对整个气膜区域进行积分,QR对整个圆周方向进行积分,ρA为空气密度.
在实际试验中,载荷的大小是给定的,且一般沿竖直方向. 因此,须通过迭代修正的方式计算给定载荷
式中:q为迭代层数,
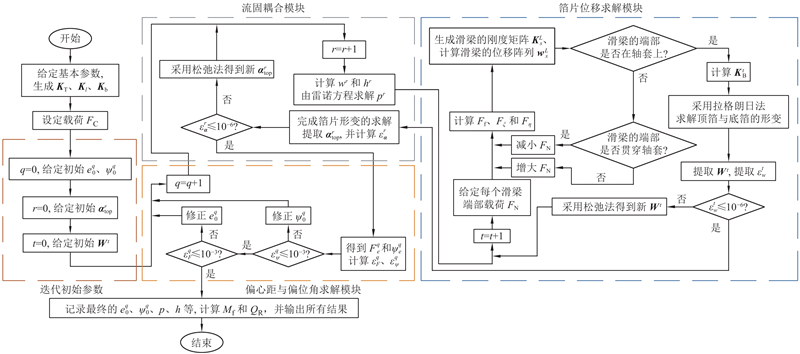
综上,当给定结构参数及载荷FC时,箔片轴承的运行参数及润滑性能的数值求解方法如图9所示,包括箔片位移求解模块、流固耦合模块和偏心距与偏位角求解模块.
图 9
图 9 箔片轴承润滑性能参数的数值求解流程图
Fig.9 Flowchart of numerical solution for lubrication performance parameters of foil bearing
2. 算例研究
2.1. 模型的试验验证
通过MATLAB编程实现图9中的计算流程. 为了检验所建模型的准确性,搭建试验台进行验证.
图 10
图 10 滑梁式箔片轴承与试验台照片及试验原理图
Fig.10 Photographs of sliding beam foil bearing and test stand, and schematic of test principle
表 1 轴承结构参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| L0/mm | 2.25 | R/mm | 14.00 | |
| d/mm | 1.40 | m | 27 | |
| LC/mm | 80.63 | n | 13 | |
| LB/mm | 25.00 | h0/μm | 10.00 | |
| γ | 0.10 | D0/mm | 2.50 | |
| t1/mm | 0.10 | Dd/mm | 1.60 | |
| t0/mm | 0.10 | lb/mm | 0.20 |
转子与伺服电机的轴通过联轴器直接相连. 箔片轴承套装在转子上,轴承上端通过细线与砝码相连. 砝码对轴承施加向上的拉力,根据力的相互作用,等价于转子对轴承施加向下的力. 轴套与力臂杆相连,力臂杆的一端以自由的方式压在压力传感器上. 当转子转速提高到一定程度时,形成流体动压润滑气膜. 随着转子的旋转,气膜受到剪切作用,使轴承套产生旋转的力矩,带动力臂杆给传感器施加压力. 当转子旋转时,通过传感器测得压力值FSEN,可以进一步计算轴承的摩擦力矩MEP:
式中:lpole为力臂杆的长度,RSL为轴套外表面半径.
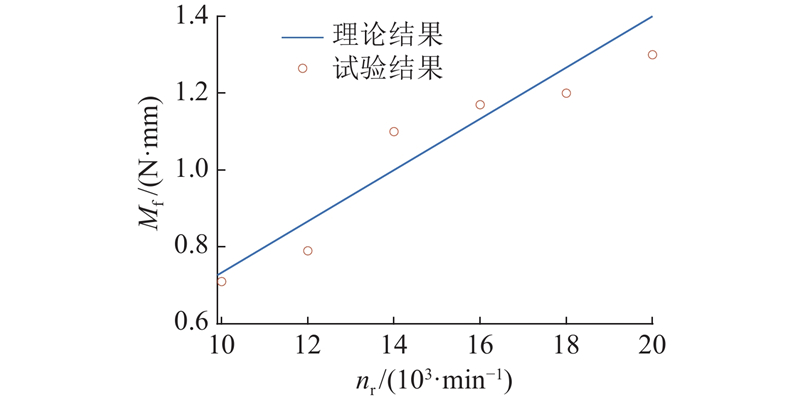
当转速较低时,轴承未起飞,转子与箔片之间存在接触摩擦. 取转速nr>1×104 r/min的试验数据与数值结果对比,如图11所示. 可以看出理论模拟结果与试验结果在数值及变化趋势方面均具有良好的一致性,两者吻合度较高,说明本研究建立的理论模型具有良好的可靠性.
图 11
图 11 摩擦力矩的试验与数值结果对比
Fig.11 Comparison of experimental and numerical results of friction torque
2.2. 算例研究
对轴承进行数值研究,轴承结构参数如表1所示. 已知大气压强P0=101 325 Pa,流体动力学黏度ηA=
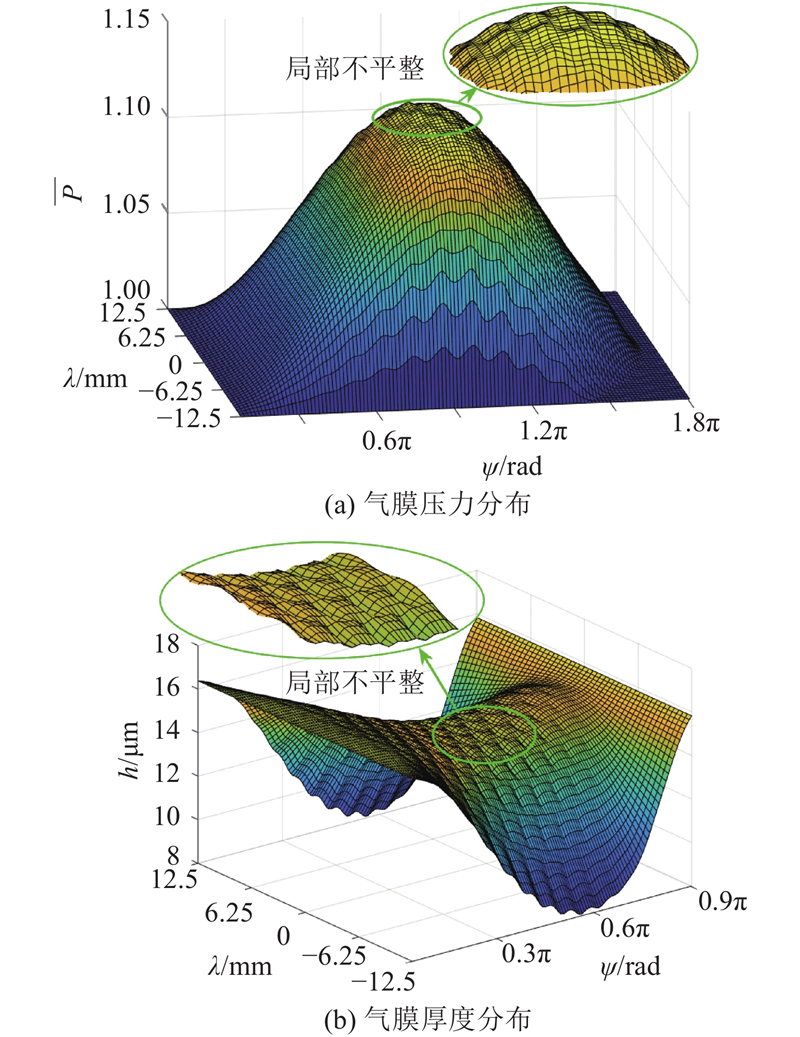
图 12
图 12 气膜压力分布及对应的厚度分布
Fig.12 Air film pressure distribution and corresponding thickness distribution
图 13
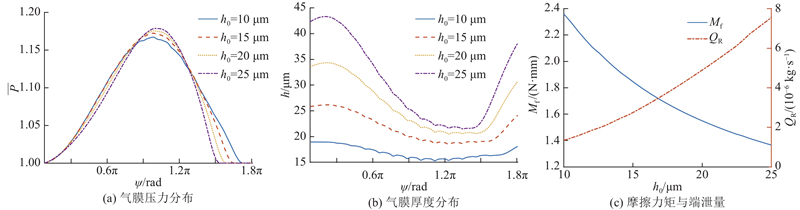
图 13 标准气膜厚度对轴承润滑性能的影响
Fig.13 Effect of standard air film thickness on bearing lubrication performance
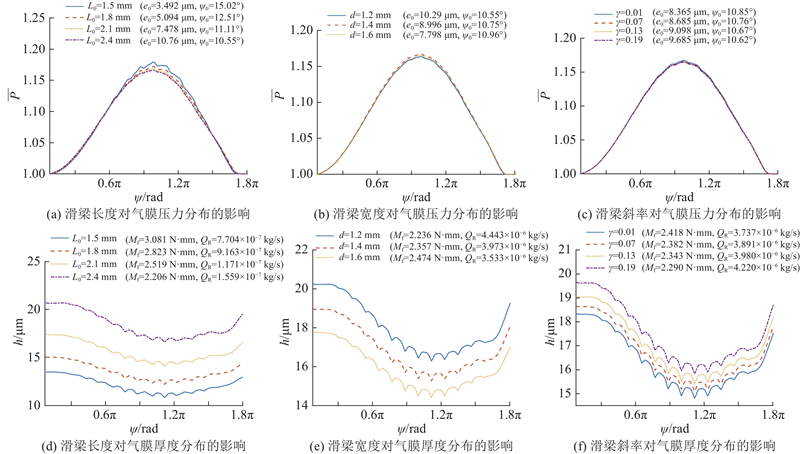
滑梁的尺寸参数受到滑梁数目与梯形形状的限制,长、宽过大将会导致结构之间的贯穿,斜率过大将不能维持滑梁的梯形形状. 研究滑梁尺寸对轴承气膜压力与厚度分布的影响,采用控制变量法,分别取
图 14
图 14 λ=0处滑梁尺寸对气膜压力和厚度分布的影响
Fig.14 Effect of sliding beam sizes on pressure and thickness distributions of air film at λ=0
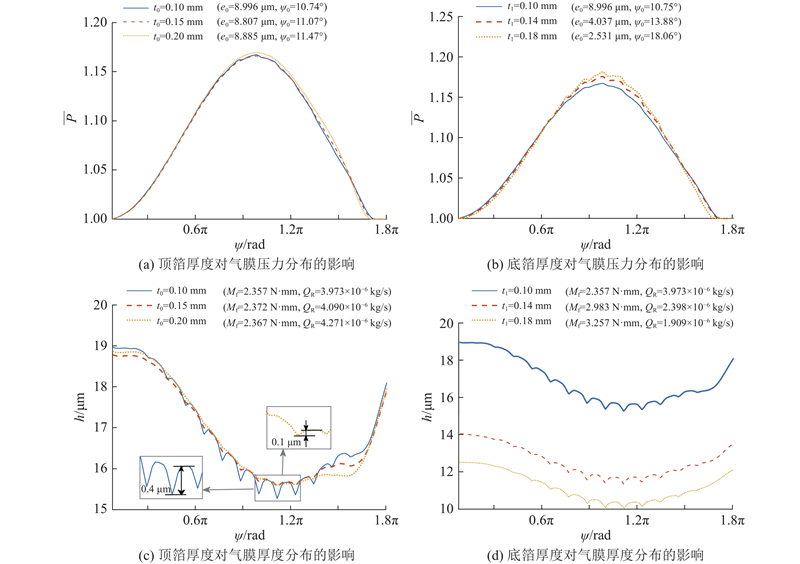
图 15
图 15 λ=0处箔片厚度对气膜压力和厚度分布的影响
Fig.15 Effect of foil thickness on pressure and thickness distributions of air film at λ=0
3. 结 论
(1) 基于Kirchhoff理论建立顶箔的有限元模型,并对底箔结构进行简化处理. 在模型中,考虑底箔连接梁之间的位移耦合,根据梁的大变形理论计算滑梁的等效刚度. 进一步建立底箔的非线性刚度矩阵,并计算箔片的形变. 采用等温雷诺方程计算气膜压力分布,通过流固耦合方法构建滑梁式空气箔片轴承的力学模型,计算在特定载荷下轴承的性能参数. 该模型的数值结果与试验结果良好地吻合.
(2) 结合具体的算例,研究箔片的结构参数对轴承性能的影响. 结果表明,随着轴承与转子初始间隙的增大,气膜动压区域减小,气膜的最大压力上升,摩擦力矩减小,端泄量增大;滑梁尺寸和底箔厚度对气膜的影响是通过改变滑梁支撑刚度实现的,当滑梁对顶箔的支撑刚度增大时,气膜厚度减小,气膜的最大压力增大. 由于滑梁对顶箔的支撑不连续,气膜厚度与气膜压力呈现局部不平整现象,并且随着压强的增大与顶箔厚度的减小,局部不平整现象加剧.
(3) 通过数值计算方法研究滑梁结构参数对滑梁箔片轴承润滑性能的影响,得出一系列规律和结论. 然而,影响箔片轴承润滑性能的因素还有很多,例如表面粗糙度、温度、振动、形位公差等. 在今后的研究中还需要进一步地把这些因素纳入考虑范围,进行更加全面和深入的研究,以更准确地评估和优化滑梁箔片轴承的润滑性能.
参考文献
Analysis of gas-lubricated foil journal bearings
[J].DOI:10.1115/1.3254697 [本文引用: 1]
Effects of membrane stresses in the prediction of foil bearing performance
[J].DOI:10.1080/10402009408983264 [本文引用: 1]
Misalignment in a complete shell gas foil journal bearing
[J].DOI:10.1080/10402009408983365 [本文引用: 1]
波箔片气体动压径向轴承气膜压力分布特点
[J].DOI:10.3969/j.issn.1000-3762.2008.01.008 [本文引用: 1]
Characteristics of film pressure distribution of bump foil gas bearings
[J].DOI:10.3969/j.issn.1000-3762.2008.01.008 [本文引用: 1]
The dynamic performance analysis of foil journal bearings considering Coulomb friction: rotating unbalance response
[J].DOI:10.1080/10402000802192685 [本文引用: 1]
Compliant foil bearing structural stiffness analysis—part II: experimental investigation
[J].DOI:10.1115/1.2921644 [本文引用: 1]
The role of radial clearance on the performance of foil air bearings
[J].DOI:10.1080/10402000208982578 [本文引用: 1]
Feasibility investigation of a compressor rotor supported by gas foil bearings with inhomogeneous bump foils
[J].DOI:10.1177/13506501211004668 [本文引用: 1]
考虑波箔变形的波箔型气体箔片轴承润滑性能的数值研究
[J].
Numerical study on the lubrication performance of bump-type gas foil bearings with considering the deformation of bump foil
[J].
三瓣式气体箔片径向轴承的静动态特性
[J].DOI:10.3969/j.issn.1004-132X.2017.15.010 [本文引用: 1]
Static and dynamic performances of a three-pad gas foil journal bearing
[J].DOI:10.3969/j.issn.1004-132X.2017.15.010 [本文引用: 1]
Study of load carrying mechanism of a novel three-pad gas foil bearing with multiple sliding beams
[J].DOI:10.1016/j.ymssp.2019.106372
Linear stability and nonlinear rotor responses of the gas foil bearing with multiple sliding beams
[J].DOI:10.1177/09544062231163717 [本文引用: 1]
三瓣结构的滑梁式空气箔片轴承润滑力学建模及数值研究
[J].
Lubrication mechanics model and numerical study of sliding beam type gas foil bearing with three-pad structure
[J].
滑梁式空气箔片轴承力学分析及疲劳寿命计算方法
[J].
Mechanical performance and fatigue life calculation method of sliding beam air foil bearing
[J].