注浆法因具有操作简便、对施工环境的适应性强的优点,被广泛应用于不同地层的防渗加固工程中[9]. 注浆技术的原理为通过注浆泵对浆液施加压力,使其渗入土体孔隙中,浆液凝固后与土体共同形成固结体或增强体从而提高土体的完整性,以达到防渗加固的目的[10]. 因此,浆液能否顺利渗入土体孔隙是注浆工程中的关键. 已有研究表明,全风化花岗岩地层具有致密性,土体颗粒间排列紧密,孔隙细微[11-12]. 常规水泥基浆材在较低的注浆压力下很难渗入地层,而过大的注浆压力又会造成劈裂,破坏土体结构,且注浆均匀性难以保证. 此外,压力过大有可能引发地层抬升和一系列相关问题[13]. 传统的化学浆材可注性良好,但存在环境污染性、耐久性差的问题. 因此亟需一种可注性强、耐久性良好、绿色环保的新型注浆材料.
此外,诸多学者对硅溶胶注浆加固效果及其扩散规律开展了研究,刘灿平[16]以固砂体抗压强度为关键指标,通过单因素试验及正交试验确定纳米硅溶胶溶液的最优配比并进行了砂土灌浆数值模拟. 结果表明:在最优配比下,硅溶胶固砂体养护28 d后的抗压强度最大可以达到862 kPa;当灌浆压力为1.0 MPa,砂土孔隙率为0.4时,硅溶胶浆液在砂土中最终扩散半径达到1.47 m. 周春花[17]通过自行设计的微管微压注浆设备,采用硅溶胶对低渗透性粉砂进行室内渗透注浆试验. 发现硅溶胶溶液中二氧化硅质量分数较低时浆液扩散更为均匀且扩散范围近似为圆柱体,注浆结石体在50 kPa竖向应力下的抗剪强度最大为83.27 kPa. 上述研究表明硅溶胶的可注性强且防渗加固效果良好,在加固全风化花岗岩地层方面具有较强的应用前景.
为了量化硅溶胶的可注性,众多学者开展了广泛的研究. Fraccica等[18]将不同类型的浆液注入渗透系数梯度设置的粉砂混合物中研究浆液的可注性,结果表明硅溶胶渗透注浆可适用于渗透系数为10−3~10−6 m/s的土体. 在现场研究方面,Funehag[19]在瑞典哈兰萨斯隧道防渗工程中利用硅溶胶对渗透系数为10−7 m/s的裂隙岩体进行注浆,成功将岩体渗透系数降低至10−9 m/s. 测得全风化花岗岩土体的渗透系数范围为10−5~10−6 m/s,因此理论上硅溶胶能够实现全风化花岗岩土体中的渗透注浆. 但目前硅溶胶注浆加固的研究对象主要为砂土,硅溶胶注浆对全风化花岗岩土体的防渗加固效果及其在全风化花岗岩土体中的渗透规律鲜有人研究. 此外,目前对硅溶胶渗透扩散规律的研究尚缺乏坚实的渗透注浆理论支撑.
本研究采用硅溶胶浆液对全风化花岗岩土体进行防渗加固并通过无侧限抗压强度试验、三轴压缩试验以及变水头渗透试验具体分析防渗加固效果. 通过自制注浆设备在实验室内开展注浆模拟试验,探明硅溶胶在全风化花岗岩土体中的渗透扩散规律. 为了准确地预测硅溶胶浆液的扩散范围,考虑浆液黏度变化及土体迂曲度的影响,对传统渗透注浆理论公式进行修正. 在模拟实验中对修正公式进行验证. 研究旨在为工程实践提供科学可行的指导与理论依据,解决全风化花岗岩地层防渗加固处理的难题.
1. 试验材料
1.1. 全风化花岗岩
图 1
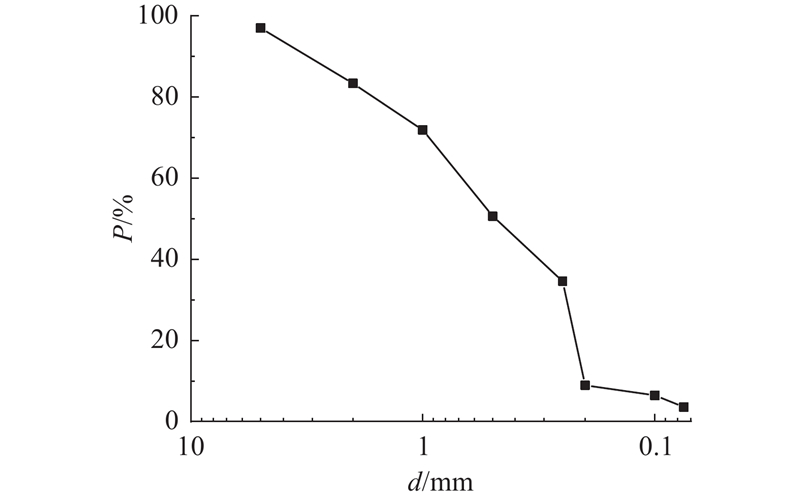
图 1 全风化花岗岩土样颗粒级配曲线
Fig.1 Granular gradation curve of completely weathered granite
1.2. 纳米硅溶胶
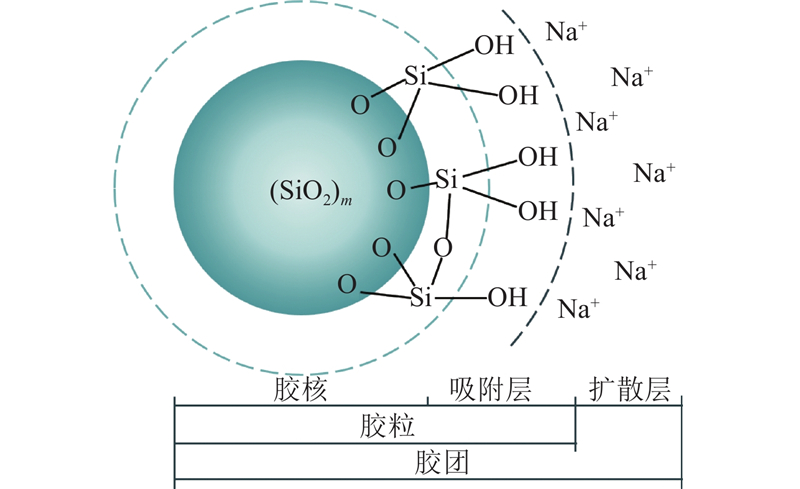
纳米硅溶胶是由二氧化硅纳米颗粒在水中均匀分散所形成的胶体溶液. 杨微等[22]指出纳米硅溶胶胶团具有典型的双电层结构,如图2所示,由胶核与双电层(吸附层与扩散层)2部分构成. 胶团的中心为胶核,H+离子与SiO32−吸附在胶核表面组成吸附层并形成硅羟基(―Si―OH). 胶核与吸附层共同组成胶粒,碱金属离子在胶粒外围形成扩散层. 硅溶胶胶粒之间通过双电层间的静电排斥保持力学平衡,在加入NaCl或其他强电解质溶液后,双电层厚度减小,静电排斥力减弱,相邻胶粒表面的硅羟基发生脱水缩合反应形成硅氧烷键(Si―O―Si),硅溶胶胶团缓慢聚集成具有三维网状结构的固体凝胶. 纳米硅溶胶及其凝胶体如图3所示.
图 2
图 3
纳米硅溶胶的化学成分不会对环境产生影响,为环境友好型材料. 研究所用硅溶胶采购于山东省临沂市科翰硅制品有限公司,二氧化硅质量分数为29%~31%,平均粒径为7~10 nm,黏度≤9 mPa·s.
2. 试验方案与方法
2.1. 试验方案
目前国内外学者广泛认为硅溶胶的增强机制是源于不同胶粒表面的硅羟基发生脱水缩合反应所形成的硅氧烷键(Si―O―Si),硅氧烷键的数量越多则凝胶体的强度与抗渗性能越强. 硅溶胶凝胶过程中形成硅氧烷键的数量与硅溶胶溶液中二氧化硅颗粒的质量分数(ws)和胶凝剂溶液中溶质的质量分数即氯化钠溶液中氯化钠的质量分数(wn)相关. 在一定区间内,ws越大则凝胶过程中所形成的硅氧烷键数量越多,强度及抗渗性能越强. 当ws过大而wn很低时,胶凝反应不充分,强度会有所降低. wn过大也可能使得硅溶胶过度交联,从而降低凝胶强度[22]. 因此,硅溶胶的强度与抗渗性能主要与3种因素有关:ws、硅胶比(硅溶胶溶液与强电解质溶液的质量比,用m表示)和wn. 此外,硅溶胶浆液的凝胶时间也与上述3种因素密切相关,ws或wn增大均会导致凝胶时间缩短,而m增大则会延长凝胶时间.
硅溶胶的强度、抗渗性和凝胶时间均与ws、m、wn这3种因素相关. 因此,本研究以上述3种因素为试验变量设置正交试验,ws梯度为30%、25%和20%,m梯度为4∶1、6∶1和8∶1,wn梯度为8%、10%和12%,具体方案见表1,此外,计算得到硅溶胶与胶凝剂混合后浆液中二氧化硅颗粒的质量分数与氯化钠的质量分数辅助分析,表中分别记作wsm和wnm. 测试不同配比下硅溶胶浆液的黏度时变性,探索上述3种因素对浆液黏度及凝胶时间的影响规律;测试硅溶胶加固体的力学特性及渗透特性,探索上述3种因素对硅溶胶加固全风化花岗岩的影响规律.
表 1 硅溶胶浆液配比正交试验方案
Tab.1
| 编号 | 试样 | ws/% | m | wn/% | wsm/% | wnm/% |
| 1 | S30-4-8 | 30 | 4∶1 | 8 | 24.0 | 1.6 |
| 2 | S30-6-10 | 30 | 6∶1 | 10 | 25.7 | 1.4 |
| 3 | S30-8-12 | 30 | 8∶1 | 12 | 26.7 | 1.3 |
| 4 | S25-4-10 | 25 | 4∶1 | 10 | 20.0 | 2.0 |
| 5 | S25-6-12 | 25 | 6∶1 | 12 | 21.4 | 1.7 |
| 6 | S25-8-8 | 25 | 8∶1 | 8 | 22.2 | 0.9 |
| 7 | S20-4-12 | 20 | 4∶1 | 12 | 16.0 | 2.4 |
| 8 | S20-6-8 | 20 | 6∶1 | 8 | 17.1 | 1.1 |
| 9 | S20-8-10 | 20 | 8∶1 | 10 | 17.8 | 1.1 |
在硅溶胶浆液渗透扩散规律研究方面,由于硅溶胶浆液具有显著的黏度时变性,且全风化花岗岩土体具有典型的多孔介质的特征,须同时考虑浆液的黏度时变性以及土体的迂曲度才能更好地反映硅溶胶在全风化花岗岩中的渗透扩散规律,但目前尚未有同时考虑上述两者因素的渗透注浆理论公式. 因此,本研究在传统渗透注浆理论公式上推导出同时考虑黏度时变性及迂曲度的理论公式. 为了探明硅溶胶在全风化花岗岩土体中的渗透扩散规律与验证公式的合理性,在室内开展注浆模拟试验.
2.2. 试验方法
2.2.1. 黏度时变性
参照标准GB/T 10247—2008《黏度测量方法》(
图 4
图 5
2.2.2. 力学特性
力学特性主要考虑无侧限抗压强度与抗剪强度. 通过无侧限抗压强度试验与三轴压缩试验探索不同配比的硅溶胶注浆后全风化花岗岩的抗压强度与抗剪强度的变化规律
1)无侧限抗压强度试验. 无侧限抗压强度试验方法参照JCT 2037—2010《丙烯酸盐灌浆材料》(
图 6
2)三轴压缩试验. 在内径为39.1 mm,高度为80.0 mm的ABS圆柱体模具内,按无侧限抗压强度试验中相同方法制作加固体,每种配比制备3个试样,养护龄期为7 d. 三轴压缩试验类型为不固结不排水(UU),剪切速率为0.04 mm/min,围压梯度设置为100、300、600 kPa.
2.2.3. 渗透特性
通过变水头渗透试验测量加固体的渗透系数研究其渗透特性. 试样制作方法如下:使用保鲜膜包裹环刀并用橡皮筋双层固定,将硅溶胶浆液灌入环刀中,在持续轻柔搅拌下将预先称量好的土体缓慢灌入浆液中,使土体沉降,最终在环刀内形成土体与浆液混合均匀的试样. 用保鲜膜覆盖在环刀顶部于自然条件下养护7 d后,将环刀装入TST-55型变水头渗透仪中开始进行渗透试验,重新开始计时,持续监测加固体渗透系数变化至28 d.
2.2.4. 渗透扩散规律
在室内开展注浆模拟试验探明硅溶胶在全风化花岗岩土体中的渗透扩散规律. 注浆模拟试验装置如图7所示,由供压装置及模型箱组成. 空气压缩机负责提供气压并连接稳压阀从而保证其压力稳定,通过储浆桶将气压转换为注浆压力最终将硅溶胶浆液注入到模型箱内的土体中.
图 7
模型箱内径为28 cm,高为30 cm. 注浆管长度为38 cm,距底端6 cm和10 cm加工2排注浆花孔,孔径为4 mm,呈梅花型布置. 注浆模拟试验共进行3组,其中,全风化花岗岩土体干密度分别设定为1.30、1.36、1.42 g/cm3,含水质量分数均设定为1%以方便观察浆液扩散范围. 注浆时间设定为30 min,注浆压力设定为10 kPa. 注浆结束7 d后,开挖土体得到注浆结石体并测量其尺寸即可确定硅溶胶浆液在各组土体中的扩散范围.
3. 试验结果与分析
3.1. 硅溶胶黏度时变性分析
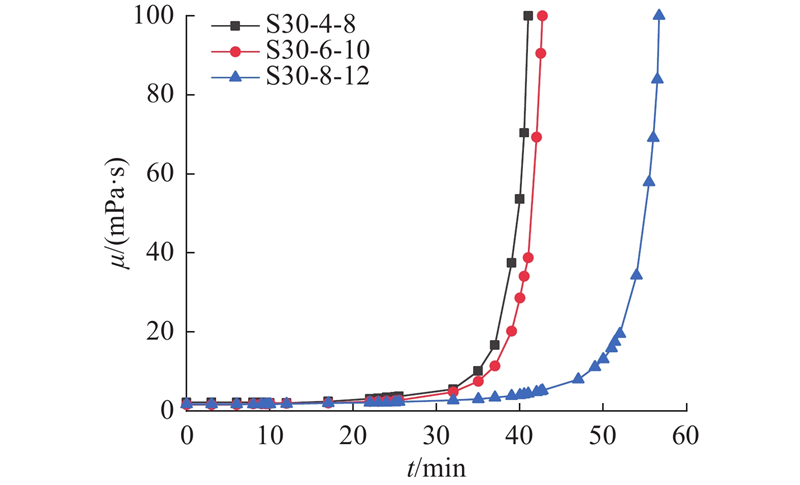
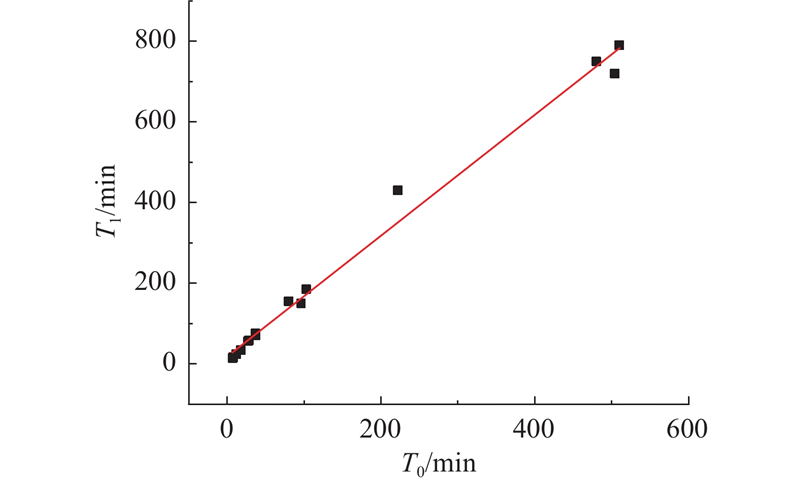
以S30-4-8、S30-6-10和S30-8-12配比硅溶胶浆液为例,浆液黏度μ随时间t的变化曲线如图8所示,其余配比下的硅溶胶浆液黏度变化曲线特征类似. 试验结果表明:硅溶胶浆液的初始黏度较低,在1~2 mPa·s范围内,表现出较强的可注性,而后黏度随时间逐步升高直至完全凝胶. 硅溶胶浆液的黏度变化曲线均存在明显拐点,拐点前黏度基本保持不变,拐点后黏度急剧上升. 参考Zhang等[24]的研究,取浆液黏度达到初始黏度2倍时所对应的时间为拐点时间,记作T0,硅溶胶浆液完全凝胶时所对应的时间记作T1. 正交试验方案中硅溶胶浆液的T0与T1见表2,由于样本点较少,为了便于进一步分析,补充测量其他配比下硅溶胶浆液的T0与T1,结果见表2. 研究发现T0与T1表现出线性函数关系,两者的拟合直线如图9所示,拟合直线表达式为T1=
图 8
图 8 不同配比硅溶胶浆液黏度随时间的变化曲线
Fig.8 Viscosity change curve of silica sol slurry with time under different ratios
表 2 不同配比硅溶胶浆液的T0及T1
Tab.2
| 试验 | 编号 | 试样 | T0/min | T1/min |
| 正交试验中硅溶胶浆液 | 1 | S30-4-8 | 28 | 58 |
| 2 | S30-6-10 | 27 | 56 | |
| 3 | S30-8-12 | 37 | 75 | |
| 4 | S25-4-10 | 18 | 34 | |
| 5 | S25-6-12 | 37 | 70 | |
| 6 | S25-8-8 | 504 | 720 | |
| 7 | S20-4-12 | 7 | 13 | |
| 8 | S20-6-8 | 510 | 790 | |
| 9 | S20-8-10 | 480 | 750 | |
| 补充试验中硅溶胶浆液 | 10 | S30-4-10 | 8 | 16 |
| 11 | S30-8-10 | 103 | 185 | |
| 12 | S30-6-8 | 96 | 150 | |
| 13 | S30-6-12 | 12 | 24 | |
| 14 | S25-6-10 | 80 | 155 | |
| 15 | S20-6-10 | 222 | 430 |
图 9
图 9 硅溶胶浆液黏度拐点时间与其凝胶时间的拟合直线
Fig.9 Linear fit between viscosity inflection time and gel time of silica sol slurry
为了定量分析硅溶胶浆液的黏度拐点时间、凝胶时间与硅溶胶溶液中二氧化硅颗粒的质量分数(ws)、硅胶比(m)、胶凝剂溶液中溶质的质量分数即氯化钠溶液中氯化钠的质量分数(wn)的关系,参考Zhang等[24]的研究引入参数λ,λ的表达式如下:
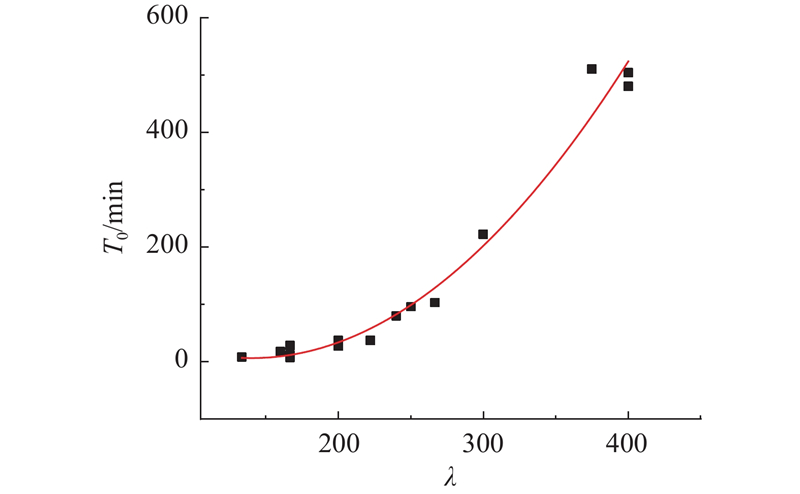
T0与λ的拟合曲线如图10所示,拟合曲线表达式为T0=
图 10
图 10 硅溶胶浆液黏度拐点时间与参数λ的拟合曲线
Fig.10 Fitting curve between viscosity inflection time of silica sol slurry and parameter λ
3.2. 硅溶胶加固体力学特性分析
3.2.1. 无侧限抗压强度试验结果分析
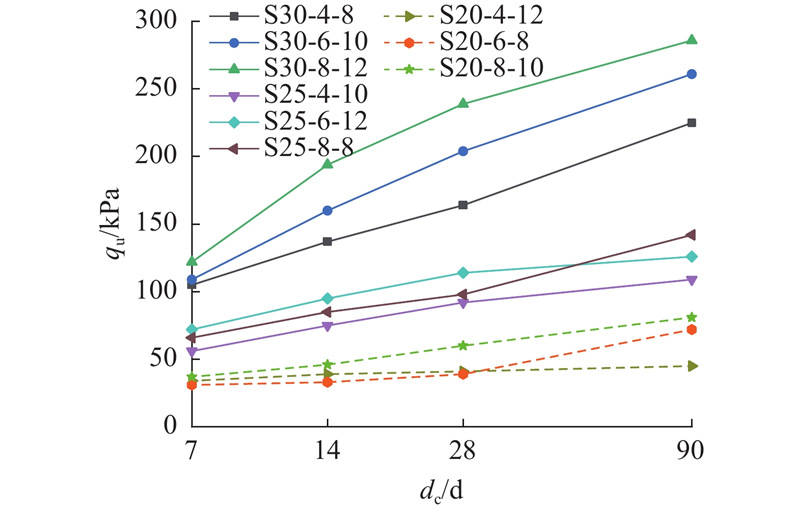
不同配比硅溶胶加固体在不同养护天数dc下的无侧限抗压强度qu如图11所示. 试验结果表明:硅溶胶加固体抗压强度随着养护天数的增加而不断增长,这是由于硅烷醇基团之间的缩合反应随时间的延长持续进行,生成硅氧烷键的数量越来越多,使得内部结构愈加致密.
图 11
图 11 不同配比硅溶胶加固体在不同养护天数下的无侧限抗压强度
Fig.11 Unconfined compressive strength of silica sol reinforced soil under different ratios and different curing days
硅溶胶加固体抗压强度与硅溶胶溶液中二氧化硅颗粒的质量分数(ws)、硅胶比(m)、氯化钠溶液中氯化钠的质量分数(wn)这3种因素密切相关,具体关系如下.
1)ws是影响硅溶胶加固体抗压强度的最主要因素,ws越大则加固体抗压强度越大. S30-4-8、S30-6-10和S30-8-12硅溶胶加固体7 d抗压强度均大于100 kPa,90 d抗压强度最高可达到286 kPa,远高于其他配比的硅溶胶加固体,根本原因在于ws越高,硅溶胶凝胶时脱水缩合反应生成的硅氧烷键数量越多,加固体强度越大.
2)wn增大会提升硅溶胶加固体的早期强度,但加固体的长期强度仍然由ws决定. 以S20-4-12、S20-6-8硅溶胶加固体为例,根据表1,硅溶胶与胶凝剂混合后,S20-4-12中ws为16.0%,wn为2.4%,S20-6-8中ws为17.1%,wn为1.1%. S20-4-12硅溶胶加固体7、14 、90 d的抗压强度分别为34、39、45 kPa,S20-6-8对应的抗压强度分别为31、33、72 kPa. S20-4-12与S20-6-8相比,wn偏大,ws偏小,因此其加固体短期强度例如7 、28 d的抗压强度偏大,长期强度例如90 d的抗压强度反而偏小. 这种现象的根本原因在于wn越大则脱水缩合反应越快,早期生成硅氧烷键数量越多,其强度越高,但最终生成的硅氧烷键数量由ws所决定.
3)m增大会导致硅溶胶与胶凝剂混合后的ws增大,wn减小. 因此,硅胶比增大可能会影响加固体的短期强度,但加固体的长期强度会明显提高.
3.2.2. 三轴压缩试验结果分析
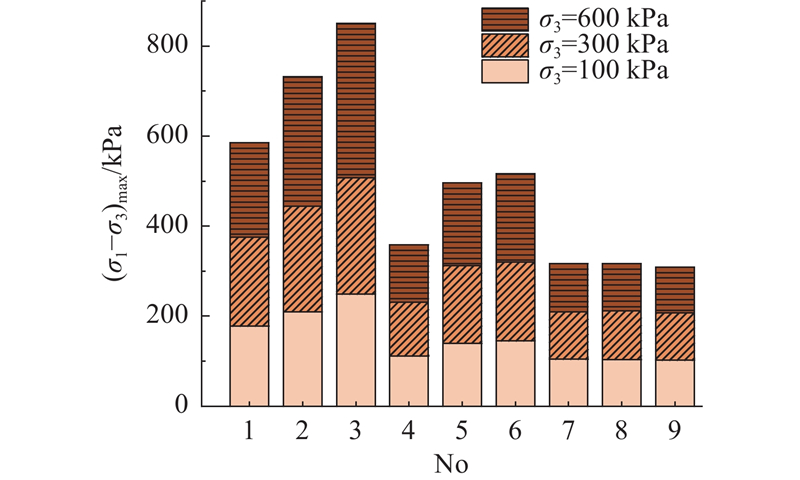
不同配比硅溶胶加固体在100、300、600 kPa围压下的最大偏应力
图 12
图 12 不同配比硅溶胶加固体在不同围压下的最大偏应力
Fig.12 Maximum deviatoric stress of silica sol reinforced soil under different ratios and different confining pressures
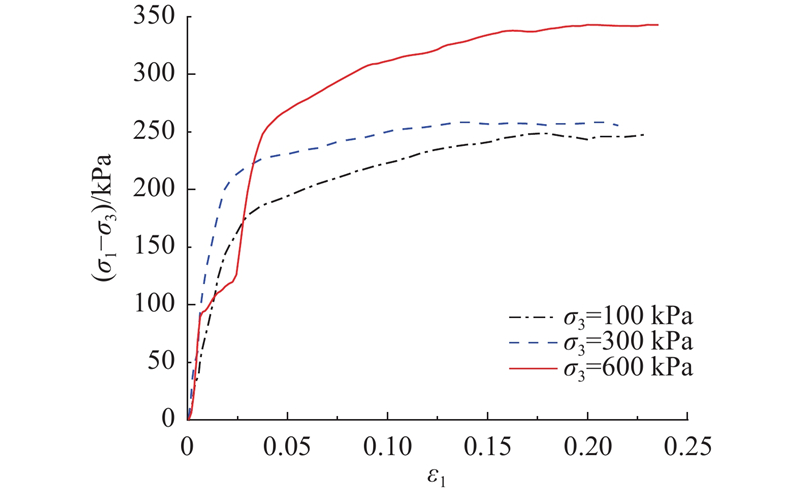
图 13
图 13 S30-8-12硅溶胶加固体的应力-应变曲线
Fig.13 Stress-strain curve of S30-8-12 silica sol reinforced soil
表 3 不同配比硅溶胶加固体的抗剪强度指标
Tab.3
| 编号 | 试样 | c/kPa | φ/(°) |
| 1 | S30-4-8 | 84.3 | 1.8 |
| 2 | S30-6-10 | 95.1 | 2.5 |
| 3 | S30-8-12 | 104.3 | 4.4 |
| 4 | S25-4-10 | 53.3 | 0.9 |
| 5 | S25-6-12 | 67.8 | 2.1 |
| 6 | S25-8-8 | 57.9 | 1.7 |
| 7 | S20-4-12 | 48.1 | 0.5 |
| 8 | S20-6-8 | 47.9 | 0.7 |
| 9 | S20-8-10 | 49.6 | 0.3 |
3.3. 硅溶胶加固体渗透特性分析
不同配比硅溶胶加固体在养护天数dc分别为0、7、14和28下的渗透系数K见表4. 加固体的抗渗性能与硅溶胶浆液配比有关,当硅溶胶与胶凝剂混合后浆液中的ws与wn较大时,加固体初期的渗透系数即可达到10−8 cm/s数量级,后持续稳定在这一数量级,例如S30-4-8、S30-6-10、S25-6-12等. 当混合后浆液中的ws或wn较小时,加固体初期渗透系数为10−5~10−6 cm/s,随着试验的进行,渗透系数逐渐降低,最终同样稳定在10−8 cm/s数量级. 这种现象的根本原因在于ws与wn较大时,前期即可生成大量的硅氧烷键,结构已经足够致密,因此加固体早期的渗透系数即可达到较低水平. ws或wn较小时,前期生成的硅氧烷键较少,内部结构不够紧密,因此加固体早期的渗透系数偏大,但随着时间的延长,硅烷醇基团之间的缩合反应随持续进行,生成硅氧烷键的数量越来越多,使得内部结构愈加致密,加固体的渗透系数最终也能达到较低水平. 此外,测得全风化花岗岩土体的渗透系数为10−3~10−4 cm/s数量级,表明硅溶胶注浆后土体的抗渗性能得到了显著加强.
表 4 不同配比硅溶胶加固体在不同养护天数下的渗透系数
Tab.4
| 编号 | 试样 | K/(cm·s−1) | |||
| dc=0 | dc=7 | dc=14 | dc=28 | ||
| 1 | S30-4-8 | 1.20×10−8 | 1.40×10−8 | 1.35×10−8 | 1.38×10−8 |
| 2 | S30-6-10 | 1.77×10−8 | 1.68×10−8 | 1.52×10−8 | 1.47×10−8 |
| 3 | S30-8-12 | 1.02×10−8 | 1.36×10−8 | 1.23×10−8 | 1.05×10−8 |
| 4 | S25-4-10 | 3.99×10−8 | 3.00×10−8 | 2.82×10−8 | 2.73×10−8 |
| 5 | S25-6-12 | 2.94×10−8 | 2.39×10−8 | 2.36×10−8 | 2.35×10−8 |
| 6 | S25-8-8 | 2.36×10−5 | 9.41×10−6 | 2.81×10−6 | 1.59×10−8 |
| 7 | S20-4-12 | 3.34×10−5 | 6.69×10−6 | 1.46×10−6 | 1.09×10−7 |
| 8 | S20-6-8 | 5.24×10−6 | 1.81×10−6 | 4.15×10−8 | 2.60×10−8 |
| 9 | S20-8-10 | 4.01×10−6 | 1.21×10−6 | 2.43×10−8 | 2.42×10−8 |
3.4. 硅溶胶渗透规律分析
3.4.1. 同时考虑黏度时变性及迂曲度的理论公式
在本研究中,探讨硅溶胶在全风化花岗岩土体中的渗透规律须遵循以下基本假定:1)全风化花岗岩土体均质,各向同性. 2)硅溶胶在渗透扩散过程中始终处于层流状态,并符合达西定律. 3)硅溶胶浆液视为牛顿流体,不可压缩. 4)注浆过程中土体无压缩或压缩很小,即不考虑压密注浆. 5)忽略重力影响.
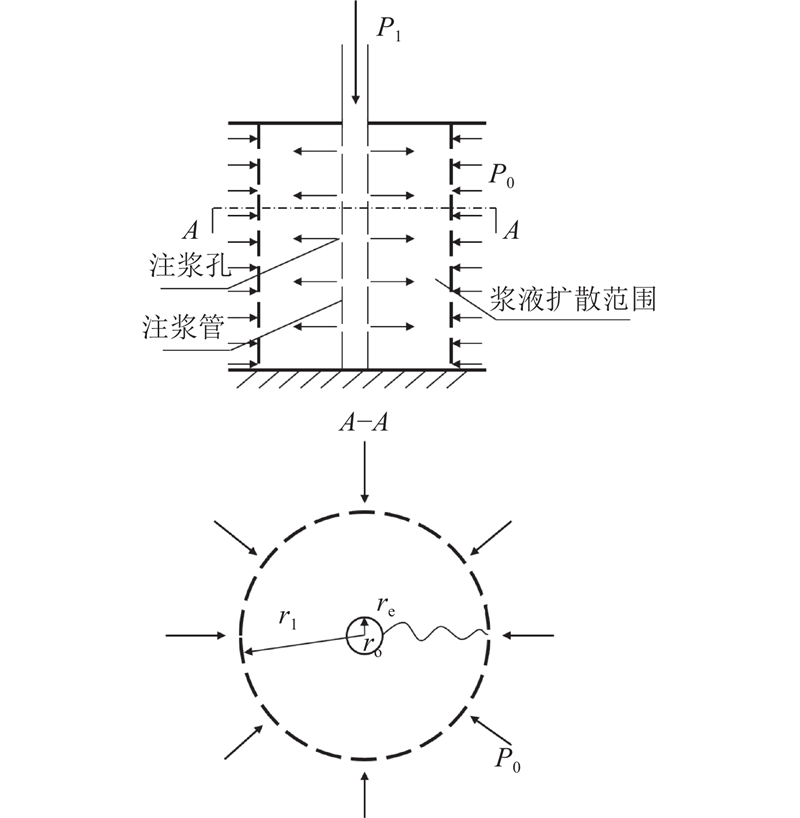
注浆模拟试验中注浆孔为梅花形布置,因此理论上硅溶胶浆液在全风化花岗岩土体中为柱形扩散,示意图如图14所示. 图中,P1为注浆压力,P0为孔隙水压力,re为实际扩散路径长度,r1为浆液最终扩散半径. r0为注浆孔半径.
图 14
同时考虑浆液黏度时变性及土体迂曲度的柱形扩散渗透注浆理论公式推导如下:
式中:Q为浆液渗透量,v为浆液的渗流速度,A为浆液渗透面的总横截面积,r为浆液等效扩散半径,K为渗透系数,β(t)为t时刻浆液与水的黏度系数比值,Γ为迂曲度,P为浆液流动过程中受到的压力,h为浆液等效扩散高度.
等式两侧积分,得到
整理后,得到
得出柱形扩散渗透注浆理论公式:
式中:n为孔隙率.
根据戴邵衡等[25]的研究成果,假设地层为各向同性,迂曲度Γ计算公式为
3.4.2. 注浆模拟试验结果分析
注浆模拟试验中各组土体参数见表5. 参考硅溶胶浆液的凝胶时间及加固体的力学、抗渗性能,选定浆液配比为S25-8-8. 在此配比下,硅溶胶加固体养护28 d后无侧限抗压强度达到98 kPa,渗透系数低至1.59×10−8 cm/s,凝胶时间为720 min,可以满足大多数注浆工程要求.
表 5 注浆模拟试验各组土体参数
Tab.5
| 编号 | ρd/(g·cm−3) | n/% | Γ | K/(cm·s−1) |
| 1 | 1.30 | 50.0 | 1.250 | 1.32×10−3 |
| 2 | 1.36 | 47.7 | 1.260 | 5.80×10−4 |
| 3 | 1.42 | 45.0 | 1.275 | 2.73×10−4 |
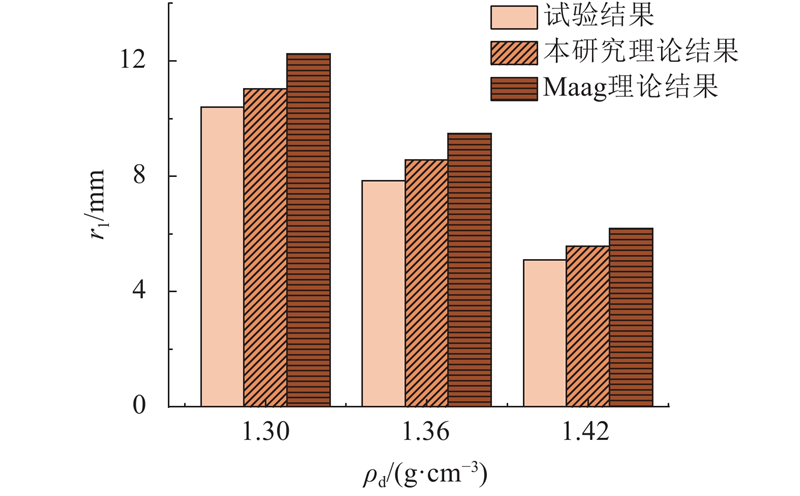
各组注浆结石体尺寸如图15所示,直径分别为10.4、7.85、5.10 cm,表明硅溶胶浆液在干密度分别为1.30、1.36、1.42 g/cm3的全风化花岗岩土体中实际扩散半径分别为10.4、7.85、5.10 cm. 根据式(3)计算得到各组试验中浆液理论扩散半径分别为11.03、8.56、5.58 cm,若不考虑浆液黏度时变性及土体迂曲度,根据传统的Maag理论渗透注浆理论公式计算得到各组试验中浆液扩散半径分别为12.24、9.48、6.18 cm. 将2种理论计算结果与试验结果进行对比,结果如图16所示. Maag理论计算结果与本研究理论计算结果均大于试验结果,其中Maag理论计算结果平均偏大19.8%,本研究理论计算结果平均偏大8.1%. 因此,同时考虑浆液黏时变性及迂曲度的渗透注浆理论更能准确描述硅溶胶在全风化花岗岩土体中的渗透扩散情况,估算其渗透扩散范围.
图 15
图 16
图 16 硅溶胶浆液在不同干密度土体中的扩散半径结果对比
Fig.16 Comparison of diffusion radius results of silica sol slurry in soils with different dry densities
4. 结 论
(1)硅溶胶浆液的初始黏度低至1~2 mPa·s,表现出优异的可注性. 硅溶胶浆液黏度的拐点时间(T0)与硅溶胶溶液中二氧化硅颗粒的质量分数(ws)、硅胶比(m)、氯化钠溶液中氯化钠的质量分数(wn)密切相关,本研究提出了相应公式. 实际工程中,可以根据具体需求确定浆液黏度的拐点时间,再通过调节ws、m以及wn来获取满足注浆要求的硅溶胶浆液.
(2)硅溶胶对全风化花岗岩的加固机制源于硅羟基发生脱水缩合反应所形成的硅氧烷键,硅氧烷键的数量越多则强度与抗渗性能越强且缩合反应会随着时间的增长持续进行. 因此,硅溶胶对全风化花岗岩的防渗加固效果会随着时间的增长而不断增强且ws越大,生成硅氧烷键数量越多,加固效果越好. 加固体养护28 d后的渗透系数低至10−8 cm/s数量级且抗压强度最高达到239 kPa,在养护90 d后抗压强度最高达到286 kPa.
(3)通过室内注浆模拟试验发现硅溶胶在全风化花岗岩土体中具备良好的可注性. 在注浆压力为10 kPa下,将硅溶胶注入至干密度分别为1.30、1.36 、1.42 g/cm3的全风化花岗岩土体中,浆液的扩散半径分别达到10.40、7.85、5.10 cm.
(4)推导出同时考虑浆液黏度时变性和土体迂曲度的渗透注浆理论公式,可准确地估算出硅溶胶在全风化花岗岩土体中的渗透扩散范围,为实际注浆工程提供科学指导和理论依据.
(5)尽管本研究取得了一些重要成果,但仍存在不足之处,主要在于通过制作并测量硅溶胶加固体的力学强度和渗透系数的方法来研究硅溶胶对全风化花岗岩的加固效果,存在一定的局限性. 为了更贴合实际情况,下一步研究拟进行现场注浆试验,并在注浆后取原状土体进行强度性能测试,可以更好地反映硅溶胶的实际加固效果.
参考文献
广东梅州花岗岩风化壳剖面的可见光-短波红外反射光谱特征及其对风化强度的指示
[J].
Visible to shortwave-infrared spectroscopic characteristics and weathering intensity indicators of a weathering-crust-type REE deposit in granite bedrock, from Meizhou, Guangdong Province
[J].
Chemical weathering indices and how they relate to the mechanical parameters of granite regolith from Southern China
[J].DOI:10.1016/j.catena.2022.106400 [本文引用: 1]
赣南花岗岩风化带岩土体强度特征及边坡破坏模式分析
[J].
Strength characteristics of granite weathering zone and analysis of slope failure mode in south Jiangxi Province
[J].
全风化花岗岩与花岗岩残积土的判别及物理力学性质对比
[J].
Identification and physical mechanical property comparison between completely decomposed granite and granite residual soil
[J].
海底强风化花岗岩K0固结三轴试验尺寸效应
[J].
Specimen size effect of strongly weathered granite of seabed in triaxial tests under K0-consolidation condition
[J].
Experimental and analytical studies on the influence of weathering degree and ground-environment analog conditions on the tribological behavior of granite
[J].DOI:10.1016/j.enggeo.2022.106644 [本文引用: 1]
富水全风化花岗岩隧道注浆加固技术研究
[J].
Study on grouting reinforcement technology of water rich fully weathered granite tunnel
[J].
全风化花岗岩富水地层注浆治理研究与应用
[J].
Study and application of grouting governing of completely weathered granite in water-rich stratum
[J].
含CaCl2水基聚合物钻井液沿井周地层渗透规律研究
[J].
Study on permeability law of water-based polymer drilling fluid containing CaCl2 in wellbore formation
[J].
全风化花岗岩地层中高固相离析浆液灌浆机理研究
[J].
A study of grouting mechanism of high solid phase segregation grout in fully weathered granite
[J].
厦门花岗岩残积土的压缩变形特性及其微观机制
[J].
Compression characteristics and microscopic mechanism of Xiamen granite residual soil
[J].
Formulation and comparison of algorithms for frictional contact problems
[J].DOI:10.1002/(SICI)1097-0207(19980515)42:1<145::AID-NME358>3.0.CO;2-L [本文引用: 1]
Design of grouting with silica Sol in hard rock: new design criteria tested in the field, Part II
[J].DOI:10.1016/j.tust.2006.12.004 [本文引用: 1]
Drip sealing of tunnels in hard rock: a new concept for the design and evaluation of permeation grouting
[J].DOI:10.1016/j.tust.2009.09.008 [本文引用: 1]
Permeation grouting of silt-sand mixtures
[J].DOI:10.1016/j.trgeo.2022.100800 [本文引用: 1]
Sealing of narrow fractures in hard rock: a case study in Hallandsas, Sweden
[J].
Effect of dilution and contaminants on sand grouted with colloidal silica
[J].DOI:10.1061/(ASCE)1090-0241(1999)125:6(461) [本文引用: 1]
Fissure grouting mechanism accounting for the time-dependent viscosity of silica Sol
[J].DOI:10.1021/acsomega.1c04216 [本文引用: 2]