(5) $\begin{split} &f\left(\lambda_1, \lambda_2, \cdots, \lambda_n\right)=\\ &\qquad \left\{\begin{array}{l}\left\{{\dfrac{1}{N} \displaystyle\sum_{i=1}^N \dfrac{\mu\left(\lambda_1, \lambda_2, \cdots, \lambda_n\right)-\mu_i^*}{\mu_i^*}}\right\}^{1/2}, \\\quad {{\mathrm{average}}}\left(\mu\left(\lambda_1, \lambda_2, \cdots, \lambda_n\right)\right) \geqslant \\\qquad {{\mathrm{average}}}\left(\mu_i^*\right) ;\\-\left\{{\dfrac{1}{N} \displaystyle\sum_{i=1}^N\dfrac{\mu\left(\lambda_1, \lambda_2, \cdots, \lambda_n\right)-\mu_i^*}{\mu_i^*} }\right\}^{1/2}, \\ \quad {\text{其他}}.\end{array}\right.\end{split} $
[1]
OLDECOP L A, ALONSO E E Theoretical investigation of the time-dependent behaviour of rockfill
[J]. Géotechnique , 2007 , 57 (3 ): 289 - 301
[本文引用: 1]
[2]
SOWERS G F, WILLIAMS R C, WALLACE T S. Compressibility of broken rock and the settlement of rockfills [C]// 6th International Conference on Soil Mechanics and Foundation Engineering . Montreal: [s. n. ], 1965: 561−565.
[本文引用: 1]
[3]
MAHINROOSTA R, ALIZADEH A, GATMIRI B Simulation of collapse settlement of first filling in a high rockfill dam
[J]. Engineering Geology , 2015 , 187 : 32 - 44
DOI:10.1016/j.enggeo.2014.12.013
[本文引用: 1]
[4]
JIA Y, CHI S Back-analysis of soil parameters of the Malutang II concrete face rockfill dam using parallel mutation particle swarm optimization
[J]. Computers and Geotechnics , 2015 , 65 : 87 - 96
DOI:10.1016/j.compgeo.2014.11.013
[本文引用: 1]
[5]
SHU X, BAO T, LI Y, et al VAE-TALSTM: a temporal attention and variational autoencoder-based long short-term memory framework for dam displacement prediction
[J]. Engineering with Computers , 2022 , 38 (4 ): 3497 - 3512
DOI:10.1007/s00366-021-01362-2
[本文引用: 1]
[6]
ZHU Y, XIE M, ZHANG K, et al A dam deformation residual correction method for high arch dams using phase space reconstruction and an optimized long short-term memory network
[J]. Mathematics , 2023 , 11 (9 ): 2010
DOI:10.3390/math11092010
[7]
LI Y, HARIRI-ARDEBILI M A, DENG T, et al A surrogate-assisted stochastic optimization inversion algorithm: parameter identification of dams
[J]. Advanced Engineering Informatics , 2023 , 55 : 101853
DOI:10.1016/j.aei.2022.101853
[本文引用: 1]
[8]
TONINI D. Observed behavior of several Italian arch dams [J]. Journal of the Power Division , 1956, 82(6): False.
[本文引用: 1]
[9]
陈久宇 应用实测位移资料研究刘家峡重力坝横缝的结构作用
[J]. 水利学报 , 1982 , 13 (12 ): 12 - 20
[本文引用: 1]
CHEN Jiuyu An investigation of linking action of transverse joints in Liujiaxia gravity dam by analyzing observed deflection data
[J]. Journal of Hydraulic Engineering , 1982 , 13 (12 ): 12 - 20
[本文引用: 1]
[10]
SALAZAR F, MORÁN R, TOLEDO M Á, et al Data-based models for the prediction of dam behaviour: a review and some methodological considerations
[J]. Archives of Computational Methods in Engineering , 2017 , 24 (1 ): 1 - 21
DOI:10.1007/s11831-015-9157-9
[本文引用: 1]
[11]
CAO E, BAO T, YUAN R, et al Hierarchical prediction of dam deformation based on hybrid temporal network and load-oriented residual correction
[J]. Engineering Structures , 2024 , 308 : 117949
DOI:10.1016/j.engstruct.2024.117949
[本文引用: 1]
[12]
JIA Y, CHI S Back-analysis of soil parameters of the Malutang II concrete face rockfill dam using parallel mutation particle swarm optimization
[J]. Computers and Geotechnics , 2015 , 65 : 87 - 96
DOI:10.1016/j.compgeo.2014.11.013
[本文引用: 1]
[13]
ZHOU W, LI S, MA G, et al Parameters inversion of high central core rockfill dams based on a novel genetic algorithm
[J]. Science China Technological Sciences , 2016 , 59 (5 ): 783 - 794
DOI:10.1007/s11431-016-6017-2
[本文引用: 1]
[14]
康飞, 李俊杰, 许青 堆石坝参数反演的蚁群聚类RBF网络模型
[J]. 岩石力学与工程学报 , 2009 , 28 (Suppl.2 ): 3639 - 3644
[本文引用: 1]
KANG Fei, LI Junjie, XU Qing Ant colony clustering radial basis function network model for inverse analysis of rockfill dam
[J]. Chinese Journal of Rock Mechanics and Engineering , 2009 , 28 (Suppl.2 ): 3639 - 3644
[本文引用: 1]
[15]
ZHOU X, SUN X, LI Y, et al Creep parameter inversion for high CFRDs based on improved BP neural network response surface method
[J]. Soft Computing , 2022 , 26 (18 ): 9527 - 9541
DOI:10.1007/s00500-022-06735-3
[本文引用: 1]
[16]
宋子屹. 基于云神经网络的土石坝坝料动力参数反演研究 [D]. 郑州: 华北水利水电大学, 2022.
[本文引用: 1]
SONG Ziyi. Inversion study of dynamic parameters of earth and rock dam materials based on cloud neural network [D]. Zhengzhou: North China University of Water Resources and Electric Power, 2022.
[本文引用: 1]
[17]
李少林, 王朝晴, 周伟, 等 高心墙堆石坝瞬变-流变参数解耦反分析方法及变形预测
[J]. 长江科学院院报 , 2018 , 35 (9 ): 86 - 91
[本文引用: 2]
LI Shaolin, WANG Zhaoqing, ZHOU Wei, et al Decoupling inversion of instantaneous and rheological parameters and deformation prediction of high core-wall rockfill dam
[J]. Journal of Yangtze River Scientific Research Institute , 2018 , 35 (9 ): 86 - 91
[本文引用: 2]
[18]
杨荷, 周伟, 马刚, 等 基于响应面法的高堆石坝瞬变-流变参数反演方法
[J]. 岩土力学 , 2016 , 37 (6 ): 1697 - 1705
[本文引用: 1]
YANG He, ZHOU Wei, MA Gang, et al Inversion of instantaneous and rheological parameters of high rockfill dams based on response surface method
[J]. Rock and Soil Mechanics , 2016 , 37 (6 ): 1697 - 1705
[本文引用: 1]
[19]
柯虎 高心墙堆石坝蓄水变形和裂缝机理分析
[J]. 水电与新能源 , 2020 , 34 (1 ): 44 - 51
[本文引用: 1]
KE Hu Analysis of the impoundment deformation and cracking mechanism of a high core wall rockfill dam
[J]. Hydropower and New Energy , 2020 , 34 (1 ): 44 - 51
[本文引用: 1]
[20]
CHEN C, LU X, LI J, et al A novel settlement forecasting model for rockfill dams based on physical causes
[J]. Bulletin of Engineering Geology and the Environment , 2021 , 80 (10 ): 7973 - 7988
DOI:10.1007/s10064-021-02403-2
[本文引用: 1]
[21]
吴中如, 陈继禹. 大坝原型观测资料分析方法和模型 [J]. 河海大学科技情报, 1989, 9(2): 48–52, 54–64.
[本文引用: 1]
WU Zhongru, CHEN Jiyu. Analysis method and model of dam prototype observation data [J]. Advances in Science and Technology of Water Resources , 1989, 9(2): 48–52, 54–64.
[本文引用: 1]
[22]
刘正云, 顾冲时 探讨较优的土石坝变形时效模型
[J]. 长江科学院院报 , 2002 , 19 (1 ): 21 - 24
[本文引用: 1]
LIU Zhengyun, GU Chongshi Probe into relatively better time-effect model of earth-rock dam’s deformation
[J]. Journal of Yangtze River Scientific Research Institute , 2002 , 19 (1 ): 21 - 24
[本文引用: 1]
[23]
张艺. 基于观测资料的土石坝后期变形研究 [D]. 大连: 大连理工大学, 2019.
[本文引用: 1]
ZHANG Yi. Research on the later deformation of earth-rock dam based on observation data [D]. Dalian: Dalian University of Technology, 2019.
[本文引用: 1]
[24]
李国英, 米占宽, 傅华, 等 混凝土面板堆石坝堆石料流变特性试验研究
[J]. 岩土力学 , 2004 , 25 (11 ): 1712 - 1716
[本文引用: 2]
LI Guoying, MI Zhankuan, FU Hua, et al Experimental studies on rheological behaviors for rockfills in concrete faced rockfill dam
[J]. Rock and Soil Mechanics , 2004 , 25 (11 ): 1712 - 1716
[本文引用: 2]
[25]
沈珠江, 赵魁芝 堆石坝流变变形的反馈分析
[J]. 水利学报 , 1998 , 29 (6 ): 1 - 6
[本文引用: 1]
SHEN Zhujiang, ZHAO Kuizhi Back analysis of creep deformation of rockfill dams
[J]. Journal of Hydraulic Engineering , 1998 , 29 (6 ): 1 - 6
[本文引用: 1]
[26]
DUNCAN J M, CHANG C Y Nonlinear analysis of stress and strain in soils
[J]. Journal of the Soil Mechanics and Foundations Division , 1970 , 96 (5 ): 1629 - 1653
DOI:10.1061/JSFEAQ.0001458
[本文引用: 1]
[27]
周雄雄. 高心墙堆石坝湿化变形与数值模拟方法研究 [D]. 大连: 大连理工大学, 2020.
[本文引用: 1]
ZHOU Xiongxiong. Study on the wetting deformation and the numerical simulation method of HCRFD [D]. Dalian: Dalian University of Technology, 2020.
[本文引用: 1]
[28]
郭德全, 严军, 杨兴国, 等 瀑布沟高土石坝三维非线性有限元分析
[J]. 人民黄河 , 2014 , 36 (5 ): 93 - 95
[本文引用: 1]
GUO Dequan, YAN Jun, YANG Xingguo, et al The 3-D nonlinear FEM analysis of pubugou high rockfill dam
[J]. Yellow River , 2014 , 36 (5 ): 93 - 95
[本文引用: 1]
[29]
庄文宇, 张如九, 徐建军, 等 基于IAGA-BP算法的高拱坝-坝基力学参数反演分析
[J]. 清华大学学报: 自然科学版 , 2022 , 62 (8 ): 1302 - 1313
[本文引用: 1]
ZHUANG Wenyu, ZHANG Rujiu, XU Jianjun, et al Inversion analysis to determine the mechanical parameters of a high arch dam and its foundation based on an IAGA-BP algorithm
[J]. Journal of Tsinghua University: Science and Technology , 2022 , 62 (8 ): 1302 - 1313
[本文引用: 1]
[30]
叶晓峰, 周伟, 马刚, 等 基于反演参数的心墙堆石坝坝顶裂缝成因研究
[J]. 武汉大学学报: 工学版 , 2022 , 55 (3 ): 220 - 228
[本文引用: 1]
YE Xiaofeng, ZHOU Wei, MA Gang, et al Study on the cause of crest cracking of earth-core rockfill dam based on inversion parameters
[J]. Engineering Journal of Wuhan University , 2022 , 55 (3 ): 220 - 228
[本文引用: 1]
[31]
江金龙. 改进遗传算法及其在波束形成中的应用 [D]. 南京: 河海大学, 2005.
[本文引用: 1]
JIANG Jinlong. Improved genetic algorithm with application to beam-forming for smart antenna [D]. Nanjing: Hohai University, 2005.
[本文引用: 1]
[32]
CHICCO D, WARRENS M J, JURMAN G The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation
[J]. PeerJ Computer Science , 2021 , 7 : e623
DOI:10.7717/peerj-cs.623
[本文引用: 1]
[33]
刘祖德 土石坝变形计算的若干问题
[J]. 岩土工程学报 , 1983 , 5 (1 ): 1 - 13
[本文引用: 1]
LIU Zude Some problems about the calculation of deformation of earth-rock dams
[J]. Chinese Journal of Geotechnical Engineering , 1983 , 5 (1 ): 1 - 13
[本文引用: 1]
[34]
张雯昕. 考虑不确定性的土石坝湿化变形参数反演研究 [D]. 郑州: 华北水利水电大学, 2020.
[本文引用: 1]
ZHANG Wenxin. Research on back analysis of wet deformation parameters of earth-rock dam considering uncertainty [D]. Zhengzhou: North China University of Water Resources and Electric Power, 2022.
[本文引用: 1]
[35]
程欣悦, 马刚, 张贵科, 等 考虑监测数据时序特征和空间分布的堆石坝参数反演研究
[J]. 水力发电学报 , 2024 , 43 (5 ): 54 - 67
[本文引用: 1]
CHENG Xinyue, MA Gang, ZHANG Guike, et al Study on parameter inversion of rockfill dams considering time series features and spatial distribution of monitoring data
[J]. Journal of Hydroelectric Engineering , 2024 , 43 (5 ): 54 - 67
[本文引用: 1]
[36]
朱晟, 路德任 基于改进粒子群算法的面板堆石坝流变反演分析
[J]. 岩石力学与工程学报 , 2022 , 41 (Suppl.1 ): 2971 - 2978
[本文引用: 1]
ZHU Sheng, LU Deren Rheological inversion analysis of CFRD based on improved particle swarm optimization algorithm
[J]. Chinese Journal of Rock Mechanics and Engineering , 2022 , 41 (Suppl.1 ): 2971 - 2978
[本文引用: 1]
Theoretical investigation of the time-dependent behaviour of rockfill
1
2007
... 堆石坝变形控制与破坏机理研究对大坝安全具有重要意义. 目前研究主要将堆石坝变形分为填筑期的瞬时变形和竣工后的后期变形. 堆石料具有流变和湿化特性,使得大坝竣工后仍会发生长达数年甚至数十年的后期变形[1 -2 ] . 心墙堆石坝在初次蓄水过程中,因上游堆石料的湿化变形,坝体会产生明显沉降,变形过大将会导致坝体产生明显的不均匀沉降,甚至引发坝顶裂缝. 可见,土石坝竣工后受蓄水影响产生的湿化变形和受时间影响产生的流变变形会对坝体结构安全产生不利影响,甚至可能导致工程故障或破坏,因此对土石坝变形的分析研究十分必要. ...
1
... 堆石坝变形控制与破坏机理研究对大坝安全具有重要意义. 目前研究主要将堆石坝变形分为填筑期的瞬时变形和竣工后的后期变形. 堆石料具有流变和湿化特性,使得大坝竣工后仍会发生长达数年甚至数十年的后期变形[1 -2 ] . 心墙堆石坝在初次蓄水过程中,因上游堆石料的湿化变形,坝体会产生明显沉降,变形过大将会导致坝体产生明显的不均匀沉降,甚至引发坝顶裂缝. 可见,土石坝竣工后受蓄水影响产生的湿化变形和受时间影响产生的流变变形会对坝体结构安全产生不利影响,甚至可能导致工程故障或破坏,因此对土石坝变形的分析研究十分必要. ...
Simulation of collapse settlement of first filling in a high rockfill dam
1
2015
... 数值模拟是预测大坝应力变形与分析安全特性的重要手段. 在进行模拟时,选择合适的力学模型和准确的参数尤为关键. 在传统模拟中,瞬时、湿化和流变变形往往采用单独的模型,而获取坝料力学参数的途径主要包括现场取样试验和基于监测数据的参数反演[3 ] . 研究表明,试验获得的参数因扰动性和尺寸效应的影响,常与实际工程中的力学参数不同[4 ] . 例如,流变变形持续多年,而室内流变试验结果多在数周或数月内完成,导致模拟结果常与监测值差异明显. 因此,结合监测数据反演后期变形模型参数对于准确预测大坝后期变形至关重要. ...
Back-analysis of soil parameters of the Malutang II concrete face rockfill dam using parallel mutation particle swarm optimization
1
2015
... 数值模拟是预测大坝应力变形与分析安全特性的重要手段. 在进行模拟时,选择合适的力学模型和准确的参数尤为关键. 在传统模拟中,瞬时、湿化和流变变形往往采用单独的模型,而获取坝料力学参数的途径主要包括现场取样试验和基于监测数据的参数反演[3 ] . 研究表明,试验获得的参数因扰动性和尺寸效应的影响,常与实际工程中的力学参数不同[4 ] . 例如,流变变形持续多年,而室内流变试验结果多在数周或数月内完成,导致模拟结果常与监测值差异明显. 因此,结合监测数据反演后期变形模型参数对于准确预测大坝后期变形至关重要. ...
VAE-TALSTM: a temporal attention and variational autoencoder-based long short-term memory framework for dam displacement prediction
1
2022
... 随着大坝安全监测精度的不断提高,基于原型观测资料分析大坝变形规律与安全特性已成为分析大坝变形的重要手段[5 -7 ] . Tonini[8 ] 分析并总结了影响大坝变形的因素,首次将大坝变形分离为受水压、温度和时间因素影响的3个部分,并基于回归分析法构建了第1个大坝变形数学模型. 陈久宇[9 ] 结合刘家峡枢纽工程,利用逐步回归分析方法,建立了基于水位、时间和温度3个因素的统计模型,对大坝沉降变形做出了预测. 近年来,深度学习和人工智能算法逐渐应用于大坝安全监测数据分析,提高了变形预测精度[10 -11 ] . ...
A dam deformation residual correction method for high arch dams using phase space reconstruction and an optimized long short-term memory network
0
2023
A surrogate-assisted stochastic optimization inversion algorithm: parameter identification of dams
1
2023
... 随着大坝安全监测精度的不断提高,基于原型观测资料分析大坝变形规律与安全特性已成为分析大坝变形的重要手段[5 -7 ] . Tonini[8 ] 分析并总结了影响大坝变形的因素,首次将大坝变形分离为受水压、温度和时间因素影响的3个部分,并基于回归分析法构建了第1个大坝变形数学模型. 陈久宇[9 ] 结合刘家峡枢纽工程,利用逐步回归分析方法,建立了基于水位、时间和温度3个因素的统计模型,对大坝沉降变形做出了预测. 近年来,深度学习和人工智能算法逐渐应用于大坝安全监测数据分析,提高了变形预测精度[10 -11 ] . ...
1
... 随着大坝安全监测精度的不断提高,基于原型观测资料分析大坝变形规律与安全特性已成为分析大坝变形的重要手段[5 -7 ] . Tonini[8 ] 分析并总结了影响大坝变形的因素,首次将大坝变形分离为受水压、温度和时间因素影响的3个部分,并基于回归分析法构建了第1个大坝变形数学模型. 陈久宇[9 ] 结合刘家峡枢纽工程,利用逐步回归分析方法,建立了基于水位、时间和温度3个因素的统计模型,对大坝沉降变形做出了预测. 近年来,深度学习和人工智能算法逐渐应用于大坝安全监测数据分析,提高了变形预测精度[10 -11 ] . ...
应用实测位移资料研究刘家峡重力坝横缝的结构作用
1
1982
... 随着大坝安全监测精度的不断提高,基于原型观测资料分析大坝变形规律与安全特性已成为分析大坝变形的重要手段[5 -7 ] . Tonini[8 ] 分析并总结了影响大坝变形的因素,首次将大坝变形分离为受水压、温度和时间因素影响的3个部分,并基于回归分析法构建了第1个大坝变形数学模型. 陈久宇[9 ] 结合刘家峡枢纽工程,利用逐步回归分析方法,建立了基于水位、时间和温度3个因素的统计模型,对大坝沉降变形做出了预测. 近年来,深度学习和人工智能算法逐渐应用于大坝安全监测数据分析,提高了变形预测精度[10 -11 ] . ...
应用实测位移资料研究刘家峡重力坝横缝的结构作用
1
1982
... 随着大坝安全监测精度的不断提高,基于原型观测资料分析大坝变形规律与安全特性已成为分析大坝变形的重要手段[5 -7 ] . Tonini[8 ] 分析并总结了影响大坝变形的因素,首次将大坝变形分离为受水压、温度和时间因素影响的3个部分,并基于回归分析法构建了第1个大坝变形数学模型. 陈久宇[9 ] 结合刘家峡枢纽工程,利用逐步回归分析方法,建立了基于水位、时间和温度3个因素的统计模型,对大坝沉降变形做出了预测. 近年来,深度学习和人工智能算法逐渐应用于大坝安全监测数据分析,提高了变形预测精度[10 -11 ] . ...
Data-based models for the prediction of dam behaviour: a review and some methodological considerations
1
2017
... 随着大坝安全监测精度的不断提高,基于原型观测资料分析大坝变形规律与安全特性已成为分析大坝变形的重要手段[5 -7 ] . Tonini[8 ] 分析并总结了影响大坝变形的因素,首次将大坝变形分离为受水压、温度和时间因素影响的3个部分,并基于回归分析法构建了第1个大坝变形数学模型. 陈久宇[9 ] 结合刘家峡枢纽工程,利用逐步回归分析方法,建立了基于水位、时间和温度3个因素的统计模型,对大坝沉降变形做出了预测. 近年来,深度学习和人工智能算法逐渐应用于大坝安全监测数据分析,提高了变形预测精度[10 -11 ] . ...
Hierarchical prediction of dam deformation based on hybrid temporal network and load-oriented residual correction
1
2024
... 随着大坝安全监测精度的不断提高,基于原型观测资料分析大坝变形规律与安全特性已成为分析大坝变形的重要手段[5 -7 ] . Tonini[8 ] 分析并总结了影响大坝变形的因素,首次将大坝变形分离为受水压、温度和时间因素影响的3个部分,并基于回归分析法构建了第1个大坝变形数学模型. 陈久宇[9 ] 结合刘家峡枢纽工程,利用逐步回归分析方法,建立了基于水位、时间和温度3个因素的统计模型,对大坝沉降变形做出了预测. 近年来,深度学习和人工智能算法逐渐应用于大坝安全监测数据分析,提高了变形预测精度[10 -11 ] . ...
Back-analysis of soil parameters of the Malutang II concrete face rockfill dam using parallel mutation particle swarm optimization
1
2015
... 目前,多数学者采用高精度、高效率的智能优化算法和机器学习方法进行参数反演. 部分学者结合工程实际对粒子群[12 ] 、遗传算法[13 ] 之类的代表性优化算法进行改进,以提升收敛效率与计算精度,从而增强反演性能;另有学者将神经网络与蚁群[14 ] 、遗传[15 ] 及云变换[16 ] 等优化算法结合,兼顾神经网络的学习能力与优化算法的寻优能力,实现参数反演的高效计算. 可见,基于人工智能算法的参数反演方法已经开始成为了主流. 然而,当前的参数反演中大多忽视所使用原型监测数据的组成,即造成大坝变形的力学成因,这将影响参数反演的合理性和可靠性. ...
Parameters inversion of high central core rockfill dams based on a novel genetic algorithm
1
2016
... 目前,多数学者采用高精度、高效率的智能优化算法和机器学习方法进行参数反演. 部分学者结合工程实际对粒子群[12 ] 、遗传算法[13 ] 之类的代表性优化算法进行改进,以提升收敛效率与计算精度,从而增强反演性能;另有学者将神经网络与蚁群[14 ] 、遗传[15 ] 及云变换[16 ] 等优化算法结合,兼顾神经网络的学习能力与优化算法的寻优能力,实现参数反演的高效计算. 可见,基于人工智能算法的参数反演方法已经开始成为了主流. 然而,当前的参数反演中大多忽视所使用原型监测数据的组成,即造成大坝变形的力学成因,这将影响参数反演的合理性和可靠性. ...
堆石坝参数反演的蚁群聚类RBF网络模型
1
2009
... 目前,多数学者采用高精度、高效率的智能优化算法和机器学习方法进行参数反演. 部分学者结合工程实际对粒子群[12 ] 、遗传算法[13 ] 之类的代表性优化算法进行改进,以提升收敛效率与计算精度,从而增强反演性能;另有学者将神经网络与蚁群[14 ] 、遗传[15 ] 及云变换[16 ] 等优化算法结合,兼顾神经网络的学习能力与优化算法的寻优能力,实现参数反演的高效计算. 可见,基于人工智能算法的参数反演方法已经开始成为了主流. 然而,当前的参数反演中大多忽视所使用原型监测数据的组成,即造成大坝变形的力学成因,这将影响参数反演的合理性和可靠性. ...
堆石坝参数反演的蚁群聚类RBF网络模型
1
2009
... 目前,多数学者采用高精度、高效率的智能优化算法和机器学习方法进行参数反演. 部分学者结合工程实际对粒子群[12 ] 、遗传算法[13 ] 之类的代表性优化算法进行改进,以提升收敛效率与计算精度,从而增强反演性能;另有学者将神经网络与蚁群[14 ] 、遗传[15 ] 及云变换[16 ] 等优化算法结合,兼顾神经网络的学习能力与优化算法的寻优能力,实现参数反演的高效计算. 可见,基于人工智能算法的参数反演方法已经开始成为了主流. 然而,当前的参数反演中大多忽视所使用原型监测数据的组成,即造成大坝变形的力学成因,这将影响参数反演的合理性和可靠性. ...
Creep parameter inversion for high CFRDs based on improved BP neural network response surface method
1
2022
... 目前,多数学者采用高精度、高效率的智能优化算法和机器学习方法进行参数反演. 部分学者结合工程实际对粒子群[12 ] 、遗传算法[13 ] 之类的代表性优化算法进行改进,以提升收敛效率与计算精度,从而增强反演性能;另有学者将神经网络与蚁群[14 ] 、遗传[15 ] 及云变换[16 ] 等优化算法结合,兼顾神经网络的学习能力与优化算法的寻优能力,实现参数反演的高效计算. 可见,基于人工智能算法的参数反演方法已经开始成为了主流. 然而,当前的参数反演中大多忽视所使用原型监测数据的组成,即造成大坝变形的力学成因,这将影响参数反演的合理性和可靠性. ...
1
... 目前,多数学者采用高精度、高效率的智能优化算法和机器学习方法进行参数反演. 部分学者结合工程实际对粒子群[12 ] 、遗传算法[13 ] 之类的代表性优化算法进行改进,以提升收敛效率与计算精度,从而增强反演性能;另有学者将神经网络与蚁群[14 ] 、遗传[15 ] 及云变换[16 ] 等优化算法结合,兼顾神经网络的学习能力与优化算法的寻优能力,实现参数反演的高效计算. 可见,基于人工智能算法的参数反演方法已经开始成为了主流. 然而,当前的参数反演中大多忽视所使用原型监测数据的组成,即造成大坝变形的力学成因,这将影响参数反演的合理性和可靠性. ...
1
... 目前,多数学者采用高精度、高效率的智能优化算法和机器学习方法进行参数反演. 部分学者结合工程实际对粒子群[12 ] 、遗传算法[13 ] 之类的代表性优化算法进行改进,以提升收敛效率与计算精度,从而增强反演性能;另有学者将神经网络与蚁群[14 ] 、遗传[15 ] 及云变换[16 ] 等优化算法结合,兼顾神经网络的学习能力与优化算法的寻优能力,实现参数反演的高效计算. 可见,基于人工智能算法的参数反演方法已经开始成为了主流. 然而,当前的参数反演中大多忽视所使用原型监测数据的组成,即造成大坝变形的力学成因,这将影响参数反演的合理性和可靠性. ...
高心墙堆石坝瞬变-流变参数解耦反分析方法及变形预测
2
2018
... 土石坝的变形是由自重荷载、湿化、流变效应等多种力学因素作用形成的,故其监测数据是瞬时、流变与湿化变形的耦合值[17 ] . 土石坝数值模拟应针对不同力学成因选用相应模型,如静力本构、流变模型、湿化模型等,以体现力学成因的对应关系. 当前土石坝参数反演中,多数将施工期变形视为瞬时变形、蓄水期视为湿化变形、稳定运行期视为流变变形,分时段进行各模型的参数反演,未考虑各时期监测数据其实是几种变形的耦合值,并未将力学成因的一一对应关系体现出来[18 ] ;亦有学者直接进行多模型参数联合反演,但过程复杂且结果可靠性有限. 因此,须结合大坝数值模拟力学模型和监测资料力学成因分析,对监测数据进行力学成因解耦,分别反演对应的本构和模型参数,以提高土石坝参数反演的合理性和可靠性. ...
... 由于本研究聚焦于大坝湿化流变变形,而E-B模型参数主要影响填筑过程中的变形,其对研究结果的影响较小,故参数取值直接参考本工程相关研究成果[17 ,28 ] ,参数如表2 所示. 其中,$\gamma $ K 为切线模量系数,n 为切线模量指数,R f 为破坏比,c 为材料凝聚力,$\varphi_0 $ $\Delta \varphi $ $K_{\mathrm{b}} $ m 分别为体积模量系数和指数. ...
高心墙堆石坝瞬变-流变参数解耦反分析方法及变形预测
2
2018
... 土石坝的变形是由自重荷载、湿化、流变效应等多种力学因素作用形成的,故其监测数据是瞬时、流变与湿化变形的耦合值[17 ] . 土石坝数值模拟应针对不同力学成因选用相应模型,如静力本构、流变模型、湿化模型等,以体现力学成因的对应关系. 当前土石坝参数反演中,多数将施工期变形视为瞬时变形、蓄水期视为湿化变形、稳定运行期视为流变变形,分时段进行各模型的参数反演,未考虑各时期监测数据其实是几种变形的耦合值,并未将力学成因的一一对应关系体现出来[18 ] ;亦有学者直接进行多模型参数联合反演,但过程复杂且结果可靠性有限. 因此,须结合大坝数值模拟力学模型和监测资料力学成因分析,对监测数据进行力学成因解耦,分别反演对应的本构和模型参数,以提高土石坝参数反演的合理性和可靠性. ...
... 由于本研究聚焦于大坝湿化流变变形,而E-B模型参数主要影响填筑过程中的变形,其对研究结果的影响较小,故参数取值直接参考本工程相关研究成果[17 ,28 ] ,参数如表2 所示. 其中,$\gamma $ K 为切线模量系数,n 为切线模量指数,R f 为破坏比,c 为材料凝聚力,$\varphi_0 $ $\Delta \varphi $ $K_{\mathrm{b}} $ m 分别为体积模量系数和指数. ...
基于响应面法的高堆石坝瞬变-流变参数反演方法
1
2016
... 土石坝的变形是由自重荷载、湿化、流变效应等多种力学因素作用形成的,故其监测数据是瞬时、流变与湿化变形的耦合值[17 ] . 土石坝数值模拟应针对不同力学成因选用相应模型,如静力本构、流变模型、湿化模型等,以体现力学成因的对应关系. 当前土石坝参数反演中,多数将施工期变形视为瞬时变形、蓄水期视为湿化变形、稳定运行期视为流变变形,分时段进行各模型的参数反演,未考虑各时期监测数据其实是几种变形的耦合值,并未将力学成因的一一对应关系体现出来[18 ] ;亦有学者直接进行多模型参数联合反演,但过程复杂且结果可靠性有限. 因此,须结合大坝数值模拟力学模型和监测资料力学成因分析,对监测数据进行力学成因解耦,分别反演对应的本构和模型参数,以提高土石坝参数反演的合理性和可靠性. ...
基于响应面法的高堆石坝瞬变-流变参数反演方法
1
2016
... 土石坝的变形是由自重荷载、湿化、流变效应等多种力学因素作用形成的,故其监测数据是瞬时、流变与湿化变形的耦合值[17 ] . 土石坝数值模拟应针对不同力学成因选用相应模型,如静力本构、流变模型、湿化模型等,以体现力学成因的对应关系. 当前土石坝参数反演中,多数将施工期变形视为瞬时变形、蓄水期视为湿化变形、稳定运行期视为流变变形,分时段进行各模型的参数反演,未考虑各时期监测数据其实是几种变形的耦合值,并未将力学成因的一一对应关系体现出来[18 ] ;亦有学者直接进行多模型参数联合反演,但过程复杂且结果可靠性有限. 因此,须结合大坝数值模拟力学模型和监测资料力学成因分析,对监测数据进行力学成因解耦,分别反演对应的本构和模型参数,以提高土石坝参数反演的合理性和可靠性. ...
高心墙堆石坝蓄水变形和裂缝机理分析
1
2020
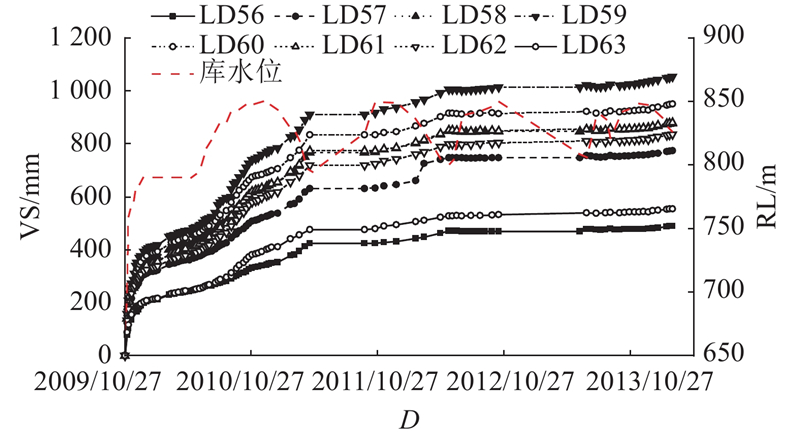
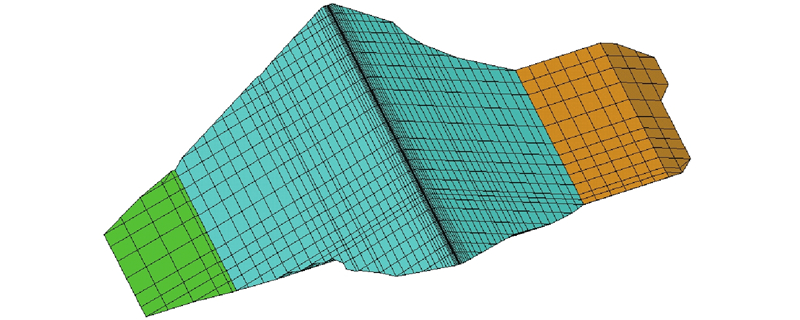
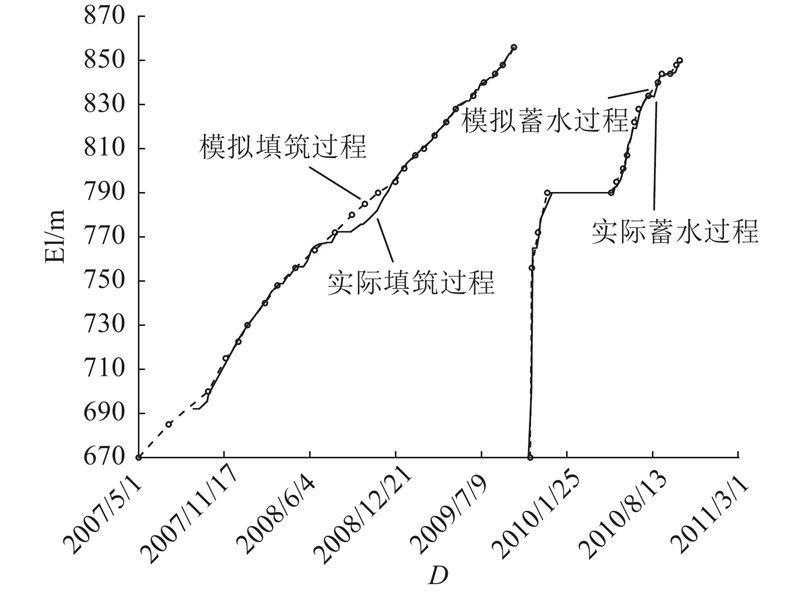
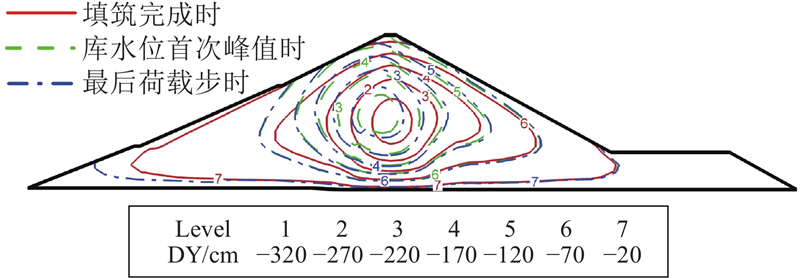
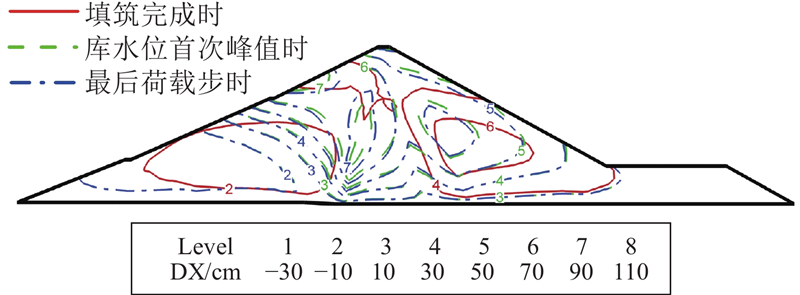
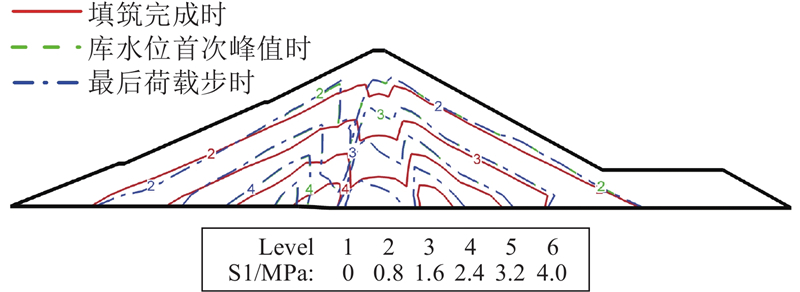
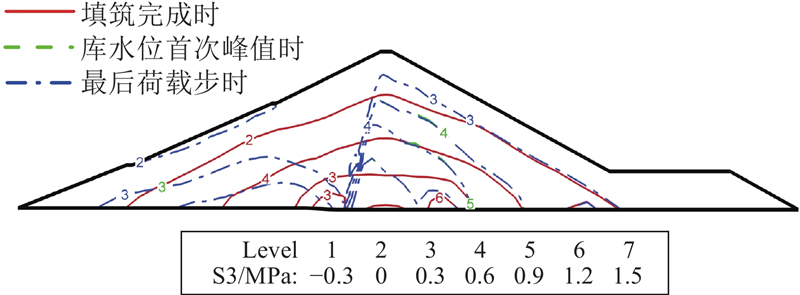
... 瀑布沟心墙堆石坝典型剖面如图1 所示,最大坝高为186 m,坝顶宽度为14 m,底宽为96 m,上游坝坡坡度为1∶2.00与1∶2.25,下游坝坡坡度为1∶1.80. 心墙顶宽为4 m,上、下游侧坡度均为1∶0.25. 正常蓄水位为850.0 m,死水位为790.0 m. 2004年3月大坝开工,2009年9月填筑完成. 分2段蓄水,第1阶段为2009年11月1日—12月13日,首次蓄水至死水位,第2阶段为2010年5月8日—10月13日,二次蓄水至正常蓄水位. 2010年8月26日现场巡视时发现坝顶出现纵向裂缝,库水位约为842.2 m. 裂缝位于坝轴线下游约5.5~6.0 m,基本平行于坝轴线,裂缝长约为230 m,最大缝宽约为5 cm,深度约为1.0~2.5 m[19 ] . ...
高心墙堆石坝蓄水变形和裂缝机理分析
1
2020
... 瀑布沟心墙堆石坝典型剖面如图1 所示,最大坝高为186 m,坝顶宽度为14 m,底宽为96 m,上游坝坡坡度为1∶2.00与1∶2.25,下游坝坡坡度为1∶1.80. 心墙顶宽为4 m,上、下游侧坡度均为1∶0.25. 正常蓄水位为850.0 m,死水位为790.0 m. 2004年3月大坝开工,2009年9月填筑完成. 分2段蓄水,第1阶段为2009年11月1日—12月13日,首次蓄水至死水位,第2阶段为2010年5月8日—10月13日,二次蓄水至正常蓄水位. 2010年8月26日现场巡视时发现坝顶出现纵向裂缝,库水位约为842.2 m. 裂缝位于坝轴线下游约5.5~6.0 m,基本平行于坝轴线,裂缝长约为230 m,最大缝宽约为5 cm,深度约为1.0~2.5 m[19 ] . ...
A novel settlement forecasting model for rockfill dams based on physical causes
1
2021
... 土石坝沉降影响因素包括坝型、剖面形状、坝址地形地质、筑坝材料、施工技术与质量、温度、库水位和时间等,考虑过多因素会增加计算量,降低模型精度,难以准确反映大坝沉降真实情况. 因此,在保证计算精度和效率的前提下,选择适当的影响因素是建立沉降统计模型的关键[20 ] . 在具体大坝工程中,坝型、剖面形状、坝址地形地质、筑坝材料等因素已确定,研究主要考虑填筑过程、上下游水位和时间的影响[21 ] . 本研究聚焦坝顶沉降变形,因测点起测时间在大坝填筑完成之后,无填筑过程变形数据,且测点高程一致,仅考虑水位和时间因素的影响. 建立沉降统计模型[22 -23 ] 如下: ...
1
... 土石坝沉降影响因素包括坝型、剖面形状、坝址地形地质、筑坝材料、施工技术与质量、温度、库水位和时间等,考虑过多因素会增加计算量,降低模型精度,难以准确反映大坝沉降真实情况. 因此,在保证计算精度和效率的前提下,选择适当的影响因素是建立沉降统计模型的关键[20 ] . 在具体大坝工程中,坝型、剖面形状、坝址地形地质、筑坝材料等因素已确定,研究主要考虑填筑过程、上下游水位和时间的影响[21 ] . 本研究聚焦坝顶沉降变形,因测点起测时间在大坝填筑完成之后,无填筑过程变形数据,且测点高程一致,仅考虑水位和时间因素的影响. 建立沉降统计模型[22 -23 ] 如下: ...
1
... 土石坝沉降影响因素包括坝型、剖面形状、坝址地形地质、筑坝材料、施工技术与质量、温度、库水位和时间等,考虑过多因素会增加计算量,降低模型精度,难以准确反映大坝沉降真实情况. 因此,在保证计算精度和效率的前提下,选择适当的影响因素是建立沉降统计模型的关键[20 ] . 在具体大坝工程中,坝型、剖面形状、坝址地形地质、筑坝材料等因素已确定,研究主要考虑填筑过程、上下游水位和时间的影响[21 ] . 本研究聚焦坝顶沉降变形,因测点起测时间在大坝填筑完成之后,无填筑过程变形数据,且测点高程一致,仅考虑水位和时间因素的影响. 建立沉降统计模型[22 -23 ] 如下: ...
探讨较优的土石坝变形时效模型
1
2002
... 土石坝沉降影响因素包括坝型、剖面形状、坝址地形地质、筑坝材料、施工技术与质量、温度、库水位和时间等,考虑过多因素会增加计算量,降低模型精度,难以准确反映大坝沉降真实情况. 因此,在保证计算精度和效率的前提下,选择适当的影响因素是建立沉降统计模型的关键[20 ] . 在具体大坝工程中,坝型、剖面形状、坝址地形地质、筑坝材料等因素已确定,研究主要考虑填筑过程、上下游水位和时间的影响[21 ] . 本研究聚焦坝顶沉降变形,因测点起测时间在大坝填筑完成之后,无填筑过程变形数据,且测点高程一致,仅考虑水位和时间因素的影响. 建立沉降统计模型[22 -23 ] 如下: ...
探讨较优的土石坝变形时效模型
1
2002
... 土石坝沉降影响因素包括坝型、剖面形状、坝址地形地质、筑坝材料、施工技术与质量、温度、库水位和时间等,考虑过多因素会增加计算量,降低模型精度,难以准确反映大坝沉降真实情况. 因此,在保证计算精度和效率的前提下,选择适当的影响因素是建立沉降统计模型的关键[20 ] . 在具体大坝工程中,坝型、剖面形状、坝址地形地质、筑坝材料等因素已确定,研究主要考虑填筑过程、上下游水位和时间的影响[21 ] . 本研究聚焦坝顶沉降变形,因测点起测时间在大坝填筑完成之后,无填筑过程变形数据,且测点高程一致,仅考虑水位和时间因素的影响. 建立沉降统计模型[22 -23 ] 如下: ...
1
... 土石坝沉降影响因素包括坝型、剖面形状、坝址地形地质、筑坝材料、施工技术与质量、温度、库水位和时间等,考虑过多因素会增加计算量,降低模型精度,难以准确反映大坝沉降真实情况. 因此,在保证计算精度和效率的前提下,选择适当的影响因素是建立沉降统计模型的关键[20 ] . 在具体大坝工程中,坝型、剖面形状、坝址地形地质、筑坝材料等因素已确定,研究主要考虑填筑过程、上下游水位和时间的影响[21 ] . 本研究聚焦坝顶沉降变形,因测点起测时间在大坝填筑完成之后,无填筑过程变形数据,且测点高程一致,仅考虑水位和时间因素的影响. 建立沉降统计模型[22 -23 ] 如下: ...
1
... 土石坝沉降影响因素包括坝型、剖面形状、坝址地形地质、筑坝材料、施工技术与质量、温度、库水位和时间等,考虑过多因素会增加计算量,降低模型精度,难以准确反映大坝沉降真实情况. 因此,在保证计算精度和效率的前提下,选择适当的影响因素是建立沉降统计模型的关键[20 ] . 在具体大坝工程中,坝型、剖面形状、坝址地形地质、筑坝材料等因素已确定,研究主要考虑填筑过程、上下游水位和时间的影响[21 ] . 本研究聚焦坝顶沉降变形,因测点起测时间在大坝填筑完成之后,无填筑过程变形数据,且测点高程一致,仅考虑水位和时间因素的影响. 建立沉降统计模型[22 -23 ] 如下: ...
混凝土面板堆石坝堆石料流变特性试验研究
2
2004
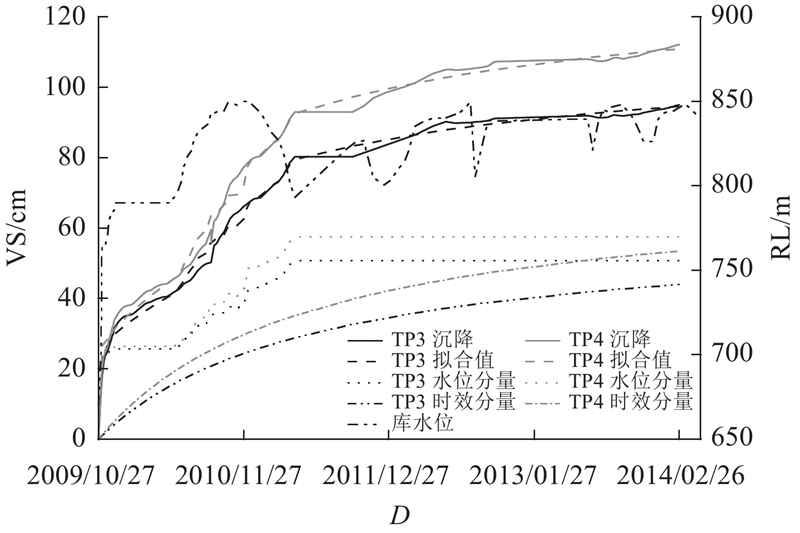
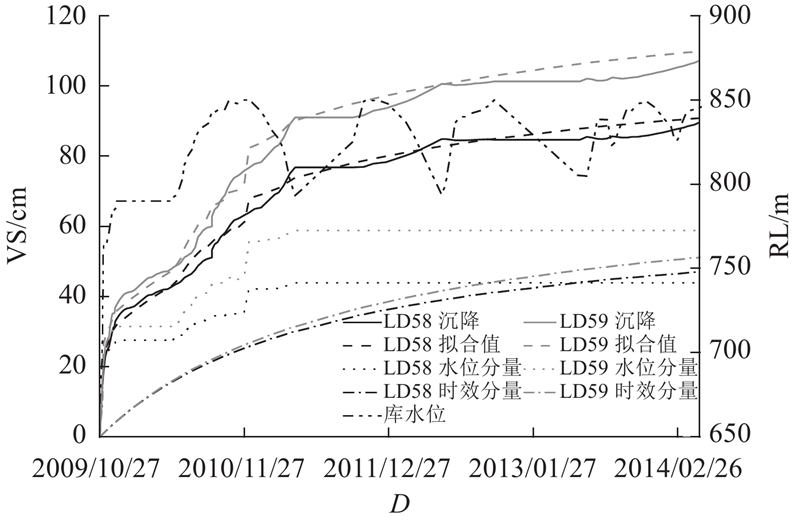
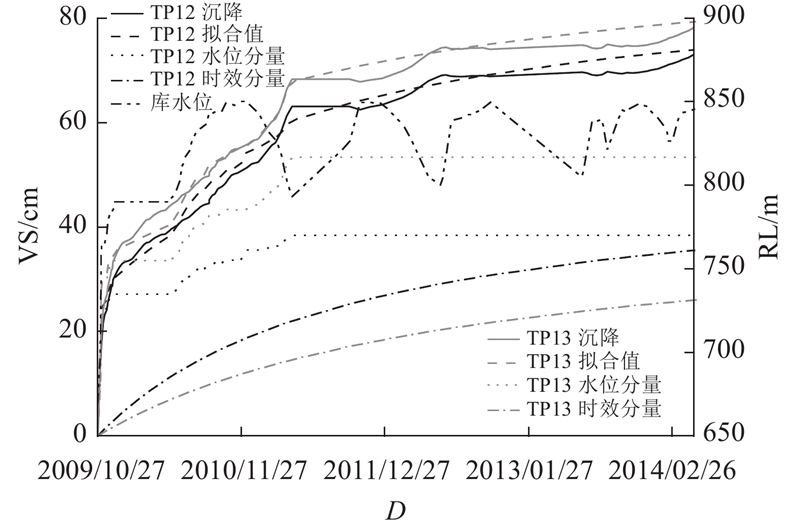
... 相关研究表明,水荷载对土石坝沉降变形产生的影响可以用与上游水位变化值H 相关的3次多项式表示[24 ] ,具体表达式如下: ...
... 在对土石坝进行有限元数值仿真计算时,须考虑材料的力学模型. 堆石料的力学模型较为复杂,具有非线性、流变、湿化变形等特性. 本研究静力瞬变模型选用E-B模型[26 ] ;湿化模型选用${E^w} $ - $ {v^w}$ [27 ] ;流变模型选用李国英七参数模型[24 ] . 本研究主要研究大坝后期流变及湿化变形,其流变和湿化模型参数通过反演获得. ...
混凝土面板堆石坝堆石料流变特性试验研究
2
2004
... 相关研究表明,水荷载对土石坝沉降变形产生的影响可以用与上游水位变化值H 相关的3次多项式表示[24 ] ,具体表达式如下: ...
... 在对土石坝进行有限元数值仿真计算时,须考虑材料的力学模型. 堆石料的力学模型较为复杂,具有非线性、流变、湿化变形等特性. 本研究静力瞬变模型选用E-B模型[26 ] ;湿化模型选用${E^w} $ - $ {v^w}$ [27 ] ;流变模型选用李国英七参数模型[24 ] . 本研究主要研究大坝后期流变及湿化变形,其流变和湿化模型参数通过反演获得. ...
堆石坝流变变形的反馈分析
1
1998
... 已有学者结合太沙基饱和土体的固结理论与土体的蠕变特性,将时效分量总结归纳为指数函数形式、对数函数形式、双曲函数形式等多个形式[25 ] . 本研究在分析瀑布沟大坝坝顶测点沉降变形发展情况后,选择了适用于本工程的双曲函数形式作为时效分量的表达式,具体表达式如下: ...
堆石坝流变变形的反馈分析
1
1998
... 已有学者结合太沙基饱和土体的固结理论与土体的蠕变特性,将时效分量总结归纳为指数函数形式、对数函数形式、双曲函数形式等多个形式[25 ] . 本研究在分析瀑布沟大坝坝顶测点沉降变形发展情况后,选择了适用于本工程的双曲函数形式作为时效分量的表达式,具体表达式如下: ...
Nonlinear analysis of stress and strain in soils
1
1970
... 在对土石坝进行有限元数值仿真计算时,须考虑材料的力学模型. 堆石料的力学模型较为复杂,具有非线性、流变、湿化变形等特性. 本研究静力瞬变模型选用E-B模型[26 ] ;湿化模型选用${E^w} $ - $ {v^w}$ [27 ] ;流变模型选用李国英七参数模型[24 ] . 本研究主要研究大坝后期流变及湿化变形,其流变和湿化模型参数通过反演获得. ...
1
... 在对土石坝进行有限元数值仿真计算时,须考虑材料的力学模型. 堆石料的力学模型较为复杂,具有非线性、流变、湿化变形等特性. 本研究静力瞬变模型选用E-B模型[26 ] ;湿化模型选用${E^w} $ - $ {v^w}$ [27 ] ;流变模型选用李国英七参数模型[24 ] . 本研究主要研究大坝后期流变及湿化变形,其流变和湿化模型参数通过反演获得. ...
1
... 在对土石坝进行有限元数值仿真计算时,须考虑材料的力学模型. 堆石料的力学模型较为复杂,具有非线性、流变、湿化变形等特性. 本研究静力瞬变模型选用E-B模型[26 ] ;湿化模型选用${E^w} $ - $ {v^w}$ [27 ] ;流变模型选用李国英七参数模型[24 ] . 本研究主要研究大坝后期流变及湿化变形,其流变和湿化模型参数通过反演获得. ...
瀑布沟高土石坝三维非线性有限元分析
1
2014
... 由于本研究聚焦于大坝湿化流变变形,而E-B模型参数主要影响填筑过程中的变形,其对研究结果的影响较小,故参数取值直接参考本工程相关研究成果[17 ,28 ] ,参数如表2 所示. 其中,$\gamma $ K 为切线模量系数,n 为切线模量指数,R f 为破坏比,c 为材料凝聚力,$\varphi_0 $ $\Delta \varphi $ $K_{\mathrm{b}} $ m 分别为体积模量系数和指数. ...
瀑布沟高土石坝三维非线性有限元分析
1
2014
... 由于本研究聚焦于大坝湿化流变变形,而E-B模型参数主要影响填筑过程中的变形,其对研究结果的影响较小,故参数取值直接参考本工程相关研究成果[17 ,28 ] ,参数如表2 所示. 其中,$\gamma $ K 为切线模量系数,n 为切线模量指数,R f 为破坏比,c 为材料凝聚力,$\varphi_0 $ $\Delta \varphi $ $K_{\mathrm{b}} $ m 分别为体积模量系数和指数. ...
基于IAGA-BP算法的高拱坝-坝基力学参数反演分析
1
2022
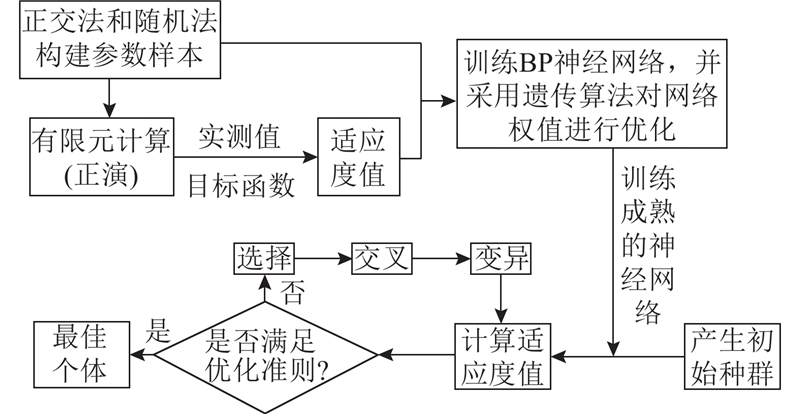
... BP神经网络通过学习和记忆,能够有效找到输入(力学参数)和输出(位移)之间的关系,从而可以近似替代有限元分析的正向计算,大大节省计算时间[29 -30 ] . 遗传算法模拟了自然选择和遗传过程,通过选择、交叉和变异操作,从初始种群逐步进化到接近最优解[31 ] ,在反演分析中,可以快速找到全局最优解. 所以本研究同时考虑智能优化算法与机器学习算法,采用BP神经网络和遗传算法结合的方法构建反演平台,对坝料的湿化与流变参数进行反演分析,基本流程如图10 所示. ...
基于IAGA-BP算法的高拱坝-坝基力学参数反演分析
1
2022
... BP神经网络通过学习和记忆,能够有效找到输入(力学参数)和输出(位移)之间的关系,从而可以近似替代有限元分析的正向计算,大大节省计算时间[29 -30 ] . 遗传算法模拟了自然选择和遗传过程,通过选择、交叉和变异操作,从初始种群逐步进化到接近最优解[31 ] ,在反演分析中,可以快速找到全局最优解. 所以本研究同时考虑智能优化算法与机器学习算法,采用BP神经网络和遗传算法结合的方法构建反演平台,对坝料的湿化与流变参数进行反演分析,基本流程如图10 所示. ...
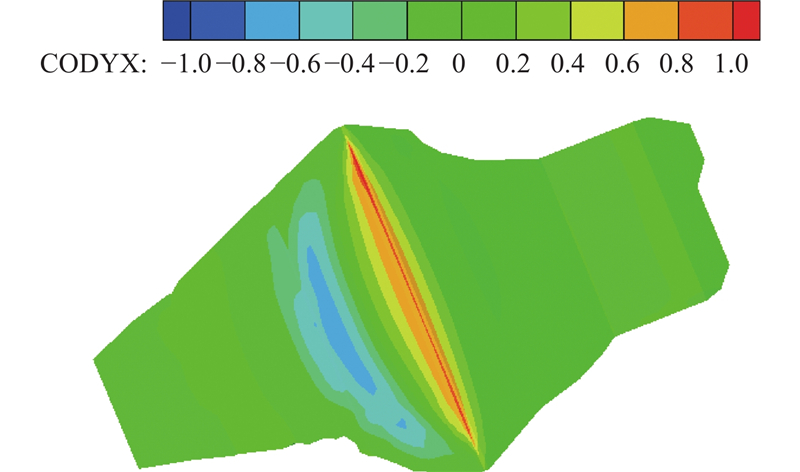
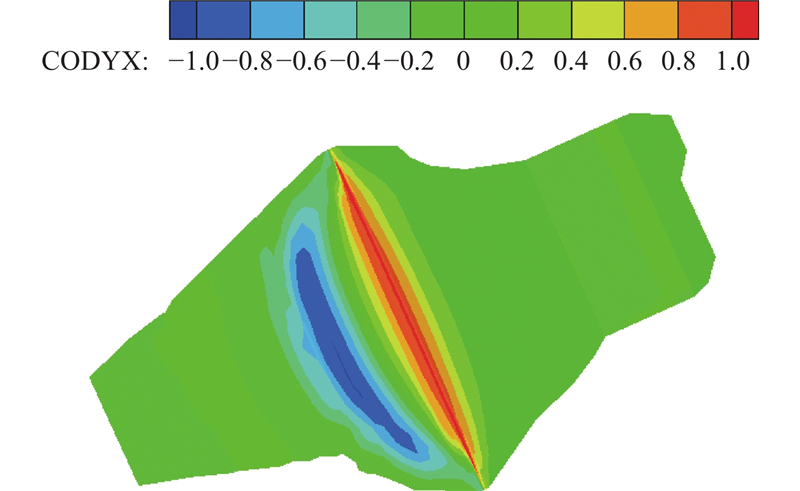
基于反演参数的心墙堆石坝坝顶裂缝成因研究
1
2022
... BP神经网络通过学习和记忆,能够有效找到输入(力学参数)和输出(位移)之间的关系,从而可以近似替代有限元分析的正向计算,大大节省计算时间[29 -30 ] . 遗传算法模拟了自然选择和遗传过程,通过选择、交叉和变异操作,从初始种群逐步进化到接近最优解[31 ] ,在反演分析中,可以快速找到全局最优解. 所以本研究同时考虑智能优化算法与机器学习算法,采用BP神经网络和遗传算法结合的方法构建反演平台,对坝料的湿化与流变参数进行反演分析,基本流程如图10 所示. ...
基于反演参数的心墙堆石坝坝顶裂缝成因研究
1
2022
... BP神经网络通过学习和记忆,能够有效找到输入(力学参数)和输出(位移)之间的关系,从而可以近似替代有限元分析的正向计算,大大节省计算时间[29 -30 ] . 遗传算法模拟了自然选择和遗传过程,通过选择、交叉和变异操作,从初始种群逐步进化到接近最优解[31 ] ,在反演分析中,可以快速找到全局最优解. 所以本研究同时考虑智能优化算法与机器学习算法,采用BP神经网络和遗传算法结合的方法构建反演平台,对坝料的湿化与流变参数进行反演分析,基本流程如图10 所示. ...
1
... BP神经网络通过学习和记忆,能够有效找到输入(力学参数)和输出(位移)之间的关系,从而可以近似替代有限元分析的正向计算,大大节省计算时间[29 -30 ] . 遗传算法模拟了自然选择和遗传过程,通过选择、交叉和变异操作,从初始种群逐步进化到接近最优解[31 ] ,在反演分析中,可以快速找到全局最优解. 所以本研究同时考虑智能优化算法与机器学习算法,采用BP神经网络和遗传算法结合的方法构建反演平台,对坝料的湿化与流变参数进行反演分析,基本流程如图10 所示. ...
1
... BP神经网络通过学习和记忆,能够有效找到输入(力学参数)和输出(位移)之间的关系,从而可以近似替代有限元分析的正向计算,大大节省计算时间[29 -30 ] . 遗传算法模拟了自然选择和遗传过程,通过选择、交叉和变异操作,从初始种群逐步进化到接近最优解[31 ] ,在反演分析中,可以快速找到全局最优解. 所以本研究同时考虑智能优化算法与机器学习算法,采用BP神经网络和遗传算法结合的方法构建反演平台,对坝料的湿化与流变参数进行反演分析,基本流程如图10 所示. ...
The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation
1
2021
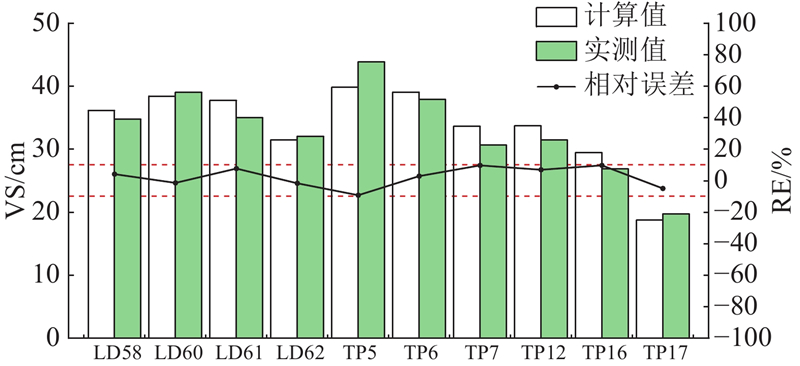
... 力学模型参数反演分析旨在寻找一组参数,使实测值与计算位移值最佳逼近. 本研究采用RMSE来判断参数的优劣性[32 ] . 同时,为了保证BP神经网络学习的有效性,将计算值比实测值偏小的样本组的RMSE取相反数,构造新的目标函数,即 ...
土石坝变形计算的若干问题
1
1983
... 刘祖德[33 ] 指出,心墙堆石坝初次蓄水时上游堆石料产生的沉降主要由湿化变形引起. 因此本研究利用沉降统计模型中的水位分量来反演湿化模型参数. 在${E^w} {\text{-}} {v^w}$ $A$ $d$ $c$ ${K_1}$ ${K_0}$ ${m_0}$ . 其中,A 、K 1 、K 0 和m 0 为计算湿化割线模量$E^w $ d 和c 为计算湿化泊松比$v^w $ $A$ $d$ $c$ ${K_1}$
土石坝变形计算的若干问题
1
1983
... 刘祖德[33 ] 指出,心墙堆石坝初次蓄水时上游堆石料产生的沉降主要由湿化变形引起. 因此本研究利用沉降统计模型中的水位分量来反演湿化模型参数. 在${E^w} {\text{-}} {v^w}$ $A$ $d$ $c$ ${K_1}$ ${K_0}$ ${m_0}$ . 其中,A 、K 1 、K 0 和m 0 为计算湿化割线模量$E^w $ d 和c 为计算湿化泊松比$v^w $ $A$ $d$ $c$ ${K_1}$
1
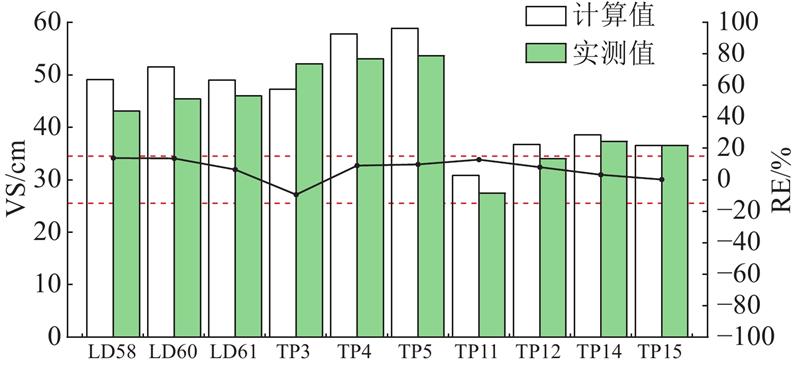
... 由于心墙对水的阻挡作用,只有上游堆石区存在湿化变形,故反演的材料分区仅为上游堆石区. 本研究基于其他案例结果[34 -35 ] ,经多次试算确定湿化模型参数初始取值范围,利用正交试验设计生成9组样本,利用随机法生成32组样本,共计41个湿化参数样本组. 随后依据3.3节中的流程进行反演分析,得到的反演结果如表3 所示. ...
1
... 由于心墙对水的阻挡作用,只有上游堆石区存在湿化变形,故反演的材料分区仅为上游堆石区. 本研究基于其他案例结果[34 -35 ] ,经多次试算确定湿化模型参数初始取值范围,利用正交试验设计生成9组样本,利用随机法生成32组样本,共计41个湿化参数样本组. 随后依据3.3节中的流程进行反演分析,得到的反演结果如表3 所示. ...
考虑监测数据时序特征和空间分布的堆石坝参数反演研究
1
2024
... 由于心墙对水的阻挡作用,只有上游堆石区存在湿化变形,故反演的材料分区仅为上游堆石区. 本研究基于其他案例结果[34 -35 ] ,经多次试算确定湿化模型参数初始取值范围,利用正交试验设计生成9组样本,利用随机法生成32组样本,共计41个湿化参数样本组. 随后依据3.3节中的流程进行反演分析,得到的反演结果如表3 所示. ...
考虑监测数据时序特征和空间分布的堆石坝参数反演研究
1
2024
... 由于心墙对水的阻挡作用,只有上游堆石区存在湿化变形,故反演的材料分区仅为上游堆石区. 本研究基于其他案例结果[34 -35 ] ,经多次试算确定湿化模型参数初始取值范围,利用正交试验设计生成9组样本,利用随机法生成32组样本,共计41个湿化参数样本组. 随后依据3.3节中的流程进行反演分析,得到的反演结果如表3 所示. ...
基于改进粒子群算法的面板堆石坝流变反演分析
1
2022
... 不同分区材料的流变参数往往不同,瀑布沟大坝共有7个材料分区,如果全部考虑,则反演参数数量庞大,容易造成维度灾难,不仅降低了反演的可靠度,还会导致有限元计算的工作量巨大. 考虑到坝体过渡层和反滤层在整个大坝结构中占比较小,对最终变形结果影响不大,故设上下游过渡区和反滤层的模型参数分别与上下游主堆石区的一致[36 ] . 因此考虑进行反演的坝料分区仅有上游堆石区、下游主堆石区、下游次堆石区以及心墙区4个分区. ...
基于改进粒子群算法的面板堆石坝流变反演分析
1
2022
... 不同分区材料的流变参数往往不同,瀑布沟大坝共有7个材料分区,如果全部考虑,则反演参数数量庞大,容易造成维度灾难,不仅降低了反演的可靠度,还会导致有限元计算的工作量巨大. 考虑到坝体过渡层和反滤层在整个大坝结构中占比较小,对最终变形结果影响不大,故设上下游过渡区和反滤层的模型参数分别与上下游主堆石区的一致[36 ] . 因此考虑进行反演的坝料分区仅有上游堆石区、下游主堆石区、下游次堆石区以及心墙区4个分区. ...