随着物联网(Internet of Things, IoT)、大数据、人工智能等新兴技术的快速发展,传统的计算网络架构难以应对大量数据的集中式处理,从而导致较高的网络延迟、带宽消耗问题. 边缘计算作为分布式架构,将计算资源部署在网络的边缘,使得终端的部分数据在边缘节点上进行计算,可以减轻中心服务器的负担,从而提高计算效率、降低网络延迟[1]. 为了适应更大规模的边缘计算任务,多层边缘计算网络应运而生[2]. 与单层的场景不同,其终端往往处于不同的边缘计算服务器覆盖范围内. 其对终端设备层和边缘层进行任务卸载,根据不同的场景需求[3-4],灵活选择边缘层中某个服务器来执行计算任务以实现最优的资源分配和性能最大化.
目前已有许多策略和算法用来解决边缘计算网络中的任务卸载问题[10]. 从通信时延和计算时延两方面出发,通过调度终端和基站的资源来降低时延或减少能耗.
刘耿旗等[11-13]分别针对边缘计算场景中的用户选择、无线资源分配和任务卸载进行研究,并提出最优的解决方案. He等[14-15]采用博弈模型来优化系统总体开销和用户平均时延. 郭煜[16]提出边缘计算中带有缓存机制的卸载策略,由于终端可能多次请求一样的任务,因此将部分处理好的结果缓存在边缘服务器从而降低整体的计算开销. Tran等[17-18]利用不同的启发式算法优化系统任务完成时间和能量的加权和. 龙隆等[19]考虑在无线频谱、算力受限下,构建系统时延并利用重构线性化、松弛法以及凸优化方法最小化所有终端设备执行任务总时延. 代美玲等[20]在考虑算力资源分配的基础上,利用拉格朗日函数和拟牛顿法分别对单用户和多用户的场景进行优化. Jiang等[21]为了维持终端用户满意度,在优化算力和频谱资源的基础上提出在线联合卸载和资源分配框架,能够在满足长期移动边缘计算(mobile edge computing,MEC)能耗约束的同时,达到接近最优的性能. Kim等[22]综合考虑用户关联、资源分配、全任务卸载,提出基于分布式定价的任务解决方案来降低时延和能量消耗. 除此之外,现有的关于用户关联的研究[23-25]是基于信道质量、信噪比之类与信道有关的参数进行优化的,没有考虑到基站算力对于用户关联的影响,但基站由于算力受限,一定程度上会影响用户关联,具体表现在基站无法无限制地承受任何用户,须保证已存在用户的通信质量.
已有研究很少同时考虑基站的算力、功率,终端的算力、任务特性,以及两者之间的频谱资源优化、用户关联、卸载决策、资源分配等重要的策略. 而这些对于多层边缘计算网络是尤为重要的. 1)基站的算力和功率同时影响用户关联. 当终端有计算任务须选择一个基站进行协同计算时,如果基站的算力充足但是没有足够的发射功率,此时任务卸载将不会带来时延增益,甚至会增大计算时延. 同样,如果基站有足够的发射功率,但是没有充足的算力,此时边缘服务器计算时延会增大. 2)频谱资源以及算力资源也同时影响卸载决策. 计算任务卸载的同时会引起额外的时延开销,如任务上传时延、边缘服务器计算时延以及任务下载时延,这3部分的时延由频谱资源以及算力资源共同决定. 在频谱资源不足的情况下,终端更倾向于在本地进行处理,反之则考虑计算卸载. 因此,在多层边缘计算网络中,终端和边缘服务器的各种限制使得如何合理进行用户关联和资源分配上存在着巨大的挑战.
本研究基于上述研究背景,综合考虑基站算力、功率、频谱分配受限的情况下,终端和基站的关联方案以及最优的卸载决策和资源分配策略. 本研究主要创新点如下. 1)建立多层边缘网络终端用户模型,考虑终端算力、基站算力、功率以及无线频谱资源受限情况下的联合优化. 首先分析边缘计算网络中的通信性能和计算时延,通信性能包括终端和基站之间的上行通信速率和下行通信速率,计算时延指终端的本地计算时延、终端将任务上传基站的时延、边缘基站计算时延和基站回传任务时延. 2)根据基站算力、功率,无线频谱资源的限制,建立最小化所有任务时延的优化问题. 3)通过问题分解,分别获得用户关联、任务卸载策略以及无线资源分配的最优解,并设计基于迭代的次优算法.
1. 系统模型
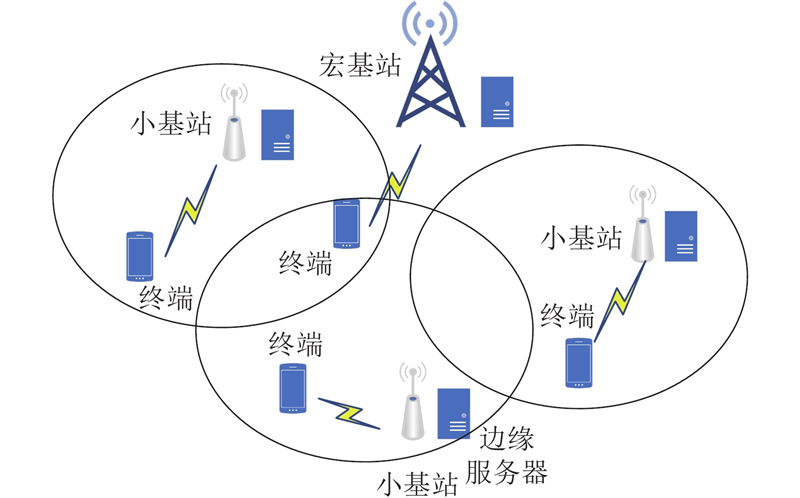
如图1所示为多层边缘计算网络示意图. 考虑一个典型的多层边缘计算场景,多个配备边缘服务器的小基站以及配备边缘服务器的宏基站组成一个多层的异构网络. 网络中随机分布着
图 1
在系统中,须同时考虑终端以及基站的计算能力和终端与基站的信道质量,来权衡终端自己处理计算任务的时间和将任务上传到基站处理,并反馈结果所带来的时延. 假设终端
基站和终端之间的通信可以采用频分复用(frequency division multiple access,FDMA)的方式复用上行和下行信道,基站和终端所分配用于通信的带宽影响计算任务上传和下载的时间,分配的带宽越高,通信速率越大,如果基站和终端之间采用其他多址接入方式也有相对应的结论,区别只在于考虑的资源复用不一样.
系统的优化目标是处理所有终端任务的时延和最小. 在这个优化目标下,由于基站算力和功率是有限的,须合理分配基站在其覆盖范围内所有终端的算力和功率. 因为终端和基站能分配的带宽总和是固定的,如果分配给基站的计算任务越多,相应分配的带宽也要越多.
2. 边缘计算网络性能分析
多层边缘计算网络中的时延主要是由通信时延和计算时延组成. 其中通信时延主要产生在终端卸载任务到边缘服务器和边缘服务器回传处理好的任务这2个过程中. 计算时延也分为2部分:1)终端本地的计算时延;2)边缘服务器处理卸载任务产生的计算时延.
2.1. 通信性能分析
使用变量
式中:
式中:
2.2. 边缘计算时延分析
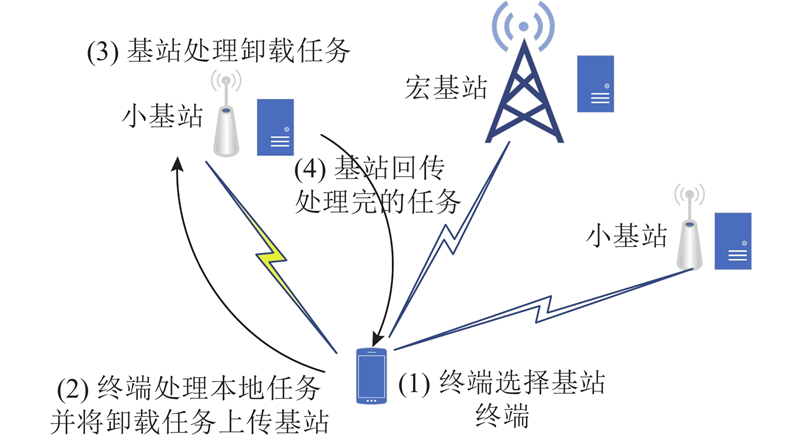
先从时延性能角度来分析用户关联、资源优化以及任务卸载优化. 如图2所示为边缘计算处理流程. 可以看出,边缘计算的时延分为4个部分. 1)终端选择一个基站,这个基站可以是小基站也可以是宏基站,终端根据自身的算力和基站的算力、功率以及频谱资源分配来计算本地计算任务和基站计算任务所占的比例. 2)终端计算本地留存的任务,产生本地计算时延作为时延衡量的一个指标,并将剩下的任务发送到基站,这些数据会经过终端和基站之间的上行信道,产生上传卸载任务的时延. 3)基站根据自身的算力以及和终端的关联情况,分配自身的算力来计算不同的终端发送过来的任务,这也是边缘卸载任务计算时延的产生. 4)基站将处理好的任务回传给终端,处理好的任务经过基站和终端之间的下行信道,产生边缘服务器回传时延,边缘计算的总体时延由本地计算时延、上传卸载任务时延、边缘卸载任务计算时延和边缘服务器回传时延构成.
图 2
设定终端
1) 本地计算时延:
式中:
2)上传卸载部分数据需要的时延:
3) 边缘服务器的处理时延:
式中:
4)边缘服务器计算完回传的时延:
终端
终端的计算时延由本地计算部分以及卸载给边缘的部分的最大值决定,这是因为卸载决策决定后,任务卸载和本地计算可以同步进行,只有2部分都完成后,该任务才能视为计算完成.
3. 边缘计算网络优化策略
3.1. 问题建模
从边缘计算的性能分析结果可知,计算时延由卸载的决策、用户关联以及资源分配共同决定. 为了提高边缘计算的效率,须通过优化用户关联、时隙分配、算力分配以及任务卸载策略,最小化所有终端任务计算的平均时延. 终端须权衡信道以及算力资源,选择合适的基站连接,并且选择最优的任务卸载策略. 该优化问题描述如下:
式中:
3.2. 问题求解
以上问题是混合整数非线性优化问题,是非凸且NP难的问题. 为了求解上述问题,首先将
式中:新增的限制条件
变量耦合导致问题变得复杂,须将这些变量分开优化. 观察上述变量可以知,问题可以分解为用户关联优化、卸载决策优化、以及无线资源分配优化.
3.2.1. 用户关联
给定
定理1 假设在边缘计算网络中存在
上述决策是一个选择问题,即针对每一个终端,在功率、算力、频谱资源已知的情况下,在考虑到信道质量和算力的基础上选择边缘计算上传、处理、回传整体时延最小的那个量,其物理意义是选择卸载后上传、处理、回传时延代价最小的那个基站.
3.2.2. 卸载决策
给定
卸载决策决定了任务上传服务器的数据量多少,当其他变量固定时,如果本地时延大于边缘计算时延,可以适当减少本地任务,将任务上传到基站,反之,可以增加本地任务,减少上传的任务. 显然,本地时延和边缘计算时延相等的卸载决策是卸载任务的最优解,定理如下.
定理2 假设在边缘计算网络中存在
证明 式(13)的第2、3个限制条件均是
则条件改写为
2个条件分别乘以
等号在
定理2表明,
3.2.3. 资源分配
当求解完用户关联以及卸载决策以后,可以分别优化
1)优化上行信道的分配,
上行频谱资源限制条件和本地计算时延条件都是线性的约束条件,边缘计算限制条件是关于
2)优化下行信道和基站功率的分配,
同样,下行频谱资源限制条件、基站功率限制条件和本地计算时延条件是线性的约束条件,在边缘计算限制条件中,
因为每个用户只能选择一个基站进行连接,这个也是凸优化问题,仍然可以用凸优化工具包求解.
3)优化基站的算力分配,
算力的分配存在闭式解,这个闭式解使得基站对于和它关联的所有用户在边缘计算时延上保持一致,即定理3.
定理3 对于基站
证明 根据定理2,将最优的卸载决策代入问题,得到
在该优化问题中,只有第2项涉及到算力的优化,且因为
由于每个基站的算力是单独优化的,根据柯西-施瓦茨不等式,使得目标函数最小的算力分配需要每个基站的算力分配满足
3.3. 联合优化算法
基于上述分析,得到如下优化算法.
1)初始化所有变量,平均分配所有的资源.
2)根据定理1获得用户关联方案.
3)根据定理2求解卸载决策.
4)分别优化与资源分配有关的变量
5)重复步骤2)~4)直到给定循环步数
通过上述步骤,可以逐步优化得到用户关联、卸载决策和资源分配方案,完整的过程描述如下.
算法 1 边缘计算策略优化
1. 初始化所有优化变量
2. For iter = 1∶I
3. 优化用户关联,根据定理1选择时延代价最小的基站
4. 优化卸载决策,根据定理2获得卸载决策
5. 优化资源分配,用凸优化工具包优化上行频谱分配、优化功率分配和下行频谱分配,根据定理3解决算力分配问题
6. end for
3.4. 复杂度分析
本研究提出的算法复杂度主要体现在各个子问题的优化中,主要考虑算法的最大迭代次数. 算法的最大迭代次数为
4. 仿真验证
考虑由多终端和多基站组成的多层边缘计算网络系统,终端具有可分解的任务,且可以将任务卸载到基站进行计算. 在计算时延参数设置上,考虑3 km
4.1. 验证资源分配的效果
资源分配是边缘计算网络中非常重要的一环,对于基站来说,不与之关联的终端可以不分配相关的资源,而与之关联的终端需要合理分配资源. 因此本研究将所提算法与以下的方法进行比较.
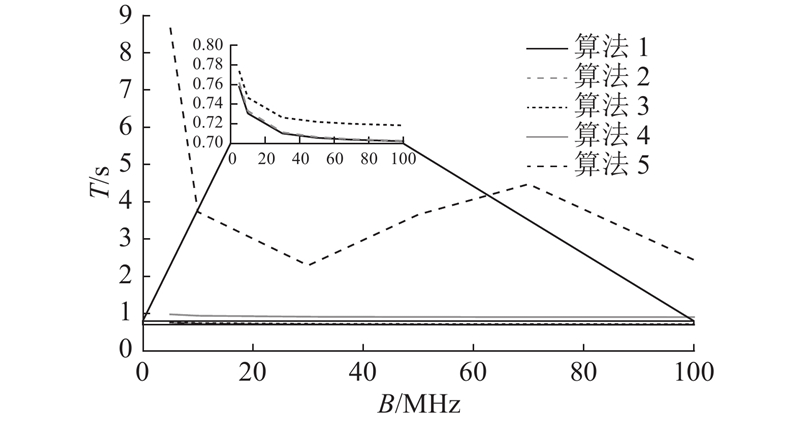
1)算法1:本研究所提出的算法,即资源分配(包括上行、下行频谱和功率)、算力优化和用户关联均须解决;
2)算法2:无线资源平均分配,但是保持用户关联优化、算力优化;
3)算法3:无线资源以及用户关联进行优化,但是算力是平均分配;
4)算法4:无线资源平均分配、用户随机关联,但是算力优化;
5)算法5:全部的变量都是随机或者平均分配.
在上述的几种方法中,为了控制变量,卸载决策均须优化,只关注资源分配.
本研究验证了带宽资源为5 ~100 MHz的不同方案下的时延性能. 仿真得到的结果如图3所示. 其中,
图 3
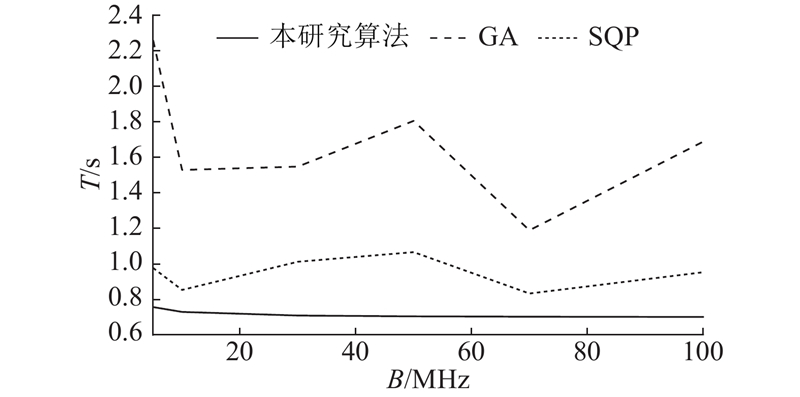
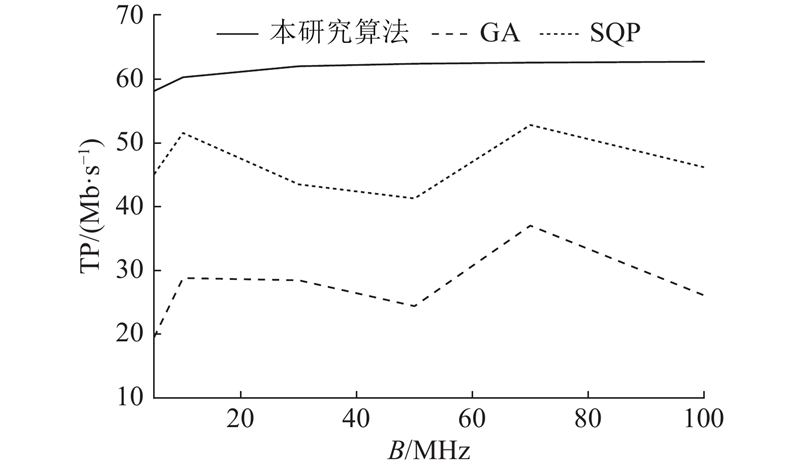
将联合优化中常用的启发式算法和近似算法与本研究提出的方法进行比较.
1) GA:模拟自然进化过程的优化算法,属于启发式搜索算法. 通过模拟物种在自然界中的生存竞争、繁殖和变异过程,逐步优化问题的解.
2) SQP:通过二次近似来解决非线性优化问题. 在每次迭代中,SQP会利用当前迭代点的信息,构造一个局部的二次近似问题,并求解该二次问题得到一个新的搜索方向. 然后,将该方向应用于当前的解,得到新的迭代点,直到收敛到一个最优解为止.
图 4
图 4 本研究算法与GA、SQP算法的时延对比
Fig.4 Latency comparison between proposed method with GA and SQP algorithms
图 5
图 5 本研究算法与GA、SQP算法的吞吐量对比
Fig.5 Throughput comparison between proposed method with GA and SQP algorithms
4.2. 验证卸载决策的重要性
卸载决策是终端根据任务量、自身算力和基站算力的情况将自身的部分任务发送到基站进行处理.
当基站的算力充足时,终端会将几乎整个的任务都发送到基站,此时,终端几乎不处理任务. 因此,考虑基站算力缺乏时,将本研究的算法与以下策略进行比较.
1)算法1:本研究所提出的算法;
2)算法6:计算任务只在本地进行;
3)算法7:计算任务只在基站进行.
进一步的,设置不同的带宽和不同的基站算力来进行验证.
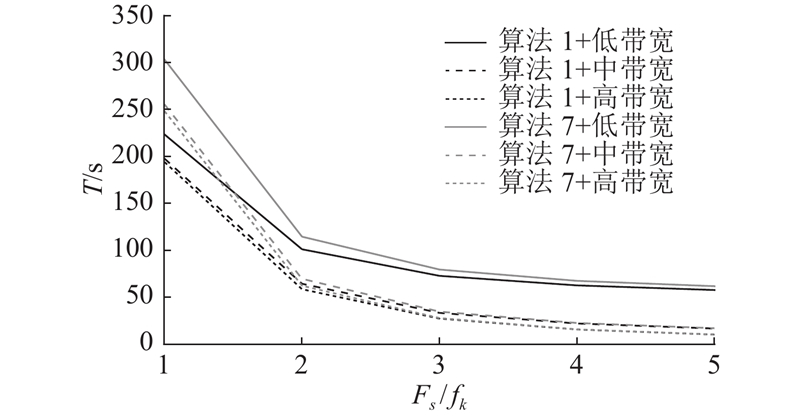
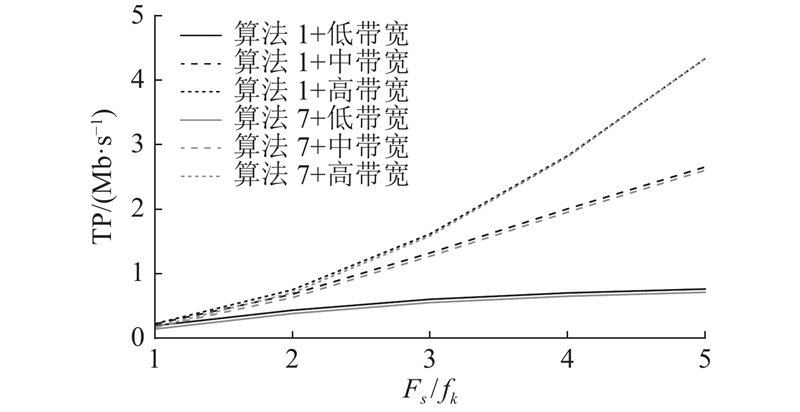
对于算法6,由于计算任务只在本地进行,整体的时延不受基站算力和无线频谱资源的影响,通过公式可以计算得到在如上的配置下,只在本地进行计算任务需要897.33 s,是个定值. 如图6、7所示,其中
图 6
图 6 不同卸载决策下的时延对比
Fig.6 Comparison of latency under different offloading decisions
图 7
图 7 不同卸载决策下的吞吐量对比
Fig.7 Throughput comparison under different offloading decisions
表 1 基站极限算力下的时延
Tab.1
| 策略 | T/s | ||
| 低带宽 | 适中带宽 | 高带宽 | |
| 算法1 | 862.73 | 856.39 | 854.43 |
| 算法6 | 897.33 | 897.33 | 897.33 |
| 算法7 | |||
4.3. 验证用户关联的效果
用户关联是终端与基站的配对情况,用户关联决定了优化的上限,因此合理的用户关联才能保证资源和算力的最优分配.
本研究提出的用户关联方案是基于信道和算力综合考量的. 为了验证本研究提出的用户关联方案的有效性,考虑以下几组方式:
1)算法1:本研究提出的用户关联策略;
2)算法8:只基于信道质量进行用户关联;
3)算法9:只基于算力进行用户关联;
4)算法10:随机用户关联.
图 8
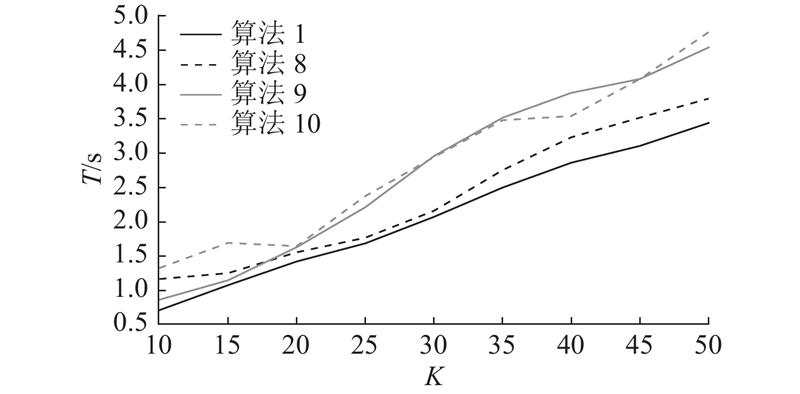
图 8 不同用户关联下的时延对比
Fig.8 Comparison of latency under different user associations
图 9
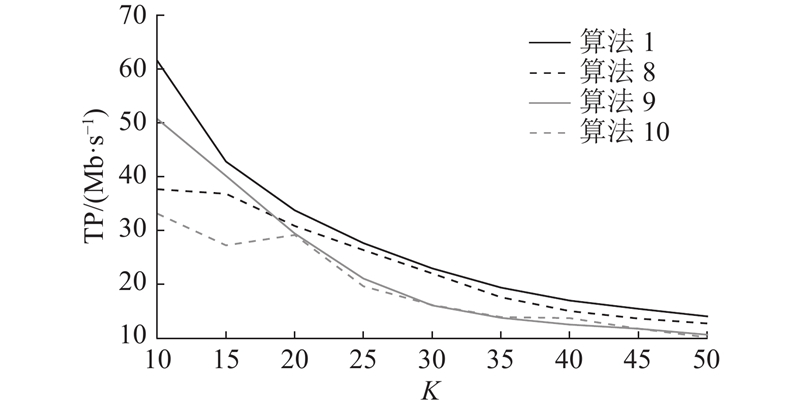
图 9 不同用户关联下的吞吐量对比
Fig.9 Comparison of throughput under different user associations
5. 结 语
在多层边缘计算网络中,终端计算任务时延的优化不仅要考虑终端和基站的关联,还要考虑到终端的任务卸载和整体的资源分配. 为了解决该问题,本研究面向多层边缘计算网络,提出联合用户关联、任务卸载和资源分配的优化策略,有效降低了终端的计算时延. 此外,通过大量仿真验证了资源分配、任务卸载和用户关联在边缘计算网络中的重要作用. 实验结果证明,本研究所提出的基于信道质量和算力的用户关联决策能够在多层边缘计算网络中更好地进行终端、基站配对和性能优化. 考虑到能耗同样是边缘计算中较为重要的性能指标,将在后续的研究中同时考虑时延和能耗性能,并引入多连接概念,探讨并设计此场景下的性能优化算法.
参考文献
面向未来移动通信的移动边缘计算研究综述
[J].
Research of mobile edge computing for future mobile communications: a review
[J].
Edge computing for the Internet of Things: a case study
[J].DOI:10.1109/JIOT.2018.2805263 [本文引用: 1]
车辆边缘计算中联合资源分配和任务卸载方案
[J].
Joint resource allocation and task offloading schemes in vehicle edge computing
[J].
基于DRL的无人机辅助MEC任务卸载算法
[J].
DRL-based unmanned aerial vehicle assisted MEC offloading algorithm
[J].
Task offloading strategies for mobile edge computing: a survey
[J].DOI:10.1016/j.comnet.2024.110791 [本文引用: 1]
Optimized task offloading strategy in IoT edge computing network
[J].DOI:10.1016/j.jksuci.2024.101942 [本文引用: 1]
基于星地协同的低时延任务卸载算法
[J].
A satellite-ground based low-latency task offloading algorithm
[J].
基于智能超表面的无人机移动边缘计算综述
[J].
Survey on UAV-enabled mobile edge computing based on reconfigurable intelligent surface
[J].
面向复杂任务的多无人机协同计算资源分配与优化
[J].
Multi-UAV cooperative computing resource allocation and optimization for complex tasks
[J].
Research on new edge computing network architecture and task offloading strategy for Internet of Things
[J].DOI:10.1007/s11276-020-02516-8 [本文引用: 1]
多边缘节点场景下的计算任务卸载算法
[J].
Computational task offloading algorithms for multi-edge node scenarios
[J].
Energy-efficient resource allocation for mobile-edge computation offloading
[J].
Energy-efficient offloading for mobile edge computing in 5G heterogeneous networks
[J].DOI:10.1109/ACCESS.2016.2597169 [本文引用: 1]
Design and implementation of user task offloading algorithm
[J].DOI:10.1063/5.0181636 [本文引用: 1]
低地球轨道卫星边缘计算场景中任务卸载与资源分配联合优化算法
[J].
Joint optimization algorithm for task offloading and resource allocation in low earth orbit satellites edge computing scenario
[J].
移动边缘计算中带有缓存机制的任务卸载策略
[J].
Tasks offloading strategy with caching mechanism in mobile margin computing
[J].
Joint task offloading and resource allocation for multi-server mobile-edge computing networks
[J].DOI:10.1109/TVT.2018.2881191 [本文引用: 1]
Computing offloading strategy using improved genetic algorithm in mobile edge computing system
[J].DOI:10.1007/s10723-021-09578-8 [本文引用: 1]
移动边缘网络下服务缓存与资源分配联合优化策略
[J].
Joint optimization strategy of service cache and resource allocation in mobile edge network
[J].
基于终端能耗和系统时延最小化的边缘计算卸载及资源分配机制
[J].
A computation offloading and resource allocation mechanism based on minimizing devices energy consumption and system delay
[J].
Joint task offloading and resource allocation for energy-constrained mobile edge computing
[J].DOI:10.1109/TMC.2022.3150432 [本文引用: 1]
Distributed task offloading and resource allocation for latency minimization in mobile edge computing networks
[J].DOI:10.1109/TMC.2024.3458185 [本文引用: 1]
基于QoS驱动的多目标优化用户动态关联研究
[J].
Research on dynamic association of multi-objective optimization users driven by QoS
[J].
异构蜂窝网络中一种基于匈牙利算法的用户关联方法
[J].
User association in heterogeneous cellular networks via the Hungarian method
[J].
基于时延优化的蜂窝D2D通信联合用户关联及内容部署算法
[J].
Joint clustering and content deployment algorithm for cellular D2D communication based on delay optimization
[J].