现有的肌肉疲劳分析研究主要分为特征提取和疲劳分类2个步骤,其中,特征提取的质量直接影响分类准确性[5]. 肌肉疲劳的时域特征主要包括平均绝对值(mean absolute value, MAV)[6]、均方根值(root mean square, RMS)[7]、积分肌电值(integral of EMG, iEMG)[8],通常会随着肌力增加和疲劳的出现而上升. 然而,由于sEMG信号具有非线性和非平稳特性且易受噪声干扰[9],频域特征相较于时域特征对噪声的敏感性较低. 因此,许多学者常使用频域特征来评估肌肉疲劳,频域特征指标常包括中值频率(median frequency, MF)[10]、平均频率(mean frequency, MNF)[11]以及功率谱密度(power spectral density, PSD)[12]等.
近年来,一些学者尝试通过利用新的指标来分析肌肉疲劳. 研究发现,在肌肉疲劳分析中,传统的时频域方法的可靠性低于样本熵、模糊近似熵这些非线性指标,且计算时间较长[13]. 熵作为衡量系统复杂性的有效方法,能够捕捉sEMG信号中伴随肌肉疲劳而发生的复杂性变化. 随着肌肉疲劳的加深,sEMG信号的复杂性逐渐降低,使得熵能够有效反映肌肉疲劳过程中的变化特征[14]. Murillo-Escobar等[15]通过结合生物力学特征和排列熵,能够更有效地区分肌肉的非疲劳和疲劳阶段. Makaram等[16]通过符号熵和网络熵分析动态收缩中的肌肉疲劳,并采用过渡网络方法研究sEMG信号的变化. 通过对信号的符号化处理,提取熵特征来表征非疲劳和疲劳状态. Hu等[17]提出分数阶模糊分散熵来分析肌肉疲劳,通过引入分数阶和改变模糊隶属函数,有效提高了算法对动态变化的灵敏度和特征提取能力.
上述这些熵指标仅从单一时间尺度上提取信号特征,难以全面反映特征信息[18]. 为了解决这一问题,Costa等[19]提出多尺度样本熵,结果表明神经信号复杂性会在不同时间尺度上发生变化,该思路广泛应用于生理信号分析. Wang等[20]提出快速精细复合多尺度样本熵(rapid refined composite multiscale sample entropy, R2CMSE),R2CMSE在多个时间尺度上相比多尺度样本熵表现出更高的计算效率和稳定性,能够有效区分疲劳和非疲劳状态. Sun等[21]将波动分散熵(fluctuation-based dispersion entropy, FDE)引入多尺度分析,提出多尺度波动分散熵(multiscale fluctuation-based dispersion entropy,MFDE),用于分析故障信号,该方法通过在不同尺度下提取信号特征,能有效识别信号中的复杂模式和异常变化. Su等[22]在MFDE的基础上进一步提出精细复合多尺度波动分散熵(refined composite multiscale fluctuation-based dispersion entropy,RCMFDE),通过RCMFDE提取多尺度故障特征,并结合支持向量机进行故障识别,实验表明该方法在特征提取与故障识别方面性能优异. 上述方法虽能在一定程度上表征肌肉疲劳,但在区分非疲劳与疲劳信号时,熵值差异不明显,反映出算法灵敏性不足,导致疲劳状态识别不准确. 同时,传统粗粒化方法在尺度增加时未能充分利用信号信息,导致信息丢失且不同尺度下的熵值波动较大,影响疲劳评估. 有学者在此基础上提出了时移粗粒化方法[23-24],但该方法计算量较大,且熵值波动问题仍然存在.
为了解决以上问题,本研究通过改进FDE来表征肌肉疲劳过程. FDE通过综合考虑时间序列的局部模式散布和波动幅度,更精确地揭示波动性变化,有效区分信号与噪声,并提供更细致的动态特征分析,特别适用于非线性数据的复杂性研究[25],但其灵敏性不足,且离散分类方式影响了信号之间的连续性和平滑过渡. 为此,本研究在FDE中引入模糊化处理,并结合Tsallis熵得到新的熵算法,同时提出平滑增强的粗粒化方法对肌肉疲劳实现多尺度分析. 基于此,本研究提出平滑增强的精细复合多尺度Tsallis波动分散熵(refined composite multiscale Tsallis fluctuation-based dispersion entropy, RCMTFDE),具体实现如下:1)针对FDE离散分类的不足,引入模糊化处理,利用高斯函数计算各数据点的隶属度,使得数据点可以同时隶属多个类别,保持数据之间的连续性和平滑性;2)针对FDE灵敏性欠佳的问题,将FDE和Tsallis熵结合,加入可调参数,提出Tsallis波动分散熵(Tsallis fluctuation-based dispersion entropy, TFDE),提升算法的灵敏性和适应性;3)针对传统粗粒化方法在处理过程中遗漏信号信息和熵值波动较大的问题,提出平滑增强的粗粒化方法. 该方法通过中位数生成粗粒化序列,以减少极端值或异常值的影响,并在每个尺度下对生成的粗粒化序列计算平均熵值,从而有效降低噪声干扰和熵值波动.
1. Tsallis熵和波动分散熵
1.1. Tsallis熵
Tsallis熵是经典香农熵的推广,在分析复杂系统的非线性特征中有着显著的应用,能够揭示肌肉疲劳过程中的复杂性变化. Tsallis熵引入了一个可调参数q来调整系统对概率分布的灵敏性,这使其更适合处理广泛的复杂系统[26].
对于一个离散概率分布{p1, p2, ···, pN},Tsallis熵定义为
式中:N为概率的离散项数;pi为第i个概率;当q=1时,Tsallis熵退化为香农熵;当q<1时,增强了对低概率、罕见波动的敏感性,能够捕捉sEMG信号中的肌肉疲劳特征[27].
1.2. 波动分散熵
给定一长度为N的单变量信号x={x1, x2, ···, xN}, FDE算法如下.
1)将原始信号中的每个数据点xj (j=1, 2, ···, N) 通过tan-sigmoid非线性映射,映射到y= {y1, y2, ···, yN}:
式中:σ和μ分别为信号x的标准差和平均值.
2)映射后的信号通过线性变换被分到时间序列zj中:
式中:R为舍入函数,c为类别的数量. 在步骤1)、2)之后,时间序列x中的每个元素都被映射到{1, 2, ···, c}中.
3)利用如下公式计算嵌入向量:
式中:m为嵌入维数,d为时间延迟,i=1,2,···,N−(m−1)d.
4)每个分散模式出现的概率通过如下公式计算:
式中:
5) FDE算法考虑的是分散模式的相邻元素之间的差异,称为基于波动的分散模式. 这样,就有了长度为m−1的向量,它们的每个元素都从−c+1变为c−1. 因此,存在(2c−1)m−1个基于波动的潜在色散模式:
2. 精细复合多尺度Tsallis波动分散熵
2.1. Tsallis波动分散熵
在原始FDE算法中,sEMG信号的每个数据点通常被映射到预定义的类别范围(1~c). 虽然这种离散化简化了计算过程,但也忽略了sEMG信号的连续性和动态变化性. sEMG信号通常包含肌肉收缩的连续电位变化,其过渡性特征可能会在硬性离散化过程中被丢失,进而影响熵值的计算精度. 因此,传统的硬性离散分类在一定程度上限制了熵算法对sEMG信号复杂性的描述.
为了解决这一问题,在FDE的线性变换后引入模糊化处理. 在信号被硬性分类到时间序列zj后,即经过式(3)处理,再利用高斯函数对每个离散点计算隶属度值,使得每个数据点可以部分隶属于多个类别:
式中:z(i)为信号的每个离散点,1≤j≤2c−1,fuzzy(i, j)为模糊隶属度矩阵中的元素.
为了确保最后的隶属度之和为1,对每个离散点的隶属度进行了归一化处理:
为了更详细地说明模糊化处理后与硬性分类的区别,以一个简单的时间序列
通过时间延时d和嵌入维数m,将模糊化处理后的数据构建为嵌入向量:
式中:i=1,2,···, N−(m−1)d;fuzzy(i,:)表示第i个数据点的模糊隶属度向量.
FDE作为衡量信号复杂性的有效工具,其通过量化信号中波动的散布程度来度量系统的复杂性. 然而,传统的FDE算法在处理具有高度非线性特征的肌肉疲劳信号时,存在一定的灵敏度不足问题. 因此,为了提升FDE的灵敏性,将模糊化后的FDE与Tsallis熵进行结合,得到TFDE算法:
式中:
2.2. 多尺度分析
2.2.1. 平滑增强的粗粒化方法
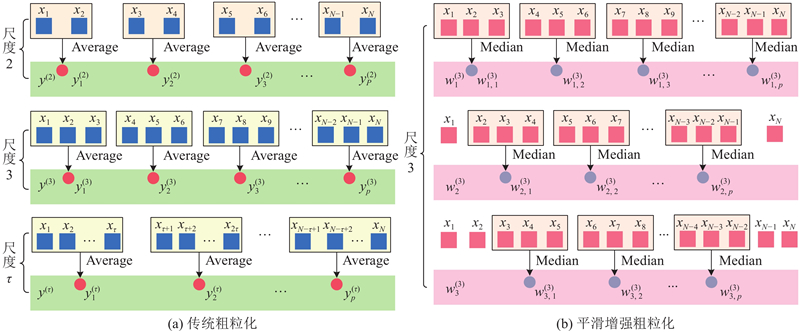
虽然目前各种多尺度熵方法能够在不同尺度下提取时间序列中的信息,但在粗粒化过程中仍存在未充分捕捉信号信息的问题. 如图1(a)所示为传统粗粒化方法. 在传统的粗粒化过程中,当τ=2时,x1和x2、x3和x4、x5和x6之间通过取平均值生成粗粒化序列
图 1
2.2.2. RCMTFDE算法
利用平滑增强的粗粒化方法对TFDE算法进行多尺度分析,通过在多个尺度下对sEMG信号的熵值进行计算,能够捕捉信号在不同时间尺度下的动态信息,从而提供更全面的肌肉疲劳分析. 其计算步骤如下.
1) 给定尺度因子τ(τ=1,2,···),然后通过平滑增强的粗粒化方法对长度为N的时间序列x={x1, x2, ···, xN}进行粗粒化,得到τ个不同的序列
式中:median为中位数函数,1≤j≤N−τ+1,1≤i≤τ.
2)对于在移动窗口序列
3)分别计算与尺度因子τ相对应的各个粗粒化序列的TFDE熵值,然后,再对τ个TFDE熵值求均值,即可得尺度τ下的RCMTFDE:
3. 数据采集与预处理
3.1. 数据采集
本实验选取年龄23~26岁、身体健康且无神经肌肉骨骼疾病的受试者,男性身高为(175±5) cm,女性身高为(158±3) cm,受试者在实验前24 h内避免参与任何高强度体育活动. sEMG信号利用深圳市润谊泰益科技公司研发生产的RTLab软件和RunE系列无线设备进行采集,采样率设为
实验时,受试者坐在实验桌前,背部保持直立,肌电传感器被精确安置于手臂肱桡肌的发达区域. 受试者的上臂垂直地面,前臂与上臂呈90°角. 实验开始前,受试者放松上臂肌肉,随后通过肱桡肌发力. 实验中,受试者单手举3 kg哑铃直至出现酸痛无力感,停止信号采集.
3.2. 数据预处理
sEMG信号的有效信息主要集中在0~500 Hz的频率范围内,而大部分能量集中在50~150 Hz的低频部分,极易受到干扰[28]. 在进行信号预处理时,首先须消除信号中的趋势项,然后使用陷波滤波器来去除50 Hz的电源干扰频率及其谐波,最后通过10~490 Hz的带通滤波器处理. 本研究选取sEMG信号的前5 s为非疲劳阶段,此时受试者能够轻松稳定地保持负重,而sEMG信号最后5 s被视为疲劳阶段,此时受试者几乎无法继续维持负重.
4. 实验结果及分析
4.1. 参数选择
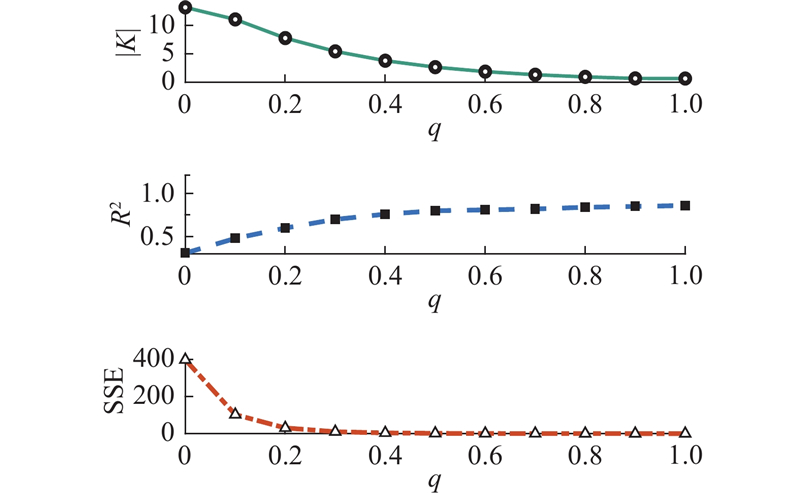
在使用RCMTFDE对sEMG信号进行分析时,选择合适的关键参数对于保证分析结果的有效性和准确性至关重要. 采用TFDE算法对5组sEMG信号进行特征提取,并对结果进行曲线拟合,得到各项指标的平均值,各项指标随q的变化结果如图2所示. 首先,斜率绝对值|K|代表了TFDE的区分肌肉疲劳的能力,随着q增大,算法的灵敏性逐渐减弱,较小的q使算法更为敏感,能够捕捉到更细微的特征变化. 其次,决定系数R2衡量了拟合效果的好坏. 随着q从1.0减小到0,R2从
图 2
文献[25]表明,嵌入维数m=3能有效捕捉信号的动态特征,避免信息冗余,适用于大多数信号分析任务;类别数c在3~9范围内结果变化不大,较小的c可减少噪声,较大的c保留更多细节,c=5既能有效抑制噪声,又能保持足够的信号信息;时间延迟d通常选择1,以保留信号有效细节信息. 因此,本研究使用RCMTFDE算法进行分析时,设置嵌入维数m=3,类别数c=5,时间延迟d=1,尺度因子τ=20.
4.2. RCMTFDE性能分析
RCMTFDE作为特征提取方法,其能否有效识别不同类型信号,是评价其性能的重要依据. 选取精细复合多尺度分散熵(RCMDE)[29]、RCMFDE、时移多尺度波动分散熵(TSMFDE)[30]、R2CMSE和时移多尺度斜率熵(RTSMSlE)[24]作为对比算法,通过比较RCMTFDE与这5种熵算法在不同噪声(高斯白噪声和1/f噪声)下的识别效果,评估算法对不同类型信号的区分能力. 高斯白噪声用于评估算法在随机干扰下的鲁棒性,而1/f噪声则更接近肌肉疲劳过程中的复杂性和非线性变化. 因此,选择这2种噪声进行性能对比,有助于全面评估算法在不同噪声环境下的表现. 实验选取高斯白噪声(WGN)和1/f噪声的长度N分别为
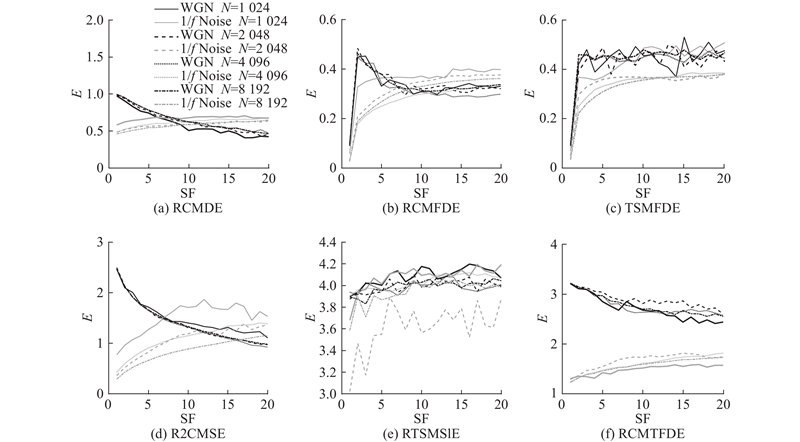
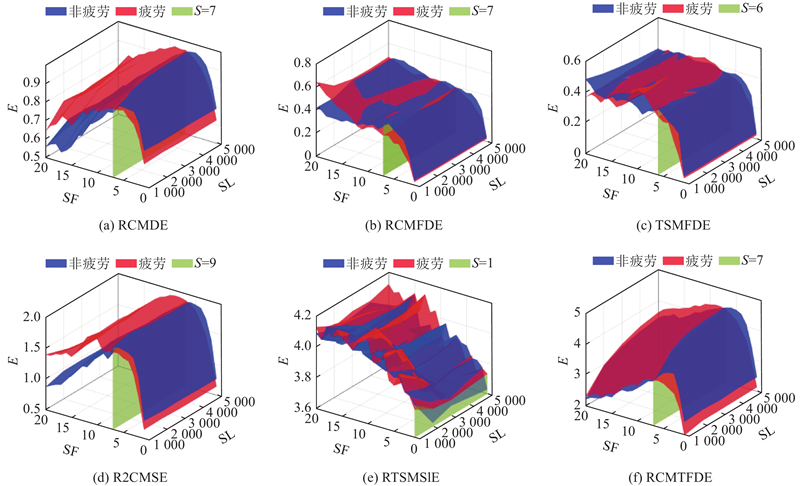
如图3所示为不同噪声长度下不同熵算法结果分布情况. 其中,E为熵值,SF为尺度因子. 可以看出,在任意尺度下,随着噪声信号长度的变化,2种类型的噪声信号的RCMTFDE熵值始终没有交叉,且呈现出明显的差异;其他熵算法的熵值则存在交叉和重叠现象,表明RCMTFDE可有效区分2种不同类型噪声信号,且稳定性强. 另外,RCMTFDE在相同类型的噪声下,熵值分布集中,重叠现象较明显,表明随着信号长度的变化,RCMTFDE的熵值变化较小,具有较好的鲁棒性. 其他熵算法随着噪声信号长度的增加,熵值分布会出现波动,其中RCMDE和R2CMSE的熵值波动较大.
图 3
图 3 不同噪声长度下不同熵算法结果分布情况
Fig.3 Distribution of entropy value under different noise lengths
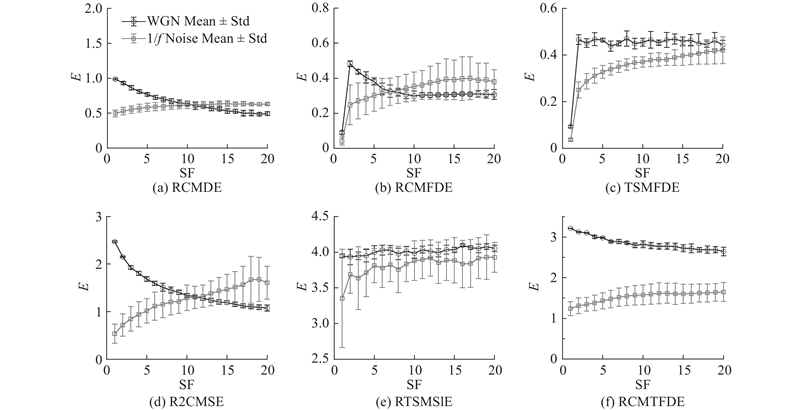
如图4所示为多尺度熵算法在不同噪声信号长度下的均值和标准差的误差条图,展示了各算法在不同噪声信号下随尺度因子的熵值变化趋势及波动幅度. 可以看出,RCMTFDE算法在不同噪声信号下的标准差整体较小,表现出了较高的稳健性. 此外,通过计算最大变异系数进一步量化了各算法的稳定性. RCMTFDE算法在高斯白噪声和1/f噪声下的最大变异系数分别为4.235和14.877,均为最低,表明其在噪声条件下的稳定性最强. 相比之下,RCMDE算法在高斯白噪声下的最大变异系数为16.905,为所有算法中最高;而R2CMSE算法在1/f噪声下的最大变异系数达到69.59,表明这些算法在对应噪声条件下的稳定性较差. 综上所述,RCMTFDE能有效识别不同类型的信号,且稳定性强.
图 4
图 4 不同噪声下不同熵方法的误差条图
Fig.4 Error bars of entropy methods across noise variations
4.3. RCMTFDE疲劳表征效果
为了验证RCMTFDE能否有效区分非疲劳和疲劳状态,须观察其在不同尺度下的熵值变化. 利用非疲劳和疲劳信号进行分析,数据长度范围为
图 5
图 5 不同尺度因子和长度下的非疲劳和疲劳信号下的熵值对比
Fig.5 Comparison of entropy values in non-fatigue and fatigue signals across scale factors and lengths
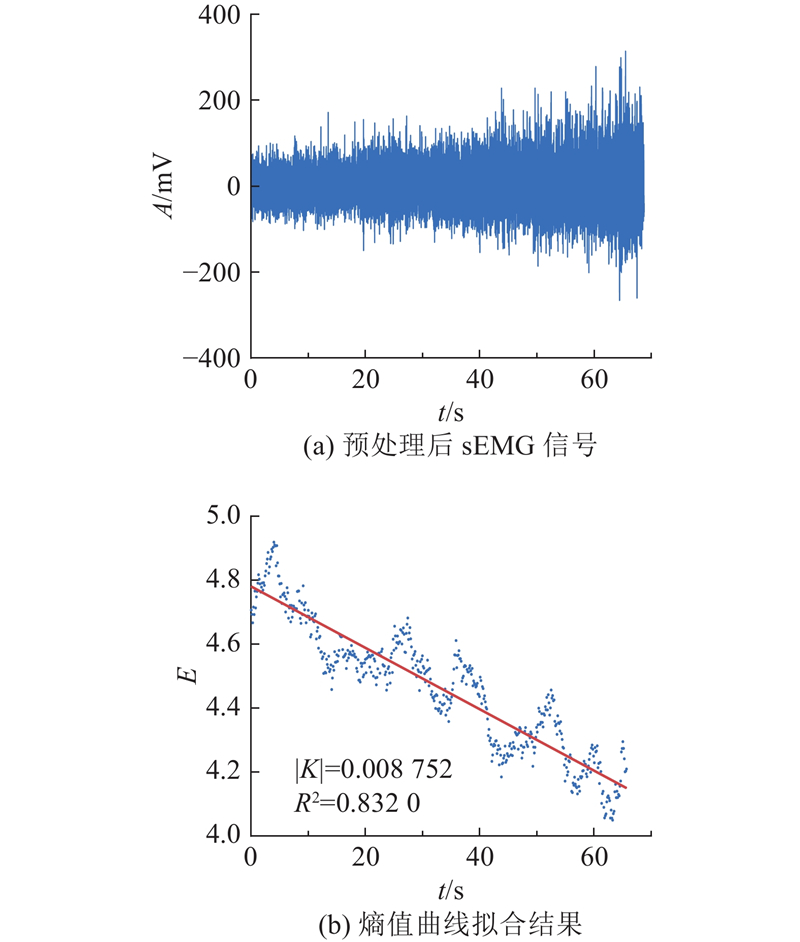
由于不同受试者的sEMG信号测量结果存在差异,须进一步探讨该分析方法对不同个体的适用性. 在熵理论中,肌肉疲劳指标可通过一条固定斜率的直线来表征. 图6(a)为受试者1的sEMG信号预处理后结果,图6(b)展示了信号的量化结果及其拟合直线. 其中,A为幅值,t为时间. 量化结果可区分非疲劳与疲劳状态,拟合直线能准确描述疲劳过程. 偏离直线的值被视为干扰,算法的抗干扰能力可通过决定系数R2来衡量,R2越大,抗干扰能力越强. 此外,直线斜率绝对值|K|越大,肌肉疲劳指标区分肌肉疲劳能力更强. 在多个尺度下寻找最佳肌肉疲劳特征,以|K|×R2为判断标准,当|K|×R2最大时,输出对应尺度下的熵值曲线.
图 6
在实验过程中,由于受试者的肌肉状态差异,不同受试者的耐力也有所不同. 选取受试者的肌肉疲劳过程单独分析,通过拟合熵值曲线计算|K|和R2,结果汇总于表1. 在6种算法中,RCMTFDE的|K|的平均值(
表 1 各受试者肌肉疲劳量化结果
Tab.1
| 受试者 | |K|/10−3 | R2 | |||||||||||
| RCMDE | RCMFDE | TSMFDE | R2CMSE | RTSMSIE | RCMTFDE | RCMDE | RCMFDE | TSMFDE | R2CMSE | RTSMSIE | RCMTFDE | ||
| 1 | |||||||||||||
| 2 | |||||||||||||
| 3 | |||||||||||||
| 4 | |||||||||||||
| 5 | |||||||||||||
| 6 | |||||||||||||
| 7 | 14.978 | ||||||||||||
| 8 | |||||||||||||
| 9 | |||||||||||||
| 10 | |||||||||||||
| 11 | |||||||||||||
| 12 | |||||||||||||
| 13 | |||||||||||||
| 14 | 10.031 | ||||||||||||
| 15 | |||||||||||||
| 平均值 | |||||||||||||
| 标准差 | |||||||||||||
对各多尺度熵的量化结果曲线进行Mann-Kendall趋势检验,验证其趋势程度和方向,数据平均结果如表2所示. 在Mann-Kendall趋势检验中,z表示数据趋势的方向和显著性:z > 0表示上升趋势,z< 0 表示下降趋势,且绝对值越大,趋势越显著. p则衡量趋势的显著性,当p小于显著性水平(0.05)时,趋势显著. 结果表明,除了RTSMSIE外,其他多尺度熵的z均为负,熵值曲线呈下降趋势. 这一趋势反映出随着肌肉疲劳加深,信号复杂性将会降低,符合肌肉疲劳状态下活动规律性增强、随机性减少的特点. RCMDE、RCMFDE、TSMFDE、R2CMSE和RCMTFDE的p均小于0.05,表明其熵值下降趋势显著. 其中,RCMTFDE的p(
表 2 Mann-Kendall趋势检验结果
Tab.2
| Mann-Kendall参数 | p | z |
| R2CMSE | − | |
| RCMDE | − | |
| RCMFDE | − | |
| RTSMSIE | − | |
| TSMFDE | − | |
| RCMTFDE | − |
4.4. 肌肉疲劳分类
为了进一步评估RCMTFDE与其他5种熵算法在区分肌肉非疲劳状态和疲劳状态的能力,将60组受试者的实验数据分为训练数据集(80%)和测试数据集(20%). 分类任务采用具有径向基函数核的支持向量机(support vector machine, SVM)分类器进行非疲劳与疲劳的分类. 为了更加全面地评估RCMTFDE算法的性能,除了与其他5种熵算法进行对比外,选取常用的传统时域特征iEMG和频域特征MF作为分类特征. 此外,为了优化模型的表现,采用K折交叉验证(K = 5)来选定最佳分类模型,并重复实验50次求取结果的平均值来体现模型的稳定性和泛化能力. 通过准确率A、灵敏度Sen、特异性Spe、精度Pre、F1值以及接收操作特征(ROC)曲线来评估模型识别疲劳状态的能力. 性能指标的表达式如下:
式中:TP、TN、FP和FN分别表示真阳性、真阴性、假阳性和假阴性样本个数.
肌肉疲劳分类结果如表3、图7所示. 从表3可以看出,基于RCMTFDE和SVM的分类模型在疲劳与非疲劳状态分类中,达到了最高的准确率96.667%,同时,其灵敏度和特异性分别为98.667%和94.667%,充分展示了模型在分类性能上的良好表现. 此外,该模型的F1高达96.800%,精度为95.287%,均高于其他特征组合. 实验结果表明,RCMTFDE算法能够更加精准地捕捉疲劳状态与非疲劳状态之间的差异,从而有效提升分类的整体性能和可靠性. 相比之下,其余特征的分类性能存在较大差异,反映了这些特征在区分疲劳与非疲劳状态时的不足. 其中,iEMG和MF特征的分类准确率仅为68.333%和74.111%,可以看出,RCMTFDE在可靠性上优于传统疲劳特征;RTSMSIE分类准确率最低,为67.000%,表明RTSMSIE在肌肉疲劳识别中具有局限性.
表 3 不同特征肌肉疲劳分类结果
Tab.3
| 特征 | 分类器 | Sen/% | Spe/% | Pre/% | F1/% | A/% |
| iEMG | SVM | 68.889 | 67.778 | 68.710 | 68.300 | 68.333 |
| MF | SVM | 66.889 | 81.333 | 81.276 | 71.204 | 74.111 |
| RCMDE | SVM | 86.222 | 86.000 | 86.636 | 85.821 | 86.111 |
| RCMFDE | SVM | 83.333 | 89.778 | 90.452 | 86.001 | 86.556 |
| TSMFDE | SVM | 85.556 | 89.556 | 89.89 | 87.136 | 87.556 |
| R2CMSE | SVM | 88.444 | 90.889 | 91.823 | 89.319 | 89.667 |
| RTSMSIE | SVM | 71.778 | 62.222 | 66.373 | 68.327 | 67.000 |
| RCMTFDE | SVM | 98.667 | 94.667 | 95.287 | 96.800 | 96.667 |
图 7
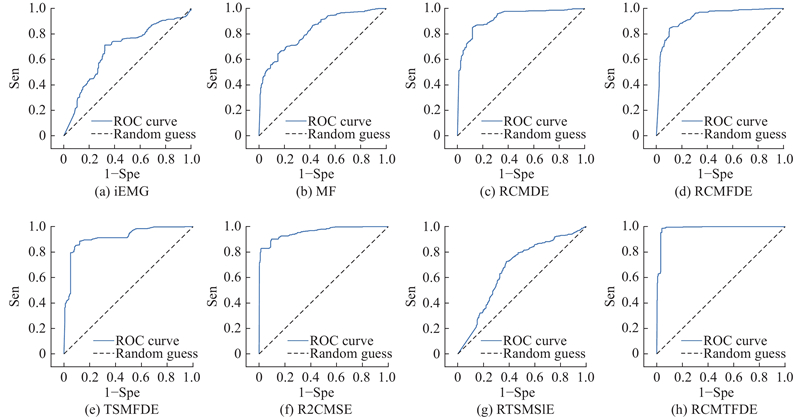
图 7 肌肉疲劳分类实验中各方法的ROC曲线对比结果
Fig.7 ROC curve results of each method in muscle fatigue classification
如图7所示展示了基于不同特征和SVM的模型在识别肌肉疲劳中的ROC曲线结果. 可以看出,基于RCMTFDE和SVM的识别框架具有最优性能,其ROC曲线下面积(AUC)达到0.985 00;基于iEMG特征的框架表现相对较差,AUC为
综上所述,本研究提出的基于RCMTFDE的肌肉疲劳识别方法,在各项评估指标中表现出色,特别是与传统特征iEMG和MF相比,RCMTFDE算法在识别精度上展现了明显的优势. 此外,与其他熵算法相比,RCMTFDE在灵敏性和信号信息提取能力方面表现突出,能够更好地捕捉肌肉疲劳的微弱变化,从而有效提升分类的准确性.
4.5. 消融实验
在RCMTFDE算法中,依次引入模糊化处理、Tsallis熵以及平滑增强的粗粒化方法,利用5组sEMG信号进行消融实验,来验证各个改进模块的独立作用,设计了6种消融对比方法:FDE、模糊化FDE、未模糊化的TFDE、模糊化的TFDE、传统粗粒化RCMTFDE以及平滑增强RCMTFDE,结果如表4所示. 可以看出,逐步引入不同改进显著提升了算法的性能. 模糊化FDE相较于FDE,在|K|和R2这2个指标上均有所增加,表明模糊化处理有效增强了算法的抗干扰能力和精确性. 仅引入Tsallis熵时,算法的灵敏性和抗干扰能力得到明显提升;而结合模糊化和Tsallis熵的TFDE算法,性能得到了进一步增强. 传统粗粒化方法RCMTFDE相比TFDE,在|K|指标上提升了59.257%,而在R2上提升了0.369%,表明RCMTFDE在特征提取方面表现出更强的能力. 平滑增强RCMTFDE的|K|略有增加,R2提升至
表 4 RCMTFDE算法的消融实验结果
Tab.4
| 算法 | FDE | 模糊化 | Tsallis熵 | 传统粗粒化 | 平滑增强粗粒化 | |K|/10−3 | R2 |
| FDE | √ | × | × | × | × | ||
| 模糊化FDE | √ | √ | × | × | × | ||
| 未模糊化TFDE | √ | × | √ | × | × | ||
| 模糊化TFDE | √ | √ | √ | × | × | ||
| 传统粗粒化RCMTFDE | √ | √ | √ | √ | × | ||
| 平滑增强RCMTFDE | √ | √ | √ | √ | √ |
5. 结 论
针对FDE离散分类和灵敏性不足的缺点,在FDE基础上引入模糊化处理,并结合Tsallis熵,提出TFDE. 在TFDE的基础上,对粗粒化方法存在信息泄露的问题进行改进,提出基于RCMTFDE的肌肉疲劳多尺度表征方法. 与其他特征进行比较分析,实验结果如下.
(1)在面对不同长度噪声时,RCMTFDE能有效区分信号,展现出更好的鲁棒性和稳定性;
(2)在分析非疲劳和疲劳信号时,RCMTFDE在两者信号之间的熵值差异更为显著,能在低尺度下有效区分疲劳状态,且熵值变化稳定;
(3)在不同受试者的肌肉疲劳量化结果中,RCMTFDE所提取的特征表现出更强的区分能力,同时RCMTFDE在灵敏性和抗干扰性方面也优于其他方法,识别出的疲劳表征趋势变化更加明显;
(4)肌肉疲劳分类实验结果表明,相较于5种熵算法和2种传统特征,所提RCMTFDE算法取得了最高的识别精度,达到96.667%,灵敏度、特异性、精度等分类指标值也均为最高,验证了所提算法在表征肌肉疲劳中的优势.
本研究所提方法存在参数设置过多以及在高尺度下区分效果减弱的问题,仍须进一步优化. 接下来可通过优化参数设置并改进高尺度下的表现,进一步完善该方法的实用性和通用性.
参考文献
Complex network properties analysis of muscle fatigue based on sEMG signals
[J].DOI:10.1109/JSEN.2022.3233047 [本文引用: 1]
Peripheral fatigue: new mechanistic insights from recent technologies
[J].DOI:10.1007/s00421-019-04264-w [本文引用: 1]
sEMG-based dynamic muscle fatigue classification using SVM with improved whale optimization algorithm
[J].DOI:10.1109/JIOT.2021.3056126 [本文引用: 1]
MFFNet: multi-dimensional feature fusion network based on attention mechanism for sEMG analysis to detect muscle fatigue
[J].DOI:10.1016/j.eswa.2021.115639 [本文引用: 1]
基于傅里叶分解方法的肌肉疲劳状态分类研究
[J].
Study of muscle fatigue state classification based on Fourier decomposition method
[J].
基于表面肌电与步态的外骨骼穿戴疲劳评测
[J].
Evaluation of exoskeleton wearing fatigue based on surface electromyography and gait
[J].
Neuromuscular fatigue in autoimmune myasthenia gravis: a cross-sectional study
[J].DOI:10.1016/j.neucli.2023.102844 [本文引用: 1]
Characterization of electromyographical signals from biceps and rectus femoris muscles to evaluate the performance of squats coupled with countermeasure gravitational load modulating bodygear
[J].DOI:10.1007/s12217-021-09899-z [本文引用: 1]
Muscle fatigue detection based on sEMG signal using autocorrelation function and neural networks
[J].DOI:10.1515/auto-2023-0207 [本文引用: 1]
Exploration and application of a muscle fatigue assessment model based on NMF for multi-muscle synergistic movements
[J].DOI:10.1109/TNSRE.2024.3393132 [本文引用: 1]
Improved algorithm of muscle fatigue detection using linear regression analysis
[J].DOI:10.1049/el.2012.2316 [本文引用: 1]
Mean frequency derived via Hilbert-Huang transform with application to fatigue EMG signal analysis
[J].DOI:10.1016/j.cmpb.2006.02.009 [本文引用: 1]
Fuzzy approximate entropy analysis of chaotic and natural complex systems: detecting muscle fatigue using electromyography signals
[J].DOI:10.1007/s10439-010-9933-5 [本文引用: 1]
Electromyographic models to assess muscle fatigue
[J].DOI:10.1016/j.jelekin.2012.02.019 [本文引用: 1]
Muscle fatigue analysis during dynamic contractions based on biomechanical features and Permutation Entropy
[J].DOI:10.3934/mbe.2020142 [本文引用: 1]
Analysis of dynamics of EMG signal variations in fatiguing contractions of muscles using transition network approach
[J].
A new fractional fuzzy dispersion entropy and its application in muscle fatigue detection
[J].
(multiscale) cross-entropy methods: a review
[J].
Analysis of fatigue in the biceps brachii by using rapid refined composite multiscale sample entropy
[J].DOI:10.1016/j.bspc.2021.102510 [本文引用: 1]
Vibration-based fault diagnosis for railway point machines using VMD and multiscale fluctuation-based dispersion entropy
[J].DOI:10.23919/cje.2022.00.075 [本文引用: 1]
Refined composite multiscale fluctuation dispersion entropy and supervised manifold mapping for planetary gearbox fault diagnosis
[J].DOI:10.3390/machines11010047 [本文引用: 1]
Gearbox fault diagnosis based on refined time-shift multiscale reverse dispersion entropy and optimised support vector machine
[J].DOI:10.3390/machines11060646 [本文引用: 1]
Refined time-shift multiscale slope entropy: a new nonlinear dynamic analysis tool for rotating machinery fault feature extraction
[J].DOI:10.1007/s11071-024-10106-y [本文引用: 2]
Amplitude- and fluctuation-based dispersion entropy
[J].DOI:10.3390/e20030210 [本文引用: 2]
Cross subject emotion identification from multichannel EEG sub-bands using Tsallis entropy feature and KNN classifier
[J].DOI:10.1186/s40708-024-00220-3 [本文引用: 1]
Tsallis entropy-based complexity-IPE casualty plane: a novel method for complex time series analysis
[J].DOI:10.3390/e26060521 [本文引用: 1]
基于sEMG信号几何特征的肌肉疲劳分类
[J].
Muscle fatigue classification based on geometric features of sEMG signal
[J].
Complexity analysis of time series based on generalized fractional order refined composite multiscale dispersion entropy
[J].DOI:10.1142/S0218127420502119 [本文引用: 1]
基于时移多尺度波动散布熵和改进核极限学习机的水电机组故障诊断
[J].
Fault diagnosis method of hydropower units based on time-shifted multiscale fluctuation dispersion entropy and improved kernel extreme learning machine
[J].