随着科学技术的快速发展和数据规模的不断扩大，各领域优化问题日益增多且愈加复杂. 传统的优化方法在计算效率和解质量上面临严峻挑战. 元启发式优化算法因其独特的仿生智能特性，逐渐引起众多学者的关注. 经典的智能优化算法如粒子群优化算法、遗传算法、蚁群优化算法，以及近年来涌现的新兴算法如鲸鱼优化算法^[1]、正余弦算法^[2]、哈里斯鹰优化算法^[3]和雪消融优化器^[4]等，凭借其强大的全局搜索能力、简单的实现方式和对复杂非线性问题的高度适应性，已成功应用于多个领域.

平衡优化器（equilibrium optimizer，EO）^[5]是Faramarzi等受动态质量平衡启发而提出的新型智能优化算法. EO凭借其独特机制，在分布式发电优化^[6]、医学图像融合^[7]和燃料电池建模^[8]等领域展现出良好的性能，但存在探索能力不足、易陷入局部最优的局限性. 为此，众多研究者提出不同的改进策略来提升其性能. 张梦溪等^[9]引入浓度平衡机制、自适应因子和基于菲克定律的扰动机制，增强了算法的全局探索能力. 周鹏等^[10]引入Tent混沌映射来提高收敛速度，利用透镜成像学习策略，防止算法陷入局部最优. Dinkar等^[11]加入基于拉普拉斯分布的随机游走策略和融合变加速系数的对立学习策略，有效平衡了EO的探索和开发能力. Atha等^[12]提出准对立混沌平衡优化器，提升了初始解的质量，减少了局部停滞. Fan等^[13]引入对立学习和混沌映射来改善种群质量，利用非线性时间控制策略提高搜索效率. Wu等^[14]引入质心对立学习策略和自学习策略，提高了EO算法的全局探索能力和寻优效果.

这些改进有效提升了EO算法在各自应用领域的求解性能，然而在应对高维复杂优化问题时，该算法的收敛精度、求解稳定性和摆脱局部桎梏的能力仍有进一步提升的空间. 本文提出基于交叉更新、分级搜索和三角拓扑精英学习策略的平衡优化器（CGTEO）. 在CEC2017测试集上，将CGTEO与9种代表性对比算法进行多维度、多方法的求解测试和对比分析.

平衡优化器算法的灵感来源于控制体积内混合动态质量平衡的物理现象，EO中的每个粒子都根据平衡候选、指数项及生成速率来更新位置，从而使算法逐步达到平衡状态.

平衡优化器算法的步骤如下.

1）初始化参数：种群规模$ N $、空间维度$ D $、最大迭代次数Iter_m. 根据式（1）产生$ N $个粒子的初始位置$ {\boldsymbol{C}} $：

(1)$ {\boldsymbol{C}} = {{\boldsymbol{C}}_{{\mathrm{min}}}}+{\bf{rand}}(N,D) \times ({{\boldsymbol{C}}_{{\mathrm{max}}}} - {{\boldsymbol{C}}_{{\mathrm{min}}}}). $

式中：$ {{\boldsymbol{C}}_{{\mathrm{max}}}} $和$ {{\boldsymbol{C}}_{{\mathrm{min}}}} $分别为搜索空间各维度的上、下限，$ {\bf{rand}}(N,D) $为产生（0, 1.0）均匀分布随机数的$ D $维矩阵.

2）进入迭代，对各个粒子进行边界条件的处理. 根据目标函数计算各粒子的适应度，将适应度最优的4个粒子记为平衡候选，对4个平衡候选粒子求算术平均值，构造平衡池.

(2)$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(}}{\mathrm{ave}}{\text{)}}}} = \frac{{{{\boldsymbol{C}}_{{\rm{eq}}{\text{(1)}}}}+{{\boldsymbol{C}}_{{\rm{eq}}{\text{(2)}}}}+{{\boldsymbol{C}}_{{\rm{eq}}{\text{(3)}}}}+{{\boldsymbol{C}}_{{\rm{eq}}{\text{(4)}}}}}}{4}, $

(3)$ {C_{{\rm{eq,pool}}}} = \left\{ {{{\boldsymbol{C}}_{{\rm{eq}}{\text{(1)}}}},{{\boldsymbol{C}}_{{\rm{eq}}{\text{(2)}}}},{{\boldsymbol{C}}_{{\rm{eq}}{\text{(3)}}}},{{\boldsymbol{C}}_{{\rm{eq}}{\text{(4)}}}},{{\boldsymbol{C}}_{{\rm{eq}}{\text{(}}{\mathrm{ave}}{\text{)}}}}} \right\}. $

式中：$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(1)}}}} $、$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(2)}}}} $、$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(3)}}}} $、$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(4)}}}} $分别为4个最佳粒子的位置，$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(}}{\mathrm{ave}}{\text{)}}}} $为4个粒子的平均位置. 在迭代过程中，每个粒子以相同的概率从平衡池中选择候选对象来更新位置.

3）执行记忆存储，每个粒子与上一代粒子的适应度进行比较，保留优质个体.

4）计算自适应系数$ t $，$ t $随着迭代次数的增加而非线性减小，如下所示：

(4)$ t = {\left(1 - \frac{{{\mathrm{Iter}}}}{{{\mathrm{Iter}}_{\mathrm{m}}}}\right)^{{a_2}{{{\mathrm{Iter}}}}/{{{\mathrm{Iter}}_{\mathrm{m}}}}}}. $

式中：$ {a_2} $为控制开发能力的常数值，$ {a_2} $越大，开发能力越好，探索能力越低；$ {\mathrm{Iter}} $为当前迭代次数.

5）开始各粒子的位置更新过程，从$ {C_{{\rm{eq,pool}}}} $随机选取候选粒子作为当前迭代的平衡候选$ {{\boldsymbol{C}}_{{\rm{eq}}}} $.

6）计算指数项系数$ {\boldsymbol{F}} $，它主要影响位置更新规则，平衡算法的全局搜索和局部搜索.

(5)$ {\boldsymbol{F}} = {a_1}{\mathrm{sign}}\;({\boldsymbol{r}} - 0.5{\boldsymbol{E}})({{\mathrm{e}}^{ - {\boldsymbol{\lambda}} t}} - {\boldsymbol{E}}). $

式中：$ {a_1} $为控制探索能力的常数值，$ {\mathrm{sign}}\;({\boldsymbol{r}} - 0.5{\boldsymbol{E}}) $决定探索和开发的方向，$ {\boldsymbol{r}} $、$ {\boldsymbol{\lambda}} $均为（0,1.0）均匀分布的随机向量，E为所有元素均为1的向量.

7）根据下式计算生成速率$ {\boldsymbol{G}} $，它作用于粒子位置更新公式中的生成项，增强算法的局部搜索能力.

(6)$ {\boldsymbol{G}} = {{\boldsymbol{G}}_0}{{\mathrm{e}}^{ - {\boldsymbol{\lambda}} (t - {t_0})}} = {{\boldsymbol{G}}_{0}}\circ {\boldsymbol{F}}. $

(7)$ {{\boldsymbol{G}}_0} = {\bf{GCP}}\circ({{\boldsymbol{C}}_{{\rm{eq}}}} - {\boldsymbol{\lambda}}\circ {\boldsymbol{C}}). $

(8)$ {\bf{GCP}} = \left\{ {\begin{array}{*{20}{c}} {0.5{{{r}}_1} {\boldsymbol{M}},}&{{{{r}}_2} \geqslant {\mathrm{GP}}}; \\ {{\boldsymbol{0}},}&{{{{r}}_2} < {\mathrm{GP}}} .\end{array}} \right. $

式中：$\circ $表示逐元素相乘；$ {r_1} $、$ {r_2} $均为（0,1.0）均匀分布的随机数；$ {\boldsymbol{M}} $为元素都为1的$ D $维向量；$ {\bf{GCP}} $为生成速率控制参数；$ {\mathrm{GP}} = 0.5 $为生成概率，指定有多少粒子使用生成项来更新其状态.

8）对粒子位置进行更新：

(9)$ {\boldsymbol{C}}({\mathrm{Iter}}+1) = {{\boldsymbol{C}}_{{\rm{eq}}}}+({\boldsymbol{C}}({\mathrm{Iter}}) - {{\boldsymbol{C}}_{{\rm{eq}}}}){\boldsymbol{F}}+\frac{{\boldsymbol{G}}}{{{\boldsymbol{\lambda}} {{V}}}}({\boldsymbol{E}} - {\boldsymbol{F}}). $

式中：V为常数.

9）判断是否符合结束条件. 若符合，则输出结果；否则，转回2）继续下一轮迭代.

通过分析式（8）、（9）可以发现，当$ {r_2} < {\mathrm{GP}} $时，若当前个体$ {\boldsymbol{C}} $与选择的平衡候选个体$ {{\boldsymbol{C}}_{{\rm{eq}}}} $相同，则个体的位置更新将停滞. 对于具有多个局部极值的复杂问题来说，EO算法的多样性和探索能力有待提高. 在EO中引入新的更新机制，当$ {r_2} < {\mathrm{GP}} $时，通过交叉算子将平衡候选个体$ {{\boldsymbol{C}}_{{\rm{eq}}}} $与随机个体组合，得到新的个体$ {{\boldsymbol{C}}_{\mathrm{p}}} $，并由该个体引导位置更新，计算公式如下所示：

(10)$ {{\boldsymbol{C}}_{{\rm{ave}}}} = \frac{{{{\boldsymbol{C}}_{{\rm{n}}1}}+{{\boldsymbol{C}}_{{\rm{n}}2}}}}{2}, $

(11)$ {{\boldsymbol{C}}_{\rm{p}}} = {{\boldsymbol{C}}_{{\rm{eq}}}} \circ {\bf{OP}}+{{\boldsymbol{C}}_{{\rm{ave}}}} \circ ({\boldsymbol{E}} - {\bf{OP}}). $

式中：$ {{\boldsymbol{C}}_{{\rm{n}}1}} $、$ {{\boldsymbol{C}}_{{\rm{n}}2}} $表示从种群中随机选择的2个不同的个体，$ {\bf{OP}} $为由二进制数（0和1）随机组成的$ D $维交叉算子. 为了增强全局搜索能力，设计搜索范围更广的正余弦系数$ {\bf{SCF}} $：

(12)$\begin{split} {\bf{SCF}} =& (0.5{\boldsymbol{E}}+t{{\boldsymbol{r}}_4} ) \circ [\sin\; (2{\text{π}} {{\boldsymbol{r}}_5}) \circ {\bf{OP}}+ \\&\cos\; (2{\text{π}} {{\boldsymbol{r}}_5}) \circ ({\boldsymbol{E}} - {\bf{OP}})]. \end{split} $

式中：$ {{\boldsymbol{r}}_4} $、$ {{\boldsymbol{r}}_5} $均为（0，1.0）均匀分布的随机数组成的向量. 此时，改进EO算法的位置更新模型为

(13)$ \begin{split} &{\boldsymbol{C}}({\mathrm{Iter}}+1) = \\&\left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{C}}_{{\text{eq}}}}+({\boldsymbol{C}}({\mathrm{Iter}}) - {{\boldsymbol{C}}_{{\text{eq}}}}) \circ {\boldsymbol{F}}+\dfrac{{\boldsymbol{G}}}{{{\boldsymbol{\lambda}} V}}\circ ({\boldsymbol{E}} - {\boldsymbol{F}}),}&{{r_2} \geqslant {\mathrm{GP}}}; \\ {{{\boldsymbol{C}}_{\text{p}}}+({\boldsymbol{C}}({\mathrm{Iter}}) - {{\boldsymbol{C}}_{\text{p}}}) \circ {\bf{SCF}}}, &{{r_2} <{\mathrm{GP}}} .\end{array}} \right.\end{split} $

在引入交叉个体$ {{\boldsymbol{C}}_{\rm{p}}} $后，为了进一步加强算法探索和开发能力之间的平衡，对$ {\mathrm{GP}} = 0.5 $进行改进，根据式（14）计算$ {\mathrm{GP}} $. 此时，$ {\mathrm{GP}} $的变化趋势如图1所示. 可知，交叉个体的引导概率较大，呈现非线性递减的趋势，因此在提高了对未知解的探索能力的同时，保证了算法的收敛性.

(14)$ {\mathrm{GP}} = {\left(1 - \frac{3}{4} \times \frac{{{\mathrm{Iter}}}}{{{\mathrm{Iter}}_{\mathrm{m}}}}\right)^{{1}/{2}}}. $

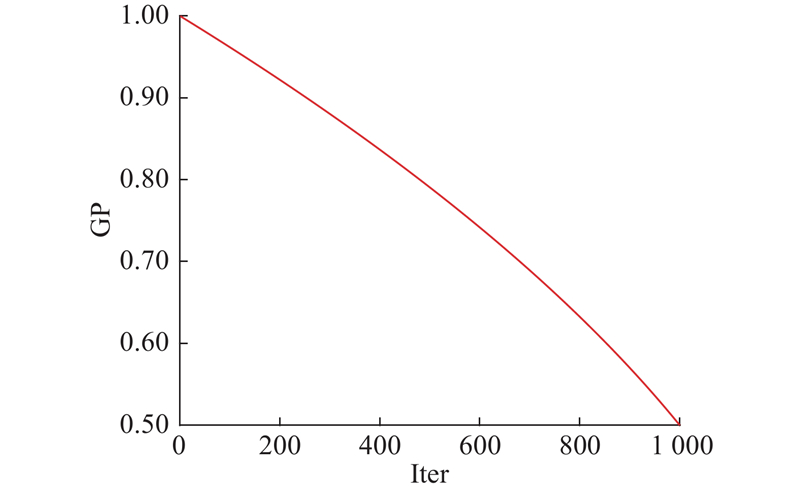
该策略通过交叉算子将平衡候选个体与更广泛的其他个体结合，可以在保持种群多样性的同时，利用优势个体的优势信息来指导搜索方向. 正余弦系数$ {\bf{SCF}} $和指数项系数$ {\boldsymbol{F}} $随着迭代的进行都呈现振荡收缩的趋势，$ {\bf{SCF}} $较$ {\boldsymbol{F}} $具有更大的取值范围，可以探索更广阔的区域. 相对于$ {\boldsymbol{F}} $来说，$ {\bf{SCF}} $在迭代后期没有减小到接近0，而是维持在[−0.5，0.5]. 这有助于算法跳出局部最优解，增强对全局最优解的搜索能力.

为了保持算法探索开发能力的平衡并提高最终的收敛精度，提出动态分级搜索策略. 将整个种群按照适应度进行排序，并由此生成精英池，精英池的组成如下所示：

(15)$ {\mathrm{B}}\_{\mathrm{pool}} = \left\{ {{{\boldsymbol{C}}_{{\text{eq}}(1)}},{{\boldsymbol{C}}_{{\text{eq}}(2)}},{{\boldsymbol{C}}_{{\text{eq}}(3)}},{{\boldsymbol{C}}_{{\text{eq}}(4)}}} \right\}. $

根据排序结果，将种群分成3个子种群，各个子种群包含的个体数量在迭代过程中动态调整. 第1个子群由适应度较优的个体组成，该部分由最优个体引导，以加快整体的收敛速度. 第2个子群由适应度中等的个体组成，该部分采用混合搜索策略，每个个体以一定的概率选择向较优个体靠近，或者在当前位置进行局部搜索，以提高算法的开发能力. 第3个子群由剩下的适应度较差的个体组成，该部分个体执行随机搜索策略，以避免算法陷入局部最优，从而提高算法找到全局最优解的能力. 分级方法如下所示：

(16)$ {\boldsymbol{C}} = \left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{C}}_a},}&{a = 1,2, \cdots ,{n_1}}; \\ {{{\boldsymbol{C}}_b},}&{b = {n_1}+1,{n_1}+2, \cdots ,{n_2}} ;\\ {{{\boldsymbol{C}}_c},}&{c = {n_2}+1,{n_2}+2, \cdots ,N} .\end{array}} \right. $

式中：$ {\boldsymbol{C}} $为总种群；$ {{\boldsymbol{C}}_a} $、$ {{\boldsymbol{C}}_b} $、$ {{\boldsymbol{C}}_c} $为按适应度分级后的子种群；$ {n_1} $和$ {n_2} $为每个子种群包含个体数量的边界，

(17)$\left. \begin{split} {n_1} =\; & {\rm{ceil}}\left( {\frac{2}{8} N+N {{\left(\frac{{{\mathrm{Iter}}}}{{{\mathrm{Iter}}_{\mathrm{m}}}} - 0.5\right)}^3}} \right), \\ {n_2} =\; & {\rm{ceil}}\left( {\frac{6}{8} N+N {{\left(\frac{{{\mathrm{Iter}}}}{{{\mathrm{Iter}}_{\mathrm{m}}}} - 0.5\right)}^3}} \right). \end{split}\right\} $

式中：$ {\rm{ceil}} $表示向上取整函数.

对于第1个子种群$ {{\boldsymbol{C}}_a} $中的较优个体，由最优个体$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(1)}}}} $引导在最有希望的区域进行布朗运动，如下所示：

(18)$ {{\boldsymbol{C}}_{{a}}}({\mathrm{Iter}}+1) = {{\boldsymbol{C}}_{{\text{eq}}(1)}}+{{\boldsymbol{B}}_{\text{m}}} \circ ({{\boldsymbol{C}}_{{\text{eq}}(1)}} - {{\boldsymbol{C}}_{{a}}}({\mathrm{Iter}})). $

式中：$ {{\boldsymbol{B}}_{\text{m}}} $为由标准正态分布生成的随机向量，表示布朗运动. 布朗运动产生动态和均匀的步长，可以充分搜索当前的最佳区域，增加找到最优解的机会.

对于第2个子种群$ {{\boldsymbol{C}}_b} $中的个体，它们的适应度位于中等级别，该子种群执行如下所示的2种搜索策略：

(19)$\begin{split} &{{\boldsymbol{C}}_{{b}}}({\mathrm{Iter}}+1) = \\&\left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{C}}_{{b}}}({\mathrm{Iter}})+{{\boldsymbol{R}}_{{{\mathrm{v}}}}} \circ({\bf{BC}} - {{\boldsymbol{C}}_{{b}}}({\mathrm{Iter}})),}& {{r_6} > {\mathrm{DP}}}; \\ {{{\boldsymbol{C}}_{{b}}}({\mathrm{Iter}})+{\bf{Gauss}} \circ {{\boldsymbol{C}}_{{b}}}({\mathrm{Iter}}),}&{{r_6} \leqslant {\mathrm{DP}}} .\end{array}} \right.\end{split} $

式中：$ {r_6} $为（0,1.0）均匀分布的随机数，$ {{\boldsymbol{R}}_{\text{v}}} $为由（0,1.0）均匀分布的随机数组成的向量，$ {\bf{BC}} $为从精英池$ {\mathrm{B}}\_{\mathrm{pool}} $中随机选择的个体，$ {\bf{Gauss}} $表示均值为0、方差为1的高斯分布，$ {\mathrm{DP}} $为决策概率. 当策略选择随机数$ {r_6} > {\mathrm{DP}} $时，个体向精英池$ {\mathrm{B}}\_{\mathrm{pool}} $中的个体学习，每次从池中随机选择较优的个体，向其作随机运动. 当$ {r_6} \leqslant {\mathrm{DP}} $时，个体在自身位置附近进行高斯变异，对当前位置进行更加精细的搜索. 经反复测试可知，$ {\mathrm{DP}} $取 0.3时效果最佳.

对于第3个子种群$ {{\boldsymbol{C}}_c} $中的较差个体，通过在搜索空间中生成一个新解，并由该新解引导它们的更新，如下所示.

(20)$ s = {r_7} \left(1 - 0.5 \dfrac{{{\mathrm{Iter}}}}{{{\mathrm{Iter}}_{\mathrm{m}}}}\right). $

(21)$ \begin{split} {{\boldsymbol{C}}_{{c}}}({\mathrm{Iter}}+1) = \;& {{\boldsymbol{C}}_{{c}}}({\mathrm{Iter}})+s \bigg[{{\boldsymbol{C}}_{\min }}+({{\boldsymbol{C}}_{\max }} - {{\boldsymbol{C}}_{\min }}) \circ \\&{\bf{rand}}\;(1,D) - {{\boldsymbol{C}}_{{c}}}({\mathrm{Iter}})\bigg]. \end{split}$

式中：$ {r_7} $为（0,1.0）均匀分布的随机数；步长$ s $在迭代过程中呈现振荡缩小的趋势，在提供多样性的同时，有利于迭代后期的深度挖掘；$ {\bf{rand}}\;(1,D) $产生由（0,1.0）均匀分布的随机数组成的$ D $维向量. 新解的引导可以增加搜索的多样性，避免算法陷入局部最优.

上述动态分级搜索策略根据个体的适应度将种群分为3个子种群，每个子种群采用不同的搜索策略. 其中最佳个体和精英池的引导搜索提高了算法的收敛速度，高斯扰动和随机新解的引导保持了种群的多样性，有助于算法跳出局部最优，提高算法的收敛精度. 每个子种群中个体数量的动态变化进一步增强了优化过程的灵活性和适应性.

为了进一步提高改进算法的求解精度，提出融合三角形拓扑单元^[15]的精英邻域学习策略. 在算法执行前2节的改进策略完成位置更新后，根据适应度对种群个体进行排序，更新式（15）所示的精英池中的4个精英个体$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(1)}}}} $、$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(2)}}}} $、$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(3)}}}} $、$ {{\boldsymbol{C}}_{{\rm{eq}}{\text{(4)}}}} $. 对它们每个个体构造三角形拓扑邻域进行学习，最后以较优的新解更新种群中对应精英个体的位置.

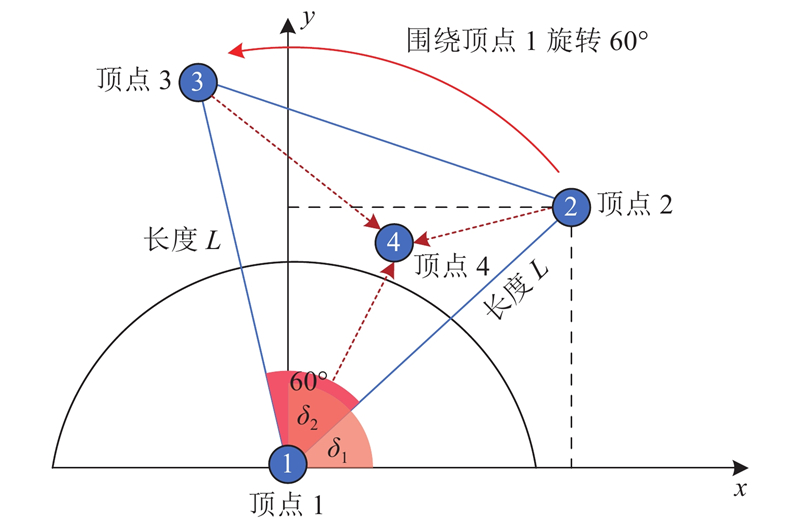
分别为4个精英个体构造三角形拓扑单元，如图2所示为三角形拓扑单元的构造示意图. 每个精英个体作为对应单元内的第1个顶点$ {{\boldsymbol{T}}_{{{k}},1}}({{k}} = 1,\cdots ,4) $，以该顶点作为起始点引出另外2条边的方向向量，计算如下：

(22)$\left. \begin{split} {{f}}({\boldsymbol{\delta}} ) =\; & [\cos\; {\delta _1},\;\cos \;{\delta _2},\cdots ,\;\cos\; {\delta _{D - 1}},\cos \;{\delta _D}], \\ {{f}}\left({\boldsymbol{\delta}} +\frac{{\text{π}} }{3}{\boldsymbol{E}}\right) =& \left[\cos \left({\delta _1}+\frac{{\text{π}} }{3}\right),\cos \left({\delta _2}+\frac{{\text{π}} }{3}\right),\cdots ,\right.\\ &\left.\cos \left({\delta _D}+\frac{{\text{π}} }{3}\right)\right]. \end{split} \right\}$

式中：$ {\boldsymbol{\delta}} = [{\delta _1},\cdots ,{\delta _D}] $，其中$ {\delta _j}(j = 1,\cdots ,D) $为$ [0,{\text{π}} ] $均匀分布的随机数. $ {\boldsymbol{\delta}} $是极坐标系中的1个方向向量，将$ {\boldsymbol{\delta}} $逆时针旋转$ {\text{π}} /3 $得到第2个方向向量，通过余弦函数将这2个方向向量转换到直角坐标系中.

(23)$ L = 12 \times {{\mathrm{exp}}\left({ - \dfrac{{{\mathrm{Iter}}}}{{{\mathrm{Iter}}_{\mathrm{m}}}}}\right)}. $

式中：$ L $为三角形拓扑单元的大小，随着迭代次数的增加而减小. 在边长为$ L $的条件下，分别形成第2个顶点$ {{\boldsymbol{T}}_{{{k}},2}} $和第3个顶点$ {{\boldsymbol{T}}_{{{k}},3}} $，如下所示：

(24)$\left. \begin{split} &{{\boldsymbol{T}}_{{{k}},2}} = {{\boldsymbol{T}}_{{{k}},1}}+L {{f}}({\boldsymbol{\delta}} ), \\ & {{\boldsymbol{T}}_{{{k}},3}} = {{\boldsymbol{T}}_{{{k}},1}}+L {{f}}\left({\boldsymbol{\delta}} +\frac{{\text{π}} }{3}{\boldsymbol{E}}\right). \end{split}\right\} $

利用式（24），由1个顶点和2个边长相等的边生成1个三角形拓扑单元. 每一组三角形拓扑单元在其内部聚合产生一个新点，该点的计算公式为

(25)$ {{\boldsymbol{T}}_{{{k}},4}} = {w_1} {{\boldsymbol{T}}_{{{k}},1}}+{w_2} {{\boldsymbol{T}}_{{{k}},2}}+{w_3} {{\boldsymbol{T}}_{{{k}},3}}. $

式中：$ {w_1} $、$ {w_2} $和$ {w_3} $为（0，1.0）均匀分布的随机数， $ {w_1}+{w_2}+{w_3} = 1 $.

在三角形拓扑单元构造完成之后，对每一组单元中的4个顶点计算适应度，找出最优个体和次优个体. 设计扰动系数$ \alpha $，将其作用于最优个体和次优个体之间的向量差，以实现对最优个体位置的扰动，如下所示.

(26)$ \alpha = 3 - 2 \times \left[{\left(\dfrac{{{{\mathrm{exp}}\;({{{{\mathrm{Iter}}}}/{{{\mathrm{Iter}}_{\mathrm{m}}}}})} - 1}}{{e - 1}}\right)^{{{{{\mathrm{exp}}\;{( {\mathrm{Iter}}/{(2 {\mathrm{Iter}}_{\mathrm{m}})})}}}}}}\right], $

(27)$ {{\boldsymbol{T}}_{{{k}},{\rm{new}}}} = {{\boldsymbol{T}}_{{{k,{\mathrm{best}}}}}}+\alpha ({{\boldsymbol{T}}_{{{k,{\mathrm{best}}}}}} - {{\boldsymbol{T}}_{{{k,{\mathrm{sbest}}}}}}). $

式中：$ \alpha $在迭代过程中从3非线性地递减到1，决定扰动区域的大小；$ {{\boldsymbol{T}}_{{{k}},{\rm{best}}}} $为第$ k $个三角形拓扑单元中的最优个体；$ {{\boldsymbol{T}}_{{{k}},{\rm{sbest}}}} $为次优个体.

使用次优个体的位置进行扰动，可以进一步减小最优个体陷入局部极值的可能性. 在生成新的个体后，为了使收敛性向更有希望的方向发展，需要比较新个体和原来三角形拓扑单元中最优个体的适应度. 根据下式所示的贪婪选择机制来确定最优个体位置的更新.

(28)$ {{\boldsymbol{T}}_{{{k,{\mathrm{best}}}}}} = \left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{T}}_{{{k,{\mathrm{new}}}}}},}& {f({{\boldsymbol{T}}_{{{k,{\mathrm{new}}}}}}) < f({T_{{{k,{\mathrm{best}}}}}})}; \\ {{{\boldsymbol{T}}_{{{k,{\mathrm{best}}}}}},}&{其他} .\end{array}} \right. $

(29)$ {{\boldsymbol{C}}_{{{{\mathrm{eq}}}}(k)}}({\mathrm{Iter}}+1) = {{\boldsymbol{T}}_{{{k,{\mathrm{best}}}}}}(k = 1,\cdots ,4). $

将最优个体的位置信息赋值给用于构造当前三角形拓扑单元的精英个体，对种群中的相应个体进行同步更新.

利用提出的基于三角形拓扑单元的精英邻域学习策略，有助于算法探索精英个体附近的潜在更优解，增加了候选个体的多样性. 通过构建三角拓扑单元和扰动最优个体位置来更新种群中的精英个体，有利于减少算法陷入局部最优的风险，提高算法的搜索效率和对全局最优解的发现概率.

对于优化算法而言，必须确保该算法具有收敛性，这是迭代进化类算法正确性的基本要求. CGTEO算法是随机进化算法，可以通过概率测度法来证明该算法具有全局收敛性. 根据全局收敛性准则和定理^[16]可知，若该算法是全局收敛的，则需要满足以下2个条件.

条件1 $ f(E(a,p )) \leqslant f(a) $，并且如果$ p \in S $，则$ f(E(a,p)) \leqslant f(p ) $. 其中，$ f $为最小化问题的目标函数；$ E $表示算法；$ S $为解空间$ {{\bf{R}}^n} $上的可测子集；$ a $为$ S $上的一个点，能够使得函数的值最小化或者在$ S $上实现可接受的函数值的下确界；$ f(a) $为当前轮迭代开始前所取得的全局最优值；$p $为算法$ E $在迭代过程中搜索到的点；$ f(E(a,p )) $表示在当前轮迭代位置更新之后生成的全局最优值. 由条件1可以看出，若$ p \in S $，则点$p $至少不会使函数值的质量变差，即最优值集合$ f(E(a,p )) $是单调非增序列.

条件2 　对于$ S $中的任意Borel子集$ A $，若其概率测度$ V[A] > 0 $，则有$ \displaystyle {\prod} _{k = 0}^\infty (1 - {\mu _k}(A)) = 0 $. 其中，$ {\mu _k}(A) $为算法$ E $第$ k $次迭代的结果在集合$ A $上的概率测度. 条件2意味着经过无穷多次迭代后，算法$ E $错过$ S $中任意Borel子集$ A $的概率为0.

引理1 （随机优化算法全局收敛定理）　　若函数$ f $可测，随机优化算法满足条件1和条件2，$ \{ {x^k}\} _{k = 1}^\infty $为算法迭代过程中产生的数列，则有$ \mathop {\lim }\limits_{k \to \infty } P[{x^k} \in {{R}}] = 1 $. 其中，$ R $为全局最优点集合，$ P[{x^k} \in {{R}}] $为算法第$ k $代的结果落在$ {{R }}$内的概率.

定理1 　CGTEO算法满足条件1.

证明：根据对算法CGTEO的描述，将$ E $定义为

$ E({{\boldsymbol{G}}_{{\text{Iter}}}},{{\boldsymbol{C}}_{i,{\text{Iter}}}}) = \left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{G}}_{{\text{Iter}}}},}&{f(g({{\boldsymbol{C}}_{i,{\text{Iter}}}})) \geqslant f({{\boldsymbol{G}}_{{\text{Iter}}}})}; \\ {g\;({{\boldsymbol{C}}_{i,{\text{Iter}}}}),}&{f(g({{\boldsymbol{C}}_{i,{\text{Iter}}}})) < f({{\boldsymbol{G}}_{{\text{Iter}}}})}. \end{array}} \right. $

$ E({{\boldsymbol{G}}_{{\text{Iter}}}},{{\boldsymbol{C}}_{i,{\text{Iter}}}}) = \left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{G}}_{{\text{Iter}}}},}&{f(h({{\boldsymbol{C}}_{i,{\text{Iter}}}})) \geqslant f({{\boldsymbol{G}}_{{\text{Iter}}}})} ;\\ {h\;({{\boldsymbol{C}}_{i,{\text{Iter}}}}),}&{f(h({{\boldsymbol{C}}_{i,{\text{Iter}}}})) < f({{\boldsymbol{G}}_{{\text{Iter}}}})} .\end{array}} \right. $

$ E({{\boldsymbol{G}}_{{\text{Iter}}}},{{\boldsymbol{C}}_{i,{\text{Iter}}}}) = \left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{G}}_{{\text{Iter}}}},}&{f(z({{\boldsymbol{C}}_{i,{\text{Iter}}}})) \geqslant f({{\boldsymbol{G}}_{{\text{Iter}}}})}; \\ {z\;({{\boldsymbol{C}}_{i,{\text{Iter}}}}),}&{f(z({{\boldsymbol{C}}_{i,{\text{Iter}}}})) < f({{\boldsymbol{G}}_{{\text{Iter}}}})}. \end{array}} \right. $

式中：函数$ g $对应融合正余弦系数的交叉更新操作，$ g\;({{\boldsymbol{C}}_{i,{\text{Iter}}}}) $为经过交叉更新后的第$ {\mathrm{Iter}} $代种群个体$ i $的位置；函数$ h $对应动态分级搜索，$ h\;({{\boldsymbol{C}}_{i,{\text{Iter}}}}) $表示经过分级搜索后的第$ {\mathrm{Iter}} $代种群个体$ i $的位置；函数$ z $对应基于三角形拓扑单元的精英邻域学习，$ z\;({{\boldsymbol{C}}_{i,{\text{Iter}}}}) $表示经过精英邻域学习后的第$ {\mathrm{Iter}} $代种群个体$ i $的位置；$ {{\boldsymbol{G}}_{{\text{Iter}}}} $为目前的全局最优解位置. 根据上述对CGTEO算法公式的定义可知，$ {{\boldsymbol{G}}_{{\text{Iter}}}} $所对应的适应度是单调非增的，并逐渐收敛到解空间的下确界，满足条件1.

定理2 　CGTEO算法满足条件2.

证明：为了满足条件2，规模为$ N $的算法种群的样本空间必须包含$ S $，即

$ S \subseteq \mathop \bigcup \limits_{i = 1}^N {M_{i,{\mathrm{Iter}}}} . $

式中：$ {M_{i,{\mathrm{Iter}}}} $为第$ {\mathrm{Iter}} $代个体$ i $的样本空间的支撑集.

对于CGTEO算法中的交叉更新位置机制，有

$ \begin{split} &g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }}) = \\&\left\{ {\begin{array}{*{20}{l}} {{{\boldsymbol{C}}_{{{{\mathrm{eq}}}}}}+({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }} - {{\boldsymbol{C}}_{{{{\mathrm{eq}}}}}}) \circ {\boldsymbol{F}}+\dfrac{{\boldsymbol{G}}}{{{\boldsymbol{\lambda}} V}} \circ ({\boldsymbol{E}} - {\boldsymbol{F}}),}&{{r_2} \geqslant {\mathrm{GP}}}; \\ {{{\boldsymbol{C}}_{{{\mathrm{p}}}}}+({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }} - {{\boldsymbol{C}}_{{{\mathrm{p}}}}}) \circ {\bf{SCF}}}, &{{r_2} < {\mathrm{GP}}} .\end{array}} \right.\end{split} $

式中：$ {{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }} $、$ {{\boldsymbol{C}}_{{{n}}_1{\text{,}}{{\mathrm{Iter}}} }} $和$ {{\boldsymbol{C}}_{{{n}}_2{\text{,}}{{\mathrm{Iter}}} }} $分别为$ {{\bf{R}}^n} $第$ {\mathrm{Iter}} $代个体$ i $、$ {n_1} $和$ n{}_2 $的样本空间，$ g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }}) $为$ {{\bf{R}}^n} $中不同于$ {{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }} $的样本空间. 在经过交叉更新机制之后，由$ {{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }} $到$ g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }}) $的概率大于0，随着迭代次数的增加，每个$ g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }}) $的闭包$ V[g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }})] $和其并集$ \displaystyle {\bigcup}_{i = 1}^N g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }}) $的闭包$ V\left[ {\displaystyle \bigcup} _{i = 1}^N g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }})\right] $都逐渐变大，故而存在一个整数$ {\mathrm{Ite}}{{\mathrm{r}}_1} $，当$ {\mathrm{Iter}} > {\mathrm{Ite}}{{\mathrm{r}}_1} $时，$ S \subseteq \left( {\displaystyle \bigcup} _{i = 1}^N g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }})\right) $.

类似地，对于CGTEO算法中经过动态分级搜索策略的个体，设支撑集的并集为$ \xi $，随着迭代次数的增加，$ V[\xi ] $逐渐变大. 对于CGTEO算法，存在正整数$ {\mathrm{Ite}}{{\mathrm{r}}_2} $，当$ {\mathrm{Iter}} > {\mathrm{Ite}}{{\mathrm{r}}_2} $时，$ S \subseteq \left(\displaystyle {\bigcup}_{i = 1}^N g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }})\right) \bigcup \xi $.

对于CGTEO算法中执行精英邻域学习策略的个体，设支撑集的并集为$ \varphi $，随着迭代次数的增加，$ V[\varphi ] $逐渐变大. 对于CGTEO算法，存在正整数$ {\mathrm{Ite}}{{\mathrm{r}}_3} $，当$ {\mathrm{Iter}} > {\mathrm{Ite}}{{\mathrm{r}}_3} $时，$ S \subseteq \left(\displaystyle {\bigcup}_{i = 1}^N g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }})\right) \bigcup \xi \bigcup \varphi $.

令$ S $的Borel子集$ A = \left(\displaystyle {\bigcup}_{i = 1}^N g({{\boldsymbol{C}}_{{{i,}}{{\mathrm{Iter}}} }})\right) \bigcup \xi \bigcup \varphi $，则有$ V[A] > 0 $，$ {\mu _i}(A) = \displaystyle \sum\nolimits_{i = 1}^N {{\mu _{i,{\mathrm{Iter}}}}(A)} = 1 $，即$ {\displaystyle \prod} _{{\mathrm{Iter}} = 0}^\infty ( $1 −$ {\mu _{{\mathrm{Iter}}}}(A)) = 0 $，满足条件2.

从上述证明可知，CGTEO算法满足条件1和条件2. 由引理1可知，CGTEO具有全局收敛性.

为了全面验证CGTEO算法在全局优化问题中的求解性能，将该算法与基本EO算法、EO相关的有效改进算法、其他具有影响力的新兴智能优化算法以及在CEC函数求解中表现优异的其他智能优化改进算法共9种对比算法进行系统化的比较分析. 所选的9种对比算法如下：平衡优化器（EO、2020）^[5]，基于反向学习和新更新规则的改进平衡优化器（m-EO、2021）^[13]，自学习策略平衡优化器（AEO、2023）^[14]，正余弦算法（SCA、2016）^[2]，哈里斯鹰优化算法（HHO、2019）^[3]，雪消融优化器（SAO、2023）^[4]，基于高斯变异和维度决策的哈里斯鹰优化算法（GCHHO、2021）^[17]，集成正弦微分协方差矩阵自适应差分进化算法（LSHADE-cnEpSin、2017）^[18]和多重自适应差分进化算法（MadDE、2021）^[19]. 实验基于权威且测试集中包含函数最丰富的IEEE CEC2017开展，从多个维度评估算法的性能.

CEC2017是当前广泛使用且函数齐全的标准测试集之一，包含单峰函数（F1、F3）、简单多峰函数（F4~F10）、混合函数（F11~F20）和复合函数（F21~F30）共29个具有不同特性和难度的测试函数，每个函数的搜索范围为[−100，100].

为了确保结果的公正性和客观性，每种算法在相同的实验环境和设置条件下独立运行30次，$ N = 30 $，$ {\mathrm{Iter}}_{\mathrm{m}} = 1\;000 $，$ D = 30、50、 100 $. 实验运行环境为Windows 10操作系统，编程环境为MATLAB R2018b. 所有算法的参数设置都与其原文献和源代码保持一致.

将9种对比算法分成3组，分别与CGTEO算法进行对比分析. 每个算法在30维、50维和100维的条件下独立运行30次，通过计算平均值、最佳值和最差值来评估算法的寻优能力. 考虑到篇幅限制，下面将展示$ D = 100 $时对CEC2017测试集中单峰函数F1、多峰函数F5~F7、混合函数F11~F13和组合函数F28~F30这10个不同类型函数的寻优结果，其余函数的测试结果与表1~3中类似，不再一一赘述，表1~3中的最佳结果以粗体显示.

为了验证CGTEO算法相较于EO及其改进算法在求解性能上的优势，将CGTEO与基本EO算法及2种新近提出的有效改进算法m-EO和AEO进行对比分析. 4种算法分别在$ D = 100 $的条件下独立运行30次，如表1所示为各算法的实验结果.

从表1可以看出，当$ D = 100 $时，本文的改进算法CGTEO在10个函数上的平均值、最佳值和最差值均明显优于EO、m-EO和AEO算法，展现出优越的寻优精度和稳定性，验证了改进策略的有效性和高维适应性.

为了分析 CGTEO 算法相比于其他新兴智能优化算法是否存在寻优优势，将CGTEO算法与SCA、HHO和SAO 3种有影响力的算法进行比较. 其中，SCA^[2]是2016年提出的新颖优化算法，HHO^[3]和SAO^[4]是较新提出的高性能优化算法. 如表2所示为4种算法在$ D = 100 $的条件下独立求解函数30次的数据.

从表2可以看出，CGTEO在4种类型函数上的平均值、最佳值和最差值均显著优于其他3种对比算法，求解效果十分出色. 可知，CGTEO在与近年提出的各类高效基准算法比较中，具有很强的全局优化能力和稳定性.

为了进一步验证CGTEO算法相对于当前先进改进算法的竞争性能，将CGTEO算法与GCHHO、LSHADE-cnEpSin和MadDE 3种改进算法进行比较分析. 其中，GCHHO是效果显著的哈里斯鹰改进算法，LSHADE-cnEpSin和MadDE分别是CEC2017、CEC2021的优胜算法，它们在求解CEC函数方面有着出色的表现，具有较大的挑战性. 如表3所示为4种算法在$ D = 100 $条件下独立运行30次结果的平均值、最佳值和最差值，其中为了节省表格空间，将LSHADE-cnEpSin简写为LSHADE-c.

从表3可以看出，当$ D = 100 $时，CGTEO在10个函数上的平均值、最佳值和最差值都在4种算法中最优. 即使相比于改进算法GCHHO和优胜算法LSHADE-cnEpSin、MadDE这些求解CEC函数时表现优越的算法，CGTEO依然展现出很强的整体优越性和竞争力.

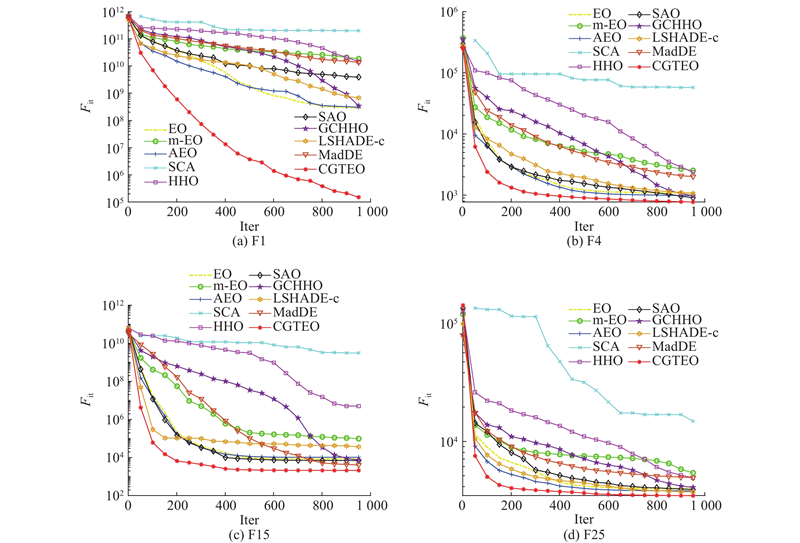
绘制CGTEO算法和9种对比算法在$ D = 100 $时求解CEC2017测试函数的收敛曲线. 如图3所示为单峰函数F1、简单多峰函数F4、混合函数F15和复合函数F25这4个函数上的收敛曲线，其他函数上的收敛情况与上述函数类似，不再逐一赘述. 其中，F_it为适应度.

从图3可以看出，CGTEO算法的收敛曲线在4个函数上始终保持着最快的收敛速度，且最终的收敛精度优于其他9种对比算法. 收敛曲线整体上更加光滑，陷入局部极值的次数较少，展现出较好的求解性能.

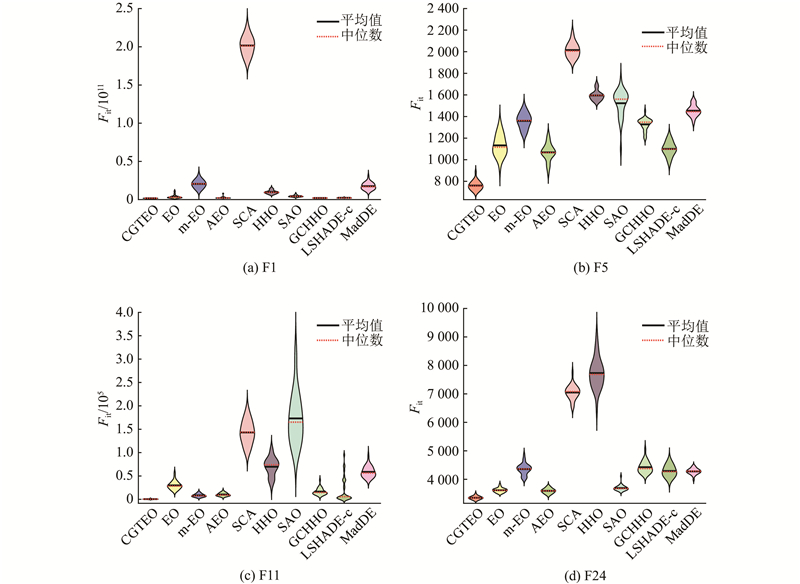
小提琴图能够显示多组数据的分布情况和概率密度. 通过绘制各算法独立求解函数30次结果的小提琴图来评估稳定性. 算法的稳定性通过观察小提琴图中求解数据的分布范围、集中程度和密度分布来衡量. 小提琴图的高度表示数据的分布范围，较短的高度意味着该算法的结果在多次运行中更集中，波动较小，具有较高的稳定性. 图的宽度反映了数据的分布密度，某一数值处的宽度越大，表示数据更多地集中在这个数值附近，数据在此处的密度越高. 小提琴图中间的实线和虚线分别表示数据的平均值和中位数. 如图4所示为CGTEO算法与其他对比算法在$ D = 100 $时求解CEC2017中F1、F5、F11、F24这4个不同类型函数的小提琴图.

从图4可以看出，对于F1、F5、F11、F24这4个函数，CGTEO算法的小提琴图高度均最短，表明该算法具有较优的稳定性. 特别是在函数F1和F11上，CGTEO的小提琴图几乎浓缩为一条横线，意味着CGTEO的求解结果能够集中收敛在最优值附近. 在函数F11和F24上，CGTEO的整体数据分布较其他算法更加集中，且在平均值处的概率密度更高，说明CGTEO较其他算法具有更好的收敛集中度和稳定性. 此外，对于求最小值优化问题来说，小提琴图的位置越靠近底部，表示算法的求解质量越好. CGTEO算法在4个函数中的小提琴图位置都最低，且平均值和中位数都低于其他对比算法，表明该算法整体寻优结果的质量较高.

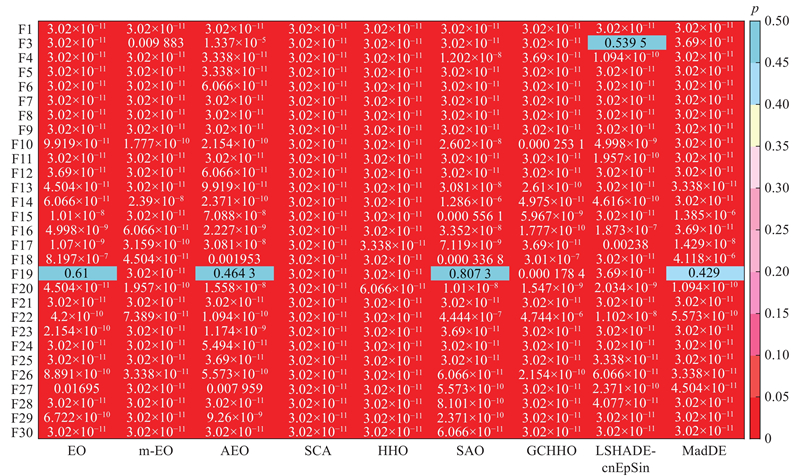
Wilcoxon秩和检验^[20]是常用的非参数统计方法，用于评估2种算法在求解结果上是否存在显著差异. 为了验证本文改进算法CGTEO的优化结果是否显著优于其他9种对比算法，采用Wilcoxon秩和检验进行统计分析. 实验中，分别将CGTEO算法与每种对比算法在CEC2017函数集上独立运行30次的求解结果进行两两比较. 若检验结果的p值小于0.05，则表示在95%的置信水平下拒绝零假设，说明2种算法之间存在显著性差异. 以热图的形式展示在$ D = 100 $时CGTEO与对比算法进行Wilcoxon秩和检验的结果，如图5所示.

热图中的颜色变化反映了数值大小的差异，从而更直观地呈现出CGTEO与其他9种对比算法的差异显著性情况. 从图5可以看出，对于CEC2017测试集中的几乎所有函数，改进算法CGTEO与其他9种对比算法的p值均小于0.05. 这说明CGTEO与其他9种对比算法的寻优结果之间存在显著性差异，结合表1~3可知，CGTEO算法明显优于其他9种算法.

本文提出融合自适应交叉更新、动态分级搜索和三角拓扑精英学习策略的平衡优化器（CGTEO）. 引入自适应交叉更新机制，增强了算法的全局搜索能力. 加入动态分级搜索策略，平衡了算法的全局探索和局部挖掘能力. 引入基于三角形拓扑单元的精英邻域学习策略，提高了算法的收敛精度和摆脱局部桎梏的能力. 利用概率测度法，证明了CGTEO具有全局收敛性. 在实验中，通过CEC2017测试套件对CGTEO与9种代表性对比算法进行性能测试，验证了CGTEO的寻优精度、收敛性能和求解稳定性均明显优于其他对比算法，且优化结果与其他算法相比具有显著性差异. 后续将考虑把算法应用于实际优化问题，并进一步改善平衡优化器的算法机制和寻优性能，拓展其在更多领域的应用可行性.