[33]
叶见曙, 李国平. 结构设计原理[M]. 4版. 北京: 人民交通出版社, 2018: 95-97.
[本文引用: 1]
[34]
戴明江, 杨鸥, 肖岩 纵筋锈蚀对钢筋混凝土梁抗剪性能影响
[J]. 工业建筑 , 2016 , 46 (11 ): 74 - 79
[本文引用: 1]
[1]
JUAREZ C A, GUEVARA B, FAJARDO G, et al Ultimate and nominal shear strength in reinforced concrete beams deteriorated by corrosion
[J]. Engineering Structures , 2011 , 33 (12 ): 3189 - 3196
DOI:10.1016/j.engstruct.2011.08.014
[本文引用: 2]
[3]
霍艳华. 锈蚀钢筋混凝土简支梁受剪承载力研究[D]. 南昌: 南昌大学, 2007.
[本文引用: 7]
HUO Yanhua. Research on shear capacity of simply supported concrete beam with corroded reinforcement [D]. Nanchang: Nanchang University, 2007.
[本文引用: 7]
[4]
ALASKAR A. Shear behaviour of slender RC beams with corroded web reinforcement [D]. Waterloo: University of Waterloo, 2013.
[本文引用: 1]
[5]
赵羽习, 金伟良 锈蚀箍筋混凝土梁的抗剪承载力分析
[J]. 浙江大学学报: 工学版 , 2008 , 42 (1 ): 19 - 24
[本文引用: 2]
ZHAO Yuxi, JIN Weiliang Analysis on shearing capacity of concrete beams with corroded stirrups
[J]. Journal of Zhejiang University: Engineering Science , 2008 , 42 (1 ): 19 - 24
[本文引用: 2]
[7]
李士彬, 张鑫, 贾留东, 等 箍筋锈蚀钢筋混凝土梁的抗剪承载力分析
[J]. 工程力学 , 2011 , 28 (Suppl.1 ): 60 - 63
[本文引用: 6]
LI Shibin, ZHANG Xin, JIA Liudong, et al Analysis for shear capacity of reinforced concrete beams with corrosion stirrups
[J]. Engineering Mechanics , 2011 , 28 (Suppl.1 ): 60 - 63
[本文引用: 6]
[8]
FENG D C, LIU Z T, WANG X D, et al Failure mode classification and bearing capacity prediction for reinforced concrete columns based on ensemble machine learning algorithm
[J]. Advanced Engineering Informatics , 2020 , 45 : 101126
DOI:10.1016/j.aei.2020.101126
[本文引用: 1]
[9]
张玉平, 马超, 李传习, 等 基于改进BP算法的混凝土热学参数反演与预测
[J]. 交通科学与工程 , 2021 , 37 (1 ): 42 - 50
DOI:10.3969/j.issn.1674-599X.2021.01.007
ZHANG Yuping, MA Chao, LI Chuanxi, et al Back analysis and prediction of thermal parameters of concrete based on improved BP algorithm
[J]. Journal of Transport Science and Engineering , 2021 , 37 (1 ): 42 - 50
DOI:10.3969/j.issn.1674-599X.2021.01.007
[10]
KUMAR A, ARORA H C, KAPOOR N R, et al Machine learning intelligence to assess the shear capacity of corroded reinforced concrete beams
[J]. Scientific Reports , 2023 , 13 (1 ): 2857
DOI:10.1038/s41598-023-30037-9
[11]
FU B, FENG D C A machine learning-based time-dependent shear strength model for corroded reinforced concrete beams
[J]. Journal of Building Engineering , 2021 , 36 : 102118
DOI:10.1016/j.jobe.2020.102118
[本文引用: 1]
[12]
NGUYEN T H, NGUYEN D T, NGUYEN D H, et al Evaluation of residual strength of corroded reinforced concrete beams using machine learning models
[J]. Arabian Journal for Science and Engineering , 2022 , 47 (8 ): 9985 - 10002
DOI:10.1007/s13369-021-06493-8
[13]
戴理朝, 王冲, 袁平, 等 基于可解释机器学习的锈蚀RC构件抗剪承载力预测模型
[J]. 吉林大学学报: 工学版 , 2024 , 54 (11 ): 3231 - 3243
[本文引用: 1]
DAI Lizhao, WANG Chong, YUAN Ping, et al Prediction model for shear capacity of corroded RC beams based on interpretable machine learning
[J]. Journal of Jilin University: Engineering and Technology Edition , 2024 , 54 (11 ): 3231 - 3243
[本文引用: 1]
[14]
于晓辉, 王猛, 宁超列 基于机器学习的钢筋混凝土柱失效模式两阶段判别方法
[J]. 建筑结构学报 , 2022 , 43 (8 ): 220 - 231
[本文引用: 1]
YU Xiaohui, WANG Meng, NING Chaolie A machine-leaning-based two-step method for failure mode classification of reinforced concrete columns
[J]. Journal of Building Structures , 2022 , 43 (8 ): 220 - 231
[本文引用: 1]
[15]
GUAN X, SUN H, HOU R, et al A deep reinforcement learning method for structural dominant failure modes searching based on self-play strategy
[J]. Reliability Engineering and System Safety , 2023 , 233 : 109093
DOI:10.1016/j.ress.2023.109093
[本文引用: 1]
[16]
LIU J, ALEXANDER J, GU Q, et al Gaussian process regression-based load-carrying capacity models of corroded prestressed concrete bridge girders for fast-screening and reliability-based evaluation
[J]. Engineering Structures , 2023 , 285 : 116040
DOI:10.1016/j.engstruct.2023.116040
[本文引用: 1]
[17]
YU Z, XIE W, YU B, et al Probabilistic prediction of joint shear strength using Gaussian process regression with anisotropic compound kernel
[J]. Engineering Structures , 2023 , 277 : 115413
DOI:10.1016/j.engstruct.2022.115413
[本文引用: 1]
[18]
SCHULZ E, SPEEKENBRINK M, KRAUSE A A tutorial on Gaussian process regression: modelling, exploring, and exploiting functions
[J]. Journal of Mathematical Psychology , 2018 , 85 : 1 - 16
DOI:10.1016/j.jmp.2018.03.001
[本文引用: 1]
[19]
HEAD J D, ZERNER M C A Broyden-Fletcher-Goldfarb-Shanno optimization procedure for molecular geometries
[J]. Chemical Physics Letters , 1985 , 122 (3 ): 264 - 270
DOI:10.1016/0009-2614(85)80574-1
[本文引用: 1]
[20]
ZHU C, BYRD R H, LU P, et al Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization
[J]. ACM Transactions on Mathematical Software , 1997 , 23 (4 ): 550 - 560
DOI:10.1145/279232.279236
[本文引用: 1]
[21]
BERGSTRA J, BARDENET R, BENGIO Y, et al. Algorithms for hyper-parameter optimization [C]//Proceedings of the 24th International Conference on Neural Information Processing Systems . Granada: Curran Associates Inc. 2011, 2546–2554.
[本文引用: 1]
[22]
李冰, 高向华, 王小惠, 等 局部区段锈蚀的钢筋混凝土梁抗剪承载力试验研究
[J]. 混凝土与水泥制品 , 2010 , (6 ): 60 - 65
DOI:10.3969/j.issn.1000-4637.2010.06.016
[本文引用: 1]
LI Bing, GAO Xianghua, WANG Xiaohui, et al Experimental study on shear capacity of reinforced concrete beam with partial section corrosion
[J]. China Concrete and Cement Products , 2010 , (6 ): 60 - 65
DOI:10.3969/j.issn.1000-4637.2010.06.016
[本文引用: 1]
[23]
杨晓明, 吴桐, 王耀耀 小剪跨比锈蚀钢筋混凝土梁受剪性能试验研究
[J]. 建筑结构学报 , 2019 , 40 (12 ): 147 - 154
[本文引用: 1]
YANG Xiaoming, WU Tong, WANG Yaoyao Experimental study on shear behavior of corroded reinforced concrete beams with low shear span ratio
[J]. Journal of Building Structures , 2019 , 40 (12 ): 147 - 154
[本文引用: 1]
[24]
陈正. 钢筋锈蚀后RC梁抗剪性能的试验研究与分析[D]. 扬州: 扬州大学, 2022.
[本文引用: 2]
CHEN Zheng. Experimental study and analysis of shear strength of RC beams due to reinforcement corrosion [D]. Yangzhou: Yangzhou University, 2022.
[本文引用: 2]
[25]
FU C, HUANG J, DONG Z, et al Shear behavior of reinforced concrete beams subjected to accelerated non-uniform corrosion
[J]. Engineering Structures , 2023 , 286 : 116081
DOI:10.1016/j.engstruct.2023.116081
[本文引用: 1]
[26]
中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB50010-2010 [S]. 北京: 中国建筑工业出版社, 2015.
[本文引用: 2]
[27]
国振喜. 简明钢筋混凝土结构计算手册[M]. 3版. 北京: 机械工业出版社, 2017: 41-58.
[本文引用: 1]
[28]
HE Y, ZHENG Y Short-term power load probability density forecasting based on Yeo-Johnson transformation quantile regression and Gaussian kernel function
[J]. Energy , 2018 , 154 : 143 - 156
DOI:10.1016/j.energy.2018.04.072
[本文引用: 1]
[29]
HAUKE J, KOSSOWSKI T Comparison of values of Pearson's and Spearman's correlation coefficients on the same sets of data
[J]. Quaestiones Geographicae , 2011 , 30 (2 ): 87 - 93
DOI:10.2478/v10117-011-0021-1
[本文引用: 1]
[30]
赵丽, 胡翮. 统计学基础[M]. 南京: 南京大学出版社, 2017: 213-216.
[本文引用: 1]
[31]
CHEN X, JEONG J C. Enhanced recursive feature elimination [C]//Proceedings of the 6th International Conference on Machine Learning and Applications . Cincinnati: IEEE, 2007: 429−435.
[本文引用: 1]
[32]
柳世涛. 受腐蚀钢筋混凝土梁抗剪性能研究[D]. 长沙: 中南大学, 2013.
[本文引用: 1]
LIU Shitao. Research on shear behavior of corroded RC beams [D]. Changsha: Central South University, 2013.
[本文引用: 1]
[34]
DAI Mingjiang, YANG Ou, XIAO Yan Influence of longitudinal bar corrosion on shear behavior of RC beams
[J]. Industrial Construction , 2016 , 46 (11 ): 74 - 79
[本文引用: 1]
1
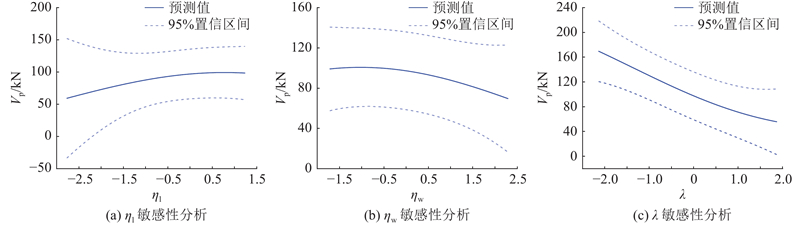
... 为了探究${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{w}}}$ $\lambda $ 图7 (a)所示为${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{l}}}$ V p 随着锈蚀率的增加而增加,其置信区间随着锈蚀率的增加而减小. 这是由于样本中存在仅箍筋锈蚀梁、箍筋和纵筋均锈蚀梁、仅纵筋锈蚀梁3种,当纵筋锈蚀率较小时,95%置信区间范围较大. 当${\eta _{\mathrm{l}}}$ 图7 (b)所示为${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{w}}}$ V p 随着锈蚀率的增加而增加,当${\eta _{\mathrm{w}}}$ 图7 (c)所示为$\lambda $ V p 随着$\lambda $ $\lambda $ 5 , 33 , 34 ]的描述较一致,表明利用GPR模型,可以较好地捕捉特征与预测结果间的映射关系. ...
纵筋锈蚀对钢筋混凝土梁抗剪性能影响
1
2016
... 为了探究${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{w}}}$ $\lambda $ 图7 (a)所示为${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{l}}}$ V p 随着锈蚀率的增加而增加,其置信区间随着锈蚀率的增加而减小. 这是由于样本中存在仅箍筋锈蚀梁、箍筋和纵筋均锈蚀梁、仅纵筋锈蚀梁3种,当纵筋锈蚀率较小时,95%置信区间范围较大. 当${\eta _{\mathrm{l}}}$ 图7 (b)所示为${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{w}}}$ V p 随着锈蚀率的增加而增加,当${\eta _{\mathrm{w}}}$ 图7 (c)所示为$\lambda $ V p 随着$\lambda $ $\lambda $ 5 , 33 , 34 ]的描述较一致,表明利用GPR模型,可以较好地捕捉特征与预测结果间的映射关系. ...
Ultimate and nominal shear strength in reinforced concrete beams deteriorated by corrosion
2
2011
... 施工质量、几何参数、材料强度等因素会导致RC梁抗剪承载力的不确定性,而锈蚀引起的力学性能退化会加剧这一问题. 受侵蚀介质的影响,箍筋比纵筋更易锈蚀,导致RC梁的剪切性能退化,破坏模式可能由延性弯曲破坏演变为脆性剪切破坏[1 ] ,使RC梁的抗剪承载力呈现高离散性和不确定性. 准确评估锈蚀RC梁的抗剪承载力对保证其服役安全具有重要意义. ...
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
锈蚀钢筋混凝土简支梁斜截面抗剪性能研究
5
2004
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
... 为了验证所建GPR模型的预测性能,对徐善华等[2 -3 ,7 ] 建立的经验模型进行比较,如表3 所示. ...
... Empirical model for calculating shear capacity of RC beam
Tab.3 模型 模型公式 文献[2 ]模型 ${V_{\mathrm{p}}} = \xi (\lambda ,{\eta _{\mathrm{w}}})\dfrac{{0.08+4{\rho _{\mathrm{l}}}}}{{\lambda - 0.3}}{f_{\mathrm{c}}}b{h_0}+\alpha ({\eta _{\mathrm{w}}})\dfrac{{0.25+0.4\lambda }}{s}{A_{{\mathrm{vc}}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\alpha ({\eta _{\mathrm{w}}}) = 1 - 0.077{\eta _{\mathrm{w}}},\;{A_{{\mathrm{vc}}}} = {A_{\mathrm{v}}}(1 - {\eta _{\mathrm{w}}}).$ $ \xi (\lambda ,{\eta _{\mathrm{w}}}) = \left\{ \begin{gathered} {\text{ }}1,\qquad\qquad\qquad\;\;{\eta _{\mathrm{w}}} \leqslant {\eta _{{\mathrm{cr}}}} ; \\ {({\eta _{\mathrm{w}}}/{\eta _{{\mathrm{cr}}}})^{0.069\lambda - 0.43}},{\eta _{\mathrm{w}}} > {\eta _{{\mathrm{cr}}}} . \\ \end{gathered} \right.\;\;{\eta _{{\mathrm{cr}}}} = 10.4(c/{d_{\mathrm{v}}}^2)+{f_{{\mathrm{cu}},{\mathrm{k}}}}/{d_{\mathrm{v}}}. $ 文献[7 ]模型 ${V_{\mathrm{p}}} = 1.75\dfrac{{{f_{\mathrm{t}}}{b_{\mathrm{c}}}{h_0}_{\mathrm{c}}}}{{\lambda +1}}+\dfrac{{{f_{{\mathrm{yvc}}}}{A_{{\mathrm{vc}}}}{h_0}}}{s}.$ ${f_{{\mathrm{yvc}}}} = {f_{{\mathrm{yv}}}}\dfrac{{1 - 1.121\;9{\eta _{\mathrm{w}}}}}{{1 - {\eta _{\mathrm{w}}}}} \geqslant 0.$ 文献[3 ]模型 ${V_{\mathrm{p}}} = \psi {f_{\mathrm{c}}}b{h_0}\left[\dfrac{{0.08}}{{\lambda - 0.3}}+\dfrac{{100{\rho _{\mathrm{l}}}}}{{\lambda {f_{\mathrm{c}}}}}\right]+\alpha \dfrac{{(0.4+0.3\lambda )}}{s}{A_{\mathrm{v}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\psi = \left\{ \begin{gathered} {\text{ }}1,{\text{ }}{\eta _{\mathrm{l}}} \leqslant 5\text{%} ; \\ 1.098 - 1.96\eta_{\mathrm{l}},{\eta _{\mathrm{l}}} > 5\text{%} . \\ \end{gathered} \right.\;\;{\text{ }}\alpha = 1 - 1.059{\eta _{\mathrm{w}}} \geqslant 0.$
基于随机森林(RF)、极端梯度提升树(Xgboost)及多层感知器(MLP),建立锈蚀RC梁抗剪承载力的确定性预测模型. ...
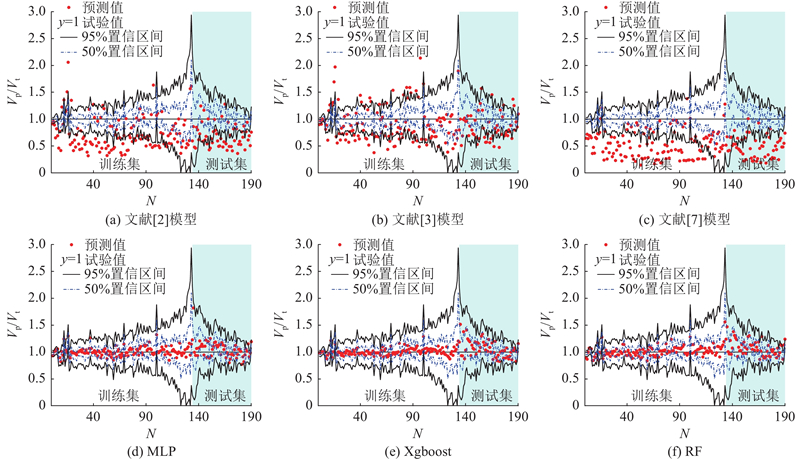
... 如表4 所示为机理模型与数据驱动模型的预测指标. 为了表示GPR模型的适用性,将GPR模型的50%置信区间与95%置信区间放置在这些模型中,如图8 所示. 结果表明,相较于机理模型,数据驱动模型具有显著优势,数据驱动模型均拥有较高的预测精度与稳定性. 在数据驱动模型中,GPR模型不仅具有最高的性能指标,而且可以输出预测值的概率区间,50%置信区间几乎包含了所有数据驱动模型的预测值,这表明GPR的置信区间具有代表性. 在3个经验模型中,文献[3 ]的模型考虑箍筋和纵筋各自锈蚀,在真实情况下箍筋先锈蚀,因此当样本纵筋锈蚀率较小时,该模型容易高估承载力. 文献[2 ,7 ]的模型仅考虑箍筋锈蚀,忽略了纵筋锈蚀的影响,这两位学者提出的方法预测结果偏于保守,更利于工程实际应用. 总体而言,GPR模型具有最强的预测性能,与经验模型与数据驱动确定性模型相比,具有较好的适用性,可以为锈蚀RC梁的概率安全性评估和概率极限状态评估提供依据. ...
... Comparison of predictive indicator of different model
Tab.4 模型 训练集 测试集 R 2 RMSE MAE R 2 RMSE MAE RF 0.978 14.101 8.311 0.916 20.813 12.765 Xgboost 0.994 7.359 4.833 0.944 16.952 11.859 MLP 0.986 11.658 7.073 0.944 17.080 11.451 GPR 0.987 10.938 7.004 0.947 16.632 11.462 文献[2 ]模型 0.780 47.460 24.540 0.577 47.897 35.182 文献[3 ]模型 0.874 34.700 28.420 0.844 28.482 23.882 文献[7 ]模型 0.642 66.121 53.210 0.430 62.023 52.141
图 8 不同模型的预测精度对比 ...
锈蚀钢筋混凝土简支梁斜截面抗剪性能研究
5
2004
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
... 为了验证所建GPR模型的预测性能,对徐善华等[2 -3 ,7 ] 建立的经验模型进行比较,如表3 所示. ...
... Empirical model for calculating shear capacity of RC beam
Tab.3 模型 模型公式 文献[2 ]模型 ${V_{\mathrm{p}}} = \xi (\lambda ,{\eta _{\mathrm{w}}})\dfrac{{0.08+4{\rho _{\mathrm{l}}}}}{{\lambda - 0.3}}{f_{\mathrm{c}}}b{h_0}+\alpha ({\eta _{\mathrm{w}}})\dfrac{{0.25+0.4\lambda }}{s}{A_{{\mathrm{vc}}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\alpha ({\eta _{\mathrm{w}}}) = 1 - 0.077{\eta _{\mathrm{w}}},\;{A_{{\mathrm{vc}}}} = {A_{\mathrm{v}}}(1 - {\eta _{\mathrm{w}}}).$ $ \xi (\lambda ,{\eta _{\mathrm{w}}}) = \left\{ \begin{gathered} {\text{ }}1,\qquad\qquad\qquad\;\;{\eta _{\mathrm{w}}} \leqslant {\eta _{{\mathrm{cr}}}} ; \\ {({\eta _{\mathrm{w}}}/{\eta _{{\mathrm{cr}}}})^{0.069\lambda - 0.43}},{\eta _{\mathrm{w}}} > {\eta _{{\mathrm{cr}}}} . \\ \end{gathered} \right.\;\;{\eta _{{\mathrm{cr}}}} = 10.4(c/{d_{\mathrm{v}}}^2)+{f_{{\mathrm{cu}},{\mathrm{k}}}}/{d_{\mathrm{v}}}. $ 文献[7 ]模型 ${V_{\mathrm{p}}} = 1.75\dfrac{{{f_{\mathrm{t}}}{b_{\mathrm{c}}}{h_0}_{\mathrm{c}}}}{{\lambda +1}}+\dfrac{{{f_{{\mathrm{yvc}}}}{A_{{\mathrm{vc}}}}{h_0}}}{s}.$ ${f_{{\mathrm{yvc}}}} = {f_{{\mathrm{yv}}}}\dfrac{{1 - 1.121\;9{\eta _{\mathrm{w}}}}}{{1 - {\eta _{\mathrm{w}}}}} \geqslant 0.$ 文献[3 ]模型 ${V_{\mathrm{p}}} = \psi {f_{\mathrm{c}}}b{h_0}\left[\dfrac{{0.08}}{{\lambda - 0.3}}+\dfrac{{100{\rho _{\mathrm{l}}}}}{{\lambda {f_{\mathrm{c}}}}}\right]+\alpha \dfrac{{(0.4+0.3\lambda )}}{s}{A_{\mathrm{v}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\psi = \left\{ \begin{gathered} {\text{ }}1,{\text{ }}{\eta _{\mathrm{l}}} \leqslant 5\text{%} ; \\ 1.098 - 1.96\eta_{\mathrm{l}},{\eta _{\mathrm{l}}} > 5\text{%} . \\ \end{gathered} \right.\;\;{\text{ }}\alpha = 1 - 1.059{\eta _{\mathrm{w}}} \geqslant 0.$
基于随机森林(RF)、极端梯度提升树(Xgboost)及多层感知器(MLP),建立锈蚀RC梁抗剪承载力的确定性预测模型. ...
... 如表4 所示为机理模型与数据驱动模型的预测指标. 为了表示GPR模型的适用性,将GPR模型的50%置信区间与95%置信区间放置在这些模型中,如图8 所示. 结果表明,相较于机理模型,数据驱动模型具有显著优势,数据驱动模型均拥有较高的预测精度与稳定性. 在数据驱动模型中,GPR模型不仅具有最高的性能指标,而且可以输出预测值的概率区间,50%置信区间几乎包含了所有数据驱动模型的预测值,这表明GPR的置信区间具有代表性. 在3个经验模型中,文献[3 ]的模型考虑箍筋和纵筋各自锈蚀,在真实情况下箍筋先锈蚀,因此当样本纵筋锈蚀率较小时,该模型容易高估承载力. 文献[2 ,7 ]的模型仅考虑箍筋锈蚀,忽略了纵筋锈蚀的影响,这两位学者提出的方法预测结果偏于保守,更利于工程实际应用. 总体而言,GPR模型具有最强的预测性能,与经验模型与数据驱动确定性模型相比,具有较好的适用性,可以为锈蚀RC梁的概率安全性评估和概率极限状态评估提供依据. ...
... Comparison of predictive indicator of different model
Tab.4 模型 训练集 测试集 R 2 RMSE MAE R 2 RMSE MAE RF 0.978 14.101 8.311 0.916 20.813 12.765 Xgboost 0.994 7.359 4.833 0.944 16.952 11.859 MLP 0.986 11.658 7.073 0.944 17.080 11.451 GPR 0.987 10.938 7.004 0.947 16.632 11.462 文献[2 ]模型 0.780 47.460 24.540 0.577 47.897 35.182 文献[3 ]模型 0.874 34.700 28.420 0.844 28.482 23.882 文献[7 ]模型 0.642 66.121 53.210 0.430 62.023 52.141
图 8 不同模型的预测精度对比 ...
7
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
... [3 , 7 ],但存在精度不足的问题. ...
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
... 为了验证所建GPR模型的预测性能,对徐善华等[2 -3 ,7 ] 建立的经验模型进行比较,如表3 所示. ...
... Empirical model for calculating shear capacity of RC beam
Tab.3 模型 模型公式 文献[2 ]模型 ${V_{\mathrm{p}}} = \xi (\lambda ,{\eta _{\mathrm{w}}})\dfrac{{0.08+4{\rho _{\mathrm{l}}}}}{{\lambda - 0.3}}{f_{\mathrm{c}}}b{h_0}+\alpha ({\eta _{\mathrm{w}}})\dfrac{{0.25+0.4\lambda }}{s}{A_{{\mathrm{vc}}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\alpha ({\eta _{\mathrm{w}}}) = 1 - 0.077{\eta _{\mathrm{w}}},\;{A_{{\mathrm{vc}}}} = {A_{\mathrm{v}}}(1 - {\eta _{\mathrm{w}}}).$ $ \xi (\lambda ,{\eta _{\mathrm{w}}}) = \left\{ \begin{gathered} {\text{ }}1,\qquad\qquad\qquad\;\;{\eta _{\mathrm{w}}} \leqslant {\eta _{{\mathrm{cr}}}} ; \\ {({\eta _{\mathrm{w}}}/{\eta _{{\mathrm{cr}}}})^{0.069\lambda - 0.43}},{\eta _{\mathrm{w}}} > {\eta _{{\mathrm{cr}}}} . \\ \end{gathered} \right.\;\;{\eta _{{\mathrm{cr}}}} = 10.4(c/{d_{\mathrm{v}}}^2)+{f_{{\mathrm{cu}},{\mathrm{k}}}}/{d_{\mathrm{v}}}. $ 文献[7 ]模型 ${V_{\mathrm{p}}} = 1.75\dfrac{{{f_{\mathrm{t}}}{b_{\mathrm{c}}}{h_0}_{\mathrm{c}}}}{{\lambda +1}}+\dfrac{{{f_{{\mathrm{yvc}}}}{A_{{\mathrm{vc}}}}{h_0}}}{s}.$ ${f_{{\mathrm{yvc}}}} = {f_{{\mathrm{yv}}}}\dfrac{{1 - 1.121\;9{\eta _{\mathrm{w}}}}}{{1 - {\eta _{\mathrm{w}}}}} \geqslant 0.$ 文献[3 ]模型 ${V_{\mathrm{p}}} = \psi {f_{\mathrm{c}}}b{h_0}\left[\dfrac{{0.08}}{{\lambda - 0.3}}+\dfrac{{100{\rho _{\mathrm{l}}}}}{{\lambda {f_{\mathrm{c}}}}}\right]+\alpha \dfrac{{(0.4+0.3\lambda )}}{s}{A_{\mathrm{v}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\psi = \left\{ \begin{gathered} {\text{ }}1,{\text{ }}{\eta _{\mathrm{l}}} \leqslant 5\text{%} ; \\ 1.098 - 1.96\eta_{\mathrm{l}},{\eta _{\mathrm{l}}} > 5\text{%} . \\ \end{gathered} \right.\;\;{\text{ }}\alpha = 1 - 1.059{\eta _{\mathrm{w}}} \geqslant 0.$
基于随机森林(RF)、极端梯度提升树(Xgboost)及多层感知器(MLP),建立锈蚀RC梁抗剪承载力的确定性预测模型. ...
... 如表4 所示为机理模型与数据驱动模型的预测指标. 为了表示GPR模型的适用性,将GPR模型的50%置信区间与95%置信区间放置在这些模型中,如图8 所示. 结果表明,相较于机理模型,数据驱动模型具有显著优势,数据驱动模型均拥有较高的预测精度与稳定性. 在数据驱动模型中,GPR模型不仅具有最高的性能指标,而且可以输出预测值的概率区间,50%置信区间几乎包含了所有数据驱动模型的预测值,这表明GPR的置信区间具有代表性. 在3个经验模型中,文献[3 ]的模型考虑箍筋和纵筋各自锈蚀,在真实情况下箍筋先锈蚀,因此当样本纵筋锈蚀率较小时,该模型容易高估承载力. 文献[2 ,7 ]的模型仅考虑箍筋锈蚀,忽略了纵筋锈蚀的影响,这两位学者提出的方法预测结果偏于保守,更利于工程实际应用. 总体而言,GPR模型具有最强的预测性能,与经验模型与数据驱动确定性模型相比,具有较好的适用性,可以为锈蚀RC梁的概率安全性评估和概率极限状态评估提供依据. ...
... Comparison of predictive indicator of different model
Tab.4 模型 训练集 测试集 R 2 RMSE MAE R 2 RMSE MAE RF 0.978 14.101 8.311 0.916 20.813 12.765 Xgboost 0.994 7.359 4.833 0.944 16.952 11.859 MLP 0.986 11.658 7.073 0.944 17.080 11.451 GPR 0.987 10.938 7.004 0.947 16.632 11.462 文献[2 ]模型 0.780 47.460 24.540 0.577 47.897 35.182 文献[3 ]模型 0.874 34.700 28.420 0.844 28.482 23.882 文献[7 ]模型 0.642 66.121 53.210 0.430 62.023 52.141
图 8 不同模型的预测精度对比 ...
7
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
... [3 , 7 ],但存在精度不足的问题. ...
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
... 为了验证所建GPR模型的预测性能,对徐善华等[2 -3 ,7 ] 建立的经验模型进行比较,如表3 所示. ...
... Empirical model for calculating shear capacity of RC beam
Tab.3 模型 模型公式 文献[2 ]模型 ${V_{\mathrm{p}}} = \xi (\lambda ,{\eta _{\mathrm{w}}})\dfrac{{0.08+4{\rho _{\mathrm{l}}}}}{{\lambda - 0.3}}{f_{\mathrm{c}}}b{h_0}+\alpha ({\eta _{\mathrm{w}}})\dfrac{{0.25+0.4\lambda }}{s}{A_{{\mathrm{vc}}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\alpha ({\eta _{\mathrm{w}}}) = 1 - 0.077{\eta _{\mathrm{w}}},\;{A_{{\mathrm{vc}}}} = {A_{\mathrm{v}}}(1 - {\eta _{\mathrm{w}}}).$ $ \xi (\lambda ,{\eta _{\mathrm{w}}}) = \left\{ \begin{gathered} {\text{ }}1,\qquad\qquad\qquad\;\;{\eta _{\mathrm{w}}} \leqslant {\eta _{{\mathrm{cr}}}} ; \\ {({\eta _{\mathrm{w}}}/{\eta _{{\mathrm{cr}}}})^{0.069\lambda - 0.43}},{\eta _{\mathrm{w}}} > {\eta _{{\mathrm{cr}}}} . \\ \end{gathered} \right.\;\;{\eta _{{\mathrm{cr}}}} = 10.4(c/{d_{\mathrm{v}}}^2)+{f_{{\mathrm{cu}},{\mathrm{k}}}}/{d_{\mathrm{v}}}. $ 文献[7 ]模型 ${V_{\mathrm{p}}} = 1.75\dfrac{{{f_{\mathrm{t}}}{b_{\mathrm{c}}}{h_0}_{\mathrm{c}}}}{{\lambda +1}}+\dfrac{{{f_{{\mathrm{yvc}}}}{A_{{\mathrm{vc}}}}{h_0}}}{s}.$ ${f_{{\mathrm{yvc}}}} = {f_{{\mathrm{yv}}}}\dfrac{{1 - 1.121\;9{\eta _{\mathrm{w}}}}}{{1 - {\eta _{\mathrm{w}}}}} \geqslant 0.$ 文献[3 ]模型 ${V_{\mathrm{p}}} = \psi {f_{\mathrm{c}}}b{h_0}\left[\dfrac{{0.08}}{{\lambda - 0.3}}+\dfrac{{100{\rho _{\mathrm{l}}}}}{{\lambda {f_{\mathrm{c}}}}}\right]+\alpha \dfrac{{(0.4+0.3\lambda )}}{s}{A_{\mathrm{v}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\psi = \left\{ \begin{gathered} {\text{ }}1,{\text{ }}{\eta _{\mathrm{l}}} \leqslant 5\text{%} ; \\ 1.098 - 1.96\eta_{\mathrm{l}},{\eta _{\mathrm{l}}} > 5\text{%} . \\ \end{gathered} \right.\;\;{\text{ }}\alpha = 1 - 1.059{\eta _{\mathrm{w}}} \geqslant 0.$
基于随机森林(RF)、极端梯度提升树(Xgboost)及多层感知器(MLP),建立锈蚀RC梁抗剪承载力的确定性预测模型. ...
... 如表4 所示为机理模型与数据驱动模型的预测指标. 为了表示GPR模型的适用性,将GPR模型的50%置信区间与95%置信区间放置在这些模型中,如图8 所示. 结果表明,相较于机理模型,数据驱动模型具有显著优势,数据驱动模型均拥有较高的预测精度与稳定性. 在数据驱动模型中,GPR模型不仅具有最高的性能指标,而且可以输出预测值的概率区间,50%置信区间几乎包含了所有数据驱动模型的预测值,这表明GPR的置信区间具有代表性. 在3个经验模型中,文献[3 ]的模型考虑箍筋和纵筋各自锈蚀,在真实情况下箍筋先锈蚀,因此当样本纵筋锈蚀率较小时,该模型容易高估承载力. 文献[2 ,7 ]的模型仅考虑箍筋锈蚀,忽略了纵筋锈蚀的影响,这两位学者提出的方法预测结果偏于保守,更利于工程实际应用. 总体而言,GPR模型具有最强的预测性能,与经验模型与数据驱动确定性模型相比,具有较好的适用性,可以为锈蚀RC梁的概率安全性评估和概率极限状态评估提供依据. ...
... Comparison of predictive indicator of different model
Tab.4 模型 训练集 测试集 R 2 RMSE MAE R 2 RMSE MAE RF 0.978 14.101 8.311 0.916 20.813 12.765 Xgboost 0.994 7.359 4.833 0.944 16.952 11.859 MLP 0.986 11.658 7.073 0.944 17.080 11.451 GPR 0.987 10.938 7.004 0.947 16.632 11.462 文献[2 ]模型 0.780 47.460 24.540 0.577 47.897 35.182 文献[3 ]模型 0.874 34.700 28.420 0.844 28.482 23.882 文献[7 ]模型 0.642 66.121 53.210 0.430 62.023 52.141
图 8 不同模型的预测精度对比 ...
1
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
锈蚀箍筋混凝土梁的抗剪承载力分析
2
2008
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
... 为了探究${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{w}}}$ $\lambda $ 图7 (a)所示为${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{l}}}$ V p 随着锈蚀率的增加而增加,其置信区间随着锈蚀率的增加而减小. 这是由于样本中存在仅箍筋锈蚀梁、箍筋和纵筋均锈蚀梁、仅纵筋锈蚀梁3种,当纵筋锈蚀率较小时,95%置信区间范围较大. 当${\eta _{\mathrm{l}}}$ 图7 (b)所示为${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{w}}}$ V p 随着锈蚀率的增加而增加,当${\eta _{\mathrm{w}}}$ 图7 (c)所示为$\lambda $ V p 随着$\lambda $ $\lambda $ 5 , 33 , 34 ]的描述较一致,表明利用GPR模型,可以较好地捕捉特征与预测结果间的映射关系. ...
锈蚀箍筋混凝土梁的抗剪承载力分析
2
2008
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
... 为了探究${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{w}}}$ $\lambda $ 图7 (a)所示为${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{l}}}$ V p 随着锈蚀率的增加而增加,其置信区间随着锈蚀率的增加而减小. 这是由于样本中存在仅箍筋锈蚀梁、箍筋和纵筋均锈蚀梁、仅纵筋锈蚀梁3种,当纵筋锈蚀率较小时,95%置信区间范围较大. 当${\eta _{\mathrm{l}}}$ 图7 (b)所示为${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{w}}}$ V p 随着锈蚀率的增加而增加,当${\eta _{\mathrm{w}}}$ 图7 (c)所示为$\lambda $ V p 随着$\lambda $ $\lambda $ 5 , 33 , 34 ]的描述较一致,表明利用GPR模型,可以较好地捕捉特征与预测结果间的映射关系. ...
锈蚀钢筋混凝土梁抗剪承载力计算的概率模型
1
2018
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
锈蚀钢筋混凝土梁抗剪承载力计算的概率模型
1
2018
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
箍筋锈蚀钢筋混凝土梁的抗剪承载力分析
6
2011
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
... 为了验证所建GPR模型的预测性能,对徐善华等[2 -3 ,7 ] 建立的经验模型进行比较,如表3 所示. ...
... Empirical model for calculating shear capacity of RC beam
Tab.3 模型 模型公式 文献[2 ]模型 ${V_{\mathrm{p}}} = \xi (\lambda ,{\eta _{\mathrm{w}}})\dfrac{{0.08+4{\rho _{\mathrm{l}}}}}{{\lambda - 0.3}}{f_{\mathrm{c}}}b{h_0}+\alpha ({\eta _{\mathrm{w}}})\dfrac{{0.25+0.4\lambda }}{s}{A_{{\mathrm{vc}}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\alpha ({\eta _{\mathrm{w}}}) = 1 - 0.077{\eta _{\mathrm{w}}},\;{A_{{\mathrm{vc}}}} = {A_{\mathrm{v}}}(1 - {\eta _{\mathrm{w}}}).$ $ \xi (\lambda ,{\eta _{\mathrm{w}}}) = \left\{ \begin{gathered} {\text{ }}1,\qquad\qquad\qquad\;\;{\eta _{\mathrm{w}}} \leqslant {\eta _{{\mathrm{cr}}}} ; \\ {({\eta _{\mathrm{w}}}/{\eta _{{\mathrm{cr}}}})^{0.069\lambda - 0.43}},{\eta _{\mathrm{w}}} > {\eta _{{\mathrm{cr}}}} . \\ \end{gathered} \right.\;\;{\eta _{{\mathrm{cr}}}} = 10.4(c/{d_{\mathrm{v}}}^2)+{f_{{\mathrm{cu}},{\mathrm{k}}}}/{d_{\mathrm{v}}}. $ 文献[7 ]模型 ${V_{\mathrm{p}}} = 1.75\dfrac{{{f_{\mathrm{t}}}{b_{\mathrm{c}}}{h_0}_{\mathrm{c}}}}{{\lambda +1}}+\dfrac{{{f_{{\mathrm{yvc}}}}{A_{{\mathrm{vc}}}}{h_0}}}{s}.$ ${f_{{\mathrm{yvc}}}} = {f_{{\mathrm{yv}}}}\dfrac{{1 - 1.121\;9{\eta _{\mathrm{w}}}}}{{1 - {\eta _{\mathrm{w}}}}} \geqslant 0.$ 文献[3 ]模型 ${V_{\mathrm{p}}} = \psi {f_{\mathrm{c}}}b{h_0}\left[\dfrac{{0.08}}{{\lambda - 0.3}}+\dfrac{{100{\rho _{\mathrm{l}}}}}{{\lambda {f_{\mathrm{c}}}}}\right]+\alpha \dfrac{{(0.4+0.3\lambda )}}{s}{A_{\mathrm{v}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\psi = \left\{ \begin{gathered} {\text{ }}1,{\text{ }}{\eta _{\mathrm{l}}} \leqslant 5\text{%} ; \\ 1.098 - 1.96\eta_{\mathrm{l}},{\eta _{\mathrm{l}}} > 5\text{%} . \\ \end{gathered} \right.\;\;{\text{ }}\alpha = 1 - 1.059{\eta _{\mathrm{w}}} \geqslant 0.$
基于随机森林(RF)、极端梯度提升树(Xgboost)及多层感知器(MLP),建立锈蚀RC梁抗剪承载力的确定性预测模型. ...
... 如表4 所示为机理模型与数据驱动模型的预测指标. 为了表示GPR模型的适用性,将GPR模型的50%置信区间与95%置信区间放置在这些模型中,如图8 所示. 结果表明,相较于机理模型,数据驱动模型具有显著优势,数据驱动模型均拥有较高的预测精度与稳定性. 在数据驱动模型中,GPR模型不仅具有最高的性能指标,而且可以输出预测值的概率区间,50%置信区间几乎包含了所有数据驱动模型的预测值,这表明GPR的置信区间具有代表性. 在3个经验模型中,文献[3 ]的模型考虑箍筋和纵筋各自锈蚀,在真实情况下箍筋先锈蚀,因此当样本纵筋锈蚀率较小时,该模型容易高估承载力. 文献[2 ,7 ]的模型仅考虑箍筋锈蚀,忽略了纵筋锈蚀的影响,这两位学者提出的方法预测结果偏于保守,更利于工程实际应用. 总体而言,GPR模型具有最强的预测性能,与经验模型与数据驱动确定性模型相比,具有较好的适用性,可以为锈蚀RC梁的概率安全性评估和概率极限状态评估提供依据. ...
... Comparison of predictive indicator of different model
Tab.4 模型 训练集 测试集 R 2 RMSE MAE R 2 RMSE MAE RF 0.978 14.101 8.311 0.916 20.813 12.765 Xgboost 0.994 7.359 4.833 0.944 16.952 11.859 MLP 0.986 11.658 7.073 0.944 17.080 11.451 GPR 0.987 10.938 7.004 0.947 16.632 11.462 文献[2 ]模型 0.780 47.460 24.540 0.577 47.897 35.182 文献[3 ]模型 0.874 34.700 28.420 0.844 28.482 23.882 文献[7 ]模型 0.642 66.121 53.210 0.430 62.023 52.141
图 8 不同模型的预测精度对比 ...
箍筋锈蚀钢筋混凝土梁的抗剪承载力分析
6
2011
... 目前,预测方法主要包括机理驱动与数据驱动2类. 一些学者基于机理模型,如极限平衡理论[1 -2 ] 、“桁架-拱”理论[3 ] 、“修正压力场”理论[4 ] 、“等效桁架”理论[5 ] 等,建立确定性预测方法. 余波等[6 ] 结合修正压力场理论和临界斜裂缝倾角模型,建立概率模型. 该类方法的计算复杂,依赖多种假定与简化,难以适应锈蚀RC梁本身的高离散性. 为了提升实用性,一些学者通过试验回归分析引入经验参数,推导了经验实用方程[3 , 7 ] ,但存在精度不足的问题. ...
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
... 为了验证所建GPR模型的预测性能,对徐善华等[2 -3 ,7 ] 建立的经验模型进行比较,如表3 所示. ...
... Empirical model for calculating shear capacity of RC beam
Tab.3 模型 模型公式 文献[2 ]模型 ${V_{\mathrm{p}}} = \xi (\lambda ,{\eta _{\mathrm{w}}})\dfrac{{0.08+4{\rho _{\mathrm{l}}}}}{{\lambda - 0.3}}{f_{\mathrm{c}}}b{h_0}+\alpha ({\eta _{\mathrm{w}}})\dfrac{{0.25+0.4\lambda }}{s}{A_{{\mathrm{vc}}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\alpha ({\eta _{\mathrm{w}}}) = 1 - 0.077{\eta _{\mathrm{w}}},\;{A_{{\mathrm{vc}}}} = {A_{\mathrm{v}}}(1 - {\eta _{\mathrm{w}}}).$ $ \xi (\lambda ,{\eta _{\mathrm{w}}}) = \left\{ \begin{gathered} {\text{ }}1,\qquad\qquad\qquad\;\;{\eta _{\mathrm{w}}} \leqslant {\eta _{{\mathrm{cr}}}} ; \\ {({\eta _{\mathrm{w}}}/{\eta _{{\mathrm{cr}}}})^{0.069\lambda - 0.43}},{\eta _{\mathrm{w}}} > {\eta _{{\mathrm{cr}}}} . \\ \end{gathered} \right.\;\;{\eta _{{\mathrm{cr}}}} = 10.4(c/{d_{\mathrm{v}}}^2)+{f_{{\mathrm{cu}},{\mathrm{k}}}}/{d_{\mathrm{v}}}. $ 文献[7 ]模型 ${V_{\mathrm{p}}} = 1.75\dfrac{{{f_{\mathrm{t}}}{b_{\mathrm{c}}}{h_0}_{\mathrm{c}}}}{{\lambda +1}}+\dfrac{{{f_{{\mathrm{yvc}}}}{A_{{\mathrm{vc}}}}{h_0}}}{s}.$ ${f_{{\mathrm{yvc}}}} = {f_{{\mathrm{yv}}}}\dfrac{{1 - 1.121\;9{\eta _{\mathrm{w}}}}}{{1 - {\eta _{\mathrm{w}}}}} \geqslant 0.$ 文献[3 ]模型 ${V_{\mathrm{p}}} = \psi {f_{\mathrm{c}}}b{h_0}\left[\dfrac{{0.08}}{{\lambda - 0.3}}+\dfrac{{100{\rho _{\mathrm{l}}}}}{{\lambda {f_{\mathrm{c}}}}}\right]+\alpha \dfrac{{(0.4+0.3\lambda )}}{s}{A_{\mathrm{v}}}{f_{{\mathrm{yv}}}}{h_0}.$ $\psi = \left\{ \begin{gathered} {\text{ }}1,{\text{ }}{\eta _{\mathrm{l}}} \leqslant 5\text{%} ; \\ 1.098 - 1.96\eta_{\mathrm{l}},{\eta _{\mathrm{l}}} > 5\text{%} . \\ \end{gathered} \right.\;\;{\text{ }}\alpha = 1 - 1.059{\eta _{\mathrm{w}}} \geqslant 0.$
基于随机森林(RF)、极端梯度提升树(Xgboost)及多层感知器(MLP),建立锈蚀RC梁抗剪承载力的确定性预测模型. ...
... 如表4 所示为机理模型与数据驱动模型的预测指标. 为了表示GPR模型的适用性,将GPR模型的50%置信区间与95%置信区间放置在这些模型中,如图8 所示. 结果表明,相较于机理模型,数据驱动模型具有显著优势,数据驱动模型均拥有较高的预测精度与稳定性. 在数据驱动模型中,GPR模型不仅具有最高的性能指标,而且可以输出预测值的概率区间,50%置信区间几乎包含了所有数据驱动模型的预测值,这表明GPR的置信区间具有代表性. 在3个经验模型中,文献[3 ]的模型考虑箍筋和纵筋各自锈蚀,在真实情况下箍筋先锈蚀,因此当样本纵筋锈蚀率较小时,该模型容易高估承载力. 文献[2 ,7 ]的模型仅考虑箍筋锈蚀,忽略了纵筋锈蚀的影响,这两位学者提出的方法预测结果偏于保守,更利于工程实际应用. 总体而言,GPR模型具有最强的预测性能,与经验模型与数据驱动确定性模型相比,具有较好的适用性,可以为锈蚀RC梁的概率安全性评估和概率极限状态评估提供依据. ...
... Comparison of predictive indicator of different model
Tab.4 模型 训练集 测试集 R 2 RMSE MAE R 2 RMSE MAE RF 0.978 14.101 8.311 0.916 20.813 12.765 Xgboost 0.994 7.359 4.833 0.944 16.952 11.859 MLP 0.986 11.658 7.073 0.944 17.080 11.451 GPR 0.987 10.938 7.004 0.947 16.632 11.462 文献[2 ]模型 0.780 47.460 24.540 0.577 47.897 35.182 文献[3 ]模型 0.874 34.700 28.420 0.844 28.482 23.882 文献[7 ]模型 0.642 66.121 53.210 0.430 62.023 52.141
图 8 不同模型的预测精度对比 ...
Failure mode classification and bearing capacity prediction for reinforced concrete columns based on ensemble machine learning algorithm
1
2020
... 数据驱动方法可以精确捕捉输入特征与输出值间的复杂映射关系,具有预测精度高、建模效率快的优点,已被广泛应用于结构强度[8 -13 ] 、破坏模式[14 ] 、决策分析[15 ] 等方面的预测. 上述数据驱动方法的输出结果是唯一确定性的,难以考虑锈蚀RC梁的自身力学性能客观不确定性和超参数拟定主观不确定性的影响. 有必要建立数据驱动的概率模型,以考虑不确定性对锈蚀RC梁抗剪承载力的影响. ...
基于改进BP算法的混凝土热学参数反演与预测
0
2021
基于改进BP算法的混凝土热学参数反演与预测
0
2021
Machine learning intelligence to assess the shear capacity of corroded reinforced concrete beams
0
2023
A machine learning-based time-dependent shear strength model for corroded reinforced concrete beams
1
2021
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
Evaluation of residual strength of corroded reinforced concrete beams using machine learning models
0
2022
基于可解释机器学习的锈蚀RC构件抗剪承载力预测模型
1
2024
... 数据驱动方法可以精确捕捉输入特征与输出值间的复杂映射关系,具有预测精度高、建模效率快的优点,已被广泛应用于结构强度[8 -13 ] 、破坏模式[14 ] 、决策分析[15 ] 等方面的预测. 上述数据驱动方法的输出结果是唯一确定性的,难以考虑锈蚀RC梁的自身力学性能客观不确定性和超参数拟定主观不确定性的影响. 有必要建立数据驱动的概率模型,以考虑不确定性对锈蚀RC梁抗剪承载力的影响. ...
基于可解释机器学习的锈蚀RC构件抗剪承载力预测模型
1
2024
... 数据驱动方法可以精确捕捉输入特征与输出值间的复杂映射关系,具有预测精度高、建模效率快的优点,已被广泛应用于结构强度[8 -13 ] 、破坏模式[14 ] 、决策分析[15 ] 等方面的预测. 上述数据驱动方法的输出结果是唯一确定性的,难以考虑锈蚀RC梁的自身力学性能客观不确定性和超参数拟定主观不确定性的影响. 有必要建立数据驱动的概率模型,以考虑不确定性对锈蚀RC梁抗剪承载力的影响. ...
基于机器学习的钢筋混凝土柱失效模式两阶段判别方法
1
2022
... 数据驱动方法可以精确捕捉输入特征与输出值间的复杂映射关系,具有预测精度高、建模效率快的优点,已被广泛应用于结构强度[8 -13 ] 、破坏模式[14 ] 、决策分析[15 ] 等方面的预测. 上述数据驱动方法的输出结果是唯一确定性的,难以考虑锈蚀RC梁的自身力学性能客观不确定性和超参数拟定主观不确定性的影响. 有必要建立数据驱动的概率模型,以考虑不确定性对锈蚀RC梁抗剪承载力的影响. ...
基于机器学习的钢筋混凝土柱失效模式两阶段判别方法
1
2022
... 数据驱动方法可以精确捕捉输入特征与输出值间的复杂映射关系,具有预测精度高、建模效率快的优点,已被广泛应用于结构强度[8 -13 ] 、破坏模式[14 ] 、决策分析[15 ] 等方面的预测. 上述数据驱动方法的输出结果是唯一确定性的,难以考虑锈蚀RC梁的自身力学性能客观不确定性和超参数拟定主观不确定性的影响. 有必要建立数据驱动的概率模型,以考虑不确定性对锈蚀RC梁抗剪承载力的影响. ...
A deep reinforcement learning method for structural dominant failure modes searching based on self-play strategy
1
2023
... 数据驱动方法可以精确捕捉输入特征与输出值间的复杂映射关系,具有预测精度高、建模效率快的优点,已被广泛应用于结构强度[8 -13 ] 、破坏模式[14 ] 、决策分析[15 ] 等方面的预测. 上述数据驱动方法的输出结果是唯一确定性的,难以考虑锈蚀RC梁的自身力学性能客观不确定性和超参数拟定主观不确定性的影响. 有必要建立数据驱动的概率模型,以考虑不确定性对锈蚀RC梁抗剪承载力的影响. ...
Gaussian process regression-based load-carrying capacity models of corroded prestressed concrete bridge girders for fast-screening and reliability-based evaluation
1
2023
... 高斯过程回归(GPR)是概率机器学习方法,具有灵活的核函数,可以量化输入特征的不确定性. Liu等[16 -17 ] 利用GPR分别建立锈蚀PC梁承载力概率模型和RC梁柱接头剪切强度概率模型,但已有模型未考虑输入特征尺度和维度的影响,且超参数拟定未利用先验知识,限制了预测性能. ...
Probabilistic prediction of joint shear strength using Gaussian process regression with anisotropic compound kernel
1
2023
... 高斯过程回归(GPR)是概率机器学习方法,具有灵活的核函数,可以量化输入特征的不确定性. Liu等[16 -17 ] 利用GPR分别建立锈蚀PC梁承载力概率模型和RC梁柱接头剪切强度概率模型,但已有模型未考虑输入特征尺度和维度的影响,且超参数拟定未利用先验知识,限制了预测性能. ...
A tutorial on Gaussian process regression: modelling, exploring, and exploiting functions
1
2018
... 高斯过程回归(GPR)是基于贝叶斯理论和统计学习理论发展的非参数回归方法,目标是建立有限子集的联合概率分布[18 ] . GPR不仅可以给出点预测,还可以给出预测值的不确定性即置信区间,记为 ...
A Broyden-Fletcher-Goldfarb-Shanno optimization procedure for molecular geometries
1
1985
... BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法是拟牛顿法,用于寻找可微标量函数的局部最小值[19 ] . 优先内存BFGS(L-BFGS)仅存储有限的历史信息逼近逆Hessian矩阵,显著减少了内存需求,提高了求解效率[20 ] . ...
Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization
1
1997
... BFGS(Broyden-Fletcher-Goldfarb-Shanno)算法是拟牛顿法,用于寻找可微标量函数的局部最小值[19 ] . 优先内存BFGS(L-BFGS)仅存储有限的历史信息逼近逆Hessian矩阵,显著减少了内存需求,提高了求解效率[20 ] . ...
1
... RC梁的抗剪承载力与材料的几何尺寸、力学性能息息相关,且这些特征间存在相关性,在锈蚀的影响下,这些特征之间的层次结构更复杂. 传统的贝叶斯优化生成连续的超参数配置,没有明确的探索和开发步骤,难以精确考虑这些特征间的复杂依赖关系. 树形分层贝叶斯估计(TPE)[21 ] 是贝叶斯优化的变体,引入树形结构和探索-开发策略,以更加高效地探索超参数空间. ...
局部区段锈蚀的钢筋混凝土梁抗剪承载力试验研究
1
2010
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
局部区段锈蚀的钢筋混凝土梁抗剪承载力试验研究
1
2010
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
小剪跨比锈蚀钢筋混凝土梁受剪性能试验研究
1
2019
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
小剪跨比锈蚀钢筋混凝土梁受剪性能试验研究
1
2019
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
2
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
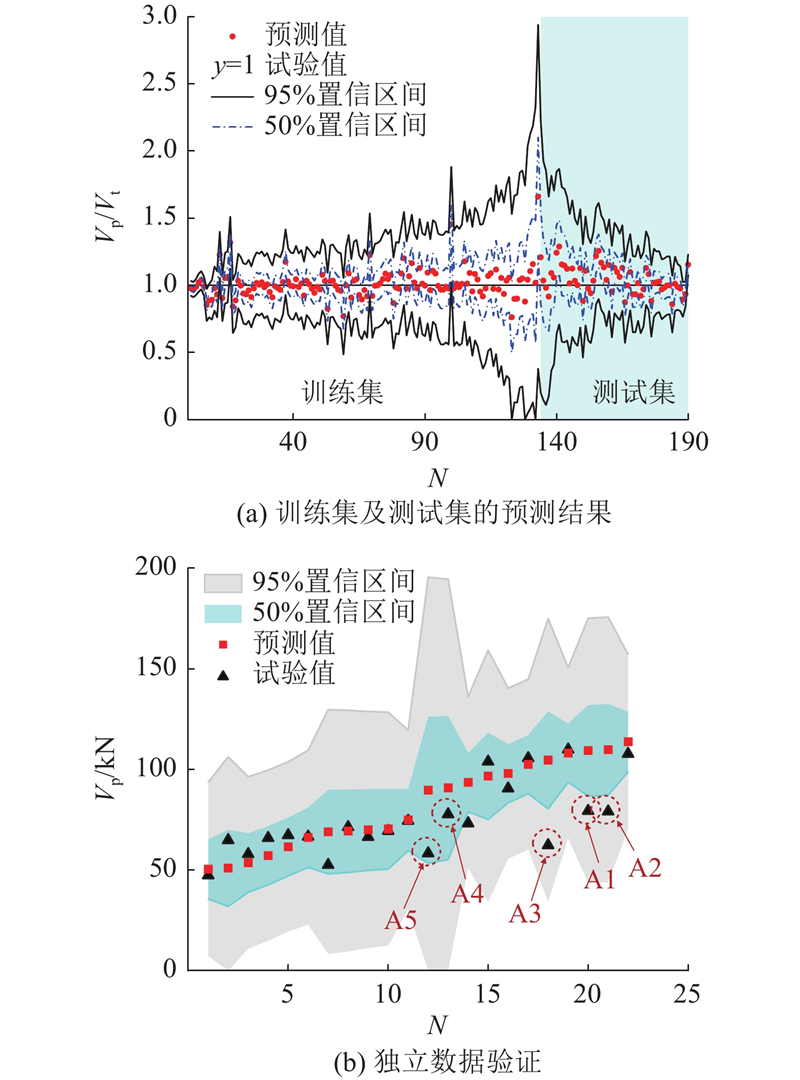
... 如图6 (a)所示为133组训练集与57组测试集的预测均值与试验值的对比分析结果. 其中,N 为梁编号,V t 为试验值. 在133组训练样本中,仅3个样本在95%置信区间外,26个样本位于50%~95%置信区间内,104个样本位于50%置信区间内. 在57组测试集样本中,仅有1个样本在95%置信区间外,17个样本位于50%~95%置信区间内,39个样本位于50%置信区间内. 如图6 (b)所示为22组独立验证集的预测效果. A1~A3样本在50%置信区间外且置信区间较大,这是由于文献[24 ]中A1~A5样本的配筋率(3.6%)在训练参数范围外,而训练参数范围内的其他样本预测较好. ...
2
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
... 如图6 (a)所示为133组训练集与57组测试集的预测均值与试验值的对比分析结果. 其中,N 为梁编号,V t 为试验值. 在133组训练样本中,仅3个样本在95%置信区间外,26个样本位于50%~95%置信区间内,104个样本位于50%置信区间内. 在57组测试集样本中,仅有1个样本在95%置信区间外,17个样本位于50%~95%置信区间内,39个样本位于50%置信区间内. 如图6 (b)所示为22组独立验证集的预测效果. A1~A3样本在50%置信区间外且置信区间较大,这是由于文献[24 ]中A1~A5样本的配筋率(3.6%)在训练参数范围外,而训练参数范围内的其他样本预测较好. ...
Shear behavior of reinforced concrete beams subjected to accelerated non-uniform corrosion
1
2023
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
2
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
... 由于该数据库中的混凝土强度采用的是圆柱体抗压强度标准值,而我国规范采用的是轴心抗压强度设计值${f_{\mathrm{c}}}$ 26 ]换算混凝土强度,换算公式如下: ...
1
... 研究人员更关注材料和性能的相对变化规律,传统的RC梁抗剪强度设计理论都是参考小尺寸梁的试验结果得到的,尚未有专门针对尺寸效应RC梁剪切强度的试验数据库,因此本文在Fu等[11 ] 建立的数据库基础上,增加了李冰等[22 ] 、杨晓明等[23 ] 及霍艳华[3 ] 的试验梁样本,共计190组,用于模型的训练与测试. 其中,70%的数据用于训练(133组),30%的数据用于测试(57组). 引入22组独立数据[24 -25 ] ,用于测试模型的泛化性能. 数据库具有14个结构的基本特征:混凝土轴心抗压强度设计值${f_{\mathrm{c}}}$ ${h_0}$ $\lambda $ ${\eta _{\text{w}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ ${\eta _{\mathrm{l}}}$ ${f_{{\mathrm{yv}}}}$ $s$ ${d_{\mathrm{v}}}$ ${f_{\mathrm{y}}}$ $h$ 表1 . 根据文献[26 ],设计使用年限为50 a的RC梁,混凝土等级通常为C20~C40(9.6~19.1 MPa),实际结构通常使用C30~C40混凝土,训练集的${f_{\mathrm{c}}}$ (12.09 ~26.85 MPa)对应C30~C60混凝土,钢筋屈服强度通常为300~500 MPa,训练集的${f_{{\mathrm{yv}}}}$ $s$ 27 ]可知,对于C20~C40混凝土,纵筋最大${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{l}}}$ ${\rho _{\mathrm{v}}}$ ${\rho _{\mathrm{v}}}$ [7 ] 对服役28 a的屋顶花架梁钢筋锈蚀率进行测定,锈蚀率最大为29.4%,训练集${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{l}}}$
Short-term power load probability density forecasting based on Yeo-Johnson transformation quantile regression and Gaussian kernel function
1
2018
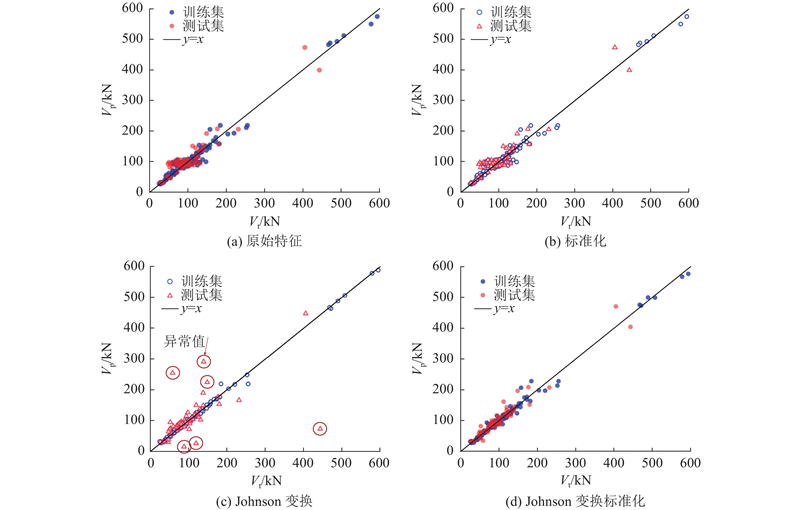
... 试验数据的分布与质量可以决定数据驱动方法所能达到的上限,而输入特征的分布具有偏态、长尾、多峰等特点,且特征间存在尺度差异. 数据特征的不同尺度与分布形态可能会对GPR的性能产生负面影响,因此本文通过Yeo-Johnson变换[28 ] 将严重偏态分布的数据尽可能映射到接近正态分布,提高模型的稳定性与预测精度. 通过最大化特征的对数似然计算最优$\lambda $
Comparison of values of Pearson's and Spearman's correlation coefficients on the same sets of data
1
2011
... 当利用数据驱动方法选择输入特征时,若输入特征存在共线性,则会导致模型出现过拟合、超参数估计不准确的问题. 为了验证特征的合理性,通常对数据库进行特征相关性分析. 用于描述连续变量的相关系数主要有Pearson和Spearman相关系数[29 ] ,Spearman相关系数用于度量2个变量间的单调关系,对于非线性关系也能较好地描述且不要求变量连续. 选择Spearman相关系数对本数据库进行相关性分析,Spearman相关系数可以采用以下近似公式计算: ...
1
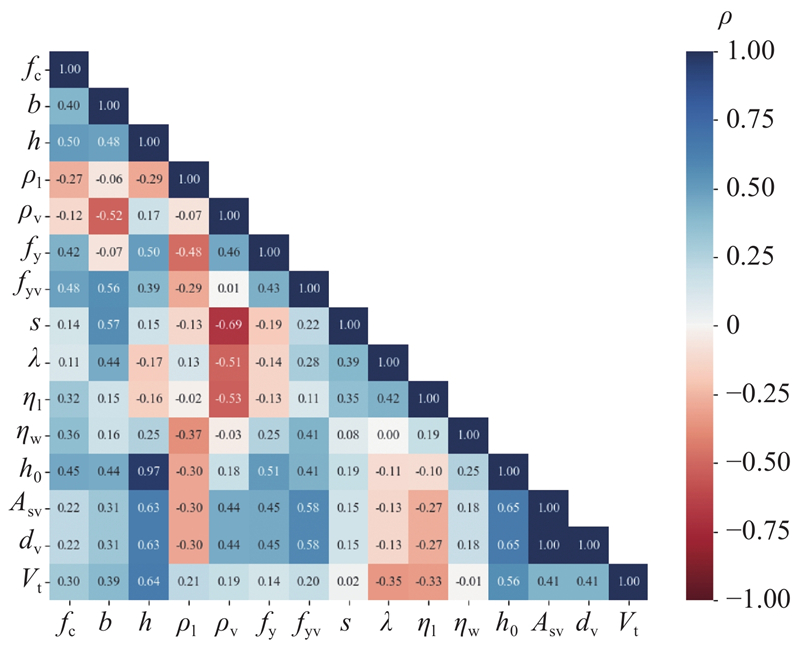
... 如图3 所示为特征间的相关性,一般认为高度相关($|\rho | \geqslant 0.8$ ) 的变量不适合作为输入变量[30 ] . $h$ ${h_0}$ ${h_0}$ ${h_0}$ $ {\rho }_{{\mathrm{v}}}={A}_{{\mathrm{sv}}}/(b s) $ ${\rho _{\mathrm{v}}}$ ${A_{{\mathrm{sv}}}}$ $b$ $s$ ${\rho _{\mathrm{v}}}$ $s$
1
... 输入特征维度的增加需要更多的数据对空间进行充分覆盖,否则难以保证模型的泛化性能. 从2.3节可知,数据库存在共线冗余的特征,因此通过特征递归消除(RFE)对输入特征进行降维. 特征递归消除(RFE)是以置换特征重要性(PFI)[31 ] 为特征重要性的判别手段,通过反复训练模型并剔除最不重要的特征,直至达到设定的特征数量或某个停止准则. 设定保留的特征数量为7,每一轮特征递归消除的特征分别为$h$ ${f_{\mathrm{y}}}$ ${d_{\mathrm{v}}}$ $s$ ${f_{{\mathrm{yv}}}}$ ${\eta _{\mathrm{l}}}$ $b$ ${A_{{\mathrm{sv}}}}$
1
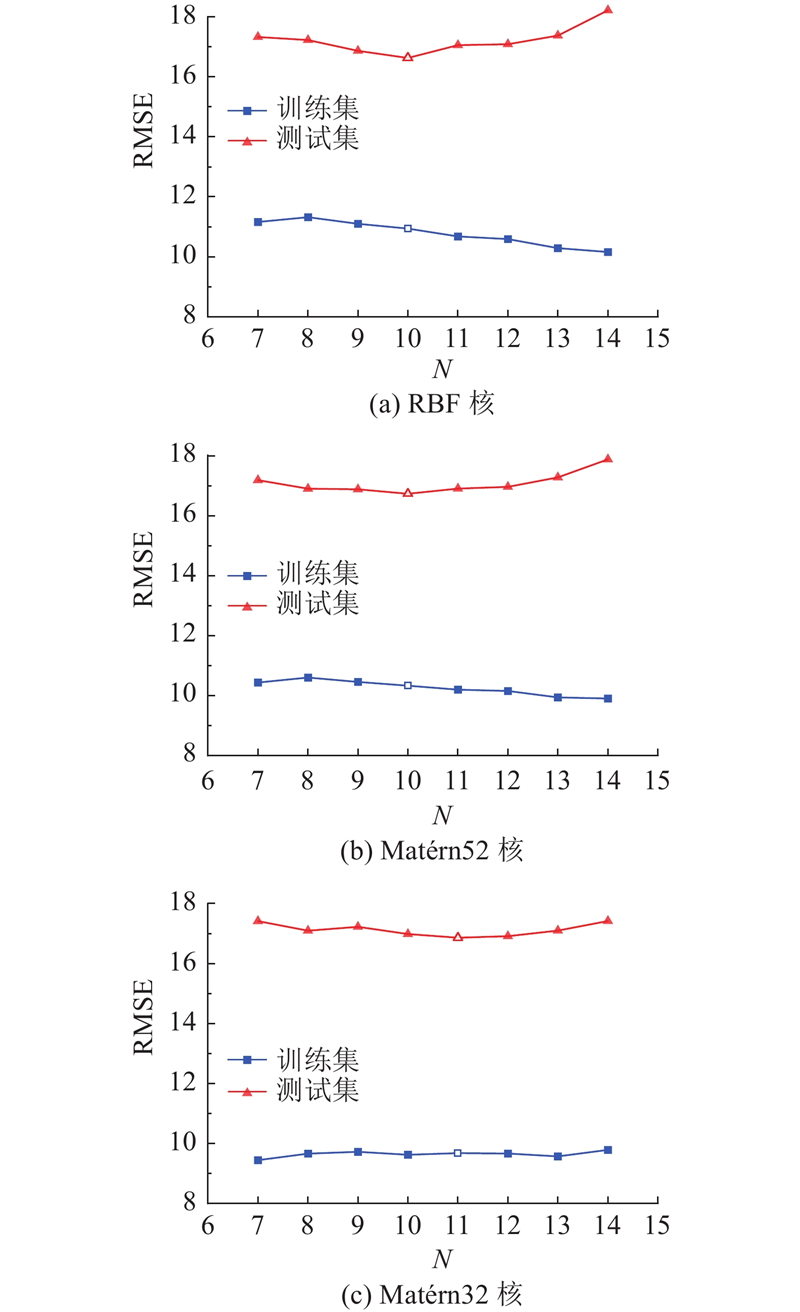
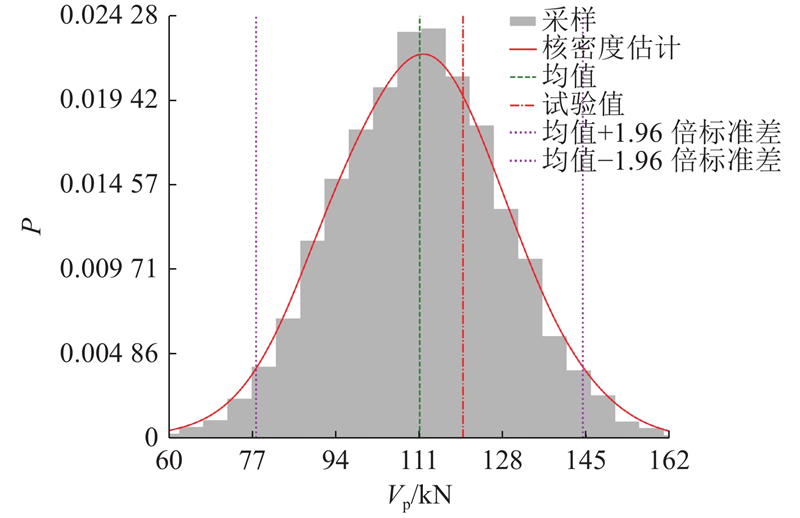
... 基于RFE与TEP-L-BFGS优化算法,建立锈蚀RC梁抗剪承载力预测GPR模型. 在该模型中,最优核函数为RBF,噪声方差为182.15,长度尺度为5.03,方差为42 757.8. 如图5 所示为文献[32 ]的A3试件预测结果. 其中,P 为预测概率密度,V p 为预测值. 该样本的预测均值为110.9 kN,试验值为119.8 kN,95%置信预测区间的上、下限分别为144.2和77.62 kN. ...
1
... 基于RFE与TEP-L-BFGS优化算法,建立锈蚀RC梁抗剪承载力预测GPR模型. 在该模型中,最优核函数为RBF,噪声方差为182.15,长度尺度为5.03,方差为42 757.8. 如图5 所示为文献[32 ]的A3试件预测结果. 其中,P 为预测概率密度,V p 为预测值. 该样本的预测均值为110.9 kN,试验值为119.8 kN,95%置信预测区间的上、下限分别为144.2和77.62 kN. ...
纵筋锈蚀对钢筋混凝土梁抗剪性能影响
1
2016
... 为了探究${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{w}}}$ $\lambda $ 图7 (a)所示为${\eta _{\mathrm{l}}}$ ${\eta _{\mathrm{l}}}$ V p 随着锈蚀率的增加而增加,其置信区间随着锈蚀率的增加而减小. 这是由于样本中存在仅箍筋锈蚀梁、箍筋和纵筋均锈蚀梁、仅纵筋锈蚀梁3种,当纵筋锈蚀率较小时,95%置信区间范围较大. 当${\eta _{\mathrm{l}}}$ 图7 (b)所示为${\eta _{\mathrm{w}}}$ ${\eta _{\mathrm{w}}}$ V p 随着锈蚀率的增加而增加,当${\eta _{\mathrm{w}}}$ 图7 (c)所示为$\lambda $ V p 随着$\lambda $ $\lambda $ 5 , 33 , 34 ]的描述较一致,表明利用GPR模型,可以较好地捕捉特征与预测结果间的映射关系. ...