城市交通拥堵源于交通供需失衡. 传统的“四阶段”交通模型未能充分考虑出行与活动之间的时空联系,目前,基于活动的模型主要依赖于居民调查问卷数据,这种依赖性限制了模型的分析深度. 随着智慧城市概念的普及,手机信令数据因其广泛的覆盖范围和庞大的数据量而成为研究的热点. 预测活动序列,需要推断出手机信令数据中居民停留点的活动类型,早期研究多采用监督学习方法[1-3],将在出行调查数据上训练的模型迁移到GPS或手机信令数据上. 通常,多源数据的异构性导致监督模型迁移存在问题. 越来越多的学者采用无监督方法,推断居民活动类型,例如基于规则[4]、结合周边POI[5-6]或时空特征[7]的方法. 这类方法容易受到噪声的影响,能够有效处理噪声的潜在狄利克雷分配模型,被广泛用于从大规模手机信令数据中推断出行目的[8-9]. 在推断出出行目的后,可以进一步提取个体活动模式.
本文利用潜在狄利克雷分配(LDA)主题生成算法推断出个体出行目的,引入nTreeClus框架识别典型的活动模式,融合多源数据并结合注意力机制,借助TFT进行建模,预测个体多步活动序列. 依据居民活动序列预测不同时段各区域的人员流动与聚集情况,为交通部门提前制定交通疏导方案、调配公共交通资源提供关键信息,进一步推动城市活动与交通系统的协同发展.
1. 数据采集与预处理
1.1. 手机信令数据
采用的手机信令数据由移动通信运营商提供,研究样本涵盖了杭州市主城区的2万名用户,记录他们在浙江省范围内2023年5月15日至21日期间的轨迹数据,共计480万条. 目前大多移动设备位置数据因其被动收集数据的性质和隐私方面的顾虑,往往缺乏重要的居民基本个人属性和社会经济属性,这一缺陷限制了研究模型在政策分析、干预效果评估或适应个体行为变化方面的能力. 在本研究中,合作的移动运营商在严格保护用户隐私的前提下,提供了脱敏处理后的用户个人和社会经济属性数据,如表1所示,有效解决了数据不足问题.
表 1 用户基本属性的含义表
Tab.1
| 序号 | 字段 | 含义 |
| 1 | BILL_NO | 手机号码 |
| 2 | SEX | 性别(0-女;1-男) |
| 3 | AGE | 年龄 |
| 4 | AGE_GROUP | 年龄分组 |
| 5 | OCCU_NAME | 职业大类 |
| 6 | INCOME_LEVEL_NAME | 收入水平 |
对手机信令数据的预处理的任务主要包括数据清洗和停留点识别. 通过数据清洗,处理手机信令数据中的乒乓数据和漂移数据,删除有跨市交通流动的用户数据,使研究专注于杭州市内的出行活动. 经过数据清洗后,将杭州市地图按50 m×50 m的栅格进行划分,若用户在一个地点的停留时间超过30 min,则该点被判定为手机用户停留点[24].
最终处理后的手机信令数据部分字段如表2所示.
表 2 处理后手机信令数据样例
Tab.2
| 手机号码 | 开始时间 | 离开时间 | 经纬度/(°) |
| 14d42c***8d9a | 2023-05-15 00:00:00 | 2023-05-15 07:01:17 | 120.255, 30.318 |
| 14d42c***8d9a | 2023-05-15 07:35:43 | 2023-05-15 17:49:13 | 120.261, 30.326 |
| 14d42c***8d9a | 2023-05-15 18:08:13 | 2023-05-15 19:56:39 | 120.291, 30.329 |
1.2. POI数据
POI(point of interest)即兴趣点,是电子地图中可以查询的各类标签. 杭州市POI数据利用网络爬虫从高德地图提供的API接口爬取,数据约89万条,部分POI数据如表3所示,研究关注手机用户在目的地的活动类型.
表 3 部分杭州市POI数据示例
Tab.3
| POI点 | 所属类型 | 经纬度/(°) | 行政区 | 详细地址 |
| 西湖文化广场 | 风景名胜、公园广场、城市广场 | 拱墅区 | 环城北路47号 | |
| 品诣美发 | 生活服务、美容美发店、美容美发店 | 上城区 | 笕桥镇麦庙街明桂南苑2幢底商2号 |
鉴于高德地图提供的POI种类繁多,为了便于分析,对POI大类进行精简,选择11个通用标签对POI分类进行概括. 这些标签被用于增强出行目的地的空间语义信息,包括餐饮服务、体育休闲服务、医疗保健服务、商务住宅、生活服务、机动车服务、公司企业、购物服务、科教文化服务、风景名胜、政府机构和社会团体. 围绕用户出行目的地(即用户停留点的地理位置)以特定半径R进行POI搜索,该半径初步设置为150 m,旨在捕捉周边的相关POI. 用户目的地的地理位置往往对应多个POI点,本研究采用重力模型对POI进行权重分配,确定最具代表性的POI标签. 在该模型中,带有POI标签c的位置l被访问的概率根据下式计算:
式中:
该方法旨在为手机用户的出行目的地赋予相应的POI概率标签,以此构建精准且贴合实际的数据表征,保障后续的用户活动行为研究.
1.3. 气象和日期数据
1)气象数据处理. 气象数据包括每日的天气情况,如晴天、阴天、雨天等. 数据从杭州气象局获取,涵盖了研究期间内的每一天. 当处理这些数据时,对每个日期的天气状况进行分类,将天气状况编码为数值形式,以便于后续的统计分析,例如将“晴天”编码为0,“阴天”编码为1,“雨天”编码为2. 通过这种方式,能够量化天气状况的影响,探究不同天气背景下居民活动模式的变化.
2)日期数据处理. 日期数据包含工作日、周末(星期六和星期日)及节假日,将这些数据进行数值编码,以便将日期类型作为影响居民活动的一个变量进行研究,例如将“工作日”编码为0,“周末”编码为1.
2. 活动类型的推断
考虑到居民在工作日的晚上通常会停留在家庭居住地,而在白天则前往工作场所,家庭/工作活动展现出显著的规律性. 基于居民日常活动的这种规律性,提出规则化方法来确定个人的家庭和工作地点. 该方法基于以下2个核心假设[23]. 1)居民在夜间(午夜12点到早晨6点)停留时间最长的位置(至少是260 min),通常被认为是家庭所在地. 2)居民在白天(早晨6点到下午4点)停留时间最长(至少是180 min)的位置,通常被认为是工作地点.
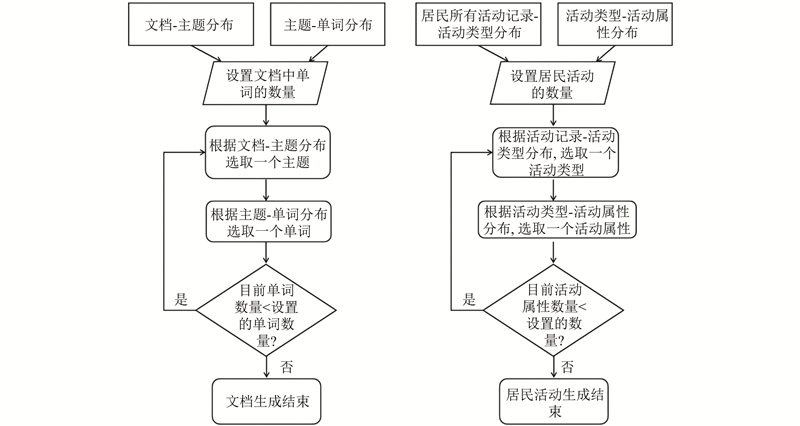
LDA被广泛用于文本挖掘中的主题识别. 该模型假设文档是通过文档到主题再到词汇的过程生成的. 根据这一假设,文档中的词汇可以通过以下2个步骤生成:1)从主题分布中抽取文档的主题;2)在特定主题下抽取相关词汇. 将LDA应用于交通活动领域,把每个用户的所有活动记录视为一个文档,居民的每次活动视为一个单词,为每次活动推断出一个潜在活动类型,为每个用户推断出一个活动链. 与LDA假设下的文档生成过程类似,认为剩余观察到的活动是如图1所示生成的.
图 1
图 1 居民活动记录与文档生成过程的对比
Fig.1 Comparison of process of resident activity record and document generation
利用困惑度指标确定LDA的主题数目为18类,根据每类主题的开始时间、持续时间、年龄群体和活动地点POI标签,将主题合并为5大类:工作活动、居家活动、娱乐活动、个人维护活动(就医相关主题)和其他活动.
3. 多日活动模式聚类
3.1. 多日活动序列的构建
为了分析居民的日常活动模式,为每位居民重建活动链,如表4所示. 传统的活动链(如“家—工作—娱乐—家”)无法体现活动发生时间的差异,因此采用时间切片法进行优化.
表 4 居民活动链的示例
Tab.4
| 手机号码 | 开始时间 | 离开时间 | 活动类型 |
| 14d42c***8d9a | 2023-05-15 00:00:00 | 2023-05-15 07:01:17 | 居家 |
| 14d42c***8d9a | 2023-05-15 07:35:43 | 2023-05-15 17:49:13 | 工作 |
| 14d42c***8d9a | 2023-05-15 18:08:13 | 2023-05-15 19:56:39 | 娱乐 |
| 14d42c***8d9a | 2023-05-15 20:31:27 | 2023-05-15 23:59:59 | 居家 |
图 2
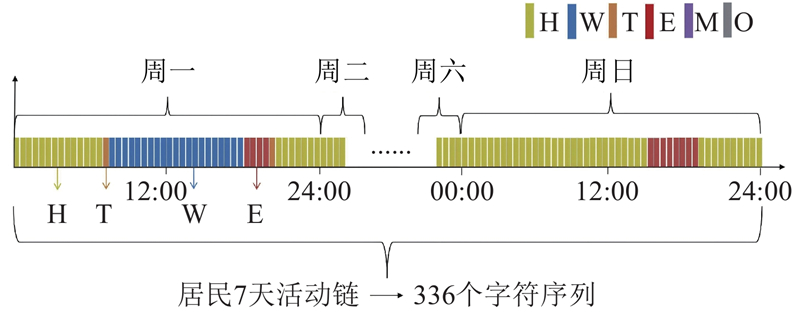
图 2 居民多日活动序列的重构
Fig.2 Reconstruction of residents' multi-day activity sequence
活动类型被编码为居家(H)、工作(W)、娱乐(E)、个人维护(M)、出行(T)及其他(O),以此直观地呈现居民一周的活动节律.
3.2. nTreeClus聚类框架
在获取居民的多日活动序列后,为了深入挖掘多日活动序列的潜在特征,需要进行向量化,以揭示子序列与序列之间的关系并衡量居民活动序列间的差异性. 采用nTreeClus框架来评估居民多日活动序列的相似性,nTreeClus融合了基于树的学习机制、k-mers技术以及自回归(auto regressive model,AR)模型对时间序列分类的独特见解. 具体来说,通过将序列分割为长度为n的子序列,应用随机森林模型追踪和学习序列中元素的交互作用. nTreeClus通过计算每个子序列在决策树叶子节点的出现频率,构建序列的向量化表示. 利用该方法,不仅提升了特征提取的深度,而且提高了聚类效率和精度.
采用平均轮廓系数(average silhouette width, ASW)作为评价聚类效果的指标,以定量评估聚类过程对居民活动序列划分的合理性[26]. 轮廓系数高的聚类结果通常表明,同一簇内的居民活动序列之间具有较高的相似性,且与其他簇保持较大的差异性,这是判断聚类效果优异的重要依据. 平均轮廓系数通过整合簇内聚度与簇间分离度的信息,量化了每个居民活动序列与其所属簇的匹配程度相对于最接近的其他簇的匹配程度. 平均轮廓系数的取值为−1~1,平均轮廓系数接近1,意味着居民活动序列与所属簇的匹配程度高,与其他簇的距离远,表明了良好的聚类质量. 平均轮廓系数接近−1,表明该活动序列可能被错误地分配到了某个簇中.
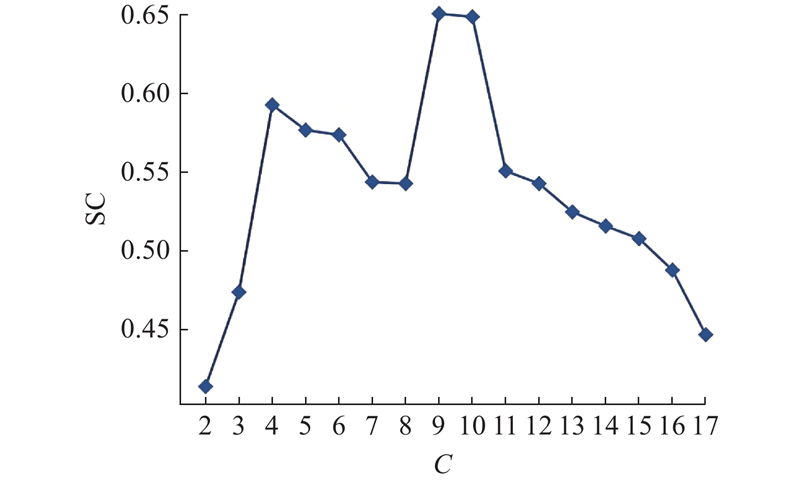
在 nTreeClus 框架中,随着聚类数量的改变,用于评估聚类效果的平均轮廓系数相应变化,如图3所示. 其中,SC为平均轮廓系数,C为簇个数. 当C = 9时,平均轮廓系数达到最大值0.651,表明模型在这一聚类数量下展现出优秀的分类效果. 其中3个簇的样本所占的总体比例相对较小,处于个位数水平,故不对这3个簇进行分析. 最终确定6种典型的多日活动模式.
图 3
3.3. 聚类结果分析
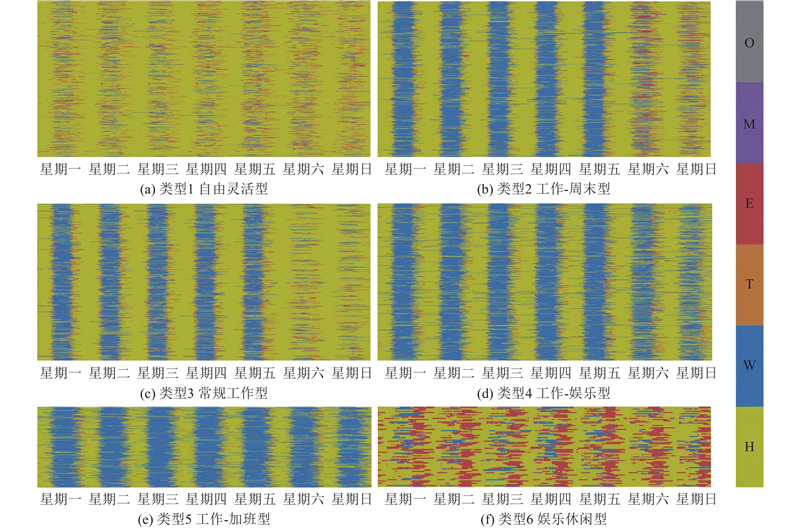
居民活动序列的聚类结果如图4所示,每个子图的横轴表示一周的时间,纵轴表示同一簇中不同居民的一周活动安排. 对于每个活动序列,活动单元按6种活动类型分别着色,即居家(H)、工作(W)、出行(T)、娱乐(E)、个人维护(M)、其他(O). 同一簇中的活动序列大多相似,活动单元的时间分布和顺序具有一致的规律性. 每个簇都可以表示一种典型的居民多日活动模式,不同的簇直观显示了居民在多日活动模式上的显著差异. 根据聚类结果分析,可以将6个类别的居民多日活动模式分别定义为“自由灵活型”、“工作-周末活动型”、“常规工作型”、“工作-娱乐型”、“工作-加班型”、“娱乐休闲型”. 类别1(自由灵活型)中,见图4(a),居民通常没有固定的工作,主要时间在家中度过,偶尔在日间参与休闲娱乐、个人维护或其他活动.
图 4
从图4(b)可以发现,类别2即工作-周末活动型中,绝大多数上班族在工作日内会有规律地在工作地点投入大量时间,典型的工作时段是从早上8点至晚上6点. 在工作结束后,他们返回住所,晚间时间主要在住所内度过. 到了周末,活动模式会有所转变,大多数居民倾向于外出进行娱乐活动、个人维护活动及其他活动. 从图4(c)可知,类别3即常规工作型,居民在工作日的活动主要以工作为中心,占据了大部分白天时间. 相较于工作-周末活动型,这一类群体中的居民下班后前往商场、餐厅、电影院等地进行娱乐活动的比例更高. 到了周末,他们多数选择宅在家中,与工作-周末活动型相比,外出娱乐的比例显著减少. 这些模式在日常生活中很常见. 通过对居民多日活动的聚类分析,发现若干不同于常规模式的活动类型,如图4(a)、(b)所示,一部分居民在工作日及周末处于持续工作的模式,这一现象揭示了杭州存在大量的高强度工作现状. 尽管类别4(工作-娱乐型)和类别5(工作-加班型)的居民在一周之中持续加班的行为上表现出共性,但两者之间仍存在差异. 具体而言,工作-加班型的居民的工作时间更长,除了工作基本上只在家中活动,没有其他活动安排,这反映出极高的工作强度. 工作-娱乐型的居民虽然同样加班,但他们的工作时间相对较短,并且在工作之余参与其他娱乐和休闲活动的频率显著更高. 最后,还发现了一种较特殊的活动模式,如图4(f)所示,娱乐休闲型的居民投入于工作的时间较少,享受相对灵活的工作时间安排,倾向于花费更多时间从事娱乐活动,特别是在下午到晚上的时间段. 这种模式往往与对特定活动有特别兴趣的群体相关联.
4. 基于多日活动序列的多步预测
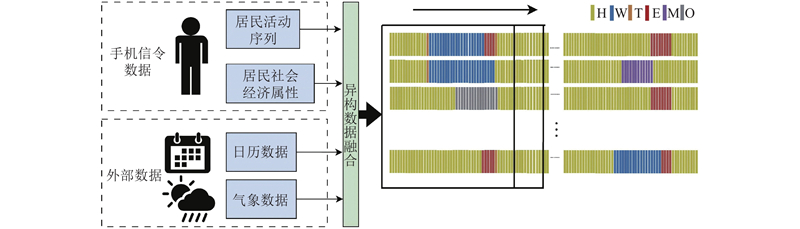
通过对居民典型多日活动模式的识别,进一步丰富了居民多日活动序列中包含的个人出行信息,这与基于活动的非集计模型范式高度契合,为自下而上构建活动需求预测模型奠定了基础. 如图5所示,利用深度学习技术将加工后的手机信令数据和外部数据进行多源异构数据融合,建立居民多日活动序列预测方法,实现个体层面的未来多个时间点的活动预测. 选取TFT模型作为基准模型,与HMM、S2SLSTM、S2SGRU进行对比,验证该方法的有效性.
图 5
图 5 多源数据下活动序列多步预测的示意图
Fig.5 Schematic diagram of multi-step prediction of activity sequence with multi-source data
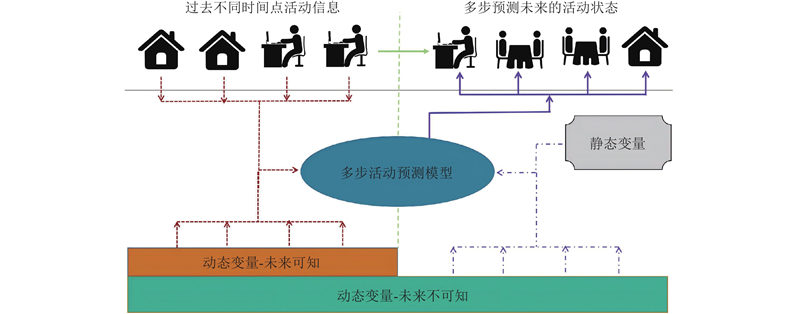
时间融合Transformer(temporal fusion Transformer,TFT)采用多头注意力机制,能够有效捕捉时间序列数据的中长期相关性,有效减小了逐步滚动预测可能导致的误差累积. 与当前大多数“黑箱”式的深度学习架构不同,TFT通过引入变量选择网络评估并量化各输入在预测过程中的重要性,具备一定的解释能力. 与常用的事后解释技术(SHAP)不同,TFT的方法考虑了时间序列数据中各时间步骤的依赖关系,提供了更符合时间序列特征的解释方式. TFT的解码器可以接收未来的已知动态特征,这使得它在预测时能够利用更多的背景信息,而标准Transformer通常只基于过去的信息进行预测. TFT的输出层能够同时预测多个未来时间步的结果. 这与标准Transformer通过迭代生成多步预测的方式相比,更强调多步预测的能力,该模型的活动多步预测功能如图6所示.
图 6
4.1. 基准模型的多步预测
为了全面评估本文扩展的TFT模型在多步分类序列预测任务中的表现,将其与一系列包括传统统计学方法和深度学习方法在内的序列预测模型进行比较. 下列模型都在交通活动序列预测的研究中有着广泛的应用基础,并被证实能够在多种预测任务中提供有效的基准. 为了确保评估的一致性和可比性,所有深度学习模型均采用交叉熵损失函数来训练. 以下是与TFT对比的基准模型简述.
1)HMM:隐马尔可夫模型(hidden Markov model,HMM)是著名的统计模型,用于描述具有隐藏状态的序列. HMM假设系统可以通过一系列不可观察的状态来表达,其中每个状态按照一定的概率产生观测数据,状态转移本身遵循一定的概率模型. 在活动序列预测中,HMM常用于建模序列数据的生成过程以及预测未来活动的概率.
2)S2S-LSTM:基于长短期记忆(long short-term memory,LSTM)网络的序列到序列模型. 该模型具有2层结构,每层含有128个隐藏单元,有效捕捉居民活动数据中的长期依赖关系. S2S-LSTM模型利用其强大的学习能力,深入分析历史活动序列,揭示时间依赖性,从而准确预测活动变化的趋势.
3)S2S-GRU:基于门控循环单元(gated recurrent unit,GRU)的序列到序列模型. 模型采用2层结构,每层含有128个隐藏单元. GRU是LSTM的一个变体,它将遗忘门和输入门合并为更新门,模型结构更简化. GRU在活动序列预测中能够更快地训练,并且在处理短序列时性能不亚于LSTM.
4.2. 实验参数与指标设置
为了保证实验的有效性和减少模型的过拟合风险,采取分层抽样策略,根据居民所属的多日活动模式划分数据:70%用于训练,10%用于验证,20%用于测试. 在模型参数设置方面,选择adam优化器,设定训练轮数为20,学习率为0.001,注意力机制的头数设置为4,隐藏层大小设置为256. 这些参数的设置旨在优化模型性能,保证准确捕捉居民活动序列的特征.
对于每一个时间点的预测是一个多分类问题,在多分类问题中,模型性能的评估通常依赖于精确率P(precision)、召回率R(recall)和F1分(F1 score). 它们共同构成了衡量标准,可以全面地反映模型在预测上的准确性和鲁棒性. 除此之外,选取微平均(micro-averaged)和加权平均(weighted-average)作为全局性能指标,因为它们不仅提供了模型性能的整体评估,而且能够兼顾各类别的不均衡分布. 以F1分数为例,这2个全局指标的计算公式为
式中:
4.3. 实验结果
如表5~7所示为各模型在居民活动序列测试集上的多步预测性能. 其中,Pm、Pw分别为微平均精确率与加权平均精确率,Rm、Rw分别为微平均召回率与加权平均召回率. 本文的分析聚焦于预测居民不同时间点下的活动类型,在所有对比模型中,S2S-GRU和S2S-LSTM这2个深度学习模型在性能上表现突出,它们的复杂网络结构能够有效捕捉居民的复杂非线性时序依赖性. HMM模型的活动预测表现较差,与其他模型相比有明显的差距. 这反映出传统统计模型在处理个体活动的随机性和复杂性时所遇到的困难,尤其是在进行多步预测的情况下. 提出的TFT模型在精确率、召回率和F1分数这几个指标上几乎都优于基准模型,微平均精确率、微平均召回率、微平均F1分数分别达到88%、88%、87%,且在F1分数上较基准模型实现了显著的提升,分别增大了11%、6%、3%. 对于相对有规律的“居家”和“工作”类活动,预测相对容易. 如何准确预测那些在时间上具有高度差异性和随机性的活动(如“娱乐”、“个人维护”、“其他”),一直是基于活动的模型需要攻克的技术难题. TFT模型在这些活动类型上与S2S-GRU相比,F1分数分别提升了31%、27%、21%,精确率分别达到68%、67%、71%. 上述结果表明了TFT模型在大规模居民活动数据集上进行多步预测的可行性,且在融合多源数据挖掘个体层面的居民活动复杂模式方面展现出了强大的能力,体现了该方法的优越性.
表 5 TFT与其他方法在精确率指标上的预测性能比较
Tab.5
| 模型 | P | Pm | Pw | |||||
| 居家 | 工作 | 娱乐 | 个人维护 | 其他 | 出行 | |||
| HMM | 85 | 78 | 25 | 20 | 22 | 12 | 78 | 76 |
| S2SLSTM | 83 | 70 | 48 | 49 | 58 | 35 | 81 | 79 |
| S2SGRU | 86 | 81 | 58 | 58 | 68 | 50 | 84 | 82 |
| TFT | 89 | 81 | 68 | 67 | 71 | 50 | 88 | 85 |
表 6 TFT与其他方法在召回率指标上的预测性能比较
Tab.6
| 模型 | R | Rm | Rw | |||||
| 居家 | 工作 | 娱乐 | 个人维护 | 其他 | 出行 | |||
| HMM | 90 | 83 | 15 | 10 | 12 | 5 | 77 | 77 |
| S2SLSTM | 91 | 78 | 25 | 20 | 38 | 2 | 81 | 81 |
| S2SGRU | 96 | 82 | 18 | 15 | 28 | 10 | 84 | 84 |
| TFT | 96 | 88 | 51 | 41 | 53 | 9 | 88 | 88 |
表 7 TFT与其他方法在F1分数上的预测性能比较
Tab.7
| 模型 | F1 | F1m | F1w | |||||
| 居家 | 工作 | 娱乐 | 个人维护 | 其他 | 出行 | |||
| HMM | 87 | 80 | 19 | 13 | 16 | 7 | 76 | 76 |
| S2SLSTM | 87 | 74 | 33 | 28 | 46 | 4 | 81 | 79 |
| S2SGRU | 91 | 82 | 27 | 24 | 40 | 16 | 84 | 81 |
| TFT | 93 | 84 | 58 | 51 | 61 | 15 | 87 | 86 |
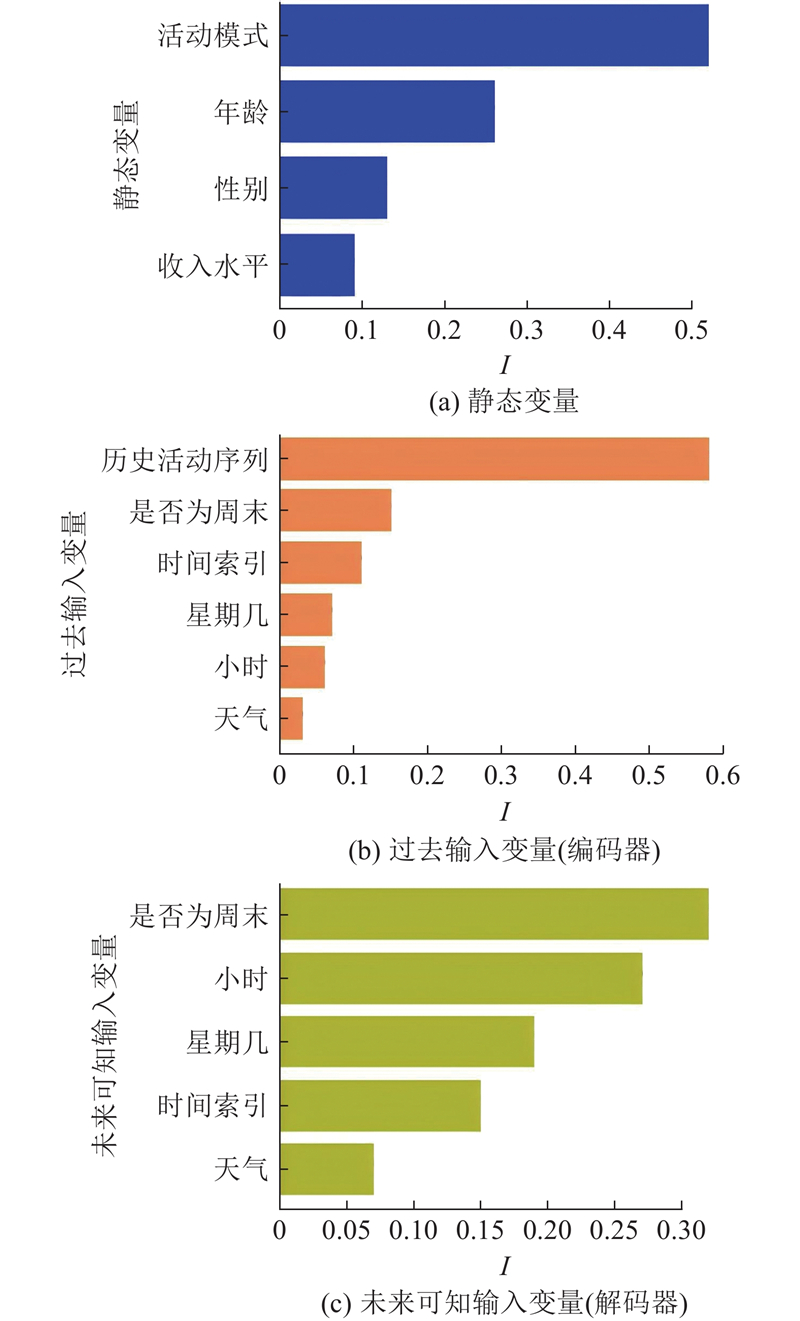
TFT模型的一个显著优势是通过对内部参数的分析,实现了较高的可解释性. 在TFT模型中,变量被分为3类,包括静态变量、动态过去可知但未来不可知的变量(编码器变量)和动态未来可知的变量(解码器变量),每类分别通过独立的变量选择网络估计变量的权重. 图7中,I为相对重要性. 如图7(a)所示,在静态变量中,居民所属的典型活动模式是相对最重要的变量,达到0.52;其次是居民的年龄,收入水平和性别的影响相对较小. 如图7(b)所示,在过去输入中,历史活动序列的重要性最高,达到0.59,这表明模型主要依赖于历史活动来预测后续活动的变化,说明居民活动具有很强的历史规律性,其次重要的特征是活动是否发生在周末. 如图7(c)所示,在未来可知的输入中,活动是否在周末发生以及活动的具体时间段是相对重要的因素.
图 7
综上所述,TFT模型通过变量选择网络提取的变量相对重要性不仅直观,而且对不同类型的数据进行了区分,有效地突出了各类数据的重要性. 模型特征重要性分析结果表明,居民的历史活动序列、所属的活动模式和是否为周末是重要变量.
5. 结 论
(1)采用聚类框架nTreeClus,解决居民多日活动序列相似性判断的难题,有效地识别出6种典型的多日活动模式,分别为自由灵活型、工作-周末活动型、常规工作型、工作-娱乐型、工作-加班型、娱乐休闲型.
(2)扩展的TFT模型在活动序列预测中全面优于基准模型,微平均精确率、召回率、F1分数分别达到88%、88%、87%. 其中,娱乐、个人维护活动的F1分数较基准模型提升超过20%. 特征重要性分析表明,“居民所属的活动模式”、“历史活动序列”和“是否为周末”是影响预测结果的关键因子.
综上,利用提出的基于多源信息、nTreeClus框架和扩展TFT模型的预测方法,显著提升了个体活动多步预测的精度,对实现城市交通智能化管理具有重要的意义. 精准的个体出行预测能够辅助交通规划,优化公共交通服务,为城市基础设施建设提供数据支持. 未来研究可以尝试在更大规模数据或不同时间尺度上进行,并将预测任务扩展至预测活动地点与出行方式.
参考文献
Real-time trip purpose prediction using online location-based search and discovery services
[J].
Machine learning for activity pattern detection
[J].DOI:10.1080/15472450.2022.2084336
Multi-day activity pattern recognition based on semantic embeddings of activity chains
[J].
Origin–destination trips by purpose and time of day inferred from mobile phone data
[J].
TripImputor: real-time imputing taxi trip purpose leveraging multisourced urban data
[J].DOI:10.1109/TITS.2017.2771231 [本文引用: 1]
Discover trip purposes from cellular network data with topic modeling
[J].
Trip purposes mining from mobile signaling data
[J].
Resident activity pattern recognition and comparison of six Sino-American metropolises
[J].DOI:10.1049/iet-its.2018.5246 [本文引用: 1]
Reconstructing human activities via coupling mobile phone data with location-based social networks
[J].
Inferring patterns in the multi-week activity sequences of public transport users
[J].
From edit distance to augmented space-time-weighted edit distance: detecting and clustering patterns of human activities in Puget Sound region
[J].
nTreeClus: a tree-based sequence encoder for clustering categorical series
[J].
Enhancing transportation systems via deep learning: a survey
[J].
Recurrent neural networks and robust time series prediction
[J].DOI:10.1109/72.279188 [本文引用: 1]
Long short-term memory
[J].DOI:10.1162/neco.1997.9.8.1735
基于深度注意力模型的个体出行多步预测研究
[J].
Multi-step prediction of individual travel based on deep attention model
[J].
Temporal fusion transformers for interpretable multi-horizon time series forecasting
[J].DOI:10.1016/j.ijforecast.2021.03.012 [本文引用: 1]
基于多源数据融合的高速公路路网短时交通流参数实时预测
[J].
Real-time prediction of short-term traffic flow parameters in expressway network based on multi-source data fusion
[J].
DeepPF: a deep learning based architecture for metro passenger flow prediction
[J].
Detecting home and work locations from mobile phone cellular signaling data
[J].
Fusing mobile phone and travel survey data to model urban activity dynamics
[J].