常见的优化策略是利用多元回归模型拟合目标函数,再应用优化算法进行求解. 回归模型通常是在静态数据上训练的,参数和结构保持不变. 这种静态特性会导致动态数据中模型参数和结构的调整无效,影响模型的整体性能和稳定性. 本研究提出改进的麻雀搜索算法优化BP模型(ISSA-BP),作为多目标优化的适应度预测函数. ISSA-BP能够在动态环境中实时处理数据,通过不断更新模型来适应新的数据模式,可以为建立更准确、更稳定的预测模型提供有效的途径,从而更好地解决自适应动态优化问题.
1. 实验简介
1.1. 加工装置
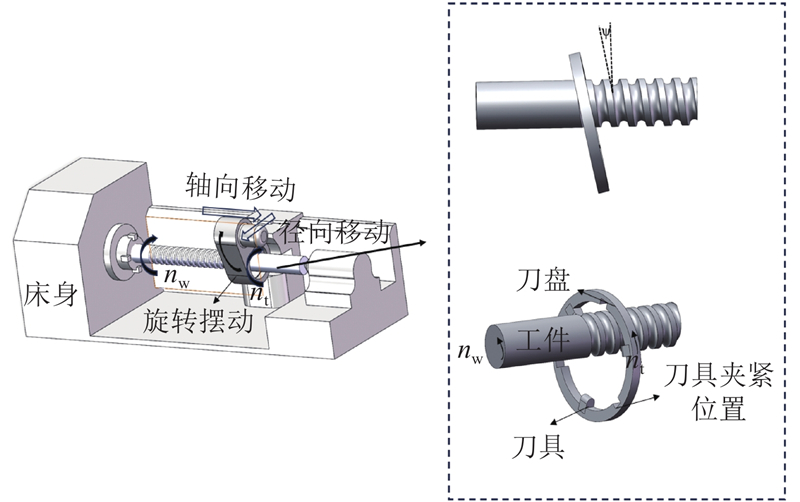
实验在数控旋风铣削加工中心(型号“HJ092X80”,汉江机床有限公司)中进行. 螺纹干式旋铣通过安装在刀盘上的多个刀具对螺纹工件进行渐进和间歇切削. 螺纹工件的间歇切削涉及4个运动过程:刀具轴向进给运动、刀具径向平移运动、刀盘旋转运动和工件旋转运动. 丝杠旋铣加工的示意图如图1所示.
图 1
1.2. 测量装置
将切削速度Vt、最大切削深度Ma、刀具个数N作为丝杠加工质量的主要影响因素. 切削力(切向Ft、径向Fr、轴向Fa)由压电传感器Kistler 9602A测量,经NI cDAQ-9189采集箱与NI-
式中:
式中:av为振动信号,
图 2
图 3
具体的实验方案与结果如表1所示.其中,Ra为粗糙度.
表 1 单因素实验方案和结果
Tab.1
| 序号 | Vt/ (m·min−1) | Ma/ mm | N | Fmax/ N | av/g | Ra/ nm | σr/ MPa |
| A1 | 60 | 0.06 | 3 | 164 | 0.471 | 143.6 | 308 |
| A2 | 100 | 0.06 | 3 | 146 | 0.441 | 132.8 | 250 |
| A3 | 140 | 0.06 | 3 | 154 | 0.388 | 107.8 | 400 |
| A4 | 180 | 0.06 | 3 | 122 | 0.393 | 116.5 | 455 |
| B1 | 140 | 0.04 | 3 | 75 | 0.395 | 117.6 | 92 |
| B2 | 140 | 0.06 | 3 | 154 | 0.388 | 107.8 | 400 |
| B3 | 140 | 0.08 | 3 | 193 | 0.378 | 126.8 | 370 |
| B4 | 140 | 0.10 | 3 | 216 | 0.374 | 204.6 | 415 |
| C1 | 140 | 0.06 | 2 | 180 | 0.359 | 109.8 | 410 |
| C2 | 140 | 0.06 | 3 | 154 | 0.388 | 107.8 | 400 |
| C3 | 140 | 0.06 | 4 | 161 | 0.413 | 92.3 | 329 |
| C4 | 140 | 0.06 | 6 | 130 | 0.494 | 81.7 | 260 |
表 2 基于单因素实验的样条插值参数及结果
Tab.2
| 序号 | Vt/ (m·min−1) | Ma/ mm | N | Fmax / N | av/g | Ra/ nm | σr/ MPa |
| 1 | 60 | 0.06 | 3 | 164 | 0.471 | 143.6 | 308 |
| 2 | 80 | 0.06 | 3 | 148 | 0.464 | 142.9 | 235 |
| 3 | 100 | 0.06 | 3 | 146 | 0.441 | 132.8 | 250 |
| 4 | 120 | 0.06 | 3 | 151 | 0.412 | 119.1 | 316 |
| 5 | 140 | 0.06 | 3 | 154 | 0.388 | 107.8 | 400 |
| 6 | 160 | 0.06 | 3 | 147 | 0.378 | 104.9 | 453 |
| 7 | 180 | 0.06 | 3 | 122 | 0.393 | 116.5 | 455 |
| 8 | 140 | 0.04 | 3 | 75 | 0.395 | 117.6 | 92 |
| 9 | 140 | 0.05 | 3 | 121 | 0.392 | 111.0 | 326 |
| 10 | 140 | 0.06 | 3 | 154 | 0.388 | 107.8 | 400 |
| 11 | 140 | 0.07 | 3 | 177 | 0.383 | 111.8 | 373 |
| 12 | 140 | 0.08 | 3 | 193 | 0.378 | 126.8 | 370 |
| 13 | 140 | 0.09 | 3 | 205 | 0.375 | 156.5 | 306 |
| 14 | 140 | 0.1 | 3 | 216 | 0.374 | 204.0 | 415 |
| 15 | 140 | 0.06 | 2 | 180 | 0.359 | 109.8 | 410 |
| 16 | 140 | 0.06 | 2.5 | 159 | 0.375 | 112.7 | 325 |
| 17 | 140 | 0.06 | 3 | 154 | 0.388 | 107.8 | 400 |
| 18 | 140 | 0.06 | 3.5 | 160 | 0.4 | 97.9 | 387 |
| 19 | 140 | 0.06 | 4 | 161 | 0.413 | 92.3 | 329 |
| 20 | 140 | 0.06 | 5 | 179 | 0.445 | 69.5 | 198 |
| 21 | 140 | 0.06 | 6 | 130 | 0.494 | 81.7 | 260 |
2. 建模方法
2.1. 麻雀搜索算法
式中:
追随者的位置更新由下式给出:
式中:
警戒者的位置更新表达如下:
式中:
2.2. 改进的麻雀搜索算法 (ISSA)
表 3 几种常见的混沌映射
Tab.3
| 映射名称 | 映射公式 | 映射范围 |
| Logistic | [0,1.0] | |
| Circle | [0,1.0] | |
| Sine | [0,1.0] | |
| Singer | [0,1.0] | |
| Cubic | [0,1.0] |
图 4
2.3. ISSA-BP预测模型的建立
SSA对BP神经网络的权值和阈值进行优化,优化后的神经网络模型具有更好的预测性能. 通过Cubic混沌映射改进的SSA具有更好的全局搜索能力和稳定性,因此利用建立的ISSA-BP,可以更好地提高模型的预测精度.
由于样本中每个维度的数据存在显著差异,必须对原始数据进行归一化,以减轻维度变化的影响. 归一化公式为
式中:
在所需样本较少的情况下,采用单隐藏层的BP神经网络对各个响应进行预测. 采用试凑法,利用下式确定隐藏层神经元数的范围:
式中:
以切削速度、最大切削深度、刀具个数为输入,切削力、振动、粗糙度及残余压应力为输出,构建BP网络. 输入层节点数m为3,单个输出的输出层节点数n为1,所以隐藏层节点数为3~12. 遍历节点数,选择归一化训练数据的最小均方误差对应值作为最佳节点数,得到各模型的隐含层节点数为9、8、4、6. 设训练目标误差为0.000 1,学习效率为0.01,训练次数为1 000,隐含层用tansig函数,输出层用purelin函数,通过trainlm函数训练.
在模型评估时,使用平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)和R2作为所建立的ISSA-BP的评价指标,判断所建立预测模型的预测精度. 各个公式表示如下:
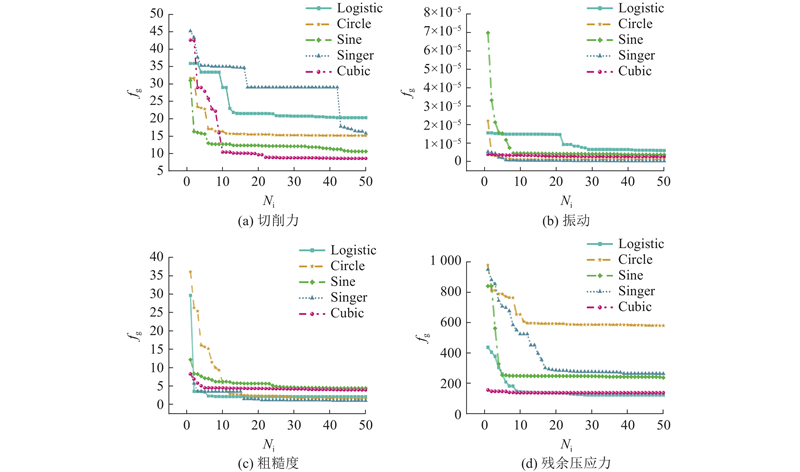
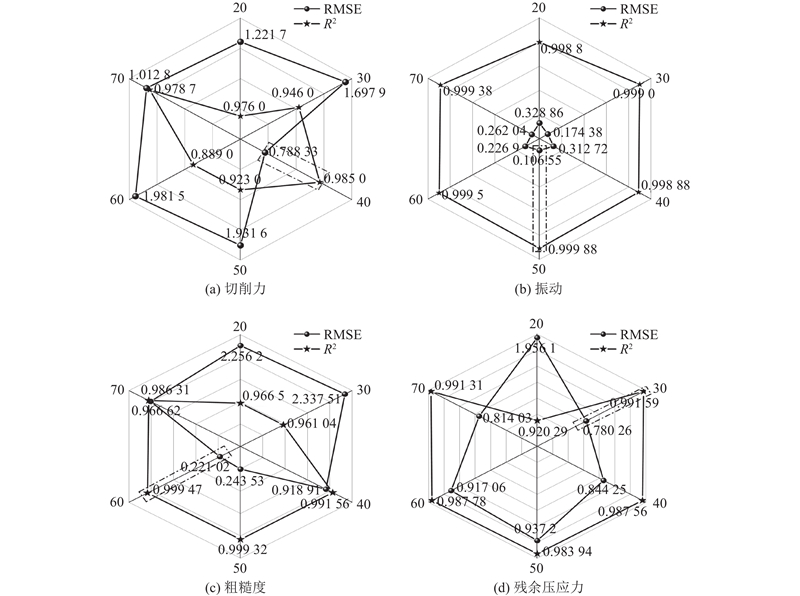
在麻雀搜索算法的参数设置中,种群数量对算法的影响较大. 若种群较小,则会导致收敛过快,从而产生局部最优的结果;若种群过大,则收敛较慢,导致迭代次数增加,从而增大了计算的复杂度. 针对不同的种群数量进行试验,观察每次试验中算法预测性能指标的变化,通过对比分析来确定最适合的种群数量. 种群对麻雀搜索算法的影响结果如图5所示. 将RMSE与R2作为ISSA-BP预测精度的评价指标,为了追求较低的RMSE及较高的R2,获得更好的预测精度,所建立的4个ISSA-BP模型的麻雀种群数分别为40、50、60、30.
图 5
目前,没有通用的方法来确定搜索者和警戒者之间的比例. 为了找到最优比例,搜索者和警戒者在一定范围内进行调整和搜索.
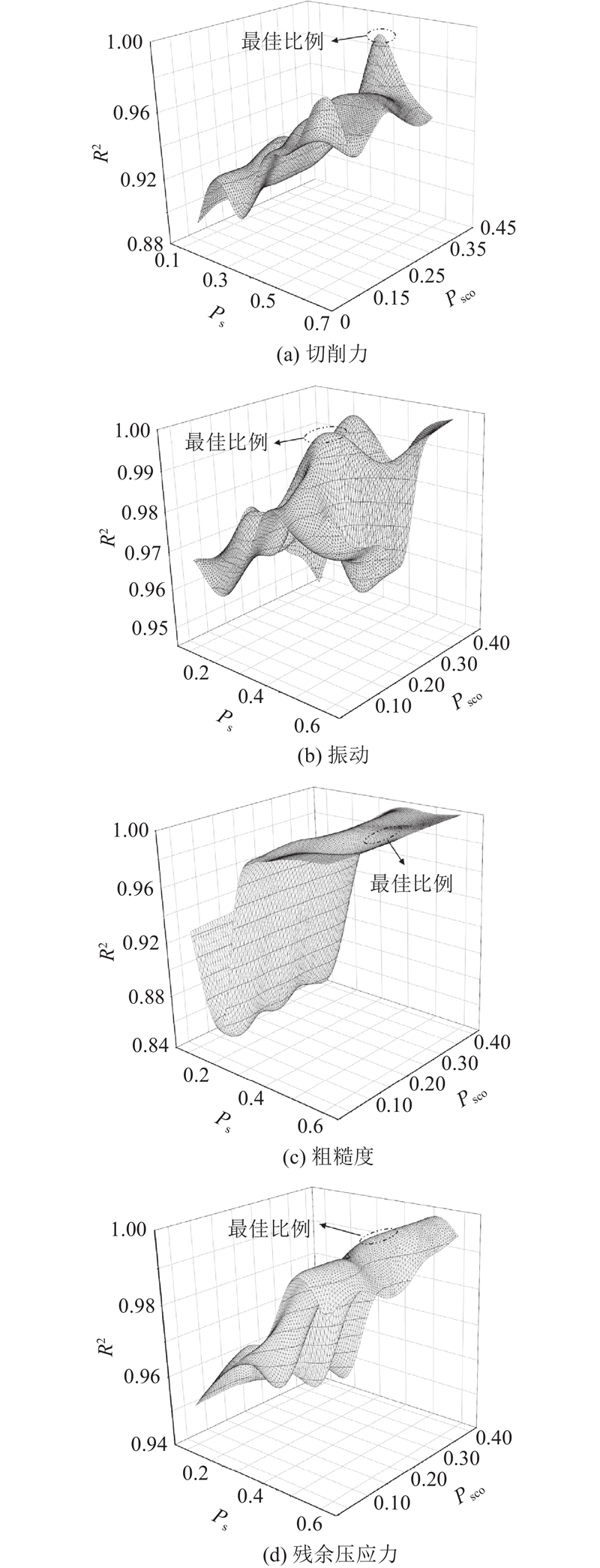
如图6所示,在建立的切削力模型中,当搜索者设置的比例Ps为0.30~0.40,警戒者比例Psco为0.35~0.40时,建立的模型预测性能更好. 在建立的振动预测模型中,搜索者的最优比例为0.30~0.35,警戒者的最优比例为0.20~0.25. 在粗糙度预测模型中,当搜索者比例为0.50~0.55,警戒者比例为0.25~0.30时,该模型显示出更好的性能. 在残余压应力预测模型中,当搜索者比例为0.40~0.45,警戒者比例为0.25~0.30时表现出更好的预测性能. 将混沌映射添加到已建立的模型中,完成最终的模型.
图 6
图 6 各种搜索者与警戒者比例的模型预测性能
Fig.6 Model prediction performance for percentage of various searchers and scouters
3. 结果与讨论
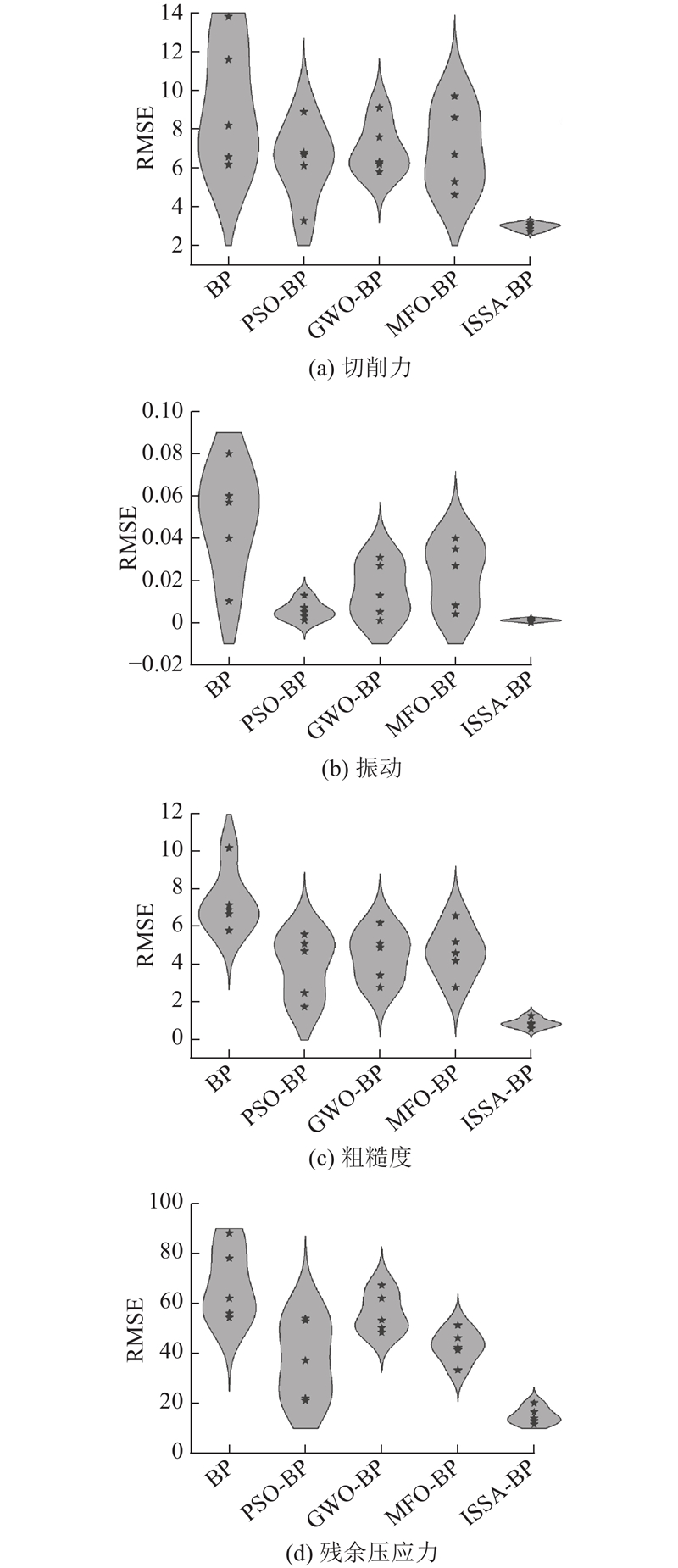
图 7
图 7 5种算法在4个指标上的RMSE对比小提琴图
Fig.7 Violin plots comparing RMSE of five algorithms across four indicators
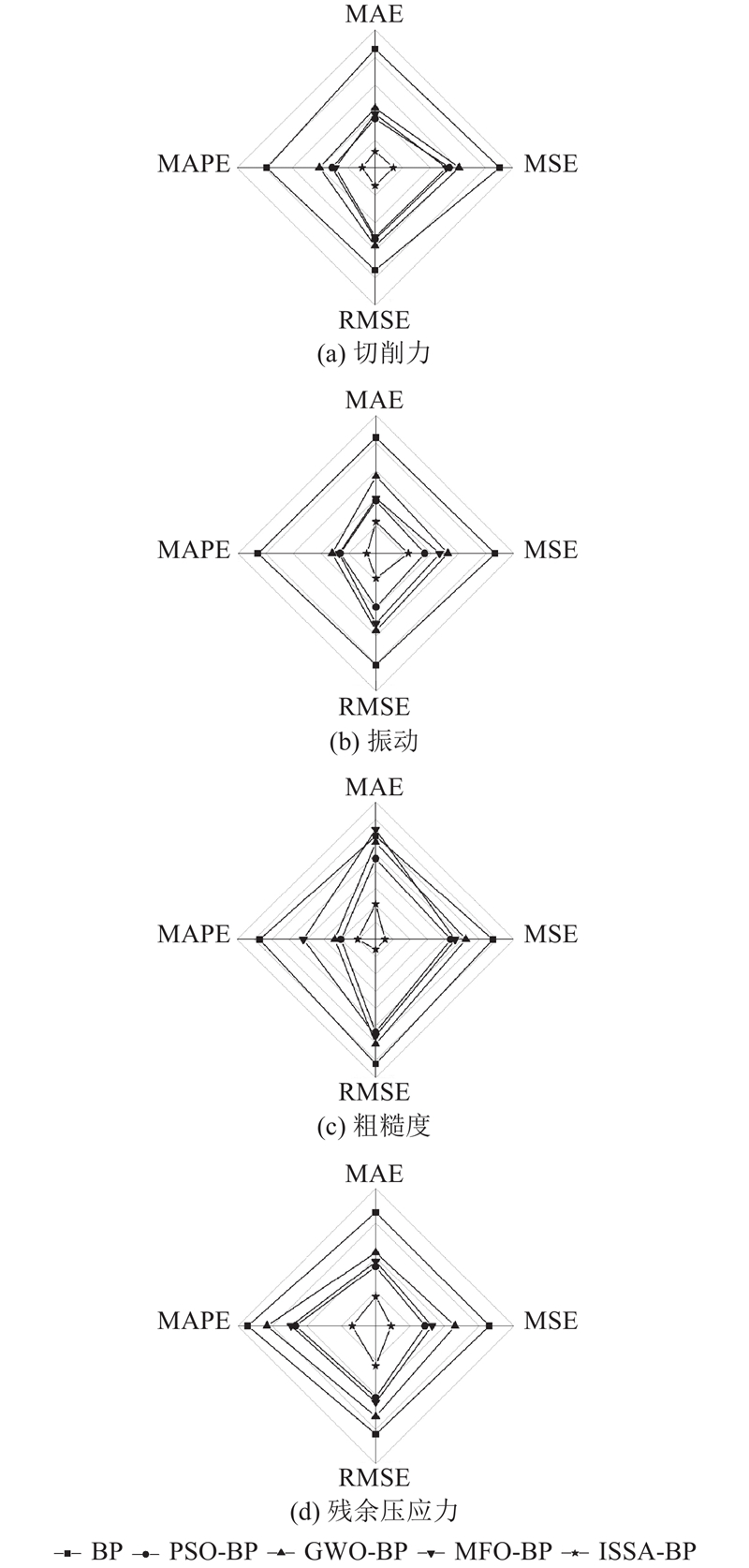
从图8可以看出,在建立的预测模型中,ISSA-BP模型在MAE、MSE、RMSE、MAPE方面表现出优异的预测性能.
图 8
图 8 5种算法模型在4项性能评估标准下的性能比较
Fig.8 Performance comparison of five algorithmic models under four performance evaluation standards
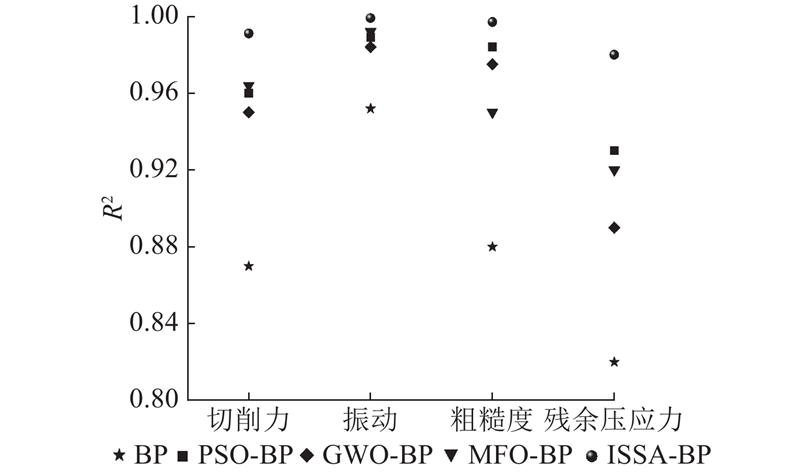
图 9
表 4 5种算法模型在4个指标上的性能对比
Tab.4
| 算法 | F/N | 算法 | av/g | |||||||||
| MAE | MSE | RMSE | MAPE | R2 | MAE | MSE | RMSE | MAPE | R2 | |||
| BP | 8.62 | 63.2 | 7.95 | 6.28 | 0.870 | BP | 6.63×10−5 | 1.54 | 0.952 | |||
| ISSA-BP | 1.19 | 9.26 | 3.04 | 0.74 | 0.991 | ISSA-BP | 3.42×10−6 | 0.12 | 0.999 | |||
| PSO-BP | 3.55 | 37.8 | 6.15 | 2.49 | 0.960 | PSO-BP | 1.54×10−5 | 0.469 | 0.989 | |||
| GWO-BP | 4.33 | 42.6 | 6.53 | 3.22 | 0.950 | GWO-BP | 3.20×10−5 | 0.57 | 0.984 | |||
| MFO-BP | 3.89 | 36.2 | 6.02 | 2.3 | 0.964 | MFO-BP | 2.61×10−5 | 0.48 | 0.992 | |||
| 算法 | Ra/nm | 算法 | ||||||||||
| MAE | MSE | RMSE | MAPE | R2 | MAE | MSE | RMSE | MAPE | R2 | |||
| BP | 3.01 | 21.17 | 4.60 | 6.70 | 0.880 | BP | 33.10 | 986.5 | 31.4 | 9.28 | 0.82 | |
| ISSA-BP | 1.03 | 1.68 | 1.29 | 1.03 | 0.997 | ISSA-BP | 8.50 | 133.2 | 11.54 | 1.71 | 0.98 | |
| PSO-BP | 2.35 | 13.56 | 3.68 | 2.00 | 0.984 | PSO-BP | 17.34 | 429.7 | 20.73 | 5.81 | 0.93 | |
| GWO-BP | 2.83 | 16.28 | 4.03 | 2.36 | 0.975 | GWO-BP | 21.46 | 689.6 | 26.25 | 7.89 | 0.89 | |
| MFO-BP | 3.20 | 14.33 | 3.79 | 4.17 | 0.950 | MFO-BP | 18.81 | 488.6 | 22.1 | 6.14 | 0.92 | |
4. 多目标优化
4.1. NSGA-III优化算法
式中:
设定的优化目标如下:最小化切削力、振动和粗糙度,最大化残余压应力. 每个决策变量都在下限和上限内,因此对切削速度、最大切削深度和刀具数量的约束范围如下:60 m/min ≤ x(1)≤ 140 m/min,0.04 mm ≤ x(2) ≤ 0.10 mm,2 ≤ x(3) ≤ 6.
4.2. 多目标优化过程
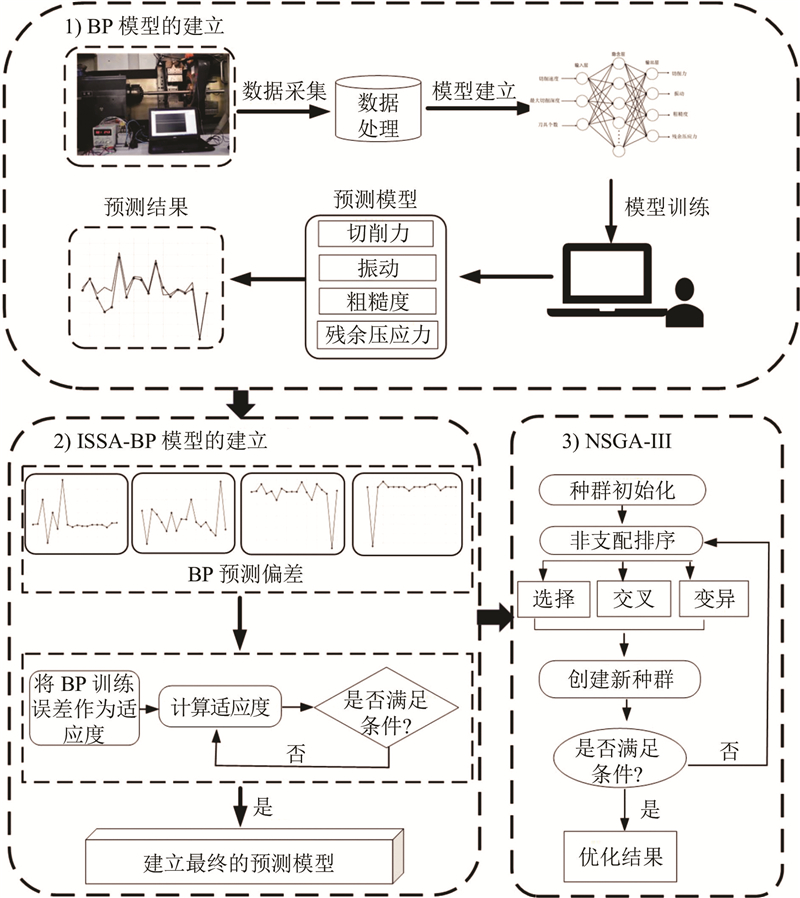
利用改进麻雀搜索算法优化 BP,建立加工参数与切削力、振动、粗糙度、残余压应力的非线性映射,得到高精度预测模型. 采用统一目标法和多目标进化算法优化,将统一评价函数作为适应度函数,引入 NSGA-III,对丝杠旋铣指标进行多目标优化,优化过程如图10所示.
图 10
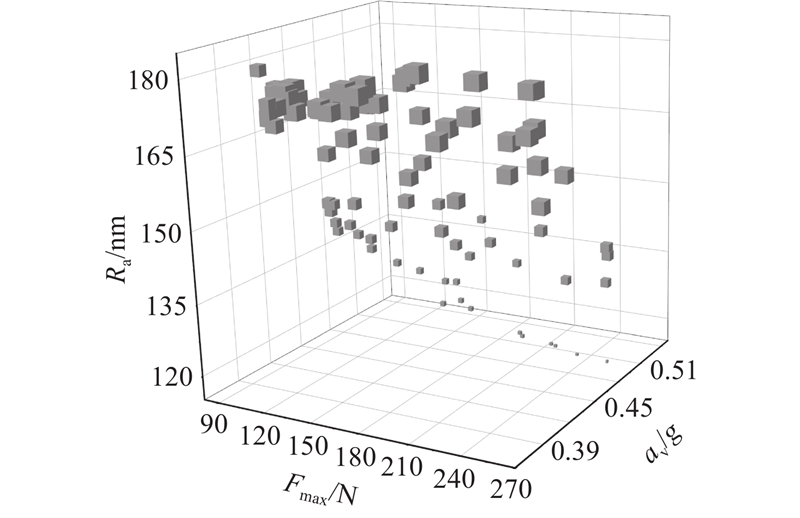
使用MATLAB 2020b,求解丝杠旋铣的多目标优化问题. 图11中,残余压应力用方块的大小表示. 可以看出,粗糙度及残余压应力之间存在权衡取舍. 当切削力增大时,工件的粗糙度呈下降趋势,这说明切削力和粗糙度是相互依存和相互关联的因素.
图 11
如表5所示为帕累托最优解集. 在丝杠加工中,每个性能指标本质上都是相互冲突的,而在帕累托最优解集中,没有一种解优于其他解,因此任何解都是可接受的解. 工艺规划人员可以根据要求在最优的解决方案集中做出合理的决策.
表 5 Pareto解集
Tab.5
| Vt/ (m·min-1) | Ma/ mm | N | Fmax/ N | av/ g | Ra/ nm | σr/ MPa |
| 140 | 0.087 | 5.4 | 161.3 | 176.8 | 619 | |
| 140 | 0.066 | 5.4 | 89.8 | 175.7 | 238 | |
| 140 | 0.075 | 4.2 | 115.6 | 174.3 | 566 | |
| 116.7 | 0.071 | 3.2 | 131.0 | 0.428 | 148.6 | 318 |
| 101 | 0.090 | 5.1 | 203.22 | 0.504 | 172.2 | 598 |
| 101 | 0.090 | 5.3 | 193.0 | 0.508 | 174.3 | 601 |
| 140 | 0.066 | 3.0 | 108.9 | 0.388 | 166.8 | 388 |
| 130.8 | 0.074 | 4.0 | 119.9 | 0.425 | 170.7 | 537 |
| 123.5 | 0.077 | 2.9 | 135.0 | 160.1 | 272 | |
| 114.5 | 0.091 | 4.5 | 195.1 | 0.499 | 171.1 | 592 |
| 97.3 | 0.098 | 5.9 | 192.5 | 0.470 | 175.4 | 599 |
| 134.9 | 0.072 | 4.1 | 110.6 | 0.417 | 172.0 | 533 |
| 116.4 | 0.066 | 3.1 | 124.5 | 0.424 | 148.3 | 313 |
| 127.1 | 0.066 | 3.4 | 113.6 | 0.416 | 157.7 | 406 |
| 140 | 0.080 | 2.9 | 147.1 | 0.373 | 206.8 | 339 |
| 106.5 | 0.078 | 3.0 | 156.6 | 0.443 | 137.1 | 200 |
| 105 | 0.080 | 3.5 | 185.7 | 0.480 | 144.2 | 362 |
| 97.6 | 0.098 | 3.5 | 240.3 | 0.505 | 132.3 | 303 |
| 116.8 | 0.100 | 3.7 | 232.9 | 0.459 | 153.9 | 485 |
| 114.5 | 0.085 | 3.7 | 178.8 | 154.8 | 479 |
5. 结 语
本研究采用改进的麻雀搜索算法与 NSGA-III 相结合的方法,开展多目标优化研究. 通过对比Logistic、Circle、Sine、Singer和Cubic 5种混沌映射改进策略,确定Cubic混沌映射为最优方案. 探究种群规模及搜索者与警戒者比例对ISSA-BP模型预测性能的影响. 结果表明,针对切削力、振动、粗糙度及残余压应力模型,最优的种群规模分别为40、50、60和30,确定各模型对应的最优的搜索者与警戒者比例. 性能对比分析显示,ISSA-BP模型在关键评价指标上均显著优于BP、PSO-BP、GWO-BP和MFO-BP 4种对比算法. 结合该模型与NSGA-III,得到Pareto解集,揭示了加工性能指标间的内在联系,如粗糙度和残余压应力近似成反比,切削力与粗糙度相互依存.
后续研究将从以下方面展开,采用正交实验设计,增加实验组数与参数的组合范围,考察各参数间的交互作用对预测模型的影响. 对现有的优化算法进行改进,提升预测精度和多目标优化的效率. 此外,引入其他多种加工场景的案例研究,得到更具普适性与实用性的优化方案,完成对最优解的有效验证.
参考文献
基于滚珠丝杠副滚珠载荷分布的摩擦力矩计算方法研究
[J].
Research on calculation method of friction moment based on ball load distribution of ball screw pair
[J].
平面滚珠丝杠副多结合面建模与动态特性分析
[J].
Modeling and dynamic characteristics analysis of multiple joint surfaces in flat ball screw pairs
[J].
基于滚珠丝杠传动的机床进给系统建模与分析
[J].DOI:10.3969/j.issn.1001-3881.2023.13.027 [本文引用: 1]
Modeling and analysis of machine tool feed system based on ball screw transmission
[J].DOI:10.3969/j.issn.1001-3881.2023.13.027 [本文引用: 1]
Predicting residual properties of ball screw raceway in whirling milling based on machine learning
[J].
Dry machining: machining of the future
[J].
AlCrBSiN复合涂层制备及高速干式切削性能
[J].
Deposition and high-speed dry cutting performance of AlCrBSiN-coated cutters
[J].
基于斜角切削理论的钛合金螺旋铣孔切削力建模
[J].
Modeling of cutting force for titanium alloy spiral milling holes based on oblique cutting theory
[J].
The fundamental roughness model for face-milling spiral bevel gears considering run-outs
[J].
In-process detection of cutting forces and cutting temperature signals in cryogenic assisted turning of titanium alloys: an analytical approach and experimental study
[J].
FE temperature and residual stress prediction in milling inserts and correlation with experimentally observed damage mechanisms
[J].
运用响应面法的Ti-6Al-4VELI钛合金铣削表面粗糙度预测模型
[J].
Prediction model for surface roughness of Ti-6Al-4V ELI titanium alloy milling using response surface methodology
[J].
A novel model considering combined effects of as-built roughness and notch for multiaxial fatigue life prediction of L-PBF Ti6Al4V
[J].
Multi-objective optimization of high-power fiber laser cutting process using data augmentation-based ANN-Adam model
[J].
Optimizing process parameters of in-situ laser assisted cutting of glass–ceramic by applying hybrid machine learning models
[J].
Integrated multi-objective optimization of rough and finish cutting parameters in plane milling for sustainable machining considering efficiency, energy, and quality
[J].
Multi-objective optimization of fiber laser cutting based on generalized regression neural network and non-dominated sorting genetic algorithm
[J].
Investigation of cutting temperature, cutting force and surface roughness using multi-objective optimization for turning of Ti-6Al-4 V (ELI)
[J].
Multi-objective optimization of milling parameters: the trade-offs between energy, production rate and cutting quality
[J].
Multi-objective optimization of cutting parameters during laser cutting of titanium alloy sheet using hybrid approach of genetic algorithm and multiple regression analysis
[J].DOI:10.1016/j.matpr.2018.10.269 [本文引用: 1]
A novel swarm intelligence optimization approach: sparrow search algorithm
[J].DOI:10.1080/21642583.2019.1708830 [本文引用: 1]
基于混沌的多策略优化麻雀算法及应用
[J].
Chaos based multi strategy optimization sparrow algorithm and its application
[J].
Trajectory control of electro-hydraulic position servo system using improved PSO-PID controller
[J].
Parameters optimization for single-track laser cladding based on MPA-SVR and A-NSGA-III
[J].
Parametric optimization of electric discharge machining of Ni Ti based shape memory alloy using NSGA II with TOPSIS55.65
[J].
An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part I: solving problems with box constraints
[J].DOI:10.1109/TEVC.2013.2281535 [本文引用: 1]