许多学者在高岩温隧道工程背景下开展了相关研究. 在高岩温隧道的温度场和初始地应力方面,赵志宏等[3]结合现场地质资料和稳态法地热研究数值模型,对川藏铁路折多山隧道温度场与热害进行初步预测,定义原始围岩温度大于50 ℃为Ⅳ级热害. 蒙伟等[4]考虑地温梯度计算岩体热应力,算得桑珠岭闪长岩隧址区岩体温度应力约为自重应力的61%,温度应力的影响不可忽视. 王才进等[5-6]深入研究岩土的导热系数,力求准确构建温度场. 高岩温隧道除了岩体出现热害以外,衬砌支护结构也会出现不同程度的劣化损坏. 王明年等[7]通过现场温度测试研究在高岩温施工过程中围岩、初支和二衬的温度变化规律,现场数据表明喷射混凝土与围岩界面最大温差近30 ℃,二衬结构温度在施工通风后虽然大幅度降低至35.5 ℃,但仍未降低至正常施工温度. 在高岩温隧道建设时期,高温通过围岩传递给衬砌,使得混凝土衬砌在不同时期均有开裂风险. 博金阳等[8]进一步揭示,高温导致混凝土水化热积聚,高地温段衬砌早期开裂风险提高,衬砌混凝土强度合格率为88%. 孙其清等[9]通过数值模拟计算发现,二衬结构安全系数在地温超过50 ℃时显著下降,超过60 ℃将不满足设计规范要求. 还有学者分析了结构或岩土的接触热阻和应力. 吴梦军等[10]提出钢-混凝土界面接触热阻确定及其等效模拟方法,确定火灾高温对钢-混凝土结构影响深度约为400 mm. 刘江等[11]考虑非线性温度分布,提出温度作用下钢-混组合梁界面滑移的挠度影响系数. Wen等[12]考虑双层饱和孔隙地层接触面间接触热阻的影响,接触热阻导致双层饱和孔隙地层间热应力偏差约25%. 张涛等[13]讨论了土体微界面接触热阻对热导率的影响,建立干砂颗粒形貌特征参数的热导率模型.
以上研究通过导热系数、比热容、热扩散系数等热物性质研究高岩温隧道温度场,分析了温度应力对隧道围岩或衬砌的不利影响,未充分考虑围岩与衬砌间微观结构在接触面上产生的附加热阻,围岩与衬砌界间接触热阻将进一步导致围岩-衬砌传热特性的非连续、非均质与整体各向异性特征. 现有结构接触热阻研究多以钢-混凝土为对象,现有岩土接触热阻研究未考虑围岩与衬砌界面接触热阻对围岩与衬砌温度分布的影响. 围岩岩性对围岩导热性能的影响不可忽视,不同岩性下围岩质量与完整性均会对界面接触热阻产生影响. 本研究考虑围岩岩性,根据岩体基本质量指标,提出热阻抗评价系数,用以评价围岩岩性对界面接触热阻的影响程度;采用数值模拟及室内实验方法,对考虑围岩岩性影响的高岩温隧道围岩-衬砌界面接触热阻计算方法进行验证.
1. 围岩-衬砌界面接触热阻计算方法
1.1. 接触模型
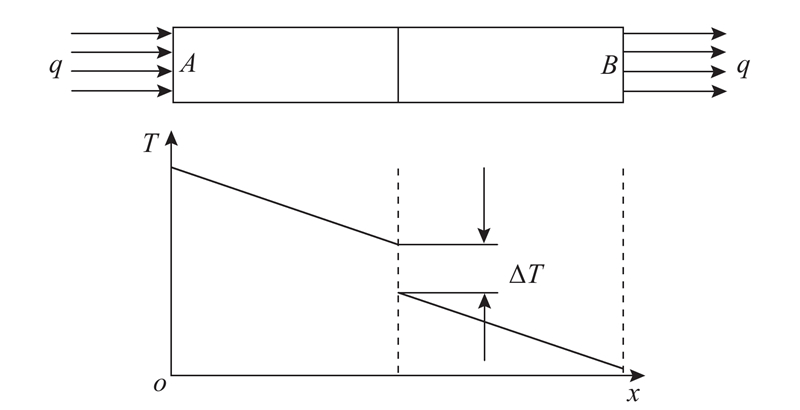
围岩与衬砌的实际接触面积仅占名义接触面积的一部分. 从微观上看,二者间的接触实际只发生在某些单独的点或面上,其余未接触的间隙由空气或其他介质填充,这使得热传递与理想状态(完全接触)相比存在损失,相当于热量的传递被附加了额外的阻力,称之为界面接触热阻. 如图1所示,界面接触热阻的影响主要表现为接触界面存在温度差∆T,即温度的跃变现象. 根据接触热阻的定义,界面接触热阻的计算式为
图 1
式中:q为通过两界面法向的热流密度,λ为导热系数, dT为热流方向上模型两端(A-B)的温差,dx为热流方向经过长度.
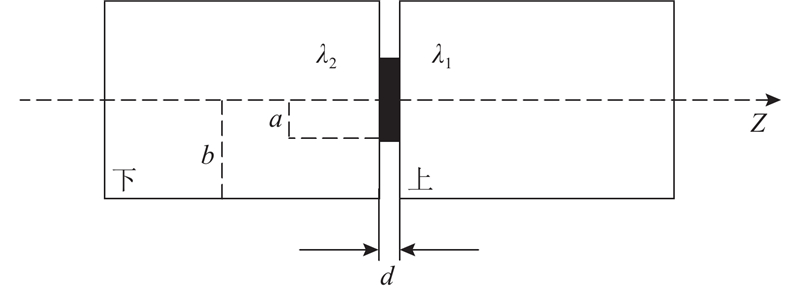
高温隧道中的高温涌水现象对隧道热环境的影响不可忽视. 高地温隧道热害分为干热型和水热型,为了简化计算与模型处理,本研究针对干热型隧道进行. 围岩与衬砌的实际接触界面在微观上由随机分布的凸峰与凹谷组成,表面接触问题较为复杂,因此使用简化接触问题的界面接触热阻模型开展接触热阻研究,本研究采用圆盘模型. 将圆盘模型的接触部分理想化为上下2个圆柱体,两者通过半径小于圆柱体的圆盘接触,其中a为圆盘半径,b为圆柱体半径,d为2个圆柱体的间隙高度,λ为导热系数,如图2所示.
图 2
1.2. 接触热阻的影响因素
式中:As为实际接触面积,A为名义接触面积,HL为相接触物体中较软物体的强度,p为接触界面的压力. 3)在高岩温隧道中,围岩等级是影响围岩-衬砌界面接触热阻的重要因素. 围岩等级由围岩岩性和围岩质量决定.
1.3. 接触界面等效导热系数
表 1 岩石导热系数
Tab.1
| 岩石种类 | λ/(W·m−1∙K−1) | 岩石种类 | λ/(W·m−1∙K−1) | |
| 玄武岩 | 1.16~4.71 | 砂岩 | 1.32~5.25 | |
| 页岩 | 1.80~4.15 | 泥岩 | 1.22~2.22 | |
| 花岗岩 | 2.63~3.55 | — | — |
在计算围岩与衬砌间的界面接触热阻时,须确定接触表面的等效导热系数λs,该系数由围岩的导热系数λr与隧道衬砌的导热系数λc得出,计算式为
1.4. 计算方法
本研究提出考虑隧道围岩岩性影响的围岩-衬砌间界面接触热阻计算方法. 质量较差、破碎松散的围岩不仅会影响隧道的安全性,其松散程度还会影响围岩的导热性能. 岩体松散程度越高,微裂纹与微孔隙数量越多,密实程度较低会导致岩体内部与外界的传热效率较差,其与衬砌在接触界面传递的热量损失越大,导致界面接触热阻增加. 在隧道施工中,衬砌周边围岩的质量会对隧道安全性产生极大的影响,质量较好、较为密实的围岩能提高隧道结构的安全性. 文献[20]使用岩体基本质量指标BQ来确定围岩基本质量等级,该指标的计算式为
式中:σs为界面粗糙度,
在理想状态下,物体表面趋近于光滑平面,可视为围岩与衬砌完全接触. 自然界中不存在理想光滑表面,因此界面接触热阻的取值大于0.
接触面因表面粗糙度存在而出现热流收缩,在干热条件下,间隙介质为空气. 进行接触面热阻问题简化,将界面接触热阻分解为固体直接接触热阻Rs和间隙介质热阻Rf,2个部分的热阻为并联关系.
间隙介质热阻可由式(9)计算得到. A=As+Af,Af为空隙面积,λs、λf分别为表面实际接触的等效导热系数与间隙中介质材料导热系数. 判断间隙介质热阻对总接触热阻的影响,
由并联公式得到总热阻
根据摩擦学,当2个固体接触面为弹性接触时,接触面实际接触面积为名义面积的1%~10%[24]. 在本研究中,岩石-混凝土接触面为弹性接触,参考Zhang等[25-26]所测岩石表面接触面积与名义面积之比,确定岩石-混凝土接触面实际接触面积占名义面积的5%. 空气导热系数λf=0.023 W/(m∙K),玄武岩(Ⅰ级围岩)与混凝土接触面等效导热系数λs=2.029 85 W/(m∙K),代入式(11)得到R=0.443Rs,综合考虑空气介质与工程安全性,取Ⅰ级围岩的热阻抗评价系数B=0.4,Ⅴ级围岩的热阻抗评价系数B=0.7. 当围岩质量及岩体完整性较好时,空隙与裂隙数量较少,岩体基本质量指标较高并具有较好的导热性能,因此热阻抗评价系数较低,界面接触热阻值较小. 当围岩质量及其完整性较差时,空隙与裂隙数量较多,导致岩体基本质量指标较低且导热性较差,同时热阻抗评价系数与界面接触热阻值增加. 在实验温度范围(20~80 ℃)内,Ⅰ级~Ⅴ级围岩热阻抗评价系数为0.4~0.7. 假设Ⅰ级到Ⅴ级围岩的岩体热阻抗评价系数根据岩体基本质量指标线性插值确定,不同围岩质量等级的岩体热阻抗评价系数如表2所示.
表 2 不同围岩质量等级的岩石热阻抗评价系数
Tab.2
| 围岩质量等级 | BQ | B |
| Ⅰ | >550 | <0.4 |
| Ⅱ | 450~550 | 0.5~0.4 |
| Ⅲ | 350~450 | 0.6~0.5 |
| Ⅳ | 250~350 | 0.7~0.6 |
| Ⅴ | <250 | >0.7 |
2. 数值模拟实验验证
2.1. 计算模型
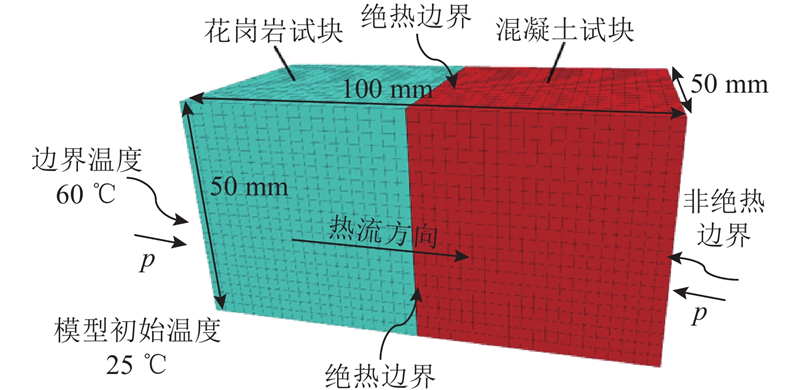
为了验证本研究所提围岩-衬砌界面接触热阻计算方法的准确性,采用有限差分数值软件FLAC3D建立计算模型. 该模型由2个边长皆为50 mm的花岗岩与混凝土立方体试块组成,如图3所示. 岩石试件为花岗岩,模型采用摩尔-库伦本构关系,混凝土试件选用C30混凝土,模型采用弹性本构关系. 数值模拟中混凝土与花岗岩界面各取等效厚度为1 mm的微小区域,设置10倍的等效导热系λs. 设置模型中的初始温度为25 ℃,温度边界条件:花岗岩试件的左侧表面温度为60 ℃,2个试件除接触表面和模型两端外其余表面均绝热,热量由花岗岩试件左侧向右侧混凝土试件传递. 轴向压力p施加在模型两端,模型在绝热边界为静态约束.
图 3
图 3 花岗岩与混凝土界面接触热阻计算模型
Fig.3 Calculation model of interfacial thermal contact resistance between granite and concrete
2.2. 计算参数
表 3 花岗岩与混凝土的计算参数
Tab.3
| 参数 | 数值 | |
| 花岗岩 | C30混凝土 | |
| γ/(kN·m−3) | 26.0 | 24.0 |
| E/GPa | 60 | 30 |
| μ | 0.18 | 0.22 |
| φ/(°) | 65 | — |
| cc/MPa | 22.5 | — |
| λ/(W∙m−1∙K−1) | 2.60 | 1.36 |
| c/(J·kg−1·K−1) | 850 | 960 |
| α/K−1 | 8.00×10−6 | 9.75×10−6 |
2.3. 相对误差
将围岩-衬砌界面之间的温差和接触界面法向热流密度代入式(1),得到界面接触热阻定义式理论结果,与式(8)求得实验结果对比,得到实验结果与理论结果的相对误差.
2.4. 实验结果
取C30混凝土和花岗岩导热系数作为模型中的导热参数代入式(5),得到界面等效导热系数
图 4
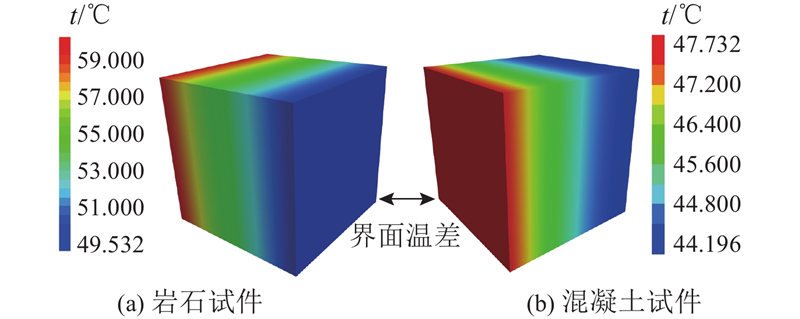
图 4 花岗岩与混凝土接触界面温差
Fig.4 Temperature difference across granite-concrete contact interface
表 4 岩石与混凝土试件的物理参数
Tab.4
| 试件 | H/MPa | σ/μm | ρ/(g·cm−3) | φ/% |
| 玄武岩(Ⅰ级) | 150 | 90 | 2.858 | 4 |
| 页岩(Ⅰ级) | 100 | 95 | 2.604 | 6 |
| 花岗岩(Ⅱ级) | 60 | 100 | 2.556 | 4 |
| 砂岩(Ⅲ级) | 45 | 105 | 2.388 | 10 |
| 泥岩(Ⅳ级) | 15 | 115 | 1.876 | 15 |
| C25试块 | 20 | 93 | 2.268 | 18 |
| C30试块 | 30 | 88 | 2.366 | 16 |
| C35试块 | 35 | 85 | 2.265 | 13 |
| C40试块 | 40 | 80 | 2.220 | 11 |
3. 围岩-衬砌界面接触热阻室内实验
3.1. 试件及实验设备
图 5
图 5 围岩-衬砌接触热阻室内实验试件
Fig.5 Laboratory specimen for testing surrounding rock-lining thermal contact resistance
粗糙度使用表面粗糙度测量仪HL223测量,量程为0~6 000 μm,分辨率为1 μm,允许误差为3 μm. 该仪器属于点式测量仪器,为此将试件表面均分为100个5 mm的正方形网格,取每个网格的中心进行粗糙度测量. 进行100次粗糙度测量,取均值代表试件的表面粗糙度. 如图6所示的固体导热系数测量仪TC3000E的导热系数测量范围为0.001~100 W/(m·K),分辨率为0.000 5 W/(m·K). TC3000E由测试仪器主机、传感器与测试软件Hotwire3.6组成. 实验中借助传感器与测试软件记录接触面两侧温差,TC3000E能够直接测量块状、粉状以及不规则物体等样品的导热系数,还能够辅助进行热流密度与界面接触热阻的计算.
图 6
3.2. 实验分组
将试件放置于20、40、60、80 ℃温度条件下,计算不同岩性下5种岩石与4种混凝土组成的围岩−混凝土界面接触热阻. 使用高低温电子万能试验机控制实验温度,实验共设计20个分组.保证岩石和混凝土试件紧密接触的情况下,使用TC3000E测量接触界面间的温差,计算实际的界面接触热阻. 为了保证实验的准确性,对试件与传感器系统进行热平衡监测. 当系统整体达到热平衡,即在软件热平衡监测功能中传感器测得的试件界面温度基本保持不变的情况下进行实验. 导热系数的测量采用软件默认的测量方式,单次测量间隔为3 min,每组测量8次,去除首次测试和剩下7次测试结果中的最大、最小值后,取平均值作为最终的测量结果. 使用电子万能实验机保证试件紧密接触,测量方式如图7所示.
图 7
图 7 围岩-衬砌接触热阻室内实验测量方式
Fig.7 Laboratory measurement mode for surrounding rock-lining thermal contact resistance
3.3. 实验结果及分析
由TC3000E测量5次花岗岩与C30混凝土试件间的导热系数值,取测量平均值作为等效导热系数
由所提界面接触热阻计算方法求得各组围岩-混凝土界面接触热阻,结果如图8所示. 可以看出,不同实验组中的界面接触热阻均呈现随温度升高而减小的趋势. 相较C25试件,C40试件的表面粗糙度略有降低,导致C40试件与不同岩石试件在实验温度为20~80 ℃的条件下界面接触热阻减低了15.63%~20.16%. 当实验温度由20 ℃升高至80 ℃时,C25、C30、C35、C40试件与不同岩石试件的界面接触热阻分别降低了5.03%~9.68%、4.39%~10.10%、1.94%~9.89%与5.05%~8.60%. 温度升高会导致试件的导热系数与体积变化,进而影响界面接触热阻,但在隧道高岩温范围(40~100 ℃)内,界面接触热阻变化幅度较小. 分析原因:温度不直接影响界面接触热阻,而是使接触表面形状发生微观变化. 在实验温度范围内,温度升高,晶体振动和自由电子运动加剧,导致接触表面形成新的平衡态,使得接触点数量和实际接触面积略微增加. 对比相同种类混凝土试件与不同种类岩石试件的界面接触热阻可知,随着围岩等级的增加,界面接触热阻均明显升高,且不同围岩等级下升高幅度差异较大. 界面接触热阻的主要影响因素为接触面粗糙度,随着围岩等级降低,岩石粗糙度上升,接触界面粗糙度变大,接触面实际接触面积减小. 以C30试件组为例,该组中Ⅰ级围岩玄武岩-混凝土界面接触热阻最低,为3.779×10−3~4.203×10−3 m2K/W. Ⅰ级围岩页岩-混凝土界面接触热阻为4.203×10−3~4.501×10−3 m2K/W,Ⅱ级围岩花岗岩-混凝土界面接触热阻为4.628×10−3~4.840×10−3 m2∙K/W,与Ⅰ级玄武岩-混凝土界面接触热阻相比分别增加了7.07%~12.09%与15.15%~22.47%. Ⅲ级围岩砂岩、Ⅳ级围岩泥岩-混凝土界面接触热阻分别为6.029×10−3~6.369×10−3、7.982×10−3~8.577×10−3 m2K/W,与Ⅰ级玄武岩-混凝土界面接触热阻相比分别增加了51.51%~59.55%和104.04%~111.24%.
图 8
图 8 不同试件组的界面接触热阻计算结果
Fig.8 Calculated interfacial thermal contact resistance for different specimen groups
当实验温度为60 ℃时,由式(1)计算得到不同岩石与混凝土试件界面接触热阻定义式理论结果与式(8)计算得到的结果的相对误差δ如表5所示. 以同样方法计算的不同温度下各实验组的相对误差,各组最大相对误差如下:20 ℃时为12.52%(C25-花岗岩)、40 ℃时为11.65%(C30-砂岩)、60 ℃时为9.53%(C35-砂岩)、80 ℃时为8.31%(C35-泥岩). 可以看出,最大相对误差小于15%(12.52%).
表 5 界面接触热阻计算结果与理论结果的相对误差
Tab.5
| 分组 | R/(10−3 m2·K·W−1) | δ/% | |
| 理论结果 | 计算结果 | ||
| C25-玄武岩 | 3.789 | 4.076 | 7.587 |
| C25-页岩 | 4.332 | 4.458 | 2.906 |
| C25-花岗岩 | 5.120 | 4.883 | −4.636 |
| C25-砂岩 | 6.866 | 6.539 | −4.766 |
| C25-泥岩 | 9.134 | 8.534 | −6.563 |
| C30-玄武岩 | 3.618 | 3.864 | 6.783 |
| C30-页岩 | 4.375 | 4.331 | −1.005 |
| C30-花岗岩 | 4.884 | 4.628 | −5.242 |
| C30-砂岩 | 6.686 | 6.072 | −9.194 |
| C30-泥岩 | 8.441 | 7.982 | −5.435 |
| C35-玄武岩 | 3.661 | 3.567 | −2.578 |
| C35-页岩 | 3.908 | 4.203 | 7.572 |
| C35-花岗岩 | 4.604 | 4.331 | −5.931 |
| C35-砂岩 | 6.148 | 5.562 | −9.528 |
| C35-泥岩 | 7.792 | 7.515 | −3.549 |
| C40-玄武岩 | 3.588 | 3.439 | −4.143 |
| C40-页岩 | 3.440 | 3.736 | 8.604 |
| C40-花岗岩 | 3.958 | 4.076 | 2.971 |
| C40-砂岩 | 5.699 | 5.477 | −3.894 |
| C40-泥岩 | 7.532 | 7.048 | −6.424 |
4. 局限与不足
1)数值模拟与室内实验均假设热流方向为接触界面法向,实际接触面上的热流方向可能受接触面微观特征和实际接触面积影响,导致热流方向偏离接触面法向. 数值模拟与室内实验中的岩石混凝土界面仅考虑热传导,忽略了接触面间复杂的热对流与热辐射. 数值模拟与室内实验将混凝土与岩石试块导热系数视为固定值,在实验温度范围(20~80 ℃)内,虽然岩石与混凝土的导热系数受温度影响较小,但是带来误差. 在混凝土与岩石界面未胶结的条件下,未考虑混凝土衬砌表面残留杂质(如脱模剂)对接触界面影响. 2)数值模拟中混凝土与岩石界面接触热阻采用薄壁模型模拟,忽略了接触面的微观结构特征,只在宏观上实现界面间温度跃变特征,未实现零厚度的接触热阻模拟. 3)在室内实验时,放置在岩石与混凝土试件之间的导热系数传感器的厚度增加了界面缝隙,在测量过程中影响界面的热阻,属于系统误差. 适当增加岩石与混凝土试件的压力能够减小传感器厚度对界面接触热阻的影响. 4)通过对实验局限的分析与相对误差计算,数值模拟和室内实验结果误差在合理范围内. 经过数值模拟和室内实验结果计算,实验结果与理论结果符合较好. 因此,所提围岩-衬砌间界面接触热阻计算方法具有一定的准确性与工程可用性.
5. 结 语
本研究基于圆盘模型的界面接触热阻计算公式提出考虑围岩岩性影响的高岩温隧道围岩-衬砌间界面接触热阻计算方法. 岩石-混凝土试件界面接触热阻室内实验结果表明,随着实验温度由20 ℃升高至80 ℃,不同混凝土试件组中岩石-混凝土的界面接触热阻均减小. 围岩等级越低(围岩质量越差),实际接触面积越小,岩石-混凝土试件间的界面接触热阻明显增大. 室内实验中Ⅳ级围岩砂岩相较Ⅰ级围岩玄武岩与混凝土间界面接触热阻增大了104.04%~111.24%. 对比界面接触热阻定义式理论计算结果与考虑围岩岩性影响的围岩-衬砌间界面接触热阻计算方法所得结果,最大相对误差为12.52%,满足15%的工程允许误差. 实验中围岩试件为完整试块,并未体现围岩的不完整性,后续研究将考虑围岩不完整性构造多裂隙岩石试块,进一步研究围岩完整性对围岩-衬砌界面热阻的影响.
参考文献
川藏铁路沿线主要不良地质条件与工程地质问题
[J].
Main unfavorable geological conditions and engineering geological problems along Sichuan-Tibet railway
[J].
高地温隧道灾变机制与灾害防控研究进展
[J].
Review on catastrophe mechanism and disaster countermeasure of high geotemperature tunnels
[J].
川藏铁路折多山段隧道温度场与热害初步预测
[J].
Preliminary prediction of temperature field and thermal damage in Zheduoshan Region along Sichuan-Tibet railway
[J].
高地温高地应力下岩体初始地应力场反演分析
[J].
Inverse analysis of the initial geostress field of rock masses under high geo-temperature and high geostress
[J].
基于人工智能算法预测土体导热系数
[J].
Prediction of thermal conductivity of soils based on artificial intelligence algorithm
[J].
热传导CPT探头的研发与应用
[J].
Development and application of heat conduction CPT probe
[J].
高岩温隧道围岩-支护结构温度场演化规律
[J].
Temperature field variation rules of rock and support structure in high rock temperature tunnel
[J].
高地温隧道衬砌混凝土早期开裂机理及防控措施
[J].
Early cracking mechanism and prevention measures for lining concrete in high geotemperature tunnel
[J].
高地温隧道二次衬砌受力特性分析
[J].
Analysis of the stress characteristics of the high ground temperature tunnel secondary lining
[J].
考虑接触热阻的钢壳沉管隧道结构火灾温度场研究
[J].
Fire temperature field of steel shell immersed tunnel structure considering contact thermal resistance
[J].
钢-混组合梁荷载-温度效应的统一解析模型
[J].
Unified analytical model for load-temperature effect of steel-concrete composite girder
[J].
Influence of thermal contact resistance on dynamic response of bilayered saturated porous strata
[J].DOI:10.1007/s11771-022-5053-2 [本文引用: 1]
考虑颗粒形貌的干砂热传导特性研究
[J].
Thermal conduction behaviors of dry sands considering effects of particle shape
[J].
界面平均温度和压力对DD5和1Cr11Ni2W2MoV材料接触热阻影响的实验研究
[J].
Experimental study on the influences of mean interface temperature and pressure on thermal contact resistance of the material DD5 and 1Cr11Ni2W2MoV
[J].
宏观接触热阻研究综述
[J].
Research overview of macroscopic thermal contact resistance
[J].
Heat flow in fractured rocks: stress and moisture-dependent thermal contact resistance
[J].DOI:10.1016/j.geothermics.2021.102113 [本文引用: 1]
北京地区基岩地层热物性参数特征
[J].
Thermal properties analysis of bedrock in Beijing
[J].
贵州主要岩石地层热物性参数特征及影响因素分析
[J].
Thermal property parameters and influencing factor analysis of main rock strata in Guizhou Province
[J].
Fire resistance of steel columns filled with bar-reinforced concrete
[J].DOI:10.1061/(ASCE)0733-9445(1996)122:1(30) [本文引用: 1]
Thermal contact conductance
[J].DOI:10.1016/0017-9310(69)90011-8 [本文引用: 3]
一种随机表面间接触热阻的计算方法
[J].
A method for calculation of contact heat resistance between two contacting surfaces
[J].
碳/碳化硅复合材料接触热阻计算方法
[J].
Engineering investigations of thermal contact resistance of C/SiC composite materials
[J].
Experimental and numerical study on the mechanical properties of the rock-concrete contact surface for consideration of ground–liner interaction in rock tunnelling
[J].DOI:10.1080/19648189.2022.2042741 [本文引用: 1]