大数据技术作为新兴关键手段,通过归纳、演绎挖掘数据内在关联,以其高预测精度、低数据需求和良好的可解释性等优势[8],在提升货运量预测工作的科学性与结果可靠性方面获得了广泛应用. 多项研究显示智能算法在预测中表现优异,如Gao等[9]融合长短期记忆网络(long short-term memory,LSTM)与其他机器学习算法,验证了融合模型在多城市数据中的有效性;Li等[10]应用LSTM预测物流需求时序,误差低于传统方法且抗外部干扰能力强;Mohammadzadeh等[11]利用LSTM捕捉非规则信息,在未过拟合情况下取得较高精度;Yin等[12]结合信息粒提取、最小二乘支持向量机与粒子群优化提升了预测效果;Yang等[13]通过灰色-马尔可夫模型进一步提高了预测精度. 随着时空影响因素被纳入交通领域的预测研究,Cai等[14]构建时空状态矩阵和改进K最近邻(k-nearest neighbor,KNN)模型,采用高斯加权欧氏距离量化时空影响,适用于短期交通流多步预测;Wu等[15]通过加权距离与状态向量改进KNN,验证了模型在多路段多时段上的适应性,表明时空融合模型优于单一时间模型. 基于LSTM处理缺失数据和残差调整的能力[16],Zou等[17]提出时空日(space-time diurnal, ST-D)方法,融合时空特征与非负性,实现高精度短期旅行时间预测,具更强鲁棒性.
本研究将时空影响因素纳入预测框架,旨在探索时空融合对精度的影响,寻求适合该场景的人工智能预测模型. 高速公路区域货运量具有较强的区域性、季节性,且行驶里程有限,受时空影响显著. 从时空角度构建数据集,整合相关影响因素建立预测模型,提高货运量预测的精度已然成为物流领域亟待解决的问题. 本研究建立基于时空信息融合的改进LSTM模型(TS-LSTM),提出适用于TS-LSTM网络模型的数据集重构方法,以期为实现更精准、可靠的货运量预测提供新途径.
1. 模型构建
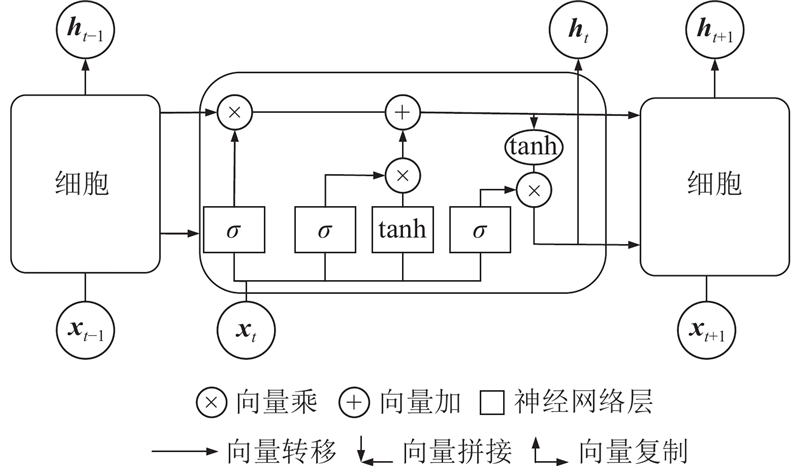
1.1. 长短期记忆网络结构
图 1
2)输入门:
3)输出门:
式中:
1.2. 基于时空信息融合的改进长短期记忆网络模型结构
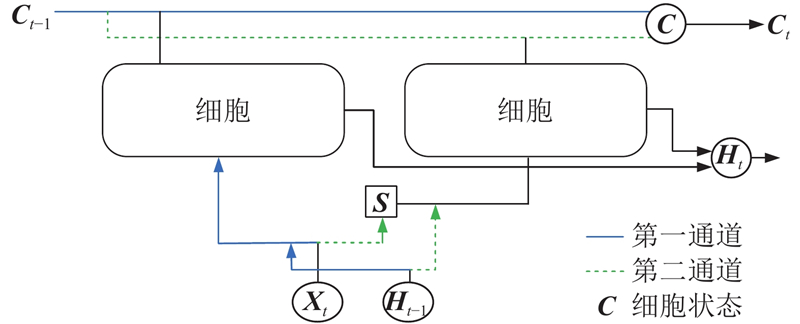
TS-LSTM的结构如图2示,TS-LSTM细胞主要从第一和第二通道分别探索数据在时间和空间维度内的隐藏信息,
图 2
图 2 基于时空信息融合的改进长短期记忆网络模型结构图
Fig.2 Structure diagram of improved long short-term memory model based on spatiotemporal information fusion
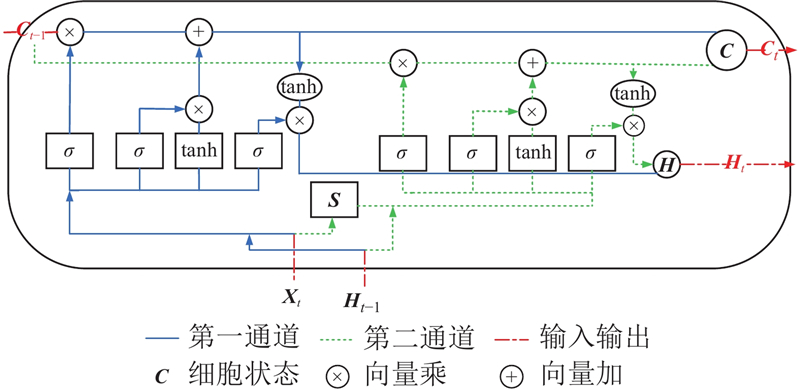
图 3
图 3 基于时空信息融合的改进长短期记忆网络模型的细胞内部结构图
Fig.3 Cell internal structure diagram of improved long short-term memory model based on spatiotemporal information fusion
式中:
在第一层中,为了将数据
1.3. 模型性能评估指标
采用均方根误差RMSE、平均绝对值误差MAE和平均绝对百分比误差MAPE评估模型的预测性能,计算式分别为
式中:
2. 时空数据集重构方法
高速公路区域货运量预测是指根据高速公路历史货运量统计数据和其他关联数据,使用预测方法对规划区域内高速公路未来时刻货运量的指标进行预测的过程. 本研究基于行政区域划分对高速公路货运量进行预测. 对货运量进行预测时,除了模型的选取至关重要之外,模型数据集的作用也不容忽视. 为了适应TS-LSTM,须建立合适的方法对时空数据进行融合重构. 货运量数据集来源于高速公路收费系统数据,原始数据集包含交通流往来数据,但不包含有效的时空信息,为此将数据中包含的潜在有效时空信息提取出来. 在完成货运量的处理之后,分别从时间和空间维度提取影响因素,实现货运量预测数据集的重构. 数据集重构前,处理工作包括:将货车往来记录按照起始点归属映射为区域货车流往来信息;对输入记录进行预处理,获取各个区域的货运量信息;在挖掘区域内货运量时间序列信息的同时,进一步挖掘空间影响因素.
2.1. 栅格划分
定义1 将统计时间间隔
定义2 将某个区域(如某个行政区、城市或者省份等)分成
定义3 当
2.2. 数据预处理
高速公路运输量数据收录188个吉林省内收费站和24个省界门架收费站的货车往来记录,以收费记录的形式存在,包含如车辆行驶路程的入站口时间、入站口收费站、行驶车道、出口时间、出站口收费站、行驶车辆类型、载重、ETC收费与否、车辆的车牌等有效信息. 省界门架收费站主要记录车辆进出省界的信息,如进出省界的时间、进出省界的收费站序号、车牌等. 观察高速公路收费系统数据发现,中长行程占据了绝大多数,运输时间都不超过1 d,因此在将数据输入组织模型时,设置每对栅格的截取时间间隔为1 d,即一天内的货物往来数量. 以2020年12月1日为例,假如从东丰县至长春市的货物运输量为486.2 t,意味着当天所有从东丰县境内的所有收费站为起点到长春市任意收费站为终点的货物总和为486.2 t. 数据预处理的具体流程及步骤如下.
1)设置吉林省全域栅格为
2)从原始数据集中筛选所需货车类型,供选择包括6种车型,编号为车型I~车型Ⅵ.
3)将载重减去对应车型的车辆平均自重之后进行加和.
4)将省内记录和门架记录根据车牌信息和时间信息进行关联,形成完整的数据记录.
5)以
6)对所有的栅格重复步骤4)和5).
7)将输入数据编码成二维矩阵格式,其中列按照网格顺序排列,行按照时间序列排序,行记录
2.3. 基于时空信息的建模数据集重构
重构预处理后的数据,货运量的影响因素主要包括2个部分:空间信息、时间信息. 空间信息即与出发网格
式中:
2.4. 区域短期货运量预测算法流程
1)对高速公路收费系统数据进行预处理,选取合适的时间间隔,统计得到每对栅格间的货运量. 2)获取栅格之间的空间权重矩阵. 3)统计并获取系统中每个栅格的历史时刻数据,即时间序列数据. 4)选定输入时空维度长度,针对子序列输入和对应输出,利用TS-LSTM进行预测. 5)完成预测后,将误差结果与其他预测模型进行比较.
3. 结果分析与模型对比
影响高速公路区域货运量序列的相关因素有时间和空间,将它们纳入预测模型特征,可增加算法的鲁棒性,提升算法的准确率. 将预处理后的数据进行重构,构成历史影响因素-未来运输量数据对,是进行货运量预测的基础,选取历史影响因素的长度对于模型的精度也至关重要.
3.1. 时空因素影响分析
选用分类与回归树(classification and regression trees, CART)算法分别计算历史时刻和邻域栅格的重要性,根据计算结果进行维度选择. 以时间维度为例,通过计算历史货运量
式中:
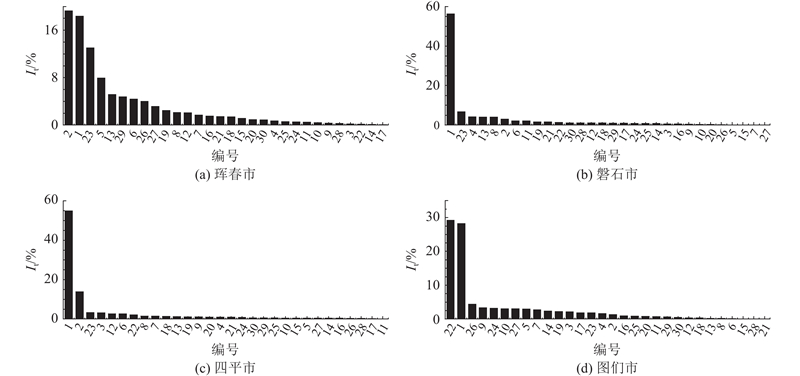
对全省每个栅格由CART算法得到的前30个时间时刻和48个空间变量的重要性进行排序. 选取珲春市、磐石市、四平市、图们市为代表格栅,其时间重要性如图4所示, 其中编号表示
图 4
图 4 举例格栅的时间重要性分析结果
Fig.4 Results of temporal importance analysis for representative grids
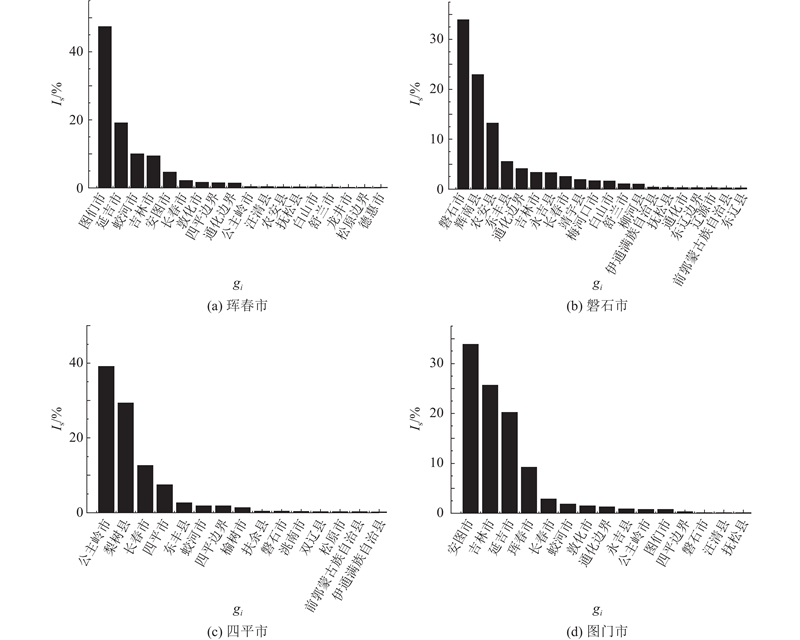
4个代表栅格的空间重要性系数如图5所示(仅展示有影响的栅格重要性),重要性系数的数值越大,表示对应的邻域对栅格的影响越大. 不同栅格受其他栅格货运量的影响不同,珲春市主要受图们市、延吉市、蛟河市、吉林市、安图市、长春市、敦化市、长春边界、通化边界的影响,比例分别为47.40%、19.11%、10.06%、9.44%、4.64%、2.22%、1.69%、1.51%、1.45%. 磐石市主要受自身、辉南县、农安县、东丰县、通化边界、吉林市、永吉县、长春市的影响,重要性分别为33.96%、22.95%、13.22%、5.52%、4.13%、3.36%、3.33%、2.58%. 四平市的空间影响变量比较少,为公主岭市、梨树县、长春市、四平市,重要性分别为39.10%、29.33%、12.65%、7.47%. 图们市受安图市、吉林市、延吉市、珲春市、长春市的影响比较大,重要性分别为33.88%、25.67%、20.26%、9.25%、2.88%. 不同栅格间的货运量关系与栅格间的货运量往来密切相关,因此获取不同栅格间的货运量矩阵作为TS-LSTM的动态输入对货运量的预测意义重大.
图 5
图 5 举例格栅的空间重要性分析结果
Fig.5 Results of spatial importance analysis for representative grids
3.2. TS-LSTM模型性能分析
为验证TS-LSTM在货运量预测上的有效性与性能优势,设计3组仿真实验:1)只考虑时间因素,即从时间维度预测每个栅格未来的货运量值;2)只考虑空间维度. 3)融合时空信息的数据集. 前2组使用传统的LSTM模型(T-LSTM和S-LSTM),第3组使用TS-LSTM. 3组实验均从仿真时间
对数据观察发现,高速公路区域货运量的波动以周为周期,因此将时间序列长度取为7 d. 设置批量大小batch_size = 10,预测未来1天的数据delay = 1,仿真迭代轮次epoch=50,训练集、测试集、验证集的比例设置为0.70∶0.15∶0.15. 实验平台为CPU Intel(R) core i5 and 12G RAM,Windows 10 64 bit Anaconda3(64 bit). 原始数据均来源于吉林省高速公路收费系统数据2020年11月—2021年11月的记录,共计25 563 256条,任意选取长春市、吉林市、松原市为格栅进行仿真实验.
如表1所示为3种模型对区域货运量预测的结果对比,日期为任意选取3个时刻,NFVT、NFVP分别为z-score标准化的实际货运量和预测货运量. T-LSTM、S-LSTM和TS-LSTM的N个栅格MAE分别为0.16、1.01、0.11,ts=
表 1 不同长短期记忆网络模型的货运量预测结果对比
Tab.1
| gi | 日期 | NFVT | T-LSTM | S-LSTM | TS-LSTM | |||||
| NFVP | er/% | NFVP | er/% | NFVP | er/% | |||||
| 长春市 | 2020–11–08 | −1.760 35 | −0.425 58 | −75.82 | − | −10.79 | − | −7.99 | ||
| 2021–01–09 | −1.041 60 | −0.987 70 | −5.17 | − | −19.15 | − | −1.63 | |||
| 2021–05–13 | 1.500 42 | 1.092 39 | −27.19 | 8.22 | 5.02 | |||||
| 吉林市 | 2020–11–09 | −1.013 21 | −0.965 39 | −4.72 | − | −41.85 | − | −1.92 | ||
| 2020–12–15 | 0.072 36 | 0.026 48 | −63.41 | 21.53 | 18.33 | |||||
| 2021–01–07 | −0.542 42 | −0.606 17 | 11.75 | − | 33.34 | − | 8.55 | |||
| 松原市 | 2020–11–14 | 0.562 48 | 0.408 93 | −27.30 | −4.14 | −1.34 | ||||
| 2021–01–27 | −2.074 66 | −2.126 46 | 2.50 | − | 33.69 | − | −0.70 | |||
| 2021–03–28 | 1.101 01 | 1.129 07 | 2.55 | −6.82 | −0.65 | |||||
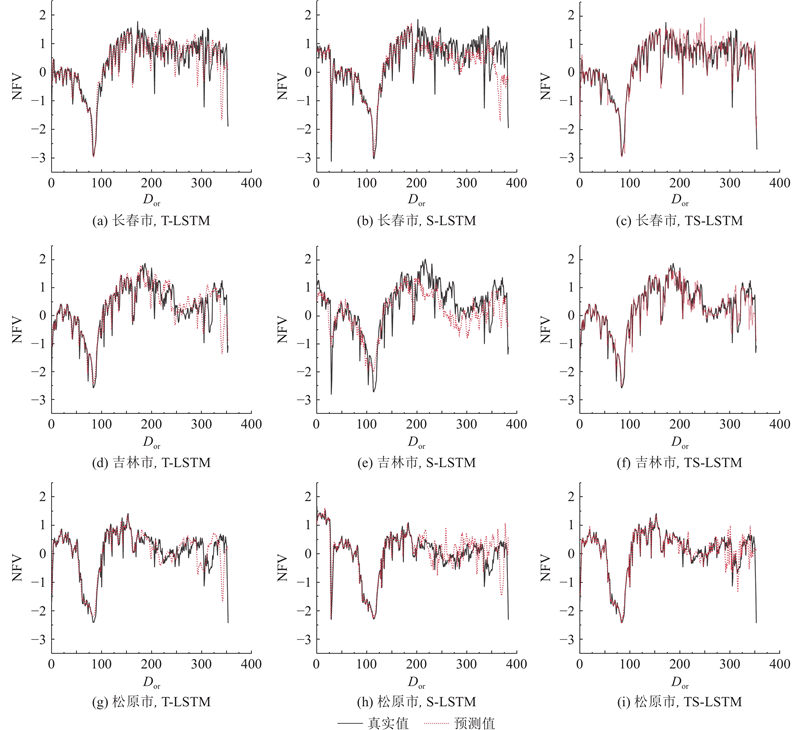
如图6所示为不同模型预测的栅格货运量变化与实际变化对比图,其中
图 6
图 6 不同长短期记忆网络模型预测年周期货运量变化的对比图
Fig.6 Comparison chart of annual cyclical freight volume changes predicted by different long short-term memory models
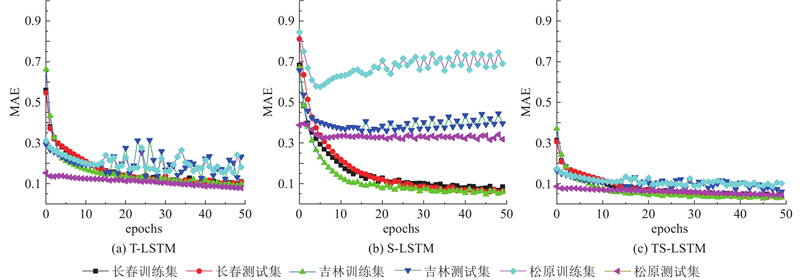
如图7所示为3种模型在3个栅格上的MAE变化. 可以看出,TS-LSTM的MAE最大、最小值比T-LSTM和S-LSTM的均有所降低. 如松原训练集,使用T-LSTM的MAE=0.25,使用S-LSTM的MAE=0.75,TS-LSTM的MAE=0.13,分别降低了48.0%和82.6%. TS-LSTM在第15轮左右达到收敛,T-LSTM和S-LSTM在第20轮收敛,而且松原和吉林的货运量预测数据稳定性远不如TS-LSTM,表明融合时空信息的模型预测精度高于只包含时间信息或者空间信息的2个模型.
图 7
图 7 不同长短期记忆网络模型的预测性能对比
Fig.7 Comparison of prediction performance among different long short-term memory models
3.3. 模型对比分析
3.3.1. 对比经典机器学习模型
基于相同的数据集,将TS-LSTM与3种经典机器学习模型进行性能对比分析,对比模型分别为全连接神经网络、单向LSTM、双向LSTM(BidLSTM),性能评估指标选取MAE、MAPE、仿真时间进行对比分析如表2所示. 可以看出TS-LSTM模型的误差均低于经典机器学习模型. 唯一的不足是TS-LSTM的仿真时间在参与对比的模型中最长,这主要是模型的内部结构不同导致的.
表 2 不同预测模型的性能指标对比
Tab.2
| 模型 | MAE | MAPE | ts/s |
| 全连接 | 0.171 3 | 104.051 1 | |
| LSTM | 0.354 5 | 150.324 2 | |
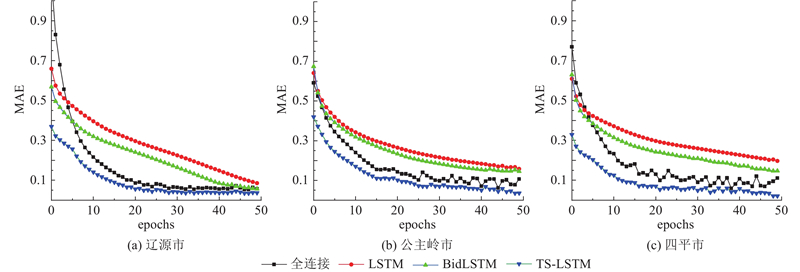
选取辽源市、公主岭市、四平市进行仿真,不同模型的MAE对比结果如图8所示. 在参与对比的模型中,TS-LSTM的预测效果最好,3个格栅的MAE分别为
图 8
图 8 不同预测模型在举例格栅中的预测性能对比
Fig.8 Comparison of prediction performance of different prediction models on representative grids
3.3.2. 对比Transformer模型
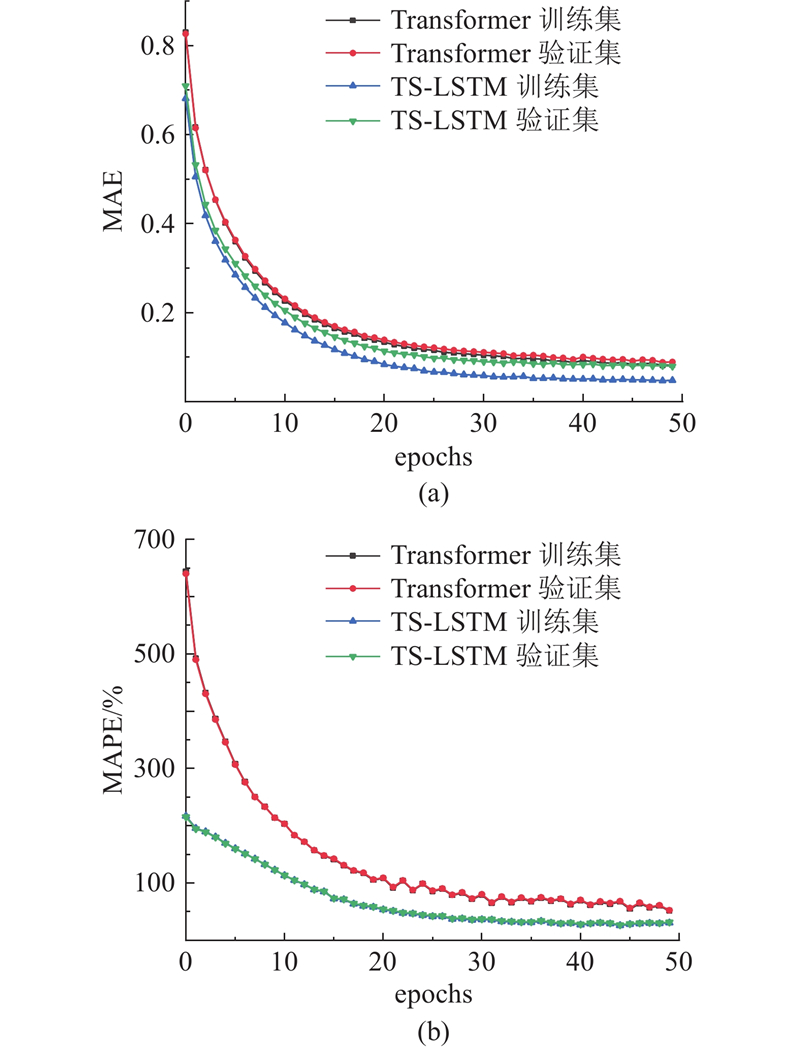
鉴于Transformer模型在时间序列预测方面的性能,将时空融合后的数据集使用Transformer与LS-LSTM进行性能比较,选取Adam优化器,其他仿真参数设置与3.2节中的参数一致,为表现模型的泛化能力,使用48个栅格的MAE和MAPE平均值进行分析,对比结果如图9所示. TS-LSTM的MAE和MAPE均低于Transformer模型,Transformer模型48个栅格训练集和验证集的MAE平均值分别约为0.082和0.089,TS-LSTM的分别约为0.048和0.080;Transformer模型48个栅格训练集和验证集的MAPE平均值分别约为51.54%和52.51%,TS-LSTM的分别为30.50%和31.69%. 相比于Transformer模型,TS-LSTM模型训练集和验证集的MAE分别降低了41%和10%,MAPE均降低了21个百分点. 显而易见,TS-LSTM的预测效果优于Transformer模型.
图 9
图 9 对比2种预测模型的泛化能力
Fig.9 Comparison of generalization capabilities between two prediction models
4. 结 语
高速公路区域货运量是多影响因素作用下的复杂动态系统,受限于数据源缺乏、统计模型区域货运量分配不均、预测精度较低,现有预测方法存在不足. 本研究以区域高速公路货运量为对象,按时空影响因素的重要性进行数据源的重构,根据数据特点设计双通道LSTM改进模型,与多种预测模型进行比较,建立在稳定性、预测精度、推广能力方面更优秀的预测模型来预测货运量的发展趋势,可为区域高速公路货运组织和物流运作提供决策依据. TS-LSTM的内部结构分别为时间和空间信息提供数据输入通道. 为了提高计算效率,算法利用机器学习进行输入信息筛选,分析时空信息的重要性,重构TS-LSTM输入的数据集,在保证精度的同时增强了模型稳定性. TS-LSTM的预测值比分别从时间和空间维度使用LSTM模型的预测值更接近实际值;TS-LSTM与经典机器学习模型的仿真对比实验结果表明,TS-LSTM能够很好地反映公路货运量的变化趋势及规律,提高预测精度;TS-LSTM比Transformer模型的预测效果好. 实验均以吉林省高速公路货运量为例进行验证,说明TS-LSTM可以作为实用性较强的高速公路货运量预测方法推广使用. 下一步将继续在数据集构建方法和预测模型方面开展相关研究.
参考文献
基于分解—集成的铁路货运需求预测研究
[J].
Railway freight demand forecasting based on decompose-ensemble method
[J].
基于灰色模型的铁路分品类货运量预测
[J].
Traffic volume forecast of railway different freight categories based on grey model
[J].
基于组合预测模型的陕西省物流需求预测
[J].
Forecasting and analysis of Shaanxi Province’s logistics demand based on combination forecasting model
[J].
Predictive scheduling with Markov chains and ARIMA models
[J].DOI:10.3390/app10176121 [本文引用: 1]
Urban freight demand forecasting: a mixed quantity/delivery/vehicle-based model
[J].DOI:10.1016/j.tre.2013.12.014 [本文引用: 1]
Regional expressway freight volume prediction algorithm based on meteorological information
[J].
Regional logistics demand prediction: a long short-term memory network method
[J].DOI:10.3390/su142013478 [本文引用: 1]
The short-term prediction of daily traffic volume for rural roads using shallow and deep learning networks: ANN and LSTM
[J].DOI:10.1007/s11227-023-05333-w [本文引用: 1]
A data-driven fuzzy information granulation approach for freight volume forecasting
[J].DOI:10.1109/TIE.2016.2613974 [本文引用: 1]
Forecast of freight volume in Xi’an based on gray GM (1, 1) model and Markov forecasting model
[J].
A spatiotemporal correlative k-nearest neighbor model for short-term traffic multistep forecasting
[J].DOI:10.1016/j.trc.2015.11.002 [本文引用: 1]
Improved k-nn for short-term traffic forecasting using temporal and spatial information
[J].DOI:10.1061/(ASCE)TE.1943-5436.0000672 [本文引用: 1]
LSTM-based traffic flow prediction with missing data
[J].DOI:10.1016/j.neucom.2018.08.067 [本文引用: 1]
A space–time diurnal method for short-term freeway travel time prediction
[J].DOI:10.1016/j.trc.2013.10.007 [本文引用: 1]
Long short-term memory
[J].DOI:10.1162/neco.1997.9.8.1735 [本文引用: 1]