随着柔性输电技术的发展,模块化多电平换流器(modular multilevel converter, MMC)在中长距离交-直-交柔性高压输电领域得到了广泛应用. MMC拓扑结构与传统电压源型换流器(voltage source converter, VSC)相似,但其上下桥臂采用级联子模块代替单个开关管,实现了多电平电压输出,使交流侧输出电压近似于标准正弦波,谐波含量极低[1]. 然而实际运行中,由于MMC内部结构或控制器与外部系统的相互作用,MMC并网系统中时常发生次同步振荡(sub-synchronous oscillation, SSO)问题,对电力系统的安全稳定运行产生影响[2-4]. Lyu等[2]指出若控制参数设计不当,在次同步振荡频段下,MMC-HVDC可能呈现负阻尼特性,与串联补偿线路相互作用时可能引发SSO. 孙雅旻等[3]通过阻抗相量法分析双馈风机与直驱风机的频域阻抗,表明当双馈、直驱风机混合并联接入MMC-HVDC时,互联系统在次同步频带存在振荡风险. Sun等[4]研究MMC-HVDC与毗邻汽轮发电机的次同步扭振互作用(sub-synchronous torsion interaction, SSTI),指出受系统强弱、负载等级、控制策略与控制参数等因素影响,MMC-HVDC可能导致发电机轴系发生次同步扭振,这一特点与传统LCC-HVDC系统的相似.
分析MMC的SSO特性的方法主要有3种:时域分析法、特征值分析法与频域分析法. 时域法优点在于能够获取系统各变量的时域响应曲线,结果精确度高,但时域法计算量庞大,需要较长的处理时间,且难以获取系统稳定程度的定量信息以及SSO产生机理[5]. 特征值法普适性强,且能提供完整的MMC小扰动特性,包括系统模式阻尼、谐振频率、稳定裕度等[6]. 然而特征值法须获知MMC互联系统的全部参数,MMC互联系统状态空间通常阶数较高,会导致“维数灾”问题,限制了特征值法在MMC次同步振荡研究中的应用[7]. 频域法包括阻抗分析法、复转矩分析法,实际应用中多采用阻抗分析法. 阻抗分析法将MMC、电网、风机等视为相互独立的子系统,分别建立各子系统的频域阻抗模型,再利用广义Nyquist判据判定互联系统的稳定性[8-9]. 阻抗分析法物理意义明确,且通过系统分块降阶规避了“维数灾”问题,其缺点在于须研究多输入多输出(multiple-in multiple-out, MIMO)系统稳定性,分析难度较高,且MIMO导致稳定性判据保守性大.
近年来,关于暂态能量函数(transient energy function, TEF)法在新能源电网中应用的研究逐渐增多. TEF法通过构造系统能量函数,并依据能量函数计算故障后系统暂态能量和临界能量,基于暂态能量与临界能量的比较来判断系统稳定性[10]. TEF法计算迅速,判稳条件简洁,并能够通过暂态能量水平反映系统稳定程度,具有实时分析电力系统稳定性的潜力. 然而,新能源电网具有电力电子设备渗透率高、交直流混合互联的特征,其详细模型的动态特性十分复杂,在能量函数构造方面存在瓶颈[11]. 因此,TEF法一度局限于传统同步发电机网络,直至Moon等[12-14]提出基于能量守恒定律的能量函数构建方法,该方法无需具体的系统元件模型,只须通过广域测量系统(wide area measurement system, WAMS)数据即可构造系统能量函数. 此方法大大降低了能量函数的构建门槛.
基于Moon的理念与端口Hamilton理论,李颖等[15-16]提出端口能量的概念,将系统整体的能量函数分解为系统中各端口流出及支路上流动的暂态能流. 陈磊等[17]对端口能量进行改进,去除端口能量的振荡分量而保留端口能量中反映能量变化趋势的部分,并将这部分定义为耗散能流(dissipating energy flow, DEF). DEF保留TEF的内核,刻画了端口元件对系统暂态能量水平变化的贡献,相比于TEF更为简明直观. 现已有研究运用DEF来分析含电力电子换流器或其他电力电子器件系统的暂态特性:Chatterjee等[18]针对2种电力电子器件(TCSC与STATCOM)开展研究,获取了低频振荡故障下2种器件的DEF表达式,并用其判别2种器件在低频振荡下的振荡源\汇特性. Ma等[19]研究了双馈风机(doubly-fed induction generator, DFIG)输出端DEF方程,分析机侧、网侧换流器控制与锁相环(phase-locked loop, PLL)对机端DEF的影响,并基于DEF的梯度构建耗散能量密度谱,以此评估DFIG并网系统的次同步振荡稳定性. 宋宇博[20]建立了直驱风机的输出端DEF函数,并研究了直驱风电场中多台风机间DEF的传播与交互作用及其对次同步振荡的影响. 然而,针对含MMC系统的DEF特性的研究尚为空白.
针对上述研究的特点及不足,从系统耗散能流的角度出发,提出新的次同步振荡分析理论. 通过 MMC 控制器建模及次同步振荡下MMC端口动态特性分析建立MMC交流侧端口DEF模型,分析MMC次同步振荡机理,并结合算例仿真结果研究各参数对DEF及MMC振荡源/汇特性的影响,从暂态能量角度展现MMC对系统整体稳定性的改变.
1. MMC与耗散能流理论简介
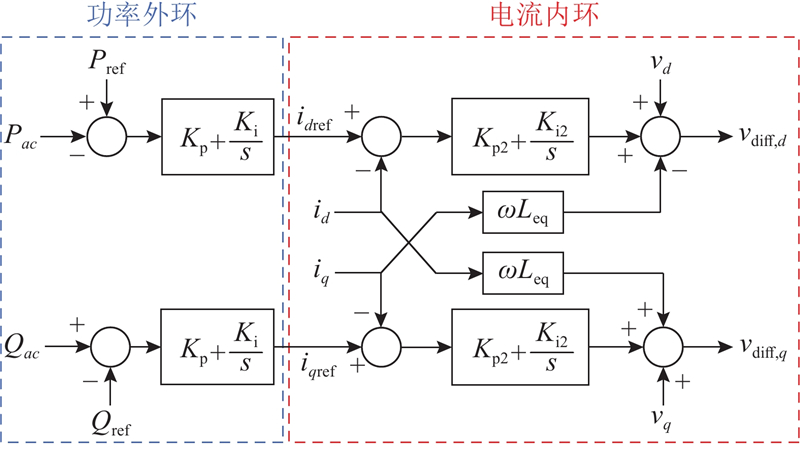
1.1. MMC拓扑结构与控制策略
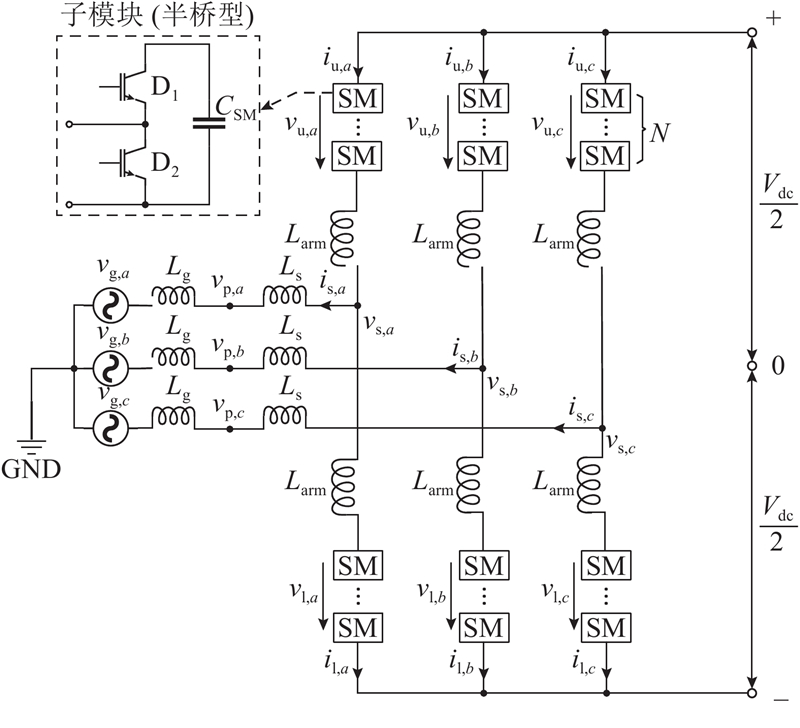
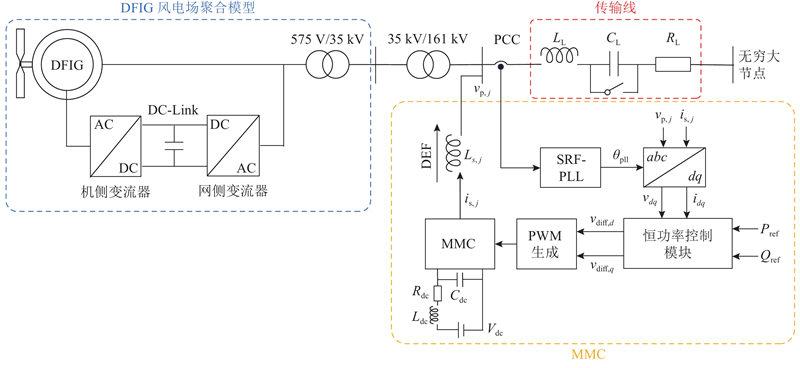
MMC拓扑结构如图1所示. 图中,
图 1
图 1 MMC拓扑结构(与一等效电网连结)
Fig.1 MMC topology (connected to an equivalent power grid)
整理可得变流器方程:
令
式中:
图 2
1.2. 耗散能流理论
陈乾等[16]提出端口能量的构造方法,可通过以下积分得到挂载在端口节点i上的设备向网络中注入的暂态能量
式中:
xy参考系与dq参考系坐标具有以下转换关系:
将式(5)代入式(4)并展开可得
式中:
式中:下标“0”表示系统稳态运行时各变量的稳态值,“
根据电力系统能量函数理论,须关注暂态过程下
2. MMC端口耗散能流特性分析
2.1. 次同步振荡下MMC端口电压扰动分析
假设系统发生次同步振荡,在MMC并网公共耦合点PCC处电压
式中:
对于含扰动分量的PCC电压
可见
MMC通过PLL跟踪
在理想PLL(无缝锁相)条件下,有
图 3
图 4
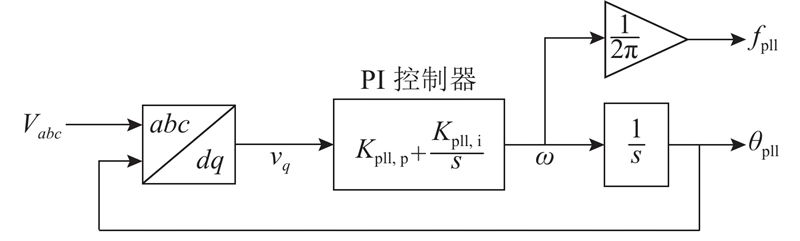
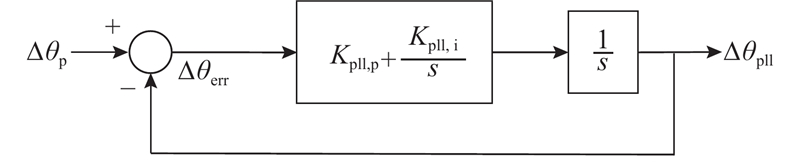
由图4可得SRF-PLL的闭环传递函数为
式中:
由式(14)可知PCC处电压的相位
式中:
将
当考虑PLL响应时,d、q轴电压均包含频率为
其中,
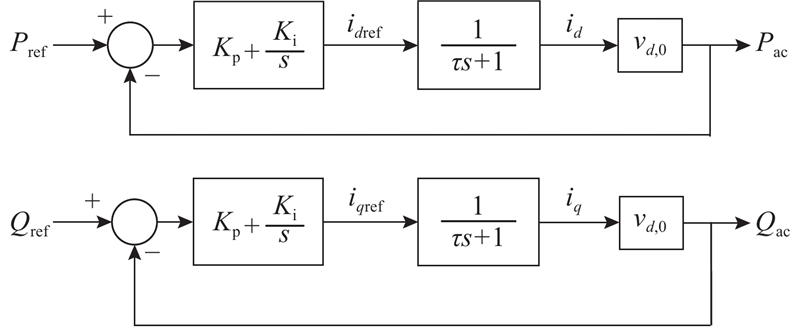
2.2. 定功率控制模式MMC端口耗散能流
考虑MMC平均值模型且假定MMC桥臂能量均衡控制器工作良好,则定功率控制模式下MMC具有以下特性.
1) MMC 交流侧、直流侧均为跟网运行(交流侧通过PLL跟踪PCC电压,直流侧跟随HVDC母线电压);
2) MMC 交流侧有功功率
图 5
基于MMC的定功率控制模式对其端口耗散能流
交流侧功率
由于电流内环的响应速度要远快于功率外环,可认为
将式(22) 、(23)代入式(21)可得
对式(24)进行小信号线性化处理. 忽略PLL的稳态跟踪误差,有
整理得到
由式(20)可知
式中:
根据式(29),可通过振荡模态、系统稳态工作点与系统控制参数计算MMC端口DEF的平均变化率
2.3. 基于耗散能流的MMC源/汇特性在线评定法
MMC端口耗散能流反映了MMC向系统注入或从系统吸收的暂态能量,因此可用于判断MMC源/汇特性,评定MMC对系统稳定性的影响. 以下是当系统中发生SSO时,实时计算MMC端口耗散能流平均变化率并据此评估MMC源/汇特性的具体步骤.
1) MMC端口变量数据采集. 在采样周期
2) 采样数据预处理. 利用二阶带通滤波器,提取MMC端口变量中的次同步扰动分量
式中:Q为品质因数,
3) 耗散能流平均变化率计算. 根据式(9)的离散化形式,计算MMC端口耗散能流的平均变化率:
4) MMC源/汇特性评定. 根据步骤3)求得的
3. 算例仿真
图 6
表 1 仿真系统参数
Tab.1
| 参数名称 | 符号 | 值 | 单位 |
| 系统额定容量 | 100 | MW | |
| 额定交流电压 | 161 | kV | |
| 系统额定频率 | 50 | Hz | |
| MMC直流侧额定电压 | 330 | kV | |
| MMC桥臂电感 | 15 | mH | |
| MMC并网电感 | 270 | mH | |
| 传输线电阻 | 2.59 | Ω | |
| 传输线电感 | 114.6 | mH | |
| 传输线串联补偿电容 | 0.14 | mF | |
| MMC控制外环比例系数 | 0.1 | — | |
| MMC控制外环积分系数 | 250 | — | |
| MMC控制内环比例系数 | 1 | — | |
| MMC控制内环积分系数 | — | ||
| PLL比例系数 | 25 | — | |
| PLL积分系数 | — | ||
| PLL微分系数 | 1 | — | |
| 无穷大节点电压 | 166 | kV |
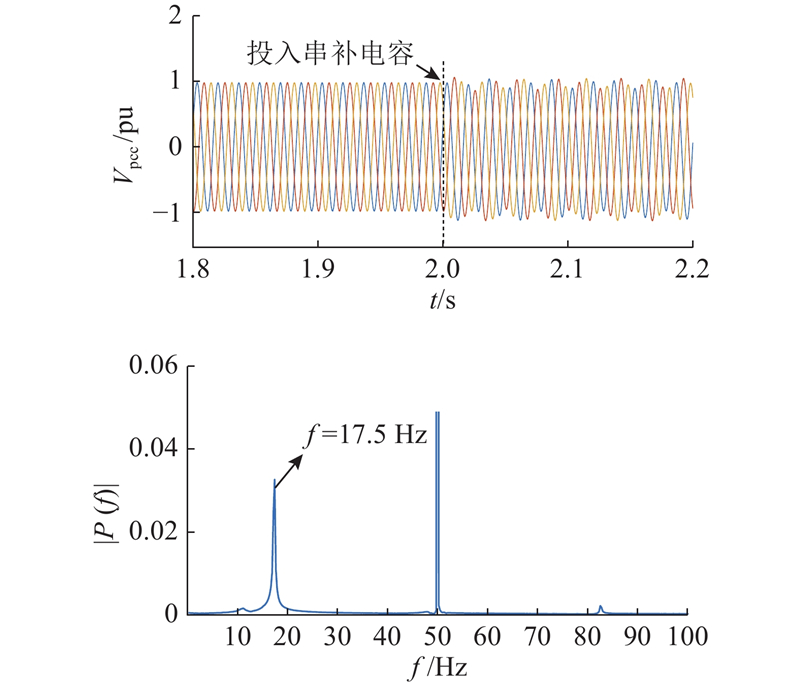
在t=2 s前,系统稳定运行,传输线上未实施串联补偿(串联补偿电容
图 7
图 8
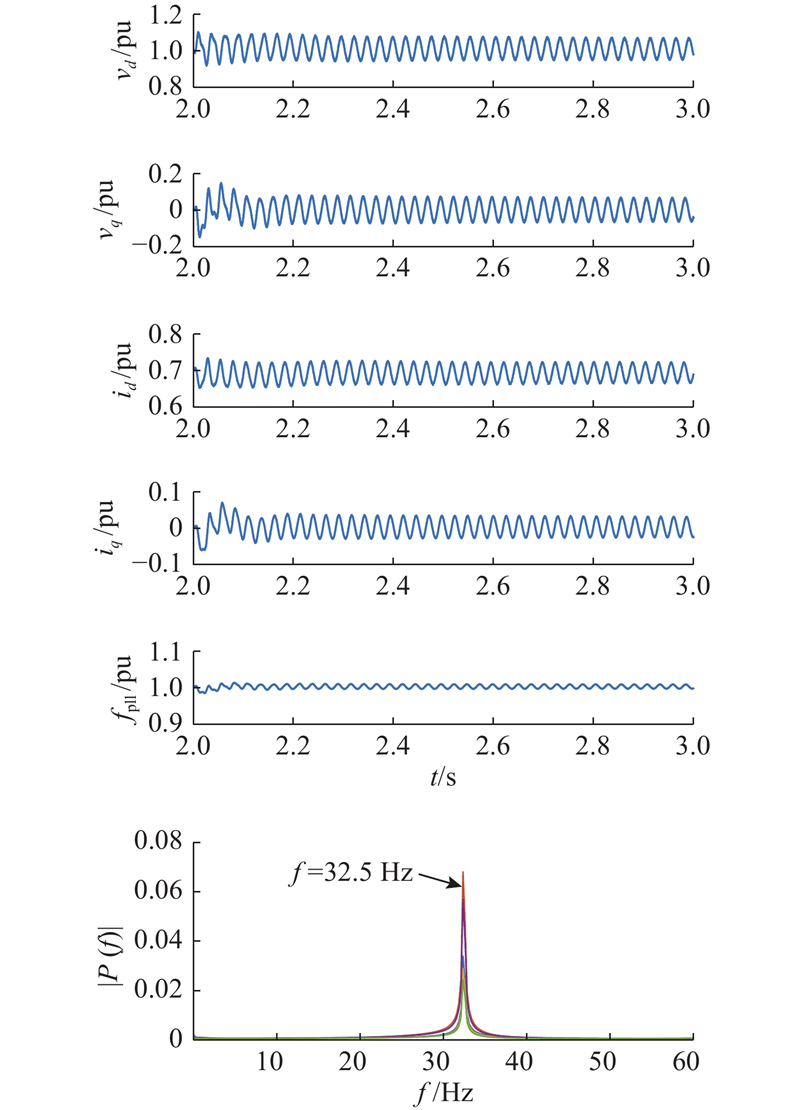
图 8 MMC端口dq轴电压、电流与PLL输出波形及频谱
Fig.8 Waveforms and frequency spectrums of dq-axis voltage and current of MMC and PLL frequency output
3.1. 不同SSO场景下MMC耗散能流模型验证
1) SSO收敛场景.
当串联补偿度设置为40%时,在t=2 s时投入串补电容
图 9
图 10
图 10
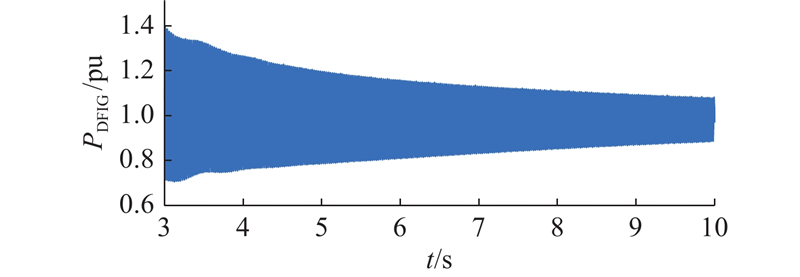
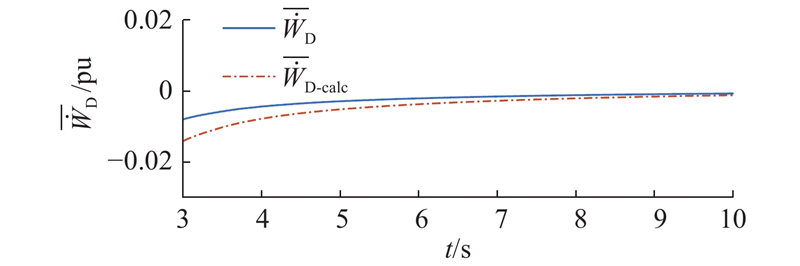
SSO收敛场景下
Fig.10
Measured and calculated values of
2) SSO发散场景.
当串联补偿度设置为45%时,在t=2 s时投入串补电容
图 11
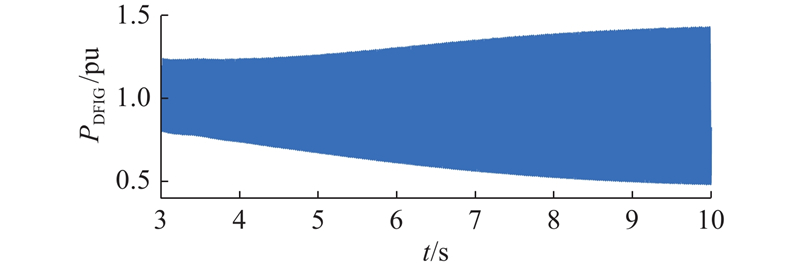
图 11 SSO发散场景下DFIG风场输出有功功率
Fig.11 Active power output of DFIG when SSO diverges
图 12
图 12
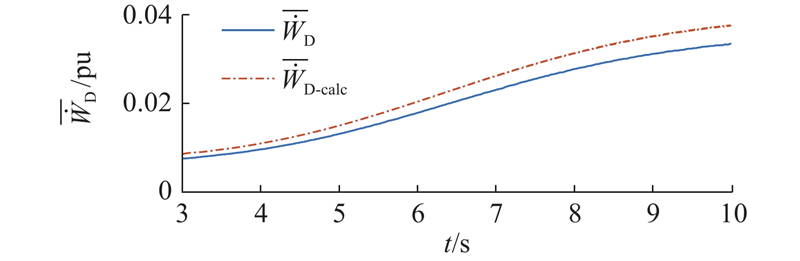
SSO发散场景下
Fig.12
Measured and calculated values of
3.2. 各参数对MMC耗散能流及系统稳定性的影响
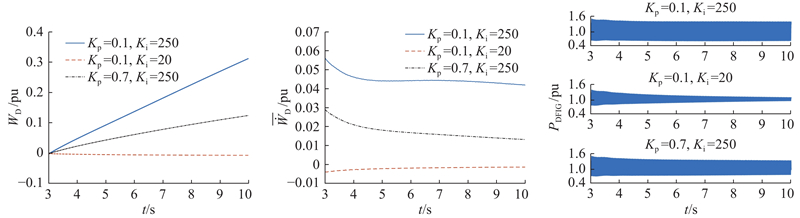
1) MMC功率外环控制参数的影响.
在不改变其他预设参数的前提下,调节MMC功率外环控制参数
如图13所示为控制外环配置(i)、(ii)、(iii)下仿真结果的对照. 配置(ii)相比于配置(i),积分系数
图 13
图 13 不同功率外环参数下的仿真实验结果
Fig.13 Simulation results under different power outer loop parameters
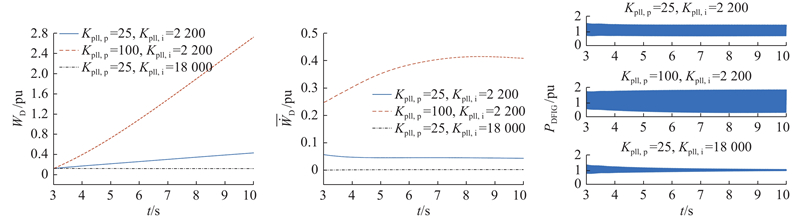
2) PLL参数的影响.
在不改变其他预设参数的前提下,研究锁相环参数
如图14所示为PLL配置(i)、(ii)、(iii)下仿真结果的对照. 配置(ii)相比于配置(i),PLL比例系数
图 14
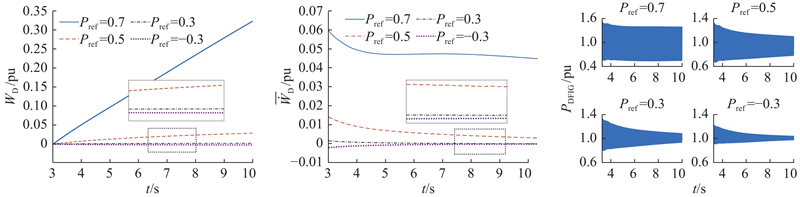
3) MMC有功功率参考值的影响.
其他预设参数不变,依次设置MMC交流侧有功功率参考值
图 15
图 15 不同MMC有功功率参考值下的实验结果
Fig.15 Simulation results under different MMC active power references
3.3. 功率环/锁相环带宽与MMC耗散能流的联系
控制带宽是控制器设计中的重要参数. 在定功率控制MMC中,定功率控制环/锁相环的带宽可由相应控制参数计算得到. 为了探究MMC功率环、锁相环带宽与MMC耗散能流的关系,在不同带宽下进行仿真实验并记录MMC端口耗散能流平均变化率,结果如下(须注意,以下结果与结论均是在MMC向外部输出功率,即
1) 功率环带宽.
MMC定功率控制框图如图5所示. 对电流内环进行整定(即Kp2/Ki2=Leq/Req)后,电流环可等效为一阶环节,即
式中:
由此可得简化后的MMC定功率控制回路,如图16所示.
图 16
定功率控制闭环传递函数为
可见定功率控制传递函数实为二阶环节,且有
其带宽可以近似计算,表达式如下:
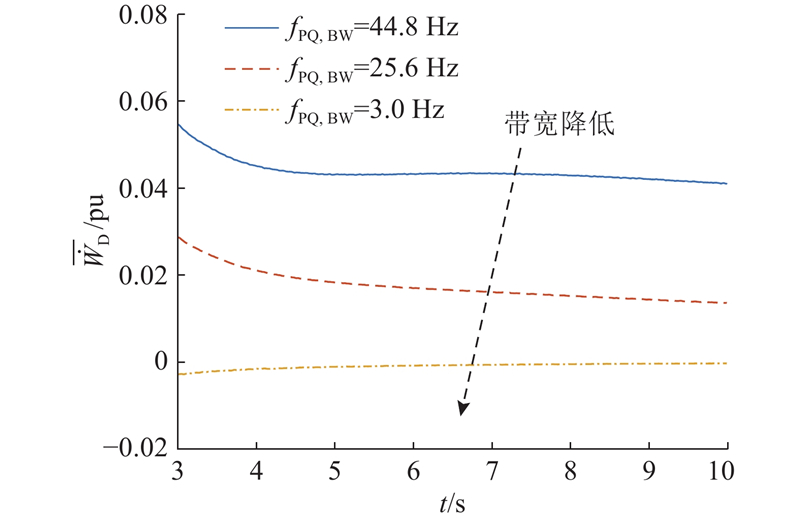
如图17所示为功率环带宽为44.8、25.6、3.0 Hz下MMC耗散能流平均变化率(
图 17
图 17
不同功率环带宽下的
Fig.17
Curves of
2) 锁相环带宽.
依据如图4所示的PLL框图,可得其闭环传递函数为
可见PLL传递函数同样为二阶环节,且有
其带宽亦可以通过式(32)近似计算.
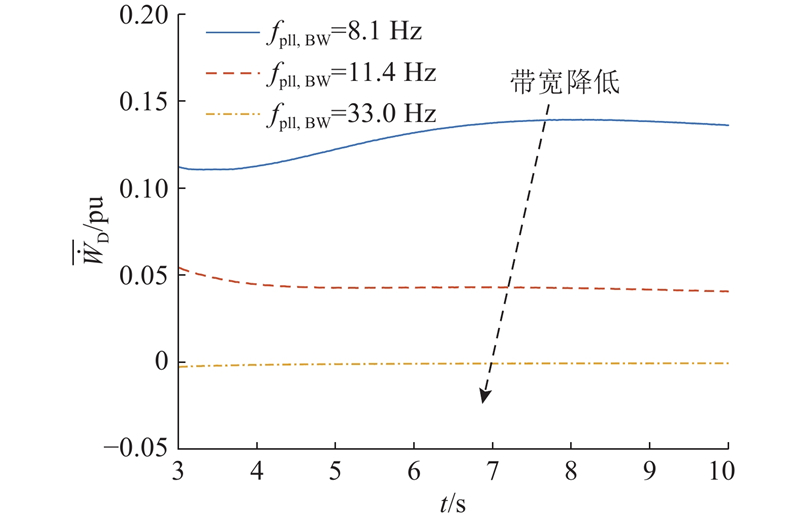
如图18所示SRF-PLL带宽fpll,BW为8.1、11.4、33.0 Hz下MMC耗散能流平均变化率曲线. 可见随着锁相环带宽增加,
图 18
图 18
不同PLL带宽下的
Fig.18
Curves of
4. 结 论
基于耗散能流理论,对次同步振荡下定功率控制MMC端口源汇特性进行研究,得出以下结论:
(1) 得出了MMC输出端DEF平均斜率的解析表达式,并验证了其正确性. DEF平均斜率与MMC恒功率控制器参数、PLL参数和MMC输出功率参考值相关.
(2) 作为MMC源/汇特性的指标,MMC端口DEF的平均斜率可评估MMC对系统稳定性的影响. 正斜率DEF代表MMC 是振荡能量源,会降低系统稳定性;负斜率DEF代表MMC 是振荡能量汇,可提高系统稳定性. 此外,DEF 平均斜率的大小反映了MMC 对系统稳定性的影响程度.
(3) 在SSO期间,MMC既可能表现为能量源也可能表现为能量汇. 利用DEF平均斜率的表达式,可以快速确定MMC的能量源/能量汇特性. 这将有助于MMC控制参数设计和SSO抑制.
未来工作将着力于探求更全面、详细的MMC端口耗散能流模型,计及MMC其他控制模式以及MMC内部环流的影响,并基于此设计抑制MMC中SSO的控制器.
参考文献
Optimal design of controller parameters for improving the stability of MMC-HVDC for wind farm integration
[J].DOI:10.1109/JESTPE.2017.2759096 [本文引用: 2]
双馈直驱风机混合接入MMC-HVDC送端系统的次同步振荡特性分析与抑制
[J].
Sub-synchronous oscillation characteristics analysis and suppression of DFIGs and PMSGs mixed access to MMC-HVDC sending-end system
[J].
Investigation of SSTI between practical MMC-based VSC-HVDC and adjacent turbogenerators through modal signal injection test
[J].
Real-time MPSoC-based electrothermal transient simulation of fault tolerant MMC topology
[J].DOI:10.1109/TPWRD.2018.2866562 [本文引用: 1]
Gole. MMC-HVDC内部谐波模态识别及其稳定性分析
[J].
Identification and stability analysis of the internal harmonic modes of the MMC-HVDC system
[J].
模块化多电平换流器数学建模方法综述
[J].
Review of modeling method of modular multilevel converter
[J].
Impedance-based stability analysis of voltage-controlled MMCs feeding linear AC systems
[J].DOI:10.1109/JESTPE.2019.2911654 [本文引用: 1]
海上风电场经MMC-HVDC并网的阻抗建模及稳定性分析
[J].
Impedance modeling and stability analysis of MMC-based HVDC for offshore wind farms
[J].
交直流混联系统的能量函数构造方法综述与探究
[J].
Review and research on construction methods of energy function for hybrid AC-DC power system
[J].
Development of an energy function reflecting the transfer conductances for direct stability analysis in power systems
[J].DOI:10.1049/ip-gtd:19971458 [本文引用: 1]
基于Hamilton实现的电力系统振荡源设备级定位
[J].
Oscillation source location in control devices of generators based on Hamiltonian realization
[J].
端口能量及其在风电系统暂态稳定分析中的应用
[J].DOI:10.7500/AEPS20140822002 [本文引用: 2]
Port energy and its application to transient stability analysis of power systems with wind generation
[J].DOI:10.7500/AEPS20140822002 [本文引用: 2]
基于振荡能量的低频振荡分析与振荡源定位 (一)理论基础与能量流计算
[J].
Low frequency oscillation analysis and oscillation source location based on oscillation energy part one: mathematical foundation and energy flow computation
[J].
Insights into dissipating energy-based source/sink characterization of TCSC and STATCOM for low-frequency oscillations
[J].DOI:10.1109/TPWRD.2022.3215929 [本文引用: 2]
Stability assessment of DFIG subsynchronous oscillation based on energy dissipation intensity analysis
[J].DOI:10.1109/TPEL.2019.2962217 [本文引用: 1]
Interconnecting power converter control role assignment in grids with multiple AC and DC subgrids
[J].DOI:10.1109/TPWRD.2023.3236977 [本文引用: 1]
Power system damping from energy function analysis implemented by voltage-source-converter stations
[J].DOI:10.1016/j.jpgr.2007.12.003 [本文引用: 1]
Use of energy function to evaluate the additional damping provided by a STATCOM
[J].DOI:10.1016/j.jpgr.2004.04.007 [本文引用: 1]
A forward compensation method to eliminate DC phase error in SRF-PLL
[J].DOI:10.1109/TPEL.2022.3142252 [本文引用: 1]