电能替代的应用在能源系统低碳转型中具有重要意义,通过相关设备将冗余的可再生能源转化成热能可以有效减少弃风弃电,提高系统调度灵活性[7]. Xu等[8]为综合能源系统开发了一种低碳经济调度方法,以解决能源效率的不确定性. 王谦等[9]提出结合碳排放权交易的工业园区综合能源系统风、光、储配置优化方案. 陈艳波等[10]指出目前工业园区的绿电消纳方法,主要包括利用蓄热元件进行储能或利用热泵和电锅炉将多余的电能转化为热量. 但以上场景仅作为示范项目进行配置,尚未实现大规模推广应用. 因此,探究清洁能源消纳场景下的工业园区蒸汽供热系统新型供汽模式,对中国工业园区的高效低碳发展具有指导意义. 本研究围绕耦合绿电的园区蒸汽供热系统,开展系统建模、特性分析及规划设计研究,以助力构建清洁低碳的新型能源系统.
1. 电热综合能源需求响应
近年来,需求侧响应技术逐渐成熟,实施需求响应管理能够降低电力用户购电费用,缓解电网调峰压力,提高电网运营可靠性. Schledorn等[11]提出Frigg框架用于在能源系统分析中整合基于价格的间接需求响应模型. 邢海军等[12]考虑多种源-荷灵活性资源提出综合能源双层调度模型,并利用目标级联分析法求解. Zhang等[13]考虑多种需求响应及其不确定性,对计及光伏-储能的住宅电动汽车充电桩规划问题开展多目标容量分配. 范帅等[14]提出智能电热网络的架构,采用两段式优化决策模型兼顾用户舒适度与负荷尖峰控制. Zhang等[15]在高度准确聚合模型的基础上设计空调系统的聚合控制策略,能提供频率调节与峰值负荷削减的需求响应服务. Pu等[16]从供给侧和需求侧解释夜间电转热价格计算机制及其环境效益,利用夜间多余的风电提供电加热. Hemmati等[17]建立结合可再生能源、储能和需求响应的可重构微电网优化调度模型,能够在提高系统灵活性与可靠性的同时减少系统运行成本与碳排放. Xie等[18]建立需求侧联合响应和共享储能的建模框架,提出考虑需求侧响应和共享储能联合调度的多区域能源系统优化调度模型. Zhong等[19]综合考虑用户响应特性与管存蓄热特性,提出蒸汽供热系统分时优化定价方法,缓解了系统的调峰压力. 张通等[20]将价格型需求响应的影响因素分为电、气分时自弹性和电-气交叉价格弹性. Pan等[21]类比电力系统的价格型需求响应和激励型需求响应,进一步构建了涵盖制冷、供热、电力和燃气的综合需求响应模型. 总体而言,当前关于需求响应理论框架及算法的研究已经较完善,其应用主要集中于在既定价格机制下提升系统运行经济性、灵活性,但较少关注价格机制本身的优化设计,并缺乏对优化价格机制如何影响系统运行的深入分析.
需求响应的核心思路在于将用户纳入管理体系,鼓励用户根据能源价格或激励措施调整用能量. 价格型需求响应通过动态定价机制来引导用户的用能行为,主要包括尖峰价格、分时价格以及实时价格3种. 本研究对象为耦合绿电的工业园区蒸汽供热系统,响应用户为工业蒸汽用户,其生产过程须按照严格的生产流程. 价格型需求响应能够给予用热企业充分的决策与响应时间,从而调整生产计划,是与其生产模式相契合的需求响应机制. 因此,本研究开展计及分时汽价的耦合绿电工业园区蒸汽供热系统需求响应研究.
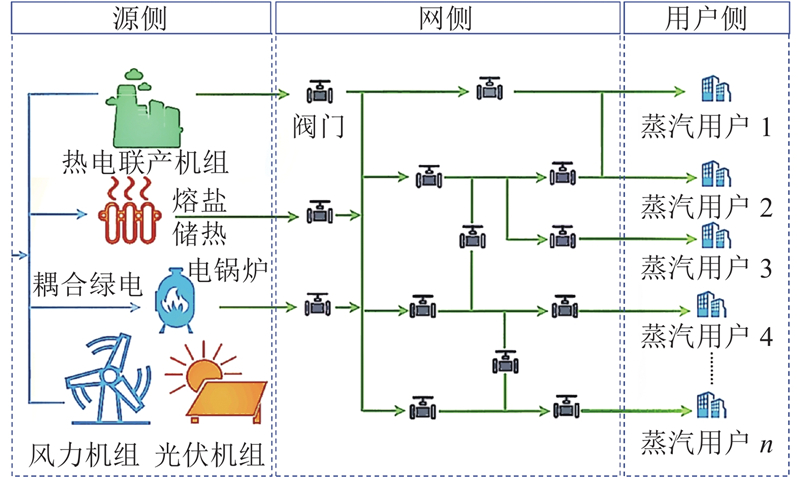
耦合绿电工业园区蒸汽供热系统基本能流结构如图1所示,由电力系统与蒸汽供热系统2部分构成,系统通过整合风力发电和光伏发电,结合电锅炉和热电联产技术,提供高效的蒸汽供热服务,并且能有效利用储热技术平衡供需,提升系统的经济性和环保性.
图 1
图 1 耦合绿电工业园区蒸汽供热系统基本能流结构图
Fig.1 Energy flow diagram of coupled green electricity industrial park steam heating system basic
本研究在厘清负荷转移特性、系统建模方法与系统效益计算理论的基础上,进一步开展分时汽价优化和双层容量配置优化研究. 通过对比分析,对将分时汽价纳入决策体系之后的系统效益变化进行量化.
2. 耦合绿电工业园区蒸汽供热系统分时汽价优化定价模型
2.1. 用户负荷转移特性
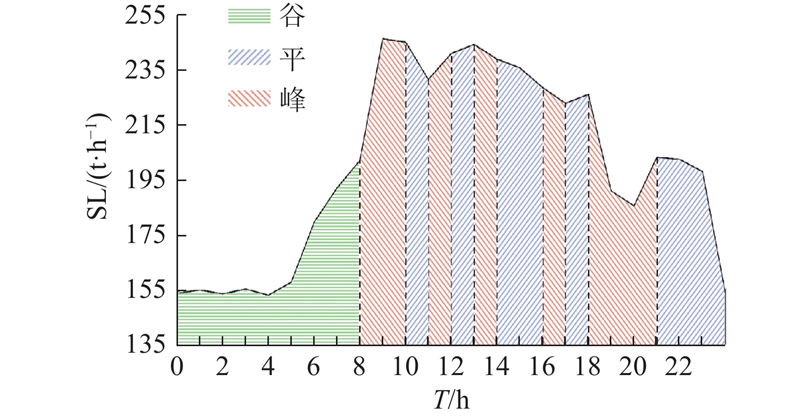
在传统的分时定价策略中,峰谷时段划分仅根据固定的负荷阈值,用户负荷高于负荷阈值上限的时段划分为峰时段,反之则划分为谷时段. 本研究考虑耦合绿电场景下的可再生能源出力波动,定义用户净负荷曲线为原用户负荷曲线减去可再生能源出力曲线;结合热源出力曲线,设置用户净负荷大于热源出力的时段为用汽高峰时段,用户净负荷小于热源出力的时段为用汽低谷时段,其余时段为平时段.
面对分时汽价的调节,园区蒸汽用户负荷转移的情况主要有3种:峰时段负荷向平时段转移,峰时段负荷向谷时段转移,以及平时段负荷向谷时段转移.
对于第i类用户,其峰-平负荷转移率εpfi表达式为
式中:下标pf表示峰-平,
考虑到负荷转移的不确定性,用梯形隶属度函数
式中:λi1、λi2、λi3和λi4 为用户响应特性所确定的隶属度参数.
考虑用户负荷转移的不确定性后的负荷转移率
式中:
2.2. 系统典型单元设备模型
电能替代改造设备具体包括电锅炉和熔融盐蓄热设备. 利用电锅炉耦合绿电,将多余电能转化为热能,可以代替原有的热源,在增加可再生能源消纳量的同时承担一部分蒸汽热负荷;也可以结合熔融盐蓄热设备将多余热量以高温熔融盐的形式储存,所存储热能在用电高峰阶段重新转化为电能并出售,在用汽高峰阶段直接输出以缓解热源供热压力.
电锅炉机组相关表达式如下:
式中:Qeb表示电锅炉制热量;Peb表示电锅炉运行功率;ηeb表示电锅炉电热转换效率;Peb,max表示设备额定功率,电锅炉运行功率受设备额定功率约束.
结合蒸汽供热系统实际工况,选用熔融盐作为蓄热介质,采用双罐式熔融盐蓄热罐,其关键参数为蓄热量,相关公式为
式中:
使用矩阵描述工业园区蒸汽供热系统拓扑结构. 对于蒸汽供热系统,将其网络结构简化为单线支路,基于图论原理,将除管道外的其他部分视作节点,节点包括源侧、用户以及中间节点,以节点-管道关联矩阵进行描述.
对于节点数为l、管段数为m、闭环回路数为k的蒸汽管网,其节点-管道关联矩阵为
其矩阵元素aij的定义如下:
由于闭合网络中节点流量守恒,可得
式中:R为各个管道内的流量向量,R=[R1,R2,···,Rm]T;Q为各个节点的净质量流量向量,Q=[Q1,Q2,···,Qm]T,一般取流入该节点为正值,流出该节点为负值.
环路-管段关联矩阵为
其矩阵元素bij的定义为
由于闭合回路中的压降与温降为0,可得
式中:ΔP为闭合网络内的压降向量,ΔP=[ΔP1, ΔP2,···,ΔPm]T,ΔT为闭合网络内的温降向量,ΔT=[ΔT1, ΔT2,···,ΔTm]T.
通过上述典型单元模块,构建耦合绿电工业园区蒸汽供热系统模型.
2.3. 系统运行模式及效益分析
实施分时汽价的目的是引导用户负荷进行转移,结合电能替代设备更有效地实现绿电消纳. 因此,负荷转移后的负荷曲线不仅应更为平滑以缓解热电机组调峰压力,而且能够在一定程度上削弱可再生能源的不确定性影响.
本研究设定相关电转热设备能够分担x比例的热负荷出力的时段为绿电时段. 在绿电/谷电时段,电能充盈,系统可直接利用绿电与谷电. 方式1为通过电锅炉加热给水,直接制取蒸汽,通过蒸汽供热管网输送给蒸汽用户使用,以辅助热电联产机组. 方式2为将多余电能转化为热量储存于高温熔融盐蓄热罐中,在电价非谷时段以及绿电资源间歇时段,释放熔盐高温蓄热罐中的高温熔融盐介质到高温蒸发器,利用蒸汽发生器加热给水制取蒸汽,降温后的介质进入低温蒸发器随后逐步回收. 系统结合蓄热装置与需求响应机制,通过将绿电与低价的谷电转换成热以满足蒸汽用户的用量需求,缓解了机组的调峰压力,实现负荷的削峰填谷,提高了系统的稳定性,该供汽模式在现如今以及未来的碳价高昂、电价普遍降低的场景中,相较于传统蒸汽供热系统供汽模式具有更好的经济优势与节能优势.
在电价非谷时段以及绿电资源间歇时段,熔融盐蓄热罐中的热量也已经完全释放,相关电转热设备无法承担x比例热负荷出力,主要依靠热电联产机组实现供需平衡,使得热电联产机组调峰压力难以得到缓解. 在外部因素确定的情况下,可以通过增加相关电转热设备的功率以及容量来实现绿电时段的占比增大,理论上能够实现全天24 h均为绿电/谷电时段,但由于过量配置电转热设备不具备经济效益,在现阶段并不现实. 更为有效的方式是通过增加分时汽价的汽价差,更大程度地引导蒸汽用户进行负荷转移以实现削峰填谷.
在系统运行过程中,耦合绿电的工业园区蒸汽供热系统须满足区域内的热负荷需求,即
式中:
系统经济效益用系统建设成本表征,系统建设成本包括设备投资成本、设备维护成本与运行成本,其计算公式为
式中:
设备投资成本由各类设备投资费用构成:
式中:
设备维护成本由设备的定期检查、维修与保养等构成,可按照一定比例折算为初始投资成本,即
式中:
耦合绿电工业园区蒸汽供热系统的运行成本由CHP机组的燃煤费用与电锅炉耗电费用构成. 标煤价格相对稳定,但在长期合同中存在一定范围的波动,电价也会因峰谷时段变化产生波动,因此设备运行成本计算公式为
式中:
系统运行过程中的收益应大于运行成本,以保证供能模式的经济性. 工业园区蒸汽供热系统收益主要以出售蒸汽为主,多余电能按上网电价出售给电力市场,因此其收益计算公式为
式中:R表示系统售汽收益, Ps表示蒸汽价格, Qs表示T时间内的总蒸汽出售量, Pe表示上网电价, Qe表示T时间内的总电力出售量.
系统环境效益用系统污染物排放量进行表征. 在系统运行过程中,风光机组运行过程中不产生污染物,因此仅考虑CHP机组燃煤所产生的污染排放,其计算公式为
式中:Ppd表示系统运行期间污染物排放总量;Pchp(t)表示t时段热电联产机组功率;Echp(j)表示热电联产机组的第j种污染物的排放系数;nw表示污染物种类总数,本研究仅考虑CO2、SO2、NOX及CO这4种污染物.
2.4. 系统分时汽价优化定价模型
蒸汽供热系统需求响应的优化目标函数为最小峰谷负荷差和最低用户购汽成本,表达式如下.
1)峰谷平均负荷差最小:
2)蒸汽用户总购汽费用最低:
式中:
采用NSGA-II算法求解,其中约束条件如下.
1)分时汽价响应后用户用汽总量不变:
2)分时汽价响应后用户购汽费用不能增加,否则用户将拒绝参与响应:
式中:Lt为响应前t时刻的原始负荷,Pt为响应前t时刻的原始电价.
3)为了避免负荷调节后发生峰谷倒置现象,设置合理的峰谷汽价比上下限:
4)为了使分时汽价响应具有较好的参与度,对各时段汽价上下限做出约束:
2.5. 系统双层优化规划方法
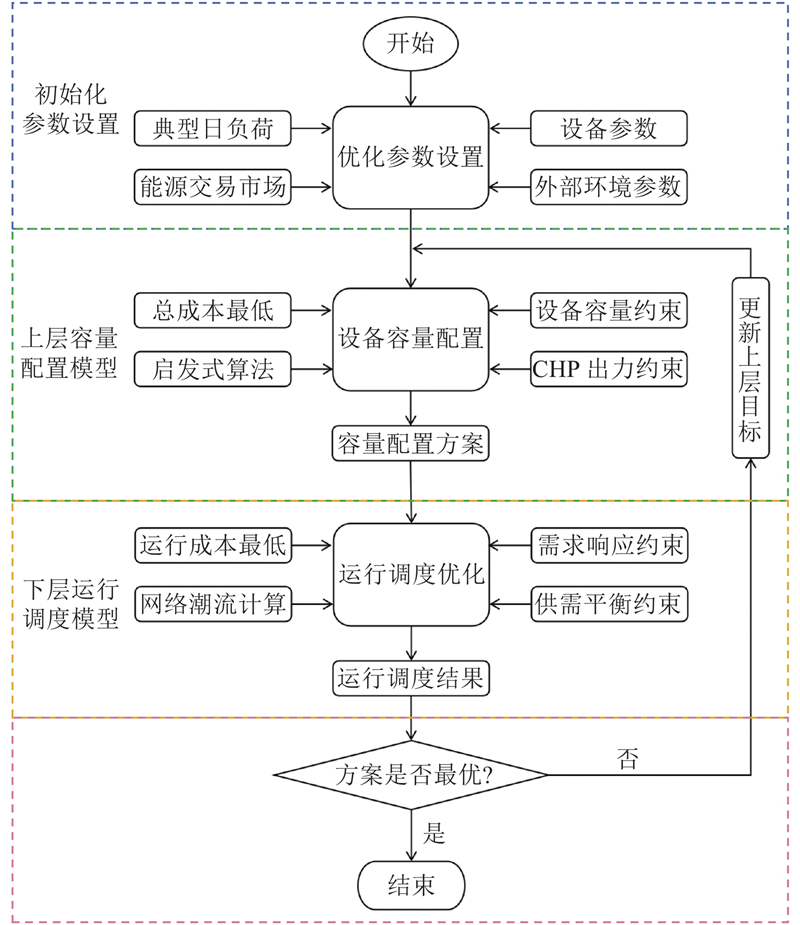
基于上述分时汽价优化结果进一步开展系统双层优化配置研究,相关配置框架图如图2所示. 上层配置模型以最小化运行周期费用为优化目标,结合下层所得的最优运行策略,确定绿电相关设备的配置容量. 下层优化调度模型根据上层模型给定的绿电相关设备容量,结合典型日的系统原始机组出力、蒸汽供热系统网络结构、环境条件及清洁电力供应情况为输入,求解出以最低系统运行成本为目标的运行调度策略. 为了更加直观地体现园区蒸汽供热系统中引入绿电相关设备后在增加可再生能源消纳能力、降低污染物排放和减少碳排放方面的积极作用,将环境效益进行显性量化,具体基于污染物排放税和碳交易成本,将这些隐性成本纳入系统运行成本中进行量化分析.
图 2
图 2 计及分时汽价的耦合绿电工业园区蒸汽供热系统双层优化配置框架
Fig.2 Coupled green electricity industrial park steam heating system bi-level optimization configuration framework considering time-of-use steam pricing
系统上层优化配置模型以最小化运行周期费用为目标函数,运行周期费用包括设备投资成本、设备维护成本和运行成本,计算公式为
式中:f(x)为系统运行成本的函数. 系统运行成本函数为下层模型反馈回上层的优化结果. 上层约束条件主要为设备容量上下限约束,采用标准遗传算法(NSGA)对上层优化配置模型进行求解.
系统下层模型以典型日的系统需求侧用户用汽负荷、系统网络结构、相关机组配置等为边界条件,求解系统运行成本最小值,其目标函数计算公式为
式中:fenv(x)表示污染物排放税.
环境效益显性量化为经济成本的表达式为
式中:Pchp(t)表示t时段热电联产机组功率;Echp(j)表示热电联产机组的第j种污染物的排放系数.
系统下层须满足网络潮流约束、供需平衡约束和设备运行约束,其中设备运行约束要求热电联产机组的热出力、电出力及其爬坡速率保证在安全范围内. 下层模型采用确定性算法开展以经济性为目标的系统调度优化,并生成对应于各个规划方案的运行调度结果.
3. 结果对比与讨论
以浙江某园区为例开展系统分时汽价优化定价研究,基于优化定价结果进一步开展系统双层优化规划研究,与传统统一定价模式下的优化规划结果进行对比分析.
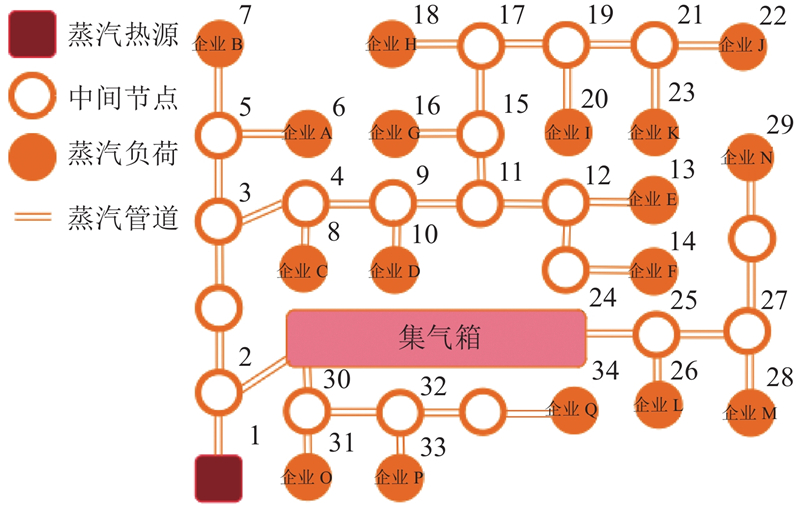
案例园区由1个热源、17个热用户及相应的管道等设备组成,共有36个节点,其出口蒸汽参数为1.3 MPa,160 t/h,270 ℃,全长超17 km,所供应的蒸汽售价为165.2元/t. 将蒸汽热源所在设为热源节点,将工业用户所在设为负荷节点,绘制系统拓扑结构如图3所示.
图 3
图 3 某园区蒸汽供热系统拓扑结构图
Fig.3 Certain power plant steam heating system topology diagram
3.1. 系统分时汽价优化结果
图 4
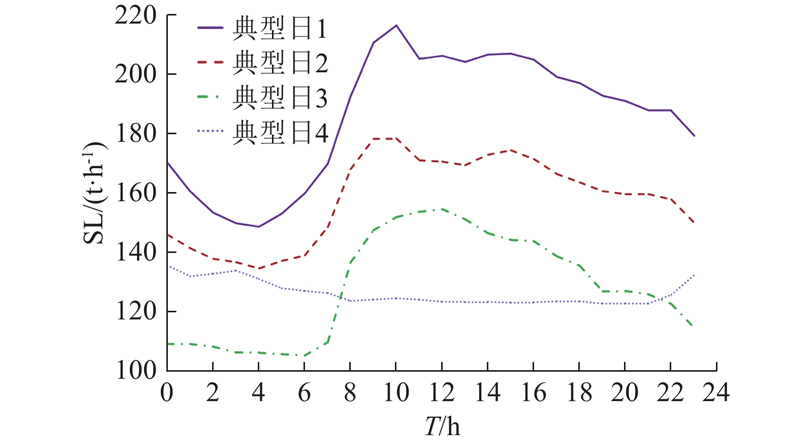
负荷聚类数据集及聚类结果表明,园区中大多数运行状况下的蒸汽需求存在明显的用汽峰谷特征,0:00—8:00期间对蒸汽需求量低,9:00—12:00期间达到用汽高峰,具有较好的削峰填谷响应潜力. 仅有少数运行日下的热负荷(图4中典型日4)不存在明显的用汽峰谷特征. 3类存在明显用汽峰谷特征的热负荷曲线整体用汽趋势近似,对应低、中、高负荷的运行状态. 结合4类典型日聚类结果及其平均负荷量大小,分别对其负荷转移率曲线进行参数设置,具体如表1所示. 其中
表 1 不同类型用户负荷响应参数设置
Tab.1
| 用户类型 | 峰-谷 | 峰-平 | 平-谷 | ||||||||
| 第1类用户 | 55.0 | 0.08 | 65.0 | 0.04 | 55.0 | 0.06 | |||||
| 第2类用户 | 45.0 | 0.10 | 55.0 | 0.06 | 35.0 | 0.08 | |||||
| 第3类用户 | 35.0 | 0.20 | 50.0 | 0.08 | 45.0 | 0.12 | |||||
| 第4类用户 | 50.0 | 0.15 | 45.0 | 0.06 | 40.0 | 0.10 | |||||
表 2 典型日系统热源出力及用户负荷数据
Tab.2
| 时间 | Qhs/(t·h−1) | Lt/(t·h−1) | 时间 | Qhs/(t·h−1) | Lt/(t·h−1) | 时间 | Qhs/(t·h−1) | Lt/(t·h−1) | ||
| 0:00 | 155.76 | 154.14 | 8:00 | 213.01 | 202.33 | 16:00 | 233.19 | 228.89 | ||
| 1:00 | 154.74 | 155.32 | 9:00 | 246.10 | 246.59 | 17:00 | 221.39 | 223.13 | ||
| 2:00 | 155.33 | 153.95 | 10:00 | 244.84 | 245.43 | 18:00 | 228.05 | 226.36 | ||
| 3:00 | 153.17 | 155.68 | 11:00 | 234.21 | 231.83 | 19:00 | 197.09 | 191.33 | ||
| 4:00 | 147.16 | 153.47 | 12:00 | 245.66 | 241.23 | 20:00 | 191.75 | 185.85 | ||
| 5:00 | 159.44 | 158.13 | 13:00 | 242.34 | 244.54 | 21:00 | 220.71 | 203.57 | ||
| 6:00 | 189.84 | 179.94 | 14:00 | 241.30 | 239.22 | 22:00 | 204.42 | 202.75 | ||
| 7:00 | 197.93 | 192.36 | 15:00 | 235.09 | 236.05 | 23:00 | 195.79 | 198.33 |
图 5
采用NSGA-II算法对系统分时汽价模型进行求解,参数设置如下:种群数量P=100;最大遗传代数N=100;交叉概率Pc=0.9;变异概率Pm=0.33.
图 6
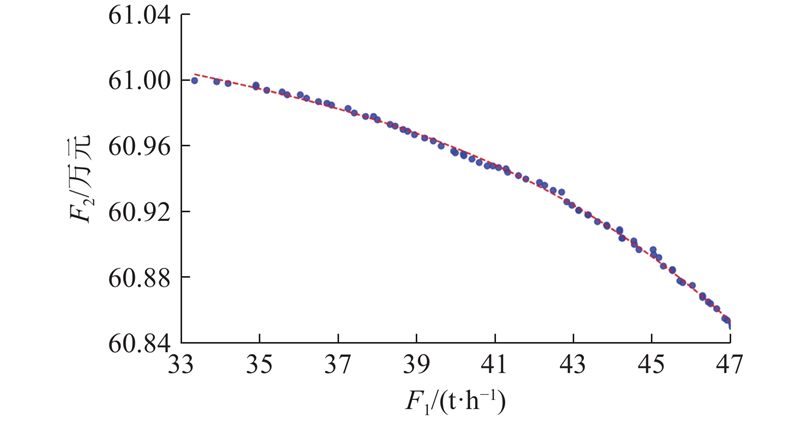
图 6 分时汽价优化目标函数帕累托解集
Fig.6 Pareto set of time-of-use steam pricing optimization objective function
表 3 分时汽价优化结果
Tab.3
| 优化结果参数 | 数值 |
| 峰时段汽价 | 210 元 |
| 平时段汽价 | 180 元 |
| 谷时段汽价 | 85 元 |
| 平均峰谷负荷差 | 32.2 t |
| 节省购汽费用 | 2.62 万元 |
| 峰谷汽价比 | 2.47 |
3.2. 系统双层优化规划结果与对比
热电厂机组年标准供热煤耗为145.14 g/(kW·h),供电煤耗为166.61 g/(kW·h),煤价为
表 4 不同来源污染物排放数据
Tab.4
| 来源 | CO2 | CO | NOx | SO2 |
| 热电联产 | 305.74 | 0.05 | 1.48 | 1.85 |
| 外购谷电 | 632.40 | 0.11 | 2.07 | 3.28 |
| 外购绿电 | 0 | 0 | 0 | 0 |
上层模型NSGA算法参数设置如下:种群数量P=50;最大遗传代数N=300;选择算子采用排序选择方法;交叉算子采用两点交叉方法,交叉点随机选择;变异率设为0.1. 下层模型使用Gurobi求解器进行确定性求解. 设置4种不同CHP机组运行出力上限作为边界条件,模拟可再生能源装机容量占比增加,CHP机组出力减小的场景. 相关设备参数见表5.
表 5 相关设备参数表
Tab.5
| 设备 | ||||
| 风力机组 | 0.024 | 8 | 22 | |
| 光伏机组 | 0.020 | 8 | 25 | |
| 电锅炉 | 0.020 | 8 | 20 | |
| 熔盐蓄热 | 50 元/(kW·h) | 0.002 | 8 | 25 |
场景1:系统中不配置任何相关设备,仅存在原始CHP机组. 作为初始对照.
场景2:设置CHP机组出力上限为额定负荷的70%,通过在系统中配置相关设备,在满足供需平衡的基础上,实现系统可再生能源消纳能力提升.
场景3:设置CHP机组出力上限为额定负荷的60%,进一步挤压燃煤机组出力上限后,相关设备容量配置增加,可再生能源消纳程度进一步提升,但是系统总收益不可避免的降低.
场景4:设置CHP机组出力上限为额定负荷的50%.
表 6 计及分时汽价的双层优化配置结果-设备容量
Tab.6
| 场景 | QPV/MW | QWT/MW | QEB/MW | QHS/(MW·h) | |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 9.34 | 15.23 | 65.41 | 169.32 |
| 3 | 0 | 55.30 | 50.59 | 158.44 | 829.23 |
| 4 | 0 | 94.69 | 87.59 | 302.37 |
表 7 计及分时汽价的双层优化配置结果-经济性
Tab.7
| 场景 | fenv(x)/万元 | F(x)/万元 | ||
| 1 | 0 | |||
| 2 | 169.32 | |||
| 3 | 829.23 | |||
| 4 |
表 8 不考虑分时汽价优化的系统双层优化配置结果-设备容量
Tab.8
| 场景 | QPV/MW | QWT/MW | QEB/MW | QHS/(MW·h) | |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 12.53 | 14.56 | 108.76 | 209.78 |
| 3 | 0 | 60.24 | 53.58 | 200.95 | 903.13 |
| 4 | 0 | 94.85 | 87.70 | 371.17 |
表 9 系统双层优化配置结果-经济性
Tab.9
| 场景 | fenv(x)/万元 | F(x)/万元 | ||
| 1 | 0 | |||
| 2 | 209.78 | |||
| 3 | 903.13 | |||
| 4 |
4. 结 语
基于耦合绿电的工业园区蒸汽供热系统模型,在系统中开展需求响应研究. 基于用户需求响应分析,提出耦合绿电工业园区蒸汽供热系统分时汽价优化定价模型,结合实际案例开展蒸汽供热系统分时汽价优化定价研究. 进一步,提出计及分时汽价的耦合绿电工业园区蒸汽供热系统双层优化配置模型,对计及分时汽价的耦合绿电工业园区蒸汽供热系统电转热设备配置容量及运行方案进行优化分析,结合实际案例进行了详细的讨论和研究. 结果表明,在系统中引入分时汽价策略能够有效削峰填谷,在某案例中的验证表明可降低58.32%的平均峰谷负荷差,在该策略下系统优化配置结果较统一汽价方案而言,运行周期内3种不同运行场景蓄热设备配置成本,投资维护成本与总成本均有所降低. 本研究提出的计及分时汽价的耦合绿电工业园区蒸汽供热系统双层优化配置方法可以有效应用于未来工业园区蒸汽生产场景.
参考文献
Thermal energy storage in district heating and cooling systems: a review
[J].DOI:10.1016/j.apenergy.2019.113474 [本文引用: 1]
Demand response and other demand side management techniques for district heating: a review
[J].DOI:10.1016/j.energy.2020.119440 [本文引用: 1]
Demand side management in district heating networks: a real application
[J].DOI:10.1016/j.energy.2019.05.131 [本文引用: 1]
Operation optimization strategy for wind-concentrated solar power hybrid power generation system
[J].DOI:10.1016/j.enconman.2018.01.040 [本文引用: 1]
Low-carbon economic dispatch of integrated energy system considering the uncertainty of energy efficiency
[J].
零碳交易下工业园区综合能源系统优化配置
[J].
Optimal allocation of integrated energy systems in industrial parks under zero carbon trading
[J].
基于大语言模型绿电预测和绿电交易的园区综合能源系统集群多目标协同运行方法
[J].
Multi-objective collaborative operation method for park-level integrated energy system cluster based on large language model for green electricity prediction and trading
[J].
Frigg 2.0: integrating price-based demand response into large-scale energy system analysis
[J].DOI:10.1016/j.apenergy.2024.122960 [本文引用: 1]
含多种灵活性资源的综合能源系统低碳优化调度
[J].
Low-carbon optimal scheduling of integrated energy system considering multiple flexible resources
[J].
Joint planning of residential electric vehicle charging station integrated with photovoltaic and energy storage considering demand response and uncertainties
[J].DOI:10.1016/j.energy.2024.131370 [本文引用: 1]
分散式电采暖负荷协同优化运行策略
[J].
Collaborative optimal operation strategy for decentralized electric heating loads
[J].
Aggregated modeling and control of air conditioning loads for demand response
[J].DOI:10.1109/TPWRS.2013.2266121 [本文引用: 1]
Feasible electricity price calculation and environmental benefits analysis of the regional nighttime wind power utilization in electric heating in Beijing
[J].DOI:10.1016/j.jclepro.2018.12.105 [本文引用: 1]
Economic-environmental analysis of combined heat and power-based reconfigurable microgrid integrated with multiple energy storage and demand response program
[J].DOI:10.1016/j.scs.2021.102790 [本文引用: 1]
Optimal scheduling of multi-regional energy system considering demand response union and shared energy storage
[J].DOI:10.1016/j.esr.2024.101413 [本文引用: 1]
Study on time-of-use pricing method for steam heating system considering user response characteristics and thermal storage capacity
[J].DOI:10.1016/j.energy.2024.131056 [本文引用: 1]
考虑需求响应和风电不确定性的能源系统调度
[J].
Energy system scheduling considering demand response and wind power uncertainty
[J].
Multi-objective and two-stage optimization study of integrated energy systems considering P2G and integrated demand responses
[J].DOI:10.1016/j.energy.2023.126846 [本文引用: 1]