[1]
LI Y, GUO W, WANG Y Emotion recognition with attention mechanism-guided dual-feature multi-path interaction network
[J]. Signal, Image and Video Processing , 2024 , 18 (1 ): 617 - 626
[本文引用: 1]
[2]
RANA A, JHA S. Emotion based hate speech detection using multimodal learning [EB/OL]. (2022-02-13) [2024-9-17]. https://arxiv.org/abs/2202.06218v1.
[本文引用: 1]
[3]
ZHANG S, ZHAO X, TIAN Q Spontaneous speech emotion recognition using multiscale deep convolutional LSTM
[J]. IEEE Transactions on Affective Computing , 2022 , 13 (2 ): 680 - 688
DOI:10.1109/TAFFC.2019.2947464
[本文引用: 1]
[4]
ZHANG S, YANG Y, CHEN C, et al Deep learning-based multimodal emotion recognition from audio, visual, and text modalities: a systematic review of recent advancements and future prospects
[J]. Expert Systems with Applications , 2024 , 237 : 121692
DOI:10.1016/j.eswa.2023.121692
[本文引用: 1]
[5]
TOISOUL A, KOSSAIFI J, BULAT A, et al Estimation of continuous valence and arousal levels from faces in naturalistic conditions
[J]. Nature Machine Intelligence , 2021 , 3 (1 ): 42 - 50
DOI:10.1038/s42256-020-00280-0
[本文引用: 1]
[7]
HERRMANN C S, STRÜBER D, HELFRICH R F, et al EEG oscillations: from correlation to causality
[J]. International Journal of Psychophysiology , 2016 , 103 : 12 - 21
DOI:10.1016/j.ijpsycho.2015.02.003
[本文引用: 1]
[8]
WU X, ZHENG W L, LI Z, et al Investigating EEG-based functional connectivity patterns for multimodal emotion recognition
[J]. Journal of Neural Engineering , 2022 , 19 (1 ): 016012
DOI:10.1088/1741-2552/ac49a7
[本文引用: 1]
[10]
WANG W Brain network features based on theta-gamma cross-frequency coupling connections in EEG for emotion recognition
[J]. Neuroscience Letters , 2021 , 761 : 136106
DOI:10.1016/j.neulet.2021.136106
[本文引用: 1]
[11]
CHENG C, ZHANG Y, LIU L, et al Multi-domain encoding of spatiotemporal dynamics in EEG for emotion recognition
[J]. IEEE Journal of Biomedical and Health Informatics , 2023 , 27 (3 ): 1342 - 1353
DOI:10.1109/JBHI.2022.3232497
[本文引用: 1]
[12]
MOON S, MOON S E, LEE J S. Resting-state fNIRS classification using connectivity and convolutional neural networks [C]// IEEE International Conference on Systems, Man, and Cybernetics . Prague: IEEE, 2022: 1724–1729.
[本文引用: 1]
[13]
MOON S E, CHEN C J, HSIEH C J, et al Emotional EEG classification using connectivity features and convolutional neural networks
[J]. Neural Networks , 2020 , 132 : 96 - 107
DOI:10.1016/j.neunet.2020.08.009
[本文引用: 7]
[14]
CHEN C J, WANG J L A new approach for functional connectivity via alignment of blood oxygen level-dependent signals
[J]. Brain Connectivity , 2019 , 9 (6 ): 464 - 474
DOI:10.1089/brain.2018.0636
[本文引用: 1]
[15]
DOSE H, MØLLER J S, IVERSEN H K, et al An end-to-end deep learning approach to MI-EEG signal classification for BCIs
[J]. Expert Systems with Applications , 2018 , 114 : 532 - 542
DOI:10.1016/j.eswa.2018.08.031
[本文引用: 1]
[16]
GUO J Y, CAI Q, AN J P, et al A Transformer based neural network for emotion recognition and visualizations of crucial EEG channels
[J]. Physica A: Statistical Mechanics and Its Applications , 2022 , 603 : 127700
DOI:10.1016/j.physa.2022.127700
[本文引用: 1]
[17]
ZHENG W, PAN B A spatiotemporal symmetrical transformer structure for EEG emotion recognition
[J]. Biomedical Signal Processing and Control , 2024 , 87 : 105487
DOI:10.1016/j.bspc.2023.105487
[本文引用: 4]
[18]
HU X, CHEN Y, YAN J, et al Masked self-supervised pre-training model for EEG-based emotion recognition
[J]. Computational Intelligence , 2024 , 40 (3 ): e12659
DOI:10.1111/coin.12659
[本文引用: 1]
[19]
DEXTER E, ROLLWAGEN-BOLLENS G, BOLLENS S M The trouble with stress: a flexible method for the evaluation of nonmetric multidimensional scaling
[J]. Limnology and Oceanography: Methods , 2018 , 16 (7 ): 434 - 443
DOI:10.1002/lom3.10257
[本文引用: 1]
[20]
KULKARNI S, PATIL P R. Analysis of DEAP dataset for emotion recognition [C]// International Conference on Intelligent and Smart Computing in Data Analytics: ISCDA 2020 . Singapore: Springer Singapore, 2021: 67–76.
[本文引用: 1]
[21]
KOBLER R J, HIRAYAMA J I, ZHAO Q, et al. SPD domain-specific batch normalization to crack interpretable unsupervised domain adaptation in EEG [EB/OL]. (2022-10-12)[2024-09-12]. https://arxiv.org/abs/2206.01323v2.
[本文引用: 1]
[22]
ZHANG G, ETEMAD A Spatio-temporal EEG representation learning on Riemannian manifold and euclidean space
[J]. IEEE Transactions on Emerging Topics in Computational Intelligence , 2024 , 8 (2 ): 1469 - 1483
DOI:10.1109/TETCI.2023.3332549
[本文引用: 3]
[23]
YIN Z, ZHAO M, WANG Y, et al Recognition of emotions using multimodal physiological signals and an ensemble deep learning model
[J]. Computer Methods and Programs in Biomedicine , 2017 , 140 : 93 - 110
DOI:10.1016/j.cmpb.2016.12.005
[本文引用: 2]
[24]
PIHO L, TJAHJADI T A mutual information based adaptive windowing of informative EEG for emotion recognition
[J]. IEEE Transactions on Affective Computing , 2020 , 11 (4 ): 722 - 735
DOI:10.1109/TAFFC.2018.2840973
[本文引用: 2]
[25]
GARG A, KAPOOR A, BEDI A K, et al. Merged LSTM Model for emotion classification using EEG signals [C]// International Conference on Data Science and Engineering . Patna: IEEE, 2019: 139-143.
[本文引用: 2]
[26]
ZHOU Z, ASGHAR M A, NAZIR D, et al An AI-empowered affect recognition model for healthcare and emotional well-being using physiological signals
[J]. Cluster Computing , 2023 , 26 (2 ): 1253 - 1266
DOI:10.1007/s10586-022-03705-0
[本文引用: 2]
Emotion recognition with attention mechanism-guided dual-feature multi-path interaction network
1
2024
... 情感识别指通过文本语言、行为表现和生理信号等信息估计或预测情绪状态[1 ] ,相较声音[2 -3 ] 、文本[4 ] 和面部图像[5 ] 等可伪装的情感信号,生理信号更能客观反应人的情感,脑电图(electroencephalogram, EEG)信号由于具有高时间分辨率、低成本和非侵入性等优点[6 ] ,成为基于生理信号的情感识别研究领域的热点. ...
1
... 情感识别指通过文本语言、行为表现和生理信号等信息估计或预测情绪状态[1 ] ,相较声音[2 -3 ] 、文本[4 ] 和面部图像[5 ] 等可伪装的情感信号,生理信号更能客观反应人的情感,脑电图(electroencephalogram, EEG)信号由于具有高时间分辨率、低成本和非侵入性等优点[6 ] ,成为基于生理信号的情感识别研究领域的热点. ...
Spontaneous speech emotion recognition using multiscale deep convolutional LSTM
1
2022
... 情感识别指通过文本语言、行为表现和生理信号等信息估计或预测情绪状态[1 ] ,相较声音[2 -3 ] 、文本[4 ] 和面部图像[5 ] 等可伪装的情感信号,生理信号更能客观反应人的情感,脑电图(electroencephalogram, EEG)信号由于具有高时间分辨率、低成本和非侵入性等优点[6 ] ,成为基于生理信号的情感识别研究领域的热点. ...
Deep learning-based multimodal emotion recognition from audio, visual, and text modalities: a systematic review of recent advancements and future prospects
1
2024
... 情感识别指通过文本语言、行为表现和生理信号等信息估计或预测情绪状态[1 ] ,相较声音[2 -3 ] 、文本[4 ] 和面部图像[5 ] 等可伪装的情感信号,生理信号更能客观反应人的情感,脑电图(electroencephalogram, EEG)信号由于具有高时间分辨率、低成本和非侵入性等优点[6 ] ,成为基于生理信号的情感识别研究领域的热点. ...
Estimation of continuous valence and arousal levels from faces in naturalistic conditions
1
2021
... 情感识别指通过文本语言、行为表现和生理信号等信息估计或预测情绪状态[1 ] ,相较声音[2 -3 ] 、文本[4 ] 和面部图像[5 ] 等可伪装的情感信号,生理信号更能客观反应人的情感,脑电图(electroencephalogram, EEG)信号由于具有高时间分辨率、低成本和非侵入性等优点[6 ] ,成为基于生理信号的情感识别研究领域的热点. ...
EEG emotion recognition based on the TimesNet fusion model
1
2024
... 情感识别指通过文本语言、行为表现和生理信号等信息估计或预测情绪状态[1 ] ,相较声音[2 -3 ] 、文本[4 ] 和面部图像[5 ] 等可伪装的情感信号,生理信号更能客观反应人的情感,脑电图(electroencephalogram, EEG)信号由于具有高时间分辨率、低成本和非侵入性等优点[6 ] ,成为基于生理信号的情感识别研究领域的热点. ...
EEG oscillations: from correlation to causality
1
2016
... 大脑的高级认知过程不仅反映在振幅和功率指标上,更关键的是体现在大脑不同区域之间的信息交流与协作中. 这种区域间的连通互动对于理解复杂的认知功能至关重要[7 ] . 现代认知神经科学表明,人类在产生与大脑相关的认知活动及行为时,大脑区域间的连通性起着至关重要的作用[8 -9 ] . EEG信号的不同电极通道放置在头皮的不同位置,代表着不同空间位置的信息,所以连通性特征矩阵中电极位置的不同排列方式构成的不同空间连通矩阵,会对情感识别网络的性能产生不同的影响. 因此,构建有效的空间连通矩阵的核心是设计合适的电极排列方式. ...
Investigating EEG-based functional connectivity patterns for multimodal emotion recognition
1
2022
... 大脑的高级认知过程不仅反映在振幅和功率指标上,更关键的是体现在大脑不同区域之间的信息交流与协作中. 这种区域间的连通互动对于理解复杂的认知功能至关重要[7 ] . 现代认知神经科学表明,人类在产生与大脑相关的认知活动及行为时,大脑区域间的连通性起着至关重要的作用[8 -9 ] . EEG信号的不同电极通道放置在头皮的不同位置,代表着不同空间位置的信息,所以连通性特征矩阵中电极位置的不同排列方式构成的不同空间连通矩阵,会对情感识别网络的性能产生不同的影响. 因此,构建有效的空间连通矩阵的核心是设计合适的电极排列方式. ...
Hemispheric asymmetries and emotions: evidence from effective connectivity
1
2018
... 大脑的高级认知过程不仅反映在振幅和功率指标上,更关键的是体现在大脑不同区域之间的信息交流与协作中. 这种区域间的连通互动对于理解复杂的认知功能至关重要[7 ] . 现代认知神经科学表明,人类在产生与大脑相关的认知活动及行为时,大脑区域间的连通性起着至关重要的作用[8 -9 ] . EEG信号的不同电极通道放置在头皮的不同位置,代表着不同空间位置的信息,所以连通性特征矩阵中电极位置的不同排列方式构成的不同空间连通矩阵,会对情感识别网络的性能产生不同的影响. 因此,构建有效的空间连通矩阵的核心是设计合适的电极排列方式. ...
Brain network features based on theta-gamma cross-frequency coupling connections in EEG for emotion recognition
1
2021
... 目前,基于DEAP (database for emotion analysis using physiological signals)的研究大多数采用数据库给出的电极通道顺序作为特征矩阵的排列顺序. Wang[10 ] 提出由于信号的容积传导效应,从电极Fp1开始将最靠近当前电极通道的电极作为顺序排列的下一个电极. Cheng等[11 ] 从左右脑半球的不对称性出发,提出从左额叶区域的电极位置开始,选择最靠近当前电极且位于同脑区半球的电极作为顺序排列的下一电极. Moon等[12 ] 利用深度优先遍历和回溯算法产生多条哈密顿路径,将一定数量的路径作为电极通道的特征矩阵排列顺序. Moon等[13 ] 认为基于物理距离的电极顺序合理但并不是最优解,通过对连通性矩阵进行视差函数降维得到新的电极排列顺序. 以上研究大多使用基于欧氏空间的电极排列顺序,然而脑电信号具有复杂、高维的特点,更适合在黎曼空间进行电极通道所表征的信息流顺序的学习. Chen等[14 ] 提出解剖学视角相距较远的区域可能在生理视角连通性较高. 因此,为了寻找脑电信号传递过程中的真正通路,本研究于黎曼空间中计算电极的排列顺序. ...
Multi-domain encoding of spatiotemporal dynamics in EEG for emotion recognition
1
2023
... 目前,基于DEAP (database for emotion analysis using physiological signals)的研究大多数采用数据库给出的电极通道顺序作为特征矩阵的排列顺序. Wang[10 ] 提出由于信号的容积传导效应,从电极Fp1开始将最靠近当前电极通道的电极作为顺序排列的下一个电极. Cheng等[11 ] 从左右脑半球的不对称性出发,提出从左额叶区域的电极位置开始,选择最靠近当前电极且位于同脑区半球的电极作为顺序排列的下一电极. Moon等[12 ] 利用深度优先遍历和回溯算法产生多条哈密顿路径,将一定数量的路径作为电极通道的特征矩阵排列顺序. Moon等[13 ] 认为基于物理距离的电极顺序合理但并不是最优解,通过对连通性矩阵进行视差函数降维得到新的电极排列顺序. 以上研究大多使用基于欧氏空间的电极排列顺序,然而脑电信号具有复杂、高维的特点,更适合在黎曼空间进行电极通道所表征的信息流顺序的学习. Chen等[14 ] 提出解剖学视角相距较远的区域可能在生理视角连通性较高. 因此,为了寻找脑电信号传递过程中的真正通路,本研究于黎曼空间中计算电极的排列顺序. ...
1
... 目前,基于DEAP (database for emotion analysis using physiological signals)的研究大多数采用数据库给出的电极通道顺序作为特征矩阵的排列顺序. Wang[10 ] 提出由于信号的容积传导效应,从电极Fp1开始将最靠近当前电极通道的电极作为顺序排列的下一个电极. Cheng等[11 ] 从左右脑半球的不对称性出发,提出从左额叶区域的电极位置开始,选择最靠近当前电极且位于同脑区半球的电极作为顺序排列的下一电极. Moon等[12 ] 利用深度优先遍历和回溯算法产生多条哈密顿路径,将一定数量的路径作为电极通道的特征矩阵排列顺序. Moon等[13 ] 认为基于物理距离的电极顺序合理但并不是最优解,通过对连通性矩阵进行视差函数降维得到新的电极排列顺序. 以上研究大多使用基于欧氏空间的电极排列顺序,然而脑电信号具有复杂、高维的特点,更适合在黎曼空间进行电极通道所表征的信息流顺序的学习. Chen等[14 ] 提出解剖学视角相距较远的区域可能在生理视角连通性较高. 因此,为了寻找脑电信号传递过程中的真正通路,本研究于黎曼空间中计算电极的排列顺序. ...
Emotional EEG classification using connectivity features and convolutional neural networks
7
2020
... 目前,基于DEAP (database for emotion analysis using physiological signals)的研究大多数采用数据库给出的电极通道顺序作为特征矩阵的排列顺序. Wang[10 ] 提出由于信号的容积传导效应,从电极Fp1开始将最靠近当前电极通道的电极作为顺序排列的下一个电极. Cheng等[11 ] 从左右脑半球的不对称性出发,提出从左额叶区域的电极位置开始,选择最靠近当前电极且位于同脑区半球的电极作为顺序排列的下一电极. Moon等[12 ] 利用深度优先遍历和回溯算法产生多条哈密顿路径,将一定数量的路径作为电极通道的特征矩阵排列顺序. Moon等[13 ] 认为基于物理距离的电极顺序合理但并不是最优解,通过对连通性矩阵进行视差函数降维得到新的电极排列顺序. 以上研究大多使用基于欧氏空间的电极排列顺序,然而脑电信号具有复杂、高维的特点,更适合在黎曼空间进行电极通道所表征的信息流顺序的学习. Chen等[14 ] 提出解剖学视角相距较远的区域可能在生理视角连通性较高. 因此,为了寻找脑电信号传递过程中的真正通路,本研究于黎曼空间中计算电极的排列顺序. ...
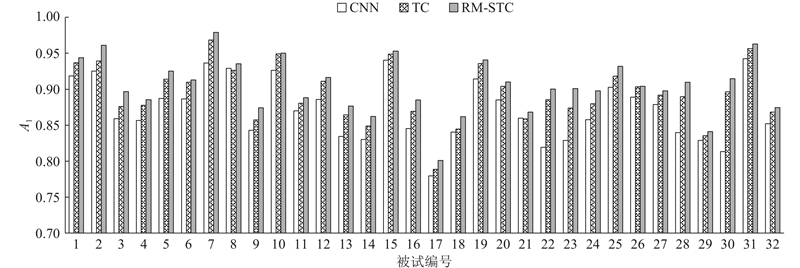
... 将提出的RM-STC网络与具有代表性的EEG情绪识别方法进行对比. 不同方法在DEAP数据库的平均准确率如表1 所示,除RM-LSTM方法外,所有对比方法的结果均来自于原文献. 其中,A 1 、A 2 分别为效价维、唤醒维识别准确率. Yin等[23 ] 使用 MESAE 对多模态信号进行二分类情感识别,Piho等[24 ] 通过KNN模型学习统计特征并进行情感分类, Garg等[25 ] 使用 Merged LSTM 模型建模特征关系进行情感识别,Moon等[13 ] 通过CNN模型学习连通性特征进而进行情感识别,Zhou等[26 ] 通过离散小波变化计算特征并通过KNN分类器进行情感识别,Zheng等[17 ] 通过STS-Transformer模型学习端到端特征进行情感识别. Zhang等[22 ] 提出黎曼流形和欧几里德空间的时空脑电表征学习,表中RM-LSTM方法为笔者复现结果. ...
... Performance comparison results of different emotion recognition models
% Tab.1 模型 A 1 A 2 MESAE[23 ] 76.17 77.19 KNN[24 ] 82.76 82.77 Merged LSTM[25 ] 84.89 83.85 CNN[13 ] 80.28 — DWT-KNN[26 ] 89.50 87.20 STS-Transformer[17 ] 89.86 86.83 RM-LSTM[22 ] 89.95 88.73 RM- STC 90.51 90.98
从表1 对比结果可见,本研究提出的RM-STC网络模型优于对比模型. 相较于机器学习中的KNN、DWT-KNN,在效价维分别提升7.75和1.01个百分点,在唤醒维分别提升8.21和3.78个百分点. 相较于深度学习MESAE、Merged LSTM、CNN、STS-Transformer、RM-LSTM模型,在效价维分别提升14.34、5.62、10.23、0.65和0.56个百分点,在唤醒维分别提升13.79、7.13、4.15和2.25个百分点. 验证了提出方法的有效性. ...
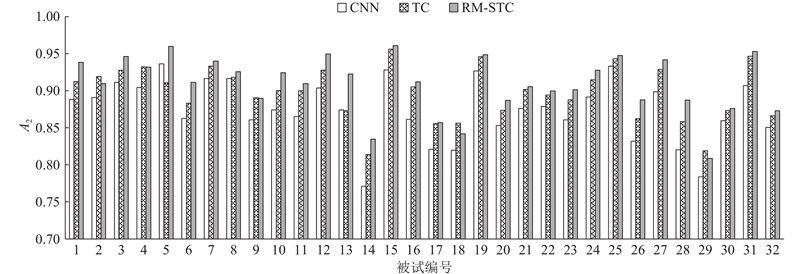
... 为了验证基于黎曼的电极排列对于CNN网络学习脑电EEG信息的有效性,进行以下消融实验,将本研究的电极排列方式与目前通用的几种排列方式进行对比. 为了更好地与文献[13 ]所提出的电极排列方式对比,识别模型均采用CNN单分支结构,具体结构见表2 . 其中,kern表示核的大小,step表示步长. ...
... Results of ablation experiment with different electrode arrangements
Tab.3 电极排列方式 A 2 /%K = 3K = 5K = 7dist[13 ] 84.54 86.90 86.82 dist-restr[13 ] 84.65 87.01 87.04 ES-PER 84.24 87.26 87.30 ES-SUM 84.98 87.13 87.37 RM-PER 85.73 87.38 87.49 RM-SUM 85.84 87.79 87.88
从表3 对比结果可见,相较于文献[13 ]提出的dist和dist-restr方法,本研究提出的RM-SUM和RM-PER方法在不同卷积核大小的条件下均有一定提升. 本研究提出的ES-SUM相较于dist和dist-restr方法略有提升. 经过配对t检验发现,基于黎曼流形的排序方法结果显著性高于基于欧氏空间的排序方法结果显著性(p <0.05)和基于常规的排序方法结果显著性(p <0.05). 表明黎曼空间更适合表征电极通道所携带的脑电信号特征,说明基于黎曼的电极排列方式可以较好地模拟脑内信息的流向,使CNN网络可以更好地卷积学习到EEG信号知识. 同时,从表中可以看出,所有被试共用同一电极排列顺序的识别率,高于为每个被试单独训练顺序的情况,可能是因为单独训练时,每个被试的样本数量较少,导致模型难以学习到最优的电极排列顺序. ...
... [
13 ]
84.65 87.01 87.04 ES-PER 84.24 87.26 87.30 ES-SUM 84.98 87.13 87.37 RM-PER 85.73 87.38 87.49 RM-SUM 85.84 87.79 87.88 从表3 对比结果可见,相较于文献[13 ]提出的dist和dist-restr方法,本研究提出的RM-SUM和RM-PER方法在不同卷积核大小的条件下均有一定提升. 本研究提出的ES-SUM相较于dist和dist-restr方法略有提升. 经过配对t检验发现,基于黎曼流形的排序方法结果显著性高于基于欧氏空间的排序方法结果显著性(p <0.05)和基于常规的排序方法结果显著性(p <0.05). 表明黎曼空间更适合表征电极通道所携带的脑电信号特征,说明基于黎曼的电极排列方式可以较好地模拟脑内信息的流向,使CNN网络可以更好地卷积学习到EEG信号知识. 同时,从表中可以看出,所有被试共用同一电极排列顺序的识别率,高于为每个被试单独训练顺序的情况,可能是因为单独训练时,每个被试的样本数量较少,导致模型难以学习到最优的电极排列顺序. ...
... 从表3 对比结果可见,相较于文献[13 ]提出的dist和dist-restr方法,本研究提出的RM-SUM和RM-PER方法在不同卷积核大小的条件下均有一定提升. 本研究提出的ES-SUM相较于dist和dist-restr方法略有提升. 经过配对t检验发现,基于黎曼流形的排序方法结果显著性高于基于欧氏空间的排序方法结果显著性(p <0.05)和基于常规的排序方法结果显著性(p <0.05). 表明黎曼空间更适合表征电极通道所携带的脑电信号特征,说明基于黎曼的电极排列方式可以较好地模拟脑内信息的流向,使CNN网络可以更好地卷积学习到EEG信号知识. 同时,从表中可以看出,所有被试共用同一电极排列顺序的识别率,高于为每个被试单独训练顺序的情况,可能是因为单独训练时,每个被试的样本数量较少,导致模型难以学习到最优的电极排列顺序. ...
A new approach for functional connectivity via alignment of blood oxygen level-dependent signals
1
2019
... 目前,基于DEAP (database for emotion analysis using physiological signals)的研究大多数采用数据库给出的电极通道顺序作为特征矩阵的排列顺序. Wang[10 ] 提出由于信号的容积传导效应,从电极Fp1开始将最靠近当前电极通道的电极作为顺序排列的下一个电极. Cheng等[11 ] 从左右脑半球的不对称性出发,提出从左额叶区域的电极位置开始,选择最靠近当前电极且位于同脑区半球的电极作为顺序排列的下一电极. Moon等[12 ] 利用深度优先遍历和回溯算法产生多条哈密顿路径,将一定数量的路径作为电极通道的特征矩阵排列顺序. Moon等[13 ] 认为基于物理距离的电极顺序合理但并不是最优解,通过对连通性矩阵进行视差函数降维得到新的电极排列顺序. 以上研究大多使用基于欧氏空间的电极排列顺序,然而脑电信号具有复杂、高维的特点,更适合在黎曼空间进行电极通道所表征的信息流顺序的学习. Chen等[14 ] 提出解剖学视角相距较远的区域可能在生理视角连通性较高. 因此,为了寻找脑电信号传递过程中的真正通路,本研究于黎曼空间中计算电极的排列顺序. ...
An end-to-end deep learning approach to MI-EEG signal classification for BCIs
1
2018
... 卷积神经网络(CNN)[15 ] 在全局特征探索方面存在一定缺陷,因此如何建立同时具有局部和全局视野的深度学习网络成为值得探讨的问题. Guo等[16 ] 提出基于深度卷积和Transformer编码器的混合网络模型. Zheng等[17 ] 提出端到端的STS-Transformer模型,直接从原始EEG信号中学习信息进行情感识别. Hu等[18 ] 提出基于CNN和Transformer的自监督预训练模型,具有优秀的泛化能力. 以上研究对于识别网络中的位置编码模块关注较少,然而位置编码可以为识别网络提供额外的空间信息. 对此,本研究将基于黎曼空间的电极排列顺序作为额外的空间位置信息映射到Transformer网络以便其可以更好地进行情感分类. ...
A Transformer based neural network for emotion recognition and visualizations of crucial EEG channels
1
2022
... 卷积神经网络(CNN)[15 ] 在全局特征探索方面存在一定缺陷,因此如何建立同时具有局部和全局视野的深度学习网络成为值得探讨的问题. Guo等[16 ] 提出基于深度卷积和Transformer编码器的混合网络模型. Zheng等[17 ] 提出端到端的STS-Transformer模型,直接从原始EEG信号中学习信息进行情感识别. Hu等[18 ] 提出基于CNN和Transformer的自监督预训练模型,具有优秀的泛化能力. 以上研究对于识别网络中的位置编码模块关注较少,然而位置编码可以为识别网络提供额外的空间信息. 对此,本研究将基于黎曼空间的电极排列顺序作为额外的空间位置信息映射到Transformer网络以便其可以更好地进行情感分类. ...
A spatiotemporal symmetrical transformer structure for EEG emotion recognition
4
2024
... 卷积神经网络(CNN)[15 ] 在全局特征探索方面存在一定缺陷,因此如何建立同时具有局部和全局视野的深度学习网络成为值得探讨的问题. Guo等[16 ] 提出基于深度卷积和Transformer编码器的混合网络模型. Zheng等[17 ] 提出端到端的STS-Transformer模型,直接从原始EEG信号中学习信息进行情感识别. Hu等[18 ] 提出基于CNN和Transformer的自监督预训练模型,具有优秀的泛化能力. 以上研究对于识别网络中的位置编码模块关注较少,然而位置编码可以为识别网络提供额外的空间信息. 对此,本研究将基于黎曼空间的电极排列顺序作为额外的空间位置信息映射到Transformer网络以便其可以更好地进行情感分类. ...
... Transformer网络的核心架构是多头自注意力模型[17 ] ,该机制能够同时关注输入序列的不同位置,从而有效捕捉长距离依赖关系,具体计算公式如下: ...
... 将提出的RM-STC网络与具有代表性的EEG情绪识别方法进行对比. 不同方法在DEAP数据库的平均准确率如表1 所示,除RM-LSTM方法外,所有对比方法的结果均来自于原文献. 其中,A 1 、A 2 分别为效价维、唤醒维识别准确率. Yin等[23 ] 使用 MESAE 对多模态信号进行二分类情感识别,Piho等[24 ] 通过KNN模型学习统计特征并进行情感分类, Garg等[25 ] 使用 Merged LSTM 模型建模特征关系进行情感识别,Moon等[13 ] 通过CNN模型学习连通性特征进而进行情感识别,Zhou等[26 ] 通过离散小波变化计算特征并通过KNN分类器进行情感识别,Zheng等[17 ] 通过STS-Transformer模型学习端到端特征进行情感识别. Zhang等[22 ] 提出黎曼流形和欧几里德空间的时空脑电表征学习,表中RM-LSTM方法为笔者复现结果. ...
... Performance comparison results of different emotion recognition models
% Tab.1 模型 A 1 A 2 MESAE[23 ] 76.17 77.19 KNN[24 ] 82.76 82.77 Merged LSTM[25 ] 84.89 83.85 CNN[13 ] 80.28 — DWT-KNN[26 ] 89.50 87.20 STS-Transformer[17 ] 89.86 86.83 RM-LSTM[22 ] 89.95 88.73 RM- STC 90.51 90.98
从表1 对比结果可见,本研究提出的RM-STC网络模型优于对比模型. 相较于机器学习中的KNN、DWT-KNN,在效价维分别提升7.75和1.01个百分点,在唤醒维分别提升8.21和3.78个百分点. 相较于深度学习MESAE、Merged LSTM、CNN、STS-Transformer、RM-LSTM模型,在效价维分别提升14.34、5.62、10.23、0.65和0.56个百分点,在唤醒维分别提升13.79、7.13、4.15和2.25个百分点. 验证了提出方法的有效性. ...
Masked self-supervised pre-training model for EEG-based emotion recognition
1
2024
... 卷积神经网络(CNN)[15 ] 在全局特征探索方面存在一定缺陷,因此如何建立同时具有局部和全局视野的深度学习网络成为值得探讨的问题. Guo等[16 ] 提出基于深度卷积和Transformer编码器的混合网络模型. Zheng等[17 ] 提出端到端的STS-Transformer模型,直接从原始EEG信号中学习信息进行情感识别. Hu等[18 ] 提出基于CNN和Transformer的自监督预训练模型,具有优秀的泛化能力. 以上研究对于识别网络中的位置编码模块关注较少,然而位置编码可以为识别网络提供额外的空间信息. 对此,本研究将基于黎曼空间的电极排列顺序作为额外的空间位置信息映射到Transformer网络以便其可以更好地进行情感分类. ...
The trouble with stress: a flexible method for the evaluation of nonmetric multidimensional scaling
1
2018
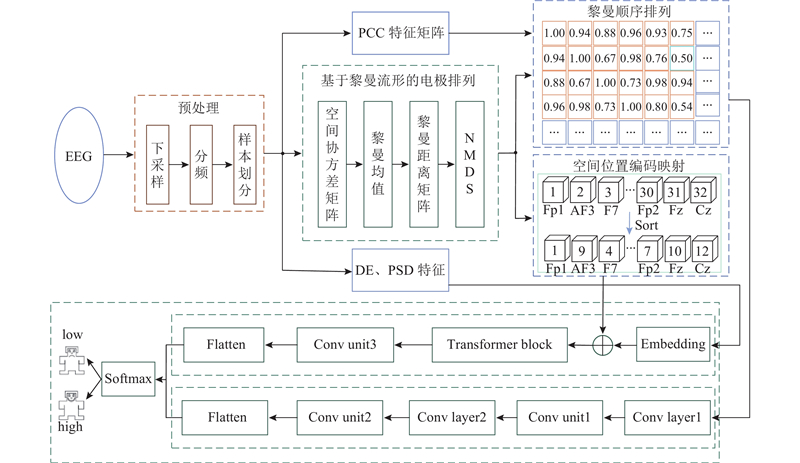
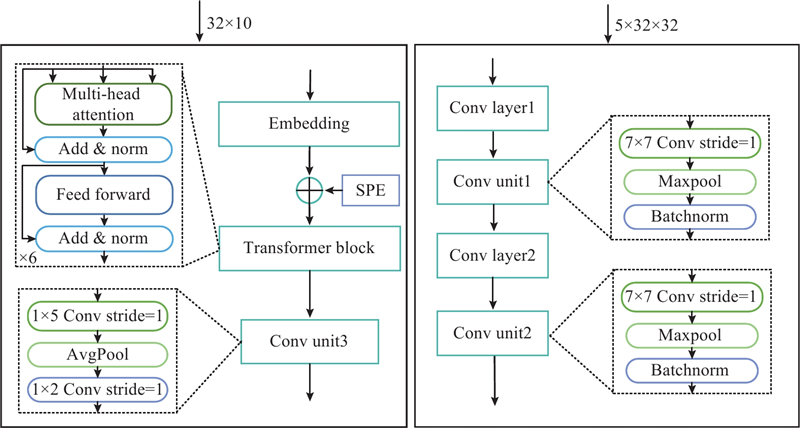
... 本研究提出的RM-STC模型整体结构如图1 所示. 针对DEAP脑电情感数据库的EEG信号进行128 Hz下采样、带通滤波预处理. 将预处理后的脑电信号分别送入3个模块进行相关运算:在PCC (Pearson correlation coefficient)特征矩阵模块计算皮尔逊相关系数;在DE (differential entropy)、PSD (power spectrum density)特征模块计算微分熵和功率谱密度;在基于黎曼流形的电极排列模块参与计算一维电极通道的排列顺序. 其中,基于黎曼流形的电极排列模块对预处理后的EEG信号进行计算,通过空间协方差矩阵将其映射到黎曼流形空间,进而在黎曼空间计算脑电通道之间的黎曼距离,获得两两电极通道之间的黎曼距离矩阵;将该距离矩阵进行非度量型多维尺度变换算法(non-metric multidimensional scaling, NMDS)[19 ] 降维处理,得到电极通道的一维排序. 这一顺序在2个模块中发挥作用:与PCC特征矩阵结合,作为黎曼顺序排列模块的输入,参与特征重排列;作用于空间位置编码映射模块,为识别网络添加电极间的空间关系信息. 将黎曼顺序排列的输出作为CNN分支网络的输入以便其更好地卷积学习局部信息,同时利用Transformer网络可以捕获长距离依赖的特点, 学习DE、PSD特征以补充全局视角,并将位置编码映射得到的电极空间位置关系添加到Transformer-CNN分支网络的向量维度进行空间编码信息嵌入,进一步丰富模型的空间编码信息. 将2个分支网络的输出进行拼接,进行二分类情感预测. ...
1
... DEAP数据库是由Kulkarni等[20 ] 建立的公开情感数据库,包含32名被试观看音乐视频片段时所产生的生理信号以及多个维度(唤醒、效价、喜欢、主导和熟悉程度)所对应的情感标签. 40个电极通道中包含32个脑电信号通道,本实验采用该32通道的EEG数据相关信息,在效价维度和唤醒维度进行二分类情感识别. ...
1
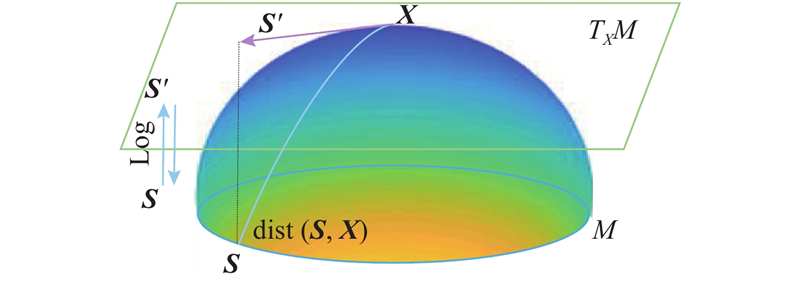
... 如图2 所示,设${{M}}$ ${T_X}M$ ${{M}}$ ${\boldsymbol{X }}\in {{M}}$ [21 ] . ...
Spatio-temporal EEG representation learning on Riemannian manifold and euclidean space
3
2024
... 黎曼均值是一组数据点在流形空间中的中心点. 因为流形空间特有的几何结构,黎曼均值的计算不能简单地通过求取平均值得到,通常须通过迭代法计算得到[22 ] . ...
... 将提出的RM-STC网络与具有代表性的EEG情绪识别方法进行对比. 不同方法在DEAP数据库的平均准确率如表1 所示,除RM-LSTM方法外,所有对比方法的结果均来自于原文献. 其中,A 1 、A 2 分别为效价维、唤醒维识别准确率. Yin等[23 ] 使用 MESAE 对多模态信号进行二分类情感识别,Piho等[24 ] 通过KNN模型学习统计特征并进行情感分类, Garg等[25 ] 使用 Merged LSTM 模型建模特征关系进行情感识别,Moon等[13 ] 通过CNN模型学习连通性特征进而进行情感识别,Zhou等[26 ] 通过离散小波变化计算特征并通过KNN分类器进行情感识别,Zheng等[17 ] 通过STS-Transformer模型学习端到端特征进行情感识别. Zhang等[22 ] 提出黎曼流形和欧几里德空间的时空脑电表征学习,表中RM-LSTM方法为笔者复现结果. ...
... Performance comparison results of different emotion recognition models
% Tab.1 模型 A 1 A 2 MESAE[23 ] 76.17 77.19 KNN[24 ] 82.76 82.77 Merged LSTM[25 ] 84.89 83.85 CNN[13 ] 80.28 — DWT-KNN[26 ] 89.50 87.20 STS-Transformer[17 ] 89.86 86.83 RM-LSTM[22 ] 89.95 88.73 RM- STC 90.51 90.98
从表1 对比结果可见,本研究提出的RM-STC网络模型优于对比模型. 相较于机器学习中的KNN、DWT-KNN,在效价维分别提升7.75和1.01个百分点,在唤醒维分别提升8.21和3.78个百分点. 相较于深度学习MESAE、Merged LSTM、CNN、STS-Transformer、RM-LSTM模型,在效价维分别提升14.34、5.62、10.23、0.65和0.56个百分点,在唤醒维分别提升13.79、7.13、4.15和2.25个百分点. 验证了提出方法的有效性. ...
Recognition of emotions using multimodal physiological signals and an ensemble deep learning model
2
2017
... 将提出的RM-STC网络与具有代表性的EEG情绪识别方法进行对比. 不同方法在DEAP数据库的平均准确率如表1 所示,除RM-LSTM方法外,所有对比方法的结果均来自于原文献. 其中,A 1 、A 2 分别为效价维、唤醒维识别准确率. Yin等[23 ] 使用 MESAE 对多模态信号进行二分类情感识别,Piho等[24 ] 通过KNN模型学习统计特征并进行情感分类, Garg等[25 ] 使用 Merged LSTM 模型建模特征关系进行情感识别,Moon等[13 ] 通过CNN模型学习连通性特征进而进行情感识别,Zhou等[26 ] 通过离散小波变化计算特征并通过KNN分类器进行情感识别,Zheng等[17 ] 通过STS-Transformer模型学习端到端特征进行情感识别. Zhang等[22 ] 提出黎曼流形和欧几里德空间的时空脑电表征学习,表中RM-LSTM方法为笔者复现结果. ...
... Performance comparison results of different emotion recognition models
% Tab.1 模型 A 1 A 2 MESAE[23 ] 76.17 77.19 KNN[24 ] 82.76 82.77 Merged LSTM[25 ] 84.89 83.85 CNN[13 ] 80.28 — DWT-KNN[26 ] 89.50 87.20 STS-Transformer[17 ] 89.86 86.83 RM-LSTM[22 ] 89.95 88.73 RM- STC 90.51 90.98
从表1 对比结果可见,本研究提出的RM-STC网络模型优于对比模型. 相较于机器学习中的KNN、DWT-KNN,在效价维分别提升7.75和1.01个百分点,在唤醒维分别提升8.21和3.78个百分点. 相较于深度学习MESAE、Merged LSTM、CNN、STS-Transformer、RM-LSTM模型,在效价维分别提升14.34、5.62、10.23、0.65和0.56个百分点,在唤醒维分别提升13.79、7.13、4.15和2.25个百分点. 验证了提出方法的有效性. ...
A mutual information based adaptive windowing of informative EEG for emotion recognition
2
2020
... 将提出的RM-STC网络与具有代表性的EEG情绪识别方法进行对比. 不同方法在DEAP数据库的平均准确率如表1 所示,除RM-LSTM方法外,所有对比方法的结果均来自于原文献. 其中,A 1 、A 2 分别为效价维、唤醒维识别准确率. Yin等[23 ] 使用 MESAE 对多模态信号进行二分类情感识别,Piho等[24 ] 通过KNN模型学习统计特征并进行情感分类, Garg等[25 ] 使用 Merged LSTM 模型建模特征关系进行情感识别,Moon等[13 ] 通过CNN模型学习连通性特征进而进行情感识别,Zhou等[26 ] 通过离散小波变化计算特征并通过KNN分类器进行情感识别,Zheng等[17 ] 通过STS-Transformer模型学习端到端特征进行情感识别. Zhang等[22 ] 提出黎曼流形和欧几里德空间的时空脑电表征学习,表中RM-LSTM方法为笔者复现结果. ...
... Performance comparison results of different emotion recognition models
% Tab.1 模型 A 1 A 2 MESAE[23 ] 76.17 77.19 KNN[24 ] 82.76 82.77 Merged LSTM[25 ] 84.89 83.85 CNN[13 ] 80.28 — DWT-KNN[26 ] 89.50 87.20 STS-Transformer[17 ] 89.86 86.83 RM-LSTM[22 ] 89.95 88.73 RM- STC 90.51 90.98
从表1 对比结果可见,本研究提出的RM-STC网络模型优于对比模型. 相较于机器学习中的KNN、DWT-KNN,在效价维分别提升7.75和1.01个百分点,在唤醒维分别提升8.21和3.78个百分点. 相较于深度学习MESAE、Merged LSTM、CNN、STS-Transformer、RM-LSTM模型,在效价维分别提升14.34、5.62、10.23、0.65和0.56个百分点,在唤醒维分别提升13.79、7.13、4.15和2.25个百分点. 验证了提出方法的有效性. ...
2
... 将提出的RM-STC网络与具有代表性的EEG情绪识别方法进行对比. 不同方法在DEAP数据库的平均准确率如表1 所示,除RM-LSTM方法外,所有对比方法的结果均来自于原文献. 其中,A 1 、A 2 分别为效价维、唤醒维识别准确率. Yin等[23 ] 使用 MESAE 对多模态信号进行二分类情感识别,Piho等[24 ] 通过KNN模型学习统计特征并进行情感分类, Garg等[25 ] 使用 Merged LSTM 模型建模特征关系进行情感识别,Moon等[13 ] 通过CNN模型学习连通性特征进而进行情感识别,Zhou等[26 ] 通过离散小波变化计算特征并通过KNN分类器进行情感识别,Zheng等[17 ] 通过STS-Transformer模型学习端到端特征进行情感识别. Zhang等[22 ] 提出黎曼流形和欧几里德空间的时空脑电表征学习,表中RM-LSTM方法为笔者复现结果. ...
... Performance comparison results of different emotion recognition models
% Tab.1 模型 A 1 A 2 MESAE[23 ] 76.17 77.19 KNN[24 ] 82.76 82.77 Merged LSTM[25 ] 84.89 83.85 CNN[13 ] 80.28 — DWT-KNN[26 ] 89.50 87.20 STS-Transformer[17 ] 89.86 86.83 RM-LSTM[22 ] 89.95 88.73 RM- STC 90.51 90.98
从表1 对比结果可见,本研究提出的RM-STC网络模型优于对比模型. 相较于机器学习中的KNN、DWT-KNN,在效价维分别提升7.75和1.01个百分点,在唤醒维分别提升8.21和3.78个百分点. 相较于深度学习MESAE、Merged LSTM、CNN、STS-Transformer、RM-LSTM模型,在效价维分别提升14.34、5.62、10.23、0.65和0.56个百分点,在唤醒维分别提升13.79、7.13、4.15和2.25个百分点. 验证了提出方法的有效性. ...
An AI-empowered affect recognition model for healthcare and emotional well-being using physiological signals
2
2023
... 将提出的RM-STC网络与具有代表性的EEG情绪识别方法进行对比. 不同方法在DEAP数据库的平均准确率如表1 所示,除RM-LSTM方法外,所有对比方法的结果均来自于原文献. 其中,A 1 、A 2 分别为效价维、唤醒维识别准确率. Yin等[23 ] 使用 MESAE 对多模态信号进行二分类情感识别,Piho等[24 ] 通过KNN模型学习统计特征并进行情感分类, Garg等[25 ] 使用 Merged LSTM 模型建模特征关系进行情感识别,Moon等[13 ] 通过CNN模型学习连通性特征进而进行情感识别,Zhou等[26 ] 通过离散小波变化计算特征并通过KNN分类器进行情感识别,Zheng等[17 ] 通过STS-Transformer模型学习端到端特征进行情感识别. Zhang等[22 ] 提出黎曼流形和欧几里德空间的时空脑电表征学习,表中RM-LSTM方法为笔者复现结果. ...
... Performance comparison results of different emotion recognition models
% Tab.1 模型 A 1 A 2 MESAE[23 ] 76.17 77.19 KNN[24 ] 82.76 82.77 Merged LSTM[25 ] 84.89 83.85 CNN[13 ] 80.28 — DWT-KNN[26 ] 89.50 87.20 STS-Transformer[17 ] 89.86 86.83 RM-LSTM[22 ] 89.95 88.73 RM- STC 90.51 90.98
从表1 对比结果可见,本研究提出的RM-STC网络模型优于对比模型. 相较于机器学习中的KNN、DWT-KNN,在效价维分别提升7.75和1.01个百分点,在唤醒维分别提升8.21和3.78个百分点. 相较于深度学习MESAE、Merged LSTM、CNN、STS-Transformer、RM-LSTM模型,在效价维分别提升14.34、5.62、10.23、0.65和0.56个百分点,在唤醒维分别提升13.79、7.13、4.15和2.25个百分点. 验证了提出方法的有效性. ...