扩频信号捕获作为卫星通信系统信号同步的第一步,其性能将直接影响通信系统的性能[3]. 传统捕获算法包括滑动相关法、匹配滤波法、并行频率捕获法、并行码相位FFT-IFFT捕获法、部分匹配滤波快速傅里叶变换PMF-FFT捕获法等,捕获灵敏度低,频偏捕获范围小,捕获时间长. 针对以上缺点,柳春[4]提出补零增加FFT点数并对PMF-FFT的加窗函数进行改进,减少扇贝损失以增大频偏捕获范围. 韩志凤等[5]提出使用复数型差分相关积分,提升FFT-IFFT算法对弱信号的捕获能力. 郭晓旭等[6]通过采用特殊的同步引导序列,对多路信号分别进行下变频,缩短FFT-IFFT算法的捕获时间. 单独提升扩频捕获算法中的一项性能指标难以满足现代低轨卫星扩频通信系统中高灵敏度通信、海量通信链路快速切换的需求.
并行码相位FFT-IFFT捕获法是目前大多数高灵敏度星载接收机采用的捕获方法. 本文针对低轨卫星扩频通信系统中传统扩频捕获算法捕获速度慢、难以同时满足大频偏捕获和高灵敏度捕获需求的问题[7],提出改进的FFT-IFFT捕获算法. 利用扫频区间的边带信息估计捕获区间,结合数字自动增益控制AGC辅助的捕获机制,解决了传统扩频捕获算法中高灵敏度与频偏捕获范围负相关、在高灵敏度捕获时容易误捕的问题,加快了捕获速度,提升了低轨卫星扩频通信系统的可靠性. 通过理论分析与实验验证,对传统算法与改进算法的性能进行对比.
1. 传统的扩频捕获算法
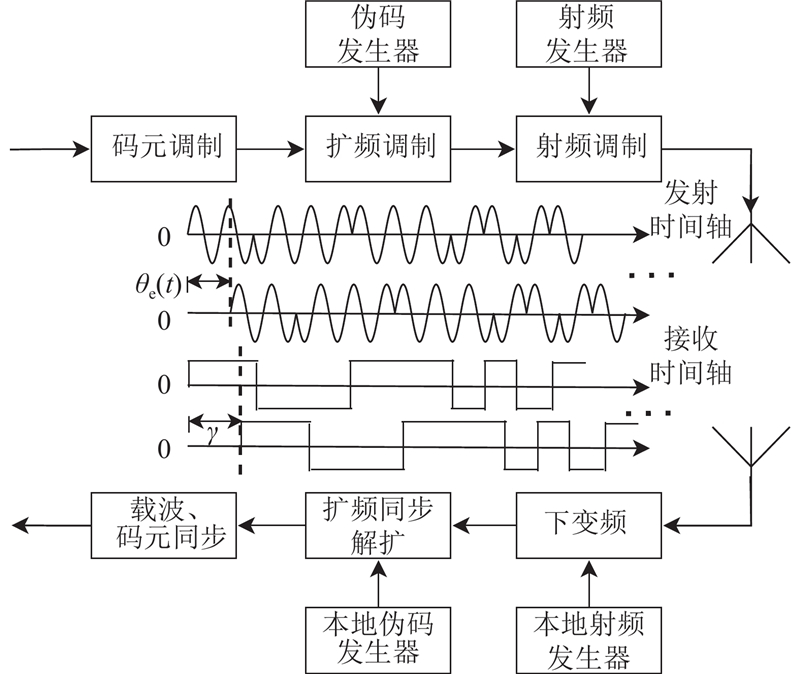
扩频捕获算法的关键是对本地信号与接收信号进行同步,只有当本地与接收信号的伪码相位同步、载波相位同步时,信号才能被正确地解扩与解调. 扩频通信系统如图1所示,发射端的伪码发生器、射频发生器分别产生伪随机序列、载波,被码元信号调制后经发射天线发射. 接收端的射频发生器产生本地载波,与接收信号的载波存在相位差
图 1
1.1. FFT-IFFT捕获算法的原理
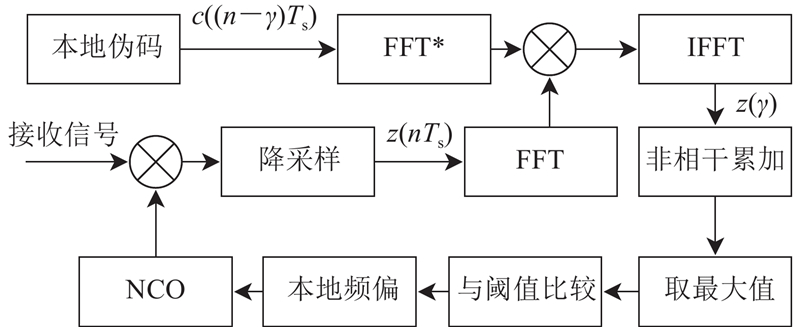
扩频通信系统中常用的捕获算法包括滑动相关法、匹配滤波法、并行频率捕获法、FFT-IFFT捕获法、PMF-FFT捕获法[8]. 为了满足大频偏高灵敏度快速捕获的需求,采用FFT-IFFT捕获法. 利用频域FFT-IFFT变换与时域卷积运算等效的特性,将伪码滑动并行化,相关结果可以表示为
式中:
图 2
对下变频后的接收信号与本地伪码信号分别进行FFT变换,并对本地伪码FFT结果取共轭,将两者相乘再进行IFFT变换,以获得相干累加增益. 时域下变频后的相关结果可以表示为
式中:
伪码具有尖锐的自相关性,当接收信号的伪码与本地伪码对齐时,
式中:
式中:
同理可得,
将同相支路与正交支路相干累加结果进行合并,得到相干累加结果
将多次FFT-IFFT结果进行累加,对非相干累加结果取模求平方,获得非相干累加结果,可以表示为
式中:
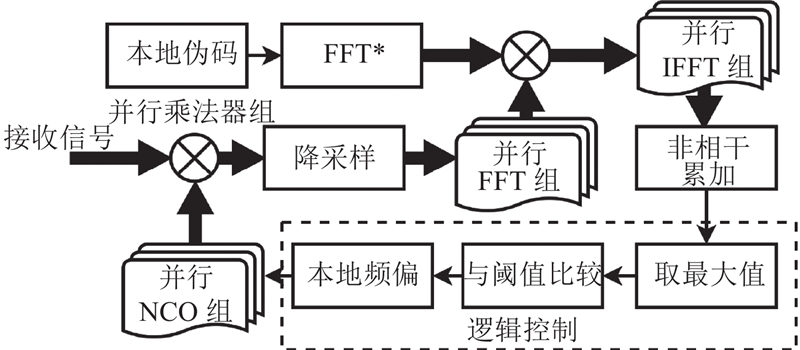
1.2. 分组并行FFT-IFFT捕获算法
图 3
设频偏范围为DOPR,FFT个数为FFTNUM,则并行FFT-IFFT组应包括1个伪码FFT模块、FFTNUM个数据FFT模块与FFTNUM个IFFT模块,并行数控振荡器NCO组包括FFTNUM个NCO模块,每个NCO的中心频点间隔为FFTR. 根据式(6)、(8)可得每一个FFT-IFFT的多普勒频偏损耗因子,即随着多普勒频偏增大而衰减的峰值,可以表示为
式中:
传统分组并行FFT-IFFT扩频捕获算法的流程如下.
1) 利用FFTNUM个并行NCO,生成频点间隔为FFTR的本地载波乘接收信号,分别下变频,降采样.
2) 将降采样后的信号分别进行
3) 重复步骤1)、2)V次,分别对FFTNUM组IFFT变换后的信号进行V次非相干累加,取其中的最大值. 若最大值大于捕获门限值,则捕获成功,取最大值组所对应的NCO频点作为频偏估计值,取最大值组
式中:
2. 改进的扩频捕获算法
2.1. 边带区间估计法
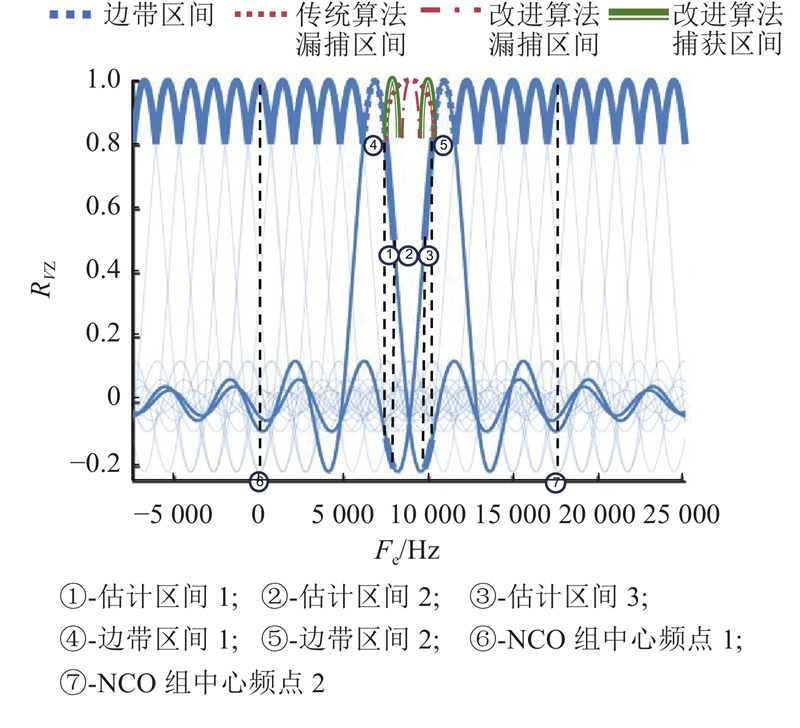
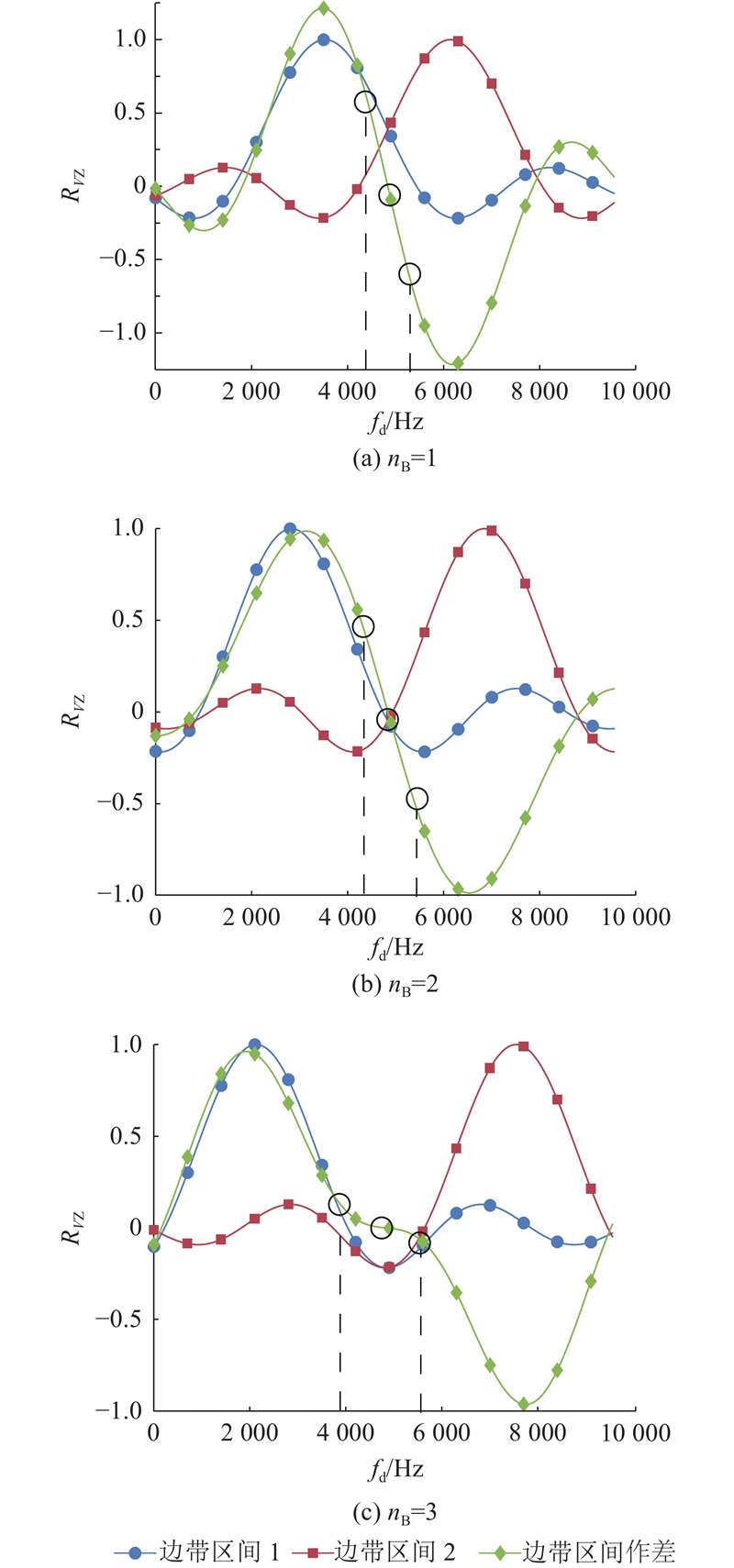
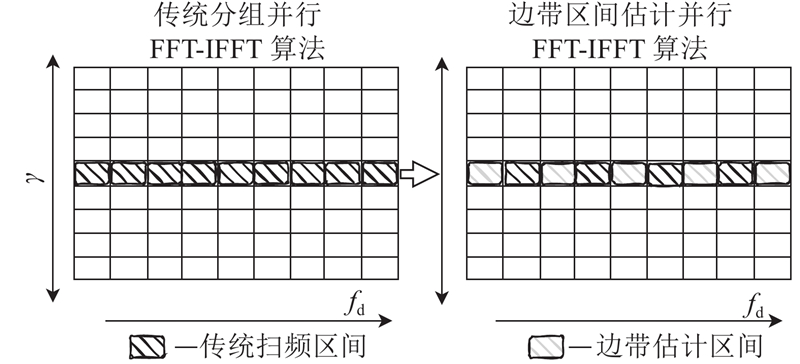
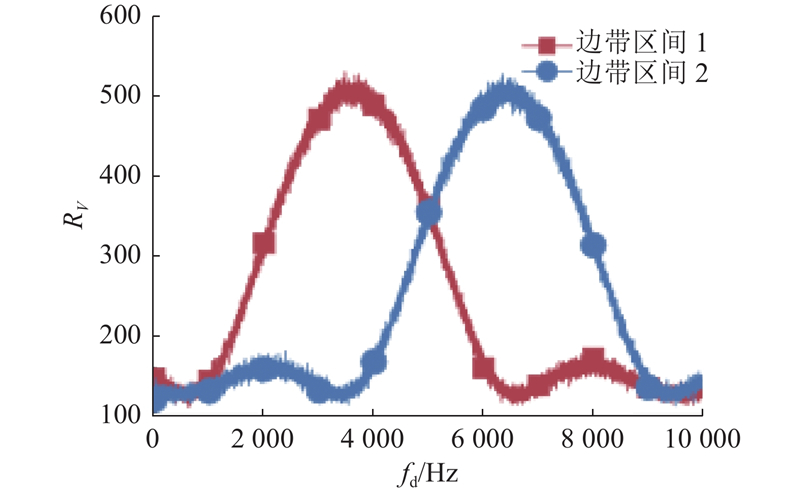
由式(10)可知,捕获时间由频偏捕获范围、并行FFT个数、累加时间与检测概率等变量共同决定. 边带区间为并行FFT-IFFT组的最外侧FFT-IFFT模块所对应的频偏区间,估计区间为2个边带区间之间等待捕获的频偏区间. 为了实现对最大多普勒频偏DOPR的100%覆盖,传统算法设置边带区间1与边带区间2的间隔为0,边带区间如图4所示,但不存在估计区间,2个扫频区间分别对应并行NCO组的中心频点1与2,扫频效率较低.
图 4
利用边带区间估计法,增大了相邻并行NCO组的中心频点间隔,减少了串行扫频次数,缩短了捕获时间,在相同的频偏捕获范围内减少了FFT使用个数,且在一定范围内,最大多普勒频偏越大,优化效果越好. 设扫频区间间隔为GAP= nB·FFTR,其中
式中:GAP为最大多普勒频偏范围.
改进算法根据作差结果将估计区间划分为3个子区间,选择1个子区间再进行一次捕获,降低了漏捕概率.
从式(6)可知,相关结果可以简化为
式中:当
式中:当
图 5
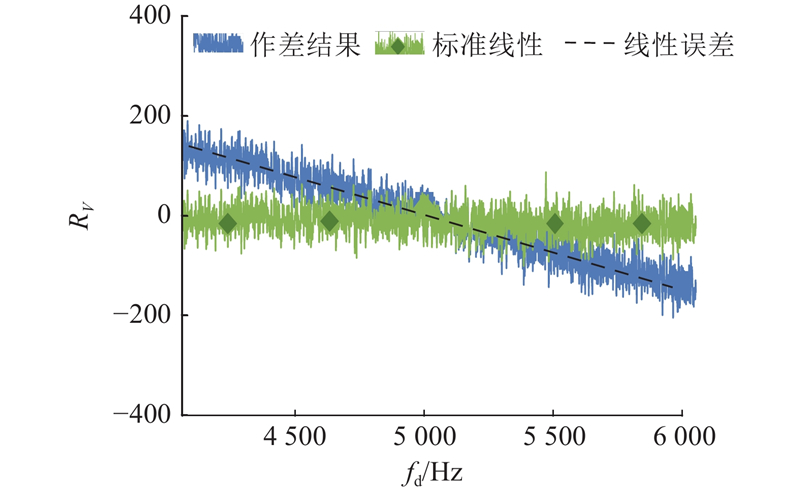
边带区间1与边带区间2的作差结果如图5所示. 结果表明,当
边带区间估计法的常规串行扫频流程与传统捕获算法相同. 若常规串行扫频未捕获,则进行一次额外的估计区间捕获,算法流程如下.
1) 进行并行FFT-IFFT变换与非相干累加. 若累加结果大于捕获门限值,则判断捕获;若小于捕获门限值,则逻辑控制单元将图3中并行NCO组的中心频点1移至中心频点2,记录边带区间1的捕获峰值.
2) 对中心频点2的并行FFT-IFFT组重复步骤1),记录边带区间2的捕获峰值.
3) 重复步骤1)、2),若常规扫频未捕获,在下一次常规扫频时,对边带区间1的捕获峰值与边带区间2的捕获峰值作差. 若差值大于归一化区间门限
2.2. 数字AGC辅助的可靠捕获机制
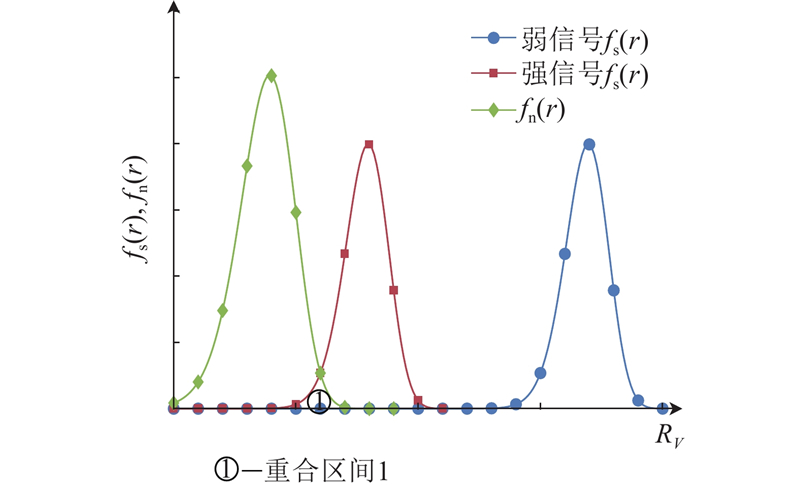
误捕现象的本质是捕获算法为满足较低的漏警概率设置较低捕获门限值,造成虚警概率增高[15]. 当峰值靠近捕获门限值时,逻辑控制单元判断锁定,但信噪比不足以支持锁相环进行跟踪. 若逻辑控制单元没有判断误捕的机制,系统将进入死循环.
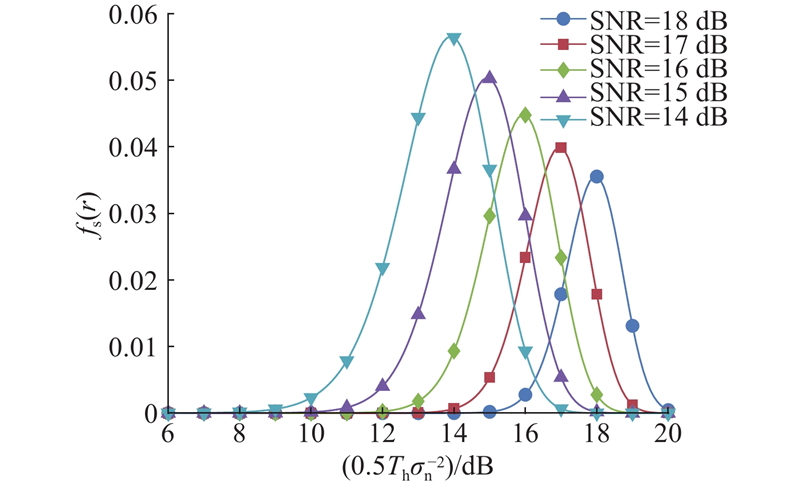
当有用信号不存在时,使用瑞利概率密度函数描述捕获概率. 当有用信号存在时,使用莱斯概率密度函数,而分布函数曲线与信噪比有关. 莱斯概率密度函数
式中:
对式(15)、(16)分别积分,可得
式中:
图 6
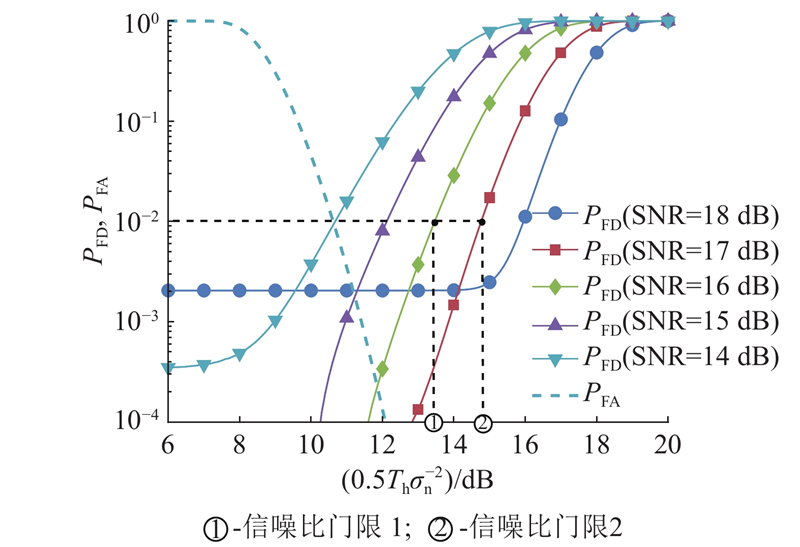
弱信号的莱斯概率密度函数与瑞利概率密度函数在区间1重合,且
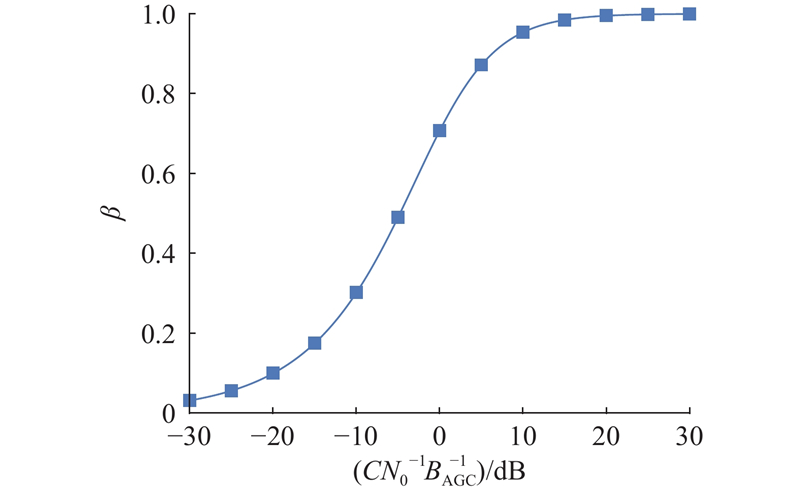
数字AGC通过反馈型环路实现,主要目的是使接收信号在一定带宽范围内维持功率不变,能够减少噪声干扰,提高信号的信噪比. 数字AGC增益因子能够反映信噪比的变化趋势[17],可以表示为
式中:
图 7
数字AGC辅助的可靠捕获机制流程如下.
1) 若
2) 判断峰值是否大于步骤1)中选择的捕获门限值. 若大于捕获门限值,则捕获成功,开启锁相环进行跟踪;若小于捕获门限值,则重捕.
3) 首次开启跟踪环路后,判断跟踪环路是否连续锁定多次. 若连续锁定多次,则判断锁定成功,否则重捕.
3. 算法性能分析
3.1. 计算复杂度的对比
边带区间估计法在相同的频偏捕获范围内,利用相邻扫频区间的边带信息,减少了FFT-IFFT组的计算次数,缩短了捕获时间,降低了算法复杂度. 算法如图8所示.
图 8
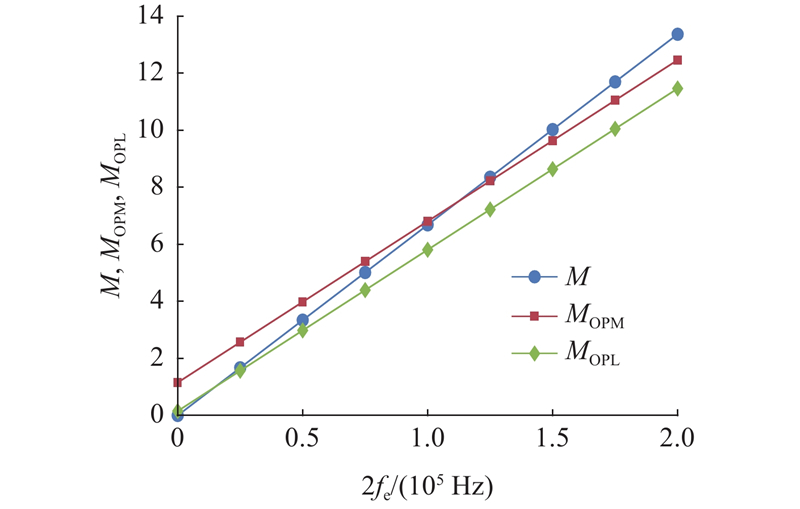
最大扫频次数是影响捕获时间与FFT-IFFT计算次数的重要因素. 改进算法与传统算法的最大扫频次数及其最大多普勒频偏的关系可以表示如下.
式中:
根据式(22)、(23)可得传统算法的FFT计算次数
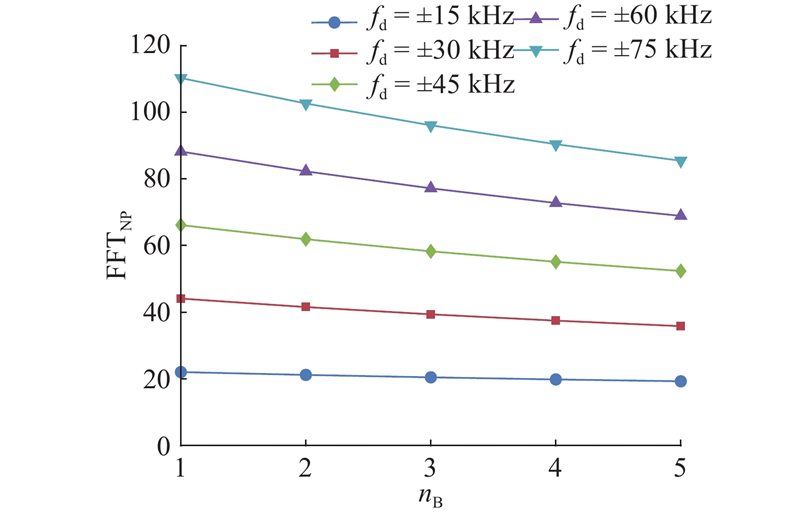
在不同的最大频偏范围下,FFT-IFFT组的计算次数与区间间隔倍数
图 9
最大扫频次数与总频偏捕获范围的关系如图10所示. 结果表明,改进算法的捕获时间比传统算法短,且优化效果随最大频偏范围的增大而上升.
图 10
3.2. 捕获概率与极限灵敏度的分析
为了计算理论极限灵敏度,需要结合最低捕获信噪比、累加增益、捕获概率等相关变量得到最低载噪比. 根据载噪比与捕获灵敏度的关系,推得极限灵敏度.
虚警概率与漏警概率过高会使非相干累加的平方损耗上升,导致捕获灵敏度下降. 本文使用数字AGC辅助的可靠捕获机制,为捕获算法选择合适的捕获门限值. 从式(2)可知,FFT-IFFT捕获算法的相干累加相关结果可以表示为
图 11
对式(17)、(18)进行变量替换,
式中:
图 12
表 1 扩频通信系统的参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| 2 | ||||
| 490 | ||||
| S-Band | — | — |
为了满足低轨卫星扩频通信系统的捕获需求,系统通信速率
相干累加与非相干累加增益可以分别表示为
非相干累加平方损耗可以表示为[19]
式中:
捕获信号的
式中:
4. 实验验证
4.1. 仿真测试
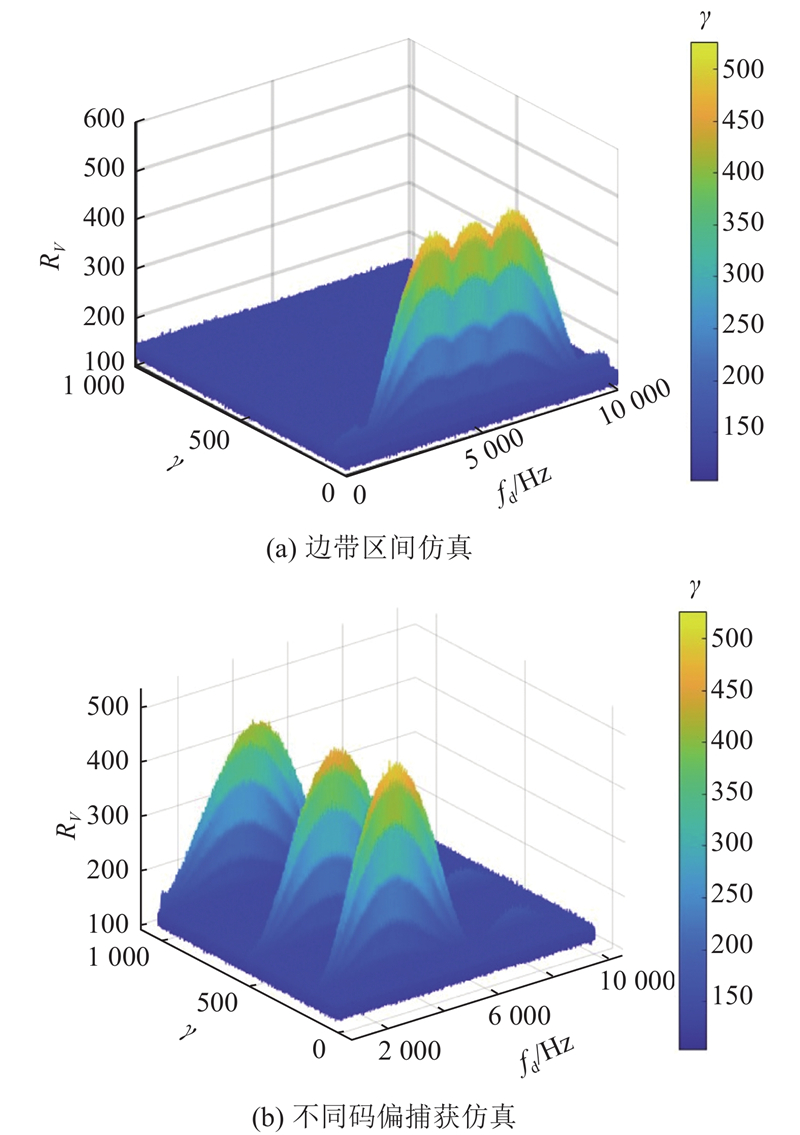
在MATLAB软件中进行仿真,设置捕获门限为350. 当码片偏移量为150~1 000时,捕获情况如图13 (a)所示. 随着码片偏移量的增大,非相干累加值逐渐下降,但非相干累加峰值清晰可见,且大于捕获门限值,表明伪码捕获性能可靠.
图 13
图 13 捕获峰值与频偏码偏的关系
Fig.13 Relationship between acquisition peak and frequency offset code offset
利用边带区间FFT-IFFT算法对伪码相位进行并行搜索,设置码片偏移量为150,边带区间捕获仿真如图13 (b)所示. 在其他码片区间内均未出现相关峰值,当码片偏移量小于150时出现明显的边带区间相关峰值,区分度明显,边带区间界限分明,且相干累加损耗小于2 dB,满足捕获信噪比最低的要求.
图 14
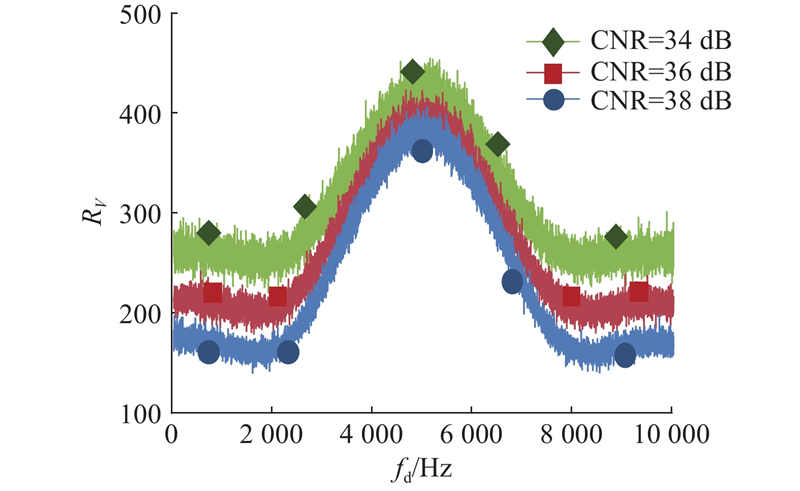
图 15
当
图 16
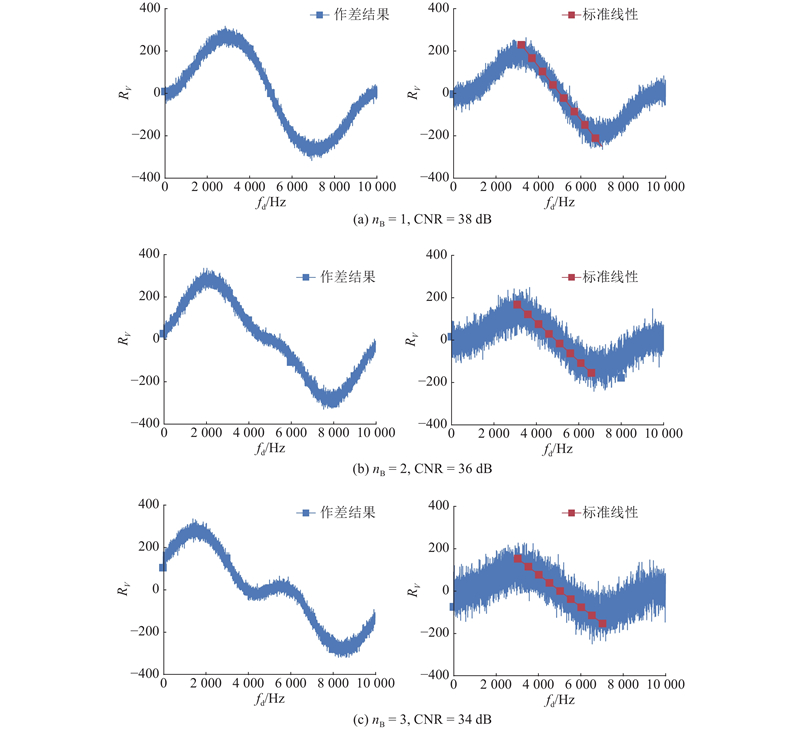
取作差结果的正、负峰值得到标准直线,将其与作差结果相减,得到线性误差,如图17所示,线性误差与横坐标重合. 结果表明,在不同的噪声强度下,边带区间作差结果满足近似线性关系.
图 17
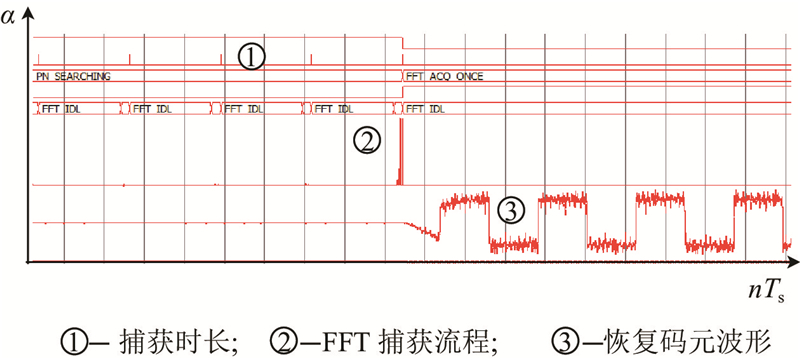
在FPGA硬件仿真平台上验证边带区间FFT-IFFT捕获算法,捕获流程如图18所示. 算法通过FPGA软件代码实现数字AGC辅助的可靠捕获机制,在信号被捕获并解调解扩后,码元信号被完整恢复. 结果表明,捕获时间低至0.8 s.
图 18
4.2. 硬件测试
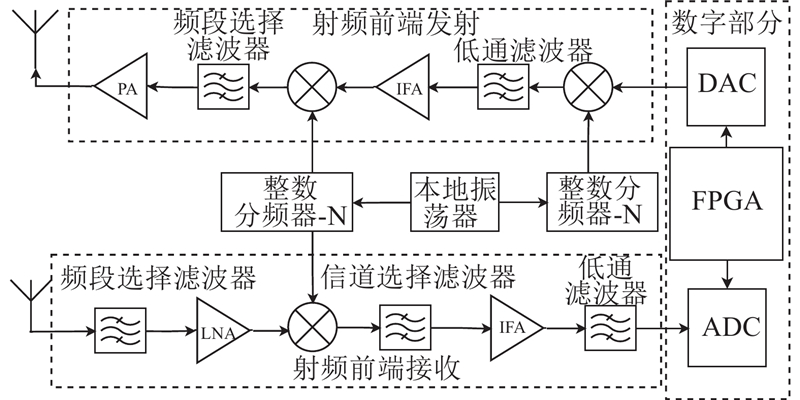
低轨卫星扩频通信系统包括射频前端硬件电路与数字信号处理模块两大部分. 前端接收部分包括接收天线、低噪声放大器LNA、混频器IFA等器件. 接收天线接收射频信号后,射频信号通过频段选择滤波器滤除带外镜像干扰,通过LNA放大,经IFA下变频至中频信号,通过滤波器与放大器处理后送入ADC模数转换芯片,FPGA用于实现扩频捕获算法. 前端发射部分除信道选择滤波器外,其他组成部分与接收部分相同,结构如图19所示.
图 19
图 20
图 21
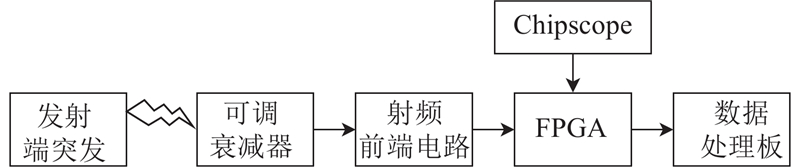
在实际的硬件平台中,利用传统及改进捕获算法的测试情况如图22所示. 设置捕获门限为
图 22
如图23所示为接收机入口功率为−120~−130 dBm情况下的解调波形对比. 可知,利用改进算法,在实测功率为−130 dBm的情况下,能够正常捕获并恢复码元信号.
图 23
表 2 捕获算法的性能指标对比
Tab.2
| 算法 | fmin/dB | |||
| 传统算法 | −128 | |||
| 改进算法 | −130 |
表 3 捕获算法的误码率结果对比
Tab.3
| P/dBm | e/10−6 | |
| 传统算法 | 改进算法 | |
5. 结 语
为了解决传统扩频捕获算法复杂度高、捕获速度慢且难以同时高动态高灵敏度捕获的问题,本文提出满足低轨卫星扩频通信系统实际应用需求的改进FFT-IFFT快捕算法. 结果表明,改进的FFT-IFFT快捕算法使用边带区间估计法,结合数字AGC辅助捕获机制,使星载接收机能够快速捕获扩频信号,有效解决了接收机在高动态低信噪比条件下容易误捕的问题,降低了误码率与丢包率,提升了通信系统的可靠性. 在卫星互联网飞速发展的时代,高性能的扩频捕获算法将使低轨卫星扩频通信系统的性能得到进一步的提升,这对安全稳定地开展航天任务具有重大意义.
参考文献
低轨互联网星座发展研究
[J].
Review on development of LEO Internet constellation
[J].
高动态卫星DSSS信号Turbo迭代捕获算法
[J].
Turbo iterative acquisition algorithm for satellite high-mobility DSSS signal
[J].
一种低轨卫星高灵敏度辅助定位服务系统
[J].
A high sensitivity auxiliary positioning service system using LEO satellites
[J].
基于差分相关积分的北斗弱信号快速捕获方法
[J].
Fast acquisition of Beidou weak signal based on differential correlation
[J].
用于星间通信的高灵敏度快捕算法
[J].DOI:10.11918/202208112 [本文引用: 1]
High sensitivity fast acquisition algorithm for inter-satellite communication
[J].DOI:10.11918/202208112 [本文引用: 1]
高灵敏度微小卫星可变带宽接收机设计
[J].
Design of variable loop bandwidth high sensitivity micro-satellite receiver
[J].
一种高动态低信噪比环境下基于多样本点串行快速傅里叶变换的信号捕获方法
[J].DOI:10.11999/JEIT200149 [本文引用: 1]
A signal acquisition method based on multi-sample serial fast Fourier transform in high dynamic and low SNR environment
[J].DOI:10.11999/JEIT200149 [本文引用: 1]
双块零扩展截断相关的长码信号快速捕获算法
[J].
A fast acquisition algorithm with DBZP truncation correlation for the long code signal
[J].
Intelligent search strategy for Doppler frequency based on fuzzy logic in DSSS signal acquisition
[J].DOI:10.1109/TAES.2023.3234456 [本文引用: 1]
一种低复杂度的低信噪比非相干直扩信号捕获算法
[J].
A low complexity acquisition algorithm for DSSS signal with low SNR and non-coherent data modulation
[J].
A stable and two-step settling digital controlled AGC loop for GNSS receiver
[J].
基于FFT的高数据率低信噪比下的长码直捕算法
[J].
Long code direct acquisition algorithm of DSSS signals based on FFT in high rate and low SNR condition
[J].