供热系统是我国重要的民生工程和城市能源转型的关键环节. 截至2021年底,北方城镇供暖面积达到162亿m²,供暖能耗达到2.12亿tce,占全国建筑总能耗的21%[1]. 当前,集中供热系统的能效偏低,主要问题如下:1)热用户负荷供需不匹配,导致“近热远冷”的现象频发;2)运行调控水平有限,管网水力热力失调. 解决上述问题的关键是对热用户负荷进行准确量化,并制定科学的运行策略,实现按需精准供热,提高经济性和能源利用效率.
本文针对以上问题,提出基于机理的供热负荷量化模型,计算二级网中各用户的实际热负荷. 结合管网的水力热力建模分析,得到二级网热力站和用户的阀门开度调节策略,实现热用户的按需供热,有效解决供热不均衡的问题.
1. 基于机理的供热负荷量化建模方法
1.1. 建筑热用户建模
在集中供热系统中,为每个房间建立的详细机理模型过于复杂,且在实际工程中难以实现. 对于同一幢建筑物而言,各房间的构造和建筑面积各不相同,建筑物内的房间有几十至几百间不等,进行如此复杂的建模工作可操作性较低. 本文对该问题进行简化,根据空间分区和几何简化原则,忽略较小因素的影响,将一整幢建筑物当作一个热用户进行考量,不考虑单一房间的详细计算分析,使得整体建模的复杂程度降低,保证了相应的建筑热负荷计算预测的可行性和准确度.
当对建筑物进行整体建模时,考虑建筑的外围护结构传热,同一幢建筑物的室内温度相同,总供热面积为建筑内每个用热房间的面积之和. 由于不同高度下建筑室外环境存在一定的差异以及建筑朝向均会对建筑的散热产生影响,计算时考虑这部分影响后,对结果进行修正. 通常供热片区内存在商业、住宅、办公楼等不同功能类型的建筑物,需要分别对这些建筑物进行建模.
1.2. 围护结构的热工特性分析
建筑墙体的作用不仅是承重和空间分隔,还可以维持室内温度稳定,减少室内外热交换. 对于建筑外墙的传热计算,主要采用以下2种方式:1)外墙的外表面通过对流与外界空气交换热量;2)外墙吸收太阳辐射热量,随后通过墙体将热量传导至室内.
式中:
由于室内外的空气温差,建筑内部的空气会通过外窗导热的方式与室外空气进行热交换. 由于玻璃及其气体夹层的热惰性相对较低,这部分在实际计算时可被忽略,通过外窗的传热可以近似为稳态传热. 相关的具体计算方法如下:
式中:
在日间,当太阳辐射直接照射到外窗时,一部分热量通过玻璃传入房间,成为房间的得热量,而剩余的热量被玻璃吸收,通过辐射和对流的方式与室内空气进行热交换. 标准太阳得热量(
式中:
室内人员热负荷可以表示为
式中:
照明热负荷可以表示为
式中:
设备热负荷可以表示为
式中:
供热系统的热负荷定义为当室外温度为
建筑围护结构的材料、窗墙比和形状系数可以决定建筑围护结构的传热系数. 建筑围护结构的基本传热负荷是在稳定条件下计算得到的,但实际负荷会受到气象条件和建筑实际情况的影响. 在计算时,需要从朝向、风力和高度3个方面对基本传热负荷进行修正,得到实际的围护结构传热负荷.
式中:βoc、βwc、βhc分别为朝向修正系数、风力附加系数、高度修正系数.
根据美国ASHRAE的《空调和制冷手册》中对热负荷计算方法的分析,建筑的渗透负荷计算公式可以表示为
式中:
构建基于机理的供热负荷量化模型. 该模型中的屋内供热负荷等于由屋内向外界的散热与室内人员、照明和设备热负荷的差值,如下所示:
典型应用场景下的建筑负荷构成示意图如图1所示.
图 1
图 1 供热负荷量化模型的典型应用场景
Fig.1 Typical application scenario for quantitative model of heating load
2. 基于负荷量化的二级网按需供热运行优化方法
2.1. 二级网运行优化方法
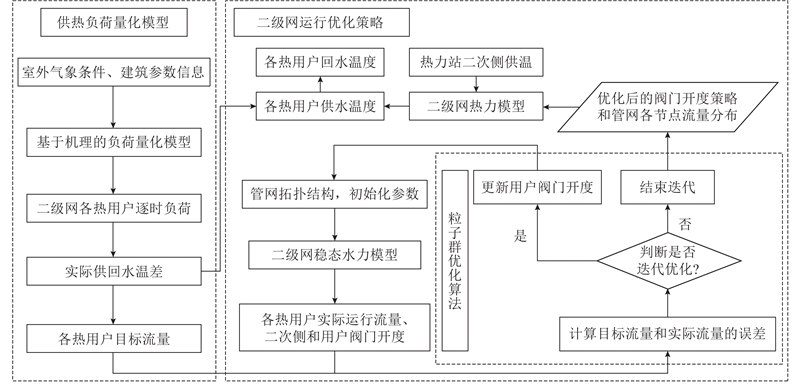
在量化计算用户真实热负荷的基础上,建立供热二级网按需运行优化方法,如图2所示. 根据二级网中各热用户的建筑类型、围护结构热工参数信息以及热用户所处地区的气象参数,采用建立的机理负荷量化模型,对二级网中各用户的逐时热负荷进行计算. 结合热用户的负荷特性和实际运行的历史供回水温差,确定各用户的推荐供回水温差,得到和热用户真实负荷对应的管网节点目标流量,初步确定二级网的总流量. 将热力站二次侧的逐时流量、水泵特性参数、管网拓扑结构、各管段长度、管径、摩擦系数、散热系数和初始阀门开度等作为初始化参数,通过水力计算模型对逐时的二级网稳态水力进行计算,得到各热用户的初始流量分布,完成初步计算. 结合基于本文负荷量化模型计算得到的各用户流量分布值,计算2组流量结果的差值的平方和,作为优化目标. 调用粒子群优化算法,将二次侧阀门和各热用户阀门作为粒子进行寻优,输出此时的各阀门开度,完成第1次迭代. 利用二级网的稳态水力模型对各用户的流量分布进行计算,分析目标函数的结果. 根据实际运行场景分析是否继续进行迭代,直至结束,输出最终的各阀门逐时开度策略和对应的流量分布. 结合热力站二次侧的供温和稳态水力的逐时计算结果,利用二级网热力模型计算得到各热用户的供水温度. 由于供热系统中水力平衡的时间较小,实际的运行调节过程可以看作是一个稳态过渡到另一个稳态的过程,因此在分析时将水力稳态的时间尺度简化为1 h,即每个小时对应一个稳态水力. 此时可以根据前面确定的推荐供回水温差,计算得到各热用户的回水温度,作为评价运行优化结果的依据.
图 2
图 2 基于用户负荷量化的二级网运行优化方法流程图
Fig.2 Flowchart of secondary network operation optimization method based on user load quantification
2.2. 粒子群优化算法
粒子群优化算法因结构简单且不须依赖问题的梯度信息,特别适用于解决那些传统优化方法难以应对的复杂问题. 图2给出二级网运行优化方法的流程图,其中粒子群算法的具体实施步骤如下.
1)初始化粒子. 本文的目标是对二级网运行中的阀门开度进行寻优,各粒子的位置为各用户的阀门开度. 粒子的位置为0~100,初始化位置均设置为30,速度为0.8.
2)计算各粒子的适应度函数值,更新粒子的速度和位置. 粒子的适应度函数值为目标流量和迭代计算流量的差的平方和,每个粒子在迭代中的最佳位置为
3)判断是否终止运行. 将迭代次数设定为粒子群优化算法的运行终止条件,当达到预设的迭代次数时,停止运行.
2.3. 管网的水力热力建模分析
1)管网的稳态水力模型.
在供热系统中,管网的水力与热力之间呈现单向耦合的关系. 水力状态的改变会直接作用于热力状态,但热力状态的调整不会对水力状态产生影响. 当进行稳态建模时,需要重点考虑管网的水力建模.
在供热管网中,管段内水的一维流动过程可以表示如下:
式中:
管网的稳态水力特性方程[21]可以表示为
式中:G为各管道流量,A 为横截面积,
在稳态水力工况下,管段中的流量是固定的. 在推导水力特性方程的过程中采用线性近似的处理方式,模型精度受基值选取的直接影响,所以采用拟牛顿法,通过迭代修正实际流量和基值之间的误差,保证方程的求解精度,得到准确的管段流量分布. 迭代过程中的流量基值可按下式进行更新:
式中:
2)管网的稳态、动态热力模型.
供热管网中流体传热的能量守恒方程为
式中:
利用傅里叶变换,将管网的关键运行参数转化为多个正弦稳态激励,结合向量的表示方法描述热力支路的特性. 管段的首末段温度关系可以表示为
式中:
热力支路的特性方程可以通过矩阵形式表示如下:
式中:
管段内各节点的汇流和分流温度约束可以表示为
式中:
结合式(17)~(19),管网支路的首末端温度计算方程可以表示为
3. 案例分析
3.1. 案例介绍
图 3
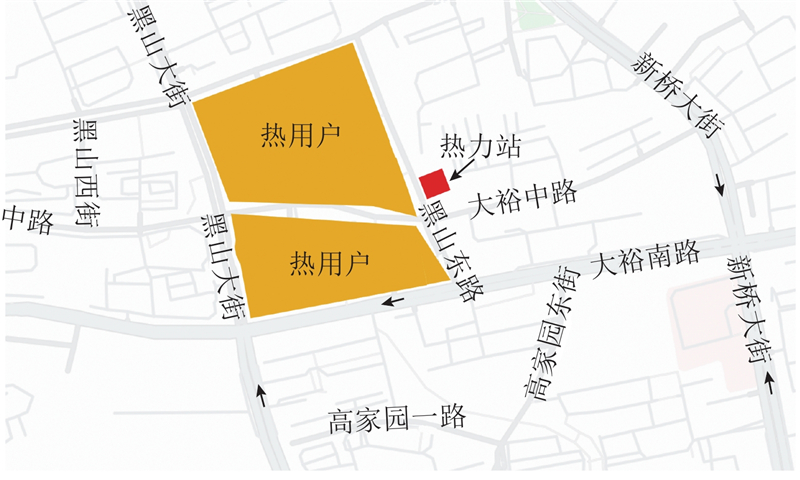
图 3 案例二级网热用户的位置分布
Fig.3 Location distribution of thermal user in case secondary network
图 4
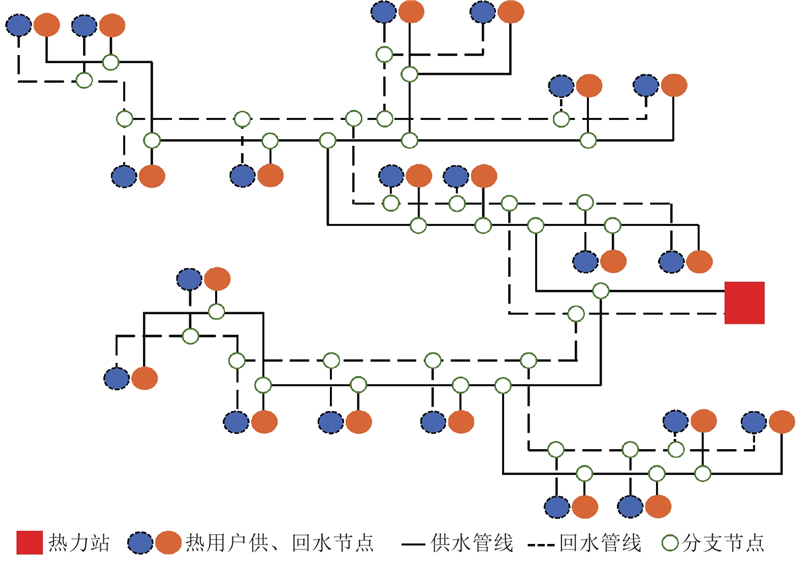
图 4 案例二级网拓扑结构节点分支的示意图
Fig.4 Illustration of node and branch configuration in case secondary network topology
图 5
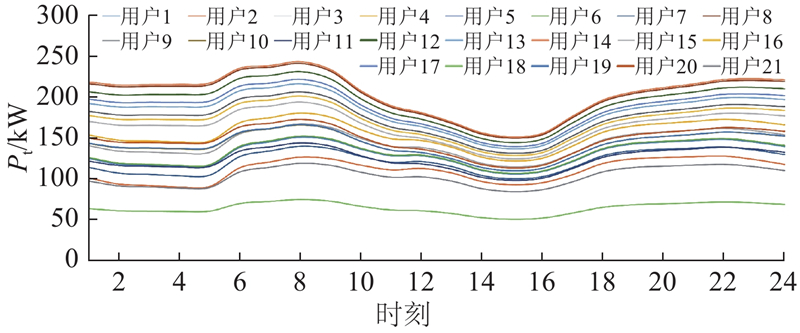
图 6
图 6 各热用户的逐时热负荷分布
Fig.6 Distribution of hourly heat demand for each thermal user
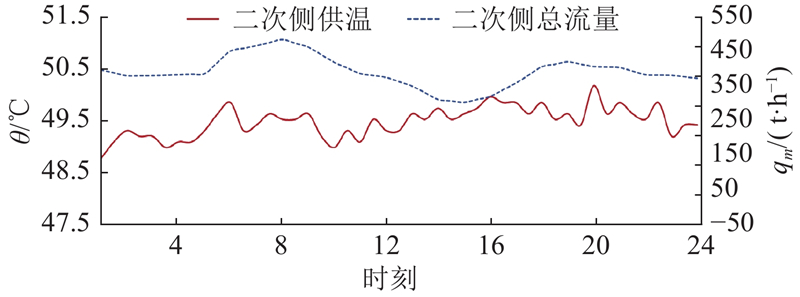
该二级网中热用户的供回水温差为6~11 ℃,流量分布会根据一天中的负荷变化产生波动. 结合实际的案例场景,该二级网热力站二次侧的供回水温度设计值分别为50、40 ℃. 案例日的历史二次侧供水温度和流量分布如图7所示.
图 7
图 7 热力站的二次侧供温和流量分布
Fig.7 Secondary side supply temperature and flow distribution at heating station
3.2. 优化结果
对各热用户在各时刻下的流量分布和阀门开度策略进行计算分析. 在粒子群优化算法的迭代过程中,调控对象是二次侧阀门和各热用户阀门,初始粒子将各阀门开度设置为30%,各阀门开度的上、下边界分别为0%和100%,粒子群数量设置为240,最大迭代次数为200,粒子群的超参数分别为
表 1 某时刻目标流量和实际流量的对比
Tab.1
| 热用户 | qmt/ (t·h−1) | qma/ (t·h−1) | kop/ % | 热用户 | qmt/ (t·h−1) | qma/ (t·h−1) | kop/ % | |
| 1 | 15.43 | 15.96 | 26.5 | 12 | 22.82 | 23.50 | 33.0 | |
| 2 | 15.03 | 14.74 | 34.5 | 13 | 25.10 | 24.59 | 32.0 | |
| 3 | 14.99 | 15.98 | 27.0 | 14 | 27.58 | 27.96 | 35.0 | |
| 4 | 21.87 | 22.45 | 31.0 | 15 | 22.11 | 21.79 | 41.5 | |
| 5 | 15.04 | 14.27 | 29.0 | 16 | 25.51 | 25.94 | 42.0 | |
| 6 | 18.59 | 18.43 | 35.5 | 17 | 26.48 | 26.68 | 41.5 | |
| 7 | 17.02 | 16.67 | 28.0 | 18 | 8.30 | 8.11 | 33.0 | |
| 8 | 20.90 | 22.16 | 30.0 | 19 | 18.73 | 18.37 | 26.0 | |
| 9 | 20.55 | 20.77 | 28.0 | 20 | 16.51 | 17.03 | 36.0 | |
| 10 | 15.05 | 14.65 | 27.5 | 21 | 14.67 | 14.21 | 34.0 | |
| 11 | 13.99 | 13.82 | 26.5 | — | — | — | — |
表2中,Ph为历史电耗,Pop为优化后电耗. 从表1、2的迭代结果对比可知,该时刻下目标质量流量和迭代计算的实际质量流量的差平方和为6.09. 综合分析可知,计算误差较小,符合实际运行场景中的要求. 根据该二级网的实际情况可知,各热用户的设计回水温度为42 ℃. 通过计算热用户的历史回水温度和设计回水温度的整体方差,分析各热用户的实际供热效果. 对比通过运行优化计算得到的回温方差,验证提出的二级网运行优化方法的有效性和优势. 各热用户的回温方差对比如图8所示. 其中,
表 2 优化后循环水泵的逐时电耗对比
Tab.2
| 时间 | Ph/ (kW·h) | Pop/ (kW·h) | 时间 | Ph/ (kW·h) | Pop/ (kW·h) | |
| 1 | 4.79 | 3.94 | 13 | 4.84 | 3.67 | |
| 2 | 4.85 | 3.87 | 14 | 4.53 | 3.07 | |
| 3 | 4.31 | 3.45 | 15 | 4.55 | 3.02 | |
| 4 | 5.08 | 4.03 | 16 | 4.49 | 3.11 | |
| 5 | 4.53 | 3.65 | 17 | 5.04 | 3.78 | |
| 6 | 5.20 | 4.73 | 18 | 4.95 | 4.09 | |
| 7 | 4.62 | 4.40 | 19 | 4.64 | 4.01 | |
| 8 | 4.84 | 4.90 | 20 | 4.42 | 4.01 | |
| 9 | 5.04 | 4.83 | 21 | 4.35 | 3.98 | |
| 10 | 4.34 | 3.87 | 22 | 4.18 | 3.78 | |
| 11 | 4.50 | 3.67 | 23 | 4.05 | 3.60 | |
| 12 | 4.58 | 3.60 | 24 | 4.13 | 3.54 |
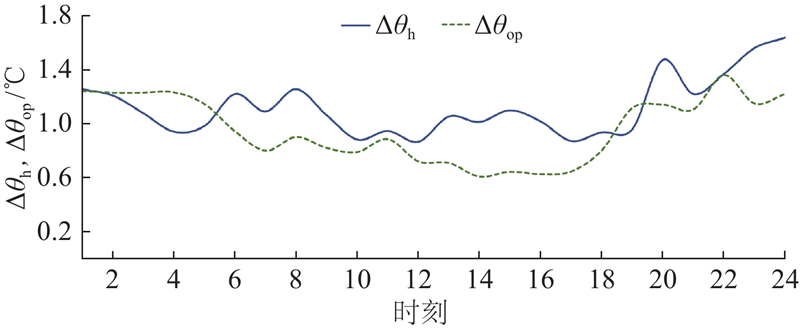
图 8
图 8 优化后热用户回温方差和历史回温方差分布的对比
Fig.8 Comparison of return water temperature variance distribution between optimized and historical condition for thermal user
根据图8中各热用户在每个时刻的回水温度方差可以看出,采用提出的基于负荷量化分析的二级网运行优化方法,在准确计算各热用户的真实热负荷的基础上,结合管网的水力热力建模分析和参数优化,与历史数据中热用户的回温方差相比,优化后回温方差的平均值整体减小12.16%. 这验证了二级网运行优化方法的有效性,解决了二级网中热量分布不均和过量供热的问题. 在热力站二次侧的回水处设有循环泵,通过对比优化前、后的水泵电耗,分析二级网运行优化方法的节能性. 基于历史和优化后的管网阻力特性,确定各管段和用户的扬程,结合管网中各管段的压差和流量关系计算循环水泵的电耗,具体的计算公式可以表示为
式中:
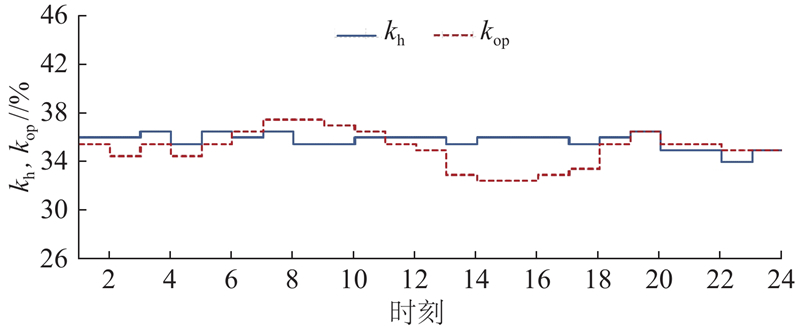
图 9
图 9 优化后热力站二次侧阀门开度策略的对比
Fig.9 Comparison of secondary side valve opening strategy at heating station after optimization
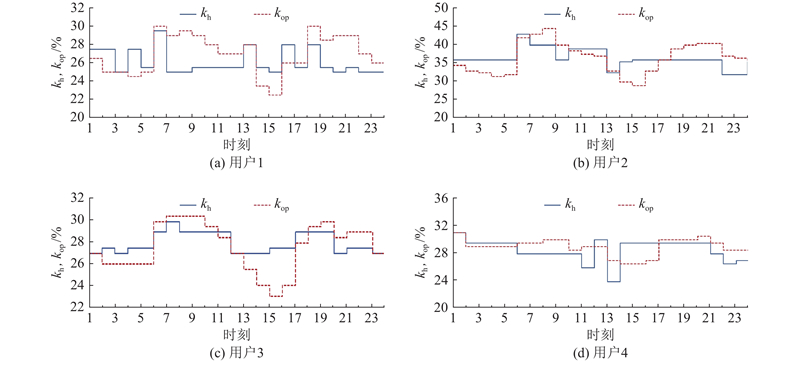
图 10
图 10 优化后热用户1~4的阀门开度策略对比
Fig.10 Comparison of valve opening strategies for thermal user 1-4 after optimization
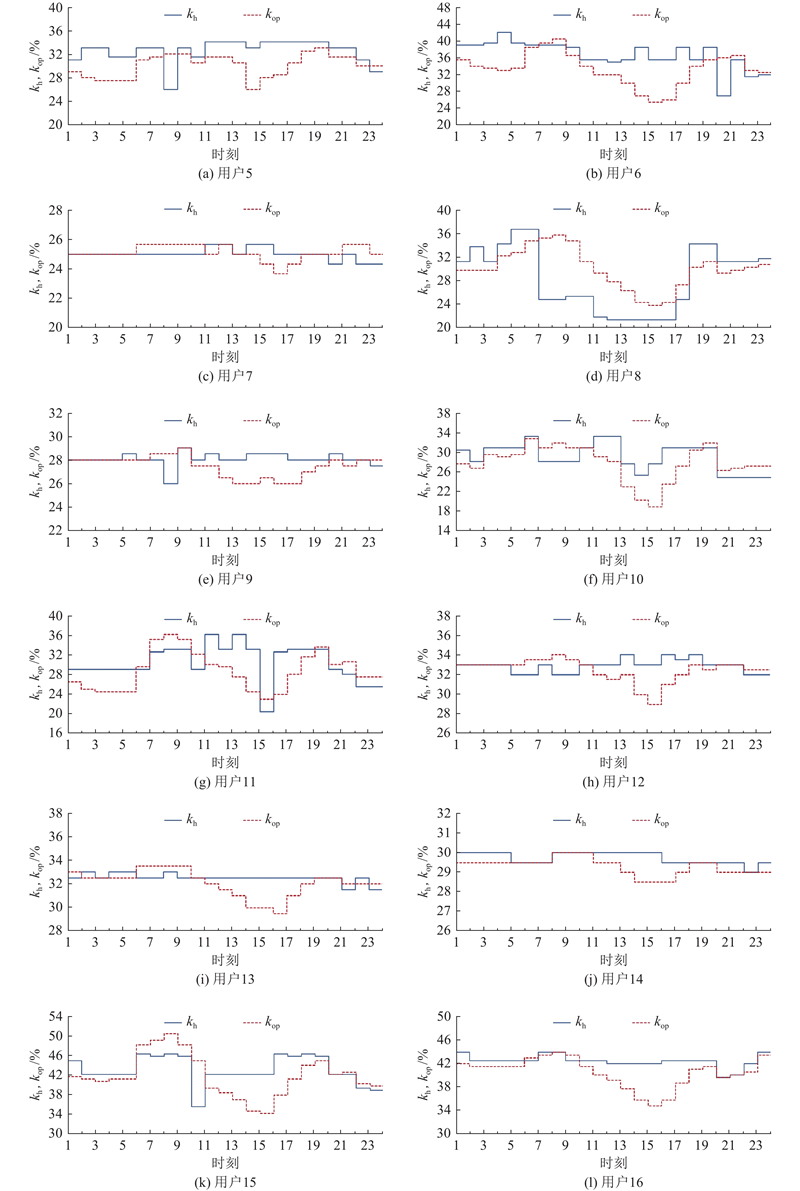
图 11
图 11 优化后热用户5~16的阀门开度策略对比
Fig.11 Comparison of valve opening strategies for thermal user 5-16 after optimization
4. 结 语
针对用户热负荷的精确评估问题,本文提出基于机理的供热负荷量化分析模型. 综合考虑热用户的负荷特性和多种实际影响因素,分析热用户的围护结构传热特性,通过热用户建模简化,在保障模型精度的同时,提升整体建模效率. 建立基于用户负荷量化的二级网运行优化方法. 案例结果表明,采用提出的二级网运行优化方法确定的阀门策略,在保证管网水力平衡的基础上,实现了用户的按需供热目标,在满足用户舒适化基本要求的基础上降低了单位面积能耗,解决了过量供热和供热不均衡的问题. 通过对比各热用户的回水温度可知,优化后各用户的整体回温方差比原来减小了12.16%,验证了本文运行优化方法的有效性. 优化后二级网循环水泵的电耗降低了16.46%,在保障用户舒适度的同时,实现了系统的节能降耗.
参考文献
基于DeST及TRNSYS软件的公共建筑能耗模型分析
[J].
Analysis of public building energy consumption model based on DeST and TRNSYS software
[J].
A statistical model of the spatial variability of weather for use in building simulation practice
[J].DOI:10.1016/j.buildenv.2021.108331
A detailed loads comparison of three building energy modeling programs: energyPlus, DeST and DOE-2.1E
[J].
绿色建筑节能技术在典型公共建筑运行中碳减排潜力评估
[J].
Assessing carbon emission reduction potential of green building energy saving technologies in operation of typical public buildings
[J].
基于混合算法优化支持向量机的供热负荷预测模型
[J].
Heat load prediction model based on support vector machine optimized by hybrid algorithm
[J].
Short-term building energy model recommendation system: a meta-learning approach
[J].DOI:10.1016/j.apenergy.2016.03.112
Research on the heat supply prediction method of a heat pump system based on timing analysis and a neural network
[J].
RC-Network based thermal bridge calculation method for transient heat transfer analysis of multidimensional building envelope details: a frequency response analysis-based method
[J].DOI:10.1016/j.enbuild.2023.113648 [本文引用: 1]
基于灰箱模型的设计阶段建筑负荷预测方法
[J].DOI:10.3969/j.issn.1003-0344.2021.03.001
A grey box model-based method for prediction of building loads in the design phase
[J].DOI:10.3969/j.issn.1003-0344.2021.03.001
Data pre-processing and optimization techniques for stochastic and deterministic low-order grey-box models of residential buildings
[J].DOI:10.1016/j.enbuild.2021.110775 [本文引用: 1]
An optimization procedure for district heating networks
[J].DOI:10.1016/j.egypro.2014.11.1107 [本文引用: 1]
Data-driven predictive model for feedback control of supply temperature in buildings with radiator heating system
[J].DOI:10.1016/j.energy.2023.128248 [本文引用: 1]
基于实际参数的集中供热系统二次网运行调节
[J].
Operational regulation of the secondary network of district heating systems based on actual parameters
[J].
基于动态水力平衡的集中供热系统二次管网节能优化调节方法研究
[J].
Study on optimal adjustment method of second pipe network in central heating system based on dynamic hydraulic balance
[J].
Heat distribution of heat exchange station in district heating system based on load forecasting
[J].DOI:10.1134/S0040601524040086 [本文引用: 1]
Investigation of control characteristics in multi-user building heating system based on demand-side adjustment
[J].DOI:10.1016/j.applthermaleng.2022.119534 [本文引用: 1]
基于粒子群优化的神经网络PID控制器在供热系统的研究
[J].
Research on neural network PID controller based on particle swarm optimization in heating system
[J].
基于遗传算法优化BP神经网络的短期热负荷预测方法研究
[J].
Optimization of BP neural network based on genetic algorithm for heat load forecasting
[J].
一种自适应模拟退火粒子群优化算法
[J].
Adaptive simulated annealing particle swarm optimization algorithm
[J].
综合能源系统分析的统一能路理论(二): 水路与热路
[J].
Energy circuit theory of integrated energy system analysis (II): hydraulic circuit and thermal circuit
[J].