叠片导磁棒式集成化速度传感器的建模与实验

doi:10.3785/j.issn.1008-973X.2025.08.004

叠片导磁棒式集成化速度传感器的建模与实验

丁川^,, 朱子帅, 夏宁, 高鹏辉, 裴升祥

1. 浙江工业大学机械工程学院，浙江杭州 310023

2. 浙江工业大学特种装备制造与先进加工技术教育部重点实验室，浙江杭州 310023

Modeling and experiment of integrated speed sensor based on laminated magnetic rod

DING Chuan^,, ZHU Zishuai, XIA Ning, GAO Penghui, PEI Shengxiang

1. School of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310023, China

2. Key Laboratory of Special Purpose Equipment and Advanced Processing Technology, Ministry of Education, Zhejiang University of Technology, Hangzhou 310023, China

收稿日期: 2024-07-11

基金资助:

国家自然科学基金资助项目（51805480）；浙江省自然科学基金资助项目（ZCLMS25E0502）.

Received: 2024-07-11

Fund supported:

国家自然科学基金资助项目（51805480）；浙江省自然科学基金资助项目（ZCLMS25E0502）.

作者简介 About authors

丁川（1986—），男，副教授，从事高性能液压元件和高速、超高压液压系统的研究.orcid.org/0000-0002-1034-2261.E-mail：chuanding@zjut.edu.cn , E-mail：chuanding@zjut.edu.cn

摘要

为了提高液压缸与速度传感器之间的集成度，提出基于磁感应式设计理念的速度传感器. 该传感器用液压缸活塞运动改变缸体不同位置的磁通量，用霍尔元件感应磁通量的变化，实现位移和速度的测量. 参考行业内叠压硅钢片的方式，通过将导磁棒离散化再叠片的方式进行涡流抑制来改善传感器的动态性能，通过公式推导和Maxwell三维仿真模型验证叠片厚度对叠片式导磁棒涡流损耗的影响. 使用叠片式导磁棒的新式传感器与标准传感器，开展对比标定实验. 结果表明，当输入正弦流量信号时，使用叠片式导磁棒的新式传感器的复现频率达到5 Hz；当输入阶跃流量信号时，响应滞后时间降至0.30 s. 结果验证了优化方案的可行性.

关键词： 液压缸 ; 速度传感器 ; Maxwell仿真 ; 叠片式导磁棒 ; 标定实验

Abstract

A speed sensor based on magnetic induction principles was proposed to improve the integration of hydraulic cylinders with speed sensor. Piston motion was employed to modulate magnetic flux distribution along the cylinder body, with Hall-effect sensors detecting flux variation to realize the measurement of displacement and speed. Eddy currents were mitigated via discretized and laminated magnetic rods to enhance dynamic response inspired by industrial laminated silicon steel stacking techniques. Theoretical analysis and Maxwell 3D simulations verified the influence of lamination thickness on eddy current losses within these rods. Comparative calibration experiments between the novel sensor based on laminated magnetic rod and conventional sensors revealed that the proposed design attained a tracking bandwidth of 5 Hz under sinusoidal flow excitation, while step-flow tests yielded a reduced response latency of 0.30 s. Results verified the feasibility of the optimized sensor configuration.

Keywords： hydraulic cylinder ; speed sensor ; Maxwell simulation ; laminated magnetic rod ; calibration experiment

PDF (3322KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

丁川, 朱子帅, 夏宁, 高鹏辉, 裴升祥. 叠片导磁棒式集成化速度传感器的建模与实验. 浙江大学学报(工学版)[J], 2025, 59(8): 1583-1589 doi:10.3785/j.issn.1008-973X.2025.08.004

DING Chuan, ZHU Zishuai, XIA Ning, GAO Penghui, PEI Shengxiang. Modeling and experiment of integrated speed sensor based on laminated magnetic rod. Journal of Zhejiang University(Engineering Science)[J], 2025, 59(8): 1583-1589 doi:10.3785/j.issn.1008-973X.2025.08.004

流量信号是评价电液系统工作特性的关键参数^[1]. 常见的容积式流量计通过计量单元将待测液体分割为等容积单元，计算单位时间内的容积单元数目变化量，实现流量测量. 由于电液系统工作压力通常为50~350 bar，流量计的一次仪表须采用非接触式计量元件. 具体而言，主要利用磁感应技术来构建一次仪表，同时需要在信号发生和采集元件之间增加结构件，以保证流量计的耐压性能.

磁感应技术利用磁场效应实现物理量的测量和检测. 目前，常见的用于流量计的磁感应元件有霍尔元件^[2-3]、基于差动变压器原理的位移传感器^[4-6]、基于变磁通原理的速度传感器^[7-9]以及基于磁致伸缩原理的位移传感器^[10-11].

霍尔元件因离散性的特点，被广泛应用于容积式流量计. 通过对作为信号发生器的霍尔元件进行布局设计，提高测量精度或动态频响. Cheong等^[12]对新型容积式正位移流量计与结合密度计的质量流量计和科里奥利质量流量计进行性能比较. 结果表明，新型流量计在低流量下具有±1%的精度，表现出更宽的量程.

位移以及速度传感器多用于伺服缸反馈或动态标定. 太原理工大学的廉自生团队基于TMR磁阻设计外置式磁感应位移传感器，通过检测活塞运动时的永磁环磁场变化来计算液压缸位移，精度为0.29%^[13-14].

磁致伸缩位移传感器利用磁性材料在磁场作用下发生尺寸变化的特点来检测磁场，具有高精度和高可靠性的优势. Su等^[15]提出具有高密封性和灵敏度可调性的磁致伸缩传感器. 通过Terfenol-D材料和光纤马赫-曾德尔干涉仪来检测磁场变化. 传感器的灵敏度可以达到−1.113 nm/mT.

笔者所在团队设计的二维活塞式动态流量计是基于“二维液压元件”设计理念的容积式流量计，曾采用霍尔元件作为传感器来测量稳态流量信号^[16-17]，并在后续的研究中尝试利用传感器获取计量元件活塞的位置或速度信号^[18-19]，以计算动态流量的变化情况. 在测量过程中出现了磁致伸缩位移传感器小量程精度不足和外接传感器占用空间较大，不利于安装的问题.

鉴于流量计对小量程和高度集成化的需求，本文基于变磁通设计的理念，提出可集成于活塞式流量计内部的磁电式速度传感器. 在阐述传感器的机械结构和工作原理后，提出将传感器内导磁棒叠片化的方法以提升性能. 通过数学建模和仿真分析，研究导磁棒叠片厚度对速度传感器动态测量性能的影响. 通过搭建原理样机完成实验研究，验证该新式速度传感器的可行性.

1. 机械机构和工作原理

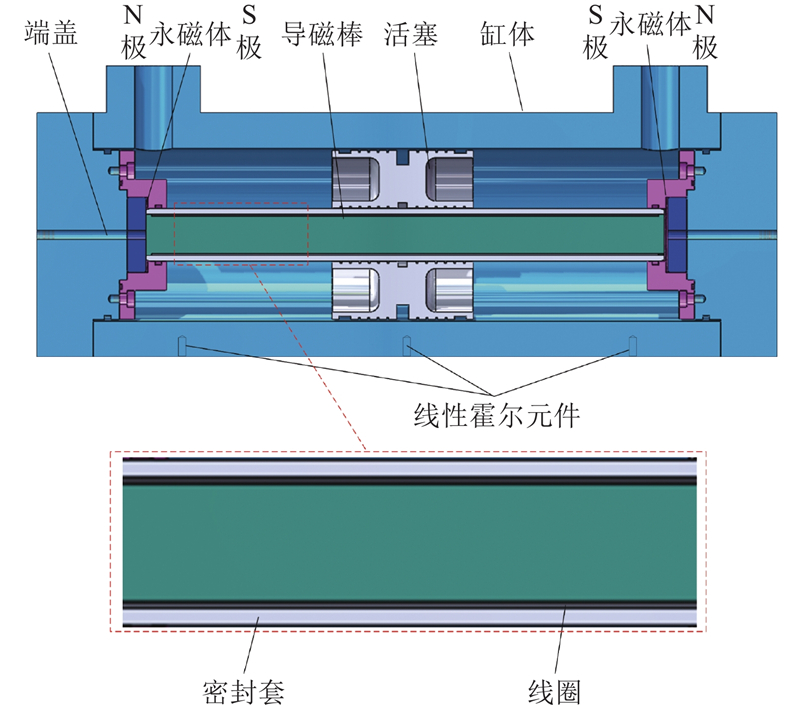
如图1所示为集成速度传感器的动态缸的结构，主要结构有端盖、缸体、活塞、永磁体、永磁体座、导磁棒、线圈、密封套. 在缸体外侧打有若干个小孔，安装线性霍尔元件. 活塞在缸体内部，可以受由缸口进入的流体作用沿导磁棒轴向移动. 导磁棒两端各有一个永磁体嵌入端盖中，并同导磁棒一起用永磁体座固定. 将线圈均匀缠绕在导磁棒上，在线圈外侧有密封套，用以保护线圈.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 集成于动态缸中的速度传感器机械结构

Fig.1 Mechanical structure of speed sensor integrated in dynamic cylinder

如图2所示，2个磁钢朝向缸体外侧的一段均为N极，缸体和上、下端盖构成一整个磁感应空间，并被活塞分成2个部分. 以导磁棒、端盖、活塞和缸体内壁为边界，形成一部分磁感线为顺时针走势，另一部分为逆时针走势的循环. 活塞移动后途经的部分磁感线走势反转，导致线圈及各线性霍尔元件安装位置上的磁通量会随着活塞的运动而实时发生变化，通过测量线性霍尔元件上的磁感应强度和线圈上由于变化的磁通量而产生的感应电动势，可以实现位移和速度的测量^[20].

图 2

新窗口打开| 下载原图ZIP| 生成PPT

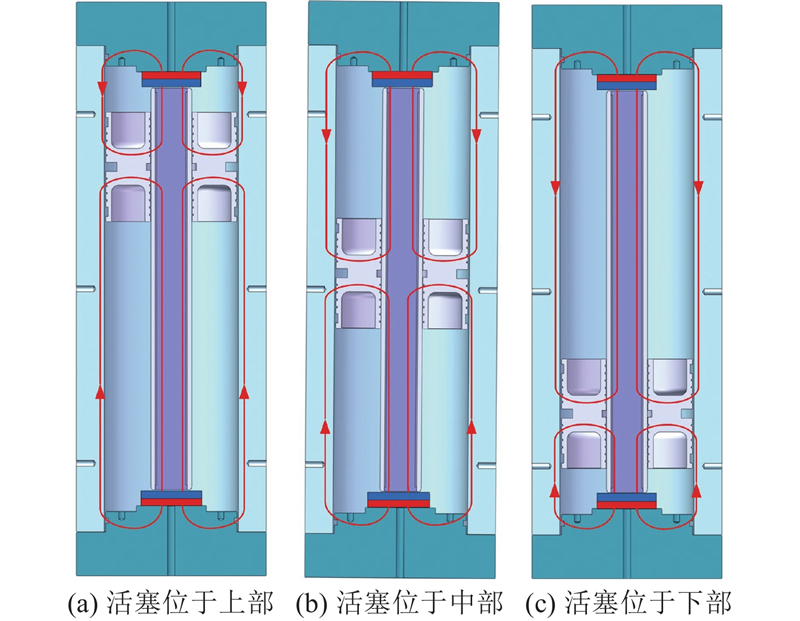
图 2 活塞移动时磁感线分布的理论示意图

Fig.2 Theoretical diagram of distribution of magnetic field line when piston is moving

2. 速度传感器的数学建模

磁电式速度传感器是利用电磁感应原理，将速度信号转换为电信号的传感器. 它具有结构简单、输出功率大、性能稳定等特点. 在使用过程中，磁电式速度传感器可能会出现幅值衰减的问题，这会影响到测量的准确性和可靠性.

磁电式传感器中的功率损耗降低了它的工作性能，功率损耗主要来源于磁滞损耗和涡流损耗2个方面. 在以铁芯为主体的磁路中，涡流损耗超过了磁滞损耗，涡流损耗比磁滞损耗大一个数量级. 导磁棒的轴向磁通量对磁电式传感器的测量性能有着直接的影响，而导磁棒截面磁性材料的面积和导磁棒的轴向磁通量成正比. 为了保障测量性能并降低涡流损耗，参考了行业内普遍采用的硅钢片叠压技术. 鉴于硅钢片的生产工艺已经非常成熟，将传感器铁芯设计成如图3所示的叠片结构^[21]. 这样的设计不仅能够有效减少涡流损耗和保证轴向磁通量，而且由于硅钢片的易获取性和经济性，能够降低制造成本.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 叠片式导磁棒截面

Fig.3 Cross-section of laminated magnetic rod

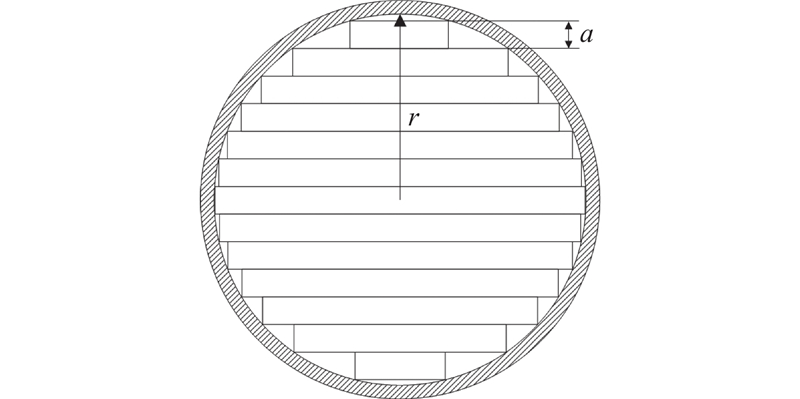
如图4所示为制作叠片结构铁芯中的铁片，薄片的厚度为$a$. 磁感应强度$B$是沿着铁片定向的.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 叠片结构的单片示意图

Fig.4 Monolithic schematic diagram of laminated structure

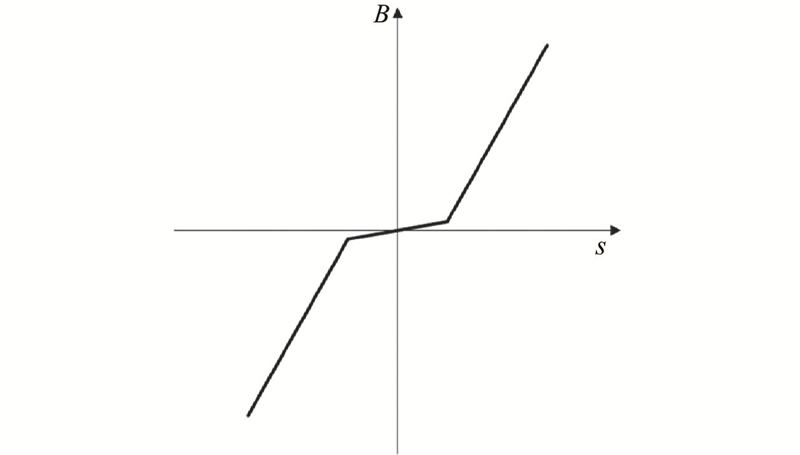
在缸体上通过线性霍尔元件来实现磁场检测. 当活塞处于缸体上端的状态时，磁感线从下往上穿过安装在缸体中部的线性霍尔元件，磁感应强度$B < 0$. 当运动部件移动到缸体中间位置时，由于磁感线分布上下对称，此时线性霍尔元件处几乎无磁感线穿过，$ B \approx 0 $. 当活塞处于缸体下端时，可以得到$B > 0$. 在活塞从上往下移动的过程中，该点处的磁感应强度会经历$B < 0$到$ B \approx 0 $再到$B > 0$的过程，如图5所示. 图中，s为活塞位移. 由于缸体上下对称，根据工程电磁场理论可知，该位移-磁感应强度曲线关于原点O对称，一个位移对应一个磁感应强度. 为了避免数据的多余度，在缸体圆周上设置2×3个线性霍尔元件，通过6个线性霍尔元件测得的位移平均值来减小误差.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 线性霍尔元件处的磁感应强度趋势

Fig.5 Trend of magnetic induction intensity at linear hall element

在线性度明显的区域，可设$B$和$ s $的关系:

(1)$ B = ks+c. $

式中：$k$为线性度，$c$为截距.

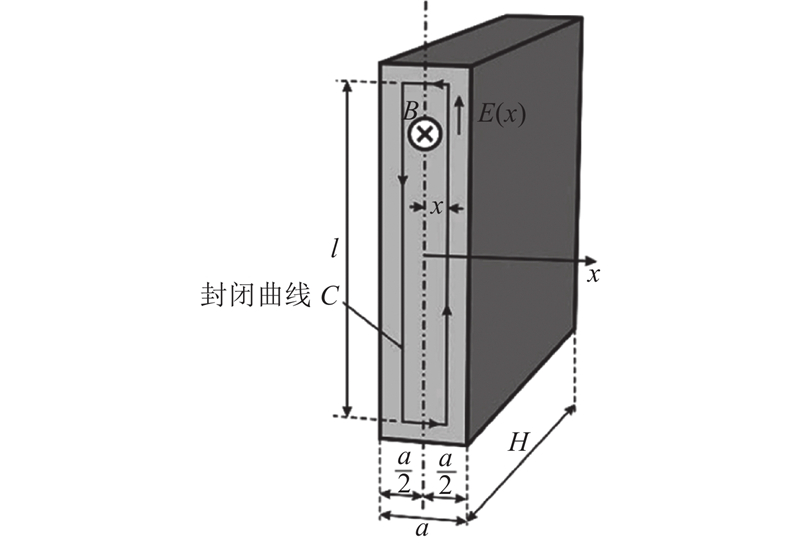
设活塞运动速度为$ v $，可得$B$和$ v $的关系：

(2)$ B = kvt+c. $

此时通过封闭曲线的磁通量为

(3)$ \varPhi = BS = al(kvt+c). $

感应电动势幅值为

(4)$ e = N\frac{{{\text{d}}\varPhi }}{{{\text{d}}t}} = Nalkv. $

电阻$R$和电导率$\sigma $的关系如下：

(5)$ R = \frac{H}{{\sigma A}}. $

式中：$A$为导体截面积.

单片导体的总功率为

(6)$ P = \frac{{{e^2}}}{R} = \frac{{\sigma {N^2}{a^3}{l^3}{k^2}{v^2}}}{H}. $

厚度$a$和薄片的高度$l$比起来很小. 在薄片的横截面上，定义宽度为$2x$的封闭曲线C. 因为 $ x{\text{ }} \leqslant a{\text{ }}/2 $，可以假设$ x{\text{ }} < < {\text{ }}l $. 在宽度为$2x$的封闭曲线中，

(7)$ {e_1} = N2xlkv. $

因为 $x < < l$，沿着封闭曲线C短边的那部分曲线积分可以忽略不计. 沿着封闭曲线C长边的感应电动势$E(x)$^[21]为

(8)$ {e_1} = 2lE(x),E(x) = Nxkv. $

电流密度为

(9)$ J(x) = \sigma E(x) = N\sigma xkv. $

单位体积焦耳损耗为

(10)$ {P_{{\text{Fe}}}}(x) = \frac{{\Delta P}}{{\Delta V}} = \frac{{{J^2}(x)}}{\sigma } = \sigma {(Nxkv)^2}. $

在尺寸为 $a \times l \times H$的单片铁磁材料中，总的损耗 ${P_{{\text{Fe}}}}$是通过空间整合得到的，

(11)$ \begin{split} {P_{{\text{Fe}}}} = &\int {_V{P_{{\text{Fe}}}}(x){\text{d}}V} = \\ & 2\int {_0^{{a}/{2}}} Hl\sigma {(Nxkv)^2} = \frac{{{a^3}}}{{12}}Hl\sigma {N^2}{k^2}{v^2}. \end{split}$

叠片结构导磁棒的总功率$ {P_{\text{T}}} $和损耗$ {P_{\text{L}}} $分别为

(12)$ {P_{\text{T}}}{\text{ = }}\frac{{\sigma {N^{\text{2}}}{a^3}{l^{{'^2}}}{k^2}{v^2}}}{H}, $

(13)$ {P_{\text{L}}}{\text{ = }}\frac{{{a^3}}}{{{\text{12}}}}H{l^{'}}\sigma {N^2}{k^2}{v^2}. $

式中：${l^{'}}$为叠片结构导磁棒所有叠片长度和，

$ {l^{'}} = \sqrt {{r^2} - 0.5{a^2}} +2\sum\limits_{i = 1}^n {\sqrt {{r^2} - {{(0.5+na)}^2}} } \text{，}n = \left[\frac{r}{a} - 0.5\right]. $

由${P_{\text{W}}}{\text{ = }}{P_{\text{T}}} - {P_{\text{L}}}$可得线圈的实际工作功率. 因$a$和$l$比起来很小，$a{l^{'}}$可以近似为圆形导磁棒的截面积，在此基础上得到活塞运动速度为$v$时的线圈感应电动势：

(14)$ {e_{\text{W}}} = \sqrt {{P_{\text{W}}}{R^{'}}} = Nkv\sqrt {{\text{π} ^2}{r^4} - {{{a^2}{H^2}}}/{{12}}} . $

式中：${R^{'}} = R{l}/{{{l^{'}}}}$.

以上从理论公式出发证明了叠片厚度的减小会增大线圈感应电动势，本文将在下一章节通过Maxwell三维仿真验证其准确性.

3. 仿真分析

为了研究导磁棒对磁感应式速度传感器的影响，基于Maxwell软件，建立三维电磁场仿真模型，开展仿真研究，如图6所示. 仿真的主要参数设置见表1.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

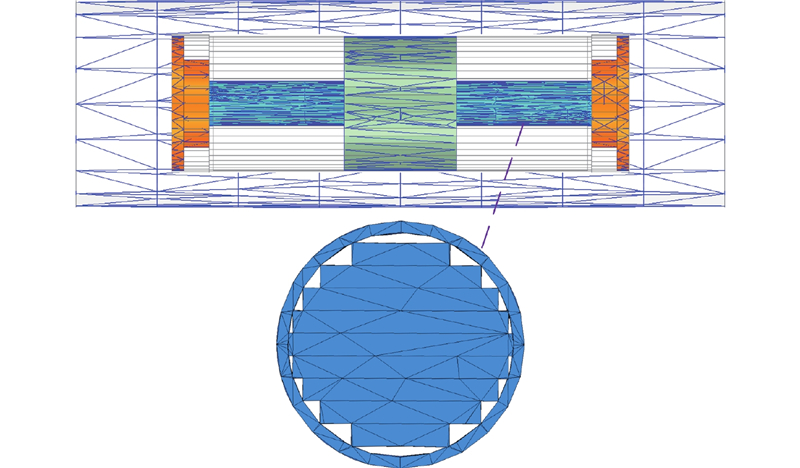
图 6 速度传感器的Maxwell三维仿真模型

Fig.6 Maxwell three-dimensional simulation model of speed sensor

表 1 速度传感器仿真模型的物理参数设置

Tab.1 Physical parameter setting of speed sensor simulation model

参数	数值	参数	数值
缸体外径/mm	130	线圈线径/mm	0.3
缸体内径/mm	92	线圈电阻/Ω	12
永磁体材料	NdFe30	导磁棒直径/mm	20
永磁体直径/mm	40	导磁棒长度/mm	275
永磁体厚度/mm	10	活塞行程/mm	200
线圈匝数	900	—	—

新窗口打开| 下载CSV

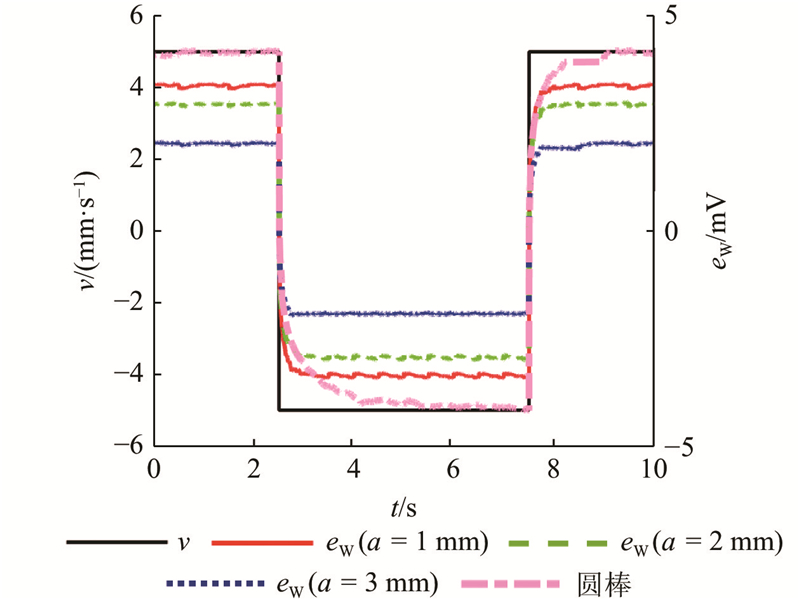
将截面圆柱形的导磁棒离散成截面为多根矩形叠加的导磁棒，每个叠片的厚度为$a$. 探究感应电动势幅值衰减现象与厚度$a$的关系. 叠片厚度$a$共有3个值，分别为1、2和3 mm.

如图7所示为未经过叠片化处理的圆棒和3种不同叠片厚度的叠片式导磁棒的阶跃仿真结果示意图. 仿真结果表明，普通圆柱形导磁棒面对阶跃信号时的滞后时间长，滞后时间约为2.4 s. 叠片式导磁棒的叠片厚度越小，面对相同阶跃信号时的滞后时间越短，叠片厚度为1、2、3 mm的导磁棒滞后时间分别约为0.05、0.07和0.10 s.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 不同加工条件下导磁棒对阶跃信号响应的影响

Fig.7 Influence of magnetic rod on step signal response under different processing conditions

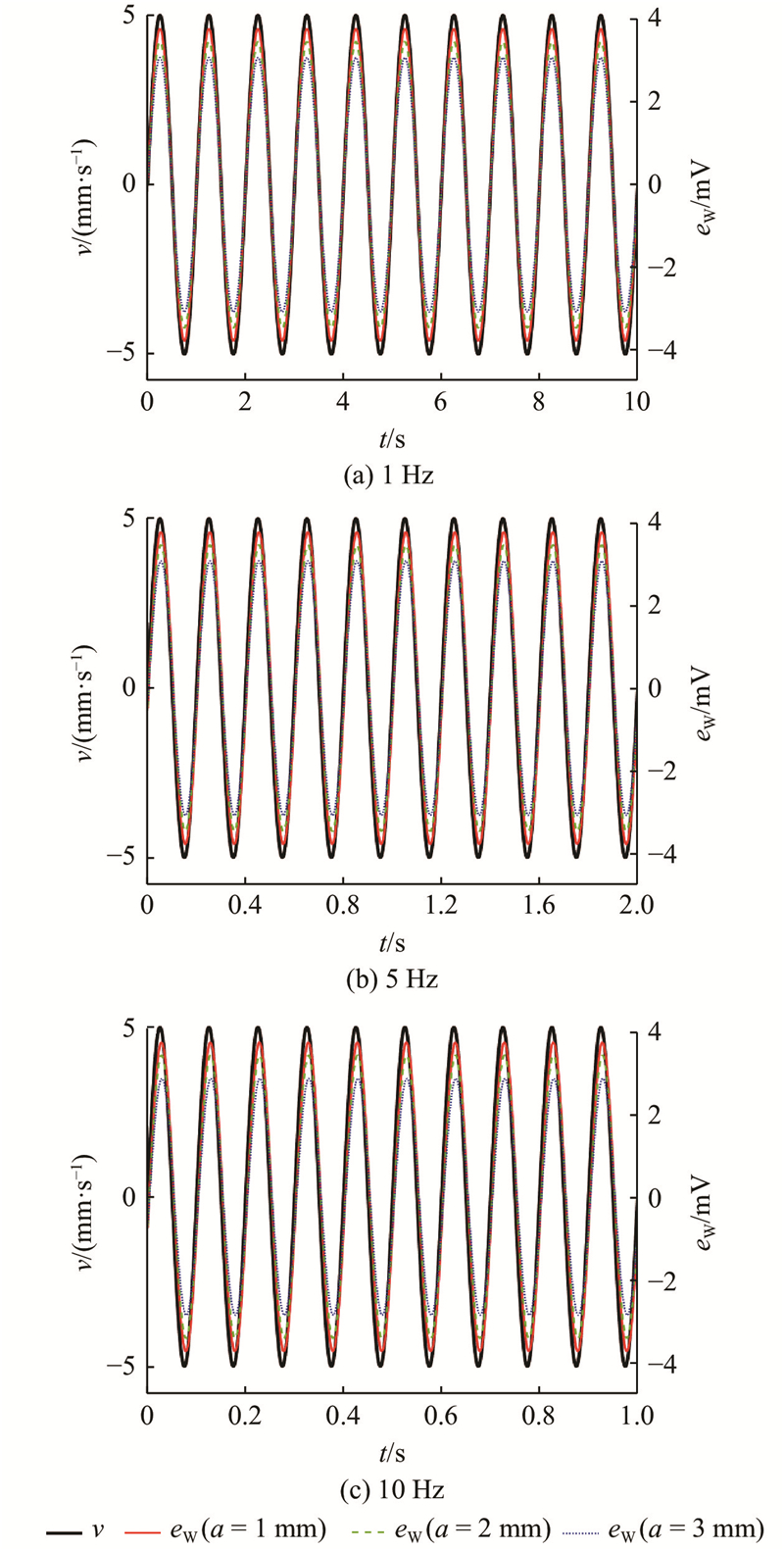
如图8所示为3种不同叠片厚度的叠片式导磁棒在1~10 Hz标准正弦信号下的仿真结果. 仿真结果表明，在1~5 Hz标准正弦信号下3种导磁棒的感应电动势基本无衰减，在10 Hz信号下叠片厚度为3 mm的导磁棒感应电动势出现约7%的幅值衰减.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8 不同频率正弦信号下叠片厚度对线圈感应电动势的影响

Fig.8 Influence of lamination thickness on coil induced electromotive force under different frequency sinusoidal signals

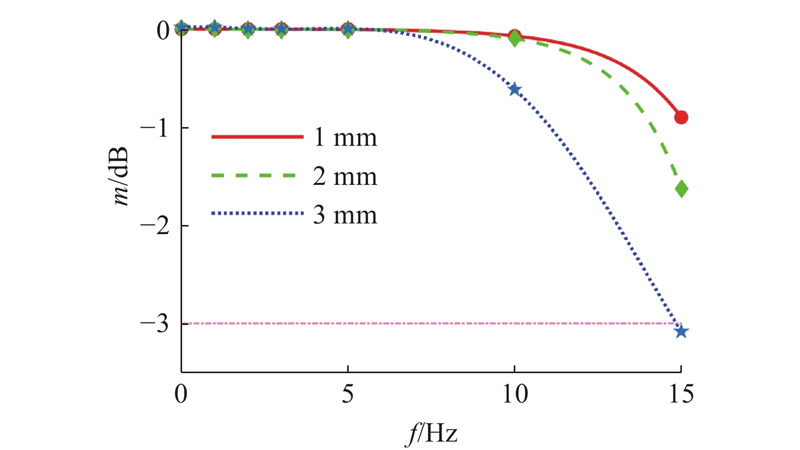
如图9所示为分别安装3种不同叠片厚度的叠片式导磁棒的磁电式传感器在面对标准正弦信号时产生的感应电动势幅度随频率f变化的仿真结果. 图中，m为感应电动势和输入电动势的幅值比. 仿真结果表明，在1~6 Hz标准正弦信号下3种导磁棒产生的感应电动势信号基本无衰减，提高了正弦信号频率. 叠片厚度为3 mm的导磁棒的感应电动势信号最先发生频率响应衰减并在约15 Hz标准正弦信号下衰减至−3 dB. 叠片厚度为1、2 mm的导磁棒的感应电动势信号能够在频率为0~10 Hz的情况下不产生明显的响应衰减，传感器处于正常工作的状态.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9 不同叠片厚度导磁棒的频率响应伯德图

Fig.9 Frequency response Bode diagram of magnetic rod with different laminated thickness

在工艺允许的范围内，叠片式导磁棒中叠片的厚度应越薄越好，越薄越能够抑制涡流.

在叠片式导磁棒中，导磁棒可以被离散成更多的叠片，兼顾导磁棒的横截面积和被切割的份数，可以在进一步减少阶跃响应时间的同时，保证感应电动势的幅值不减小. 受限于加工工艺，在实验中选择叠片厚度为2 mm的叠片式导磁棒.

4. 实验研究

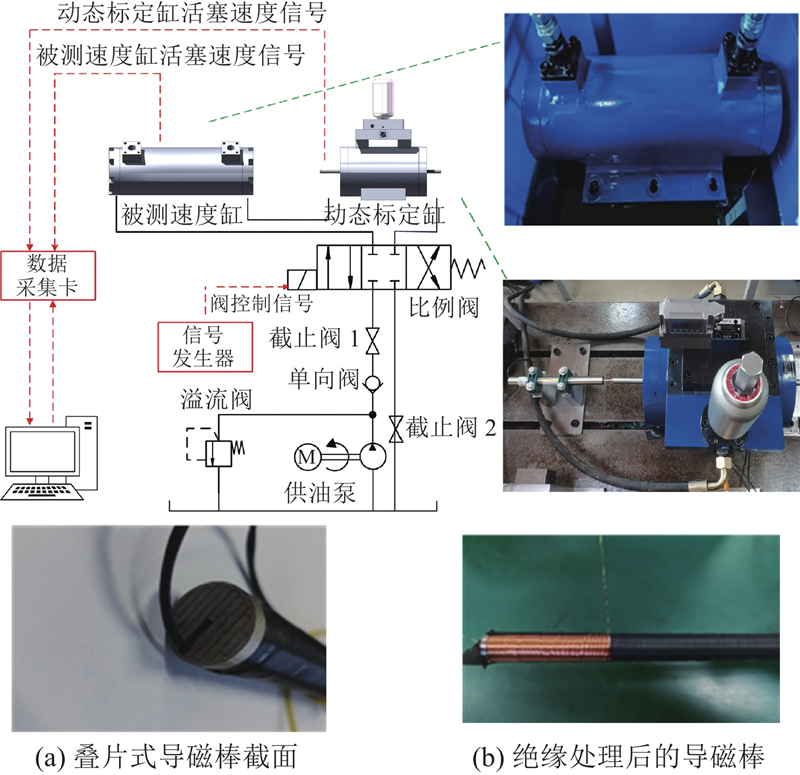
速度传感器的测量标定实验台如图10所示，流量发生部分由PC、比例伺服换向阀、信号发生器组成. 在标准动态缸安装标准速度传感器，在被测速度缸安装新式速度传感器. 实验台采用泵站供油，由溢流阀调节系统压力，信号发生器的输入控制信号控制阀口开闭. 被测速度缸和动态标定缸通过液压软管串联，当不考虑油液弹性模量时，通过上述两缸的油液的体积始终相同. 在实验过程中，将两缸活塞的位移和速度信号作为对比，能够得到磁电感应式速度传感器的动态特性.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10 叠片导磁棒式速度传感器的测量标定实验台

Fig.10 Calibration test rig of laminated magnetic rod speed sensor

如图10（a）所示为该叠片式导磁棒的截面示意图，叠片式即将原本圆形的横截面离散成多个矩形，将多个矩形长轴通过叠片的方式叠成一个类圆柱体导磁棒. 在2根矩形长轴之间插入纸片或其他绝缘材质物体，用以切断外表面上的涡流，减弱涡流效应. 如图10（b）所示为绕完线圈绝缘处理后的叠片式导磁棒示意图. 实验中所用到的各类实验仪器参数如表2所示.

表 2 测量标定实验台实验仪器的性能参数

Tab.2 Performance parameter of experimental instrument of calibration test bench

仪器	参数
比例伺服换向阀HD- 4WRPEH6C4B12L	7 MPa阀压差下公称体积流量为40 L/min，阶跃响应时间(0~100%)<10 ms，响应频率(控制电压UE±100%)为60 Hz
标准速度传感器 SD-150	测量量程为0~0.1 m/s，精度为1%，输出电压为500 mV
标准位移传感器 WY-150	测量量程为0~250 mm，精度为1%，输出电压为0~5 V
数据采集卡研华 USB-4716	16路模拟输入，采样速率为1.5×10⁵ s⁻¹
泵源	额定压力为7 MPa，额定体积流量为300 L/min
溢流阀 HD-DB10-1-10B/315	最大压力为31 MPa，最大体积流量为650 L/min

新窗口打开| 下载CSV

4.1. 稳态测量特性的比较实验

从图11可知，叠片式导磁棒型速度传感器的测量值${v_{\text{1}}}$与标准传感器的测量值${v_2}$的误差约为±1.5%. 考虑到标准传感器的测量精度误差为±1%，根据合成标准不确定度的计算公式^[22]可知

图 11

新窗口打开| 下载原图ZIP| 生成PPT

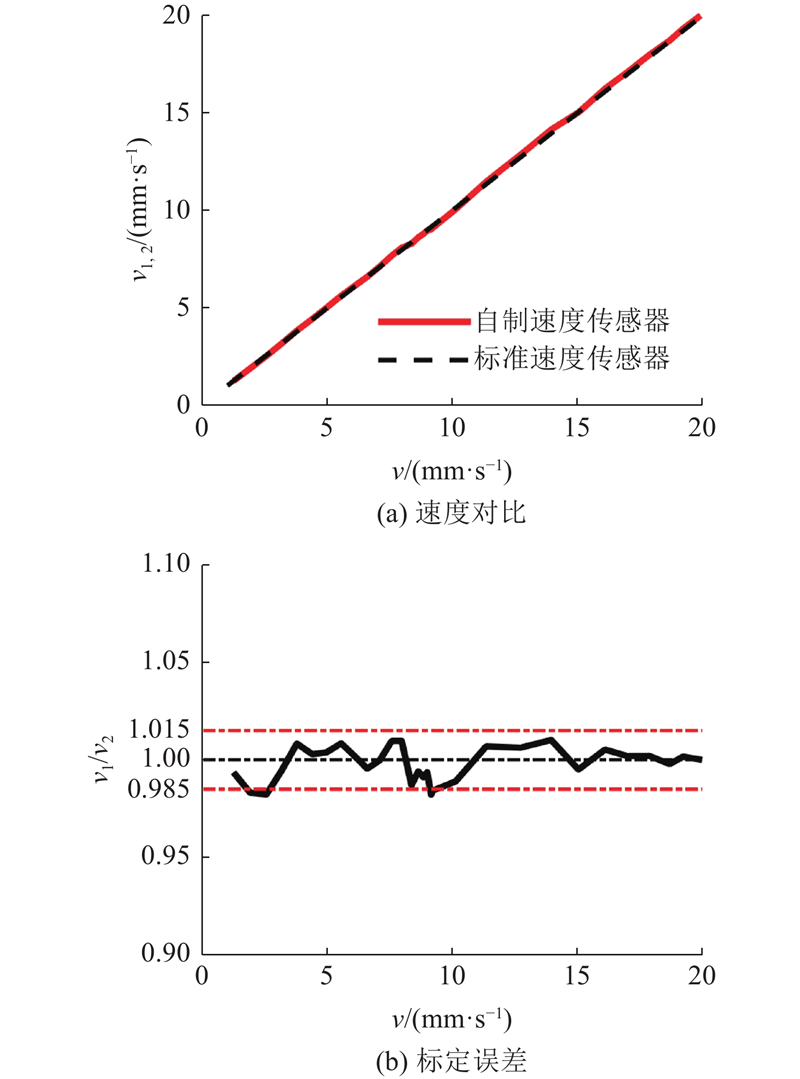
图 11 叠片式导磁棒稳态测量特性的实验结果比较

Fig.11 Comparison of experimental result of steady-state measurement characteristic of laminated magnetic rod

(15)$ {u_{\mathrm{c}}}(f) = \sqrt {\sum\limits_{i = 1}^n {u_{\mathrm{c}}^2({x_i})} } . $

该新式传感器的误差约为±1.8%.

4.2. 阶跃响应测量特性和标准正弦测量特性标定的实验

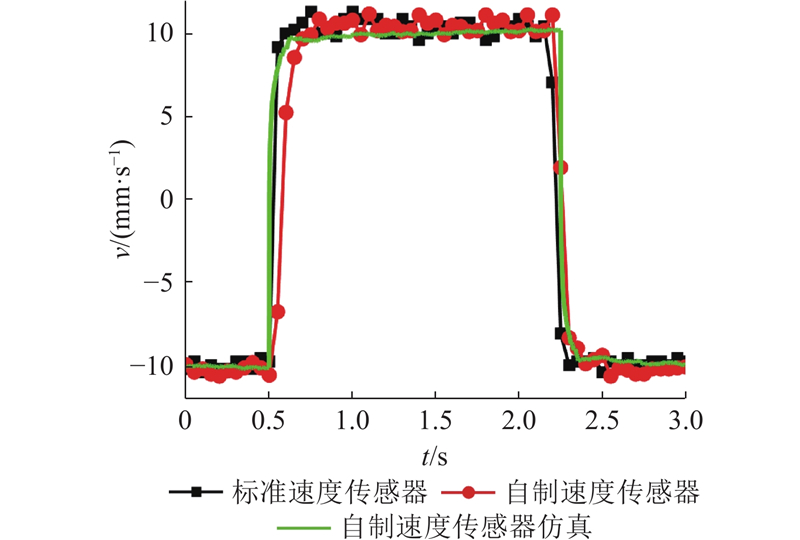
如图12所示为阶跃响应测量特性标定的实验结果示意图. 可以看出，标准速度传感器的阶跃响应好，滞后时间几乎为0 s；新式速度传感器的阶跃响应较好，滞后时间约为0.3 s.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12 叠片式导磁棒阶跃响应测量特性标定的实验结果示意图

Fig.12 Schematic diagram of experimental result of step response measurement characteristic calibration of laminated magnetic rod

如图13所示为标准正弦测量特性标定的实验结果和仿真结果对比示意图. 图13（a）、（b）表明，自制速度传感器在f ≤ 5 Hz的标准正弦信号下基本不发生信号幅值衰减的现象. 图13（c）表明，自制速度传感器在10 Hz标准正弦信号下已发生近15%的信号幅值衰减.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13 标准正弦测量特性标定实验的结果示意图

Fig.13 Result diagram of standard sinusoidal measurement characteristic calibration experiment

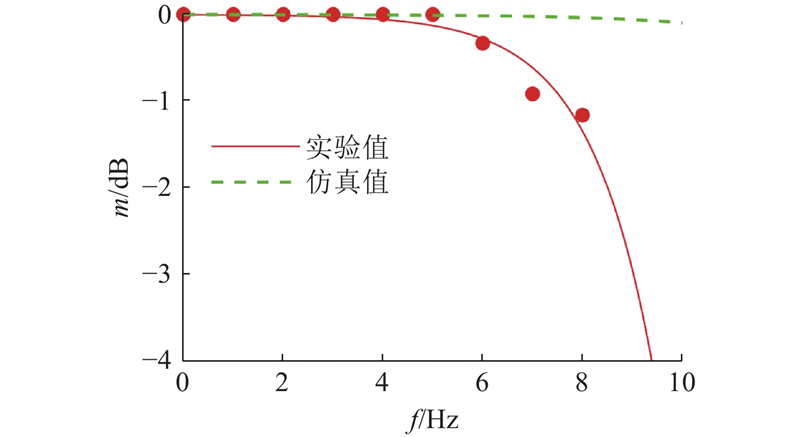
如图14所示为自制传感器仿真和实验的动态响应特性曲线，表明自制传感器在6 Hz标准正弦信号下已发生15%的信号幅值衰减. 此时测量结果的偏差较大，判断传感器已失效，故该传感器的有效工作频率小于等于5 Hz.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14 叠片导磁棒式速度传感器的频响特性

Fig.14 Frequency response characteristic of laminated magnetic rod speed sensor

5. 结　论

（1）提出磁电式速度传感器，通过叠片化导磁棒减小涡流效应，改善传感器的动态性能. 在仿真分析中，叠片式导磁棒能够有效地减少阶跃响应时间，且叠片的厚度越薄，涡流的抑制效果越好，验证了优化方案的可行性.

（2）对使用叠片式导磁棒的新式传感器与标准传感器进行对比. 实验结果表明，叠片式导磁棒能够有效削减因电涡流效应导致的幅值衰减，叠片优化后传感器的复现频率达到5 Hz，响应滞后时间短，为0.3 s.

（3）目前对导磁棒的涡流优化仅限于离散化叠片处理，之后可以基于电涡流的集肤效应原理，在导磁棒表面激光刻蚀微槽阵列. 在不会大幅减小线圈上输出的感应电动势的前提下继续减小涡流，会提升响应速度，改善幅频特性.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王松, 张天宏, 王建锋, 等

基于涡轮流量计的动态流量测量方法研究

[J]. 测控技术, 2012, 31 (11): 24- 27

DOI:10.3969/j.issn.1000-8829.2012.11.006 [本文引用: 1]

WANG Song, ZHANG Tianhong, WANG Jianfeng, et al

Study of dynamic flow rate measurement based on turbine flow meter

[J]. Measurement and Control Technology, 2012, 31 (11): 24- 27

DOI:10.3969/j.issn.1000-8829.2012.11.006 [本文引用: 1]

[2]

严加斌, 朱峰, 李军, 等

高速动车组速度传感器的电磁干扰测试与分析

[J]. 电子测量与仪器学报, 2015, (3): 433- 438

[本文引用: 1]

YAN Jiabin, ZHU Feng, LI Jun, et al

Electromagnetic interference measurement and analysis of high-speed electric multiple units speed sensor

[J]. Journal of Electronic Measurement and Instrument, 2015, (3): 433- 438

[本文引用: 1]

[3]

张柏杰

霍尔速度传感器在线检测设备的研制

[J]. 设备管理与维修, 2021, 18: 133- 134

[本文引用: 1]

ZHANG Bojie

Development of on-line detection equipment for Hall velocity sensor

[J]. Plant Maintenance Engineering, 2021, 18: 133- 134

[本文引用: 1]

[4]

LAM K, CHEN Z, NI Y, et al

A magnetorheological damper capable of force and displacement sensing

[J]. Sensors and Actuators A: Physical, 2009, 158 (1): 51- 59

[本文引用: 1]

[5]

MOCIRAN B, GLIGA M

Optimization of an inductive displacement transducer

[J]. Sensors, 2023, 23 (19): 8152

DOI:10.3390/s23198152

[6]

ANA D, STJEPAN F, BOJAN T

Methodology for eddy current losses calculation in linear variable differential transformers (LVDTs)

[J]. Sensors, 2023, 23 (4): 1760

DOI:10.3390/s23041760 [本文引用: 1]

[7]

MEHRAN M, PAVEL R, VACLAV G, et al

An axial flux eddy current sensor with perpendicular coils for speed measurement

[J]. Sensors and Actuators A: Physical, 2024, 365: 114917

DOI:10.1016/j.sna.2023.114917 [本文引用: 1]

[8]

JIANG G, CHEN S, LI Z, et al

Cylindrical-cam modulation instantaneous angular speed sensor for reciprocating-rotary machine

[J]. Mechanical Systems and Signal Processing, 2023, 205: 110860

DOI:10.1016/j.ymssp.2023.110860

[9]

MEHRAN M, PAVEL R

Rotating speed measurement using an optimized eddy current sensor

[J]. Measurement, 2023, 221: 113547

DOI:10.1016/j.measurement.2023.113547 [本文引用: 1]

[10]

WANG S, LIANG Q, LI C, et al

Design of guided wave magnetostrictive patch transducer with vertical static bias magnetic field for pipe inspection

[J]. Sensors and Actuators A: Physical, 2024, 376: 115611

DOI:10.1016/j.sna.2024.115611 [本文引用: 1]

[11]

WANG Q, LI M, GUO P, et al

Model and design of magnetostrictive flexible sensor for gesture recognition based on curvature and magnetism fusion

[J]. Measurement, 2024, 236: 115151

DOI:10.1016/j.measurement.2024.115151 [本文引用: 1]

[12]

CHEONG K, FURUICHI N, DOIHARA R, et al

A comparison between a Coriolis meter and a combination method of a volumetric positive-displacement flowmeter and a densitometer in measuring liquid fuel mass flow at low flow rates

[J]. Measurement: Sensors, 2021, 18: 100321

DOI:10.1016/j.measen.2021.100321 [本文引用: 1]

[13]

樊烨男. 基于磁感应原理的液压缸外置式位移传感技术研究[D]. 太原: 太原理工大学, 2022.

[本文引用: 1]

FAN Yenan. Research on external displacement sensing technology of hydraulic cylinder based on magnetic induction principle [D]. Taiyuan: Taiyuan University of Technology, 2022.

[本文引用: 1]

[14]

樊烨男, 高飞, 廉自生

液压缸用外置式磁感应位移传感器设计

[J]. 机电工程, 2022, 39 (6): 775- 782

DOI:10.3969/j.issn.1001-4551.2022.06.009 [本文引用: 1]

FAN Yenan, GAO Fei, LIAN Zisheng

Design of external magnetic induction displacement sensor for hydraulic cylinder

[J]. Journal of Mechanical and Electrical Engineering, 2022, 39 (6): 775- 782

DOI:10.3969/j.issn.1001-4551.2022.06.009 [本文引用: 1]

[15]

SU C, LIU X, YOU Y, et al

Highly sensitive magnetostrictive sensor with well-sealed and sensitivity tunability

[J]. Optical Fiber Technology, 2024, 84: 103737

DOI:10.1016/j.yofte.2024.103737 [本文引用: 1]

[16]

DING C, CHEN H, ZHANG C, et al. An investigation on the dynamic characteristics of a two-dimensional piston flowmeter [J]. Advances in Mechanical Engineering, 2022, 14(4): 16878132221095996.

[本文引用: 1]

[17]

丁川, 陈豪奇, 王熙, 等

二维活塞式动态流量计研究

[J]. 农业机械学报, 2022, 53 (4): 450- 458

DOI:10.6041/j.issn.1000-1298.2022.04.047 [本文引用: 1]

DING Chuan, CHEN Haoqi, WANG Xi, et al

Investigation on two-dimensional piston dynamic flowmeter

[J]. Transactions of the Chinese Society for Agricultural Machinery, 2022, 53 (4): 450- 458

DOI:10.6041/j.issn.1000-1298.2022.04.047 [本文引用: 1]

[18]

丁川, 朱海鑫, 朱宽宽, 等

单向高频正弦流量信号标定系统的建模与试验

[J]. 浙江大学学报: 工学版, 2023, 57 (12): 2375- 2380

[本文引用: 1]

DING Chuan, ZHU Haixin, ZHU Kuankuan, et al

Modeling and testing of unidirectional high-frequency sinusoidal flow signal calibration system

[J]. Journal of Zhejiang University: Engineering Science, 2023, 57 (12): 2375- 2380

[本文引用: 1]

[19]

孟彬, 杨冠政, 徐豪, 等

插装式2D电液比例流量阀的特性研究

[J]. 机械工程学报, 2022, 58 (20): 421- 437

DOI:10.3901/JME.2022.20.421 [本文引用: 1]

MENG Bin, YANG Guanzheng, XU Hao, et al

Study on characteristics of 2D cartridge electro-hydraulic proportional flow rate valve

[J]. Journal of Mechanical Engineering, 2022, 58 (20): 421- 437

DOI:10.3901/JME.2022.20.421 [本文引用: 1]

[20]

丁川, 夏宁, 周维华, 等. 集成变磁通式速度传感器的液压缸: CN115163608B [P]. 2023-06-23.

[本文引用: 1]

DING Chuan, XIA Ning, ZHOU Weihua, et al. Hydraulic cylinder integrated with variable flux speed sensor: CN115163608B [P]. 2023-06-23.

[本文引用: 1]

[21]

乌克塞维克. 电机[M]. 余龙海, 刘光军, 廖育武, 译. 北京: 机械工业出版社, 2015: 54-56.

[本文引用: 2]

[22]

唐胜睦

测量不确定度评定中灵敏系数的计算

[J]. 计量与测试技术, 2013, 40 (1): 66- 67

DOI:10.3969/j.issn.1004-6941.2013.01.034 [本文引用: 1]

TANG Shengmu

Sensitivity coefficient calculation about the evaluation of uncertainty in measurement

[J]. Metrology and Measurement Technique, 2013, 40 (1): 66- 67

DOI:10.3969/j.issn.1004-6941.2013.01.034 [本文引用: 1]

基于涡轮流量计的动态流量测量方法研究

2012

... 流量信号是评价电液系统工作特性的关键参数^[1]. 常见的容积式流量计通过计量单元将待测液体分割为等容积单元，计算单位时间内的容积单元数目变化量，实现流量测量. 由于电液系统工作压力通常为50~350 bar，流量计的一次仪表须采用非接触式计量元件. 具体而言，主要利用磁感应技术来构建一次仪表，同时需要在信号发生和采集元件之间增加结构件，以保证流量计的耐压性能. ...

基于涡轮流量计的动态流量测量方法研究

2012

高速动车组速度传感器的电磁干扰测试与分析

2015

... 磁感应技术利用磁场效应实现物理量的测量和检测. 目前，常见的用于流量计的磁感应元件有霍尔元件^[2-3]、基于差动变压器原理的位移传感器^[4-6]、基于变磁通原理的速度传感器^[7-9]以及基于磁致伸缩原理的位移传感器^[10-11]. ...

高速动车组速度传感器的电磁干扰测试与分析

2015

霍尔速度传感器在线检测设备的研制

2021

霍尔速度传感器在线检测设备的研制

2021

A magnetorheological damper capable of force and displacement sensing

2009

Optimization of an inductive displacement transducer

2023

Methodology for eddy current losses calculation in linear variable differential transformers (LVDTs)

2023

An axial flux eddy current sensor with perpendicular coils for speed measurement

2024

Cylindrical-cam modulation instantaneous angular speed sensor for reciprocating-rotary machine

2023

Rotating speed measurement using an optimized eddy current sensor

2023

Design of guided wave magnetostrictive patch transducer with vertical static bias magnetic field for pipe inspection

2024

Model and design of magnetostrictive flexible sensor for gesture recognition based on curvature and magnetism fusion

2024

A comparison between a Coriolis meter and a combination method of a volumetric positive-displacement flowmeter and a densitometer in measuring liquid fuel mass flow at low flow rates

2021

... 霍尔元件因离散性的特点，被广泛应用于容积式流量计. 通过对作为信号发生器的霍尔元件进行布局设计，提高测量精度或动态频响. Cheong等^[12]对新型容积式正位移流量计与结合密度计的质量流量计和科里奥利质量流量计进行性能比较. 结果表明，新型流量计在低流量下具有±1%的精度，表现出更宽的量程. ...

... 位移以及速度传感器多用于伺服缸反馈或动态标定. 太原理工大学的廉自生团队基于TMR磁阻设计外置式磁感应位移传感器，通过检测活塞运动时的永磁环磁场变化来计算液压缸位移，精度为0.29%^[13-14]. ...

液压缸用外置式磁感应位移传感器设计

2022

液压缸用外置式磁感应位移传感器设计

2022

Highly sensitive magnetostrictive sensor with well-sealed and sensitivity tunability

2024

... 磁致伸缩位移传感器利用磁性材料在磁场作用下发生尺寸变化的特点来检测磁场，具有高精度和高可靠性的优势. Su等^[15]提出具有高密封性和灵敏度可调性的磁致伸缩传感器. 通过Terfenol-D材料和光纤马赫-曾德尔干涉仪来检测磁场变化. 传感器的灵敏度可以达到−1.113 nm/mT. ...

... 笔者所在团队设计的二维活塞式动态流量计是基于“二维液压元件”设计理念的容积式流量计，曾采用霍尔元件作为传感器来测量稳态流量信号^[16-17]，并在后续的研究中尝试利用传感器获取计量元件活塞的位置或速度信号^[18-19]，以计算动态流量的变化情况. 在测量过程中出现了磁致伸缩位移传感器小量程精度不足和外接传感器占用空间较大，不利于安装的问题. ...

二维活塞式动态流量计研究

2022

二维活塞式动态流量计研究

2022

单向高频正弦流量信号标定系统的建模与试验

2023

单向高频正弦流量信号标定系统的建模与试验

2023

插装式2D电液比例流量阀的特性研究

2022

插装式2D电液比例流量阀的特性研究

2022

... 如图2所示，2个磁钢朝向缸体外侧的一段均为N极，缸体和上、下端盖构成一整个磁感应空间，并被活塞分成2个部分. 以导磁棒、端盖、活塞和缸体内壁为边界，形成一部分磁感线为顺时针走势，另一部分为逆时针走势的循环. 活塞移动后途经的部分磁感线走势反转，导致线圈及各线性霍尔元件安装位置上的磁通量会随着活塞的运动而实时发生变化，通过测量线性霍尔元件上的磁感应强度和线圈上由于变化的磁通量而产生的感应电动势，可以实现位移和速度的测量^[20]. ...

... 磁电式传感器中的功率损耗降低了它的工作性能，功率损耗主要来源于磁滞损耗和涡流损耗2个方面. 在以铁芯为主体的磁路中，涡流损耗超过了磁滞损耗，涡流损耗比磁滞损耗大一个数量级. 导磁棒的轴向磁通量对磁电式传感器的测量性能有着直接的影响，而导磁棒截面磁性材料的面积和导磁棒的轴向磁通量成正比. 为了保障测量性能并降低涡流损耗，参考了行业内普遍采用的硅钢片叠压技术. 鉴于硅钢片的生产工艺已经非常成熟，将传感器铁芯设计成如图3所示的叠片结构^[21]. 这样的设计不仅能够有效减少涡流损耗和保证轴向磁通量，而且由于硅钢片的易获取性和经济性，能够降低制造成本. ...

... 因为

$x < < l$

，沿着封闭曲线C短边的那部分曲线积分可以忽略不计. 沿着封闭曲线C长边的感应电动势

$E(x)$

^[21]为 ...

测量不确定度评定中灵敏系数的计算

2013

... 从图11可知，叠片式导磁棒型速度传感器的测量值

${v_{\text{1}}}$

与标准传感器的测量值

${v_2}$

的误差约为±1.5%. 考虑到标准传感器的测量精度误差为±1%，根据合成标准不确定度的计算公式^[22]可知 ...

测量不确定度评定中灵敏系数的计算

2013

... 从图11可知，叠片式导磁棒型速度传感器的测量值

${v_{\text{1}}}$

与标准传感器的测量值

${v_2}$

的误差约为±1.5%. 考虑到标准传感器的测量精度误差为±1%，根据合成标准不确定度的计算公式^[22]可知 ...

〈

〉