知识图谱由一系列的三元组$\left( {h,r,t} \right)$ h 为头实体,r 为关系,t 为尾实体. 少样本知识补全任务通常被分为2类,1)预测三元组中缺失的实体,2)预测三元组中缺失的关系. SAM的目标是预测三元组中缺失的实体,所述方法均针对预测尾实体任务. 在预测尾实体的任务中,待预测三元组称为查询三元组,表示为$\left( {{h^{\text{q}}},r,t^{\mathrm{q}}} \right)$ ${t^{\text{q}}}$ $C = \{ t_1^{\text{q}},t_2^{\text{q}}, \cdots , t_{\text{z}}^{\text{q}} \}$ S ,S 中支持三元组的数量k 称为少样本任务中的样本数,$S = \{ ( {h_1^{\text{s}},r,t_1^{\text{s}}} ),( {h_2^{\text{s}},r,t_2^{\text{s}}} ), \cdots ,( {h_k^{\text{s}},r,t_k^{\text{s}}} ) \}$ .
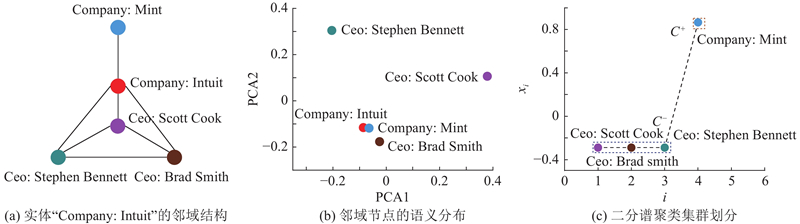
由式(3)得到2个集群${C^+} = \left\{ {V_1^+,V_2^+, \cdots ,V_a^+} \right\}$ ${C^ - } = \left\{ {V_1^ - ,V_2^ - , \cdots ,V_b^ - } \right\}$ $a+b = d$ . 如图1 (c)所示,在实体“Company: Intuit”的邻域结构中,设节点集合为$\left\{ {{V_0},{V_1},{V_2},{V_3},{V_4}} \right\}$ $\left\{ {0,1,4,4,5} \right\}$ . 4)选取${\lambda _2} = 1$ ${{\boldsymbol{X}}_2} $ 0.2887 , −0.2887 , −0.2887 , 0.8660 },依据式(3)对邻域集合$\left\{ {{V_1},{V_2},{V_3},{V_4}} \right\}$ ${C^+} = \left\{ {{V_4}} \right\}$ ${C^ - } = \left\{ {{V_1},{V_2},{V_3}} \right\}$ . 结合图1 (a)的集群效果来看,所提二分谱聚类方法可以较好地将结构上呈现集群的节点划分到同个集群中. 相比其他谱聚类方法[26 -29 ] ,所提二分谱聚类方法在实现上复杂程度更低.
[1]
杨东华, 何涛, 王宏志, 等 面向知识图谱的图嵌入学习研究进展
[J]. 软件学报 , 2022 , 33 (9 ): 3370 - 3390
[本文引用: 1]
YANG Donghua, HE Tao, WANG Hongzhi, et al Survey on knowledge graph embedding learning
[J]. Journal of Software , 2022 , 33 (9 ): 3370 - 3390
[本文引用: 1]
[2]
张天成, 田雪, 孙相会, 等 知识图谱嵌入技术研究综述
[J]. 软件学报 , 2023 , 34 (1 ): 277 - 311
ZHANG Tiancheng, TIAN Xue, SUN Xianghui, et al Overview on knowledge graph embedding technology research
[J]. Journal of Software , 2023 , 34 (1 ): 277 - 311
[3]
ZHONG L, WU J, LI Q, et al A comprehensive survey on automatic knowledge graph construction
[J]. ACM Computing Surveys , 2024 , 56 (4 ): 1 - 62
[本文引用: 1]
[4]
ZHANG N, DENG S, SUN Z, et al. Long-tail relation extraction via knowledge graph embeddings and graph convolution networks [C]// Proceedings of the 2019 Conference of the North . [S.l.]: ACL, 2019: 3016–3025.
[本文引用: 1]
[5]
WU T, MA H, WANG C, et al Heterogeneous representation learning and matching for few-shot relation prediction
[J]. Pattern Recognition , 2022 , 131 : 108830
DOI:10.1016/j.patcog.2022.108830
[本文引用: 3]
[6]
赵凯琳, 靳小龙, 王元卓 小样本学习研究综述
[J]. 软件学报 , 2021 , 32 (2 ): 349 - 369
[本文引用: 1]
ZHAO Kailin, JIN Xiaolong, WANG Yuanzhuo Survey on few-shot learning
[J]. Journal of Software , 2021 , 32 (2 ): 349 - 369
[本文引用: 1]
[7]
LU J, GONG P, YE J, et al A survey on machine learning from few samples
[J]. Pattern Recognition , 2023 , 139 : 109480
DOI:10.1016/j.patcog.2023.109480
[8]
HUANG Q, REN H, LESKOVEC J. Few-shot relational reasoning via connection subgraph pretraining [C]// Proceedings of the 36th International Conference on Neural Information Processing Systems . New York: Curran Associates, Inc., 2022: 6397–6409.
[本文引用: 1]
[9]
YUAN X, XU C, LI P, et al. Relational learning with hierarchical attention encoder and recoding validator for few-shot knowledge graph completion [C]// Proceedings of the 37th ACM/SIGAPP Symposium on Applied Computing . [S.l.]: ACM, 2022: 786–794.
[本文引用: 1]
[10]
LIANG Y, ZHAO S, CHENG B, et al TransAM: transformer appending matcher for few-shot knowledge graph completion
[J]. Neurocomputing , 2023 , 537 : 61 - 72
DOI:10.1016/j.neucom.2023.03.049
[本文引用: 3]
[11]
LI Y, YU K, ZHANG Y, et al Adaptive prototype interaction network for few-shot knowledge graph completion
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2024 , 35 (11 ): 15237 - 15250
DOI:10.1109/TNNLS.2023.3283545
[本文引用: 5]
[12]
NIU G, LI Y, TANG C, et al. Relational learning with gated and attentive neighbor aggregator for few-shot knowledge graph completion [C]// Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval . [S. l.]: ACM, 2021: 213–222.
[本文引用: 5]
[13]
ZHANG Y, QIAN Y, YE Y, et al. Adapting distilled knowledge for few-shot relation reasoning over knowledge graphs [C]// Proceedings of the 2022 SIAM International Conference on Data Mining . Philadelphia: Society for Industrial and Applied Mathematics, 2022: 666–674.
[本文引用: 3]
[14]
CAI L, WANG L, YUAN R, et al Meta-learning based dynamic adaptive relation learning for few-shot knowledge graph completion
[J]. Big Data Research , 2023 , 33 : 100394
DOI:10.1016/j.bdr.2023.100394
[本文引用: 7]
[15]
DWIVEDI V P, BRESSON X. A generalization of transformer networks to graphs [EB/OL]. (2021−01−24) [2024−05−03]. https://arxiv.org/pdf/2012.09699.
[本文引用: 1]
[16]
YING C, CAI T, LUO S, et al. Do transformers really perform badly for graph representation [C]// 35th Conference on Neural Information Processing Systems . Sydney: [s.n.], 2021: 1–19.
[本文引用: 1]
[17]
CHEN D, O’BRAY L, BORGWARDT K. Structure-aware transformer for graph representation learning [C]// Proceedings of the 39th International Conference on Machine Learning . Baltimore: PMLR, 2022: 3469–3489.
[本文引用: 1]
[18]
LUO Y, THOST V, SHI L. Transformers over directed acyclic graphs [C]// 37th Conference on Neural Information Processing Systems . [S.l.]: Curran Associates, Inc., 2023: 47764–47782.
[本文引用: 1]
[19]
LI Y, YU K, HUANG X, et al. Learning inter-entity-interaction for few-shot knowledge graph completion [C]// Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing . [S. l.]: ACL, 2022: 7691–7700.
[本文引用: 1]
[20]
SHENG J, GUO S, CHEN Z, et al. Adaptive attentional network for few-shot knowledge graph completion [C]// Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing . [S. l.]: ACL, 2020: 1681–1691.
[本文引用: 1]
[21]
陈成, 张皞, 李永强, 等 关系生成图注意力网络的知识图谱链接预测
[J]. 浙江大学学报: 工学版 , 2022 , 56 (5 ): 1025 - 1034
[本文引用: 1]
CHEN Cheng, ZHANG Hao, LI Yongqiang, et al Knowledge graph link prediction based on relational generative graph attention network
[J]. Journal of Zhejiang University: Engineering Science , 2022 , 56 (5 ): 1025 - 1034
[本文引用: 1]
[22]
VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks [C]// International Conference on Learning Representations . Vancouver: [s.n.], 2018: 1–12
[本文引用: 1]
[23]
WANG X, HE X, CAO Y, et al. KGAT: knowledge graph attention network for recommendation [C]// Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining . [S. l.]: ACM, 2019: 950–958.
[24]
YE Y, JI S Sparse graph attention networks
[J]. IEEE Transactions on Knowledge and Data Engineering , 2023 , 35 (1 ): 905 - 916
[26]
YUAN H, JI S. Structpool: structured graph pooling via conditional random fields [C]// International Conference on Learning Representations . Addis Ababa: [s.n.], 2020: 1–12.
[本文引用: 1]
[27]
BIANCHI F M, GRATTAROLA D, ALIPPI C. Spectral clustering with graph neural networks for graph pooling [C]// Proceedings of the 37th International Conference on Machine Learning . Vienna: [s. n.], 2020: 1–13.
[28]
BAEK J, KANG M, HWANG S J. Accurate learning of graph representations with graph multiset pooling [EB/OL]. (2021−06−28)[2024−05−03]. https://arxiv.org/pdf/2102.11533.
[29]
NIE F, ZHU W, LI X Unsupervised large graph embedding based on balanced and hierarchical K-means
[J]. IEEE Transactions on Knowledge and Data Engineering , 2022 , 34 (4 ): 2008 - 2019
[本文引用: 1]
面向知识图谱的图嵌入学习研究进展
1
2022
... 知识图谱是图拓扑结构数据,通常以三元组(头实体,关系,尾实体)的形式存储[1 -3 ] ,其中实体表示为节点,关系表示为连接节点的边. 这种结构化的表示方式使机器能够理解并处理复杂的语义信息,便于进行智能搜索、推理和问答等多种人工智能应用. 由于数据来源有限、信息抽取不完全以及知识验证成本高,知识图谱在实际工程应用中难以达到完备状态. 知识图谱中大量关系只有少量的支持样本[4 -5 ] . 此外,现实世界中知识是动态更新的,用于知识补全的支持样本却有限甚至稀缺. ...
面向知识图谱的图嵌入学习研究进展
1
2022
... 知识图谱是图拓扑结构数据,通常以三元组(头实体,关系,尾实体)的形式存储[1 -3 ] ,其中实体表示为节点,关系表示为连接节点的边. 这种结构化的表示方式使机器能够理解并处理复杂的语义信息,便于进行智能搜索、推理和问答等多种人工智能应用. 由于数据来源有限、信息抽取不完全以及知识验证成本高,知识图谱在实际工程应用中难以达到完备状态. 知识图谱中大量关系只有少量的支持样本[4 -5 ] . 此外,现实世界中知识是动态更新的,用于知识补全的支持样本却有限甚至稀缺. ...
A comprehensive survey on automatic knowledge graph construction
1
2024
... 知识图谱是图拓扑结构数据,通常以三元组(头实体,关系,尾实体)的形式存储[1 -3 ] ,其中实体表示为节点,关系表示为连接节点的边. 这种结构化的表示方式使机器能够理解并处理复杂的语义信息,便于进行智能搜索、推理和问答等多种人工智能应用. 由于数据来源有限、信息抽取不完全以及知识验证成本高,知识图谱在实际工程应用中难以达到完备状态. 知识图谱中大量关系只有少量的支持样本[4 -5 ] . 此外,现实世界中知识是动态更新的,用于知识补全的支持样本却有限甚至稀缺. ...
1
... 知识图谱是图拓扑结构数据,通常以三元组(头实体,关系,尾实体)的形式存储[1 -3 ] ,其中实体表示为节点,关系表示为连接节点的边. 这种结构化的表示方式使机器能够理解并处理复杂的语义信息,便于进行智能搜索、推理和问答等多种人工智能应用. 由于数据来源有限、信息抽取不完全以及知识验证成本高,知识图谱在实际工程应用中难以达到完备状态. 知识图谱中大量关系只有少量的支持样本[4 -5 ] . 此外,现实世界中知识是动态更新的,用于知识补全的支持样本却有限甚至稀缺. ...
Heterogeneous representation learning and matching for few-shot relation prediction
3
2022
... 知识图谱是图拓扑结构数据,通常以三元组(头实体,关系,尾实体)的形式存储[1 -3 ] ,其中实体表示为节点,关系表示为连接节点的边. 这种结构化的表示方式使机器能够理解并处理复杂的语义信息,便于进行智能搜索、推理和问答等多种人工智能应用. 由于数据来源有限、信息抽取不完全以及知识验证成本高,知识图谱在实际工程应用中难以达到完备状态. 知识图谱中大量关系只有少量的支持样本[4 -5 ] . 此外,现实世界中知识是动态更新的,用于知识补全的支持样本却有限甚至稀缺. ...
... 少样本知识补全任务的目的是利用模型学习支持集中三元组潜在的语义信息,推测查询三元组存在的合理性. 若查询三元组存在的合理性越高,则查询三元组中的尾实体是待预测三元组中缺失尾实体的可能性越大. 少样本知识补全任务因此转化为查询三元组与支持三元组的相似性评估任务. 在整个预测过程中,三元组的表示至关重要,对三元组的表示越准确,三元组预测得分越高,模型的评估效果越好. 词语义具有多义性,词向量预训练模型始终难以得到包含单词所有语义的向量表示. 现有知识补全方法[5 ,10 -14 ,19 -21 ] 均基于知识的预训练词向量包含的语义信息来推测查询三元组的合理性,少样本知识补全方法面临挑战:1)知识本身,三元组中的实体和关系的词向量语义信息有限,难以支持模型进行有效推理. 如图1 (a)所示为NELL-One数据集中实体“Company: Intuit”的邻域结构. 使用主成分分析算法(PCA)对邻域中所有节点的词向量进行降维,得到第一个主成分PCA1和第二个主成分PCA2,并可视化显示其语义分布,如图1 (b)所示. 可以看出,原本应该拥有相似语义的节点“Ceo: Stephen Bennett”、“Ceo: Scott Cook”、“Ceo: Brad Smith”相距较远. 2)从拓扑结构上看,呈现结构聚集性的节点应该有强相关性,从词向量的语义分布上看,这种相关性却很弱. 如果能利用拓扑结构引导模型进一步挖掘这类呈现结构集群的邻居之间潜在的语义相关性,将有利于增强模型推理. 对此,在SAM中使用如图1 (c)所示的二分谱聚类集群划分方法来挖掘邻域的拓扑结构特征. ...
... 在基于度量学习的基线模型中,多度量特征提取网络(multi-metric feature extraction network, MFEN)[5 ] 由卷积编码器捕获实体嵌入的多尺度特征,考虑了邻居节点对实体的异构影响;基于Transformer的附加匹配器(transformer appending matcher, TransAM)[10 ] 使用旋转操作提取实体的角色信息;自适应原型交互网络(adaptive prototype interaction network, APINet)[11 ] 由原型交互网络捕捉实体与关系之间的交互信息,在预测过程中使用原型网络处理关系的多层语义. 在基于元学习的基线模型中,GANA(gated and attentive neighbor aggregator)[12 ] 为两阶段学习机制,全局阶段使用图注意力网络学习支持三元组的嵌入表示,局部阶段利用查询三元组优化整个模型;自适应知识蒸馏的少样本关系推理模型 (adaptive knowledge distillation framework for few-shot relation reasoning over knowledge graph, ADK-KG)[13 ] 使用文本信息来增强邻居节点的嵌入表示,由基于知识蒸馏的元学习优化机制来更新模型参数;动态自适应关系学习模型(dynamic adapting relation learning model, DARL)[14 ] 设计动态邻居编码器来编码邻居实体,元学习器将关系元转移到查询集中,以增强模型的预测能力. ...
小样本学习研究综述
1
2021
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
小样本学习研究综述
1
2021
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
A survey on machine learning from few samples
0
2023
1
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
1
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
TransAM: transformer appending matcher for few-shot knowledge graph completion
3
2023
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
... 少样本知识补全任务的目的是利用模型学习支持集中三元组潜在的语义信息,推测查询三元组存在的合理性. 若查询三元组存在的合理性越高,则查询三元组中的尾实体是待预测三元组中缺失尾实体的可能性越大. 少样本知识补全任务因此转化为查询三元组与支持三元组的相似性评估任务. 在整个预测过程中,三元组的表示至关重要,对三元组的表示越准确,三元组预测得分越高,模型的评估效果越好. 词语义具有多义性,词向量预训练模型始终难以得到包含单词所有语义的向量表示. 现有知识补全方法[5 ,10 -14 ,19 -21 ] 均基于知识的预训练词向量包含的语义信息来推测查询三元组的合理性,少样本知识补全方法面临挑战:1)知识本身,三元组中的实体和关系的词向量语义信息有限,难以支持模型进行有效推理. 如图1 (a)所示为NELL-One数据集中实体“Company: Intuit”的邻域结构. 使用主成分分析算法(PCA)对邻域中所有节点的词向量进行降维,得到第一个主成分PCA1和第二个主成分PCA2,并可视化显示其语义分布,如图1 (b)所示. 可以看出,原本应该拥有相似语义的节点“Ceo: Stephen Bennett”、“Ceo: Scott Cook”、“Ceo: Brad Smith”相距较远. 2)从拓扑结构上看,呈现结构聚集性的节点应该有强相关性,从词向量的语义分布上看,这种相关性却很弱. 如果能利用拓扑结构引导模型进一步挖掘这类呈现结构集群的邻居之间潜在的语义相关性,将有利于增强模型推理. 对此,在SAM中使用如图1 (c)所示的二分谱聚类集群划分方法来挖掘邻域的拓扑结构特征. ...
... 在基于度量学习的基线模型中,多度量特征提取网络(multi-metric feature extraction network, MFEN)[5 ] 由卷积编码器捕获实体嵌入的多尺度特征,考虑了邻居节点对实体的异构影响;基于Transformer的附加匹配器(transformer appending matcher, TransAM)[10 ] 使用旋转操作提取实体的角色信息;自适应原型交互网络(adaptive prototype interaction network, APINet)[11 ] 由原型交互网络捕捉实体与关系之间的交互信息,在预测过程中使用原型网络处理关系的多层语义. 在基于元学习的基线模型中,GANA(gated and attentive neighbor aggregator)[12 ] 为两阶段学习机制,全局阶段使用图注意力网络学习支持三元组的嵌入表示,局部阶段利用查询三元组优化整个模型;自适应知识蒸馏的少样本关系推理模型 (adaptive knowledge distillation framework for few-shot relation reasoning over knowledge graph, ADK-KG)[13 ] 使用文本信息来增强邻居节点的嵌入表示,由基于知识蒸馏的元学习优化机制来更新模型参数;动态自适应关系学习模型(dynamic adapting relation learning model, DARL)[14 ] 设计动态邻居编码器来编码邻居实体,元学习器将关系元转移到查询集中,以增强模型的预测能力. ...
Adaptive prototype interaction network for few-shot knowledge graph completion
5
2024
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
... 在基于度量学习的基线模型中,多度量特征提取网络(multi-metric feature extraction network, MFEN)[5 ] 由卷积编码器捕获实体嵌入的多尺度特征,考虑了邻居节点对实体的异构影响;基于Transformer的附加匹配器(transformer appending matcher, TransAM)[10 ] 使用旋转操作提取实体的角色信息;自适应原型交互网络(adaptive prototype interaction network, APINet)[11 ] 由原型交互网络捕捉实体与关系之间的交互信息,在预测过程中使用原型网络处理关系的多层语义. 在基于元学习的基线模型中,GANA(gated and attentive neighbor aggregator)[12 ] 为两阶段学习机制,全局阶段使用图注意力网络学习支持三元组的嵌入表示,局部阶段利用查询三元组优化整个模型;自适应知识蒸馏的少样本关系推理模型 (adaptive knowledge distillation framework for few-shot relation reasoning over knowledge graph, ADK-KG)[13 ] 使用文本信息来增强邻居节点的嵌入表示,由基于知识蒸馏的元学习优化机制来更新模型参数;动态自适应关系学习模型(dynamic adapting relation learning model, DARL)[14 ] 设计动态邻居编码器来编码邻居实体,元学习器将关系元转移到查询集中,以增强模型的预测能力. ...
... APINet[11 ] 和DARL[14 ] 的提出者没有提供可复现的代码,因此采用论文中的实验结果进行性能对比. 在同一台服务器上复现其余4个基线模型的实验结果,得到不同模型在2个数据集上的少样本(k =3)链接预测实验结果如表2 所示. 在NELL-One中,对比MRR最好的基线模型GANA[12 ] ,SAM提升了0.018;对比Hits@10最好的基线模型APINet[11 ] ,SAM提升了0.021;对比Hits@5最好的基线模型GANA[12 ] ,SAM提升了0.024;对比Hits@1最好的基线模型ADK-KG[13 ] ,SAM提升了0.016. 在Wiki-One中,对比MRR最好的基线模型DARL[14 ] ,SAM提升了0.019;对比Hits@10最好的基线模型APINet,SAM提升了0.055;对比Hits@5最好的基线模型APINet[11 ] ,SAM提升了0.039;对比Hits@1最好的基线模型DARL[14 ] ,SAM提升了0.038. SAM优于所有基于度量学习的基线模型, 在2个数据集中对比表现最好的模型APINet,MRR、Hits@10、Hits@5、Hits@1分别提高了0.024、0.021、0.032、0.032以及0.022、0.055、0.039、0.045. 分析原因:基于度量的方法推理效果依赖于向量空间的表示,由于预训练词向量包含的语义信息有限,限制了APINet的推理能力,SAM能够较好利用邻域结构信息挖掘实体与邻居节点之间潜在的语义,增强实体的语义表示,提升模型的推理能力. SAM优于所有基于元学习的基线模型. 在NELL-One数据集上,对比表现最好的模型GANA[12 ] , MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
... [11 ],SAM提升了0.021;对比Hits@5最好的基线模型GANA[12 ] ,SAM提升了0.024;对比Hits@1最好的基线模型ADK-KG[13 ] ,SAM提升了0.016. 在Wiki-One中,对比MRR最好的基线模型DARL[14 ] ,SAM提升了0.019;对比Hits@10最好的基线模型APINet,SAM提升了0.055;对比Hits@5最好的基线模型APINet[11 ] ,SAM提升了0.039;对比Hits@1最好的基线模型DARL[14 ] ,SAM提升了0.038. SAM优于所有基于度量学习的基线模型, 在2个数据集中对比表现最好的模型APINet,MRR、Hits@10、Hits@5、Hits@1分别提高了0.024、0.021、0.032、0.032以及0.022、0.055、0.039、0.045. 分析原因:基于度量的方法推理效果依赖于向量空间的表示,由于预训练词向量包含的语义信息有限,限制了APINet的推理能力,SAM能够较好利用邻域结构信息挖掘实体与邻居节点之间潜在的语义,增强实体的语义表示,提升模型的推理能力. SAM优于所有基于元学习的基线模型. 在NELL-One数据集上,对比表现最好的模型GANA[12 ] , MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
... [11 ],SAM提升了0.039;对比Hits@1最好的基线模型DARL[14 ] ,SAM提升了0.038. SAM优于所有基于度量学习的基线模型, 在2个数据集中对比表现最好的模型APINet,MRR、Hits@10、Hits@5、Hits@1分别提高了0.024、0.021、0.032、0.032以及0.022、0.055、0.039、0.045. 分析原因:基于度量的方法推理效果依赖于向量空间的表示,由于预训练词向量包含的语义信息有限,限制了APINet的推理能力,SAM能够较好利用邻域结构信息挖掘实体与邻居节点之间潜在的语义,增强实体的语义表示,提升模型的推理能力. SAM优于所有基于元学习的基线模型. 在NELL-One数据集上,对比表现最好的模型GANA[12 ] , MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
5
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
... 在基于度量学习的基线模型中,多度量特征提取网络(multi-metric feature extraction network, MFEN)[5 ] 由卷积编码器捕获实体嵌入的多尺度特征,考虑了邻居节点对实体的异构影响;基于Transformer的附加匹配器(transformer appending matcher, TransAM)[10 ] 使用旋转操作提取实体的角色信息;自适应原型交互网络(adaptive prototype interaction network, APINet)[11 ] 由原型交互网络捕捉实体与关系之间的交互信息,在预测过程中使用原型网络处理关系的多层语义. 在基于元学习的基线模型中,GANA(gated and attentive neighbor aggregator)[12 ] 为两阶段学习机制,全局阶段使用图注意力网络学习支持三元组的嵌入表示,局部阶段利用查询三元组优化整个模型;自适应知识蒸馏的少样本关系推理模型 (adaptive knowledge distillation framework for few-shot relation reasoning over knowledge graph, ADK-KG)[13 ] 使用文本信息来增强邻居节点的嵌入表示,由基于知识蒸馏的元学习优化机制来更新模型参数;动态自适应关系学习模型(dynamic adapting relation learning model, DARL)[14 ] 设计动态邻居编码器来编码邻居实体,元学习器将关系元转移到查询集中,以增强模型的预测能力. ...
... APINet[11 ] 和DARL[14 ] 的提出者没有提供可复现的代码,因此采用论文中的实验结果进行性能对比. 在同一台服务器上复现其余4个基线模型的实验结果,得到不同模型在2个数据集上的少样本(k =3)链接预测实验结果如表2 所示. 在NELL-One中,对比MRR最好的基线模型GANA[12 ] ,SAM提升了0.018;对比Hits@10最好的基线模型APINet[11 ] ,SAM提升了0.021;对比Hits@5最好的基线模型GANA[12 ] ,SAM提升了0.024;对比Hits@1最好的基线模型ADK-KG[13 ] ,SAM提升了0.016. 在Wiki-One中,对比MRR最好的基线模型DARL[14 ] ,SAM提升了0.019;对比Hits@10最好的基线模型APINet,SAM提升了0.055;对比Hits@5最好的基线模型APINet[11 ] ,SAM提升了0.039;对比Hits@1最好的基线模型DARL[14 ] ,SAM提升了0.038. SAM优于所有基于度量学习的基线模型, 在2个数据集中对比表现最好的模型APINet,MRR、Hits@10、Hits@5、Hits@1分别提高了0.024、0.021、0.032、0.032以及0.022、0.055、0.039、0.045. 分析原因:基于度量的方法推理效果依赖于向量空间的表示,由于预训练词向量包含的语义信息有限,限制了APINet的推理能力,SAM能够较好利用邻域结构信息挖掘实体与邻居节点之间潜在的语义,增强实体的语义表示,提升模型的推理能力. SAM优于所有基于元学习的基线模型. 在NELL-One数据集上,对比表现最好的模型GANA[12 ] , MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
... [12 ],SAM提升了0.024;对比Hits@1最好的基线模型ADK-KG[13 ] ,SAM提升了0.016. 在Wiki-One中,对比MRR最好的基线模型DARL[14 ] ,SAM提升了0.019;对比Hits@10最好的基线模型APINet,SAM提升了0.055;对比Hits@5最好的基线模型APINet[11 ] ,SAM提升了0.039;对比Hits@1最好的基线模型DARL[14 ] ,SAM提升了0.038. SAM优于所有基于度量学习的基线模型, 在2个数据集中对比表现最好的模型APINet,MRR、Hits@10、Hits@5、Hits@1分别提高了0.024、0.021、0.032、0.032以及0.022、0.055、0.039、0.045. 分析原因:基于度量的方法推理效果依赖于向量空间的表示,由于预训练词向量包含的语义信息有限,限制了APINet的推理能力,SAM能够较好利用邻域结构信息挖掘实体与邻居节点之间潜在的语义,增强实体的语义表示,提升模型的推理能力. SAM优于所有基于元学习的基线模型. 在NELL-One数据集上,对比表现最好的模型GANA[12 ] , MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
... [12 ], MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
3
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
... 在基于度量学习的基线模型中,多度量特征提取网络(multi-metric feature extraction network, MFEN)[5 ] 由卷积编码器捕获实体嵌入的多尺度特征,考虑了邻居节点对实体的异构影响;基于Transformer的附加匹配器(transformer appending matcher, TransAM)[10 ] 使用旋转操作提取实体的角色信息;自适应原型交互网络(adaptive prototype interaction network, APINet)[11 ] 由原型交互网络捕捉实体与关系之间的交互信息,在预测过程中使用原型网络处理关系的多层语义. 在基于元学习的基线模型中,GANA(gated and attentive neighbor aggregator)[12 ] 为两阶段学习机制,全局阶段使用图注意力网络学习支持三元组的嵌入表示,局部阶段利用查询三元组优化整个模型;自适应知识蒸馏的少样本关系推理模型 (adaptive knowledge distillation framework for few-shot relation reasoning over knowledge graph, ADK-KG)[13 ] 使用文本信息来增强邻居节点的嵌入表示,由基于知识蒸馏的元学习优化机制来更新模型参数;动态自适应关系学习模型(dynamic adapting relation learning model, DARL)[14 ] 设计动态邻居编码器来编码邻居实体,元学习器将关系元转移到查询集中,以增强模型的预测能力. ...
... APINet[11 ] 和DARL[14 ] 的提出者没有提供可复现的代码,因此采用论文中的实验结果进行性能对比. 在同一台服务器上复现其余4个基线模型的实验结果,得到不同模型在2个数据集上的少样本(k =3)链接预测实验结果如表2 所示. 在NELL-One中,对比MRR最好的基线模型GANA[12 ] ,SAM提升了0.018;对比Hits@10最好的基线模型APINet[11 ] ,SAM提升了0.021;对比Hits@5最好的基线模型GANA[12 ] ,SAM提升了0.024;对比Hits@1最好的基线模型ADK-KG[13 ] ,SAM提升了0.016. 在Wiki-One中,对比MRR最好的基线模型DARL[14 ] ,SAM提升了0.019;对比Hits@10最好的基线模型APINet,SAM提升了0.055;对比Hits@5最好的基线模型APINet[11 ] ,SAM提升了0.039;对比Hits@1最好的基线模型DARL[14 ] ,SAM提升了0.038. SAM优于所有基于度量学习的基线模型, 在2个数据集中对比表现最好的模型APINet,MRR、Hits@10、Hits@5、Hits@1分别提高了0.024、0.021、0.032、0.032以及0.022、0.055、0.039、0.045. 分析原因:基于度量的方法推理效果依赖于向量空间的表示,由于预训练词向量包含的语义信息有限,限制了APINet的推理能力,SAM能够较好利用邻域结构信息挖掘实体与邻居节点之间潜在的语义,增强实体的语义表示,提升模型的推理能力. SAM优于所有基于元学习的基线模型. 在NELL-One数据集上,对比表现最好的模型GANA[12 ] , MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
Meta-learning based dynamic adaptive relation learning for few-shot knowledge graph completion
7
2023
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
... 少样本知识补全任务的目的是利用模型学习支持集中三元组潜在的语义信息,推测查询三元组存在的合理性. 若查询三元组存在的合理性越高,则查询三元组中的尾实体是待预测三元组中缺失尾实体的可能性越大. 少样本知识补全任务因此转化为查询三元组与支持三元组的相似性评估任务. 在整个预测过程中,三元组的表示至关重要,对三元组的表示越准确,三元组预测得分越高,模型的评估效果越好. 词语义具有多义性,词向量预训练模型始终难以得到包含单词所有语义的向量表示. 现有知识补全方法[5 ,10 -14 ,19 -21 ] 均基于知识的预训练词向量包含的语义信息来推测查询三元组的合理性,少样本知识补全方法面临挑战:1)知识本身,三元组中的实体和关系的词向量语义信息有限,难以支持模型进行有效推理. 如图1 (a)所示为NELL-One数据集中实体“Company: Intuit”的邻域结构. 使用主成分分析算法(PCA)对邻域中所有节点的词向量进行降维,得到第一个主成分PCA1和第二个主成分PCA2,并可视化显示其语义分布,如图1 (b)所示. 可以看出,原本应该拥有相似语义的节点“Ceo: Stephen Bennett”、“Ceo: Scott Cook”、“Ceo: Brad Smith”相距较远. 2)从拓扑结构上看,呈现结构聚集性的节点应该有强相关性,从词向量的语义分布上看,这种相关性却很弱. 如果能利用拓扑结构引导模型进一步挖掘这类呈现结构集群的邻居之间潜在的语义相关性,将有利于增强模型推理. 对此,在SAM中使用如图1 (c)所示的二分谱聚类集群划分方法来挖掘邻域的拓扑结构特征. ...
... 在基于度量学习的基线模型中,多度量特征提取网络(multi-metric feature extraction network, MFEN)[5 ] 由卷积编码器捕获实体嵌入的多尺度特征,考虑了邻居节点对实体的异构影响;基于Transformer的附加匹配器(transformer appending matcher, TransAM)[10 ] 使用旋转操作提取实体的角色信息;自适应原型交互网络(adaptive prototype interaction network, APINet)[11 ] 由原型交互网络捕捉实体与关系之间的交互信息,在预测过程中使用原型网络处理关系的多层语义. 在基于元学习的基线模型中,GANA(gated and attentive neighbor aggregator)[12 ] 为两阶段学习机制,全局阶段使用图注意力网络学习支持三元组的嵌入表示,局部阶段利用查询三元组优化整个模型;自适应知识蒸馏的少样本关系推理模型 (adaptive knowledge distillation framework for few-shot relation reasoning over knowledge graph, ADK-KG)[13 ] 使用文本信息来增强邻居节点的嵌入表示,由基于知识蒸馏的元学习优化机制来更新模型参数;动态自适应关系学习模型(dynamic adapting relation learning model, DARL)[14 ] 设计动态邻居编码器来编码邻居实体,元学习器将关系元转移到查询集中,以增强模型的预测能力. ...
... APINet[11 ] 和DARL[14 ] 的提出者没有提供可复现的代码,因此采用论文中的实验结果进行性能对比. 在同一台服务器上复现其余4个基线模型的实验结果,得到不同模型在2个数据集上的少样本(k =3)链接预测实验结果如表2 所示. 在NELL-One中,对比MRR最好的基线模型GANA[12 ] ,SAM提升了0.018;对比Hits@10最好的基线模型APINet[11 ] ,SAM提升了0.021;对比Hits@5最好的基线模型GANA[12 ] ,SAM提升了0.024;对比Hits@1最好的基线模型ADK-KG[13 ] ,SAM提升了0.016. 在Wiki-One中,对比MRR最好的基线模型DARL[14 ] ,SAM提升了0.019;对比Hits@10最好的基线模型APINet,SAM提升了0.055;对比Hits@5最好的基线模型APINet[11 ] ,SAM提升了0.039;对比Hits@1最好的基线模型DARL[14 ] ,SAM提升了0.038. SAM优于所有基于度量学习的基线模型, 在2个数据集中对比表现最好的模型APINet,MRR、Hits@10、Hits@5、Hits@1分别提高了0.024、0.021、0.032、0.032以及0.022、0.055、0.039、0.045. 分析原因:基于度量的方法推理效果依赖于向量空间的表示,由于预训练词向量包含的语义信息有限,限制了APINet的推理能力,SAM能够较好利用邻域结构信息挖掘实体与邻居节点之间潜在的语义,增强实体的语义表示,提升模型的推理能力. SAM优于所有基于元学习的基线模型. 在NELL-One数据集上,对比表现最好的模型GANA[12 ] , MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
... [14 ],SAM提升了0.019;对比Hits@10最好的基线模型APINet,SAM提升了0.055;对比Hits@5最好的基线模型APINet[11 ] ,SAM提升了0.039;对比Hits@1最好的基线模型DARL[14 ] ,SAM提升了0.038. SAM优于所有基于度量学习的基线模型, 在2个数据集中对比表现最好的模型APINet,MRR、Hits@10、Hits@5、Hits@1分别提高了0.024、0.021、0.032、0.032以及0.022、0.055、0.039、0.045. 分析原因:基于度量的方法推理效果依赖于向量空间的表示,由于预训练词向量包含的语义信息有限,限制了APINet的推理能力,SAM能够较好利用邻域结构信息挖掘实体与邻居节点之间潜在的语义,增强实体的语义表示,提升模型的推理能力. SAM优于所有基于元学习的基线模型. 在NELL-One数据集上,对比表现最好的模型GANA[12 ] , MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
... [14 ],SAM提升了0.038. SAM优于所有基于度量学习的基线模型, 在2个数据集中对比表现最好的模型APINet,MRR、Hits@10、Hits@5、Hits@1分别提高了0.024、0.021、0.032、0.032以及0.022、0.055、0.039、0.045. 分析原因:基于度量的方法推理效果依赖于向量空间的表示,由于预训练词向量包含的语义信息有限,限制了APINet的推理能力,SAM能够较好利用邻域结构信息挖掘实体与邻居节点之间潜在的语义,增强实体的语义表示,提升模型的推理能力. SAM优于所有基于元学习的基线模型. 在NELL-One数据集上,对比表现最好的模型GANA[12 ] , MRR、Hits@10、Hits@5、Hits@1分别提高了0.018、0.036、0.024、0.019. 在Wiki-One数据集上,对比表现较好的模型DARL[14 ] ,MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
... [14 ],MRR、Hits@10、Hits@5、Hits@1分别提高了0.019、0.082、0.058、0.038. 尽管基于元学习的方法能自动地发现和优化模型参数和超参数设置,使模型能够自动适应不同任务,但该类方法须针对不同任务进行多次反向传播和梯度更新,加大了训练的计算复杂性和时间成本. SAM在挖掘邻域信息时,没有复杂的超参数设计,模型的复杂度相对较小. 实验结果表明,在少样本条件下,所提模型能够有效挖掘到实体的邻域结构信息,实体的语义表示比其他基线模型更充分,能够有效提高查询三元组预测的准确性,泛化性良好. ...
1
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
1
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
1
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
1
... 知识补全更接近于少样本学习任务[6 -8 ] . 少样本知识补全旨在利用少量支持样本,自动构建较为完备的知识图谱,为下游人工智能应用提供良好的数据支撑. 越来越多的研究者将深度学习中的少样本学习方法应用于少样本知识补全. 现有的少样本知识补全方法主要分为2个类别:基于度量的方法和基于元学习的方法. 在基于度量的方法中,Yuan等[9 ] 考虑实体与邻居间的交互,设计分层注意力编码器来捕获交互信息. Liang等[10 ] 基于掩码机制设计全局注意力机制,捕获了实体间的交互信息. Li等[11 ] 设计原型网络,进行关系的多层语义处理,为查询样本和支持样本生成原型嵌入. 第一类方法的核心:基于不同的嵌入学习策略为知识三元组中的关系和实体学习准确的向量表示,得到查询样本和支持样本的嵌入,在同一个向量空间下度量查询样本和支持样本的相似性. 在基于元学习的方法中,Niu等[12 ] 使用关系超平面参数更新机制,建模实体之间复杂关系. Zhang等[13 ] 为了实现少样本多跳关系推理,设计出结合知识蒸馏的元学习优化机制. Cai等[14 ] 为了使元知识具备更好的语义信息,设计动态邻居编码器来融合邻居关系语义,得到实体的动态嵌入表示. 第二类方法的关键:引导模型识别并聚焦特定任务的关键参数(常被称为元参数),通过元参数调整与优化来提升模型适应新任务的能力. 主流少样本知识补全方法基于预训练词向量包含的语义信息进行推理,忽视了邻域结构对实体编码的影响. 图的结构挖掘与结构信息融合受到关注,逐渐被用于其他知识图谱任务并取得积极效果. Dwivedi等[15 ] 使用图的拉普拉斯特征向量代替Transformer编码器中的位置编码,以解决Transformer网络无法有效学习图结构特征的问题,Ying等[16 ] 使用中心性编码代替Transformer编码器中的位置编码,在注意力机制中引入空间编码以及边编码. 为了融合实体的图结构特征,Chen等[17 ] 对图谱进行子图抽取,使用图神经网络学习子图的特征,最后进行实体表示的更新. Luo等[18 ] 设计出表征节点之间连接状态的掩码矩阵并将其引入注意力机制. ...
1
... 少样本知识补全任务的目的是利用模型学习支持集中三元组潜在的语义信息,推测查询三元组存在的合理性. 若查询三元组存在的合理性越高,则查询三元组中的尾实体是待预测三元组中缺失尾实体的可能性越大. 少样本知识补全任务因此转化为查询三元组与支持三元组的相似性评估任务. 在整个预测过程中,三元组的表示至关重要,对三元组的表示越准确,三元组预测得分越高,模型的评估效果越好. 词语义具有多义性,词向量预训练模型始终难以得到包含单词所有语义的向量表示. 现有知识补全方法[5 ,10 -14 ,19 -21 ] 均基于知识的预训练词向量包含的语义信息来推测查询三元组的合理性,少样本知识补全方法面临挑战:1)知识本身,三元组中的实体和关系的词向量语义信息有限,难以支持模型进行有效推理. 如图1 (a)所示为NELL-One数据集中实体“Company: Intuit”的邻域结构. 使用主成分分析算法(PCA)对邻域中所有节点的词向量进行降维,得到第一个主成分PCA1和第二个主成分PCA2,并可视化显示其语义分布,如图1 (b)所示. 可以看出,原本应该拥有相似语义的节点“Ceo: Stephen Bennett”、“Ceo: Scott Cook”、“Ceo: Brad Smith”相距较远. 2)从拓扑结构上看,呈现结构聚集性的节点应该有强相关性,从词向量的语义分布上看,这种相关性却很弱. 如果能利用拓扑结构引导模型进一步挖掘这类呈现结构集群的邻居之间潜在的语义相关性,将有利于增强模型推理. 对此,在SAM中使用如图1 (c)所示的二分谱聚类集群划分方法来挖掘邻域的拓扑结构特征. ...
1
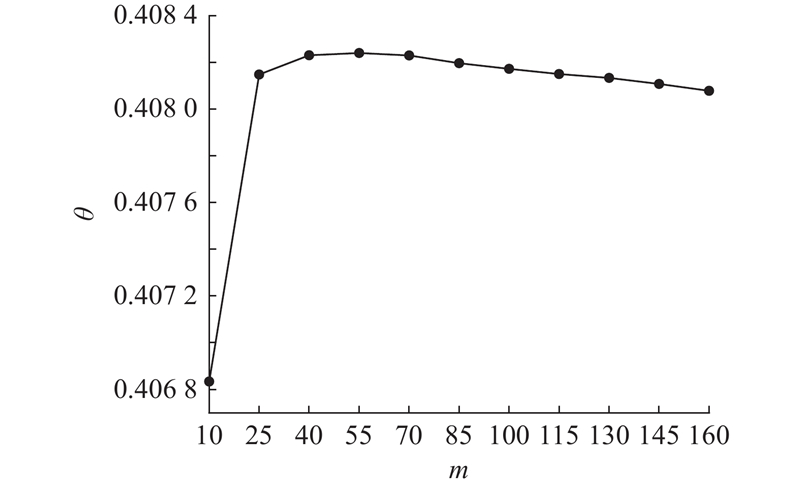
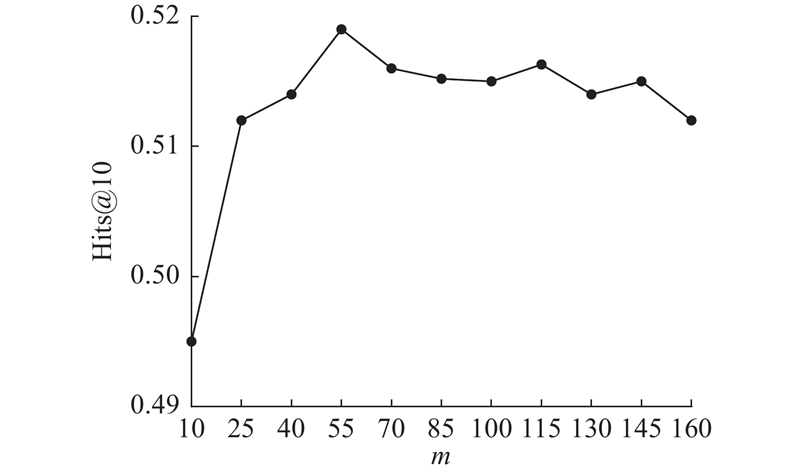
... 使用公共数据集NELL-One和Wiki-One[20 ] 评估SAM在少样本知识补全任务上的有效性. 如表1 所示为2个数据集中实体、关系和三元组的样本数量$N_{\mathrm{S}} $ . 表中,从NELL-One的三元组中划出67组预测任务,其中训练集、验证集、测试集的比例为51∶5∶11;从Wiki-One的三元组中划分出183组预测任务,其中训练集、验证集、测试集的比例为133∶16∶34. 2个数据集中,每组预测任务包含的三元组数量为50~500. 模型性能评估指标为平均倒数排名MRR和命中排名在前n 位的正确结果的平均占比Hits@n ,指标的数值越大,说明模型的性能越好. 指标计算式分别为 ...
关系生成图注意力网络的知识图谱链接预测
1
2022
... 少样本知识补全任务的目的是利用模型学习支持集中三元组潜在的语义信息,推测查询三元组存在的合理性. 若查询三元组存在的合理性越高,则查询三元组中的尾实体是待预测三元组中缺失尾实体的可能性越大. 少样本知识补全任务因此转化为查询三元组与支持三元组的相似性评估任务. 在整个预测过程中,三元组的表示至关重要,对三元组的表示越准确,三元组预测得分越高,模型的评估效果越好. 词语义具有多义性,词向量预训练模型始终难以得到包含单词所有语义的向量表示. 现有知识补全方法[5 ,10 -14 ,19 -21 ] 均基于知识的预训练词向量包含的语义信息来推测查询三元组的合理性,少样本知识补全方法面临挑战:1)知识本身,三元组中的实体和关系的词向量语义信息有限,难以支持模型进行有效推理. 如图1 (a)所示为NELL-One数据集中实体“Company: Intuit”的邻域结构. 使用主成分分析算法(PCA)对邻域中所有节点的词向量进行降维,得到第一个主成分PCA1和第二个主成分PCA2,并可视化显示其语义分布,如图1 (b)所示. 可以看出,原本应该拥有相似语义的节点“Ceo: Stephen Bennett”、“Ceo: Scott Cook”、“Ceo: Brad Smith”相距较远. 2)从拓扑结构上看,呈现结构聚集性的节点应该有强相关性,从词向量的语义分布上看,这种相关性却很弱. 如果能利用拓扑结构引导模型进一步挖掘这类呈现结构集群的邻居之间潜在的语义相关性,将有利于增强模型推理. 对此,在SAM中使用如图1 (c)所示的二分谱聚类集群划分方法来挖掘邻域的拓扑结构特征. ...
关系生成图注意力网络的知识图谱链接预测
1
2022
... 少样本知识补全任务的目的是利用模型学习支持集中三元组潜在的语义信息,推测查询三元组存在的合理性. 若查询三元组存在的合理性越高,则查询三元组中的尾实体是待预测三元组中缺失尾实体的可能性越大. 少样本知识补全任务因此转化为查询三元组与支持三元组的相似性评估任务. 在整个预测过程中,三元组的表示至关重要,对三元组的表示越准确,三元组预测得分越高,模型的评估效果越好. 词语义具有多义性,词向量预训练模型始终难以得到包含单词所有语义的向量表示. 现有知识补全方法[5 ,10 -14 ,19 -21 ] 均基于知识的预训练词向量包含的语义信息来推测查询三元组的合理性,少样本知识补全方法面临挑战:1)知识本身,三元组中的实体和关系的词向量语义信息有限,难以支持模型进行有效推理. 如图1 (a)所示为NELL-One数据集中实体“Company: Intuit”的邻域结构. 使用主成分分析算法(PCA)对邻域中所有节点的词向量进行降维,得到第一个主成分PCA1和第二个主成分PCA2,并可视化显示其语义分布,如图1 (b)所示. 可以看出,原本应该拥有相似语义的节点“Ceo: Stephen Bennett”、“Ceo: Scott Cook”、“Ceo: Brad Smith”相距较远. 2)从拓扑结构上看,呈现结构聚集性的节点应该有强相关性,从词向量的语义分布上看,这种相关性却很弱. 如果能利用拓扑结构引导模型进一步挖掘这类呈现结构集群的邻居之间潜在的语义相关性,将有利于增强模型推理. 对此,在SAM中使用如图1 (c)所示的二分谱聚类集群划分方法来挖掘邻域的拓扑结构特征. ...
1
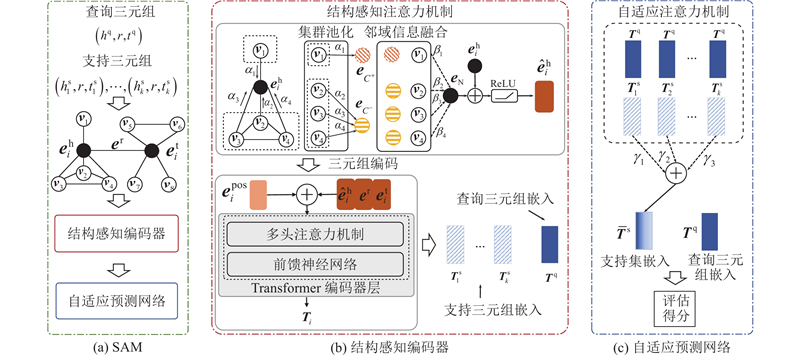
... 图注意力机制[22 -25 ] 具备一定的图结构学习能力,但是它往往只关注邻居节点对中心节点的贡献,忽视了邻居节点之间的拓扑连接对中心实体表示的影响. 为了引导模型利用邻域拓扑结构挖掘邻居节点之间潜在的语义信息,在结构感知编码器中设计结构感知注意力机制来捕获邻居结构信息,并融合到实体的嵌入表示中. 对于第i 个三元组$\left( {{h_i},r,{t_i}} \right)$ ${h_i}$ ${t_i}$
Sparse graph attention networks
0
2023
Simple and deep graph attention networks
1
2024
... 图注意力机制[22 -25 ] 具备一定的图结构学习能力,但是它往往只关注邻居节点对中心节点的贡献,忽视了邻居节点之间的拓扑连接对中心实体表示的影响. 为了引导模型利用邻域拓扑结构挖掘邻居节点之间潜在的语义信息,在结构感知编码器中设计结构感知注意力机制来捕获邻居结构信息,并融合到实体的嵌入表示中. 对于第i 个三元组$\left( {{h_i},r,{t_i}} \right)$ ${h_i}$ ${t_i}$
1
... 由式(3)得到2个集群${C^+} = \left\{ {V_1^+,V_2^+, \cdots ,V_a^+} \right\}$ ${C^ - } = \left\{ {V_1^ - ,V_2^ - , \cdots ,V_b^ - } \right\}$ $a+b = d$ . 如图1 (c)所示,在实体“Company: Intuit”的邻域结构中,设节点集合为$\left\{ {{V_0},{V_1},{V_2},{V_3},{V_4}} \right\}$ $\left\{ {0,1,4,4,5} \right\}$ . 4)选取${\lambda _2} = 1$ ${{\boldsymbol{X}}_2} $ 0.2887 , −0.2887 , −0.2887 , 0.8660 },依据式(3)对邻域集合$\left\{ {{V_1},{V_2},{V_3},{V_4}} \right\}$ ${C^+} = \left\{ {{V_4}} \right\}$ ${C^ - } = \left\{ {{V_1},{V_2},{V_3}} \right\}$ . 结合图1 (a)的集群效果来看,所提二分谱聚类方法可以较好地将结构上呈现集群的节点划分到同个集群中. 相比其他谱聚类方法[26 -29 ] ,所提二分谱聚类方法在实现上复杂程度更低. ...
Unsupervised large graph embedding based on balanced and hierarchical K-means
1
2022
... 由式(3)得到2个集群${C^+} = \left\{ {V_1^+,V_2^+, \cdots ,V_a^+} \right\}$ ${C^ - } = \left\{ {V_1^ - ,V_2^ - , \cdots ,V_b^ - } \right\}$ $a+b = d$ . 如图1 (c)所示,在实体“Company: Intuit”的邻域结构中,设节点集合为$\left\{ {{V_0},{V_1},{V_2},{V_3},{V_4}} \right\}$ $\left\{ {0,1,4,4,5} \right\}$ . 4)选取${\lambda _2} = 1$ ${{\boldsymbol{X}}_2} $ 0.2887 , −0.2887 , −0.2887 , 0.8660 },依据式(3)对邻域集合$\left\{ {{V_1},{V_2},{V_3},{V_4}} \right\}$ ${C^+} = \left\{ {{V_4}} \right\}$ ${C^ - } = \left\{ {{V_1},{V_2},{V_3}} \right\}$ . 结合图1 (a)的集群效果来看,所提二分谱聚类方法可以较好地将结构上呈现集群的节点划分到同个集群中. 相比其他谱聚类方法[26 -29 ] ,所提二分谱聚类方法在实现上复杂程度更低. ...