储备池计算(reservoir computing)是循环神经网络(recurrent neural network, RNN)的快速训练方法,优点在于可以避免梯度消失/爆炸的问题[1]. 储备池计算的核心思想是使用固定、随机且稀疏连接的大规模储备池作为RNN的隐藏层,通过输入输出层之间的训练来学习解决特定的任务. 上述训练思想已在回声状态网络(echo state networks, ESN)中成功应用[2-3]. ESN储备池内部的神经元存在循环连接(前一时刻与当前时刻的储备池之间存在连接权边),因此拥有记忆能力. ESN先随机生成输入连接权重和循环连接权重,再保持随机连接的循环网络不变以计算各时刻的内部状态,最后只需训练输出连接权重,即可得到可对网络内部状态进行分类/预测/回归的模型. 与传统的RNN相比,ESN具备更高的训练效率和便捷性,在各领域广受重视,尤其在时间序列预测任务上展现出独特优势[4-5]. 关于ESN的研究仍存在瓶颈,如在储备池拓扑结构设计方面,传统储备池是随机网络,其不确定性导致性能波动较大. 如何让储备池具有自适应、自组织、自演化的复杂结构是新兴的研究课题.
自然界及人类社会中的大量复杂网络存在自适应、自组织、自演化的特点,例如生物神经网络[6]、社交网络[7]、交通网络[8]等. 复杂网络[9-10]由大量节点和连接构成,节点之间的连接关系呈现多样性和复杂性. 相关研究表明,具有无标度特性的复杂网络比随机网络更适合作为储备池的拓扑结构[11]. 现有工作主要采用无标度网络的经典构造算法——BA(Barabasi-Albert)算法来生成储备池,该算法依赖于增长机制和偏好连接(preferential attachment, PA),具有幂律的度分布[12]. 但BA算法也存在局限:一方面,该算法只能描述幂律指数γ=3的无标度网络;另一方面,网络在增长过程中,越旧的节点具有越高的度数,而新增的节点不可能出现度数大的情况. 基于BA算法的适应度模型由此诞生[13],该模型通过引入可调参数对偏好连接机制进行细化. Tsiotas[14]提出适应度的时间动态概念,利用随网络增长而变化的拓扑适应度生成无标度网络,其中适应度由度、聚类系数、中间度、接近度和特征向量中心性控制. 为了更好解释社交网络的动态性,Behera等[7]引入基于加权介数的模型,模型节点连接的标准是加权介数中心性而不是度数,介数中心性在网络增长的每一步都被计算,能更准确地描述各种真实社交网络. 还有方法通过修改偏好连接机制,使连接到定点的概率与该定点的度数非线性相关,这种机制被称为非线性偏好连接(nonlinear preferential attachment, NPA)[15].
以上算法都是通过一个接一个添加节点的方式生成无标度网络,构建不灵活且速度慢. Wang等[16-17]提出随机图构造算法,称为Chung-Lu(CL)算法,可以灵活简单地构建出复杂网络. Fasino等[18]进一步证明通过适当选择参数,CL算法可以生成具有多种性质的无标度网络,如具有指定幂律指数的网络以及具有理想平均度和最大期望度的网络. 遗憾的是,尚未有研究工作将CL算法构造的无标度网络应用于ESN储备池设计. 本研究利用基于随机矩阵理论的CL算法生成具有理想平均度的无标度网络,并将其作为ESN储备池拓扑结构;针对CL算法在构造无标度网络过程中出现的度值偏差问题,引入随机剪枝和度值剪枝对网络连边进行剪枝.
1. 方法描述
1.1. 回声状态网络简介
传统的ESN包括输入层、大规模储备池和输出层,假设它们的神经元个数分别为I、N、O. ESN的特点是全连接的输入权重
式中:
式中:[·;·]为2个向量的上下拼接操作. 3)求解
式中:
1.2. 回声状态网络储备池的图表示
将ESN储备池抽象为无向加权图G = {V, E, A};其中V为节点(神经元)的集合(
1.3. Chung-Lu算法
CL算法生成的图通常用G(w)表示,
与节点i相连的理想边数,即节点i的理想度值为
以上为生成N个节点的随机图
定义1 当
1.4. 具有无标度性质的Chung-Lu算法
CL算法允许提前设定图G(w)的度分布,选择满足幂律度分布的参数w即可生成具有任意指数的幂律网络. 假设
根据定义1可知,G中节点的最大度值为
同理可得G中节点的最小度值为
当
式(11)的假设存在一些问题. 对于节点i之后的其余节点,存在度值和节点i的度值相同的情况,因此对于
用式(12)生成的理想度向量w仍然存在问题,即
定义2 当
式中:中间变量
定义3 当
存在常数
对于节点
那么有以下结论:1)
须注意式(15)必须满足,如果不满足该条件,则无法获得任意的度向量w. 如果d(N)的上限是常数,则该条件意味着最大理想度值m(N)的增长速度不得快于
定义4 令
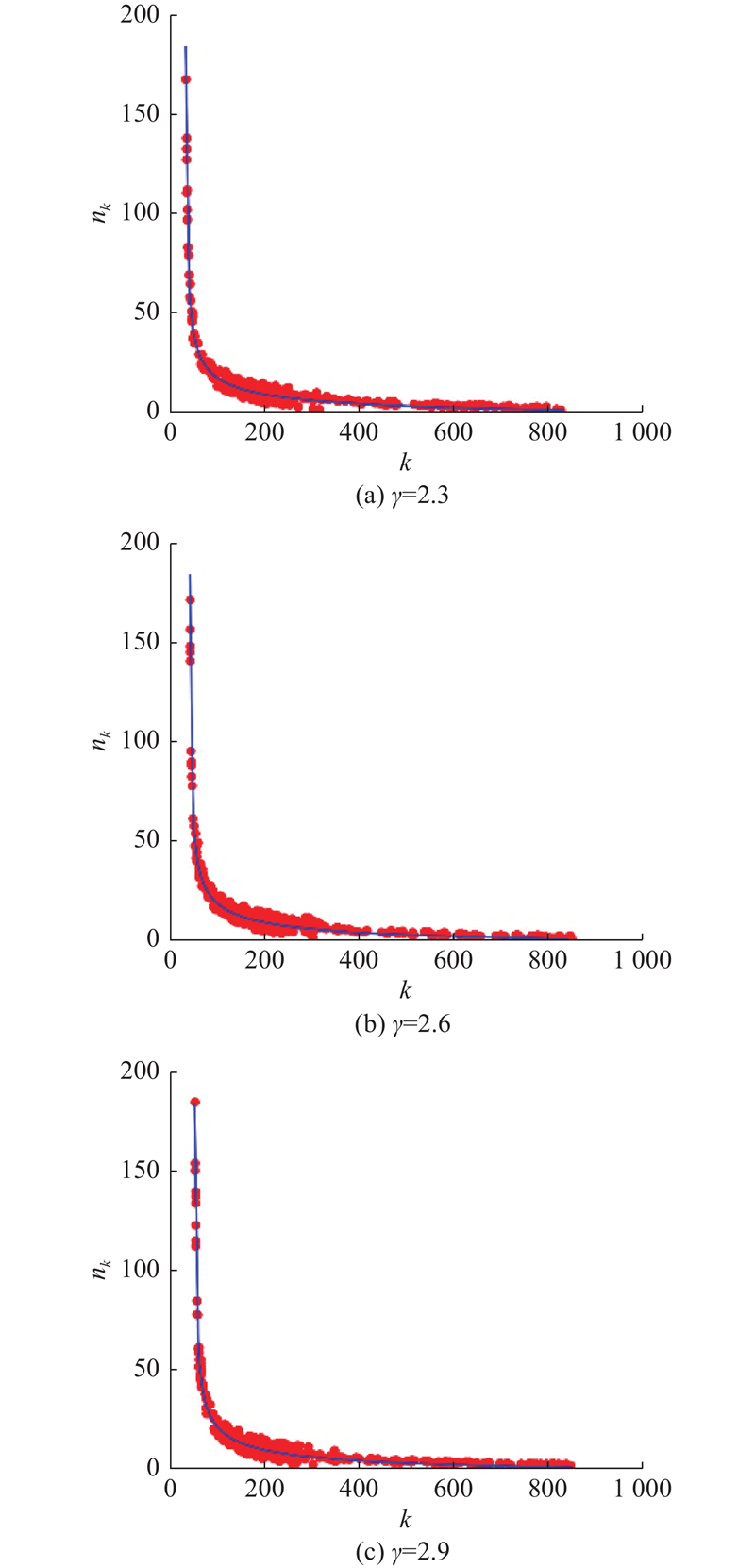
基于以上4个定义,通过改进的CL算法可以生成满足无标度幂律性质的网络G(w). 如图1所示为改进CL算法生成的具有不同幂律指数的无标度网络的节点度分布. 该图显示了度值k与度值数量
图 1
图 1 改进Chung-Lu算法生成无标度网络的节点度分布
Fig.1 Node degree distribution of scale-free network generated by improved Chung-Lu algorithm
2. 基于剪枝机制的无标度回声状态网络
本研究提出利用改进Chung-Lu算法生成具有理想平均度的无标度网络,并将其作为ESN储备池拓扑结构. 该储备池具有2个可调参数:幂律指数
1)将ESN储备池抽象为无向加权图
2)初始化幂律指数和理想平均度值,根据
3)根据w计算储备池边的数量M. M=
4)计算理想度向量
5)生成储备池边的行列索引集合I和J. 先生成随机向量
6)行索引集合和列索引集合的数量均为M个. 分别依次取出I和J中的元素,组成非零边的下标,最终得到具有M条边的稀疏矩阵A. 例如I={2,1,4},J={3, 2, 6},由于是无向图,那么A中
7)在步骤3)中为了抵消重复边,额外增加了储备池的理想边数,会导致真实的平均度值与mean(w)有差距,且随着理想平均度值d的增大,差距会越来越大. 为了解决该问题,对稀疏矩阵A进行剪枝处理. 根据真实的平均度值与mean(w)的差值计算剪枝的总边数n,接着选择以下2种机制进行剪枝. 随机剪枝:随机选择稀疏矩阵A中的n条边,赋予
8)将矩阵A中的非零边赋予区间[−1, 1]中符合均匀分布的权重值.
基于上述步骤,引入剪枝机制的无标度ESN模型,训练过程见算法1.
算法1 无标度ESN模型的训练算法
输入:ESN模型参数、幂律指数
输出:训练完成的CL-ESN模型
1. 初始随机生成满足均匀分布条件的
2. 根据选定参数幂律指数
3. 根据式(16)和(19)初始化c和最大理想度m,再根据c、m和式(17)得到参数
4. 根据w与M=
5. 根据式(20)计算理想度向量
6. 生成储备池边的行列索引集合I和J. 先生成随机向量
7. 对稀疏矩阵A,根据真实的平均度值与mean(w)的差值计算剪枝的总边数n,并进行剪枝.
8. 将A中的非零边赋予区间[−1,1]中符合均匀分布的权重值,生成具有无标度性质的初始储备池连接权重
9. 通过比例因子
10. 设置储备池初始内部状态x(0) = 0,利用输入变量
11. 从s+1时刻开始收集储备池的内部状态,根据式(2)、(3)得到扩展状态矩阵X和输出矩阵Y.
12. 根据式(4)计算网络的输出权重矩阵
13. 训练结束.
3. 实验及结果分析
3.1. 数据集
3.1.1. Mackey-Glass数据集
MG数据集是混沌时间序列预测模型的基准数据集,广泛用于测试神经网络对非线性混沌系统的辨识能力. 该数据集由时滞微分方程给出:
当
3.1.2. Multiple Superimposed Oscillator数据集
某个正弦信号的预测任务相对简单,仅需有限的记忆容量就能预测网络的下一步输出. 不过预测不是整数倍频率叠加的正弦波是具有挑战性的任务,原因是正弦信号的波长可能非常长,导致预测困难. 为了解决这个问题,Fu等[23]提出使用多重叠加振荡器(multiple superimposed oscillator, MSO)的定义:
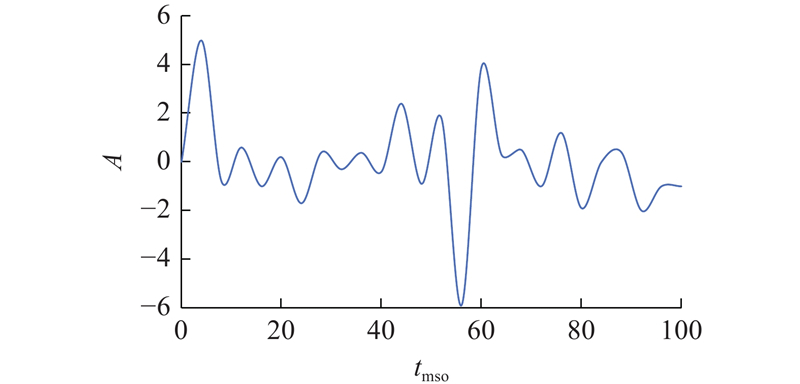
式中:tmso为MSO采样时间步. 在MSO数据集中,要求模型能够同时管理多个独立的内部状态. 传统的ESN模型中储备池神经元通常存在相互耦合现象,这与MSO数据集的要求相反. 为了更好处理MSO数据集,必须对ESN储备池的结构进行优化. 本节生成10 000个数据点,随后对MSO数据集进行标准化的预处理操作,以确保数据的一致性. 处理过后的数据如图2所示. 图中,A为振荡信号幅值.
图 2
图 2 MSO数据集的前10 000个数据点(步长为0.1)
Fig.2 First 10 000 data points of MSO dataset (step size is 0.1)
3.2. 评价指标
3.2.1. 均方误差
选用均方误差MSE作为模型预测性能的评价指标,计算式为
式中:
3.2.2. 富人俱乐部系数
富人俱乐部系数RC用来评估网络中高度连通节点的紧密程度. 该参数通常基于节点的度来衡量节点的重要性,一般而言,富人俱乐部的定义主要关注节点的拓扑结构,不考虑权重:
式中:
3.2.3. 平均百分比误差
平均绝对百分比误差MAPE的计算式为
MAPE越小,表示模型的准确性较高.
3.2.4. 运行时间
运行时间tr是指从构造储备池开始到训练出输出连接矩阵的总时间.
3.3. 实验分析
基于前期工作基础,实验设置储备池N=500,CL算法参数幂律指数γ=2.3、2.6、2.9,理想平均度数的范围在[10, 200],步长为10. 考虑到运行的随机性,每组参数迭代运行10次取均值.
3.3.1. 无标度性质对比
图 3
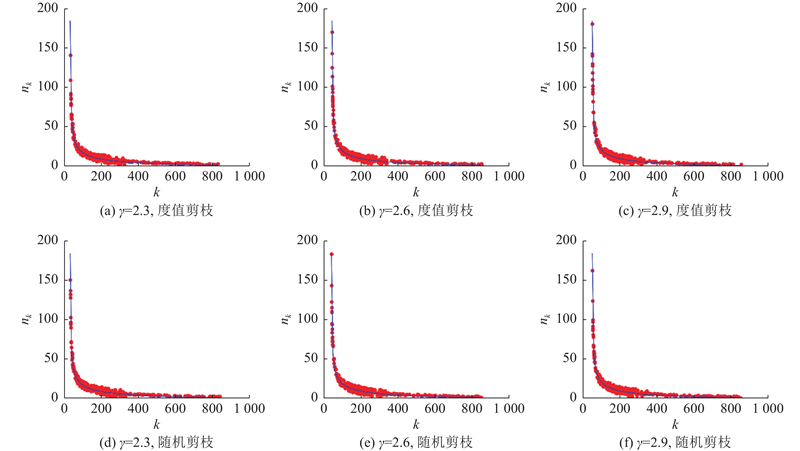
图 3 不同幂律指数下经不同机制剪枝后的节点度分布
Fig.3 Node degree distribution after pruning by different mechanisms with different power-law indexes
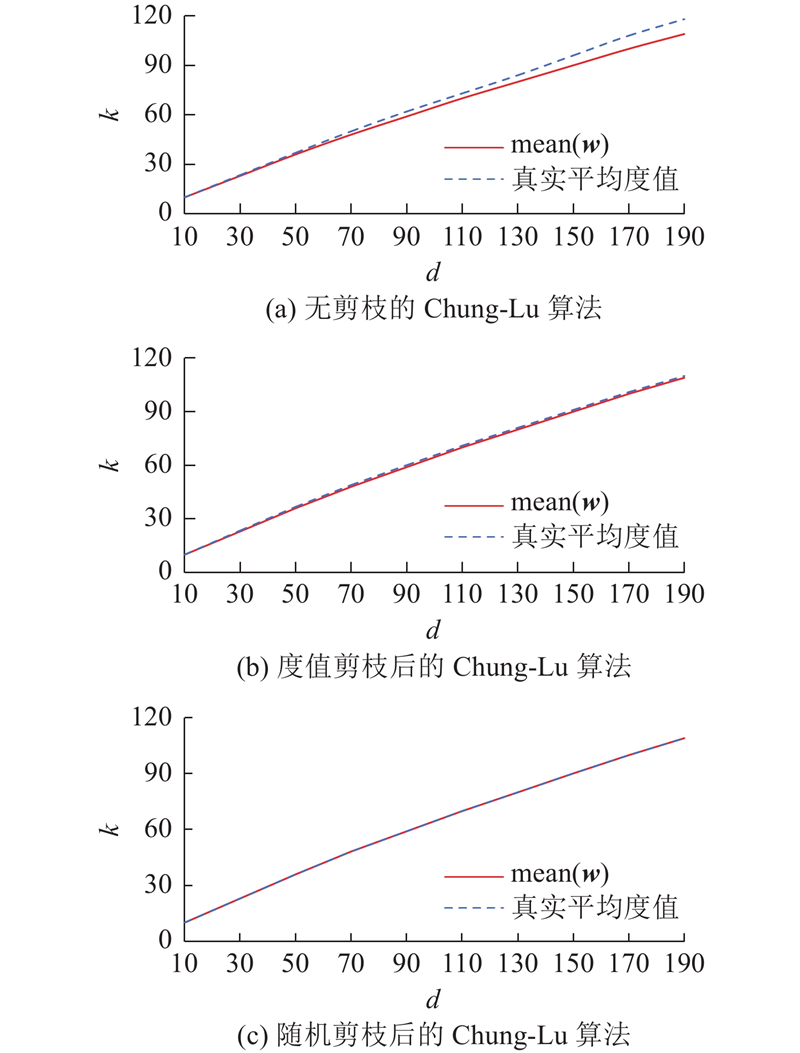
如图4所示为当
图 4
图 4 不同机制下理想平均度值与真实平均度值的对比
Fig.4 Comparison between ideal average degree and real average degree under different mechanisms
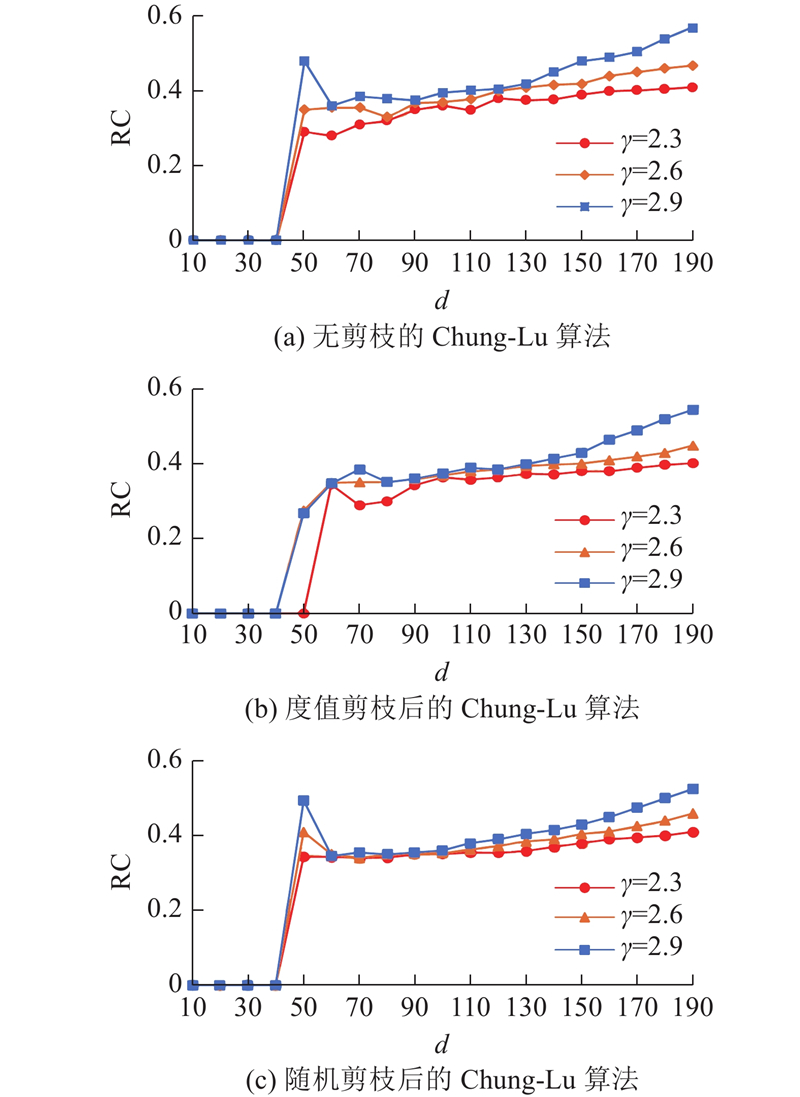
如图5所示为有无剪枝机制的算法关于不同幂律指数的理想平均度值d和富人俱乐部系数RC之间的关系,设置的富人俱乐部的阈值度为100. 由图可知,在3种幂律指数下,随着理想平均度值的增加,RC开始为0,然后整体呈上升趋势,但在局部出现一些波动. 这表明节点更倾向于与度值大的节点连接,使度值大的节点在网络中具有更重要的地位,形成不平等的连接,导致富者愈富的现象,即高度连接的节点越来越集中在少数节点上. 这种现象与无标度网络的特征是一致的. 另外,
图 5
图 5 不同机制下不同幂律指数的富人俱乐部系数的对比
Fig.5 Comparison of rich club coefficient with different power law indexes under different mechanisms
3.3.2. 基于Chung-Lu算法的回声状态网络的预测性能对比
在
表 1 基于Chung-Lu算法的储备池稀疏度
Tab.1
| d | Rc | ||
| 无剪枝 | 度值剪枝 | 随机剪枝 | |
| 50 | |||
| 100 | |||
| 150 | |||
| 200 | |||
表 2 基于Chung-Lu算法的回声状态网络均方误差
Tab.2
| d | MG-16数据集 | MG-17数据集 | MSO数据集 | ||||||||
| MSE0 | MSE1 | MSE2 | MSE0 | MSE1 | MSE2 | MSE0 | MSE1 | MSE2 | |||
| 50 | |||||||||||
| 100 | |||||||||||
| 150 | |||||||||||
| 200 | |||||||||||
表 3 基于Chung-Lu算法的回声状态网络平均绝对百分比误差
Tab.3
| d | MG-16数据集 | MG-17数据集 | MSO数据集 | ||||||||
| MAPE0 | MAPE1 | MAPE2 | MAPE0 | MAPE1 | MAPE2 | MAPE0 | MAPE1 | MAPE2 | |||
| 50 | |||||||||||
| 100 | |||||||||||
| 150 | |||||||||||
| 200 | |||||||||||
表 4 基于Chung-Lu算法的回声状态网络运行时间
Tab.4
| d | MG-16数据集 | MG-17数据集 | MSO数据集 | ||||||||
| tr,0/s | tr,1/s | tr,2/s | tr,0/s | tr,1/s | tr,2/s | tr,0/s | tr,1/s | tr,2/s | |||
| 50 | |||||||||||
| 100 | |||||||||||
| 150 | |||||||||||
| 200 | |||||||||||
3.3.3. 多种无标度网络构造方法的预测性能对比
根据无标度性质的对比实验以及预测性能的对比实验可知,基于随机剪枝的CL算法优于无剪枝或度值剪枝的CL算法,为此选用所提算法与BA算法及其各种变体生成不同的储备池并得到相应的ESN,对比它们对混沌时间序列的预测精度,平均绝对百分比误差和运行时间. 对比实验算法为BA算法[12],MC[24],MCC[25],MCE[26],已经被证明可构建无标度网络. BA算法是在度值k控制下生成的适应算法;MC为在聚类系数控制下生成的适应算法;MCC为在紧密中心性(closeness centrality, CC)控制下生成的适应算法,紧密中心性用于衡量某节点与其他节点之间的紧密程度,表示该节点到其他节点的平均最短路径长度的倒数;MCE是在特征向量中心性(eigenvector centrality, CE)控制下生成的适应算法,特征向量中心性是基于节点在网络中的连接程度和邻居节点的中心性来计算的,简单来讲就是相邻的邻居节点越重要,该节点越重要. 如表5所示,设置参数
表 5 不同数据集下不同方法构建的回声状态网络预测性能对比
Tab.5
| 构建算法 | MG-16数据集 | MG-17数据集 | MSO数据集 | ||||||||
| MSE | MAPE | tr/s | MSE | MAPE | tr/s | MSE | MAPE | tr/s | |||
| 本研究 | |||||||||||
| BA算法 | |||||||||||
| MC | |||||||||||
| MCC | |||||||||||
| MCE | |||||||||||
4. 结 语
脑科学的研究表明人脑可能具有内禀的网络特性,即无标度特性,它使得大脑内的神经元有枢纽和层级感. 为了模拟大脑网络的构造过程,本研究提出基于随机矩阵理论的Chung-Lu构造算法生成无标度网络,并将其作为ESN的储备池. 为了解决度值偏差,引入度值剪枝和随机剪枝2种机制删除冗余边,提升网络的鲁棒性. 度值剪枝有可能破坏网络中节点度大的节点,性能不如随机剪枝. 实验表明,基于剪枝机制的CL算法构建的网络,仍能保持无标度网络的幂律特性. 相比于BA算法及其变体,所提算法不再依赖于增长和偏好连接,因此构建灵活且速度快,并且在混沌时间序列预测方面具有更好的效果. 在未来的工作中,将着眼于利用不同类型的时间序列数据集,对提出的 ESN模型进行更全面的验证,以检验其在各种实际应用背景下的鲁棒性和有效性.
参考文献
One-shot bipedal robot dynamics identification with a reservoir-based RNN
[J].DOI:10.1109/ACCESS.2023.3277977 [本文引用: 1]
FastESN: fast echo state network
[J].DOI:10.1109/TNNLS.2022.3167466 [本文引用: 1]
A fast parametric and structural transfer leaky integrator echo state network for reservoir computing
[J].DOI:10.1109/TSMC.2024.3358567 [本文引用: 1]
Computational efficiency of multi-step learning echo state networks for nonlinear time series prediction
[J].DOI:10.1109/ACCESS.2022.3158755 [本文引用: 1]
Parameterizing echo state networks for multi-step time series prediction
[J].DOI:10.1016/j.neucom.2022.11.044 [本文引用: 1]
Extreme multistability in a hopfield neural network based on two biological neuronal systems
[J].
MR-IBC: mapreduce-based incremental betweenness centrality in large-scale complex networks
[J].DOI:10.1007/s13278-020-00636-9 [本文引用: 2]
Multimodal urban mobility and multilayer transport networks
[J].DOI:10.1177/23998083221108190 [本文引用: 1]
基于节点相似性和网络嵌入的复杂网络社区发现算法
[J].DOI:10.11896/jsjkx.210200009 [本文引用: 1]
Complex network community detection algorithm based on node similarity and network embedding
[J].DOI:10.11896/jsjkx.210200009 [本文引用: 1]
复杂网络能控性鲁棒性研究进展
[J].
Recent progress in controllability robustness of complex networks
[J].
A small-world topology enhances the echo state property and signal propagation in reservoir computing
[J].DOI:10.1016/j.neunet.2019.01.002 [本文引用: 1]
Historical payoff can not overcome the vaccination dilemma on Barabási–Albert scale-free networks
[J].DOI:10.1016/j.chaos.2019.109453 [本文引用: 2]
A novel method for detecting new overlapping community in complex evolving networks
[J].DOI:10.1109/TSMC.2017.2779138 [本文引用: 1]
Detecting differences in the topology of scale-free networks grown under time-dynamic topological fitness
[J].DOI:10.1038/s41598-020-67156-6 [本文引用: 1]
An investigation into the trend stationarity of local characteristics in media and social networks
[J].DOI:10.3390/systems10060249 [本文引用: 1]
Anomaly detection with subgraph search and vertex classification preprocessing in Chung-Lu random networks
[J].DOI:10.1109/TSP.2018.2866847 [本文引用: 1]
Spectral similarity for Barabási–Albert and Chung-Lu models
[J].DOI:10.1016/j.physa.2018.10.050 [本文引用: 1]
Generating large scale-free networks with the Chung-Lu random graph model
[J].DOI:10.1002/net.22012 [本文引用: 1]
A robust variable selection method for sparse online regression via the elastic net penalty
[J].DOI:10.3390/math10162985 [本文引用: 1]
A pseudo-inverse decomposition-based self-organizing modular echo state network for time series prediction
[J].DOI:10.1016/j.asoc.2021.108317
High precision error prediction algorithm based on ridge regression predictor for reversible data hiding
[J].DOI:10.1109/LSP.2021.3080181 [本文引用: 1]
Dynamics analysis of Mackey-Glass model with two variable delays
[J].DOI:10.3934/mbe.2020249 [本文引用: 1]
Link prediction algorithm based on clustering coefficient and node centrality
[J].
Weight-adaptive channel pruning for CNNs based on closeness-centrality modeling
[J].DOI:10.1007/s10489-023-05164-5 [本文引用: 1]
Link prediction of complex network based on eigenvector centrality
[J].DOI:10.1088/1742-6596/2337/1/012018 [本文引用: 1]