[1]
崔建勋, 要甲, 赵泊媛 基于深度学习的短期交通流预测方法综述
[J]. 交通运输工程学报 , 2024 , 24 (2 ): 50 - 64
[本文引用: 1]
CUI Jianxun, YAO Jia, ZHAO Boyuan Review on short-term traffic flow prediction methods based on deep learning
[J]. Journal of Traffic and Transportation Engineering , 2024 , 24 (2 ): 50 - 64
[本文引用: 1]
[2]
AHMED M S, COOK A R Analysis of freeway traffic time-series data by using box-jenkins techniques
[J]. Transportation Research Record , 1979 , (722 ): 1 - 9
[本文引用: 1]
[4]
TONG J, GU X, ZHANG M, et al. Traffic flow prediction based on improved SVR for VANET [C]// Proceedings of the 4th International Conference on Advanced Electronic Materials, Computers and Software Engineering . Changsha: IEEE, 2021: 402–405.
[本文引用: 1]
[5]
CHENG S, LU F, PENG P, et al Short-term traffic forecasting: an adaptive ST-KNN model that considers spatial heterogeneity
[J]. Computers, Environment and Urban Systems , 2018 , 71 : 186 - 198
DOI:10.1016/j.compenvurbsys.2018.05.009
[本文引用: 1]
[6]
ZAREMBA W, SUTSKEVER I, VINYALS O. Recurrent neural network regularization [EB/OL]. (2015–02–19)[2024–07–01]. https://arxiv.org/pdf/1409.2329.
[本文引用: 1]
[7]
HOCHREITER S, SCHMIDHUBER J Long short-term memory
[J]. Neural Computation , 1997 , 9 (8 ): 1735 - 1780
DOI:10.1162/neco.1997.9.8.1735
[8]
ZHANG R, SUN F, SONG Z, et al Short-term traffic flow forecasting model based on GA-TCN
[J]. Journal of Advanced Transportation , 2021 , 2021 (1 ): 1338607
[9]
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need [EB/OL]. (2023–08–02)[2024–07–01]. https://arxiv.org/pdf/1706.03762.
[本文引用: 1]
[10]
WANG H, PENG J, HUANG F, et al. MICN: multi-scale local and global context modeling for long-term series forecasting [C]// The Eleventh International Conference on Learning Representations . Kigali: [s. n.], 2023: 1–22.
[本文引用: 1]
[11]
ZHANG X, HUANG K, LIU C, et al. Urban short-term traffic flow prediction algorithm based on CNN-LSTM model [C]// Proceedings of the 3rd International Conference on Consumer Electronics and Computer Engineering . Guangzhou: IEEE, 2023: 214–217.
[本文引用: 1]
[12]
史昕, 曹凤腾, 纪艺, 等 基于多尺度时空特征与软注意力机制的交通流预测方法
[J]. 计算机工程 , 2024 , 50 (12 ): 346 - 357
[本文引用: 1]
SHI Xin, CAO Fengteng, JI Yi, et al Traffic flow prediction method based on multi-scale spatio-temporal features and soft attention mechanism
[J]. Computer Engineering , 2024 , 50 (12 ): 346 - 357
[本文引用: 1]
[13]
WU H, HU T, LIU Y, et al. TimesNet: temporal 2D-variation modeling for general time series analysis [EB/OL]. (2023–04–12)[2024–07–01]. https://arxiv.org/pdf/2210.02186.
[本文引用: 1]
[14]
WANG X, WANG Z, YANG K, et al. MPPN: multi-resolution periodic pattern network for long-term time series forecasting [EB/OL]. (2023–06–12)[2024–07–01]. https://arxiv.org/pdf/2306.06895.
[本文引用: 1]
[15]
赵顗, 沈玲宏, 马健霄, 等 综合小波分解和BP神经网络的交通小区生成交通短时预测
[J]. 重庆交通大学学报: 自然科学版 , 2021 , 40 (11 ): 60 - 66
[本文引用: 1]
ZHAO Yi, SHEN Linghong, MA Jianxiao, et al Traffic short-term prediction generated by wavelet decomposition and BP neural network of traffic zone
[J]. Journal of Chongqing Jiaotong University: Natural Science , 2021 , 40 (11 ): 60 - 66
[本文引用: 1]
[16]
SASAL L, CHAKRABORTY T, HADID A. W-Transformers: a wavelet-based transformer framework for univariate time series forecasting [C]// Proceedings of the 21st IEEE International Conference on Machine Learning and Applications . Nassau: IEEE, 2022: 671–676.
[本文引用: 1]
[17]
博格斯, 马科维奇. 小波与傅里叶分析基础[M]. 2版. 芮国胜, 康健, 译. 北京: 电子工业出版社, 2010: 173–194.
[本文引用: 1]
[18]
LIU Y, ZHENG H, FENG X, et al. Short-term traffic flow prediction with Conv-LSTM [C]// Proceedings of the 9th International Conference on Wireless Communications and Signal Processing . Nanjing: IEEE, 2017: 1–6.
[本文引用: 1]
[19]
陈峰浩. 基于时空特征分析的多步交通流量预测研究[D]. 杭州: 浙江科技大学, 2024: 1–59.
[本文引用: 1]
CHEN Fenghao. Research on multi-step traffic flow prediction based on spatio-temporal feature analysis [D]. Hangzhou: Zhejiang University of Science and Technology, 2024: 1–59.
[本文引用: 1]
[21]
FANG Y, QIN Y, LUO H, et al. When spatio-temporal meet wavelets: disentangled traffic forecasting via efficient spectral graph attention networks [C]// Proceedings of the IEEE 39th International Conference on Data Engineering . Anaheim: IEEE, 2023: 517–529.
[本文引用: 1]
[22]
HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition [C]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition . Las Vegas: IEEE, 2016: 770–778.
[本文引用: 1]
[23]
闫旭, 范晓亮, 郑传潘, 等 基于图卷积神经网络的城市交通态势预测算法
[J]. 浙江大学学报: 工学版 , 2020 , 54 (6 ): 1147 - 1155
[本文引用: 1]
YAN Xu, FAN Xiaoliang, ZHENG Chuanpan, et al Urban traffic flow prediction algorithm based on graph convolutional neural networks
[J]. Journal of Zhejiang University: Engineering Science , 2020 , 54 (6 ): 1147 - 1155
[本文引用: 1]
[24]
SUN Y, ZHANG G, YIN H Passenger flow prediction of subway transfer stations based on nonparametric regression model
[J]. Discrete Dynamics in Nature and Society , 2014 , 2014 (1 ): 397154
[本文引用: 1]
[25]
LIVIERIS I E, PINTELAS E, PINTELAS P A CNN–LSTM model for gold price time-series forecasting
[J]. Neural Computing and Applications , 2020 , 32 (23 ): 17351 - 17360
DOI:10.1007/s00521-020-04867-x
[本文引用: 1]
[26]
BAI S, KOLTER J Z, KOLTUN V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling [EB/OL]. (2018–04–19)[2024–07–01]. https://arxiv.org/pdf/1803.01271.
[本文引用: 1]
[27]
GUO S, LIN Y, FENG N, et al Attention based spatial-temporal graph convolutional networks for traffic flow forecasting
[J]. Proceedings of the AAAI Conference on Artificial Intelligence , 2019 , 33 (1 ): 922 - 929
DOI:10.1609/aaai.v33i01.3301922
[本文引用: 1]
[28]
LIU M, ZENG A, CHEN M, et al. SCINet: time series modeling and forecasting with sample convolution and interaction [C]// 36th Conference on Neural Information Processing Systems . New Orleans: [s. n.], 2022, 1–13.
[本文引用: 1]
[29]
LEE G, GOMMERS R, WASELEWSKI F, et al PyWavelets: a Python package for wavelet analysis
[J]. The Journal of Open Source Software , 2019 , 4 (36 ): 1237
DOI:10.21105/joss.01237
[本文引用: 1]
基于深度学习的短期交通流预测方法综述
1
2024
... 城市规模的急剧扩张和交通体系复杂性的日益增加,亟须交通应急管理系统与突发事件响应提升效能. 智能交通系统作为交通应急管理的重要信息化手段[1 ] ,主要通过交通流预测技术对现有交通运行状况和异常情况进行分析、评估和预测,达到为交管部门先期预警、高效决策提供支撑的目的. ...
基于深度学习的短期交通流预测方法综述
1
2024
... 城市规模的急剧扩张和交通体系复杂性的日益增加,亟须交通应急管理系统与突发事件响应提升效能. 智能交通系统作为交通应急管理的重要信息化手段[1 ] ,主要通过交通流预测技术对现有交通运行状况和异常情况进行分析、评估和预测,达到为交管部门先期预警、高效决策提供支撑的目的. ...
Analysis of freeway traffic time-series data by using box-jenkins techniques
1
1979
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
Traffic flow forecasting: comparison of modeling approaches
1
1997
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
1
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
Short-term traffic forecasting: an adaptive ST-KNN model that considers spatial heterogeneity
1
2018
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
1
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
Long short-term memory
0
1997
Short-term traffic flow forecasting model based on GA-TCN
0
2021
1
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
1
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
1
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
基于多尺度时空特征与软注意力机制的交通流预测方法
1
2024
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
基于多尺度时空特征与软注意力机制的交通流预测方法
1
2024
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
1
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
1
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
综合小波分解和BP神经网络的交通小区生成交通短时预测
1
2021
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
综合小波分解和BP神经网络的交通小区生成交通短时预测
1
2021
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
1
... 交通流预测模型主要分为数理统计学模型[2 -3 ] 、机器学习模型[4 -5 ] 及深度学习模型[6 -9 ] . 深度学习模型因具有强大的非线性拟合及深层特征提取能力,已成为交通流预测的主流方法. 在时域周期特征的建模研究中,Wang等[10 ] 利用多尺度等距卷积方法,学习描述交通流序列最主要的季节周期性特征,并辅之趋势特征,进行预测模型构建. Zhang等[11 ] 利用单一长短时记忆(long short term memory,LSMT)模型分析交通流周期性中的日周期、月周期,并结合序列的邻近特征构建交通预测模型. 史昕等[12 ] 在日周期、周周期、邻近时序基础上,通过提出双向增强注意力进一步学习时间依赖关系,以实现对交通流周期性特征的充分学习. 上述研究虽然在时域中有效捕捉了交通流的多尺度周期特征,但忽略了原始交通序列中噪声和异常值的潜在影响,致使交通流的关键周期特征提取不充分,影响了模型预测精度. 为此,研究者转向频域角度构建模型. Wu等[13 ] 利用傅里叶变换将交通流数据从时域转换至频域,以获得原始交通流的显著周期特征,进一步利用二维卷积方法实现对交通流关键周期特性的充分学习. Wang等[14 ] 针对时序上下文感知语义单元,通过傅里叶变换挖掘不同显著周期模式,结合通道自适应机制学习显著周期模式间的复杂关联,以此提升模型预测的准确性. 在上述频域研究中,傅里叶变换有效提取了交通流的关键周期特征,却忽视了时序数据的全局非线性关系,且难以处理路网时序特性转移问题,导致基于傅里叶变换的模型难以有效捕捉交通流的趋势和瞬时波动特征,影响模型预测性能.传统时域、频域分析方法的局限性使研究者转而采用可同时进行时频域分析的小波变换方法,并将该方法应用于构建交通流预测模型. 在时频域周期特征的建模研究中,赵顗等[15 ] 在利用小波分解获得交通流量趋势和波动分量的基础上,分别使用前馈神经网络提取交通流的趋势和瞬时波动特征,以完成交通流预测任务. Sasal等[16 ] 针对最大重叠离散小波变换后的趋势分量和波动分量构建Transformer模型,以捕捉各分量序列的非线性趋势特征和波动特征. 上述方法针对小波变换分解后的趋势分量和波动分量分别建模,有效学习了交通流序列的趋势特性和瞬时波动特性,解决了时序趋势和波动瞬时特性转移的问题. 然而,该类建模方法在小波变换解耦后,未能充分重视趋势分量的内在周期性及波动分量瞬时变化特点进行特定建模,在捕捉原始序列的多尺度周期性特征与动态波动特征方面存在不足. ...
1
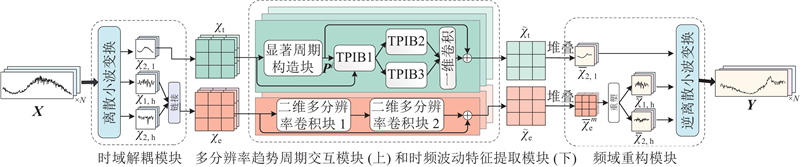
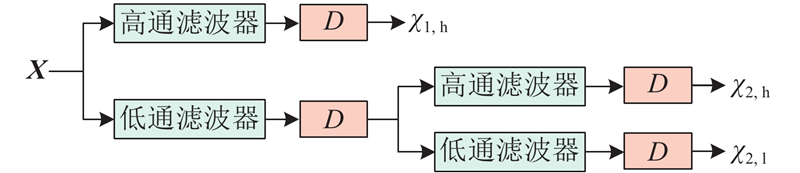
... 如图1 所示,MTPDI由时域解耦模块、MTPI、时频波动特征提取模块及频域重构模块组成. 时域解耦模块通过离散小波变换[17 ] (discrete wavelet transform, DWT)实现交通时序数据的解耦操作,生成具有多分辨率特性的趋势分量和波动分量. MTPI通过显著周期构造块提取趋势分量的显著周期特征,以此表征不易受噪声干扰的显著周期特性. 在此基础上,趋势周期交互块(trend and period interaction block,TPIB)将趋势分量的奇偶子序列分别与显著周期特征融合,实现趋势周期奇偶子序列间的交互操作,达到深度挖掘交通时序数据趋势、周期规律深层非线性特征的目的. 时频波动特征提取模块基于高频波动分量,利用二维多分辨率卷积块实现各区域节点交通流量瞬时变化特性的充分捕获. 频域重构模块基于逆离散小波变换(inverse discrete wavelet transform,IDWT)将趋势分量和波动分量从频域重构至时域,得到模型最终预测结果. ...
1
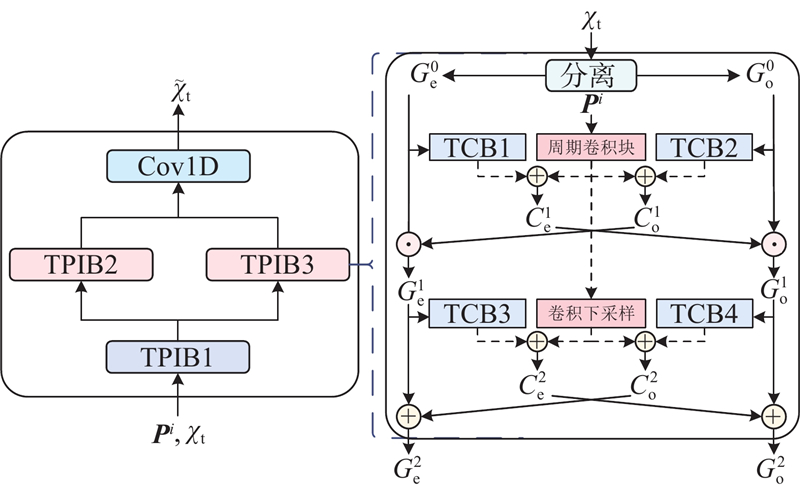
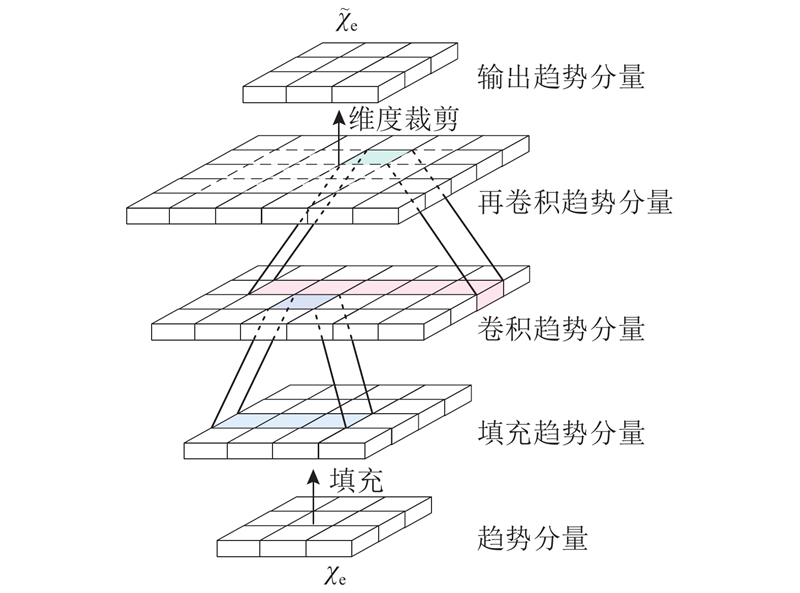
... 周期性作为交通时序数据的关键特性,是影响交通流量精准预测的重要因素. 传统交通流周期特性建模方法侧重于提取时域空间的不同时间尺度周期特征,并且时间粒度越细呈现的序列波动性越强[18 -19 ] ,导致了在时域上准确识别序列趋势性和周期性的局限性. 本研究1)设计MTPI,以具有多分辨率特性的趋势分量作为输入,通过显著周期构造块,将一维趋势分量在频谱域中转换为二维周期矩阵,采用周期卷积操作对二维周期矩阵进行显著周期特征提取. 2)通过下采样的方式将趋势特征分割为含有关键时间依赖信息的趋势奇偶子序列,结合趋势卷积进行趋势特征的高度抽象. 3)趋势奇偶子序列与显著性周期特征融合后,实现周期奇偶子序列间的多分辨率交互. 显著周期构造块的计算式为 ...
1
... 周期性作为交通时序数据的关键特性,是影响交通流量精准预测的重要因素. 传统交通流周期特性建模方法侧重于提取时域空间的不同时间尺度周期特征,并且时间粒度越细呈现的序列波动性越强[18 -19 ] ,导致了在时域上准确识别序列趋势性和周期性的局限性. 本研究1)设计MTPI,以具有多分辨率特性的趋势分量作为输入,通过显著周期构造块,将一维趋势分量在频谱域中转换为二维周期矩阵,采用周期卷积操作对二维周期矩阵进行显著周期特征提取. 2)通过下采样的方式将趋势特征分割为含有关键时间依赖信息的趋势奇偶子序列,结合趋势卷积进行趋势特征的高度抽象. 3)趋势奇偶子序列与显著性周期特征融合后,实现周期奇偶子序列间的多分辨率交互. 显著周期构造块的计算式为 ...
1
... 周期性作为交通时序数据的关键特性,是影响交通流量精准预测的重要因素. 传统交通流周期特性建模方法侧重于提取时域空间的不同时间尺度周期特征,并且时间粒度越细呈现的序列波动性越强[18 -19 ] ,导致了在时域上准确识别序列趋势性和周期性的局限性. 本研究1)设计MTPI,以具有多分辨率特性的趋势分量作为输入,通过显著周期构造块,将一维趋势分量在频谱域中转换为二维周期矩阵,采用周期卷积操作对二维周期矩阵进行显著周期特征提取. 2)通过下采样的方式将趋势特征分割为含有关键时间依赖信息的趋势奇偶子序列,结合趋势卷积进行趋势特征的高度抽象. 3)趋势奇偶子序列与显著性周期特征融合后,实现周期奇偶子序列间的多分辨率交互. 显著周期构造块的计算式为 ...
An algorithm for the machine calculation of complex Fourier series
1
1965
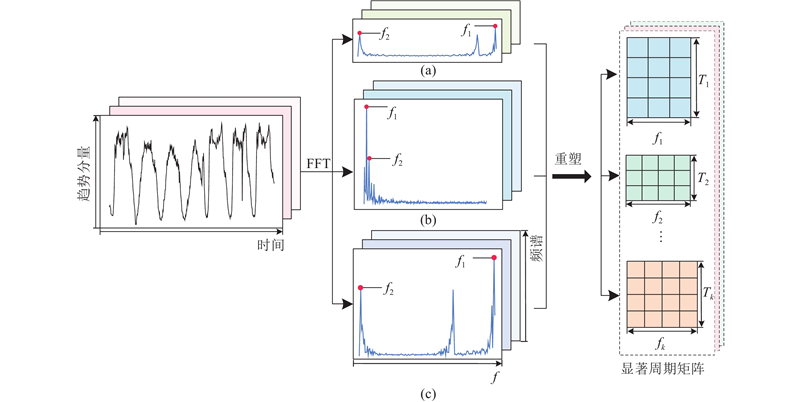
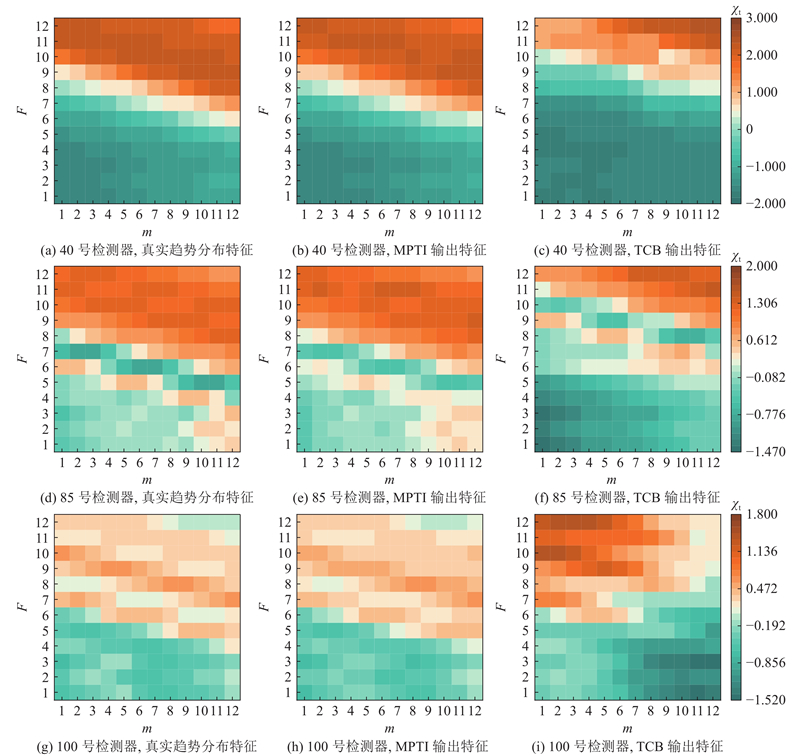
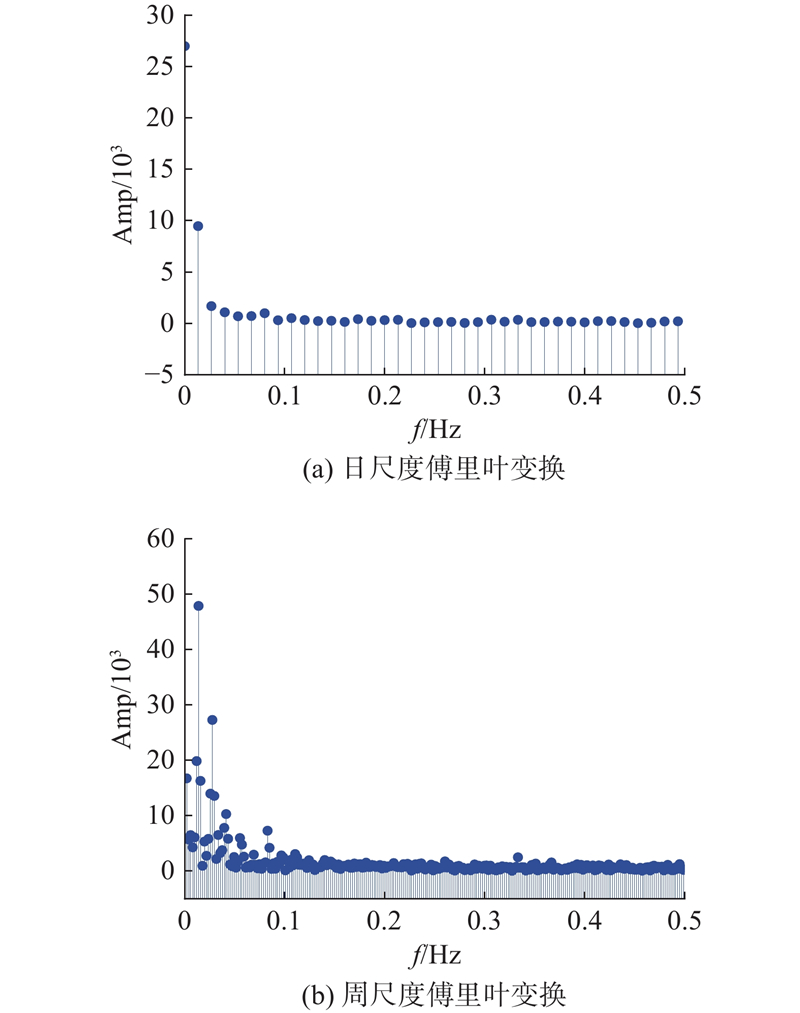
... 式中:$ \text{FFT}(\cdot) $ [20 ] ;$ \text{Amp}(\cdot) $ $ \text{Avg}(\cdot) $ ${\text{To}}{{\text{p}}_k}$ $ B $ $k$ ${f_i}$ $i \in k$ $k \in {{\boldsymbol{Z}}}$ $ T $ ${T_i}$ $ \text{Padding}(\cdot) $ ${T_i}$ $i$ $ {{{\boldsymbol{P}}}^i} \in {{{\bf{R}}}^{{f_i} \times {p_i} \times V}} $ . 如图3 所示,在布设170个检测器的PeMSD8数据集中,以第一个检测器节点7 d交通流数据经小波变换后的趋势分量来计算显著周期矩阵的具体过程. (a)、(b)及(c)为不同时间尺度下的趋势分量进行快速傅里叶变换后的频谱值,之后结合频率与周期的关系得出多个显著周期矩阵$ {{{\boldsymbol{P}}}^i} $ . MTPI采用周期卷积块捕获复杂和多尺度的显著周期特征, ...
1
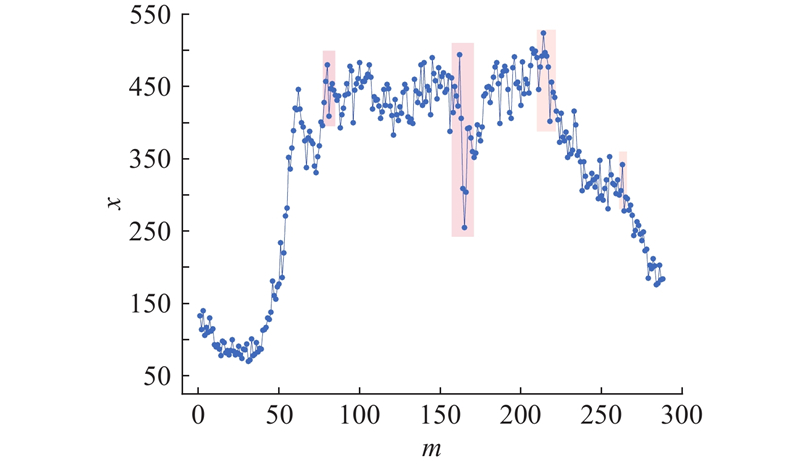
... 受交通事故、天气及道路维护等突发事件影响,原始交通数据频繁出现瞬时波动突变点[21 ] . 如图5 所示,在第150、200个时间片附近存在显著高梯度突变点,呈现交通状况的瞬时波动变化,原因是时序数据中的趋势性、周期性及瞬时波动特性相互交织,致使模型学习复杂瞬时波动特性困难. 原始交通流量数据的高频波动分量具有瞬时性和波动性,其数据局部相关性强且相邻数据点之间存在高度相关性.本研究以突发性高梯度变化的高频波动分量作为时频波动特征提取模块的输入,通过构建二维多分辨率卷积块来充分提取原始交通数据的波动特征,从而与趋势分量经由频域重构模块实现交通流预测. 时频波动特征提取模块由$c$ [22 ] 组成,计算式为 ...
1
... 受交通事故、天气及道路维护等突发事件影响,原始交通数据频繁出现瞬时波动突变点[21 ] . 如图5 所示,在第150、200个时间片附近存在显著高梯度突变点,呈现交通状况的瞬时波动变化,原因是时序数据中的趋势性、周期性及瞬时波动特性相互交织,致使模型学习复杂瞬时波动特性困难. 原始交通流量数据的高频波动分量具有瞬时性和波动性,其数据局部相关性强且相邻数据点之间存在高度相关性.本研究以突发性高梯度变化的高频波动分量作为时频波动特征提取模块的输入,通过构建二维多分辨率卷积块来充分提取原始交通数据的波动特征,从而与趋势分量经由频域重构模块实现交通流预测. 时频波动特征提取模块由$c$ [22 ] 组成,计算式为 ...
基于图卷积神经网络的城市交通态势预测算法
1
2020
... 以Python 3.8.0并基于PyTorch 1.8的开发环境实现交通流预测模型的构建和训练,实验运行均在Linux服务器上. 服务器配置信息为CPU: 16 vCPU Intel(R) Xeon(R) Gold 6430,GPU: RTX 4090(24 GB),操作系统:Ubuntu 18.04. 为了综合评估模型的整体预测性能,以平均绝对误差MAE、均方根误差RMSE以及平均绝对百分误差MAPE作为时序数据预测模型评估指标[23 ] . MAE衡量预测误差的绝对大小,RMSE表示预测误差的平均偏差程度,MAPE提供预测误差的相对百分比. 上述评价指标的数值越低,说明模型预测的效果越好. ...
基于图卷积神经网络的城市交通态势预测算法
1
2020
... 以Python 3.8.0并基于PyTorch 1.8的开发环境实现交通流预测模型的构建和训练,实验运行均在Linux服务器上. 服务器配置信息为CPU: 16 vCPU Intel(R) Xeon(R) Gold 6430,GPU: RTX 4090(24 GB),操作系统:Ubuntu 18.04. 为了综合评估模型的整体预测性能,以平均绝对误差MAE、均方根误差RMSE以及平均绝对百分误差MAPE作为时序数据预测模型评估指标[23 ] . MAE衡量预测误差的绝对大小,RMSE表示预测误差的平均偏差程度,MAPE提供预测误差的相对百分比. 上述评价指标的数值越低,说明模型预测的效果越好. ...
Passenger flow prediction of subway transfer stations based on nonparametric regression model
1
2014
... 选择6种基准线模型:历史平均模型(HA)[24 ] 、支持向量机回归(SVR)、长短期记忆-卷积神经网络(CNN_LSTM)[25 ] 、时间卷积神经网络(TCN)[26 ] 、基于注意力的时空图卷积网络(ASTGCN)[27 ] 、下采样卷积交互网络(SCINet)[28 ] . 将历史时间窗口$ m $ $h $ [29 ] 执行DWT和IDWT操作,分解层数为2. 2)MTPI采用的卷积核数量为3,显著周期构造块的卷积层数为3,卷积核数量依次为(3,5,7),显著周期个数$ k = 2 $
A CNN–LSTM model for gold price time-series forecasting
1
2020
... 选择6种基准线模型:历史平均模型(HA)[24 ] 、支持向量机回归(SVR)、长短期记忆-卷积神经网络(CNN_LSTM)[25 ] 、时间卷积神经网络(TCN)[26 ] 、基于注意力的时空图卷积网络(ASTGCN)[27 ] 、下采样卷积交互网络(SCINet)[28 ] . 将历史时间窗口$ m $ $h $ [29 ] 执行DWT和IDWT操作,分解层数为2. 2)MTPI采用的卷积核数量为3,显著周期构造块的卷积层数为3,卷积核数量依次为(3,5,7),显著周期个数$ k = 2 $
1
... 选择6种基准线模型:历史平均模型(HA)[24 ] 、支持向量机回归(SVR)、长短期记忆-卷积神经网络(CNN_LSTM)[25 ] 、时间卷积神经网络(TCN)[26 ] 、基于注意力的时空图卷积网络(ASTGCN)[27 ] 、下采样卷积交互网络(SCINet)[28 ] . 将历史时间窗口$ m $ $h $ [29 ] 执行DWT和IDWT操作,分解层数为2. 2)MTPI采用的卷积核数量为3,显著周期构造块的卷积层数为3,卷积核数量依次为(3,5,7),显著周期个数$ k = 2 $
Attention based spatial-temporal graph convolutional networks for traffic flow forecasting
1
2019
... 选择6种基准线模型:历史平均模型(HA)[24 ] 、支持向量机回归(SVR)、长短期记忆-卷积神经网络(CNN_LSTM)[25 ] 、时间卷积神经网络(TCN)[26 ] 、基于注意力的时空图卷积网络(ASTGCN)[27 ] 、下采样卷积交互网络(SCINet)[28 ] . 将历史时间窗口$ m $ $h $ [29 ] 执行DWT和IDWT操作,分解层数为2. 2)MTPI采用的卷积核数量为3,显著周期构造块的卷积层数为3,卷积核数量依次为(3,5,7),显著周期个数$ k = 2 $
1
... 选择6种基准线模型:历史平均模型(HA)[24 ] 、支持向量机回归(SVR)、长短期记忆-卷积神经网络(CNN_LSTM)[25 ] 、时间卷积神经网络(TCN)[26 ] 、基于注意力的时空图卷积网络(ASTGCN)[27 ] 、下采样卷积交互网络(SCINet)[28 ] . 将历史时间窗口$ m $ $h $ [29 ] 执行DWT和IDWT操作,分解层数为2. 2)MTPI采用的卷积核数量为3,显著周期构造块的卷积层数为3,卷积核数量依次为(3,5,7),显著周期个数$ k = 2 $
PyWavelets: a Python package for wavelet analysis
1
2019
... 选择6种基准线模型:历史平均模型(HA)[24 ] 、支持向量机回归(SVR)、长短期记忆-卷积神经网络(CNN_LSTM)[25 ] 、时间卷积神经网络(TCN)[26 ] 、基于注意力的时空图卷积网络(ASTGCN)[27 ] 、下采样卷积交互网络(SCINet)[28 ] . 将历史时间窗口$ m $ $h $ [29 ] 执行DWT和IDWT操作,分解层数为2. 2)MTPI采用的卷积核数量为3,显著周期构造块的卷积层数为3,卷积核数量依次为(3,5,7),显著周期个数$ k = 2 $