随着城市化和汽车保有量的增加，交通拥堵问题日益严重^[1]. 短时交通流预测作为智能交通系统（intelligent transportation systems, ITS）的关键技术，能够通过预测未来短时间内的交通流，优化交通管理^[2]. 短时预测面临交通流的时间变异性及气象相关因素的挑战.

传统的短时交通流预测方法如通过网格搜索优化超参数的差分自回归移动平均模型^[3]（autoregressive integrated moving average model, ARIMA）、基于卡尔曼滤波器和随机游走模型误差校准的混合双卡尔曼滤波模型^[4]（hybrid dual Kalman filter, H-KF²）是基于线性和统计的方法，能够进行短时交通流预测，但在处理交通流数据的非线性和复杂性方面存在局限性. 深度学习模型被大量应用于短时交通流预测，Fang等^[5]提出放宽预测误差高斯分布假设至任意分布的长短期记忆网络（long short-term memory, LSTM），Xia等^[6]提出使用残差注意力机制改进的门控循环单元（gated recurrent unit, GRU）. 这些基于循环网络的方法计算复杂度高、训练时间长，在处理长期依赖关系时表现欠佳. Zhang等^[7]的实验表明，时间卷积网络（temporal convolutional network, TCN）凭借因果卷积、扩张卷积和残差连接的设计，在短时交通流预测上相比循环神经网络（recurrent neural networks, RNN）有更高的准确度和效率. 由于交通流的时空特性，图卷积网络^[8]（gated recurrent unit, GCN）成为捕捉交通流时空特征的主流方法，但该方法依赖其他节点的交通流信息，在缺乏图结构数据的情况下，应用受到限制. 深度学习模型有良好的预测性能，该模型通常假设数据有稳定的统计特性，导致时间序列中的高度非线性变化难被有效捕捉. 研究者为此尝试将时间序列分解为更具代表性的成分. Zhao等^[9-11]利用经验模态分解（empirical mode decomposition, EMD）将交通流序列分解为稳定的子序列，并分别将这些子序列输入神经网络进行预测；邴其春等^[12-14]采用变分模态分解（variational mode decomposition, VMD）处理交通流时间序列，并将分解后的结果输入深度学习网络进行建模和预测. EMD在噪声抑制和分解精度方面存在不足，容易导致模态混叠问题；VMD能够提升分解精度，但参数选择复杂，在处理非线性和非平稳数据时效果一般. 此外，逐一分解并分别预测的方式会增加计算量，降低效率. 值得注意的是，时间信息对交通流的影响较大，未能充分利用这一信息会削弱预测效果，特征过多则可能导致模型复杂度增加并引发过拟合.

本研究构建融合自适应噪声完备集合经验模态分解（complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN）和软阈值时间卷积网络（soft thresholding temporal convolutional network, STTCN）的短时交通流预测算法. 1）为了增强模型对非线性特征的捕捉并控制计算复杂度，利用CEEMDAN的高分解精度和噪声抑制能力，将交通流时序分解为高频和低频成分. 2）为了提升模型的时间敏感性，提出时间戳编码方法，充分考虑交通流随时间变化的特征. 3）为了提高模型性能和计算效率，基于最大信息系数（maximal information coefficient, MIC），筛选天气和时间特征，减少冗余. 4）为了提升模型在高噪声环境下的预测精度，改进时间卷积网络，提出软阈值时间卷积网络，在残差块之后和跳跃连接之前加入软阈值过滤机制，通过黏菌优化算法（slime mould algorithm, SMA）优化软阈值参数.

CEEMDAN通过将信号分解为多个本征模态函数（intrinsic mode functions, IMFs），有效分离时间序列中的细节和趋势，使深度学习模型在捕捉交通流历史数据中的高度非线性特征的能力增强. 该过程的原理：在原始信号中引入自适应噪声，通过多次分解和平均提取IMFs，使每个IMFs能够准确反映信号的内在特征^[15]. 在分解过程中，自适应噪声的水平根据数据特性自动调整，以确保分解的精度并有效抑制噪声的影响. CEEMDAN的自适应机制减少了参数设置的需求，突破了传统方法在捕捉非线性特征方面的局限性. 该方法在每次分解时动态调整噪声，减少了模态混叠现象，能够精确地分离不同频率的信号成分.

将CEEMDAN的算法步骤如下. 1）对原始信号$ x(t) $添加白噪声，得到

(1)$ {x_i}(t) = x(t)+{\beta _0}{\omega _i}(t). $

式中：$ {\beta _0} $为用于控制噪声幅度的系数，$ {\omega _i}(t) $为标准白噪声，t为时间索引. 2）使用EMD对$ {x_i}(t) $进行第一组分解，得到残差$ {r_1}(t) $：

(2)$ {I_{{\mathrm{IMF1}}}}(t) = \frac{1}{U}\sum\limits_{i = 1} {{I_{{\mathrm{IMF1}}}}^i} (t)， $

(3)$ {r_1}(t) = x(t) - {I_{{\text{IMF1}}}}(t). $

式中：$ {I_{{\mathrm{IMF1}}}}(t) $为一阶固有模态分量，$ U $为实验次数. 3）使用EMD分解添加自适应噪声后的$ {I_{{\mathrm{IMF1}}}}(t) $，得到二阶模态分量$ {I_{{\mathrm{IMF2}}}}(t) $和残差$ {r_2}(t) $：

(4)$ {r_1}(t)+{\beta _1}{M_1}({\omega _i}(t)) = {I_{{\mathrm{IMF2}}}}(t)+{r_2}(t). $

式中：$ {\beta _1} $为控制二次噪声幅度的系数，$ {M_1} $为一阶固有模态分量算子. 4）重复步骤3），计算$k+1$阶模态分量和残差，直到残差成为单调函数，不能再被进一步提取IMFs. 通过这种分解方法，CEEMDAN能够更加准确地捕捉交通流数据中的复杂非线性特征，为短时交通流预测提供更加精细的信号成分.

在处理交通流数据时，须考虑时间依赖性. 本研究设计如下时间戳编码方法. 1）基础时间分解：将时间数据分解为年、月、日、时、分、秒等基础时间单位. 2）附加规则设计：根据短时交通流预测的需要，设计并加入额外的时间分解规则，如区分是否为工作日，考虑早晚高峰期. 3）特征组合：将基础时间单位与附加规则结合，生成具有丰富时间特征的时间戳编码数据. 通过精细化的时间分解和附加规则设计，预测模型能够更好地理解和预测交通流的变化，增强模型对不同时间场景的适应能力.

在短时交通流预测中，影响因素众多，但并非所有因素都对模型有效. 引入天气和时间特征虽然增加了信息量，但也可能导致模型复杂度增加，引发效率下降和过拟合问题. 因此，特征选择至关重要，其目的是通过筛选出有效的特征，构建最优特征子集，以降低模型复杂度并减少数据冗余.

MIC是基于信息论的统计量，用于量化2个变量之间的关系强度. MIC构建基于互信息（mutual information, MI）概念，能够捕捉变量之间的各种关系形式，包括线性、非线性及更复杂的依赖结构. 通过计算特征与目标变量间的MIC，能够筛选出最相关的特征. MI衡量2个随机变量X与Y的相互依赖性 ^[16]，计算式为

(5)$ {Q_{{\text{MI}}}}(X,Y) = \sum\limits_{x \in X} {\sum\limits_{y \in Y} P } (x,y){{\mathrm{l b}}}\left( {\frac{{P(x,y)}}{{P(x)P(y)}}} \right). $

式中：$ P(x,y) $为X和Y的联合概率分布，$ P(x) $和$ P(y) $分别为X和Y的边际概率分布. 在计算MIC时，对于X和Y的数据集，考虑不同的网格划分来构建二维直方图，并在这些直方图上计算MI. 定义MIC为所有可能划分的归一化互信息的最大值，归一化过程确保了结果不受网格尺寸和划分数量的影响. MIC的计算式^[17]为

(6)$ {Q_{{\text{MIC}}}}(X,Y) = {{\mathrm{max}} _{\mathrm{g}}}\left( {\frac{{{Q_{{\text{MI}}}}(X,Y)}}{{{\mathrm{lb}}\;(\min\; ({n_X},{n_Y}))}}} \right). $

式中：$ {\max _{\mathrm{g}}} $为在所有可能的网格划分中寻找最大值；$ {n_X} $和$ {n_Y} $分别为网格划分中X和Y的箱数；$ {\mathrm{lb}}\;(\min\; ({n_X},{n_Y})) $为归一化因子，用于调整不同划分格局下的互信息值.

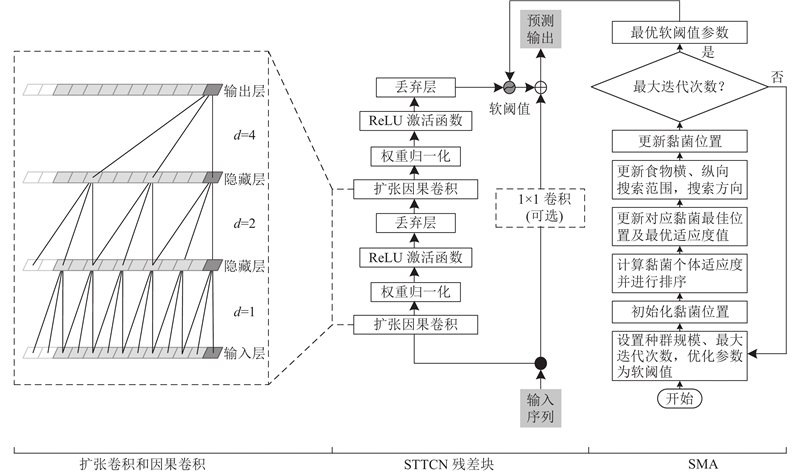
如图1所示为STTCN-SMA的网络结构，主要由TCN、STTCN残差块和SMA共3个部分组成.

TCN是专为时间序列数据设计的神经网络结构，核心特征包括因果卷积和扩张卷积. 因果卷积确保模型只利用当前及过去信息，保持数据的因果性. 扩张卷积通过扩展卷积核的范围，在不增加参数或复杂度的情况下处理更长的时间序列. 这种结构使TCN进行时间序列预测和分析时具有高效又准确的性能. 相比传统的RNN，TCN使用一维卷积层来有效捕获长期时间依赖关系，并行计算、局部依赖性、参数共享和空间局部性等卷积操作使其展现出良好的计算效率和性能. TCN的卷积公式^[18]为

(7)$ F(s) = ({\boldsymbol{X}} * {}_df)(s) = \sum\limits_{i = 0}^{k - 1} {f(i) \cdot } {X_{s - d \cdot i}}. $

式中：$ F(s) $为时间步$ s $对应的卷积输出，$ {\boldsymbol{X}} $为输入序列，$ * {}_d $为膨胀卷积操作符，$ f $为卷积核，$ f(i) $为卷积核在第$ i $位置的权重值，$ {X_{s - d \cdot i}} $为输入序列$ {\boldsymbol{X}} $在时间步$ s - d \cdot i $的值，$ d $为膨胀率. 在卷积操作中，如果滤波器的频谱与噪声信号的频谱重叠较大，噪声会在卷积过程中被放大. 1个TCN残差块通过2次卷积来提取特征，且在实际应用中，多个残差块通常会被堆叠使用，这样的多次卷积操作可能会进一步放大噪声，影响网络的最终输出.

为了降低TCN对噪声的敏感性，本研究设计软阈值机制，将其应用于TCN的残差块之后、跳跃连接之前. 该机制通过设定特定的阈值，将低于阈值的特征值置为0，保留超出阈值的特征值. 这种特征过滤方法可以减少卷积操作中的噪声影响. 软阈值机制未被应用于跳跃连接，主要原因是跳跃连接直接将输入信号传递到网络深层，不涉及卷积操作，不会放大噪声. 保留跳跃连接中的原始信息对网络的学习效果和整体性能至关重要. 在残差块之后、跳跃连接之前引入软阈值机制，可以有效减少卷积过程中引入的噪声，保留关键的原始信息. 与丢弃层（dropout）相比，软阈值更注重提高模型在噪声数据上的表现，处理复杂或杂乱信号的鲁棒性增强.

软阈值参数由SMA自动选择和优化. SMA的设计灵感来源于黄色黏菌（Physarum polycephalum）的行为模式，通过模拟黏菌高效的路径优化行为来优化神经网络的参数. SMA的优化过程分为3个主要步骤：接近食物、包围食物和抓取食物. 1）个体黏菌通过感知环境中的食物浓度梯度，朝着浓度较高的方向移动，逐步接近食物源. 2）一旦黏菌接近食物，它们会在食物附近形成稠密的聚集区域，将食物包围. 3）黏菌通过信息交换和互相影响的方式，进一步调整自身的位置和状态，最终成功抓取食物，完成优化搜索过程. 与其他优化算法（如海洋捕食者算法和樽海鞘优化算法）相比，SMA在精度和稳定性方面性能更优越^[19]. 利用SMA对软阈值参数进行选择和优化，可以较为准确地确定最佳的参数值.

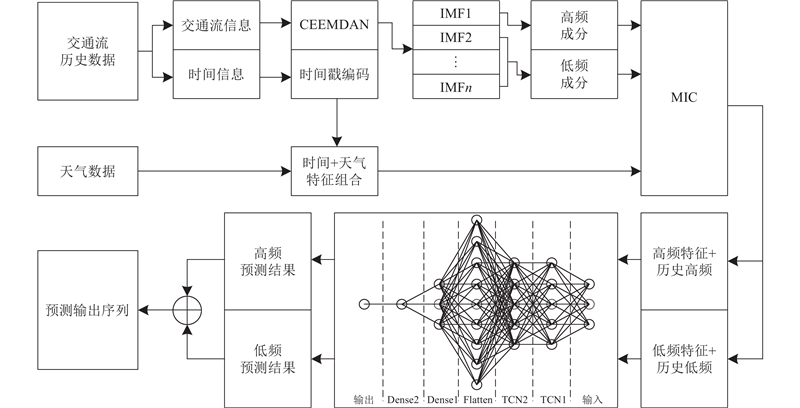
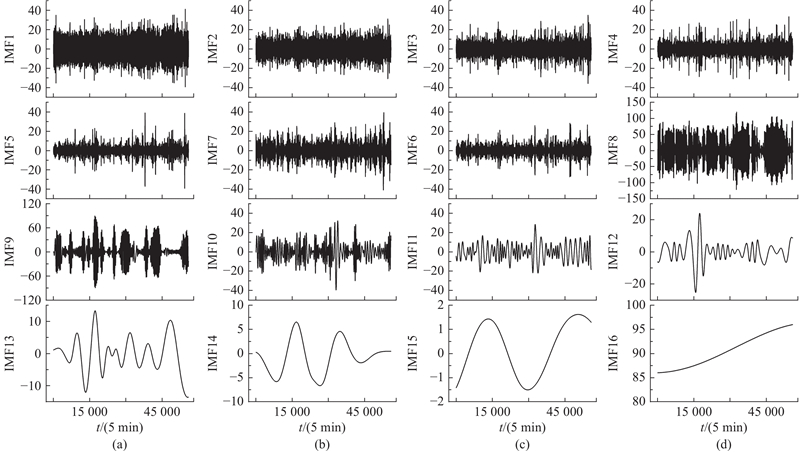
本研究所提算法结构如图2所示，具体过程如下. 1）将交通流历史数据分为交通流信息和时间信息2个部分，为模型训练和特征提取做好准备. 2）使用CEEMDAN分解交通流信息，结果如图3所示. 图中，IMF1为高频成分，其余部分被重构为低频成分. 在特征构建阶段，时间信息经过编码后与天气信息结合，形成综合特征集. 3）利用MIC计算各特征与高、低频成分的相关性，并基于相关性结果，分别选取与这2种成分最相关的2个特征用于模型预测. 在模型预测阶段，选取的特征与历史高、低频成分被输入SMA优化的软阈值时间卷积网络（STTCN-SMA）中进行预测. STTCN由2个时间卷积层（TCN1、TCN2）、1个展开层（Flatten）和2个全连接层（Dense1、Dense2）组成. 4）将高、低频成分的预测结果重构，得到最终的预测结果.

数据来源于真实采集的浙江省某高速路口交通流量，每5 min采集一次数据. 包含55 872条记录，按照6∶2∶2划分为训练集、验证集、测试集. 交通流数据进行最大-最小归一化处理，计算式^[20]为

(8)$ x' = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}. $

式中：$ x $为待归一化的数据，$ {x_{\max }} $、$ {x_{\min }} $分别为待归一化数据的最大值和最小值.

设计未分解的SVR、RNN、GRU、LSTM、TCN，分解的EMD-TCN（E-T）、VMD-TCN（V-T）、CEEMDAN-TCN（C-T）、CEEMDAN-MIC-TCN（C-M-T）、CEEMDAN-MIC-STTCN-GA（C-M-S-G）、CEEMDAN-MIC-STTCN-BOA（C-M-S-B）和CEEMDAN-MIC-STTCN-SMA（C-M-S-S）模型. SVR模型配置包括径向基函数核，正则化参数C=0.01，核函数参数γ=0.4，$\varepsilon $=0. RNN、GRU和LSTM均设置2层隐藏层，每层8个单元，使用ReLU激活函数，输出层单元采用线性激活函数，批大小为8，训练周期为100. TCN模型为2层结构，每层8个滤波器和大小为3的卷积核，扩张率逐步递增，依次为 1、2、4、8. 所有的分解模型在高低频处理上参数设置一致，包括64个滤波器和大小为3的卷积核，扩张率均为[1,4,8]，在C-M-S-G、C-M-S-B和C-M-S-S中，软阈值化参数分别通过遗传算法（genetic algorithm, GA）、贝叶斯优化算法（Bayesian optimization algorithm, BOA）和SMA优化，批大小为128，周期为100. 均使用1 h的数据来预测5 min的数据，输入步长为12，预测步长为1，使用均方误差MSE、对称平均绝对百分比误差SMAPE、绝对偏差AD作为评价指标，计算式分别为

(9)$ {{{\text{MSE}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({{\hat y}_i} - {y_i})}^2}} ， $

(10)$ {{{\text{SMAPE}}}} = \frac{{100{\text{%}} }}{n}\sum\limits_{i = 1}^n {\frac{{|{{\hat y}_i} - {y_i}|}}{{(|{{\hat y}_i}|+|{y_i}|)/2}}} ， $

(11)$ {{{\text{AD}}}} = \frac{1}{{\displaystyle\sum\nolimits_{i = 1}^n {{y_i}} }} \cdot \sum\limits_{i = 1}^n {|{{\hat y}_i} - {y_i}|} . $

式中：$ {y_i} $为实际值，$ {\hat y_i} $为预测值，$n$为样本数量.

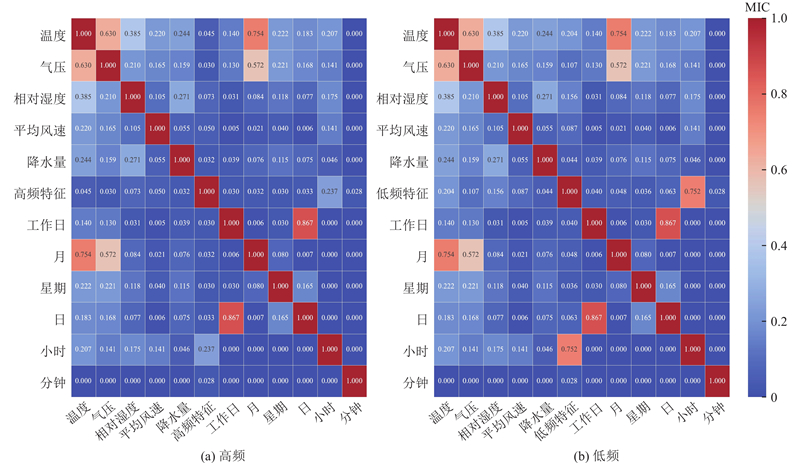
如图4所示，分析时间和天气特征与高、低频交通流之间的最大信息系数.由图可知，最相关特征分别为高频交通流中的小时和相对湿度，低频交通流中的小时和温度. 小时特征在高、低频流量中均显示出较高的相关性，MIC分别为0.237和0.752，表明时间变化对交通流具有重要影响. 在高频流量中，相对湿度的MIC为0.073；在低频流量中，温度的MIC为0.204，虽然与交通流的相关性不如小时，但也是值得关注的特征. 在后续的预测模型中，将为高频流量添加小时和相对湿度作为特征，为低频流量添加小时和温度作为特征，以进一步提高预测的准确性.

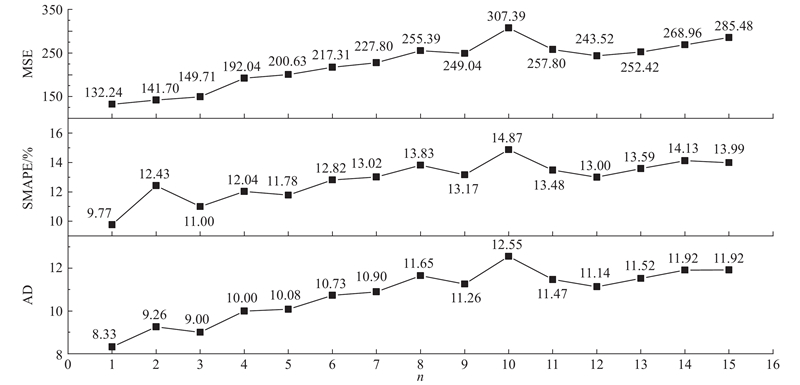
根据分解实验结果，选择只将IMF1归类为高频成分，将其他的IMFs合并为低频成分. 实验使用C-T模型，结果如图5所示，n为高频IMFs个数. 当仅将IMF1归类为高频成分时，得到最低的MSE（132.24，以每5分钟的车辆数计算，单位为车辆数的平方）、SMAPE（9.77%）以及AD（8.33，以每5分钟的车辆数计算，单位为车辆数）. 随着高频成分中IMFs的数量增加，误差逐渐增加，尤其是当高频成分达到10个或更多IMFs时，误差明显增大. 出现这种现象的原因：高频IMFs包含大量瞬时噪声和快速变化的细节，合并这些IMFs会抵消成分细节，导致预测精度下降. 若将每个IMFs分别输入神经网络进行预测会因IMFs数量众多导致计算量过大，不适合实际应用. 本研究在后续模型中将采用高、低频分类方法.

如表1所示为不同时序预测模型的评价指标. 相比SVR、GRU、LSTM、RNN，TCN在MSE、SMAPE和AD上分别平均降低了约4.44%、4.18%和4.14%. TCN使用一维卷积网络捕捉时间序列中的依赖关系，在处理长时间依赖问题时表现更为出色. 虽然RNN、LSTM和GRU也能处理长时间依赖，但在这种应用中，它们可能会因梯度消失或梯度爆炸的问题，难以有效地学习远程依赖关系. 相比E-T、V-T，C-T在MSE、SMAPE和AD上分别平均下降了约29.45%、16.25%和14.91%. 与其他分解方法相比，CEEMDAN通过逐步添加噪声的独特方式，更精确地分解了复杂的非平稳信号. 与EMD相比，CEEMDAN通过引入白噪声，有效解决了EMD中常见的模态混叠问题，使信号的分解更加稳定和细致. 与VMD相比，CEEMDAN的噪声添加机制更擅长捕捉信号中的瞬时变化和细节；尤其是在只将IMF1归类为高频成分时，CEEMDAN能更准确地分离出信号中的细节和噪声. 这种精准的分解不仅提升了模型的预测准确性，还使模型能够敏锐地捕捉数据中的微妙变化，为交通流时序数据的分析提供更可靠的支持. CEEMDAN的应用增强预测结果的精度，在处理复杂信号时更具优势. 相比C-M-S-G、C-M-S-B，C-M-S-S在MSE、SMAPE和AD上分别平均降低了约10.02%、2.91%和4.88%. 作为更先进的优化方法，SMA通过模拟黏菌的智能觅食行为，能够更准确地获取时间卷积网络中的软阈值参数. SMA的核心机制是模拟黏菌在复杂环境中寻找最佳食物源的过程，这使得该算法在高维非线性优化问题上表现出色. 与传统的GA和BOA相比，SMA能够更有效地探索全局最优解，避免陷入局部最优，使模型的预测准确度得到提升. 总的来说，本研究提出的模型（C-M-S-S）具有最高的预测精度，相较于其他模型，MSE、MAPE和AD分别平均下降了约54.97%、30.07%和34.39%.

如图6所示，设置TCN、C-T和C-M-T共3种模型来验证各个模块的有效性，n_v为车辆数. 在表1中，相比TCN，C-T的MSE、SMAPE和AD分别降低了约49.38%、26.56%和27.31%，表明CEEMDAN在提升预测精度方面具有一定的效果. 观察图6（b）和图6（d）可以得到，分解后的模型在预测波动和趋势变化时表现得更加准确. C-M-T模型通过新增时间特征和特征筛选环节，MSE、SMAPE和AD相较于C-T模型分别降低了9.33%、−7.98%和3.24%. SMAPE略有增加. 原因是SMAPE更关注误差相对于真实值的百分比，对较小的真实值更敏感. 对比图6（d）和图6（f）可以看出，C-M-T模型在预测波峰和波谷时更接近真实值，表明通过引入时间特征并进行合理的特征筛选，有助于提高TCN的预测精度和模型的泛化能力. 对比C-M-S-S与C-M-T模型，发现通过在TCN中引入软阈值机制并利用SMA优化软阈值参数后，MSE、SMAPE和AD分别降低了约19.49%、14.60%和11.66%. 由图6（f）和（h）可以看出，所提模型在预测曲线的精度和细节捕捉能力方面有了进一步提升.

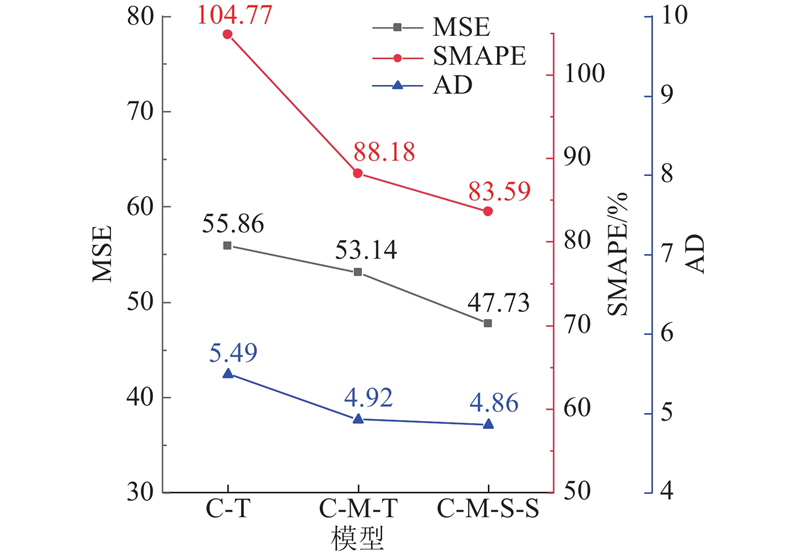
结合如表2所示的优化后软阈值和如图7所示不同分解模型的高频评价指标进行对比分析，表中$\eta _1 $、$\eta _2 $分别为第一、二层TCN的软阈值. 由表可知，软阈值机制在高频成分模型的第一层TCN中起作用，$\eta _1= $0.139. 由于高频成分通常含有大量噪声，通过设定软阈值，能够有效滤除噪声，提升信号处理的精度. 由图可以看出，所提模型相较于其他分解模型，MSE、SMAPE和AD平均下降了约6.21%、6.68%和3.31%. 结果表明，软阈值机制在高噪声数据建模中发挥了作用，提高了模型的预测能力.

本研究提出融合自适应噪声完备集合经验模态分解和软阈值时间卷积网络的短时交通流预测算法，通过实际数据验证算法的有效性. 研究表明，CEEMDAN分解结合时间戳编码以及MIC特征筛选，有效提高了预测精度，软阈值机制增强了算法对噪声的处理能力. 在多项实验中，所提算法在3个性能评价指标上的表现均优于其他算法，展现了该算法在短时交通流预测中的优势. 未来将提升算法在中长期交通流预测中的准确性，进一步优化算法在长期趋势和周期性变化中的捕捉能力. 本研究所提预测算法有望集成至智能交通系统中，实现实时预测与动态管理的无缝衔接，助力提升交通管理的智能化与效率.