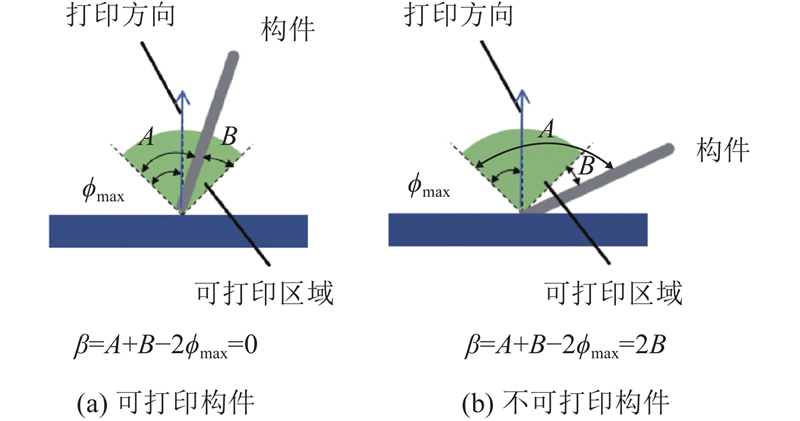
3D打印技术在建筑、航空航天和生物医学等领域得到广泛应用[1-3]. 传统3D打印采用三轴设备,在3D打印过程中须添加支撑结构,不仅会造成材料的浪费,还会增加支撑结构拆除的难度. 在金属3D打印中,拆除支撑结构还可能会损坏构件[4]. 与三轴方法相比,多轴3D打印引入旋转打印平台,在打印过程中打印方向可动态调整,制造灵活性更高,有助于缓解甚至解决悬垂效应带来的支撑问题. 多轴3D打印领域的研究主要集中在具有5个或6个自由度(DOF)的打印系统上[5]. Li等[6]提出基于向量场的曲面层切片和打印路径规划方法,用来消除支撑结构、防止碰撞并提高打印构件的机械性能. Dai等[7]采用两阶段分解方法克服多轴3D打印中的悬垂问题:将零件分解为曲面打印层后,进一步分解为曲线打印路径. Xu等[8-9]也提出组件分解打印方法,将给定的结构分解为多个单独的部分,通过为各部分指定不同的打印方向来避免悬垂问题,但该方法未考虑打印碰撞问题. 上述研究主要关注打印路径规划以及减少使用支撑结构和打印时间等方面[10-11],研究多针对已知形状的结构,多轴3D打印与结构设计优化相结合的研究鲜见.
结构优化领域的理论基础可追溯至Michell的开创性工作[12]. 该领域研究主要分为离散桁架优化与连续体拓扑优化. 对于连续体拓扑优化方法,Bendsøe等[13]提出通过计算在均质同性材料中引入周期性分布小孔的极小值来构造各向异性材料在空间中的最优分布,推动了连续体拓扑优化方法的发展. 后来逐渐发展出各种优化分支,如双向渐进结构优化法(bidirectional evolutionary structural optimization, BESO)[14]、水平集法[15]、移动可变形组件法(moving morphable component, MMC)[16-17]和可移动变形孔洞法(moving morphable voids, MMVs)[18-19]等连续体拓扑优化方法. 对于离散桁架优化方法,Dorn[20]提出基结构法并对桁架结构进行优化. Gilbert等[21]在基结构法的基础上提出的构件添加法,显著降低了计算成本且得到最优解. He等[22]引入几何优化方法进一步简化了结构布局. 在实际应用中,连续体优化方法更适于处理高体积比(优化结构与设计域的比值)问题,离散桁架优化更适于处理低体积比问题. 考虑到悬垂效应在低体积比问题中更为明显[23],本研究主要关注离散桁架优化方法.
在连续体拓扑优化中,基于密度解决悬垂问题是常用的方法. 根据附近元素的存在状况来评估单个元素的可打印性,Gaynor等[24]提出楔形过滤器,用于设计由常规网格组成的自支撑结构,Garaigordobil等[25]使用边缘检测方法识别和消除优化结构中的悬垂特征. 还有研究者采用前沿传播技术[26-27]和水平集方法[28-29]来解决悬垂问题. 在离散桁架优化领域,He等[30]在传统布局和几何桁架优化方法中添加硬性角度约束,实现了桁架结构自支撑. 林晓阳等[31-32]利用结构布局、几何优化算法,考虑力学性能与3D打印可制造型的优化方法,生成三维桁架自支撑优化结构,开展了实际模型打印测试. 上述方法虽可有效得到自支撑结构,但主要面向三轴3D打印,考虑悬垂约束还会明显增加优化结构的体积. 在结构优化与多轴3D打印相结合方面,Lu等[33]将设计域分解为多个分区,再利用优化方法确定每个分区的局部打印方向. 该方法适用于二维桁架结构,在解决三维问题时会出现数值计算困难的情况. 本研究将问题扩展到三维桁架结构,针对多轴3D打印中三维自支撑桁架结构优化存在数值稳定性差、可打印性指标低的问题,提出基于多轴3D打印的两步优化方法.
1. 数值方法
为了克服多轴3D打印中的悬垂效应,优化生成自支撑结构. 从传统的布局优化中获得下界解,再考虑悬垂约束,步骤如下. 1)识别结构的打印曲面:使用新的优化方法来识别给定结构的打印曲面,使结构可打印比例(无悬垂体积/总体积)最大化. 步骤1)中结构保持不变,无法保证结构被完全打印. 当结构可打印比例低于设定阈值时,执行步骤2). 2)结构和打印曲面整体优化:以步骤1)的结果为起点,同时对结构和打印曲面进行优化. 基于几何优化的问题,进一步提高结构的可打印比率和结构性能.
1.1. 传统的布局和几何优化方法
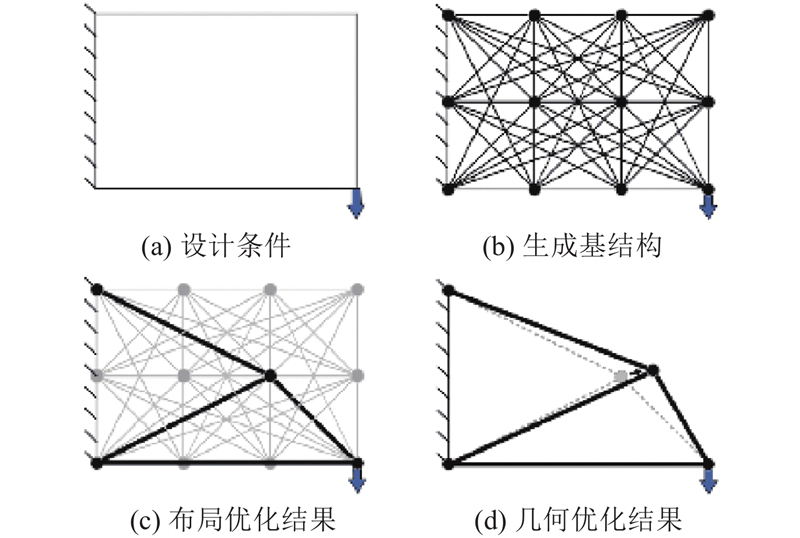
通过布局优化方法,得到特定设计条件(如设计域、载荷和边界约束)下高效的结构布局. 如图1所示,该过程分3步:指定设计域、载荷和边界条件,生成节点和潜在构件以形成基结构,通过求解优化问题来确定最佳布局. 结构布局优化数学模型为
图 1
式中:
式中:
1.2. 二维问题中的打印方向识别方法
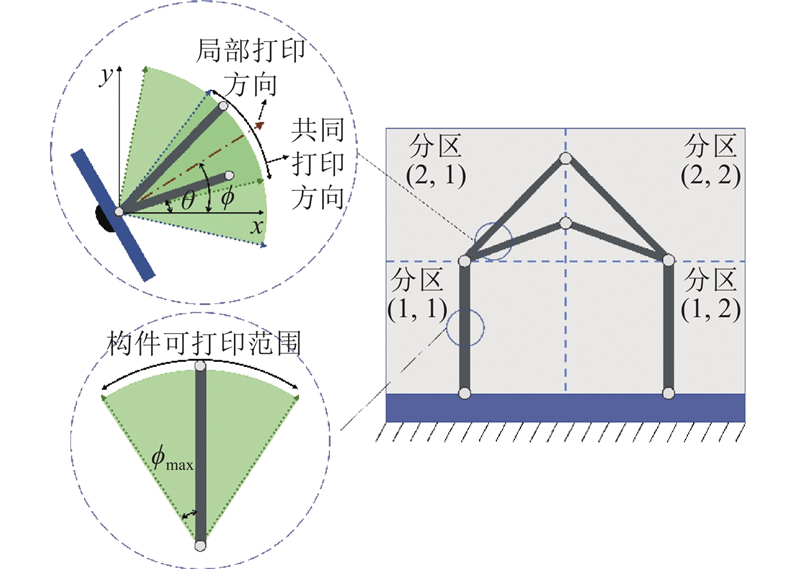
在二维问题中,将设计域划分为多个矩形分区,假定每个分区对应1个局部打印方向;根据分区内部构件方向确定相应分区的局部打印方向,识别原理如图2所示. 在分区(2,1)中,每根构件都有各自的可打印范围. 当不同构件的可打印范围存在重叠区域时,这些构件能够沿着重叠区域的共同打印方向顺利打印,定义重叠区域为共同打印范围. 若多根构件不存在共同打印范围,则选择可使结构无法打印体积最小化的方向作为最优局部打印方向. 打印方向识别方法的数学模型为
图 2
式中:
1.3. 三维问题中的打印方向识别方法
1.3.1. 设计域分割
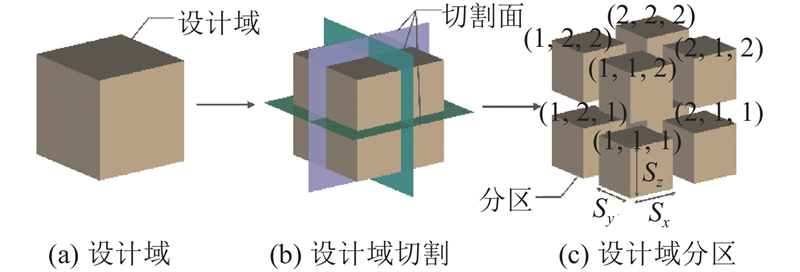
与2D方法类似,三维问题中用切割面将设计域分割成若干立方体分区,如图3所示.
图 3
1.3.2. 局部打印方向的表示
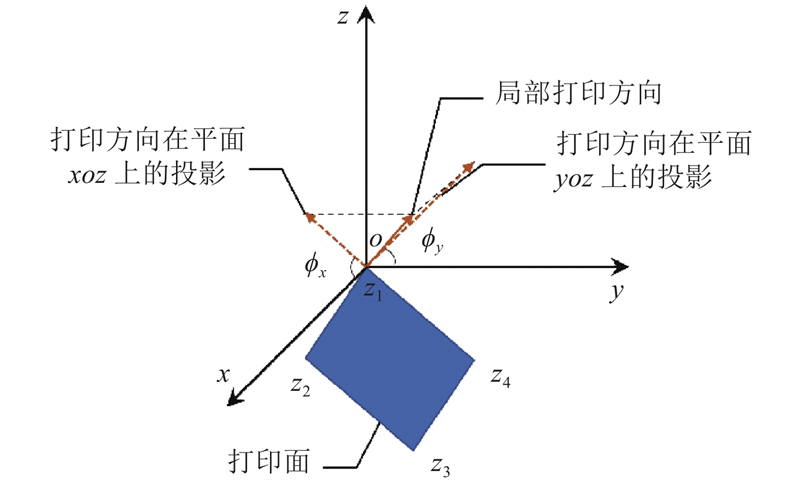
二维问题中的悬垂违反值利用局部打印方向和构件方向计算. 简单起见,在三维问题中,将局部打印方向和构件方向投影到2个相互垂直的平面
图 4
式中:
图 5
1.3.3. 打印面连续约束
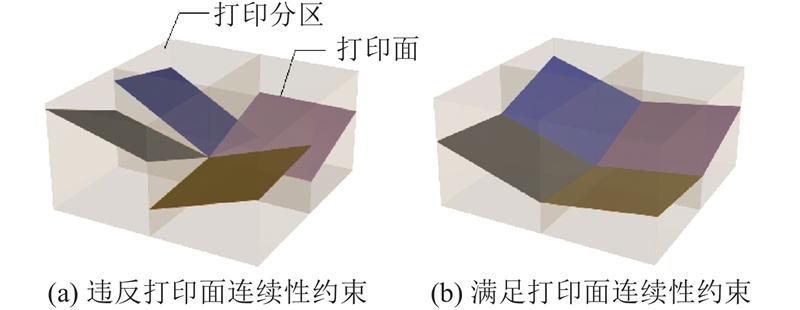
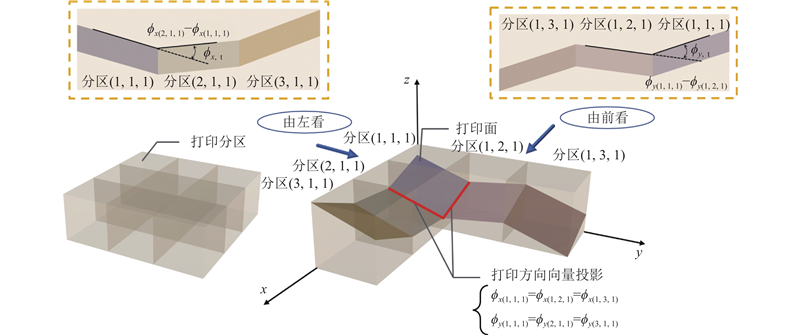
与二维问题不同,在三维问题中,相邻的局部打印面须完全连接,以确保整体打印面的连续性,如图6所示. 通过约束条件2来限制局部打印方向:
图 6
式中:
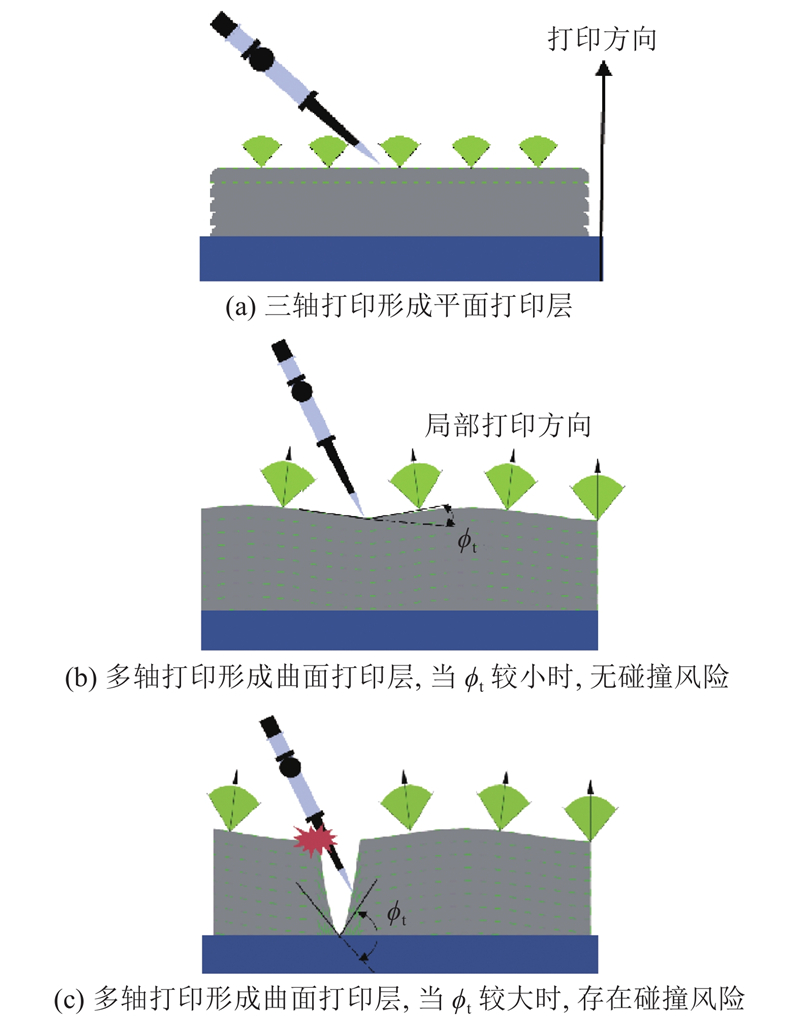
1.3.4. 打印碰撞问题
曲面若有较大旋转角可能会导致打印喷嘴与已打印的部件发生碰撞,为此设置如图7所示的约束条件3,限制相邻分区之间的投影打印旋转角:
图 7
1.3.5. 打印面优化公式
将3D打印面的优化问题表示为
式中:
1.4. 整体优化方法
优化结构是确定的,由式(7)得到的打印面不能保证该结构完全可打印. 为了减少悬垂构件,进行优化问题整合并调整结构和打印面:结合式(2)和式(7)并调整1)由因子
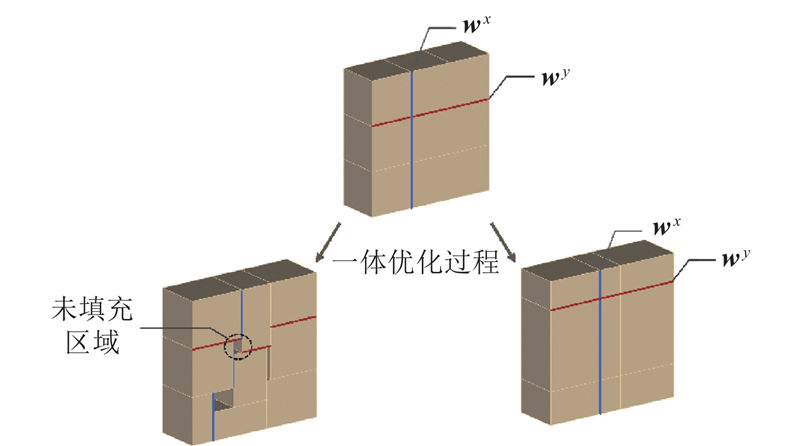
2)每根构件的悬垂违反值根据其最初的分区计算得到,因此添加节点坐标以限制每个节点在设计域最初的分区内移动. 3)将分区边界视为额外的变量,增加整体问题的设计自由度. 如图8所示,在优化过程中,未填充区域会导致规划打印路径时无法完全填充打印层,因此同一行、列排列的分区须共用边界位置变量
图 8
图 8 同层中分区边界位置变量对优化过程的影响
Fig.8 Influence of boundary position variables of partitions in same layer on optimization process
式中:
式(9)是非线性非凸问题,初始解会对最终优化结果的质量造成显著影响[36]. 本研究提出迭代的半整体方法,得到悬垂构件更少的式(9)初始解,提高最终优化结果的质量. 该方法从求解式(7)得到的弯曲打印面开始. 在已知打印面的情况下,由式(4)计算基结构和潜在构件的投影悬垂违反值
1.5. 优化方法流程
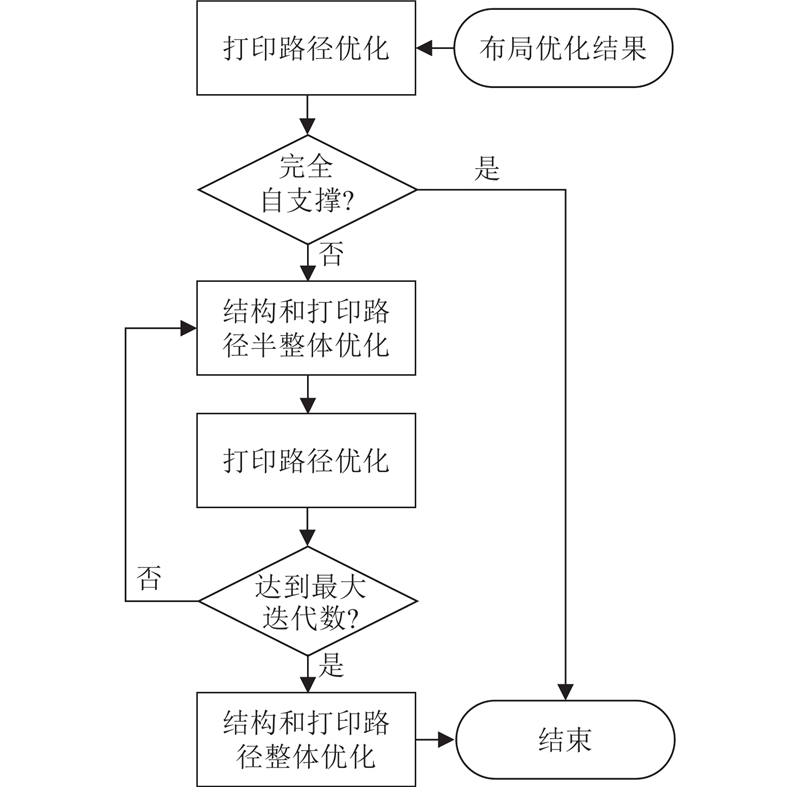
本研究提出的优化方案综合了结构设计、打印路径规划和迭代改进3个关键环节,不仅使打印出的结构满足力学性能要求,还能够在多轴3D打印过程中实现自支撑,减少支撑材料的使用. 如图9所示为所提方法的流程图. 1)利用布局优化方法对结构进行初步设计,确定构件的位置和尺寸,以满足设计域、载荷和边界条件的要求. 2)对于非自支撑部分,由式(7)进一步优化打印路径,提高结构的可打印性. 引入迭代的半整体优化方法,在已知打印面的基础上,重新计算基结构和潜在构件的投影悬垂违反值,据此调整结构布局. 4)再次运用式(7)细化打印面,实现更优的打印效果. 5)结合结构优化和打印路径规划的结果,进行整体优化,确保最终的结构设计在力学性能和打印可行性之间达到最佳平衡. 优化流程的设计旨在通过逐步迭代和多阶段优化,实现结构设计的最优化和打印路径的高效规划.
图 9
图 9 基于多轴3D打印的自支撑桁架结构优化方法的流程图
Fig.9 Flow chart of optimization method for self-supporting truss structures based on multi-axis 3D printing
2. 多轴3D打印
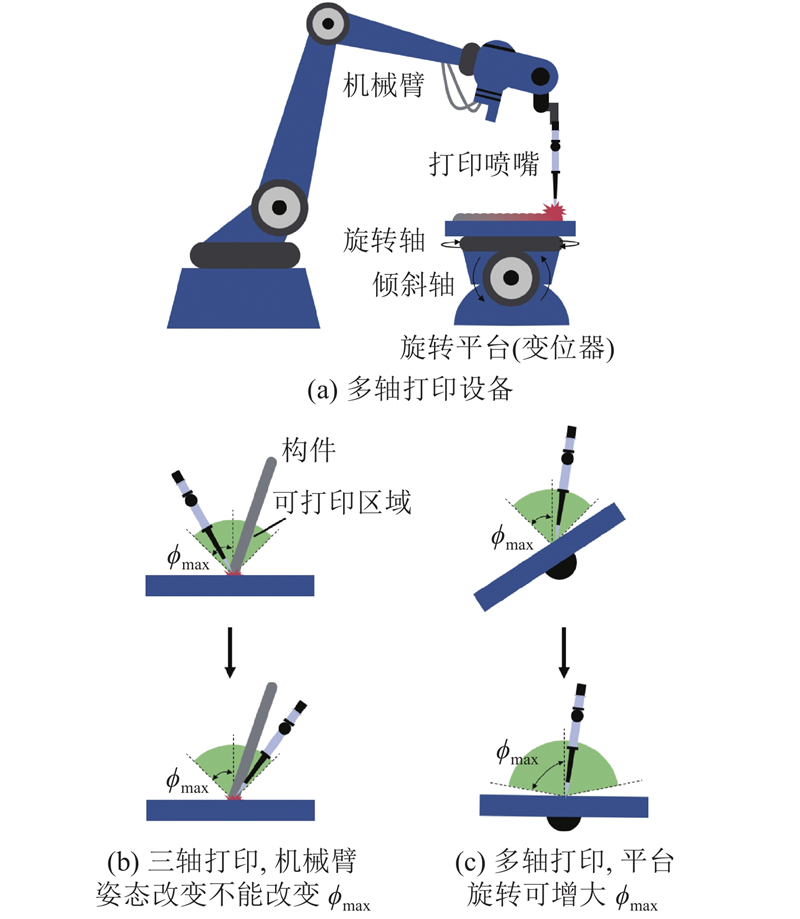
如图10所示,多轴3D打印机由机械臂以及安装在机械臂上的打印喷嘴和旋转打印平台组成. 打印平台可在打印过程中旋转、倾斜至不同角度,从而实现曲面打印. 多轴3D打印增加了局部打印位置上的最大悬垂角,有利于应对悬垂问题.
图 10
图 11
3. 数值算例
引入结构可打印比例(无悬垂体积与总体积的比值),量化结构在不依赖外部支撑条件下的成功打印程度. 总悬垂违反度
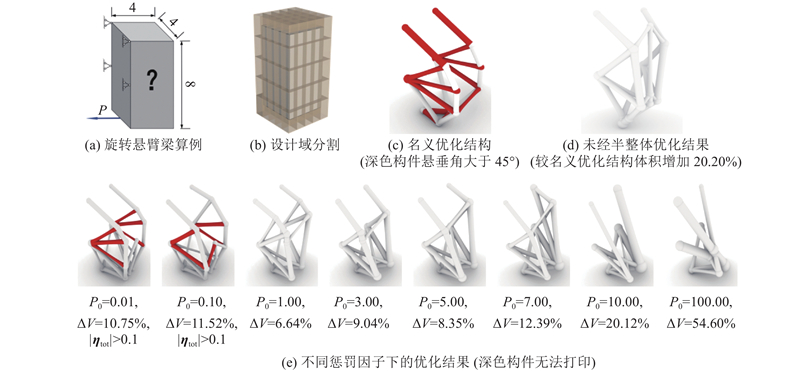
3.1. 惩罚因子对优化结果的影响
惩罚因子
图 12
图 12 旋转悬臂梁算例优化结果
Fig.12 Optimization results of rotating cantilever arithmetic example
如图13所示为当
图 13
3.2. 最大悬垂角对优化结果的影响
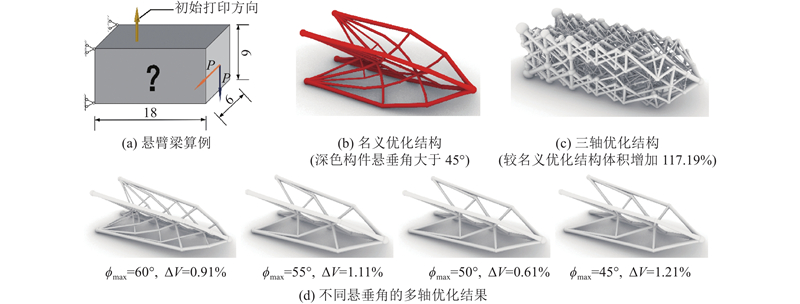
如图14所示,选择悬臂梁算例分析最大悬垂角对优化结果的影响,设置
图 14
3.3. 分区尺寸对优化结果的影响
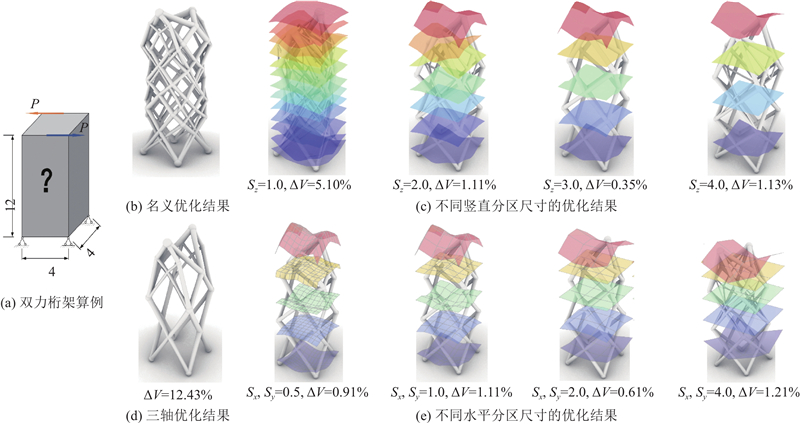
如图15所示,分2组研究分区尺寸对优化结果的影响,设置
图 15
图 15 双力桁架算例优化结果
Fig.15 Optimization results of two-load truss arithmetic example
4. 多轴打印测试
使用如图16所示的多轴3D打印系统进行优化结构的打印测试. 在多轴3D打印系统中,送丝和加热系统集成于KUKA机器人(KR 10 R1100-2),熔融沉积成型(fused deposition modeling, FDM)打印喷头挤出线材,旋转打印平台提供2个额外的自由度(旋转和倾斜). 倾斜轴旋转范围为±120°,底座平台半径为200 mm,打印平台表面至倾斜中心轴的距离为170 mm. 在打印过程中,通过KUKA smartPAD控制多轴打印系统. 打印模型的设计域尺寸为60 mm×60 mm×120 mm. PLA打印线材直径为1.75 mm;喷嘴直径为0.6 mm;喷嘴温度设定为210 ℃;温床温度为50 ℃;层高为0.4 mm,打印速度为30 mm/s.
图 16
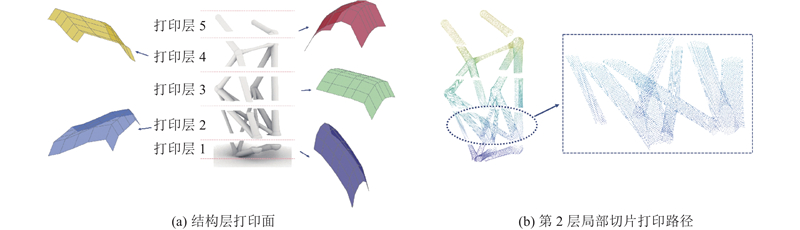
以图12的旋转悬臂梁为例,如图17所示,打印路径的生成包括3个步骤. 1)在Rhino软件[37]中,基于优化结构[38]中的节点坐标和构件横截面积生成STL格式的结构模型;2)使用获得的打印面对模型进行切片,生成打印路径轮廓层;3)使用锯齿形图案[39]填充每层的内部打印路径,设置间距为0.4 mm,填充内缩长度为0.1 mm. 使用不同打印方向,打印过程及最终模型如图18所示. 优化打印面使打印过程无需支撑且不发生碰撞,但打印结构表面存在轻微的缺陷,如图18(e)中标记的C构件处. 缺陷产生的原因:1)同层打印方向的突然变化导致表出现刨削现象[6];2)多轴打印系统在多轴运动时存在恒定的机器误差,在90°倾斜角度下测量约为1 mm. 问题1)可以通过调整打印路径实现相邻局部打印方向的平滑过渡来解决[40];问题2)可以通过测量不同倾斜角度的运动误差,并在打印路径的生成过程中考虑误差校正解决. 虽然存在误差,但是所提方法成功克服了悬垂效应. 悬垂效应最明显的结构构件是图中标记的构件A和B,其悬垂角为71°. 为此,打印该构件时,旋转平台的倾斜角调整为59.3°. 2根构件在没有任何支撑结构的情况下被成功打印,体现了方法的有效性.
图 17
图 18
5. 结 语
针对多轴3D打印,本研究提出考虑悬垂约束的3D桁架结构优化方法,采用两步优化方法得到优化结构及其弯曲打印面: 第一步识别得到优化结构的理想打印面,第二步采用整体优化同时优化结构及其打印面,提高结构性能并最大限度减少悬垂构件. 考虑整体问题的非线性和非凸性质,提出半整体方法提高了第二步初始解的质量. 选取数值算例进行优化分析,使用多轴3D打印系统对经典算例进行打印验证,证明所提方法的有效性. 1)考虑悬垂约束时,与基于三轴打印的方法相比,基于多轴打印的方法的灵活性更强. 2)分区尺寸的选择会直接影响优化结果. 当分区边界与节点紧密对齐时,可以通过迭代过程实现优化结果的改进,增强整体优化效果. 3)在打印验证过程中,局部构打印方向的变化导致轻微的表面缺陷,但悬垂效应被成功克服. 所提方法可以生成自支撑结构,带来的材料体积增加可忽略不计,证明了多轴3D打印桁架结构的设计和制造方面的优势及可行性.当前研究在突变曲率区域表面质量控制及多材料结构扩展方面仍存在局限. 后续将重点开展打印路径光顺优化算法开发,并探索工艺参数动态适配机制,以拓展该方法在复杂曲面构件中的工程应用.
参考文献
Multi-material additive manufacturing in architecture and construction: a review
[J].DOI:10.1016/j.jobe.2021.103603 [本文引用: 1]
A review on metal additive manufacturing for intricately shaped aerospace components
[J].DOI:10.1016/j.cirpj.2022.07.005
Additive manufacturing processes in medical applications
[J].DOI:10.3390/ma14010191 [本文引用: 1]
Research on support-free WAAM based on surface/interior separation and surface segmentation
[J].DOI:10.1016/j.jmatprotec.2021.117240 [本文引用: 1]
A review of multiple degrees of freedom for additive manufacturing machines
[J].DOI:10.1080/0951192X.2020.1858510 [本文引用: 1]
Vector field-based curved layer slicing and path planning for multi-axis printing
[J].DOI:10.1016/j.rcim.2022.102362 [本文引用: 2]
Support-free volume printing by multi-axis motion
[J].
Curved layer based process planning for multi-axis volume printing of freeform parts
[J].DOI:10.1016/j.cad.2019.05.007 [本文引用: 2]
Generation of efficient iso-planar printing path for multi-axis FDM printing
[J].DOI:10.3390/jmmp5020059 [本文引用: 1]
FDM五轴3D打印支撑消减算法研究
[J].
Study on elimination-reduction algorithm of support in five-axis 3D printing
[J].
The limits of economy of material in frame-structures
[J].
Generating optimal topologies in structural design using a homogenization method
[J].DOI:10.1016/0045-7825(88)90086-2 [本文引用: 1]
Computational efficiency and validation of bi-directional evolutionary structural optimisation
[J].DOI:10.1016/S0045-7825(99)00309-6 [本文引用: 1]
Structural optimization using sensitivity analysis and a level-set method
[J].DOI:10.1016/j.jcp.2003.09.032 [本文引用: 1]
A new topology optimization approach based on moving morphable components (MMC) and the ersatz material model
[J].DOI:10.1007/s00158-015-1372-3 [本文引用: 1]
Lagrangian description based topology optimization: a revival of shape optimization
[J].DOI:10.1115/1.4032432 [本文引用: 1]
Structural topology optimization through explicit boundary evolution
[J].
Explicit three dimensional topology optimization via moving morphable void (MMV) approach
[J].DOI:10.1016/j.cma.2017.05.002 [本文引用: 1]
Automatic design of optimal structures
[J].
Layout optimization of large-scale pin-jointed frames
[J].DOI:10.1108/02644400310503017 [本文引用: 2]
Rationalization of trusses generated via layout optimization
[J].DOI:10.1007/s00158-015-1260-x [本文引用: 3]
On preventing the dripping effect of overhang constraints in topology optimization for additive manufacturing
[J].DOI:10.1007/s00158-021-03077-w [本文引用: 1]
Topology optimization considering overhang constraints: eliminating sacrificial support material in additive manufacturing through design
[J].DOI:10.1007/s00158-016-1551-x [本文引用: 1]
A new overhang constraint for topology optimization of self-supporting structures in additive manufacturing
[J].DOI:10.1007/s00158-018-2010-7 [本文引用: 1]
Continuous front propagation-based overhang control for topology optimization with additive manufacturing
[J].DOI:10.1007/s00158-017-1880-4 [本文引用: 1]
Overhang control in topology optimization: a comparison of continuous front propagation-based and discrete layer-by-layer overhang control
[J].DOI:10.1007/s00158-021-02887-2 [本文引用: 1]
Topology optimization of 3D self-supporting structures for additive manufacturing
[J].DOI:10.1016/j.addma.2016.06.010 [本文引用: 1]
An additive manufacturing filter for topology optimization of print-ready designs
[J].DOI:10.1007/s00158-016-1522-2 [本文引用: 1]
Conceptual design of AM components using layout and geometry optimization
[J].
Layout and geometry optimization design for 3D printing of self-supporting structures
[J].DOI:10.1016/j.istruc.2023.105699 [本文引用: 1]
Design of optimal truss components for fabrication via multi-axis additive manufacturing
[J].DOI:10.1016/j.cma.2023.116464 [本文引用: 1]
On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming
[J].DOI:10.1007/s10107-004-0559-y [本文引用: 1]
Application of layout optimization to the design of additively manufactured metallic components
[J].DOI:10.1007/s00158-016-1426-1 [本文引用: 1]
Volume decomposition for multi-axis support-free and gouging-free printing based on ellipsoidal slicing
[J].DOI:10.1016/j.cad.2021.103135 [本文引用: 1]