太阳能无人机的能量主要由光伏电池提供,而光伏电池板的输出功率受光照强度、环境温度之类因素的影响,存在波动性与昼夜间歇性的问题. 为了向负载提供连续可靠的能量,往往会在无人机供电系统中加入蓄电池之类的储能装置. 在光/储一体化的太阳能无人机的应用场景中,其能量管理系统可按照负载母线电压是否可控分为不控型结构与受控性结构;可按照分布方式分为集中式结构与分布式结构;可按照电路拓扑结构分为两端口结构与三端口结构[1]. 采用三端口变换器(three port converter, TPC)将新能源装置、储能装置与负载同时连接,相较于传统的采用多个两端口变换器的供电架构,优势显著:器件数量减少,系统功率密度和效率提高,且无须建立额外的通信线路就可以实现集中统一控制. 因此,三端口变换器在太阳能无人机、电动汽车和燃料电池等领域获得了广泛的关注与应用.
半隔离拓扑[7-12]的开关元件数量少、集成度高并且控制相对简单,获得了广泛的研究. Qian等[8]提出TPC拓扑,所用到的开关器件少,并且可以实现原边主管的软开关. Wu等[9]提出Buck-Boost集成移相全桥的拓扑结构. 孙孝峰等[10]集成双向Buck-Boost与原边全桥结构实现开关元件,实现了器件复用. 王杉杉等[11]在上述研究的基础上加入辅助电感构成的额外回路,能够减少电感数量,实现主管软开关并且优化蓄电池电流波形. 孙孝峰等[12]将LLC谐振腔与交错并联Buck-Boost电路结合,采用脉冲宽度调制和脉冲频率调制混合调制的策略,实现端口功率的灵活控制. 王荣闯等[13]提出基于大信号建模的解耦控制策略,能够在全功率范围内实现TPC的功率解耦. Zhang等[14]将LLC谐振腔与复合全桥结构结合,提出新的TPC拓扑构建方式,但其电路采用移相控制与脉冲频率调制混合控制,控制环路的控制量不可避免地参与多条功率路径,导致控制环路之间存在功率耦合的问题.
本研究提出基于LLC谐振型的半隔离TPC拓扑结构,其结构简单,光伏端口与蓄电池端口共用开关元件,开关器件的数量减少,功率密度得到提高. 该变换器采用移相控制,能够灵活控制3个端口之间的功率流动.利用时域分析的方法,分析LLC谐振腔的运行模态与变换器的增益特性,并在此基础上提出简单有效的解耦控制策略,能够大大降低控制环路之间存在的功率耦合问题,优化系统的动态性能. 最后搭建500 W试验样机,验证所提三端口变换器及解耦策略的有效性.
1. 工作原理
1.1. 拓扑原理
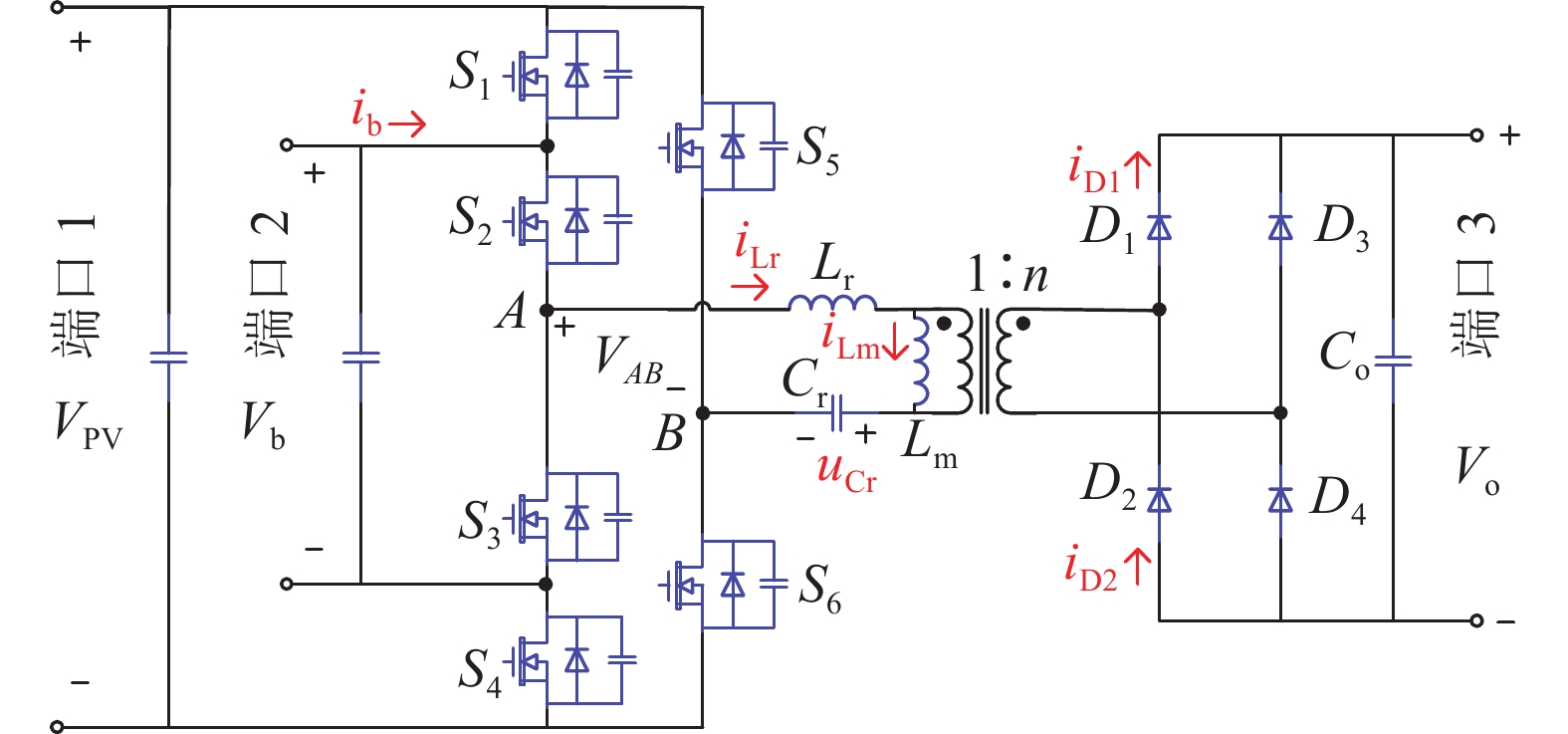
如图1所示为所提出的复合全桥LLC集成三端口变换器的拓扑结构. 开关管S1~S4构成一个复合桥臂,开关管S5、S6构成一个普通桥臂,由谐振电感Lr、谐振电容Cr与高频变压器励磁电感Lm构成的LLC谐振网络分别连接在复合桥臂的中点A与普通桥臂的中点B上,其中Lr和Cr两谐振元件的谐振频率
图 1
1.2. 工作模式分析
光伏端口输出功率大小用PPV表示,蓄电池端口功率用Pb表示,负载上的输出功率用Po表示,三端口变换器根据端口功率的不同可以分为3种功率传输模式.
1)功率传输模式Ⅰ:单输入单输出模式(single input single output, SISO). 其又可以分为2种子模式. (a)功率传输模式Ⅰ A:光伏端口退出最大功率点跟踪(maximum power point tracking, MPPT)运行模式,并且作为输入侧电源单独向负载供电,此时PPV=Po;(b)功率传输模式Ⅰ B:光伏端口不参与工作,蓄电池端口单独向负载供电,此时Pb=Po;
2)功率传输模式Ⅱ:双输入单输出模式(dual input single output, DISO). 当PPV<Po时,光伏端口和蓄电池端口共同向负载供电.
3)功率传输模式Ⅲ:单输入双输出模式(single input dual output, SIDO). 当PPV>Po时,光伏端口多余的能量由蓄电池储存,光伏端口为负载供电的同时也为蓄电池充电.
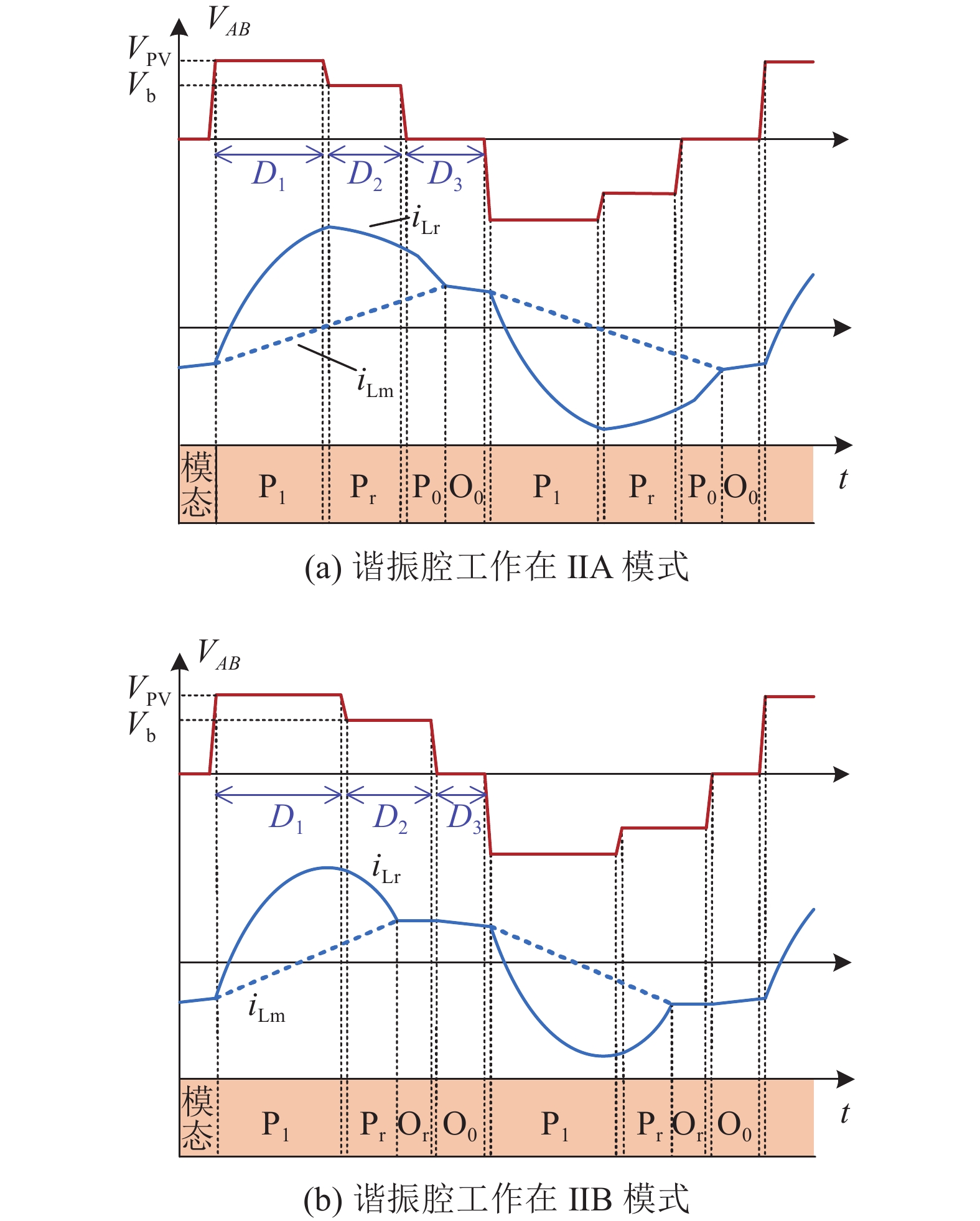
当3个端口共同参与工作时,定义3对开关:S1与S4、S2与S3和S5与S6. 开关管S1/S4与S5/S6、S1/S4与S2/S3、S2/S3与S5/S6之间的移相角分别为θ1、θ2、θ3. 根据移相角定义对应的占空比分别为D1、D2、D3,其中D1=θ1/(2π),D2=θ2/(2π),D3=θ3/(2π). 每对开关管均采用50%占空比互补导通的方式. 如图2(a)~(c)所示分别为电路处于DISO、SIDO和蓄电池单独供电工作模式下,电路主要元件的运行波形图.
图 2
图 2 不同功率传输模式下主要工作波形
Fig.2 Key operation waveforms under different power transmission modes
如图3所示为谐振腔工作状态图. 根据占空比的不同,谐振腔中谐振电流波形也存在2种不同的情况,以下针对DISO模式进行详细分析. 1)当D1、D2较小时,在VAB等于零电平之前,谐振电流iLr未能等于励磁电感电流iLm,在VAB=0后,加在原边谐振腔两端的电压变为0电压,谐振腔中继续进行Lr与Cr的两谐振元件的谐振过程,直至iLr=iLm,如图3(a)所示,此工作模式称为Ⅱ A模式. 2)当D1、D2较大时,在VAB等于零电平之前,谐振电流iLr已经等于励磁电感电流iLm,在iLr=iLm之后,谐振腔中的谐振过程转变成Lr、Lm与Cr这3个原件之间的谐振过程,在VAB=0后,三元件谐振过程持续进行,如图3(b)所示,此工作模式称为Ⅱ B模式. SIDO模式与DISO类似,同样存在2种不同的工作模式,即存在模式ⅢA与ⅢB. 当电路处于功率传输模式Ⅰ时,电路变为单输入单输出工作状态,此时移相占空比D3仍用于实现输出电压的稳定控制.
图 3
1.3. 电路模态分析
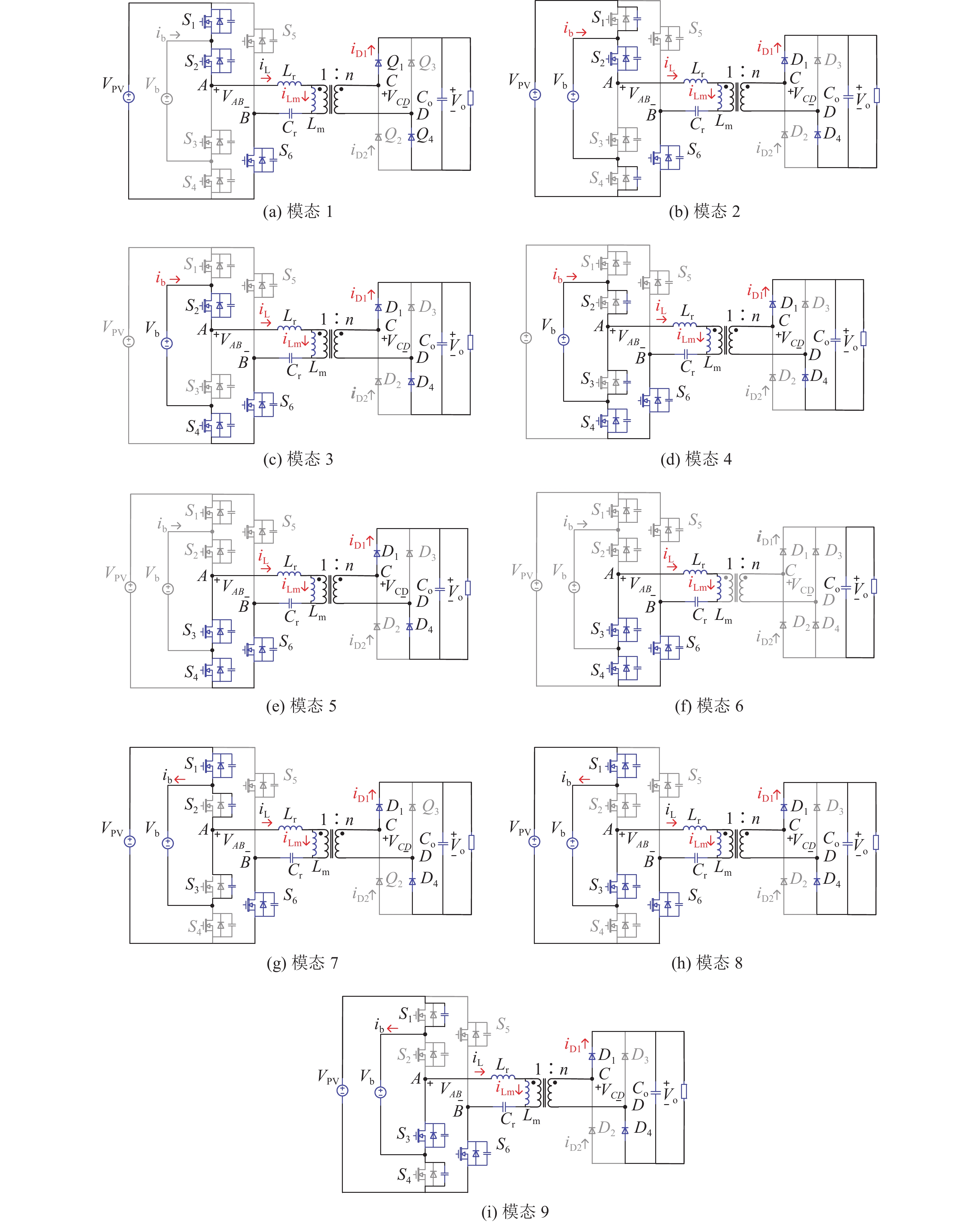
图 4
图 4 三端口运行模式下各个模态下的等效电路图
Fig.4 Equivalent circuit diagrams under three port operation modes
式中:Zr为特征阻抗,Zr=(Lr/Cr)1/2.
1)阶段1 [t0,t1),如图4(a)所示. 在t0时刻,开关管S6导通,谐振腔中Lr与Cr发生谐振,原边谐振腔两端电压VAB=VPV,谐振电流iLr由负值开始正向增加,谐振频率为fr,励磁电感电流iLm线性增加,此模式称为P1谐振模态. iLr、iLm、uCr的归一化时域表达式如下:
式中:θ=2πfrt;M为电压增益,M=nVo/VPV;m为励磁电感与谐振电感之比,m=Lm/Lr;r为端口电压之比,r=Vb/VPV.
2)阶段2 [t1,t2),如图4(b)所示. 在t1时刻,开关管S1关断,进入S1与S4的死区时间中,谐振电流iLr给S1的输出电容充电,给S4的输出电容放电,当S4管的输出电容上电压降为0后,S4的体二极管导通,S4实现ZVS开通.
3)阶段3 [t2,t3),如图4(c)所示. 在t2时刻,开关管S4开通,电流流经S4并联二极管,原边谐振腔两端电压VAB=Vb=rVPV,谐振腔中Lr与Cr继续谐振过程,励磁电感电流iLm继续线性增加,此模式称为Pr谐振模态. iLr、iLm、uCr的归一化的时域表达式如下:
4)阶段4 [t3,t4),如图4(d)所示. 在t3时刻,开关管S2关断,进入S2与S3的死区时间中,谐振电流iLr给S3的输出电容放电,当S3管的输出电容上电压降为0后,S3的体二极管导通,S3实现ZVS开通.
5)阶段5 [t4,t5),如图4(e)所示. 在t4时刻,开关管S3开通,电流流经S3、S4并联二极管,原边谐振腔两端电压VAB=0,由于谐振电流iLr仍大于励磁电感电流iLm,谐振腔继续发生Lr与Cr元件的谐振过程,励磁电感电流iLm继续线性增加,当iLr=iLm时,该阶段结束. 此模式称为P0谐振模态. iLr、iLm、uCr的归一化的时域表达式如下:
6)阶段6 [t5,t6),如图4(f)所示. 在t5时刻,iLr=iLm,副边二极管电流降为0,副边D1、D4二极管实现零电流关断. 同时,谐振腔进入Lr、Lm与Cr这3个元件的谐振状态,原边谐振腔两端电压VAB=0,此模式称为O0谐振模态. iLr、iLm、uCr、uLm的归一化的时域表达式如下:
式中:k=(1+m)−1/2.
7)阶段7 [t6,t7). 在t6时刻,开关管S6关断,进入S5与S6的死区时间中,谐振电流iLr与励磁电感电流iLm相同,共同给S6的输出电容充电,给S5的输出电容放电,当S5管的输出电容上电压降为0后,S5的体二极管导通,S5实现ZVS开通.
2. 电路模型
2.1. 变换器增益特性
由于原边谐振腔两端电压VAB为含有5种电平的矩形奇对称矩形波,除去基波成分外还含有非常丰富的高次谐波成分,因此采用基波近似法(first harmonic approximation, FHA)分析该三端口LLC谐振型电路增益会带来一定的误差. 本研究采用时域分析法,结合前文列写的各个运行模态的电路时域状态方程对电路增益进行分析.
如图2(a)所示,谐振电感电流iLr、谐振电容电压uCr、励磁电感电流iLm在一个开关周期内具有连续性,同时相应的谐振原件波形具有奇对称性,可以列出以下方程:
根据归一化的输出电流相同,可以列出:
式中:Ro为负载大小.
对于运行模式Ⅱ下,根据谐振电感电流iLr与励磁电感电流iLm相等的时刻是否滞后VAB=Vb电平结束的时刻,可以判断出电路运行在模态ⅡA或模态ⅡB,模式Ⅲ下A或B模式的判断同样可以基于这一边界条件.
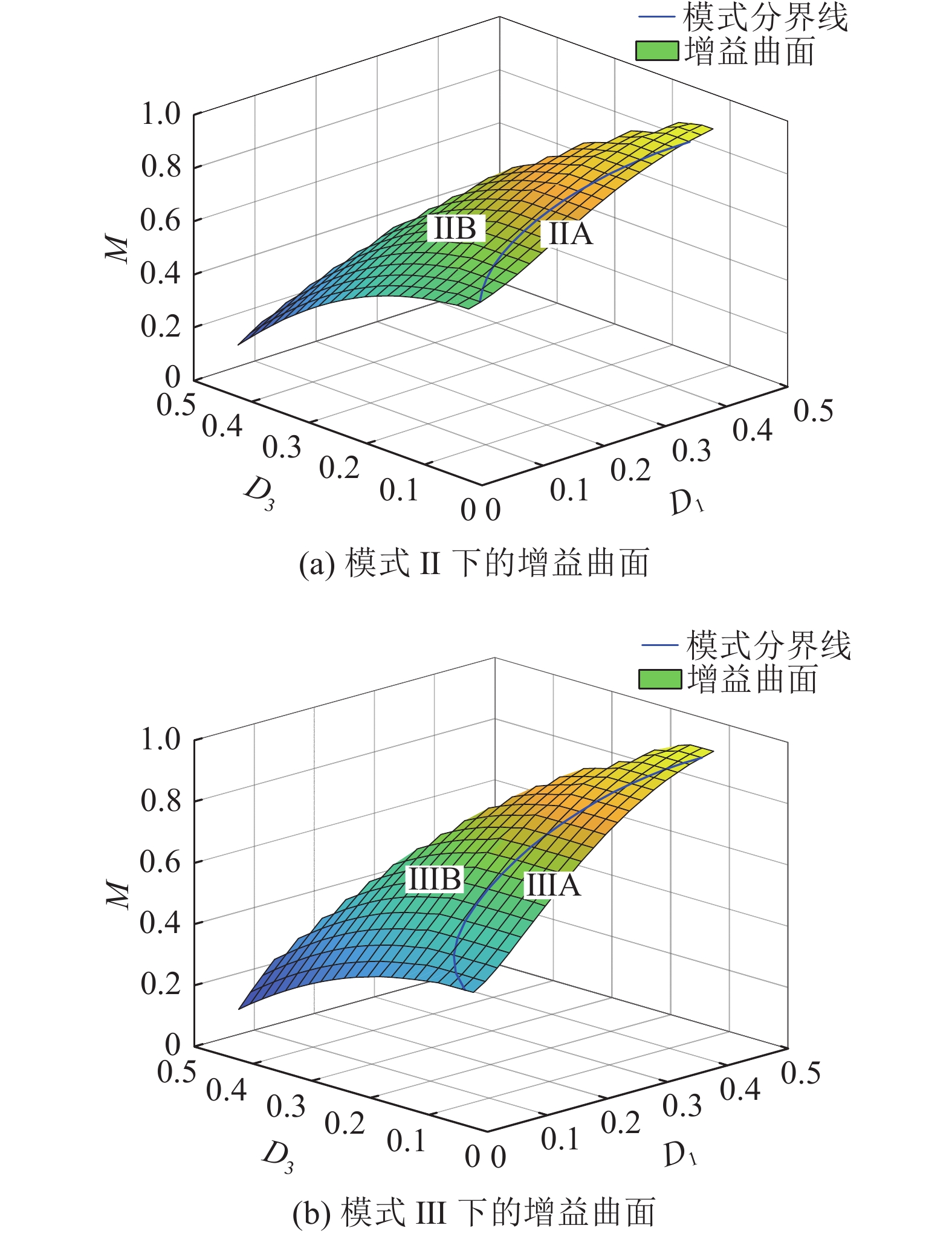
根据式(2)~(7)可以得到描述该电路在ⅡA模式运行状态下的一组稳态方程组,对于给定负载Ro=80 Ω、励磁电感与谐振电感比值m=40/5.39、特征阻抗Zr=
图 5
2.2. 控制策略
2.2.1. 控制方式
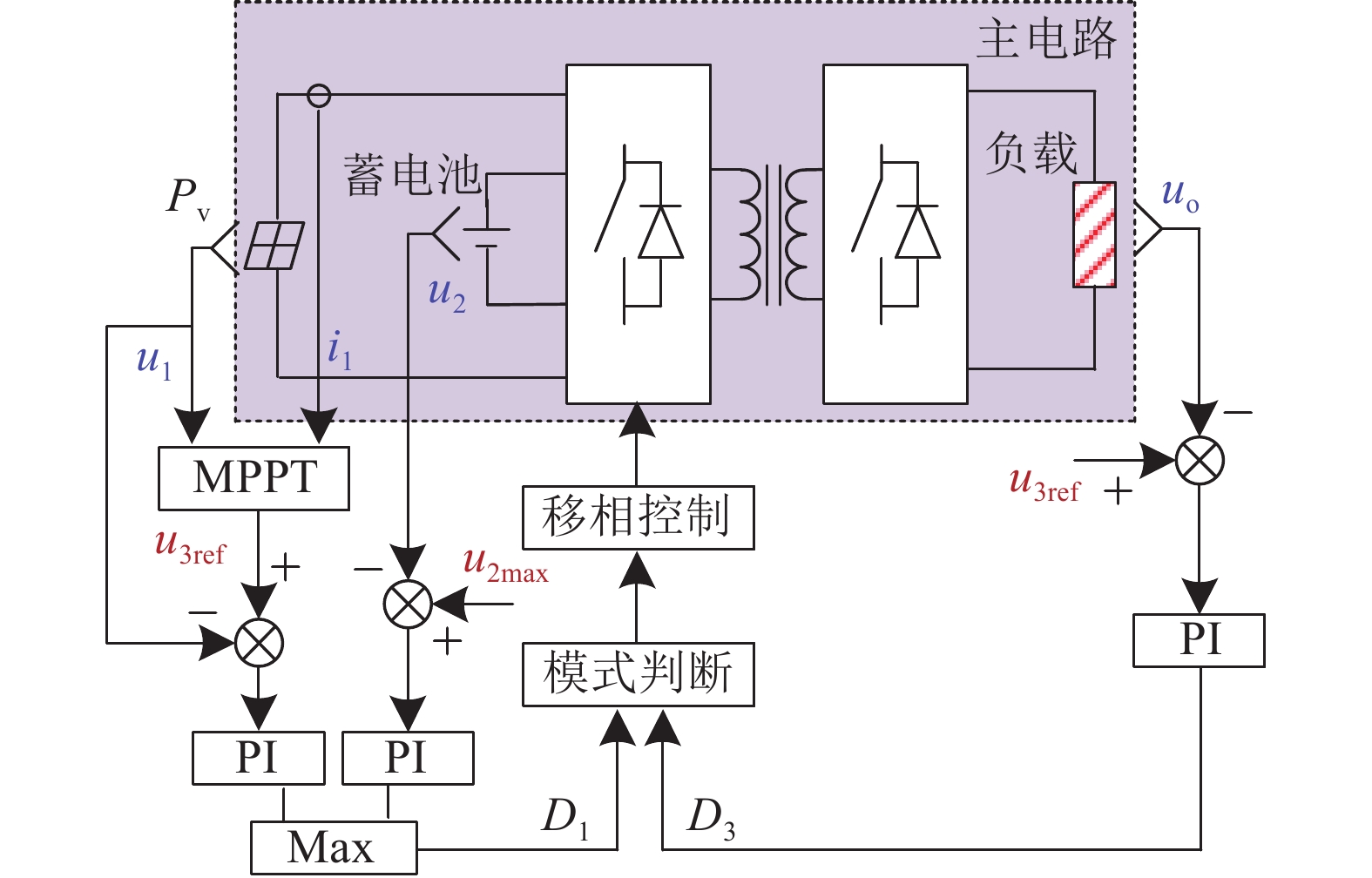
在光伏-蓄电池联合供电的应用场景下,须同时控制输出电压的稳定与光伏端口输出功率的大小. 提出的LLC谐振型三端口电路采用移相控制的方式,开关频率fs始终等于谐振频率fr,移相角D1、D2、D3之和始终等于半个开关周期,即D1+D2+D3=0.5,故实际只存在2个自由的控制变量. 移相角D1用来控制端口1上输出功率的大小,即用于端口1上光伏组件MPPT功能的实现. 移相角D3用于控制输出电压的稳定,同时根据D3的大小决定电路的工作模式:当负载增大且此时PPV<Po时,D3逐渐减小,此时D3<0.5−D1,即D2移相角为正值,电路处于功率传输模式Ⅱ;当负载逐渐减小时,D3逐渐增大,当D3>0.5−D1,即D2移相角由正变为负值时,电路的功率传输模式变为模式Ⅲ. 模式Ⅱ与模式Ⅲ之间的切换为连续过程,当端口功率发生变化时,电路能够实现自然平滑的切换过程. 电路对应的控制框图如图6所示.
图 6
当电路工作在功率传输模式Ⅰ时,电路变为单输入单输出运行模式,当光伏端口单独供电时,蓄电池端口被开关管旁路;当蓄电池单独供电时,光伏端口被开关管旁路. 在模式Ⅰ中,移相角D3同样用于控制输出电压的稳定.
2.2.2. 解耦控制
由于变换器原边开关管的高度复用,结合如图5所示的增益曲面可以发现,移相角D1不仅影响光伏端口的输入功率,还直接影响输出电压的增益. 在外界环境发生变化时,为了实现MPPT功能,须不断调节占空比D1,进而会影响以D3为控制量的输出电压控制环的波动,进而导致输出电压的跳动,影响负载的供电质量. 为了削弱D1控制量的变化对输出电压带来的影响,须设计解耦控制环路. 在分析时,认为蓄电池端口电压在短时间尺度内的波动较小,故认为Vb保持不变. 根据前文分析,采用时域分析的方法可以求解出在固定负载大小的条件下,输出电压增益M与D1、D3之间的关系,但是状态方程联立得到的为超越方程组,难以得到解析解.
为了进一步得到归一化的输出电压增益M与D1和D3之间的数学表达式,采用多项式逼近的计算方法,利用MATLAB软件进行求解. 当负载变化时,须根据相应的负载条件计算对应的增益曲面与拟合增益表达式. 在负载满载Ro=80 Ω、励磁电感与谐振电感比值m=40/5.39、特征阻抗Zr=
表 1 拟合曲面多项式系数
Tab.1
| ⅡA模态 | ⅡB模态 | ⅢA模态 | ⅢB模态 |
| a11=−3.433 | a12=−6.119 | a21=−3.106 | a22=−2.968 |
| b11= | b12=−4.448 | b21=− | b22= |
| c11= | c12=2.72 | c21=− | c22=− |
| d11=− | d12=2.857 | d21=−1.423 | d22=− |
| e11= | e12=− | e21=1.156 | e22=1.096 |
| f11= | f12= | f21= | — |
| — | g12= | — | — |
表 2 解耦多项式系数
Tab.2
| ⅡA模态 | ⅡB模态 | ⅢA模态 | ⅢB模态 |
| A11=a11 | A12=a12 | A21=a21 | A22=a22 |
| B11=0.5b11/a11 | B12=b12 | B21=0.5b21/a21 | B22=0.5b22/a22 |
| C11=0.5c11/a11 | C12=c12 | C21=0.5c21/a21 | C22=0.5c22/a22 |
| D11=d11−0.25b112/a11 | D12=d12 | D21=d21−0.25b212/a21 | D22=−0.25b222/a22 |
| E11=e11−0.5b11c11/a11 | E12=e12 | E21=e21−0.5b21c21/a21 | E22=d22−0.5b22c22/a22 |
| F11=f11−0.25c112/a11 | F12=f12 | F21=f21−0.25c212/a21 | F22=e22−0.25c222/a22 |
| — | G12=g12 | — | — |
当负载在半载到满载之间变化时,为了简化时域分析的复杂程度,依旧采用满载条件进行拟合系数的计算,即依旧采用如式(8)所示的结果进行增益拟合,但拟合结果精度随着负载的减小会逐渐降低. 如表3所示为固定占空比的条件下,时域分析计算得到的不同负载条件下增益与拟合曲面得到的增益之间的对比. 表中,Pf为拟合计算准确度. 拟合增益的准确程度随着负载的减小而逐渐降低,但依旧可以用于后续解耦环路的设计,并且采用同一组拟合系数可以减小实际系统中解耦环路的计算量.
表 3 不同负载下的增益特性对比
Tab.3
| M | Pf/% | |
| 80 | 99.98 | |
| 100 | 99.18 | |
| 150 | 97.86 | |
| 200 | 97.08 | |
| 400 | 95.69 |
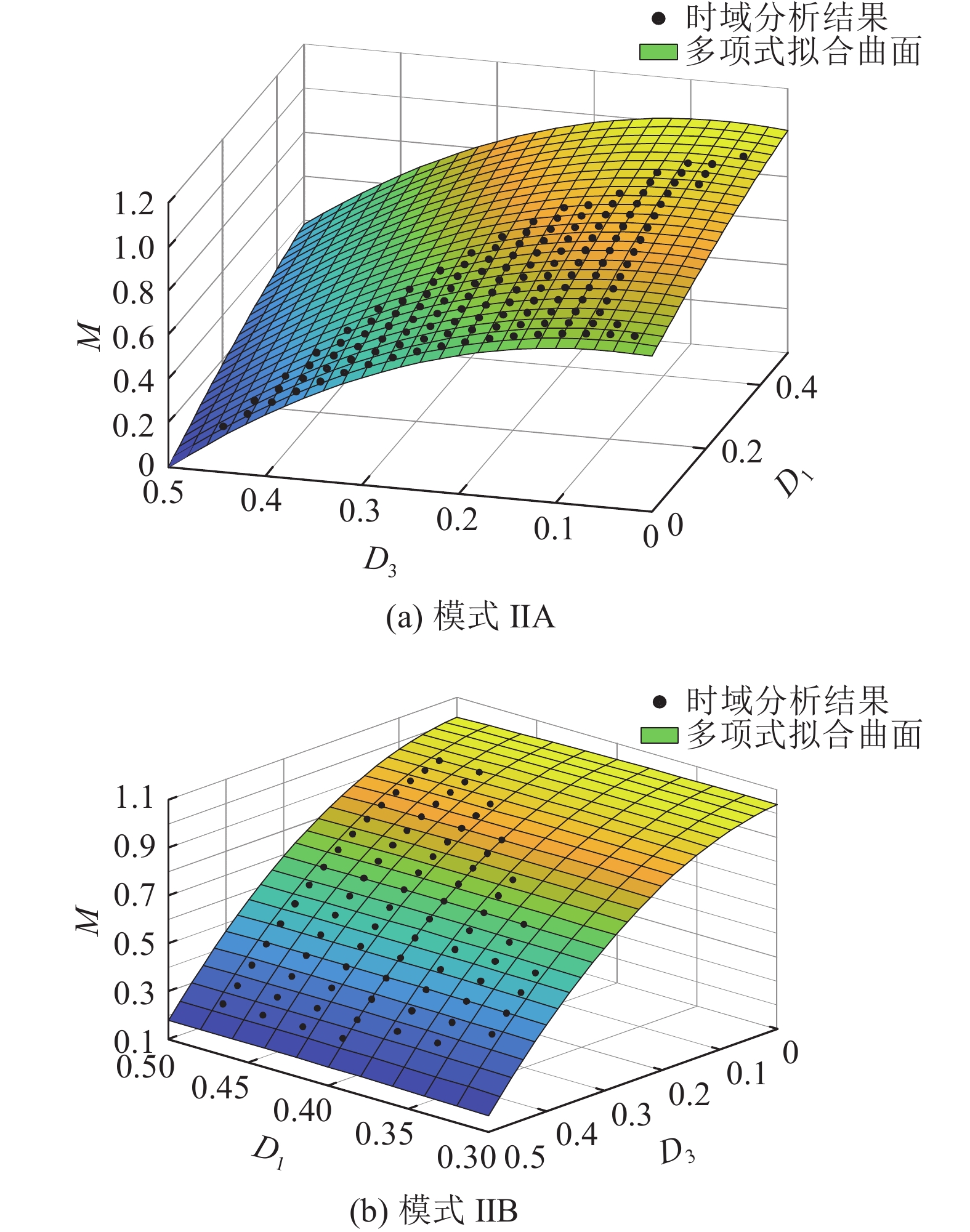
如图7(a)、(b)所示分别为运行模式Ⅱ A、Ⅱ B条件下,采用时域分析和多项式拟合结果得到的变换器归一化的直流增益的比较. 可以看到,利用多项式拟合得到的结果与时域分析结果基本一致.
图 7
各模式之间的边界条件同样可以通过式(2)~(7)进行求解. 如图2(a)所示,当P0模态的占空比恰好为0时,可以求出Ⅱ A与Ⅱ B或者Ⅲ A与Ⅲ B模态之间的边界状态. 在与式(8)相同的电路参数的状态下,利用多项式逼近的拟合方法可以得出:
式(10)、(11)中多项式系数如表4所示.
表 4 运行边界多项式系数
Tab.4
| 模态Ⅱ | 模态Ⅲ |
| a1=2.101 | a2=7.128 |
| b1=−2.585 | b2=−6.238 |
| c1= | c2=1.223 |
| d1=− | d2= |
模式Ⅱ与模式Ⅲ之间的边界可以通过固定电压增益M,求解当D2占空比恰好为0时的D1移相角来确定. 在与式(8)相同的电路参数的状态下,即M=
式(12)为模式Ⅱ与模式Ⅲ之间的运行边界.
通过上述分析,在电路运行时,利用式(12)可以判断出电路当前运行的具体模态:当D1>
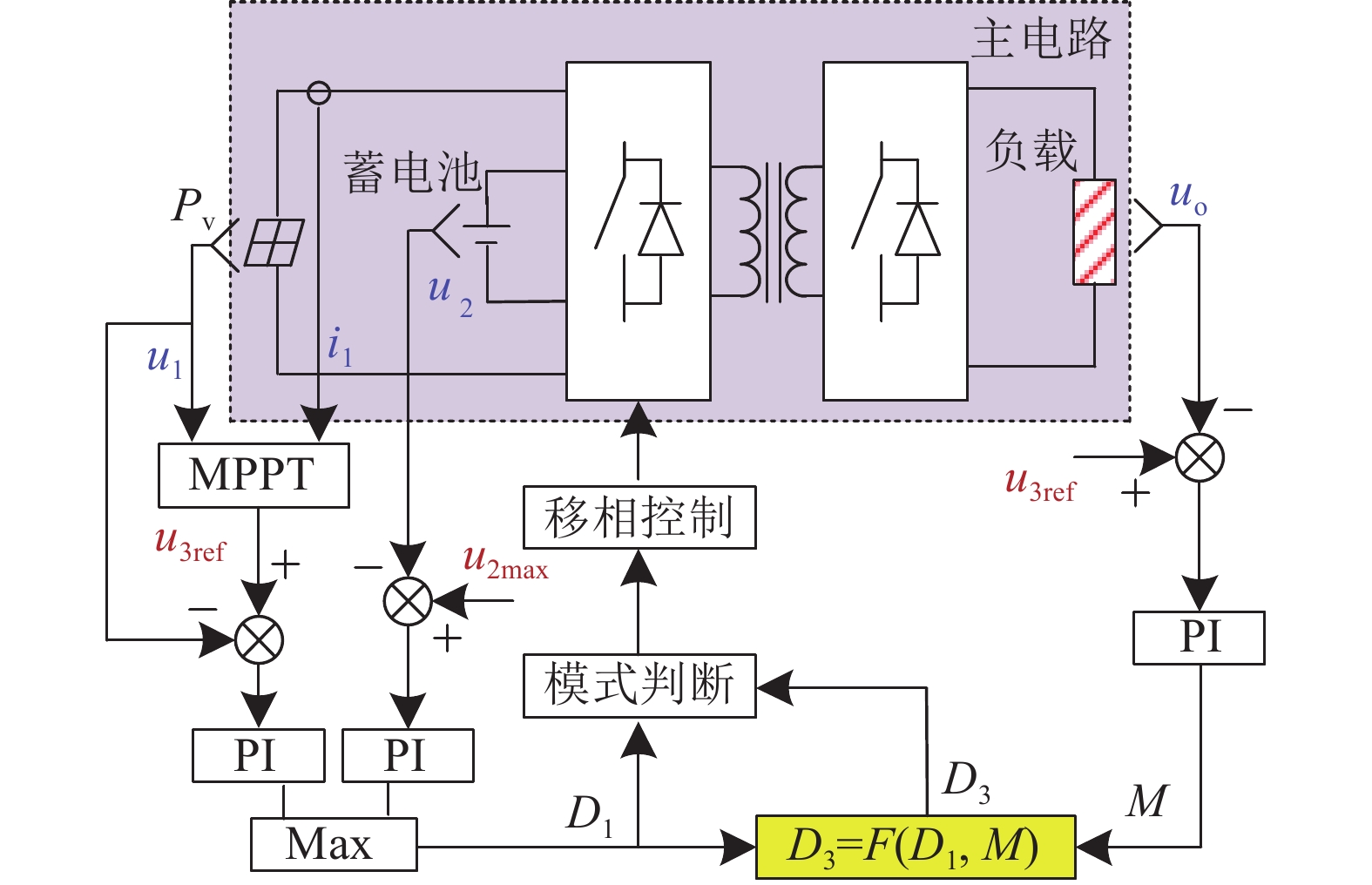
图 8
图 8 加入解耦控制的系统控制框图
Fig.8 System control block diagram incorporating decoupling control
图 9
3. 实验验证
图 10
表 5 样机主要参数
Tab.5
| 参数 | 数值 | 参数 | 数值 | |
| 光伏电压VPV/V | 80~120 | 谐振电容Cr/nF | 470 | |
| 蓄电池电压Vb/V | 50~75 | 励磁电感Lm/μH | 40 | |
| 输出电压Vo/V | 200 | 变压器变比n1∶n2 | 1∶3 | |
| 输出功率Po/W | 0~500 | 谐振频率fr/kHz | 100 | |
| 谐振电感Lr/μH | 5.39 | 开关频率fs/kHz | 100 |
3.1. 稳态运行谐振腔波形
如图11(a)所示为在VPV=100 V,Vb=75 V,输出负载功率为500 W的工作条件下,在D1=0.1时,采用移相控制的方式得到的谐振腔工作波形. 在此条件下,光伏端口与蓄电池端口都向外输出功率,变换器在DISO模式下工作,即工作模式Ⅱ下,同时谐振电流在VAB=Vb电平持续期间仍未谐振到与励磁电感电流相同,故谐振腔此时处于工作模式ⅡA. 如图11(b)所示为相同端口条件下,D1=0.4时得到的谐振腔工作波形,在此条件下,光伏端口向外输出功率,蓄电池作为负载吸收多余的功率,变换器处于SIDO模式,即工作模式Ⅲ下,同时在VAB=Vb电平持续期间iLr谐振与到iLm相等的状态,因而谐振腔处于ⅢB工作模式. 在实验样机中,因理论上蓄电池电流波形不连续,为了减小蓄电池端口上的电压电流尖峰,在蓄电池端口并联容值为440 μF的电解电容,如图11(a)所示,在并联电容后,蓄电池端口电流有效值为4.9 A,如图11(b)所示,蓄电池电流有效值为−4.3 A,电流ib经过电解电容滤波后表现为连续形式,但电流有效值与理论分析结果保持一致.
图 11
3.2. 工作模式切换波形
图 12
3.3. 解耦控制波形
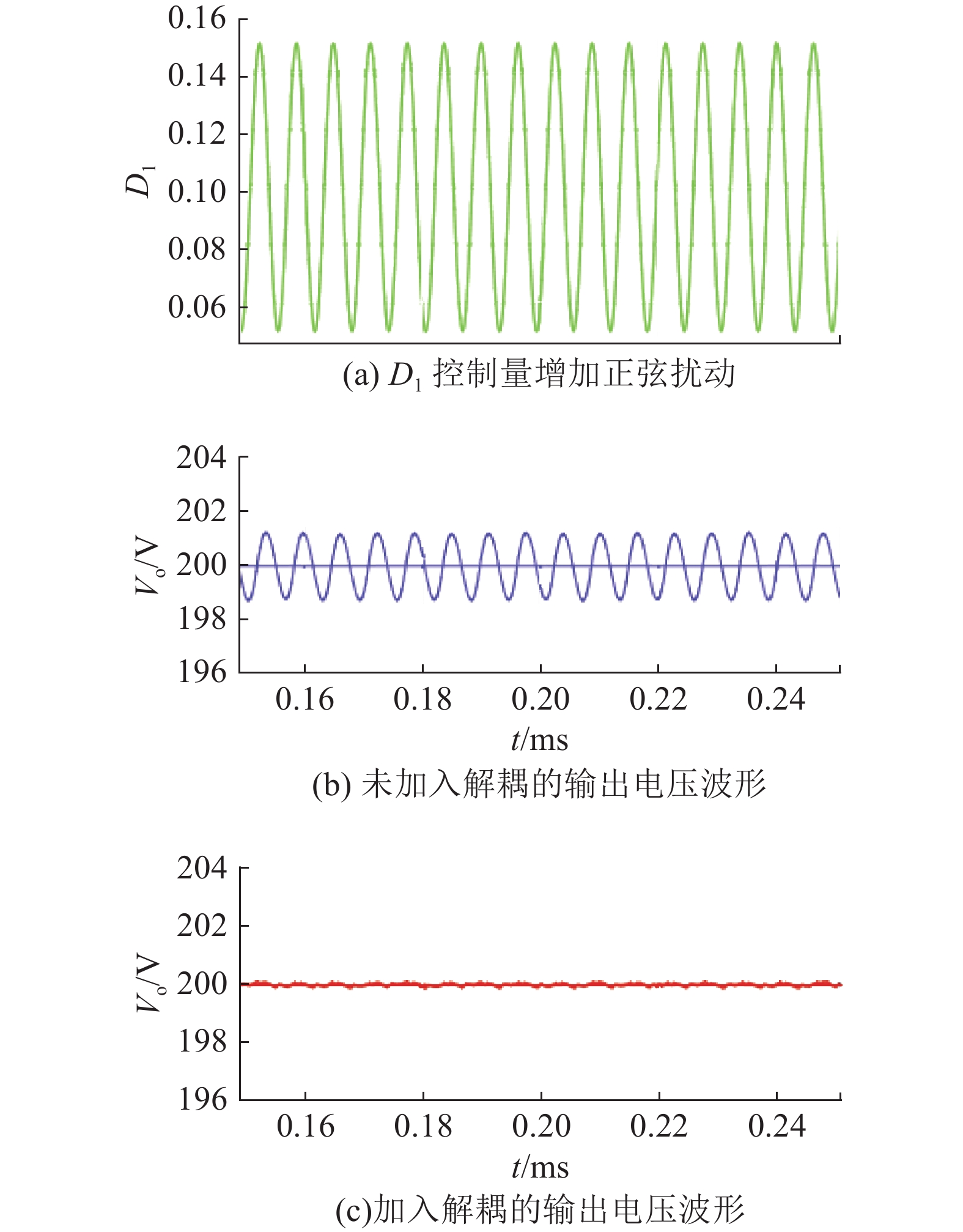
如图13所示为电路状态发生变化时,电路中各关键元件波形的变化,其中VPV=100 V,Vb=75 V,输出电压Vo=200 V,输出功率保持500 W满载功率,在D1占空比从0.4跳变到0.1后,分别在有、无解耦控制的条件下,输出电压Vo、蓄电池端口电流ib的变化情况. 当D1占空比从0.4跳变到0.1后,蓄电池端口电流由−4.5 A跳变到5.2 A,光伏端口功率从830 W跳变到100 W,跳变前后变换工作模式由SIDO模式切换为DISO模式. 当不加入解耦控制算法时,D1控制量的跳动在引起光伏端口功率跳动的同时,会明显引起输出电压Vo的波动,震荡幅度ΔVo约为30 V,调整时间ts约为800 ms;当加入解耦控制算法后,震荡幅度ΔVo<5 V,调整时间ts<320 ms,大大降低了D1控制量的波动对输出电压控制回路的影响.
图 13
如图14所示为输出功率在400 W功率条件下,D1占空比从0.4跳变到0.1后,分别在有、无解耦控制的条件下,输出电压Vo、蓄电池端口电流ib的变化情况. 当D1占空比从0.4跳变到0.1后,蓄电池端口电流由−3.7 A跳变到4.1 A,光伏端口功率从680 W跳变到95 W,跳变前后变换工作模式由SIDO模式切换为DISO模式. 当不加入解耦控制算法时,D1控制量的跳动在引起光伏端口功率跳动的同时,会明显引起输出电压Vo的波动,震荡幅度ΔVo约为25 V,调整时间ts约为600 ms;当加入解耦控制算法后,震荡幅度ΔVo<5 V,调整时间ts<280 ms,大大降低了D1控制量的波动对输出电压控制回路的影响.
图 14
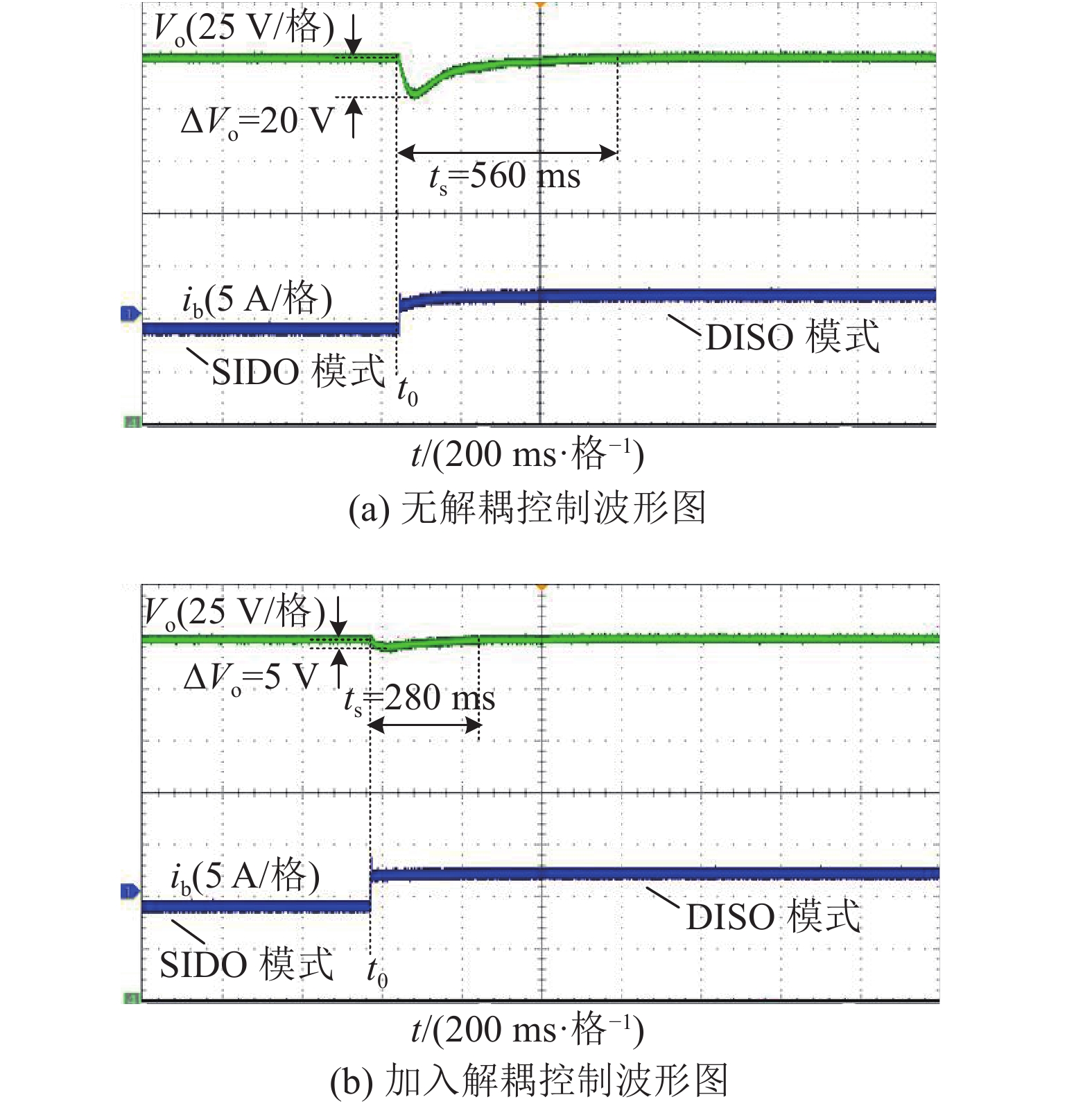
如图15所示为输出功率在200 W轻载条件下,D1占空比从0.4跳变到0.1后,分别在有、无解耦控制的条件下,输出电压Vo、蓄电池端口电流ib的变化情况. 当D1占空比从0.4跳变到0.1后,蓄电池端口电流由−2.3 A跳变到1.7 A,光伏端口功率从370 W跳变到70 W,跳变前后变换工作模式由SIDO模式切换为DISO模式. 当不加入解耦控制算法时,D1控制量的跳动在引起光伏端口功率跳动的同时,会明显引起输出电压Vo的波动,震荡幅度ΔVo约为20 V,调整时间ts约为560 ms;当加入解耦控制算法后,震荡幅度ΔVo<5 V,调整时间ts<280 ms,大大降低了D1控制量的波动对输出电压控制回路的影响.
图 15
4. 结 语
本研究提出针对LLC谐振型三端口变换器的解耦控制方法,理论分析和实验表明:基于时域分析方法,能够准确描述移相控制策略下的三端口变换器增益特性;通过多项式拟合的方式,能够得到电路增益与各控制量之间的数学表达式,进而实现解耦控制环路的设计;解耦控制策略简单有效,能够大大降低2个控制环路之间的功率耦合程度,提升系统动态响应能力.
参考文献
一种独立光储发电系统用宽输入范围非隔离三端口变换器
[J].
A wide input range non-isolated three-port converter for stand-alone PV storage power generation system
[J].
Novel three-port converter with high-voltage gain
[J].DOI:10.1109/TPEL.2013.2285477 [本文引用: 1]
Three-port DC-DC converter for stand-alone photovoltaic systems
[J].DOI:10.1109/TPEL.2014.2331343 [本文引用: 1]
Idling port isolation control of three-port bidirectional converter for EVs
[J].
An integrated three-port bidirectional DC-DC converter for PV application on a DC distribution system
[J].DOI:10.1109/TPEL.2012.2236580 [本文引用: 1]
Modeling and control of three-port DC/DC converter interface for satellite applications
[J].
Multiport converters based on integration of full-bridge and bidirectional DC-DC topologies for renewable generation systems
[J].DOI:10.1109/TIE.2013.2254096 [本文引用: 1]
双Buck/Boost集成双有源桥三端口DC-DC变换器
[J].
Dual buck/boost integrated dual active bridge three-port DC-DC converter
[J].
一种应用于航天器分布式供电系统的ZVS三端口DC-DC变换器
[J].
A ZVS three-port dc-dc converter of distributed power supply system applied in spacecraft
[J].
交错并联双向Buck/Boost集成LLC谐振型三端口直流变换器
[J].
Interleaved bidirectional buck/boost and LLC integrated three-port DC-DC converter
[J].
光伏-蓄电池联合供电系统中三端口变换器的解耦控制研究
[J].
Research on decoupling control of three-port converter in photovoltaic-battery generation system
[J].
A three-port LLC resonant DC/DC converter
[J].DOI:10.1109/JESTPE.2019.2902425 [本文引用: 1]