[1]
SELVARAJU DR S Application of composite in marine industry
[J]. Journal of Engineering Research and Studies , 2011 , 2 : 89 - 91
[本文引用: 1]
[3]
洪毅. 高性能复合材料螺旋桨的结构设计及水弹性优化 [D]. 哈尔滨: 哈尔滨工业大学, 2011.
[本文引用: 1]
HONG Yi. Structure design and hydroelastic optimization of high performance composite propeller [D]. Harbin: Harbin Institute of Technology, 2010.
[本文引用: 1]
[4]
周鑫, 童喆益, 杨文凯, 等 大厚度船用复合材料螺旋桨桨叶设计与成型工艺
[J]. 船舶工程 , 2022 , 44 (9 ): 24 - 28
[本文引用: 3]
ZHOU Xin, TONG Zheyi, YANG Wenkai, et al Design and molding process of large thichness marine composite propeller blade
[J]. Ship Engineering , 2022 , 44 (9 ): 24 - 28
[本文引用: 3]
[5]
杨文志, 朱锡, 陈悦, 等 复合材料螺旋桨RTM成型工艺研究
[J]. 材料科学与工艺 , 2015 , 23 (6 ): 87 - 92
[本文引用: 1]
YANG Wenzhi, ZHU Xi, CHEN Yue, et al Research on RTM molding process of composite propeller
[J]. Materials Science and Technology , 2015 , 23 (6 ): 87 - 92
[本文引用: 1]
[6]
SEARLE T, CHUDLEY J, SHORT D, et al Are composite propellers the way forward for small boats
[J]. Mater World , 1994 , (2 ): 69 - 70
[本文引用: 1]
[8]
王晓飞, 蔡智奇, 文秀芳, 等 风轮叶片树脂与成型工艺研究进展
[J]. 化工新型材料 , 2012 , 40 (1 ): 31 - 34
DOI:10.3969/j.issn.1006-3536.2012.01.010
[本文引用: 1]
WANG Xiaofei, CAI Zhiqi, WEN Xiufang, et al Advance in studies of thermosetting resin and molding process of rotor blades
[J]. New Chemical Materials , 2012 , 40 (1 ): 31 - 34
DOI:10.3969/j.issn.1006-3536.2012.01.010
[本文引用: 1]
[9]
张鸿名. 船用复合材料螺旋桨成型工艺研究 [D]. 哈尔滨: 哈尔滨工业大学, 2009.
[本文引用: 1]
ZHANG Hongming. Manufacture and technique of marine composite material propeller [D]. Harbin: Harbin Institute of Technology, 2009.
[本文引用: 1]
[10]
陆九如. 碳纤维复合材料薄壁曲面构件纤维铺放方法研究 [D]. 上海: 东华大学, 2023.
[本文引用: 1]
LU Jiuru. Investigation of carbon fiber placement method for thin-walled composite shells [D]. Shanghai: Donghua University, 2023.
[本文引用: 1]
[11]
宋超, 李勇, 还大军, 等. 航空发动机复合材料叶片曲面可铺性研究[J]. 航空制造技术, 2015, 58(增2): 63–66.
[本文引用: 1]
SONG Chao, LI Yong, HUAN Dajun, et al. Study on placeability of composite blade surface of aeroengine [J]. Aeronautical Manufacturing Technology , 2015, 58(Suppl.2): 63–66.
[本文引用: 1]
[12]
GAN M C, TAN S T, CHAN K W Flattening developable bi-parametric surfaces
[J]. Computers and Structures , 1996 , 58 (4 ): 703 - 708
[本文引用: 1]
[14]
王立冬. 碳纤维预浸料层间滑移性能研究及在热隔膜成型中的应用[D]. 上海: 上海交通大学, 2020.
[本文引用: 1]
WANG Lidong. Investigation on inter-Ply slipping behavior of carbon fiber prepreg and its application in hot diaphragm forming [D]. Shanghai: Shanghai Jiao Tong University, 2020.
[本文引用: 1]
[15]
赵盼, 史耀耀, 康超, 等 复合材料机器人纤维铺放工艺参数优化
[J]. 西北工业大学学报 , 2018 , 36 (4 ): 693 - 700
DOI:10.3969/j.issn.1000-2758.2018.04.013
[本文引用: 1]
ZHAO Pan, SHI Yaoyao, KANG Chao, et al Optimization of process parameters for robotic fibre placement
[J]. Journal of Northwestern Polytechnical University , 2018 , 36 (4 ): 693 - 700
DOI:10.3969/j.issn.1000-2758.2018.04.013
[本文引用: 1]
[16]
柯映林, 曲巍崴, 李江雄, 等 碳纤维复合材料结构件自动铺放技术与装备研究进展
[J]. 机械工程学报 , 2023 , 59 (20 ): 401 - 435
DOI:10.3901/JME.2023.20.401
[本文引用: 1]
KE Yinglin, QU Weiwei, LI Jiangxiong, et al Researches on automated placement technologies and equipment for carbon fiber reinforced composites: a state-of-the-art review
[J]. Journal of Mechanical Engineering , 2023 , 59 (20 ): 401 - 435
DOI:10.3901/JME.2023.20.401
[本文引用: 1]
[17]
秦永利, 祝颖丹, 范欣愉, 等 纤维曲线铺放制备变刚度复合材料层合板的研究进展
[J]. 玻璃钢/复合材料 , 2012 , (1 ): 61 - 66
QIN Yongli, ZHU Yingdan, FAN Xinyu, et al Research and development on variable-stiffness composite laminates manufactured by variable angle tow placement
[J]. Fiber Reinforced Plastics/Composites , 2012 , (1 ): 61 - 66
[18]
BRAMPTON C J, WU K C, KIM H A New optimization method for steered fiber composites using the level set method
[J]. Structural and Multidisciplinary Optimization , 2015 , 52 (3 ): 493 - 505
DOI:10.1007/s00158-015-1256-6
[本文引用: 1]
[19]
CHEN X, WU Z, NIE G, et al Buckling analysis of variable angle tow composite plates with a through-the-width or an embedded rectangular delamination
[J]. International Journal of Solids and Structures , 2018 , 138 : 166 - 180
DOI:10.1016/j.ijsolstr.2018.01.010
[20]
LIGUORI F S, ZUCCO G, MADEO A, et al Postbuckling optimisation of a variable angle tow composite wingbox using a multi-modal Koiter approach
[J]. Thin-Walled Structures , 2019 , 138 : 183 - 198
DOI:10.1016/j.tws.2019.01.035
[本文引用: 1]
[21]
都涛. 基于碳纤维预浸料铺放的工艺参数分析与试验研究[D]. 杭州: 浙江大学, 2018.
[本文引用: 1]
DU Tao. Analysis and experiment study of lay-up process parameters based on carbon fiber prepreg lay-up [D]. Hangzhou: Zhejiang University, 2018.
[本文引用: 1]
[22]
LUKASZEWICZ D H A. Optimisation of high-speed automated layup of thermoset carbon-fiber reimpregnates [D]. Bristol: University of Bristol, 2011.
[本文引用: 1]
[23]
AIZED T, SHIRINZADEH B Robotic fiber placement process analysis and optimization using response surface method
[J]. The International Journal of Advanced Manufacturing Technology , 2011 , 55 (1 ): 393 - 404
[本文引用: 1]
[24]
LI K, LIU X, JIN Y, et al Structural strength and laminate optimization of composite connecting bracket in manned spacecraft using a genetic algorithm
[J]. Applied Composite Materials , 2019 , 26 (2 ): 591 - 604
DOI:10.1007/s10443-018-9736-7
[本文引用: 1]
[25]
孙海涛, 熊鹰, 黄政 复合材料螺旋桨纤维铺层的影响及预变形设计
[J]. 华中科技大学学报: 自然科学版 , 2014 , 42 (5 ): 116 - 121
[本文引用: 1]
SUN Haitao, XIONG Ying, HUANG Zheng Effect of stacking mode of composite laminates and pre-deformed design of composite marine propellers
[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition , 2014 , 42 (5 ): 116 - 121
[本文引用: 1]
[26]
BLASQUES J P, BERGGREEN C, ANDERSEN P Hydro-elastic analysis and optimization of a composite marine propeller
[J]. Marine Structures , 2010 , 23 (1 ): 22 - 38
DOI:10.1016/j.marstruc.2009.10.002
[本文引用: 1]
[28]
ALMEIDA J H S, BITTRICH L, JANSEN E, et al Buckling optimization of composite cylinders for axial compression: a design methodology considering a variable-axial fiber layout
[J]. Composite Structures , 2019 , 222 : 110928
DOI:10.1016/j.compstruct.2019.110928
[本文引用: 1]
Application of composite in marine industry
1
2011
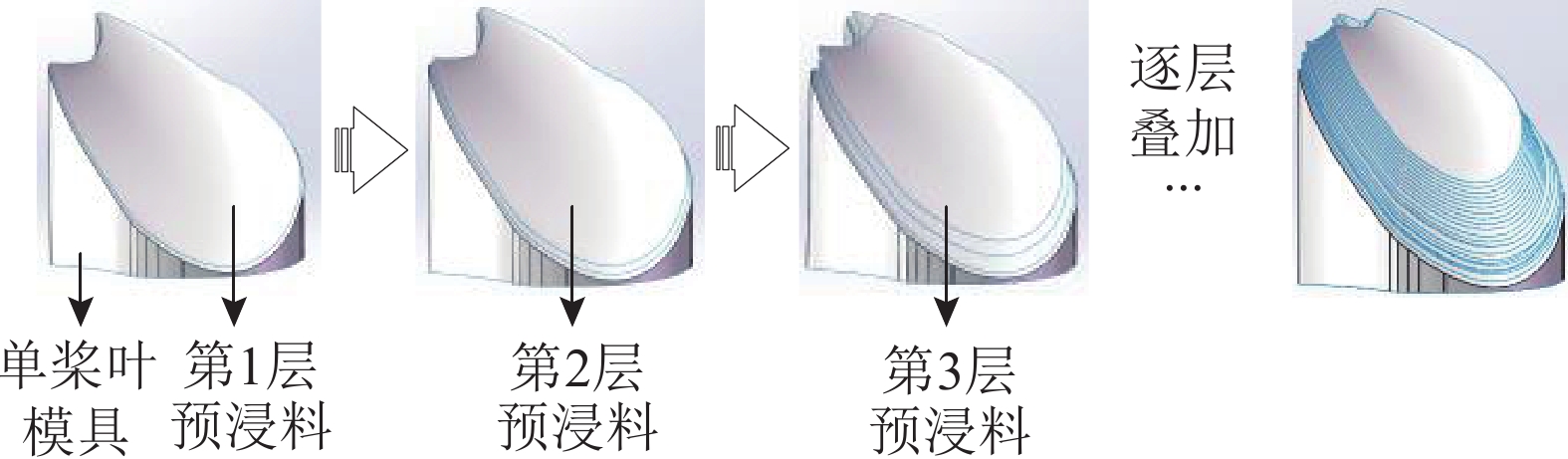
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
A new start for marine propellers?
1
2004
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
1
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
1
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
大厚度船用复合材料螺旋桨桨叶设计与成型工艺
3
2022
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
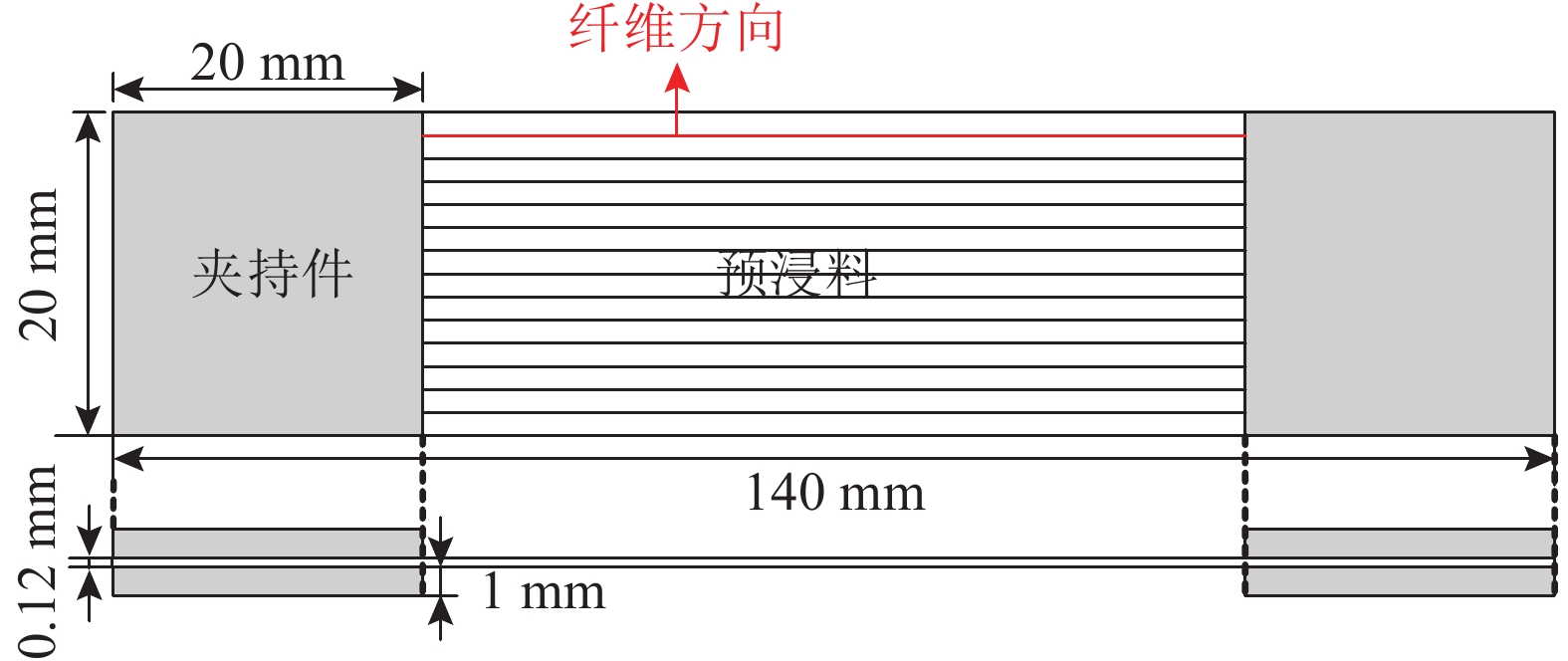
... T300单向碳纤维预浸料属性[4 ] ...
... Properties of T300 unidirectional carbon fiber prepreg[4 ] ...
大厚度船用复合材料螺旋桨桨叶设计与成型工艺
3
2022
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
... T300单向碳纤维预浸料属性[4 ] ...
... Properties of T300 unidirectional carbon fiber prepreg[4 ] ...
复合材料螺旋桨RTM成型工艺研究
1
2015
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
复合材料螺旋桨RTM成型工艺研究
1
2015
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
Are composite propellers the way forward for small boats
1
1994
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
Optimization and experiment of composite marine propellers
1
2009
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
风轮叶片树脂与成型工艺研究进展
1
2012
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
风轮叶片树脂与成型工艺研究进展
1
2012
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
1
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
1
... 碳纤维复合材料具有拉伸强度高、模量大、密度小、比强度高、比模量高等特性,在船用螺旋桨方面拥有广阔的发展前景. 碳纤维复合材料螺旋桨成型工艺的精度对螺旋桨的性能有着重要影响[1 ] . 目前,复合材料螺旋桨有RTM[2 ] (resin transfer moulding)、模压成型[3 ] 之类的制备工艺,国内外学者对此也有大量研究,例如,周鑫等[4 ] 为了保证大厚度桨叶制备的精准度,以桨叶几何型值的确定作为设计和研究切入点,开展了大厚度船用复合材料螺旋桨桨叶设计与成型工艺的研究,提出一种大厚度复合材料螺旋桨叶的制备方案. 杨文志等[5 ] 提出采用树脂传递模塑成型技术制作螺旋桨模型,制定了模具制备、纤维剪裁和铺层实施方案以及工艺流程,提出了适合复杂型线纤维布剪裁和铺层的实施方案来确保螺旋桨叶复杂曲面的制备精度. Searle等[6 ] 利用RTM技术和真空融合工艺制作复合材料螺旋桨叶,进一步提高其制备质量. Lin等[7 ] 利用RTM技术制作小直径大侧斜的复合材料螺旋桨. 王晓飞等[8 -9 ] 对RTM成型原理和研究进展进行了对比. 研究表明,无论哪种成型工艺,碳纤维复合材料螺旋桨叶的逐层铺设都是其中的必要环节. 由于逐层铺设的制备工艺、复合材料本身强烈的各向异性、较弱的层间强度以及船用螺旋桨叶所具有的变截面、大曲率几何特征等问题,预浸料铺层的层间误差会随铺放过程不断累积,导致复合材料螺旋桨叶的制备误差远比其他各向同性材料桨叶的制备误差大,这也制约着复合材料螺旋桨在船舶方面的发展与应用. ...
1
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
1
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
1
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
1
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
Flattening developable bi-parametric surfaces
1
1996
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
Design of plane developments of doubly curved surfaces
1
1997
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
1
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
1
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
复合材料机器人纤维铺放工艺参数优化
1
2018
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
复合材料机器人纤维铺放工艺参数优化
1
2018
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
碳纤维复合材料结构件自动铺放技术与装备研究进展
1
2023
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
碳纤维复合材料结构件自动铺放技术与装备研究进展
1
2023
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
纤维曲线铺放制备变刚度复合材料层合板的研究进展
0
2012
纤维曲线铺放制备变刚度复合材料层合板的研究进展
0
2012
New optimization method for steered fiber composites using the level set method
1
2015
... 接触属性的设置对预浸料铺层的仿真结果有着直接影响,由于预浸料铺层在铺放过程中接触关系最复杂,为了明确表达这种接触关系,在上表面与预浸料铺层下表面之间建立具有法向硬接触属性和切向惩罚函数接触属性的面对面接触,选用有限滑移接触跟踪法,来准确模拟层间的真实接触状态. 在仿真过程中,压载模具、预浸料铺层以及底层模具三者之间的接触关系会随着载荷和位移变形而不断发生变化. 因此,在模型中须考虑法向硬接触以及切向基于惩罚函数的摩擦接触. 根据复合材料与金属接触的接触研究经验值,将摩擦因数设定为0.3[18 ] . 为了减少底层模具与压载模具因位置偏移对预浸料铺层层间误差结果的影响,在压载模具叶根端点处创建参考点,并对其建立约束,限制所有平移自由度. 同时,对该参考点施加垂直向下的压力载荷,其移动距离为参考点到底层模具对应位置端点的距离. 此外,对下表面与预浸料铺层上表面建立面对面接触. 对于预浸料铺层,限制其横向平移自由度,以限制水平方向的位移,从而提高初始分析步的收敛性. ...
Buckling analysis of variable angle tow composite plates with a through-the-width or an embedded rectangular delamination
0
2018
Postbuckling optimisation of a variable angle tow composite wingbox using a multi-modal Koiter approach
1
2019
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
1
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
1
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
1
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
Robotic fiber placement process analysis and optimization using response surface method
1
2011
... 国内外学者对于碳纤维铺层的曲面铺放以及层间问题进行了一系列研究,例如,陆九如[10 ] 提出对碳纤维复合材料薄壁曲面构件的纤维铺放方法. 宋超等[11 ] 开展复合材料叶片曲面可铺性分析研究,提出基于预浸料纤维变形及纤维铺放方向双约束的复杂曲面复合材料构件可铺性分析方法. Gan等[12 ] 提出基于约束全局优化算法的恒定测地曲率曲面划分方法. Azariadis等[13 ] 给出基于约束全局优化算法的恒定测地曲率曲面划分方法. 王立冬[14 ] 研究预浸料的成型起皱会导致层间滑移并建立了考虑相对滑移位移及工艺参数影响的层间滑移模型. 赵盼等[15 ] 建立铺放工艺参数对层间结合度的多层作用机理模型. 国内外学者在复合材料自动铺放工艺规划技术、自动化铺放装备研制、铺丝过程的纤维特性以及铺放工艺规划软件开发等方面探讨了高端复合材料构件制造面临的核心技术问题[16 -20 ] . 都涛[21 ] 开发预浸料性能的试验方法,探究铺放工艺参数对国产碳纤维预浸料成型的影响规律,并结合固化后复合材料构件性能,对预浸料的铺放质量进行系统性评价,以确定合适的铺放工艺参数. Lukaszewicz[22 ] 研究铺放温度和铺放压力对预浸料层间相互作用的影响,进而对铺放过程中微观尺度下的非固化预浸料成型行为进行预测. Aized等[23 ] 提出一种定性铺放质量评价方法,在认为预浸料与模具之间以及预浸料铺层之间充分贴合的情况下,将铺放质量分为5级,分别为不能接受的、一般的、好的、非常好的以及极好的. ...
Structural strength and laminate optimization of composite connecting bracket in manned spacecraft using a genetic algorithm
1
2019
... 成型工艺的优劣在很大程度上决定了螺旋桨性能的发挥. 由于螺旋桨具有变曲率及复杂多变的几何特征,通过成型质量试验研究纤维铺层对螺旋桨水动力性能及结构变形特性的影响具有较高难度. 基于优化算法和有限元算法的螺旋桨成型工艺质量研究逐渐趋于成熟,包括基于遗传算法的铺层设计优化[24 ] 、结合面元法与有限元法的迭代分析法[25 ] . Blasques等[26 ] 提出基于定制纤维铺放工艺的优化方法,通过有限元屈曲分析初步评估了该工艺在制备过程中对缺陷的敏感性. 卢秉贺等[27 ] 针对复合材料在各向异性条件下设计难度较大的问题,运用有限元方法开展结构分析,并进行了铺层设计及其过渡策略的优化. Almeida等[28 ] 聚焦于柔性复合材料螺旋桨的设计与优化,通过有限元分析建立螺旋桨的水弹性模型,并以此为基础指导铺层方案的制定 ...
复合材料螺旋桨纤维铺层的影响及预变形设计
1
2014
... 成型工艺的优劣在很大程度上决定了螺旋桨性能的发挥. 由于螺旋桨具有变曲率及复杂多变的几何特征,通过成型质量试验研究纤维铺层对螺旋桨水动力性能及结构变形特性的影响具有较高难度. 基于优化算法和有限元算法的螺旋桨成型工艺质量研究逐渐趋于成熟,包括基于遗传算法的铺层设计优化[24 ] 、结合面元法与有限元法的迭代分析法[25 ] . Blasques等[26 ] 提出基于定制纤维铺放工艺的优化方法,通过有限元屈曲分析初步评估了该工艺在制备过程中对缺陷的敏感性. 卢秉贺等[27 ] 针对复合材料在各向异性条件下设计难度较大的问题,运用有限元方法开展结构分析,并进行了铺层设计及其过渡策略的优化. Almeida等[28 ] 聚焦于柔性复合材料螺旋桨的设计与优化,通过有限元分析建立螺旋桨的水弹性模型,并以此为基础指导铺层方案的制定 ...
复合材料螺旋桨纤维铺层的影响及预变形设计
1
2014
... 成型工艺的优劣在很大程度上决定了螺旋桨性能的发挥. 由于螺旋桨具有变曲率及复杂多变的几何特征,通过成型质量试验研究纤维铺层对螺旋桨水动力性能及结构变形特性的影响具有较高难度. 基于优化算法和有限元算法的螺旋桨成型工艺质量研究逐渐趋于成熟,包括基于遗传算法的铺层设计优化[24 ] 、结合面元法与有限元法的迭代分析法[25 ] . Blasques等[26 ] 提出基于定制纤维铺放工艺的优化方法,通过有限元屈曲分析初步评估了该工艺在制备过程中对缺陷的敏感性. 卢秉贺等[27 ] 针对复合材料在各向异性条件下设计难度较大的问题,运用有限元方法开展结构分析,并进行了铺层设计及其过渡策略的优化. Almeida等[28 ] 聚焦于柔性复合材料螺旋桨的设计与优化,通过有限元分析建立螺旋桨的水弹性模型,并以此为基础指导铺层方案的制定 ...
Hydro-elastic analysis and optimization of a composite marine propeller
1
2010
... 成型工艺的优劣在很大程度上决定了螺旋桨性能的发挥. 由于螺旋桨具有变曲率及复杂多变的几何特征,通过成型质量试验研究纤维铺层对螺旋桨水动力性能及结构变形特性的影响具有较高难度. 基于优化算法和有限元算法的螺旋桨成型工艺质量研究逐渐趋于成熟,包括基于遗传算法的铺层设计优化[24 ] 、结合面元法与有限元法的迭代分析法[25 ] . Blasques等[26 ] 提出基于定制纤维铺放工艺的优化方法,通过有限元屈曲分析初步评估了该工艺在制备过程中对缺陷的敏感性. 卢秉贺等[27 ] 针对复合材料在各向异性条件下设计难度较大的问题,运用有限元方法开展结构分析,并进行了铺层设计及其过渡策略的优化. Almeida等[28 ] 聚焦于柔性复合材料螺旋桨的设计与优化,通过有限元分析建立螺旋桨的水弹性模型,并以此为基础指导铺层方案的制定 ...
基于Hypersizer的复合材料结构铺层设计和铺层过渡设计
1
2011
... 成型工艺的优劣在很大程度上决定了螺旋桨性能的发挥. 由于螺旋桨具有变曲率及复杂多变的几何特征,通过成型质量试验研究纤维铺层对螺旋桨水动力性能及结构变形特性的影响具有较高难度. 基于优化算法和有限元算法的螺旋桨成型工艺质量研究逐渐趋于成熟,包括基于遗传算法的铺层设计优化[24 ] 、结合面元法与有限元法的迭代分析法[25 ] . Blasques等[26 ] 提出基于定制纤维铺放工艺的优化方法,通过有限元屈曲分析初步评估了该工艺在制备过程中对缺陷的敏感性. 卢秉贺等[27 ] 针对复合材料在各向异性条件下设计难度较大的问题,运用有限元方法开展结构分析,并进行了铺层设计及其过渡策略的优化. Almeida等[28 ] 聚焦于柔性复合材料螺旋桨的设计与优化,通过有限元分析建立螺旋桨的水弹性模型,并以此为基础指导铺层方案的制定 ...
基于Hypersizer的复合材料结构铺层设计和铺层过渡设计
1
2011
... 成型工艺的优劣在很大程度上决定了螺旋桨性能的发挥. 由于螺旋桨具有变曲率及复杂多变的几何特征,通过成型质量试验研究纤维铺层对螺旋桨水动力性能及结构变形特性的影响具有较高难度. 基于优化算法和有限元算法的螺旋桨成型工艺质量研究逐渐趋于成熟,包括基于遗传算法的铺层设计优化[24 ] 、结合面元法与有限元法的迭代分析法[25 ] . Blasques等[26 ] 提出基于定制纤维铺放工艺的优化方法,通过有限元屈曲分析初步评估了该工艺在制备过程中对缺陷的敏感性. 卢秉贺等[27 ] 针对复合材料在各向异性条件下设计难度较大的问题,运用有限元方法开展结构分析,并进行了铺层设计及其过渡策略的优化. Almeida等[28 ] 聚焦于柔性复合材料螺旋桨的设计与优化,通过有限元分析建立螺旋桨的水弹性模型,并以此为基础指导铺层方案的制定 ...
Buckling optimization of composite cylinders for axial compression: a design methodology considering a variable-axial fiber layout
1
2019
... 成型工艺的优劣在很大程度上决定了螺旋桨性能的发挥. 由于螺旋桨具有变曲率及复杂多变的几何特征,通过成型质量试验研究纤维铺层对螺旋桨水动力性能及结构变形特性的影响具有较高难度. 基于优化算法和有限元算法的螺旋桨成型工艺质量研究逐渐趋于成熟,包括基于遗传算法的铺层设计优化[24 ] 、结合面元法与有限元法的迭代分析法[25 ] . Blasques等[26 ] 提出基于定制纤维铺放工艺的优化方法,通过有限元屈曲分析初步评估了该工艺在制备过程中对缺陷的敏感性. 卢秉贺等[27 ] 针对复合材料在各向异性条件下设计难度较大的问题,运用有限元方法开展结构分析,并进行了铺层设计及其过渡策略的优化. Almeida等[28 ] 聚焦于柔性复合材料螺旋桨的设计与优化,通过有限元分析建立螺旋桨的水弹性模型,并以此为基础指导铺层方案的制定 ...