浙江大学学报(工学版)

浙江大学学报(工学版), 2025, 59(5): 1083-1091 doi: 10.3785/j.issn.1008-973X.2025.05.021

土木工程、交通工程

网络级道路交通运行状态的深度学习识别方法

罗义凯,, 辛苡琳, 徐金华, 陈桂珍, 李岩,

1. 长安大学 运输工程学院，陕西 西安 710064

2. 比亚迪汽车有限公司，陕西 西安 710018

Deep learning method for recognizing network-level road traffic state

LUO Yikai,, XIN Yilin, XU Jinhua, CHEN Guizhen, LI Yan,

1. College of Transportation Engineering, Chang’an University, Xi’an 710064, China

2. BYD Automobile Limited Company, Xi’an 710018, China

通讯作者: 李岩, 男, 教授, 博导. orcid.org/0000-0002-5010-4735. E-mail: lyan@chd.edu.cn

收稿日期: 2024-02-27  

基金资助: 国家自然科学基金资助项目（51408049）；陕西省自然科学基础研究计划资助项目（2020JM-237）.

Received: 2024-02-27  

Fund supported: 国家自然科学基金资助项目（51408049）；陕西省自然科学基础研究计划资助项目（2020JM-237）.

作者简介 About authors

罗义凯（1998—），男，博士生，从事深度学习和智能交通的研究.orcid.org/0009-0007-9024-4656.E-mail：lyk@chd.edu.cn , E-mail：lyk@chd.edu.cn

摘要

为了精准、实时、高效地掌握道路网各区域交通运行状态，基于网约车轨迹数据提取相关运行参数，对研究区域进行时空单元划分，构建将特征提取与聚类过程融合的深度聚类网络模型，对交通状态进行分类. 对聚类结果量化获取类别标签，结合集成学习、贝叶斯优化和轻量梯度提升机，提出交通状态识别模型. 西安市网约车数据测试的结果表明，道路运行状态可以分为畅通、缓行、轻度拥堵、中度拥堵和严重拥堵5种类型，严重拥堵路段占比在早晚高峰时段明显增加，平峰时段有所减少. 所提聚类模型的效果均优于对比模型，交通状态识别模型计算的精确率、召回率、F1分数和准确率分别为0.982 1、0.984 4、0.983 3、0.983 9.

关键词： 网络级道路 ; 交通运行状态 ; 深度聚类 ; 轨迹数据 ; 轻量梯度提升机

Abstract

The research area was divided into spatiotemporal units, and a deep clustering network model that integrated feature extraction and clustering process was constructed based on the trajectory data of online car-hailing to extract relevant operation parameters to identify traffic states in order to accurately, real-time and efficiently grasp the traffic operation state of various areas in the road network. The clustering results were quantified to obtain category labels, and a traffic state identification model was proposed combining integrated learning, Bayesian optimization and light gradient boosting machine. The test results of Xi'an online car-hailing data show that road operation states can be divided into 5 types: smooth, slow, mild congestion, moderate congestion and severe congestion. The proportion of severely congested road sections increases significantly during morning and evening peak periods and decreases during off-peak periods. The proposed clustering model performs better than the comparison models, with the precision, recall, F1-score and accuracy of the traffic state identification model being 0.982 1, 0.984 4, 0.983 3 and 0.983 9 respectively.

Keywords： network-level road ; traffic operation state ; deep clustering ; trajectory data ; light gradient boosting machine

PDF (1388KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

罗义凯, 辛苡琳, 徐金华, 陈桂珍, 李岩. 网络级道路交通运行状态的深度学习识别方法. 浙江大学学报(工学版)[J], 2025, 59(5): 1083-1091 doi:10.3785/j.issn.1008-973X.2025.05.021

LUO Yikai, XIN Yilin, XU Jinhua, CHEN Guizhen, LI Yan. Deep learning method for recognizing network-level road traffic state. Journal of Zhejiang University(Engineering Science)[J], 2025, 59(5): 1083-1091 doi:10.3785/j.issn.1008-973X.2025.05.021

道路交通运行状态的识别对预防交通事故至关重要. 以往针对交通状态识别的对象多聚焦于单路段或某一交叉口，缺乏对道路网络的整体性分析[1]. 实时了解整个道路网的交通运行状况不仅有利于交通拥堵疏导，为驾驶人提供精准的路径信息，而且能够挖掘道路中的潜在风险，为信号灯调控、道路设计及城市规划等提供依据.

交通运行状态的识别常分为指标选取、状态划分和识别方法3部分[2]. 常用的指标有交通流量、道路拥堵率、车辆平均速度和车道平均速度差值(DSpeed)、延迟时间、道路饱和度、驾驶效率和低速比、车辆密度、车间距和排队长度等[3-7]. 相较于选取单一指标，利用多指标结合的方法能够更全面、准确地反映交通运行状态. 在识别之前，须对交通运行状态进行划分，从数据角度出发的聚类算法常被用于类别划分. 苏俊杰等[8]通过k-means 聚类方法，提出基于控制策略的交通状态识别模型. 李晓璐等[9]利用改进的模糊C均值(fuzzy c-means, FCM)算法对特征参数进行聚类，建立基于多分类器支持向量机的交通状态识别模型. k-means和FCM是基于距离度量的聚类算法，由多元交通运行参数构成的高维时序数据在进行聚类时受“维度效应”的影响[10]. 在高维空间中，样本之间的距离变得模糊，导致聚类效果下降. 传统的提取特征方法由于与聚类目标不匹配，会使状态划分不能达到预期效果[11].

近年来，基于机器学习的交通状态识别方法受到广泛的关注. 该方法通过聚类算法获取标签后，利用监督学习识别得到道路所处的交通状态. 常用的XGBoost和LightGBM模型在单路段状态识别中表现优异[12]，然而道路网络中各路段的运行状态相互关联，简单地对单个路段的识别进行累加，不能构建整体道路网络的识别模型.

针对上述问题，本文基于网约车的轨迹数据选取多元指标，在深度聚类(deep embedded clustering, DEC) [13-14]和分类的联合使用下，提出网络级的交通运行状态识别方法.

1. 方法简介

提出的方法可以分为以下几步. 1）利用网约车轨迹数据能够真实反映道路运行状态的特性，对研究区域进行时空划分和轨迹点地图匹配. 2）针对多元指标搭建交通运行状态深度聚类网络模型(traffic state deep embedded clustering, TS-DEC)，对时空单元聚类. 该模型通过构建基于LSTM的深度自编码神经网络，对高维时序数据进行降维和特征提取[15]，利用K-means在特征空间上聚类. 3）为使聚类结果具有实际意义，将聚类结果量化. 4）构建Bagging-Bo-LightGBM识别模型，对整个道路网各个时空单元进行实时、准确的交通运行状态识别[16-17]. 方法流程如图1所示.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   网络级道路交通运行状态识别方法的流程图

Fig.1   Flowchart of network-level road traffic state recognition method


1.1. 数据处理

本文数据处理的对象为网约车轨迹数据，它通过车辆上配备的GPS定位设备获取车辆的位置信息，定期发送车辆的运行状态数据. 由于信号丢失、定位误差及其他原因，往往造成轨迹数据的缺失和异常. 针对缺失数据，在将数据按车辆编号和订单编号分组的基础上，计算每一个出行链中当前记录对应的时间戳与上一相邻记录时间戳的差值，筛选出差值大于采样间隔的索引，即可找出缺失值. 针对偏移出正常道路的异常轨迹点，选用考虑航向和距离约束的滑动窗口地图匹配算法[18]，使用Arcgis软件建立缓冲区[19]，进行异常轨迹点和异常轨迹段的捕捉. 针对缺失值和剔除的异常值，采用最近邻插补法[20]填补空缺数据，地图匹配算法的流程如图2所示. 网约车轨迹点缺失和异常的示意图如图3所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   考虑航向和距离约束的滑动窗口地图匹配算法的流程

Fig.2   Flowchart of sliding window map matching algorithm with heading and distance constraint


网约车在正常行驶前后这2段时间的行驶状态与路网其他车辆的运行状态不同. 为了使网约车轨迹数据能够尽可能地还原路网的真实交通运行状态，须剔除这2段时间的轨迹数据，只保留正常行驶部分的数据. 按照一般汽车的起步加速度约为3 m/s2计算，将9 s作为网约车起步加速到维持正常行驶速度的时间，删除前9 s的采样记录，同理减速阶段删除后9 s的采样记录.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   网约车轨迹点缺失和异常的示意图

Fig.3   Illustration of missing and anomalous trajectory point in ride-hailing data


1.2. 指标体系

选取以下交通运行参数作为交通运行的评价指标.

1)平均速度. 平均速度是反映道路交通状态的重要指标，以同一时空单元内所有网约车的运行速度的平均值作为平均速度.

2)平均加速度. 加速度反映了车辆在单位时间内运行速度的变化率，是表征交通运行状况的重要参数，平均加速度是同一时空单元内车辆在运行过程中的加速度的平均值.

3)速度标准差. 运行速度标准差用来衡量各运行速度偏离平均速度的程度，反映了运行速度分布的离散程度.

4)设计速度一致性. 设计速度一致性是用于表示道路交通实际运行速度与设计速度一致程度的指标，道路的设计速度是在各方面条件都良好的情况下最理想的行车速度[21].

5)平均停车次数. 平均停车次数是同一时空单元内车辆停车次数的平均值.

6)速度不平衡率. 速度不平衡率是与平均速度之差的绝对值超出平均速度50%的运行速度个数占所有运行速度个数的比值.

以上6个交通运行参数能够从运行速度大小、变化率、分布的离散程度、与设计速度一致性、交通运行的连续性和可控性较全面地反映道路运行状态.

1.3. 深度聚类网络模型

经典聚类使用表征学习将数据以矢量化的形式表示特征，然而这会使数据复杂化，导致这些方法难以处理高维度大批量的数据. DEC的核心思想是结合无监督学习和深度学习，在数据输入传统聚类前进行深度表征，对深度表征学习和聚类联合优化. 学习到的高质量特征有助于提升聚类算法的性能，聚类结果可以引导神经网络学习更好的特征. 这种方法使得聚类在高维空间中更加有效，可以处理大规模数据.

1.3.1. 模型的特征处理器部分

为了能够有效地从交通运行参数构成的高维时间序列及时序特征差异中提取所需的特征，将LSTM引入特征提取过程，利用时序特征无监督学习的优势，构建深度自编码神经网络(autoencoder, AE) [22]. 作为TS-DEC模型的一部分，基于LSTM的深度自编码神经网络取代了传统聚类手工设计的特征处理器，以重构输入信号为目标，输入层的数据同时用作输出层的期望输出来指定模型的收敛方向，可以自动地从无标签的数据中学习特征.

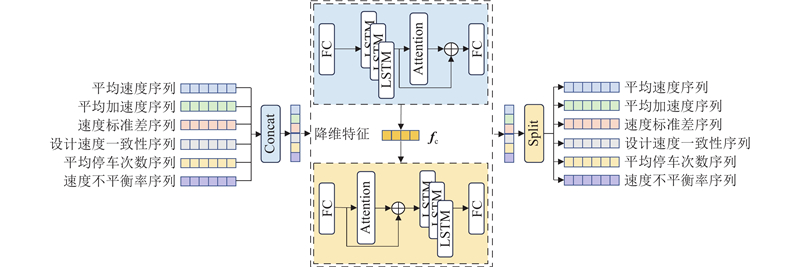
基于LSTM的深度自编码神经网络结构如图4所示，时序注意力编码器在多层LSTM网络两端加入2个全连接层FC，该编码器的作用是学习高维时序数据中隐含的交通运行状态特征的低维表示，即利用非线性映射$ {f}_{\theta }:\boldsymbol{X}\to \boldsymbol{Z} $（$ \mathrm{其}\mathrm{中}\boldsymbol{X} $为交通运行参数的原始参数空间，$ \boldsymbol{Z} $为潜在特征空间），将输入的高维复合向量$ \boldsymbol{x} $映射到低维的潜在特征空间中，以提取低维交通状态特征向量$ {\boldsymbol{f}}_{{{\mathrm{c}}}} $. 其中，利用多层LSTM网络提取变量的时序特征，左端全连接层的输出神经元个数大于输入神经元个数，旨在增加输入向量的维度，使编码的信息不低于实际有效的信息，提升神经网络的拟合能力，右端全连接层旨在对高维特征向量降维，并过滤冗余信息. 在特征提取过程中加入注意力机制，调整不同参数的时序序列对应特征的权重. 时序注意力解码器的作用是将低维特征向量$ {\boldsymbol{f}}_{{{\mathrm{c}}}} $还原到初始维度，实现对输入向量$ \boldsymbol{x} $的重构，其结构设计和编码器相反.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   基于LSTM的深度自编码神经网络

Fig.4   Deep self-coding neural network based on LSTM


将各时空单元的时序向量$ \bar{\boldsymbol{v}} $（平均速度）、$ \bar{\boldsymbol{a}} $（平均加速度）、$ {\boldsymbol{\sigma }}_{\boldsymbol{v}} $（速度标准差）、$ {\boldsymbol{D}}_{{{\mathrm{C}}}} $（设计速度一致性）、$ {{{\boldsymbol{C}}}}_{\mathrm{{{s}{t}{o}{p}}}} $（平均停车次数）和$ \boldsymbol{R} $（速度不均衡率），通过拼接函数Concat组合为复合向量$ \boldsymbol{x}=[\bar{\boldsymbol{v}},\bar{\boldsymbol{a}}, {\boldsymbol{\sigma }}_{\boldsymbol{v}},{\boldsymbol{D}}_{{{\mathrm{C}}}}, {\boldsymbol{C}}_{{\mathrm{stop}}}, {\boldsymbol{R}}] $作为深度自编码神经网络的输入，其中$ \boldsymbol{x}\in \boldsymbol{X} $. 以输入向量$ \boldsymbol{x} $与重构向量$ \tilde{\boldsymbol{x}} $的重构误差$ {L}_{\mathrm{R}\mathrm{E}} $作为神经网络模型的损失.

$ {L}_{\mathrm{R}\mathrm{E}}=\frac{1}{6 T}\sum _{t=1}^{T}{||{\boldsymbol{x}}_{{t}}-{\tilde{\boldsymbol{x}}}_{{t}}||}_{2}^{2}. $

式中：$ T\mathrm{为} $输入序列的最大时间索引，$ {\boldsymbol{x}}_{{t}} $、$ {\tilde{\boldsymbol{x}}}_{{t}} $分别为$ t $时段的输入序列和输出的重构序列.

1.3.2. 模型聚类的步骤

深度聚类网络模型将聚类过程与特征提取过程结合，作为端到端的网络模型. 通过特征提取过程，将原始参数空间$ \boldsymbol{X} $映射到低维特征空间$ \boldsymbol{Z} $，在该映射中优化聚类效果. 将聚类过程中的损失反馈给特征提取过程，2个过程相互促进. TS-DEC模型的步骤如下.

算法1　TS-DEC深度聚类
输入：经数据处理的高维时序数据
步骤：
//依据DEC算法中KL散度(Kullback-Leibler divergence, KL)的聚类方法
1）通过LSTM深度自编码神经网络，获取特征分布空间$ \boldsymbol{Z} $及特征映射$ {f}_{\theta } $.
2）采用K-means算法，确定$ \boldsymbol{Z} $中的初始聚类中心$ {\boldsymbol{\mu }}_{{j}}\left\{{\boldsymbol{\mu }}_{{j}}\in \boldsymbol{Z},j=1,2, \cdots ,k\right\} $.
3） while 总损失$ L $未趋于稳定 do
4）计算特征空间中提取的特征与聚类中心的软分配$ q $，使用学生t分布来衡量特征向量$ {\boldsymbol{z}}_{{i}} $与聚类中心$ {\boldsymbol{\mu }}_{{j}} $之间的相似性，采用$ {\boldsymbol{z}}_{{i}} $与$ {\boldsymbol{\mu }}_{{j}} $之间的归一化相似性进行软分配.
5）计算软分配分布$ q $与辅助目标分布$ p $之间的KL散度，将二者的KL散度作为聚类损失$ {L}_{{\mathrm{C}}} $，以KL散度最小化作为聚类目标.
6）模型的总损失$ L $由特征提取过程产生的重构误差$ {L}_{\mathrm{R}\mathrm{E}} $和聚类过程产生的聚类误差$ {L}_{{\mathrm{C}}} $组成.
7） 迭代更新模型.
8） end while
输出：交通状态特征矩阵、聚类类别

学生t分布下$ {\boldsymbol{z}}_{{i}} $分配给$ {\boldsymbol{\mu }}_{{j}} $的概率$ {q}_{ij} $为

$ {q}_{ij}=\frac{{\left(1+{||{\boldsymbol{z}}_{{i}}-{\boldsymbol{\mu }}_{{j}}||}^{2}/\alpha \right)}^{-\frac{\alpha +1}{2}}}{{\displaystyle \sum }_{{j'}}{\left(1+{||{\boldsymbol{z}}_{{i}}-{\boldsymbol{\mu }}_{{{j'}}}||}^{2}/\alpha \right)}^{-\frac{\alpha +1}{2}}}. $

式中：$ {\boldsymbol{z}}_{{i}} $为模型输入的复合向量$ {\boldsymbol{x}}_{{i}}\in \boldsymbol{X} $经自编码神经网络提取的特征向量，$ {\boldsymbol{z}}_{{i}}={f}_{\theta }\left({\boldsymbol{x}}_{{i}}\right)\in \boldsymbol{Z} $；$ \alpha $为学生t分布的自由度.

设置辅助目标分布$ p $的目的是在聚类时能够学习高置信度特征向量来优化整体的聚类效果，辅助目标分布$ p $和聚类损失$ {L}_{\mathrm{C}} $的公式如下.

${p}_{ij}=\frac{{q}_{ij}^{2}/{\displaystyle \sum} _{i}{q}_{ij}}{{\displaystyle \sum} _{{j'}}\left({q}_{i{j'}}^{2}/{\displaystyle \sum} _{i}{q}_{ij}\right)}. $

$ {L}_{{\mathrm{C}}}={\mathrm{KL}}\left(P\right|\left|Q\right)=\sum _{i}\sum _{j}{p}_{ij}\mathrm{ln}\;\frac{{p}_{ij}}{{q}_{ij}}. $

模型的总损失$ L $由特征提取过程产生的网络损失$ {L}_{{\mathrm{RE}}} $和聚类过程产生的$ {L}_{{\mathrm{C}}} $组成.

$ L=\gamma {L}_{{\mathrm{RE}}}+\left(1-\gamma \right){L}_{{\mathrm{C}}}. $

式中：$ \gamma $为权重平衡系数.

1.4. 识别模型

为了实现对各个时空单元的交通状态实时识别，使用贝叶斯优化(Bayesian optimization, BO)优化LightGBM的超参数，包含决策树叶子节点数量$ \omega $、最大深度$ \alpha $、学习率$ \eta $和树的数量$ \tau $. 为了进一步提高模型的准确性，提升应对大规模数据的能力和泛化能力，采用集成学习中的Bagging算法，将多个子模型的识别结果进行组合，构建Bagging-Bo-LightGBM集成模型.

模型会根据预测值和真实值之间的误差来迭代更新本地决策树和全局树中的节点信息，使模型输出的类别标签不断逼近训练数据集中的真实标签. 模型的目标函数如下：

$ {{\mathrm{Obj}}}^{t}=\sum _{i=1}^{n}L\left({y}_{i,}{\hat{y}}_{i}^{t}\right)+\sum _{i=1}^{t}\mathrm{\varOmega }\left({f}_{i}\right). $

式中：$ {y}_{i} $为真实值，$ {\hat{y}}_{i}^{t} $为模型第$ t $次的预测值，$ n $为样本数量，$ \varOmega $为模型正则项.

算法2　Bagging-Bo-LightGBM识别模型
输入：LightGBM超参数向量$ \boldsymbol{x}=[{\mathrm{num}}\_{\mathrm{leaves,max}}\_ {\mathrm{depth}},\eta ,{\mathrm{n}}\_ {\mathrm{estimators}}] $、训练数据集$ D $（包含提取后的特征和标签向量）
步骤：
//贝叶斯优化lightGBM超参数过程
1）初始化：超参数、贝叶斯网络结构、迭代次数$ T $.
2） 定义目标函数：准确率$ f\left(\boldsymbol{x}\right) $ .
3）定义超参数空间联合先验分布$ P\left(\boldsymbol{x}\right)={\prod }_{i=1}^{d}P\left({x}_{i}\right) $.
4）选择初始参数点$ ({x}_{1},{x}_{2}{,\cdots ,x}_{n}) $, 计算目标函数值.
5）使用高斯过程(Gaussian process, GP)拟合代理模型，$ \hat{f}\left(\boldsymbol{x}\right)\sim{{\mathrm{G}}}{{\mathrm{P}}}\left(m\left(\boldsymbol{x}\right),k\left(\boldsymbol{x},\bar{\boldsymbol{x}}\right)\right) $.
6） for $ t=\mathrm{1,2},\cdots ,T $ do
7） 依据高斯过程后验分布找到下一个参数点 $ {\boldsymbol{x}}_{\boldsymbol{n}+1} $.
8） $ {\boldsymbol{x}}_{\boldsymbol{n}+1}={\mathrm{argmax}}\;\left\{\mu \left(\boldsymbol{x}\right)+k\sigma \left(\boldsymbol{x}\right)\right\} $.
9） 使用$ {\boldsymbol{x}}_{\boldsymbol{n}+1} $计算目标函数$ f\left(\boldsymbol{x}\right) $值.
10） 更新代理模型.
11）end for
//在优化超参数的基础上，使用Bagging优化分类过程
12）初始化：子采样率、子模型数量$ m $.
13）for $ i=\mathrm{1,2}, \cdots ,m $ do
14） 对训练集$ D $中所有样本进行i次有放回的抽样，生成训练子集$ {D}_{i} $.
15） 在子训练集$ {D}_{i} $上训练基本模型$ {M}_{i} $.
16） end for
17）使用所有基本模型$ {M}_{i} $进行预测，并统计预测结果.
18）采用软投票(soft voting, SV)，对分类结果加权平均.
19）最终的分类结果$ {C}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}} $可以表示为$ {C}_{\mathrm{fi}\mathrm{n}\mathrm{a}\mathrm{l}}={\mathrm{argmax}}_{{{C}}} \left(\sum _{i=1}^{m}{m}^{-1}{P}_{i}\left({{C}}\right)\right) $，其中$ {P}_{i}\left({{C}}\right) $为预测概率.
输出：Bagging和Bo共同优化后的LightGBM集成模型

2. 实例验证

2.1. 数据采集

采用西安市滴滴盖亚网约车的轨迹数据集，数据记录了2018年10月8日至10月15日的592 140条订单的轨迹数据. 轨迹点采样时间间隔为3 s，研究区域的经纬度范围分别为（108.92759, 108.99588）和（34.20623，34.24339），包含二环南路、长安路、曲江大道等不同等级的道路，如图5所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   网约车轨迹数据的采集区域

Fig.5   Collection area of ride-hailing trajectory data


如表1所示为部分轨迹数据的组成，含订单编号、车辆编号、经度、纬度、时间戳. 经数据处理后，共得到15 311 980个有效轨迹点，综合考虑研究目的、精度及研究范围内轨迹点的数量等因素，选取5 min为时间间隔，150 m为空间网格大小，对轨迹数据进行时空单元划分.

表 1   网约车轨迹数据的样例

Tab.1  Sample data of online car-hailing trajectory

订单编号车辆编号经度/(°)纬度/(°)时间戳
79b55f7533……e14c06bccc0bcb8012……f81a5827108.9460134.25298153912798
79b55f7533……e14c06bccc0bcb8012……f81a5827108.9460234.25296153912801
79b55f7533……e14c06bccc0bcb8012……f81a5827108.9460734.25293153912804
79b55f7533……e14c06bccc0bcb8012……f81a5827108.9460834.25292153912807
79b55f7533……e14c06bccc0bcb8012……f81a5827108.9460834.25293153912811

新窗口打开| 下载CSV


2.2. 聚类模型的结果

2.2.1. 聚类结果的分析

对TS-DEC模型进行迭代训练，训练过程中模型总损失$ L $的变化如图6所示. 当迭代次数$ {E}_{{\mathrm{p}}} $>2 000时，损失基本不再下降且保持稳定，模型能够收敛，表明设计的特征提取器和聚类算法具有可行性.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   深度聚类模型的损失函数

Fig.6   Loss function of deep embedded clustering model


TS-DEC模型采用肘部法则选取最佳的聚类数目，采用组内误差平方和(WSSE)作为评价指标. 如图7所示，拐点对应的聚类数目为5，因此将路网交通运行状态划分为5类.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   时空单元的聚类数目

Fig.7   Number of cluster for spatio-temporal unit


为了进一步观察TS-DEC模型在隐空间获取聚类特征的分离程度，将由6个交通运行参数组成的6维隐变量降至3维，并在3维空间中展示可视化结果. 可视化效果如图8所示. 图中，F1 、F2、F3为隐变量的3个特征.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   深度聚类特征的三维可视化

Fig.8   Three-dimensional visualization of deep embedded clustering feature


2.2.2. 对比实验

选取以下4种模型验证TS-DEC模型的可靠性，分别是K-means、FCM、结合随机森林(random forest, RF)与K-means的聚类模型以及结合AE与K-means的聚类模型，选取轮廓系数$ {S}_{{\mathrm{c}}} $和$ {C}_{\mathrm{h}} $指数对模型聚类质量进行评估. 其中$ {S}_{{\mathrm{c}}} $越接近1，$ {C}_{\mathrm{h}} $指数越大，说明类簇越紧凑，聚类效果越好.

从表2可以看出，基于初始数据直接聚类的方法对应的$ {S}_{{\mathrm{c}}} $和$ {C}_{\mathrm{h}} $都相对较小，原因在于输入指标为高维数据，影响聚类结果. 采用随机森林和自编码器进行特征提取后再聚类的方法，聚类效果有所提高. 所提模型的$ {S}_{{\mathrm{c}}} $和$ {C}_{\mathrm{h}} $分别为0.886 3和204168.57，聚类效果更好.

表 2   不同模型对时空单元的聚类效果评估

Tab.2  Evaluation of spatiotemporal unit clustering by different models

模型$ {S}_{{\mathrm{c}}} $$ {C}_{{\mathrm{h}}} $
K-means0.492 265 713.11
FCM0.469 168 899.26
RF-K-means0.684 592 241.37
AE-K-means0.711 6117 002.29
TS-DEC0.886 3204 168.57

新窗口打开| 下载CSV


2.3. 交通运行状态等级的量化

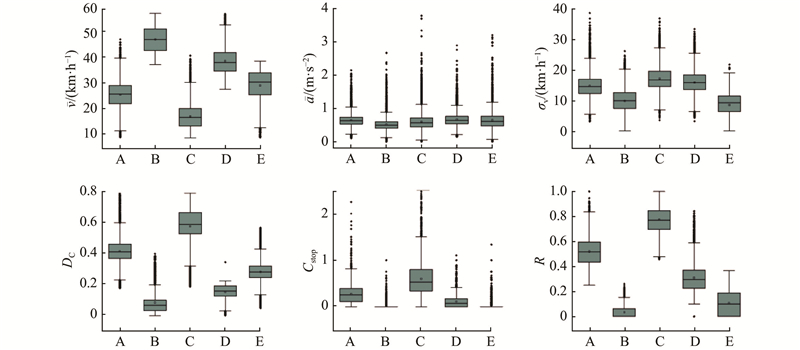
利用TS-DEC模型，将交通运行状态聚为5类，以A、B、C、D、E编号. 为了使聚类结果更具有现实意义，须对各类别的交通状态等级进行量化. 根据图9中各类别的指标分布，通过对各类别的指标分布特征进行比较和分析，对其状态等级进行量化. 具体量化如下.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   对应交通运行状态指标的分布特征

Fig.9   Distribution characteristic of corresponding traffic state indicator


由于类别C的平均速度均值最小为17.032 km/h，平均加速度指标相对较大，速度标准差、设计速度一致性、平均停车次数和速度不均衡率指标均明显大于其他类别，表明该类别内的交通运行缓慢，交通运行状态复杂，速度分布混乱，交通在运行过程中受到的限制较强烈. 该类别对应的交通运行特征与交叉口和拥堵路段的交通运行特征基本相同，因此将交通状态等级设为5级.

类别B的平均速度均值最大为46.112 km/h，其他指标最小且分布较集中，表明此类别内的交通运行通畅，交通运行的连续性和一致性较好，将等级设置为1级.

类别D和类别E的各项指标都与类别B较接近，类别D的平均速度均值较类别E大22.6%，设计速度一致性指标的均值比类别E小29.2%，但类别E的平均加速度、速度标准差、平均停车次数和速度不均衡均低于类别D. 类别E对应的交通运行特征为：虽然行驶速度相对较慢，但是运行状态较平稳有序. 将类别E的等级设为2级，类别D设为3级.

类别A的各项指标都与类别C较接近，且平均加速度较大，速度标准差、设计速度一致性、平均停车次和速度不均衡率指标明显高于类别B、D、E，表明该类别下的交通运行较拥堵. 将类别A设为4级.

各类别对应的交通运行等级如表3所示.

表 3   交通运行状态的量化结果

Tab.3  Quantified ranking result of traffic state

类别等级运行状态
A4中度拥堵
B1畅通
C5严重拥堵
D3轻度拥堵
E2缓行

新窗口打开| 下载CSV


2.4. 分布特征的分析

对交通运行状态进行等级划分后，以30 min为统计单元，选取6:00—18:00各等级对应的路段在所有路段中的占比$P_{\mathrm{r}} $进行统计分析，如图10所示. 从各等级路段占比的整体情况来看，早晚高峰现象较明显. 在高峰期间，畅通路段占比会明显减小，拥堵路段占比会明显增加，研究结果与实际情况相符.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   各等级路段时间占比的分布特征

Fig.10   Distribution characteristic of time proportion by every level road


利用交通运行状态划分结果，可以研究各等级路段占比的时间分布，还能够获取研究范围内同一时段不同路段对应的交通运行等级空间分布. 当研究空间分布时，对路段流向进行上、下行分隔处理. 如图11所示为早高峰8:00—8:05上行和下行路段交通运行状态的空间分布. 图中，Ls为状态标签. 从图11可以看出，上、下行对应的空间分布特征存在一定的差异，交叉口的拥堵等级普遍高于普通路段，主要道路如二环南路、长安路对应的拥堵等级较高.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

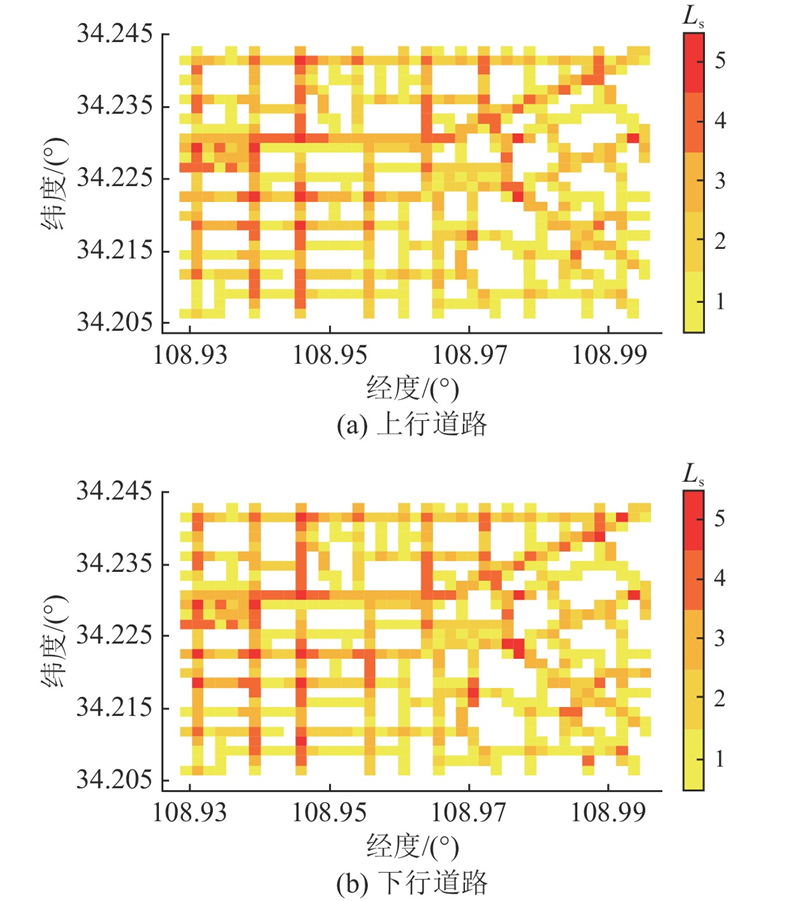
图 11   道路交通运行状态的全局空间分布云图

Fig.11   Global spatial distribution contour map of road traffic state


2.5. 识别模型结果

模型的输入为自编码神经网络提取的特征矩阵，标签向量为深度聚类类别结果. 输出为预测的类别.

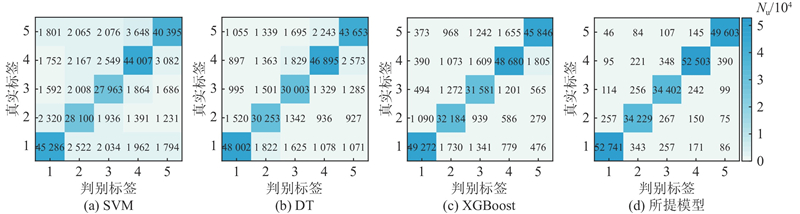
将数据按7∶3划分为训练集和测试集，引入支持向量机(SVM)、决策树(DT)及XGBoost 3种模型与所提模型进行对比分析. 识别结果对应的混淆矩阵如图12所示，共计227 231个时空单元. 图中，Nu为时空单元的个数. 其中Bagging-Bo-LightGBM集成模型的识别准确率最高，共计准确识别223 478个时空单元的状态等级.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   各交通运行状态识别模型的混淆矩阵

Fig.12   Confusion matrix of every traffic state identification model


选取精确率P (precision)、召回率R (recall)、召回率的调和平均数$ {F}_{1-{\mathrm{score}}} $和准确率$ {A}_{{\mathrm{cc}}} $(accuracy)作为模型分类效果的评价指标，根据混淆矩阵计算评价指标. 如表4所示，所提模型的精确率为0.982 1，召回率为0.984 4，${F}_{1-{\mathrm{score}}} $为0.983 3，准确率为0.983 9，具有最优的识别效果.

表 4   各交通运行状态识别模型的评价结果

Tab.4  Evaluation result of every traffic state identification model

分类模型PR$ {F}_{1-{\mathrm{score}}} $$ {A}_{{\mathrm{cc}}} $
SVM0.815 40.819 20.817 30.817 7
DT0.868 50.883 20.873 80.874 9
XGBoost0.908 30.919 60.913 60.915 4
所提模型0.982 10.984 40.983 30.983 9

新窗口打开| 下载CSV


3. 结　论

（1）利用网约车轨迹数据，结合时空单元划分，选择与交通运行状态相关的6个参数，构建评价指标体系. 利用建立的深度聚类模型，有效避免了“维数灾难”，提取了有效特征，开发了集成学习识别模型，实现对每个时空单元状态的实时精准识别. 利用该方法，可以全面了解道路网各个区域实时的交通运行状态.

（2）通过西安市的数据实例验证，TS-DEC模型将道路交通运行状态划分为5类，相较于传统聚类效果更优，识别模型的精确率高达98.21%. 通过分时段、分空间上下行对道路网交通运行状态的分析，可以研究拥堵路段和拥堵时段，实时、精准地识别全局交通运行状态有利于交通规划，具有现实意义.

（3）未来会有更加有效的、可用于道路交通运行状态挖掘的交通数据，后续研究可以基于这些数据挖掘更有价值的运行特征. 在网络级交通运行状态的识别框架中加入预测模型，通过对各个时空单元交通状态的分步预测，提升道路的服务水平.

参考文献

张琦, 陈红, 周继彪, 等

道路开口对临近交叉口交通安全的影响

[J]. 浙江大学学报: 工学版, 2021, 55 (4): 720- 726

[本文引用: 1]

ZHANG Qi, CHEN Hong, ZHOU Jibiao, et al

Effect of roadway access on traffic safety at adjacent intersection

[J]. Journal of Zhejiang University: Engineering Science, 2021, 55 (4): 720- 726

[本文引用: 1]

XIE J Y, GIRSHICK R, FARHADI A. Unsupervised deep embedding for clustering analysis [C]// International Conference on Machine Learning . New York: JMLR, 2016: 478-487.

[本文引用: 1]

黎茂盛, 李杭聪

基于交叉口车牌识别数据的网络交通状态分类方法

[J]. 哈尔滨工业大学学报, 2023, 55 (11): 82- 90

[本文引用: 1]

LI Maosheng, LI Hangcong

Classification method of network traffic state based on electronic police data at intersections

[J]. Journal of Harbin Institute of Technology, 2023, 55 (11): 82- 90

[本文引用: 1]

李岩, 王泰州, 徐金华, 等

面向动态交通分配的交通需求深度学习预测方法

[J]. 交通运输系统工程与信息, 2024, 24 (1): 115- 123

LI Yan, WANG Taizhou, XV Jinhua, et al

Traffic demand prediction method based on deep learning for dynamic traffic assignment

[J]. Journal of Transportation Systems Engineering and Information Technology, 2024, 24 (1): 115- 123

JAVANI B, BABAZADEH A, CEDRER A

Path-based capacity-restrained dynamic traffic assignment algorithm

[J]. Transportmetrica B: Transport Dynamics, 2019, 7 (1): 741- 746

DOI:10.1080/21680566.2018.1496861     

郭璘, 周继彪, 董升, 等

基于改进K-means算法的城市道路交通事故分析

[J]. 中国公路学报, 2018, 31 (4): 270- 279

GUO Lin, ZHOU Jibiao, DONG Sheng, et al

Analysis of urban road traffic accidents based on improved k-means algorithm

[J]. China Journal of Highway and Transport, 2018, 31 (4): 270- 279

XU J H, LUO W B, LI Y, et al

A multi-directional recurrent graph convolutional network model for reconstructing traffic spatiotemporal diagram

[J]. Transportation Letters, 2024, 16 (5): 405- 415

DOI:10.1080/19427867.2023.2198829      [本文引用: 1]

苏俊杰, 柴干, 季文韬

基于投影寻踪的快速路交织区交通状态识别方法

[J]. 交通信息与安全, 2019, 37 (2): 114- 119

[本文引用: 1]

SU Junjie, CHAI Gan, JI Wentao

Traffic state discrimination method for interchange areas in expressways based on projection pursuit

[J]. Journal of Transport Information and Safety, 2019, 37 (2): 114- 119

[本文引用: 1]

李晓璐, 于昕明, 杜崇, 等

基于权值优化的 FCM-MSVM 算法及其在高速公路状态识别中的应用

[J]. 北京交通大学学报, 2018, 42 (4): 72- 78

[本文引用: 1]

LI Xiaolu, YU Xinming, DU Chong, et al

FCM-MSVM algorithm based on weight optimization and its application in highway state discrimination

[J]. Journal of Beijing Jiaotong University, 2018, 42 (4): 72- 78

[本文引用: 1]

LIU J, KHATTAK A J

Delivering improved alerts, warnings, and control assistance using basic safety messages transmitted between connected vehicles

[J]. Transportation Research Part C: Emerging Technologies, 2016, 68 (3): 83- 100

[本文引用: 1]

XU J H, LI Y R, LU W, et al

A heterogeneous traffic spatio-temporal graph convolution model for traffic prediction

[J]. Physica A: Statistical Mechanics and its Applications, 2024, 641: 129746

DOI:10.1016/j.physa.2024.129746      [本文引用: 1]

丁瑞, 刘俊, 蒋艳, 等

基于车辆加速度数据的互通立交匝道驾驶风险分析

[J]. 交通信息与安全, 2021, 39 (1): 17- 25

[本文引用: 1]

DING Rui, LIU Jun, JIANG Yan, et al

Driving risks of interchange ramps based on vehicle acceleration data

[J]. Journal of Transport Information and Safety, 2021, 39 (1): 17- 25

[本文引用: 1]

张鑫, 张卫华

快速路合流区主线不同交通状态下的安全性分析

[J]. 吉林大学学报: 工学版, 2022, 52 (6): 1308- 1314

[本文引用: 1]

ZHANG Xin, ZHANG Weihua

Safety analysis of main line under different traffic conditions in expressway confluence area

[J]. Journal of Jilin University: Engineering and Technology Edition, 2022, 52 (6): 1308- 1314

[本文引用: 1]

ZENG Q, GUO Q, WONG S C, et al

Jointly modeling area-level crash rates by severity: a Bayesian multivariate random-parameters spatio-temporal Tobit regression

[J]. Transportmetrica A: Transport Science, 2019, 15 (2): 1867- 1884

DOI:10.1080/23249935.2019.1652867      [本文引用: 1]

李岩, 曾明哲, 朱才华, 等

基于多点线圈联合数据的高速公路匝道影响范围识别

[J]. 交通运输系统工程与信息, 2022, 22 (3): 53- 62

[本文引用: 1]

LI Yan, ZENG Mingzhe, ZHU Caihua, et al

Identification of freeway ramp influence areas based on multi-point loop data

[J]. Journal of Transportation Systems Engineering and Information Technology, 2022, 22 (3): 53- 62

[本文引用: 1]

张存保, 彭汉辉, 张珊, 等

雾天高速公路实时交通安全状态评价方法

[J]. 中国安全科学学报, 2017, 27 (4): 110- 115

[本文引用: 1]

ZHANG Cunbao, PENG Hanhui, ZHANG Shan, et al

Real-time traffic safety evaluation method for freeway in fog

[J]. China Safety Science Journal, 2017, 27 (4): 110- 115

[本文引用: 1]

MALIN F, NORROS I, INNAMAA S

Accident risk of road and weather conditions on different road types

[J]. Accident Analysis and Prevention, 2019, 122 (2): 181- 188

[本文引用: 1]

吴兵, 翟犇, 卢建涛, 等

基于安全风险的恶劣天气下高速公路建议车速确定方法

[J]. 同济大学学报: 自然科学版, 2020, 48 (11): 1570- 1578

[本文引用: 1]

WU Bing, ZHAI Ben, LU Jiantao, et al

Determination of freeway recommended speed based on safety risk under adverse weather conditions

[J]. Journal of Tongji University: Natural Science, 2020, 48 (11): 1570- 1578

[本文引用: 1]

吕能超, 彭凌枫, 吴超仲, 等

基于视频轨迹参数的边缘率减速标线驾驶行为效果评价方法

[J]. 安全与环境学报, 2021, 21 (2): 461- 469

[本文引用: 1]

LV Nengchao, PENG Lingfeng, WU Chaozhong, et al

Valuative judgment of the driving behaviors of the edge rate deceleration bars based on the video trajectory parameters

[J]. Journal of Safety and Environment, 2021, 21 (2): 461- 469

[本文引用: 1]

YUAN J, ABDELATY M, WANG L, et al

Utilizing bluetooth and adaptive signal control data for real-time safety analysis on urban arterials

[J]. Transportation Research Part C: Emerging Technologies, 2018, 97 (5): 114- 127

[本文引用: 1]

杨飞, 姜海航, 刘好德, 等

基于GPS轨迹数据的不同交通状态下交通方式识别流程优化方法

[J]. 交通运输系统工程与信息, 2020, 20 (4): 83- 89

[本文引用: 1]

YANG Fei, JIANG Haihang, LIU Haode, et al

Procedure optimization method based on GPS trajectory data for transportation mode recognition under different traffic conditions

[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20 (4): 83- 89

[本文引用: 1]

BEJANI M M, GHATEE M

A context aware system for driving style evaluation by an ensemble learning on smartphone sensors data

[J]. Transportation Research Part C: Emerging Technologies, 2018, 89 (14): 303- 320

[本文引用: 1]

/

〈 〉