很多学者对渐开线斜齿轮泵的几何流量特性进行研究. 赵亮等[5]将斜齿轮近似看作由无数个无限薄的直齿轮叠加而成,以齿宽方向上的中截面为基准面,采用扫过面积法得到泵的流量脉动率,认为斜齿轮泵不具有减小流量脉动的功能. 周骥平等[6]对文献[5]的计算公式进行修订,结果表明,斜齿轮泵的流量脉动与齿数、齿宽、模数及螺旋角有关,在主要参数相同的条件下,斜齿轮泵的流量脉动小于直齿轮泵. 甘学辉等[7]采用能量守恒法,推导得到斜齿轮泵瞬时几何流量的解析表达式,认为在保证不窜油条件下减小齿轮重叠系数、齿宽、模数、齿数或增大螺旋角,有利于降低泵的流量脉动. 周兰美[8]根据能量守恒定律导出异齿数斜齿轮泵瞬时几何流量和流量不均匀系数的计算公式,结果表明,当主、从动齿轮齿数相等时,流量不均匀系数与模数无关,随着螺旋角的增大而增大,增大齿数有利于减小流量脉动. Huang等[9]采用扫过面积法导出斜齿轮泵瞬时几何流量与啮合线长度间的关系式,研究结果表明,增大模数、减少齿数可以增大排量,但流量脉动变大. Liu等[10]通过CFD仿真分析转速和螺旋角对斜齿轮泵流量不均匀系数的影响,结果表明,流量不均匀系数对转速的变化更敏感,增大螺旋角会减小流量不均匀系数. 卞革[11]利用Pumplinx,针对螺旋角和齿宽对斜齿轮泵流量输出特性的影响进行仿真计算,结果表明,增大螺旋角可以减小流量不均匀系数. 杨国来等[12]推导渐开线斜齿轮泵困油的数学模型,对困油特性进行研究,结果表明,随着螺旋角和齿宽的增大,困油角度逐渐减小;困油体积随齿轮转角呈抛物线变化规律. Ransegnola等[13]采用多控制体积法,即将每一个齿槽看成单独的控制体,轮齿退出或进入齿槽引起控制体容积变化产生吸油或排油,给出斜齿轮泵瞬时几何流量的计算式,结果表明,斜齿轮泵的平均流量小于直齿轮泵,流量脉动的最大值与最小值之差不变. Mazzei等[14]结合集中参数法和CFD方法,对斜齿轮泵的流量压力特性及出口压力脉动特性进行对比研究,但没有讨论泵的瞬时流量特性. 为了改善渐开线齿形泵的输出流量脉动特性,Zhao等[15-16]综合渐开线齿形圆弧齿形的优点,提出圆弧-渐开线-圆弧复合新齿形,结合集中参数法、CFD仿真法及实验,研究新齿形泵的瞬时几何流量特性、压力脉动特性,但受动态流量不易测试的限制,仅给出泵的瞬时几何流量特性的计算值. 因齿形的差异性,这种齿轮泵的瞬时几何流量曲线近似为方波,无法反映渐开线齿形泵的流量特性.
目前对外啮合斜齿轮泵瞬时几何流量特性的研究以理论推导解析和CFD仿真计算方法为主,从已有的渐开线齿形斜齿轮泵文献来看,斜齿结构对泵瞬时几何流量特性影响的研究结果尚不完全一致. 液压泵几何流量特性的计算分析是容积式泵设计的基础问题,与泵的效率评估、流量压力脉动、振动噪声等性能密切相关. 本文从容积式泵依靠密封容积变化完成吸排油这一基本原理出发,探究渐开线外啮合斜齿轮泵瞬时几何流量的计算方法,以期揭示斜齿结构对泵瞬时几何流量特性的影响规律.
1. 排油密封容腔轴向切片的叠加原理
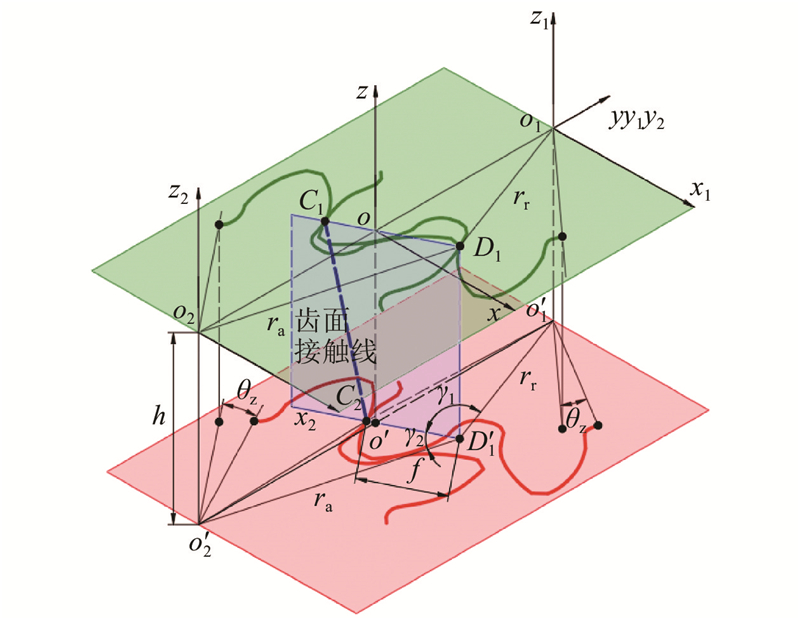
外啮合斜齿轮泵排油密封容腔由主从动齿轮、前后泵盖及泵体等零件组成,如图1所示为工作原理简图(为了清晰起见,隐去了前后泵盖及泵体). 图中,主动齿轮为左旋,从动齿轮为右旋,前后端面齿廓滞后角为β0,齿间夹角为α0.
图 1
以图1中所示的位置为齿轮工作参考起始点,此时前一对啮合齿即主动齿轮的A1齿与从动齿轮的B1齿处于全齿宽啮合阶段,齿间接触密封线C1H1将泵左侧的吸油腔与右侧的排油腔隔开,C1、H1点分别为前、后端面对应齿的齿廓啮合点. 后一对齿A2、B2刚进入啮合,啮合点为D1,对应前端面主动齿轮A2齿齿廓的齿根点和从动齿轮B2齿齿廓的齿顶点. C1D1连线为齿轮前端面齿廓啮合线,C1、D1、H1 3点所在的平面为齿轮啮合平面. 前一对齿A1B1在退出全齿宽啮合瞬间,后一对齿A2B2进入全齿宽啮合,能够确保既无困油、吸排油腔,又能可靠隔开. 若同时有2对齿处于全齿宽啮合,则出现困油现象. 当主动齿轮顺时针旋转时,啮合点D1沿啮合线下移,对应A2齿上啮合点由齿根向齿顶移动,B2齿上啮合点由齿顶向齿根移动,A2B2齿接触密封线通过D1点向齿轮后端面延伸,且与C1H1平行,当齿轮转过的角度等于滞后角β0时,A2、B2齿进入全齿宽啮合. 当齿轮啮合转动齿间夹角α0时,排油密封容腔体积变化一个周期. 为了方便排油密封容腔体积的计算,可以将齿轮沿齿宽方向等切分为n片,相应的排油密封容腔被切分为n个,故排油腔总体积的变化规律等同于n个切片体积之和的变化规律.
如图2所示为当齿轮转过一个齿间距时,典型啮合位置排油密封容腔切片阴影的示意图. 如图2(a)、(b)所示为齿轮处于图1起始位置时以前端面为参考的第1层切片和第n层切片的轴向投影图. 当齿轮转过角度小于β0时,各层齿啮合状况与此类似,A2、B2齿啮合接触线长度随转角的增大而增长,在该阶段仅第1对齿处于全齿宽啮合. 如图2(c)、(d)所示为当齿轮转过角度大于β0,2对齿同时进入全齿宽啮合时第1层切片和第n层切片的轴向投影图. 图中,C1Cn、D1Dn连线分别为2对啮合齿的接触密封线. 此时,排油密封容腔被分割为困油区和排油区2部分,当设置有卸荷槽时,困油区容积减小时与排油腔沟通,反之则与吸油腔沟通. 当齿轮继续转动,第1对齿脱离全齿宽啮合而仅有第2对齿处于全齿宽啮合时,第1层切片和第n层切片的轴向投影图如图2(e)、(f)所示,此时A2、B2齿接触密封线将排油腔与吸油腔隔开. 当图1中A2齿转至A1齿位置时,泵完成一个排油工作周期.
图 2
图 2 排油密封容腔典型切片的轴向投影图
Fig.2 Axial projection of typical section of discharge seal chamber
2. 计算域轮廓曲线数学模型的建立
排油密封容腔切片计算域轮廓曲线主要由齿顶圆弧、齿侧渐开线曲线、齿根过渡曲线、齿底圆弧及排油口直线5部分组成. 各层切片轮廓因斜齿结构的形状相似但相位不同,每层齿轮啮合点坐标与齿轮转角和层数有关.
2.1. 斜齿轮轴向不同切片轮廓方程间的关系
图 3
图 3 斜齿轮轴向不同切片位置的示意图
Fig.3 Diagram of different axial slicing positions of helical gear
以前端面第1层切片即图3中上部切片轮廓为参考基准,则距基准切片轴向距离为h的下部切片的轮廓相对基准面轮廓的相位滞后角为
式中:β为螺旋角,r为分度圆半径.
若基准面主动齿轮齿廓上任一点在x1o1y1坐标系内的坐标为(x1,y1),则下部切片所处的平面内,相位滞后θz的主动齿轮齿廓上对应点坐标在xoy坐标系中可以表示为(x,y),可用下式求得:
式中:rw为节圆半径.
同理,在下部切片所处的平面内,从动齿轮齿廓上任一点(x2,y2)相对应点的坐标在xoy坐标系中可用下式计算:
2.2. 渐开线齿廓曲线的参数方程
以主动齿轮渐开线齿廓曲线为例说明,渐开线上任一点在随主动齿轮同步转动的相对坐标系下的直角坐标方程[17]为
式中:μk为滚动角,
齿顶圆ra处的压力角最大,其值为
为了方便后续积分点的计算,式(4)中引入参数t1,其取值范围为
式中:
从动齿轮渐开线齿廓曲线在x2o2y2坐标系下的方程为
式中:
将式(6)、(7)分别代入式(2)、(3),可得主、从动齿轮轴向不同切片渐开线齿廓曲线在xoy坐标系下的参数方程.
2.3. 齿根过渡曲线的参数方程
滚切加工时滚刀的节线与被加工齿轮的节圆相切,并作纯滚动. 若采用双圆弧滚刀加工,则齿根过渡曲线方程[18]为
式中:e、φ为与刀具有关的参数,ρ为刀具圆弧半径,ζ为变位系数,γ为在端面压力角至90 °之间变化的角度,m为模数.
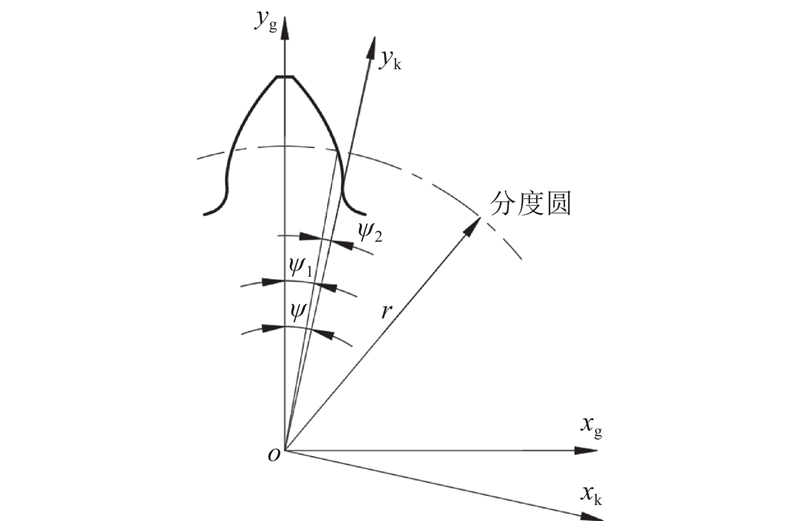
由于建立齿根过渡曲线所用的坐标系与建立渐开线时不同,如图4所示,两坐标系相差角度ψ,为分度圆上的展角与半个齿厚对应的角之和.
图 4
图 4 齿廓曲线建模坐标系关系的示意图
Fig.4 Diagram of coordinate system relationship for tooth profile curve
式中:z为齿数,s为齿厚,d为分度圆直径,αt为端面压力角.
主动齿轮齿根过渡曲线在x1o1y1坐标系下的参数方程为
同理,从动齿轮齿根过渡曲线在x2o2y2坐标系下的参数方程为
将式(10)、(11)代入式(2)、(3),可得主动齿轮轴向不同切片齿根过渡曲线在xoy坐标系下的参数方程.
2.4. 齿顶圆及齿根圆方程
齿顶圆与齿根圆方程均为圆方程,主动齿轮上的齿顶与齿根圆方程分别为
式中:rf为齿根圆半径.
同理,从动齿轮上的齿顶与齿根圆方程分别为
2.5. 啮合线方程和各层齿轮啮合点的坐标
为了便于求解啮合点坐标,须给出啮合线方程. 渐开线齿轮啮合线为两齿轮基圆的一条内公切线,将两圆半径代入点到直线的距离公式,可得公切线方程,则齿轮泵的啮合线方程为
式中:a为齿轮的实际中心距.
齿轮啮合接触点将吸排油腔隔开,是密封容腔各层切片体积计算的积分端点. 由于齿廓啮合曲线为渐开线曲线,啮合点坐标的求解可以归结为参数t1、t2的计算.
从图3可知,C1、D1分别为基准面上前、后一对齿的啮合点,此时D1为后一对齿刚进入啮合时的起始啮合点. 联立式(14)、(16),可得起始啮合点D1坐标,进而得到rr的长度.
在
由图3中的几何关系可得,啮合点C2到o1′、o2′的距离r1、r2分别为
式中:f为啮合点到节点的距离,
3. 计算方法及计算流程
3.1. 斜齿轮泵不窜油的条件及困油卸荷槽的位置
仅对不窜油即吸排油腔可靠隔开的斜齿轮泵结构进行讨论,斜齿轮泵不发生窜油的条件[19]为
式中:αat为齿顶圆压力角,
当式(21)取等号时,斜齿轮泵既不发生困油也不发生窜油. 对于斜齿轮任意切片上的齿廓,经历的双点啮合角度为
式中:εα为斜齿轮端面重合度.
当式(21)取大于号时,斜齿轮泵存在困油现象,须开设卸荷槽. 通常前后侧板或泵盖卸荷槽开设位置对应齿轮泵轴向中截面困油面积为最小时的位置,如图5所示为矩形卸荷槽开设位置及中截面最小困油阴影区.
图 5
从图5可知,以前端面为基准,当齿轮转至中截面困油区面积最小的位置时,齿轮的转角为
将式(23)代入渐开线方程,可得对称卸荷槽开设的位置.
3.2. 一个啮合周期齿轮转角的区间划分
由排油密封容腔轴向切片叠加原理及困油卸荷槽开设位置可知,一个啮合周期的齿轮转角
1)
2)
3)
对于不考虑卸荷槽作用即不考虑困油区排油作用的斜齿轮泵,当
3.3. 计算流程
由格林公式可知,由闭合曲线围成的单连通区域的面积可以表示为在该曲线上曲线积分的一半. 将排油腔沿轴向切成n片,第i层排油腔的横截面积为
式中:L为排油腔边界轮廓.
斜齿轮泵排油腔总容积为
改变时间,对应主从动齿轮进入新的转角位置,可得斜齿轮泵排油腔容积随时间的变化量,进而得到泵的瞬时几何流量为
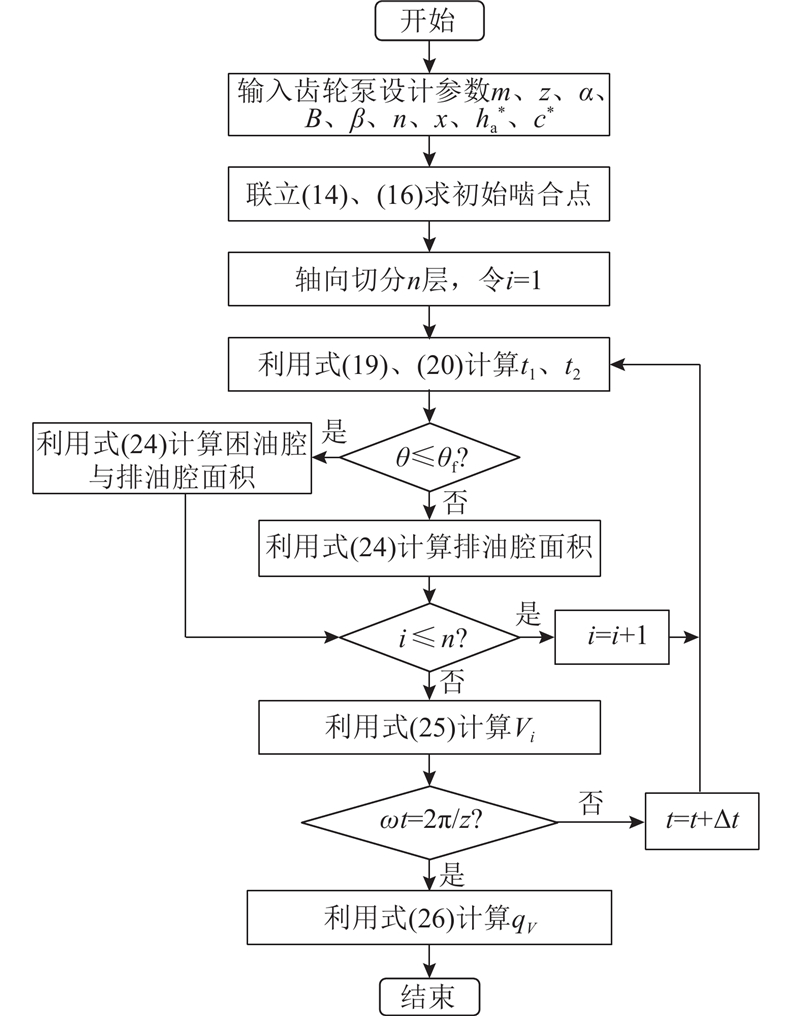
泵的瞬时几何流量计算流程如图6所示.
图 6
图 6 斜齿轮泵瞬时几何流量计算的流程图
Fig.6 Flow chart for instantaneous geometric flow calculation of helical gear pump
4. 计算案例及分析
4.1. 排油腔密封容积的计算与验证
表 1 斜齿轮泵的结构参数
Tab.1
| 参数 | 数值 |
| z | 10 |
| mn/mm | 3 |
| β/(°) | 11 |
| nr(/r·min−1) | 2 400 |
| αn/(°) | 28 |
| a/mm | 30 |
| ζ/mm | − |
| B/mm | 12.5 |
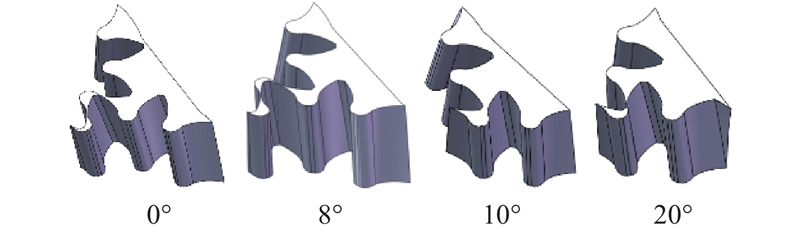
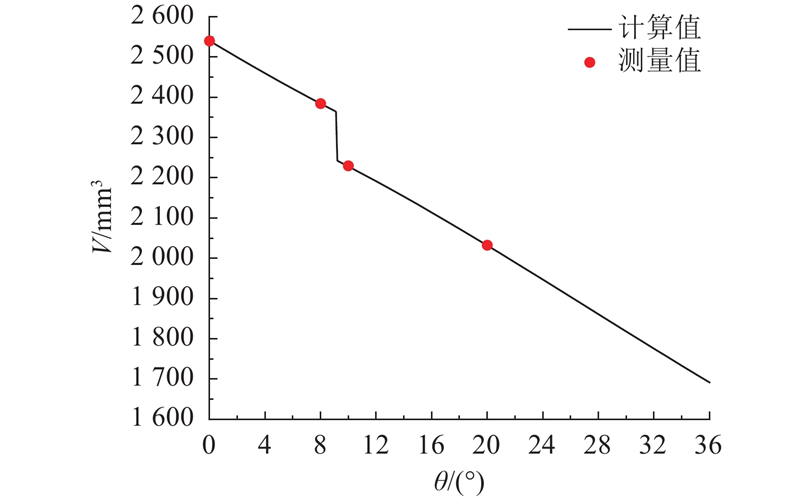
将参数代入斜齿轮泵齿廓曲线模型,计算得到齿廓曲线坐标点,导入Solidworks软件生成斜齿轮的三维模型,装配抽取排油腔体积如图7所示. 通过三维软件测得,当典型齿轮转角位置为0°、8°、10°、20°时,排油腔体积分别为2 539. 796、 2 384. 205、2 229. 488、2 032. 442 mm3.
图 7
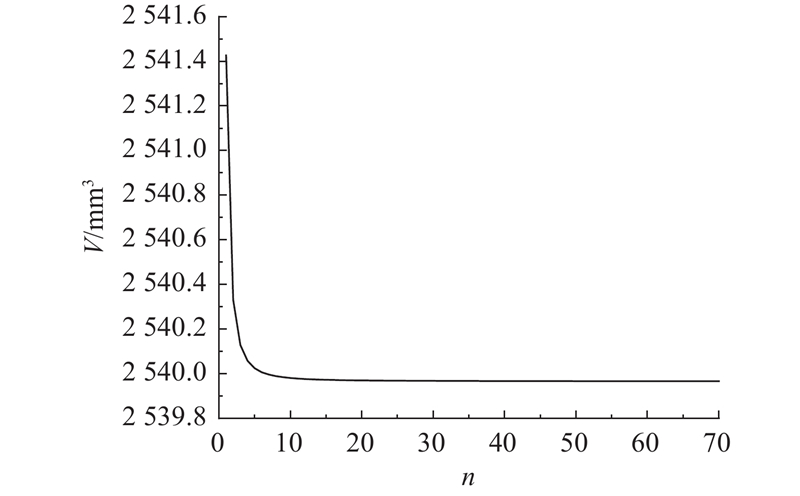
当采用叠加法计算时,所取层数n对计算精度有一定的影响. 当n取不同值时,计算得到
图 8
图 8 0°时排油腔容积随层数的变化曲线
Fig.8 Curve of discharge chamber volume with layer number at zero degree
图 9
图 9 排油腔容积随转角变化曲线
Fig.9 Volume of discharge chamber with different gear rotation angle
4.2. 瞬时几何流量的计算结果对比
式中:u0为中截面齿轮啮合点到节点的距离.
图 10
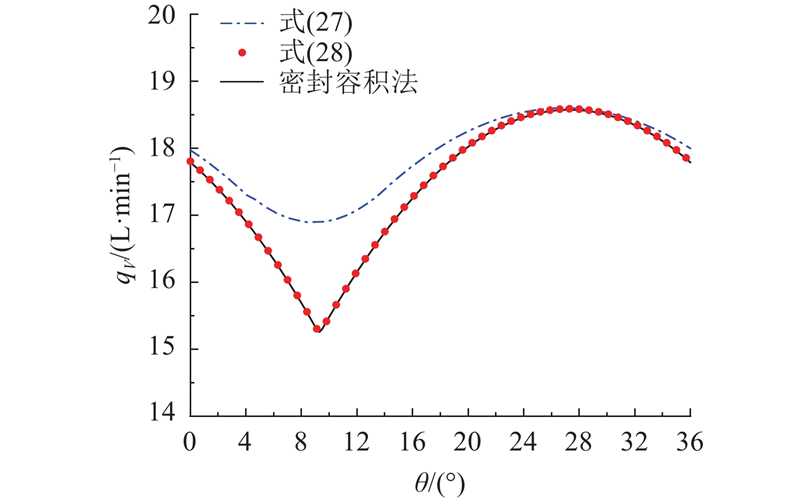
图 10 利用3种计算方法得到的瞬时几何流量对比图
Fig.10 Comparison of instantaneous geometric flow curve obtained by three methods
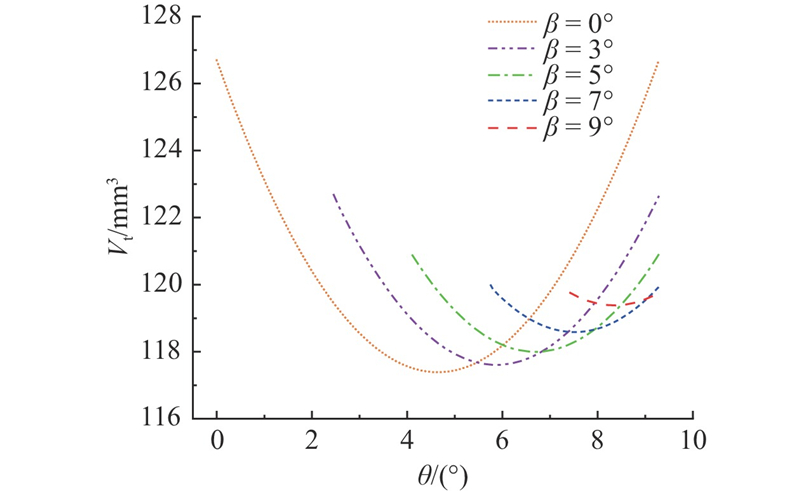
4.3. 螺旋角对瞬时几何流量的影响
图 11
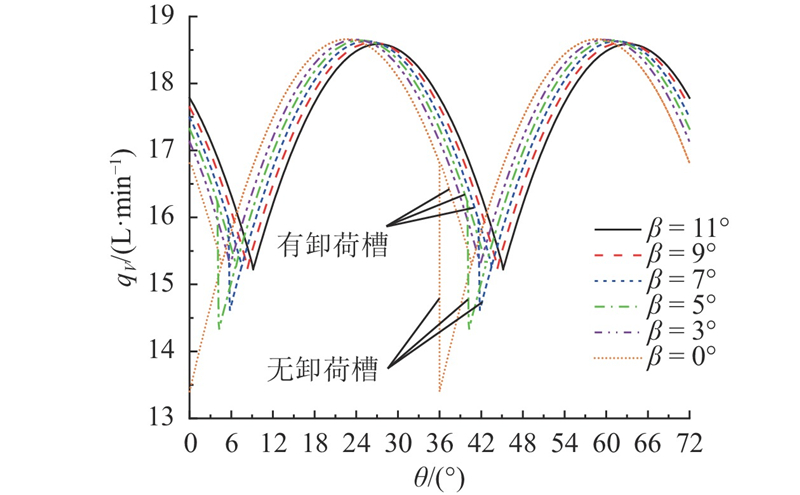
图 11 不同螺旋角下泵的瞬时几何流量曲线
Fig.11 Instantaneous geometric flow curves of helical gear pump with different helical angle
表 2 不同螺旋角下的流量特性
Tab.2
| β/(°) | qVm/(L·min−1) | δ/% |
| 11 | 17.4 602 | 19. 359 |
| 9 | 17.4 961 | 19. 336 |
| 7 | 17.5 143 | 19. 323 |
| 7(无卸荷槽) | 17.4 802 | 22. 971 |
| 5 | 17.5 274 | 19. 314 |
| 5(无卸荷槽) | 17.4 582 | 24. 824 |
| 3 | 17.5 354 | 19. 307 |
| 直齿 | 17.5 388 | 19. 305 |
| 直齿(无卸荷槽) | 17.3 263 | 29. 849 |
图 12
图 12 不同螺旋角下的困油容积变化曲线
Fig.12 Trapped oil volume curve with different helical angle
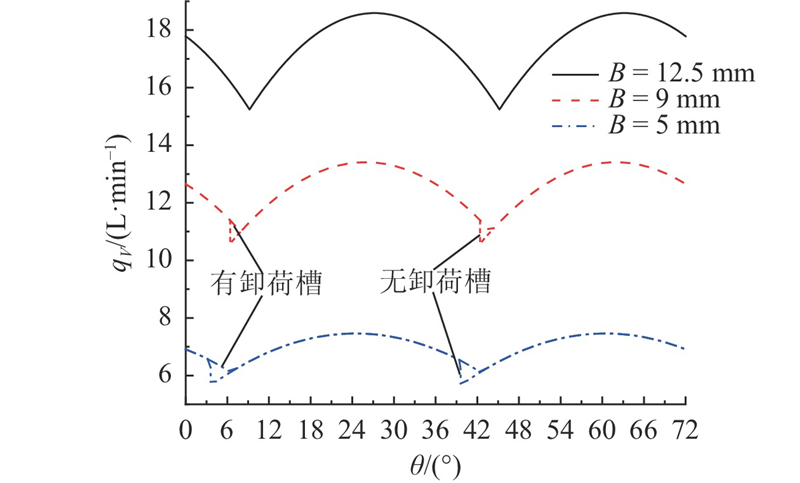
4.4. 齿宽对瞬时几何流量的影响
图 13
图 13 不同齿宽下的瞬时几何流量曲线
Fig.13 Instantaneous geometric flow curve with different tooth widths
表 3 不同齿宽下的流量特性
Tab.3
| B/mm | qVm/(L·min−1) | δ/% |
| 12.5 | 17.460 2 | 19. 359 |
| 9(有卸荷槽) | 12.603 9 | 19. 329 |
| 9(无卸荷槽) | 12.577 8 | 22. 053 |
| 5(有卸荷槽) | 7.012 5 | 19. 310 |
| 5(无卸荷槽) | 6.980 9 | 25. 247 |
5. CFD数值计算
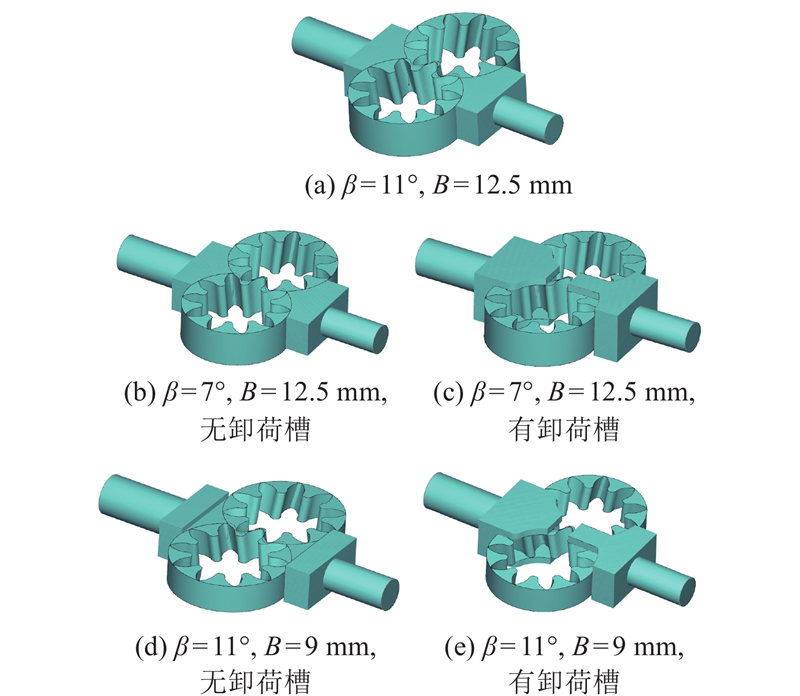
为了进一步验证本文计算方法的有效性,选取5组典型结构参数:
5.1. 计算模型
图 14
图 14 不同螺旋角和齿宽下的齿轮泵流体计算域
Fig.14 Fluid domain of gear pump with different helical angles and tooth widths
图 15
图 15
Fig.15 Meshing of helical gear pump with β=11° , B=12.5 mm
5.2. CFD计算结果
为了减小CFD仿真中边界条件设置对泵瞬时几何流量计算的影响,选取较低的泵进出口压差为边界条件,进口设为大气压力,出口设为2倍大气压力. 不考虑介质的压缩性及空化现象,对
图 16
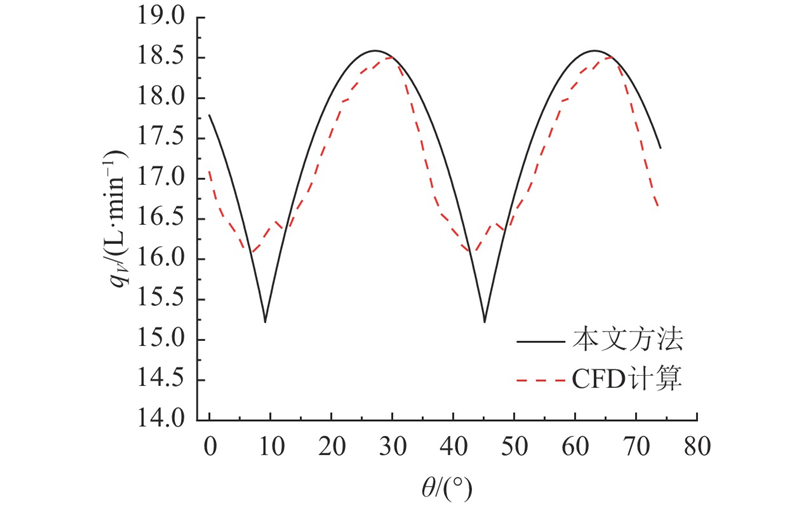
图 16 利用CFD与提出方法得到的瞬时流量曲线
Fig.16 Instantaneous flow curves by using CFD and proposed method
从图16可见,利用2种方法所得泵的瞬时几何流量脉动频率一致,根据CFD计算得到的流量脉动幅度略小,平均流量为17.254 3 L/min,比本文计算结果低1.18%. 计算结果的差异性主要源于CFD模型中为了保证流体域连通,在啮合齿侧处留有间隙,泵的密封排油腔几何形状与理论形状不完全相同,加之流场计算时齿侧及齿顶存在泄漏会对计算结果产生影响. 总的来说,二者的波形变化趋势基本相同,可以验证本文计算方法的有效性.
为了在更加贴合工程实际的条件下考察螺旋角与齿宽对斜齿轮泵输出流量特性的影响规律,将出口压力设置为2 MPa,同时考虑介质空化的影响,选用Singhal全空化模型描述,对5种结构参数的斜齿轮泵进行仿真计算. 泵的输出流量特性曲线如图17所示.
图 17
图 17 不同结构参数下泵瞬时输出流量的CFD计算结果
Fig.17 Instantaneous output flow curve of pump by CFD under different structural parameters
从图17可见,在CFD模拟中,由于泵内部流动结构的复杂性,当齿宽相同、螺旋角不同或螺旋角相同、齿宽不同时所得斜齿轮泵的瞬时输出流量曲线的平滑性不及集中参数的计算结果,但随着螺旋角的增大,瞬时输出流量曲线的滞后角增大,这与本文计算方法的结果一致.
利用CFD方法计算所得的平均流量与流量脉动率如表4所示.
表 4 利用CFD方法计算得到的泵的流量特性
Tab.4
| β/(°) | B/mm | 是否开设卸荷槽 | qVm/(L·min−1) | δ/% |
| 11 | 12.5 | 临界状态无困油 | 16.782 | |
| 7 | 12.5 | 是 | 16.690 | |
| 7 | 12.5 | 否 | 19.423 | |
| 11 | 9.0 | 是 | 16.762 | |
| 11 | 9.0 | 否 | 19.086 |
从表4可见,出口压力增大后因泄漏,泵输出平均流量降低为16.2 417 L/min. 齿宽一定,增大螺旋角,则泵的平均输出流量降低,流量脉动率增大. 螺旋角一定,增大齿宽,则泵的平均输出流量增大,流量脉动率降低. 当齿宽和螺旋角不变,开设卸荷槽结构时,泵的平均输出流量增大,流量脉动率变小.
6. 结 论
(1)利用提出的斜齿轮泵瞬时几何流量计算方法所得的结果与文献[13]的计算结果一致性良好,二者的平均偏差为0.056%. 密封容腔体积的计算结果与Solidworks三维软件测量结果吻合度高,二者的平均偏差为0. 026%,验证了计算方法的有效性.
(2)对于有困油现象、排油侧未开设卸荷槽结构的斜齿轮泵,齿宽一定,增大螺旋角使平均输出流量略微增大,流量脉动率降低;螺旋角一定,增大齿宽使平均输出流量增大,流量脉动率降低.
(3)对于排油侧有卸荷槽结构的斜齿轮泵,齿宽一定,增大螺旋角使流量脉动率略微升高,平均输出流量略微下降. 螺旋角一定,增大齿宽使平均输出流量增大,流量脉动率略微升高.
参考文献
Models for flow rate simulation in gear pumps: a review
[J].DOI:10.3390/en10091261 [本文引用: 1]
基于运动法的航空发动机高速燃油齿轮泵卸荷槽设计与验证
[J].
Design and verification of relief groove for aero-engine high-speed fuel gear pump based on motion method
[J].
高速高压燃油齿轮泵典型卸荷槽对比分析研究
[J].
Comparative analysis on relief grooves of high-speed and high-pressure aeroengine fuel gear pumps
[J].
斜齿齿轮泵流量输出特性分析
[J].DOI:10.3321/j.issn:0577-6686.1999.05.022 [本文引用: 2]
Analysis of helical gear pump for flow output property
[J].DOI:10.3321/j.issn:0577-6686.1999.05.022 [本文引用: 2]
斜齿齿轮泵小脉动输出特性
[J].DOI:10.3901/JME.2000.12.018 [本文引用: 1]
Small pulse output characteristics of helical gear pump
[J].DOI:10.3901/JME.2000.12.018 [本文引用: 1]
液压齿轮泵的性能研究
[J].
Research on performance of hydraulic gear pump
[J].
外啮合异齿数斜齿轮泵流量脉动和流量特性的研究
[J].
Study on flow pulsation and flow characteristics of external helical gear pump with different number of teeth
[J].
Geometric displacement optimization of external helical gear pumps
[J].DOI:10.1243/09544062JMES1398 [本文引用: 1]
渐开线外啮合斜齿轮泵困油特性研究
[J].
Trapped oil characteristics study on external helical involute gear pump
[J].
A comparison of helical and spur external gear machines for fluid power applications: design and optimization
[J].
Helical gear pump: a comparison between a lumped parameter and a computational fluid dynamics-based approaches
[J].DOI:10.3390/fluids8070193 [本文引用: 1]
Analysis of continuous-contact helical gear pumps through numerical modeling and experimental validation
[J].
渐开线齿轮齿根过渡曲线计算及在 UG 中精确建立齿轮三维模型
[J].
Accurate involute gear tooth root transition curve drawing and gear 3D modeling in UG
[J].