浙江大学学报(工学版)

浙江大学学报(工学版), 2025, 59(5): 1018-1030 doi: 10.3785/j.issn.1008-973X.2025.05.015

机械工程

自适应齿轮箱稀疏表示原子构建方法

周昶清,, 侯耀春, 武鹏,, 杨帅, 吴大转

1. 上海船舶设备研究所，上海 200031

2. 浙江大学 能源工程学院，浙江 杭州 310027

Adaptive sparse representation atom construction method for gearbox diagnosis

ZHOU Changqing,, HOU Yaochun, WU Peng,, YANG Shuai, WU Dazhuan

1. Shanghai Marine Equipment Research Institute, Shanghai 200031, China

2. College of Energy Engineering, Zhejiang University, Hangzhou 310027, China

通讯作者: 武鹏，男，副研究员. orcid.org/0000-0003-0746-3342. E-mail: roc@zju.edu.cn

收稿日期: 2024-03-29  

基金资助: 核技术研发科研资助项目.

Received: 2024-03-29  

Fund supported: 核技术研发科研资助项目.

作者简介 About authors

周昶清（1999—），男，硕士生，从事信号处理与故障诊断的研究.orcid.org/0009-0006-8264-4222.E-mail：cqzhou@zju.edu.cn , E-mail：cqzhou@zju.edu.cn

摘要

针对传统稀疏表示算法在齿轮箱信号干扰较多的情况下最优原子寻优效果不佳的问题，开发基于非对称高斯啁啾模型的改进原子寻优方法，以实现在低信噪比环境中获得更佳性能的目标. 利用具有多参数形状多变的非对称高斯啁啾模型，构建小波原子. 利用构建的小波原子，通过脉冲特征增强方法得到原始振动信号的特征增强信号. 通过最大化高斯条件下的循环平稳性检验指标，寻找与故障脉冲最匹配的小波原子参数，通过多重增强稀疏表示算法分离出故障瞬态分量. 通过公开数据集与故障模拟实验中齿轮箱故障数据集，验证了本文方法的有效性，并与原始方法和其他方法进行对比，证明了本文方法能够在齿轮箱信号存在较多干扰的情况下构建较优的稀疏表示原子.

关键词： 齿轮箱 ; 故障诊断 ; 稀疏表示 ; 非对称高斯啁啾模型 ; 脉冲特征增强

Abstract

An improved atom pursuit method based on the asymmetric Gaussian chirplet model (AGCM) was developed to achieve better performance in low signal-to-noise ratio environment in order to address the issue of poor optimal atom pursuit performance in traditional sparse representation algorithms under strong interference conditions in gearbox. Wavelet atoms were constructed by using AGCM with multi-parameter and variable shapes. Then a feature-enhanced signal was obtained through an impulse enhancement method. Atom parameters most compatible with fault impulses were identified by maximizing a statistical index under Gaussian hypothesis. Then fault transient components were separated through a multiple enhancement sparse representation algorithm. The effectiveness of the proposed method was validated by using both public dataset and gearbox fault simulation dataset. Comparative analysis with original methods and other existing approaches demonstrates that the proposed method can construct superior sparse representation atoms under strong interference conditions in gearbox signals.

Keywords： gearbox ; fault diagnosis ; sparse representation ; asymmetric Gaussian chirplet model ; impulse enhancement method

PDF (4602KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

周昶清, 侯耀春, 武鹏, 杨帅, 吴大转. 自适应齿轮箱稀疏表示原子构建方法. 浙江大学学报(工学版)[J], 2025, 59(5): 1018-1030 doi:10.3785/j.issn.1008-973X.2025.05.015

ZHOU Changqing, HOU Yaochun, WU Peng, YANG Shuai, WU Dazhuan. Adaptive sparse representation atom construction method for gearbox diagnosis. Journal of Zhejiang University(Engineering Science)[J], 2025, 59(5): 1018-1030 doi:10.3785/j.issn.1008-973X.2025.05.015

齿轮箱作为透平机械系统的核心传动部件，凭借其高扭矩承载能力和结构稳定性被广泛应用. 在重载、高温、高速等极端工况下，齿轮箱易发生故障并引发连锁性机械故障，导致重大经济损失甚至安全事故[1-3]. 据统计[4]可知，齿轮与滚动轴承是故障高发元件，基于振动加速度传感器的非侵入式监测技术因其高信噪比特性成为主流的诊断手段[5-6].

尽管振动信号蕴含丰富的健康信息，但实际的采集信号常受多源干扰耦合的影响. 利用传统的时频域分析方法，难以有效地分离复合故障特征，尤其当传感器固定于箱体时，各部件的振动信号相互混叠，显著增加了特征提取难度. 稀疏表示技术通过构建匹配字典提取瞬态冲击特征，逐渐成为研究热点. Huang等[7]采用极大极小凹惩罚函数与傅里叶基字典，实现齿轮多分量信号的分离. Wang等[8]基于小波和相关滤波，提出结合瞬态建模和参数识别的旋转机械故障特征检测方法. 通过瞬态周期参数识别实现故障定位. 针对齿轮箱复合故障振动信号的多重特征提取问题，基于Wang等[8]的研究，Li等[9]提出新的多重增强稀疏表示（multiple enhanced sparse decomposition，MESD）方法. 利用MESD算法，能够同时分离和提取齿轮与滚动轴承的谐波分量和瞬态特征，利用广义极大极小凹惩罚（generalized minimax concave，GMC）作为稀疏正则化项，避免了使用L1范数正则化带来的低估高振幅特征分量的影响[10]，保证了稀疏表示的准确性. Zhou等[11]构建非对称高斯啁啾模型（asymmetric Gaussian chirplet model，AGCM）时频原子，用于匹配故障脉冲波形，结合探路者算法（pathfinder algorithm，PFA）优化参数匹配.

齿轮箱复杂的传递路径导致轴承故障冲击易被齿轮啮合振动掩盖，现有方法在实测信号处理中面临显著的挑战. 利用稀疏分解算法，虽然能够分离多源瞬态分量，但受限于传感器安装位置导致的信号混叠，在实际应用中存在原子匹配精度下降的问题.

本文聚焦平行轴齿轮箱，提出改进型原子寻优方法，增强MESD算法的工程适用性. 通过优化特征原子匹配机制，为复杂工况下的复合故障诊断提供新思路.

1. 多重增强稀疏表示方法的原理

从齿轮箱中采集到的复合振动信号往往包含较大的噪声，因此齿轮箱信号建模为

$ \boldsymbol{y}={\boldsymbol{x}}_{1}+{\boldsymbol{x}}_{2}+{\boldsymbol{x}}_{3}+\boldsymbol{n} . $
(1)

式中：$ \boldsymbol{y} $表示一段长度为$ N $的一维振动信号，$ {\boldsymbol{x}}_{1} $、$ {\boldsymbol{x}}_{2} $与$ {\boldsymbol{x}}_{3} $分别为滚动轴承瞬态分量、齿轮瞬态分量和谐波分量，$ \boldsymbol{n} $为噪声信号. 在对$ {\boldsymbol{x}}_{i} $（$ i=1, 2, 3） $建立对应的字典$ {\boldsymbol{D}}_{i} $后，$ {\boldsymbol{x}}_{i} $可以表示为

$ {\boldsymbol{x}}_{i}={\boldsymbol{D}}_{i}{\boldsymbol{c}}_{i}. $
(2)

式中：$ {\boldsymbol{c}}_{i} $为系数分解得到的参数. 根据Selesnick[12]提出的方法，可以将齿轮箱复合振动信号的分解建模为

$ \left. \begin{array}{l} \mathrm{arg}\underset{{\boldsymbol{c}}_{1},{\boldsymbol{c}}_{2},{\boldsymbol{c}}_{3}}{\mathrm{min}}{\lambda }_{1}\mathrm{\varPsi }\left({\boldsymbol{c}}_{1}\right)+{\lambda }_{2}\mathrm{\varPsi }\left({\boldsymbol{c}}_{2}\right)+{\lambda }_{3}\mathrm{\varPsi }\left({\boldsymbol{c}}_{3}\right);\\\mathrm{s}.\mathrm{t}.\;{||\boldsymbol{y}-{\boldsymbol{D}}_{1}{\boldsymbol{c}}_{1}-{\boldsymbol{D}}_{2}{\boldsymbol{c}}_{2}-{\boldsymbol{D}}_{3}{\boldsymbol{c}}_{3}||}_{2}\le \xi . \end{array}\right\} $
(3)

式中：$ \varPsi \left(\cdot \right) $为广义极小极大非凸惩罚项[12]；$ {\boldsymbol{D}}_{i} $为$ {\boldsymbol{x}}_{i} $对应的字典，$ {\boldsymbol{D}}_{i}\in {\bf{R}}^{N\times N} $；$ {\boldsymbol{c}}_{i} $为稀疏表示系数，$ {\boldsymbol{c}}_{i}\in {\bf{R}}^{N\times 1} $；$ {\lambda }_{i} $为代价函数中调整数据保真度和稀疏度的约束参数；$ \xi $为受到噪声标准差影响的参数. 利用平方包络谱分析获得的瞬态分量，可得对应的故障特征，实现齿轮箱的故障诊断.

引入二阶系统的单位脉冲响应函数来表示故障. 考虑滚动轴承瞬态分量为单侧衰减形式，与拉普拉斯函数的波形相似. 选择拉普拉斯函数来构造滚动轴承的小波基稀疏字典：

$\begin{split} {D}_{1}\left(t,{\tau }_{1}\right)= &{A}_{1}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-{\zeta }_{1}}{\sqrt{1-{\zeta }_{1}^{2}}}2{\text{π}} {f}_{1}\left(t-{\tau }_{1}\right)\right)\times \\&\mathrm{s}\mathrm{i}\mathrm{n}\left(2{\text{π}} {f}_{1}\left(t-{\tau }_{1}\right)\right).\end{split} $
(4)

考虑到齿轮瞬态分量的波形是双侧衰减的，这与Morlet小波的波形相似. 采用Morlet小波构造齿轮小波基稀疏字典：

$\begin{split} {D}_{2}\left(t,{\tau }_{2}\right)=& {A}_{2}\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-{\zeta }_{2}}{\sqrt{1-{\zeta }_{2}^{2}}}{\left[2{\text{π}} {f}_{2}\left(t-{\tau }_{2}\right)\right]}^{2}\right)\times \\&\mathrm{c}\mathrm{o}\mathrm{s}\left(2{\text{π}} {f}_{2}\left(t-{\tau }_{2}\right)\right). \end{split}$
(5)

式中：$ {A}_{i} $为归一化参数，$ {f}_{i} $为共振频率，$ {\zeta }_{i} $为阻尼比，$ {\tau }_{i} $为时间指数.

由于$ {f}_{i} $、$ {\zeta }_{i} $与$ {\tau }_{i} $的取值直接影响小波基与相应暂态分量的相关性，采用Wang等[8]提出的相关系数滤波法，选择最优的参数.通过最大化每个时间系数$ {\tau }_{i} $下对应的小波基字典的相关系数，得到最优的参数$ {\bar{f}}_{i} $、$ {\bar{\zeta }}_{i} $和$ {\bar{\tau }}_{i} $.

当齿轮系统存在制造或安装错误分布式故障时，齿轮啮合振动的幅值随之发生变化，从而产生谐波分量. 将谐波字典建模为

$\begin{split} {D}_{3}\left(t\right)=\;&\mathrm{cos}\left(2{\text{π}} i{f}_{{\mathrm{r}}}t+{\phi }_{i}\right); \\&i\in \left\{mz\pm k|m=\mathrm{1,2},\cdots ,{m}_{0},k=\mathrm{1,2},\cdots ,{k}_{0}\right\}.\end{split} $
(6)

式中：$f_{\mathrm{r}} $为转动频率，$ z $为齿数，$ {m}_{0} $与$ {k}_{0} $应根据原子的频率能够覆盖最大的啮合频率的准则进行选择.

在字典构造完成后，稀疏表示的核心问题变成了MESD代价函数的建立和求解. MESD的代价函数可以表示为

$ F\left({\boldsymbol{c}}_{1},{\boldsymbol{c}}_{2},{\boldsymbol{c}}_{3}\right)= \frac{1}{2}{\left\|\boldsymbol{y}-\sum _{i=1}^{3}{\boldsymbol{D}}_{i}{\boldsymbol{c}}_{i}\right\|}_{2}^{2}+\sum _{i=1}^{3}{\lambda }_{i}{\mathrm{\varPsi }}_{{\boldsymbol{B}}_{i}}\left({\boldsymbol{c}}_{i}\right). $
(7)

式中：$ {\mathrm{\varPsi }}_{{\boldsymbol{B}}_{i}}\left({\boldsymbol{c}}_{i}\right) $为$ {\boldsymbol{c}}_{i} $对应的GMC惩罚函数. GMC惩罚函数可以表示为

$ {\mathrm{\varPsi }}_{{\boldsymbol{B}}_{i}}\left({\boldsymbol{c}}_{i}\right)={||{\boldsymbol{c}}_{i}||}_{1}- \mathrm{arg}\underset{{\boldsymbol{\upsilon }}_{i}}{\mathrm{min}}\left\{{||{\boldsymbol{\upsilon }}_{i}||}_{1}+\frac{1}{2}{||{\boldsymbol{B}}_{i}\left({\boldsymbol{c}}_{i}-{\boldsymbol{\upsilon }}_{i}\right)||}_{2}^{2}\right\}. $
(8)

式中：$ {\boldsymbol{B}}_{i} $与$ {\boldsymbol{\upsilon }}_{i} $分别为对应的矩阵和向量. 由于$ \boldsymbol{B} $很难直接求出来，根据文献[12]的方法，将$ \boldsymbol{B} $初始设置如下：

$ {\boldsymbol{B}}_{i}=\sqrt{\frac{\gamma }{{\lambda }_{i}}}{\boldsymbol{D}}_{i}. $
(9)

式中：$\gamma $为MESD方法的超参数，$\gamma \in [0,1.0] $.

代价函数可以表示为

$ F\left({\boldsymbol{c}}_{1},{\boldsymbol{c}}_{2},{\boldsymbol{c}}_{3},{\boldsymbol{\upsilon }}_{1},{\boldsymbol{\upsilon }}_{2},{\boldsymbol{\upsilon }}_{3}\right)={F}_{1}+{F}_{2}. $
(10)

$ {F}_{1}=\frac{1}{2}{\left\|\boldsymbol{y}-\sum _{i=1}^{3}{\boldsymbol{D}}_{i}{\boldsymbol{c}}_{i}\right\|}_{2}^{2}. $
(11)

$ {F}_{2}=\sum _{i=1}^{3} \left({\lambda }_{i}{||{\boldsymbol{c}}_{i}||}_{1}-{\lambda }_{i}{||{\boldsymbol{\upsilon }}_{i}||}_{1}-\frac{\gamma }{2}{||{\boldsymbol{D}}_{i}\left({\boldsymbol{c}}_{i}-{\boldsymbol{\upsilon }}_{i}\right)||}_{2}^{2}\right). $
(12)

使用FBS（forward-backward splitting，FBS）算法[13]来求解代价函数，以$ {\boldsymbol{c}}_{1}^{{\mathrm{opt}}} $为例，迭代过程如下.

$ {\boldsymbol{\omega }}_{1}^{\left(k\right)}={\boldsymbol{c}}_{1}^{\left(k\right)}-{2\mu }_{1}{\boldsymbol{G}}_{1}. $
(13)

$\left. \begin{array}{l}{\boldsymbol{G}}_{1}=\left[{\boldsymbol{D}}_{1}^{\mathrm{T}}\left({\boldsymbol{D}}_{1}\boldsymbol{Q}+{\boldsymbol{D}}_{2}{\boldsymbol{c}}_{2}^{\left(k\right)}+{\boldsymbol{D}}_{3}{\boldsymbol{c}}_{3}^{\left(k\right)}-\boldsymbol{y}\right)\right],\\ \boldsymbol{Q}={\boldsymbol{c}}_{1}^{\left(k\right)}+\gamma \left({\boldsymbol{\upsilon }}_{1}^{\left(k\right)}-{\boldsymbol{c}}_{1}^{\left(k\right)}\right).\end{array}\right\} $
(14)

$ {\boldsymbol{\theta }}_{1}^{\left(k\right)}={\boldsymbol{\upsilon }}_{1}^{\left(k\right)}-2{\mu }_{1}\gamma {\boldsymbol{D}}_{1}^{\mathrm{T}}{\boldsymbol{D}}_{1}\left({\boldsymbol{\upsilon }}_{1}^{\left(k\right)}-{\boldsymbol{c}}_{1}^{\left(k\right)}\right). $
(15)

$ {\boldsymbol{c}}_{1}^{(k+1)}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\left({\boldsymbol{\omega }}_{1}^{\left(k\right)},{\mu }_{1}{\lambda }_{1}\right). $
(16)

$ {\boldsymbol{\upsilon }}_{1}^{(k+1)}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\left({\boldsymbol{\theta }}_{1}^{\left(k\right)},{\mu }_{1}{\lambda }_{1}\right). $
(17)

阈值为$ T $的软阈值函数$ \mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\left(\cdot \right) $可以表示为

$ \mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\left(x,T\right)=x\cdot \mathrm{m}\mathrm{a}\mathrm{x}\left\{\mathrm{0,1}-{T}/{\left|x\right|}\right\}. $
(18)

通过上述的迭代过程，可以得到齿轮箱的滚动轴承与齿轮瞬态分量：$ {\boldsymbol{x}}_{1}={\boldsymbol{D}}_{1}{\boldsymbol{c}}_{1} $，$ {\boldsymbol{x}}_{2}={\boldsymbol{D}}_{2}{\boldsymbol{c}}_{2} $.

2. 最优原子寻优算法的理论基础

2.1. 广义似然比指标

针对现有的统计指标无法很好地区分信号的非高斯性和非平稳性的问题，Antoni等[14]提出能够单独量化非高斯性与非平稳性的统计指标系统方法论. 该方法通过零假设（the null hypotheses）和备择假设（the alternative hypotheses）来区分设备的健康状态和异常状态，每个假设都由不同的概率密度函数来表征.

以$ {H}_{0} $表示零假设，$ {H}_{1} $表示备择假设，分别表示信号的2种状态：通常$ {H}_{1} $反映出信号中一些统计特性（或症状）的存在，$ {H}_{0} $表示正常情况. 对于一段离散的时域信号，以$ x\left(n\right) $表示时刻$ n $的幅值，以向量$ \boldsymbol{x}={\left[x\left(0\right),x\left(1\right),\cdots ,x\left(L-1\right)\right]}^{\mathrm{T}} $表示测量到的长度为$ L $的样本信号，以$ {p}_{X}\left(\boldsymbol{x}|{H}_{0},{\boldsymbol{\theta }}_{0}\right) $和$ {p}_{X}\left(\boldsymbol{x}|{H}_{1},{\boldsymbol{\theta }}_{1}\right) $分别表示信号$ \boldsymbol{x} $在$ {H}_{0} $和$ {H}_{1} $假设下的概率密度函数，其中$ {\boldsymbol{\theta }}_{0} $、$ {\boldsymbol{\theta }}_{1} $分别为假设$ {H}_{0} $和$ {H}_{1} $的参数集合向量：

$ \left. \begin{array}{c}{H}_{0}:{\boldsymbol{x}}\sim {p}_{X}\left(\boldsymbol{x}|{H}_{0},{\boldsymbol{\theta }}_{0}\right),\\ {H}_{1}:{\boldsymbol{x}}\sim {p}_{X}\left(\boldsymbol{x}|{H}_{1},{\boldsymbol{\theta }}_{1}\right).\end{array} \right\}$
(19)

广义似然比（generalized likelihood ratio，GLR）检验具有几个有利的属性，包括最优性. GLR[15-16]被定义为

$ \mathrm{\varLambda }\left(\boldsymbol{x}\right)=\frac{\underset{{\boldsymbol{\theta }}_{1}}{\mathrm{sup}}{p}_{X}\left(\boldsymbol{x}|{H}_{1},{\boldsymbol{\theta }}_{1}\right)}{\underset{{\boldsymbol{\theta }}_{0}}{\mathrm{sup}}{p}_{X}\left(\boldsymbol{x}|{H}_{0},{\boldsymbol{\theta }}_{0}\right)}=\frac{{p}_{X}\left(\boldsymbol{x}|{H}_{1},{\hat{\boldsymbol{\theta }}}_{1}\right)}{{p}_{X}\left(\boldsymbol{x}|{H}_{0},{\hat{\boldsymbol{\theta }}}_{0}\right)}. $
(20)

式中：$ {\hat{\boldsymbol{\theta }}}_{0} $和$ {\hat{\boldsymbol{\theta }}}_{1} $为2个模型的极大似然估计（maximum-likelihood estimates，MLEs）.

对GLR取对数以简化计算，对数GLR的结果可以表示为

$\begin{split} \mathrm{ln}\;\mathrm{\varLambda }\left(\boldsymbol{x}\right)=\;&\sum _{n=0}^{L-1}\mathrm{ln}\;{p}_{X}\left(x\left(n\right)|{H}_{1},{\hat{\boldsymbol{\theta }}}_{1}\right)- \\&\sum _{n=0}^{L-1}\mathrm{ln}\;{p}_{X}\left(x\left(n\right)|{H}_{0},{\hat{\boldsymbol{\theta }}}_{0}\right)= {L}_{{{H}}_{1}}\left(\boldsymbol{x}\right)-{L}_{{{H}}_{0}}\left(\boldsymbol{x}\right).\end{split} $
(21)

式中：$ {L}_{{{H}}_{{i}}}\left(\boldsymbol{x}\right) $为信号$ \boldsymbol{x} $在${{{H}}_{{i}}} $假设下的对数极大似然估计，定义如下所示的状态检测指标：

$ {I}_{{{H}}_{1}/{{H}}_{0}}\left(\boldsymbol{x}\right)=c\cdot \frac{{L}_{{{H}}_{1}}\left(\boldsymbol{x}\right)-{L}_{{{H}}_{0}}\left(\boldsymbol{x}\right)}{L}\geqslant 0. $
(22)

式中：$ L $为信号长度，使$ L $向无穷大增长时，起到归一化的效果，使得指标渐进恒定；$ c > 0 $为校准因子，可以简化表达式. GLR≥1，因此$ \mathrm{ln}\;\mathrm{\varLambda }\left(\boldsymbol{x}\right)\geqslant 0 $，$ {I}_{{{H}}_{1}/{{H}}_{0}}\geqslant 0 $.

在高斯假设的循环平稳性检验中，$ {H}_{0} $假设描述一段平稳信号，$ {H}_{1} $假设描述一段已知样本周期为$ N $个样本点的循环平稳信号. $ {H}_{0} $与$ {H}_{1} $如下所示：

$ \left.\begin{array}{c}{H}_{0}:{\boldsymbol{x}}\sim {N}_{\mathrm{P}\mathrm{D}\mathrm{F}}\left(\boldsymbol{x};0,{\sigma }^{2}\boldsymbol{I}\right),\\ {H}_{1}:{\boldsymbol{x}}\sim {N}_{\mathrm{P}\mathrm{D}\mathrm{F}}\left(\boldsymbol{x};0,\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\sigma }^{2}\left(n\right)\right)\right).\end{array}\right\}$
(23)

式中：$ {N}_{\mathrm{P}\mathrm{D}\mathrm{F}}\left(\cdot \right) $为高斯分布概率密度函数；$ \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\cdot \right) $为对角矩阵；$ \boldsymbol{I} $为单位矩阵；$ {\sigma }^{2}\left(n\right) $为周期为$ N $的方差，即$ {\sigma }^{2}\left(n\right)={\sigma }^{2}\left(n+N\right),N\in \bf{N} $.

在高斯假设下，高斯循环平稳（Gaussian cyclostationary，GCS）信号的对数似然函数为

$ {{L}}_{\mathrm{G}\mathrm{C}\mathrm{S}}\left(\boldsymbol{x}\right)=\mathrm{ln}\prod _{n=0}^{L-1}\frac{{{\mathrm{exp}}}\;{[-{{\left|x\left(n\right)\right|}^{2}}/({c{\hat{\sigma }}^{2}\left(n\right))}]}}{{\left(c{\text{π}} {\hat{\sigma }}^{2}\left(n\right)\right)}^{\frac{1}{c}}}. $
(24)

式中：

$c= \left\{\begin{array}{l} 2,x\left(n\right)为实信号;\\ 1,x\left(n\right)为复信号.\end{array}\right. $

$ {{\sigma }}^{2}\left(n\right) $的极大似然估计为

$ {{\hat \sigma }}^{2}\left(n\right) = {s}^{2}\left(n\right)=\frac{1}{K}\sum _{k=0}^{K-1}{\left|x\left(n+kN\right)\right|}^{2}. $
(25)

式中：$ K=\left\lfloor {L/N} \right\rfloor $为采样信号持续时间内周期$ N $的循环次数，$ \left\lfloor {\cdot} \right\rfloor $表示向下取整. 将式(25)代入式(24)，可以得到

$ {L}_{\mathrm{G}\mathrm{C}\mathrm{S}}\left(\boldsymbol{x}\right)=-\frac{L}{c}\left[\mathrm{ln}\left(c{\text{π}} e\right)+\left\langle{\mathrm{ln}\left({s}^{2}\left(n\right)\right)}\right\rangle\right]. $
(26)

在高斯假设下，高斯平稳（Gaussian stationary，GS）信号具有时不变的方差，即$ {\sigma }^{2}\left(n\right)\equiv {\sigma }^{2} $. $ {\sigma }^{2} $的极大似然估计$ {\hat{\sigma }}^{2} $为

$ {\hat{\sigma }}^{2}= \frac{1}{L}\sum _{n=0}^{L-1}{\left|x\left(n\right)\right|}^{2}=\frac{1}{K}\sum _{k=0}^{K-1}{s}^{2}\left(n\right)=\left\langle{{s}^{2}\left(n\right)}\right\rangle. $
(27)

因此，高斯平稳信号的对数似然函数为

$ {L}_{\mathrm{G}\mathrm{S}}\left(\boldsymbol{x}\right)=-\frac{L}{c}\left[\mathrm{ln}\left(c{\text{π}} e\right)+\mathrm{ln}\left\langle{{s}^{2}\left(n\right)}\right\rangle\right]. $
(28)

式中：$ \left\langle{\cdot }\right\rangle $为算术平均算子.

根据式(22)、(26)、(28)可得，测试高斯循环平稳假设与高斯平稳假设的标量指标为

$ \begin{split} {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}}\left(\boldsymbol{x}\right)=&c\cdot \frac{{L}_{\mathrm{G}\mathrm{C}\mathrm{S}}\left(\boldsymbol{x}\right)-{L}_{\mathrm{G}\mathrm{S}}\left(\boldsymbol{x}\right)}{L}=\\&\mathrm{ln}\left\langle {s}^{2}\left(n\right){} \right\rangle -\left\langle {\mathrm{ln}\left({s}^{2}\left(n\right)\right)} \right\rangle .\end{split} $
(29)

2.2. 非对称高斯啁啾模型

非对称高斯啁啾模型是高斯啁啾模型的扩展. 通过在高斯啁啾模型中引入额外的不对称因子，可以构建具有不对称衰减的小波原子AGCM. AGCM的形式[11]为

$\left. \begin{split} W\left(t\right)=&E\left(t-\tau \right)F\left(t-\tau \right),\\E\left(t\right)=&\mathrm{e}\mathrm{x}\mathrm{p}\left[-\chi \left(1-\delta \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(mt\right)\right){t}^{2}\right],\\F\left(t\right)=&\mathrm{cos}\left(f\left(t\right)+\gamma {\left(t\right)}^{2}+\theta \right).\end{split}\right\} $
(30)

式中：$ \chi $为带宽系数，$ \chi > 0 $；$ \delta $为不对称系数，$ \delta \in \left(-\mathrm{1,1}\right) $；$ \tau $为时间系数；$ f $为固有频率；$ \gamma $为啁啾率；$ \theta \in \left[\left.\mathrm{0,2}{\text{π}} \right)\right. $为相位；$ E\left(t\right) $为包络部分；$ F\left(t\right) $为频率部分；$ \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(mt\right) $为双曲正切函数，其中$ m $为正整数，该函数是符号函数的平滑逼近，负责在很短的时间内改变$ \delta $的符号，使得$ E\left(t\right) $在峰值点前、后具有2种不同衰减率的高斯函数. AGCM的形状由可调参数向量$ \boldsymbol{q}=\left[\chi ,\delta ,\tau ,f,\gamma ,\theta \right] $决定.

2.3. 脉冲特征增强方法

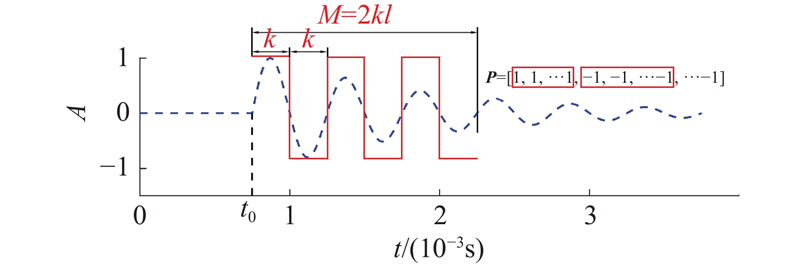
Lin等[17]为了提高微弱故障冲击的信噪比，提出利用脉冲振荡结构特性的特征增强方法. 典型的脉冲响应衰减振动如图1所示. 图中，A为幅值，t为时间.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   脉冲响应方波的示意图

Fig.1   Diagram of impulse response square wave


脉冲的衰减振动从$ {t}_{0} $时刻开始，可以看出，脉冲响应的振幅逐渐衰减到零，振荡的波峰和波谷以相同的间隔交替出现. 将间隔记为$ {k}_{{\mathrm{t}}} $，以采样点数为单位. 为了强化原始信号的故障特征，构建具有归一化幅度和与脉冲响应相同持续时间的高、低电平方波$ \boldsymbol{P}=[\mathrm{1,1},\cdots 1,-1,-1,\cdots -1,\cdots ,-1] $，如图1的方波所示. 图中，$ k $为高电平或低电平的持续时间，$ l $为模式中高电平的数量，$ M=2kl $为所定义的方波长度. 对于一段存在故障冲击的振动信号，当固有频率$ f $和采样频率$ {f}_{{\mathrm{s}}} $均已知时，理论上的间隔$ {k}_{{\mathrm{t}}} $可以计算为

$ {k}_{{\mathrm{t}}}={{f}_{{\mathrm{s}}}}/{(2f)}. $
(31)

当预先定义的方波$ \boldsymbol{P} $与包含噪声的原始信号同步，即$ k={k}_{{\mathrm{t}}} $时，方波$ \boldsymbol{P} $与原始信号的内积运算将放大脉冲响应的幅值. 此外，由于构造的方波具有正负交替的特性，内积运算具有降噪的效果. 选取合适的$ k $，可以使得构建的方波$ \boldsymbol{P} $有增强噪声信号中的故障特征的性质.

对于一段包含故障冲击的振动信号$ \boldsymbol{y}\in {\bf{R}}^{N} $，通过方波$ \boldsymbol{P} $构造的结构矩阵$ \boldsymbol{S}\in {\bf{R}}^{N\times (N+M-1)} $为

$ \boldsymbol{S}=\left[\begin{array}{*{20}{c}} {\boldsymbol{P}}&{}&{}&{}&{\boldsymbol{0}} \\ {}&{\boldsymbol{P}}&{}&{}&{} \\ {}&{}&{\boldsymbol{P}}&{}&{} \\ {}&{}&{}& \ddots &{} \\ {\boldsymbol{0}}&{}&{}&{}&{\boldsymbol{P}} \end{array}\right]. $
(32)

为了保持信号的一致性，将原始信号$ \boldsymbol{y}\in {\bf{R}}^{N} $通过零填充扩展为$ {\boldsymbol{y}}_{0}\in {\bf{R}}^{N+M-1} $，则冲击增强后的信号为

$ {\boldsymbol{y}}_{k}=\boldsymbol{S}{\boldsymbol{y}}_{0}. $
(33)

3. 研究内容

以向量$ {\boldsymbol{q}}_{1}=\left[{\chi }_{1},{\delta }_{1},{\tau }_{1},{f}_{1},{\gamma }_{1},{\theta }_{1}\right] $表示构造滚动轴承瞬态分量字典的AGCM参数向量，$ {\boldsymbol{q}}_{2}=\left[{\chi }_{2},{\delta }_{2},{\tau }_{2}, {f}_{2}, {\gamma }_{2},{\theta }_{2}\right] $表示构造齿轮瞬态分量字典的AGCM参数向量. 根据式(4)、(5)可知，滚动轴承的瞬态分量为单侧衰减形式，用于构造滚动轴承分量字典的AGCM的参数$ {\delta }_{2}\in \left(\left.\mathrm{0,1.0}\right]\right. $. 由于齿轮的瞬态分量为双侧衰减形式，用于构造齿轮分量字典的AGCM的参数$ {\delta }_{2}=0 $. 对于恒定转速下的脉冲信号，由于$ \gamma $变化很小，取$ {\gamma }_{1}={\gamma }_{2}=0 $. 虽然AGCM能够通过参数向量得到较广的变化范围，但如何寻找到最优的AGCM参数是待解决的优化问题. 通过脉冲特征增强方法，利用AGCM构造原子，得到脉冲特征增强后的信号$ {\boldsymbol{y}}_{0} $. 原始的脉冲特征增强方法的设计目标是增强信号内的脉冲成分，因此使用方波$ \boldsymbol{P} $构造结构矩阵，与补零后的原始信号相乘进行特征增强.

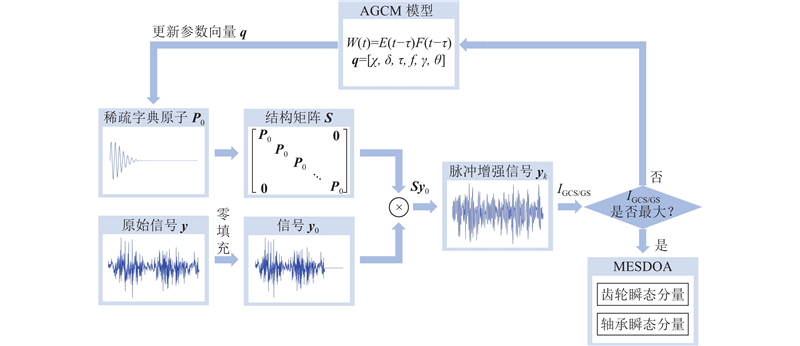
原始脉冲特征增强方法采用峭度作为最优增强结果的遴选标准. 鉴于峭度对随机冲击具有敏感性，且齿轮的啮合冲击易导致峭度偏大，提出通过构建广义似然比指标$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $作为最优$ {\boldsymbol{y}}_{0} $的寻优目标函数，对AGCM进行最优选取，获得滚动轴承与齿轮瞬态分量最佳的稀疏表示原子.

将基于AGCM与脉冲增强的最优字典的MESD方法称为使用最优原子的多种增强稀疏表示方法（multiple enhanced sparse decomposition with optimal atom，MESDOA），MESDOA方法的示意图如图2所示. 图中，$ {\boldsymbol{P}}_{0} $表示AGCM生成的小波.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   MESDOA方法最优原子构造的示意图

Fig.2   Schematic diagram of optimal atomic construction of MESDOA method


结合滚动轴承故障冲击与齿轮故障冲击的特点，对AGCM的参数向量$ \boldsymbol{q} $的优化进行如下简化. AGCM对原子影响最大的参数为带宽系数和固有频率；对于滚动轴承对应的原子，可以将不对称系数设置为$ {\delta }_{1}=0.99 $，以对应单侧脉冲的形式. 通过AGCM生成的小波$ {\boldsymbol{P}}_{0} $先生成结构矩阵，再与信号$ {\boldsymbol{y}}_{0} $相乘进行脉冲增强，且$ \boldsymbol{S} $具有时移特性，因此AGCM的参数$ \tau $与$ \theta $均可以取零. 基于此，AGCM需要优化的参数简化为$ \boldsymbol{q}=\left[\chi ,f\right] $，可以使用遍历寻优的方法进行优化.

4. 算法实验验证与对比分析

4.1. 实验介绍

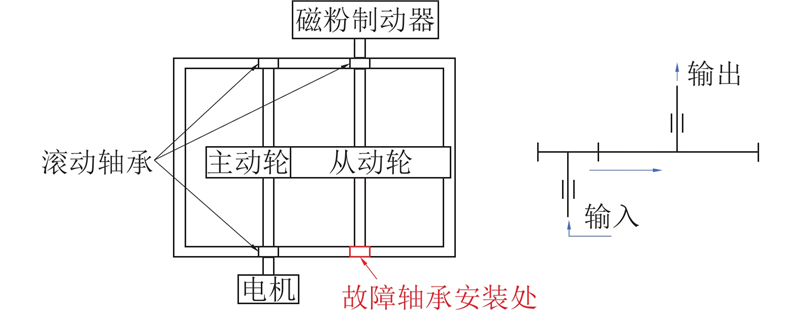
为了验证本文方法针对固定在齿轮箱外壳处的振动传感器采集到的振动信号的表现，开展齿轮箱故障模拟实验，对算法进行验证. 实验台的实物图与结构简图如图3、4所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   齿轮箱故障模拟实验台

Fig.3   Gearbox fault simulation test bench


图 4

新窗口打开| 下载原图ZIP| 生成PPT

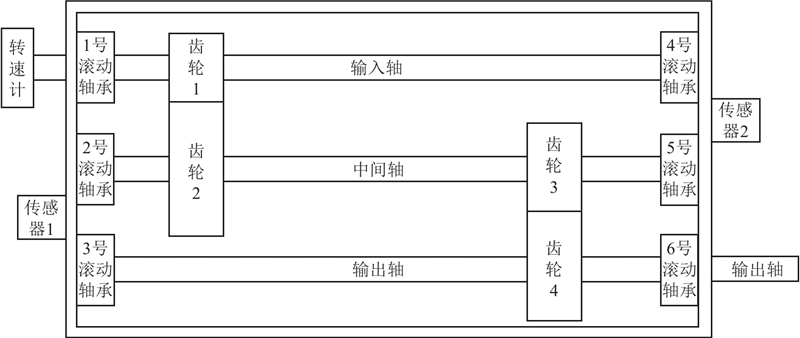
图 4   齿轮箱故障模拟实验台的齿轮箱结构简图

Fig.4   Gearbox structure diagram of gearbox fault simulation test bench


该实验台的主体部分从左到右分别为电机、单级平行轴齿轮箱、磁粉制动器. 电机转速由控制柜控制，实时转速在设定转速上下小幅波动. 单级平行轴齿轮箱为斜齿或直齿齿轮箱，主动轮齿数为30，从动轮齿数为70. 磁粉制动器提供扭矩负载，模拟实际工况. 将振动传感器分别固定于齿轮箱顶部、右侧从动轴附近、前侧、左侧主动轴附近以及后侧. 将振动传感器连接到数采仪，进行振动数据采集，采样频率设置为$ 50\;\mathrm{k}\mathrm{H}\mathrm{z} $. 该实验台可以模拟齿轮箱内的齿轮故障与滚动轴承故障，故障轴承的安装位置位于从动轴近电机侧. 以斜齿齿轮为例，滚动轴承故障元件如图5所示，齿轮故障元件如图6所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   齿轮箱斜齿齿轮故障元件图

Fig.5   Diagram of faulty component of helical gear in gearbox


图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   齿轮箱滚动轴承故障元件图

Fig.6   Gearbox rolling bearing fault component diagram


实验为模拟齿轮箱在常转速条件下的各类齿轮故障与滚动轴承故障. 在实验过程中，主动轴转速从$ 500\;\mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n} $开始，以$ 500\;\mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n} $的步长增加，到$ 3\; 500\;\mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n} $为止，共计7类转速. 各个转速工况下有2种负载，分别为$ 4 $、$ 8\;\mathrm{N}\cdot \mathrm{m} $，每种故障类型理论上进行14种工况的实验. 实验仅模拟主动轮、从动轮与滚动轴承各部件发生单一故障的情况，不包含跨故障元件的复合故障，仅在斜齿齿轮箱中模拟滚动轴承故障，包括直齿齿轮箱与斜齿齿轮箱共计18组实验.

为了保证算法在不同数据集中的有效性，采用PHM 2009齿轮箱数据集[18]作为验证数据集. PHM 2009齿轮箱数据集实验的齿轮箱结构如图7、8所示，振动数据由齿轮箱输入轴侧和输出轴侧的传感器进行采集. 该采集系统使用2种齿轮，即直齿与斜齿，输入轴与中间轴间的齿数比为1∶3，中间轴与输出轴间的齿数比为3∶5. 数据集的振动信号分别在齿轮箱主动轴转速为$ 1 \;800 $、$ 2\; 100 $、$ 2 400 $、$ 2 \;700 $、$ 3 \;000\;\mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n} $，高负载与低负载的情况下进行实验，每种工况实验重复2次，通过数采仪采集传感器1（通道1）、传感器2（通道2）与转速计（通道3）的信号，采样频率为$ f_{\mathrm{s}}={200\;000}/{3}\approx 66 \;666.67\;\mathrm{H}\mathrm{z} $，每组实验采集4 s的信号.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   PHM 2009数据集实验台与齿轮箱内部实物图

Fig.7   PHM 2009 data set experimental bench and gearbox internal physical diagram


图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   PHM 2009数据集齿轮箱的结构图

Fig.8   Structure diagram of PHM 2009 data set gearbox


4.2. 算法效果的验证

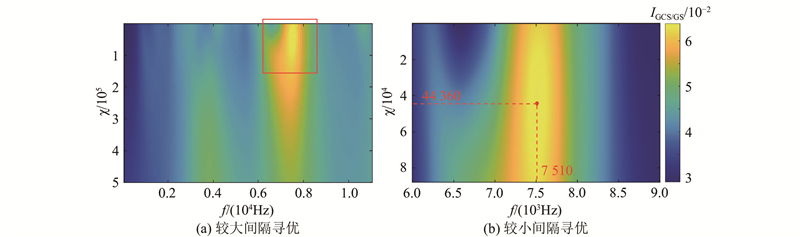
为了验证MESDOA的效果，以PHM 2009数据集的“直齿7”在主动轴转速为$ 3\;000\mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n} $，承受高负载时的数据的滚动轴承故障分量的稀疏字典对应的AGCM寻优过程为例，结果如图9所示. 图中，f为频率，$\chi $为带宽系数.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   PHM 2009“直齿7”滚动轴承分量AGCM原子遍历寻优结果图

Fig.9   AGCM atom optimization diagram of spur 7 data of PHM 2009 data set’s rolling bearing component


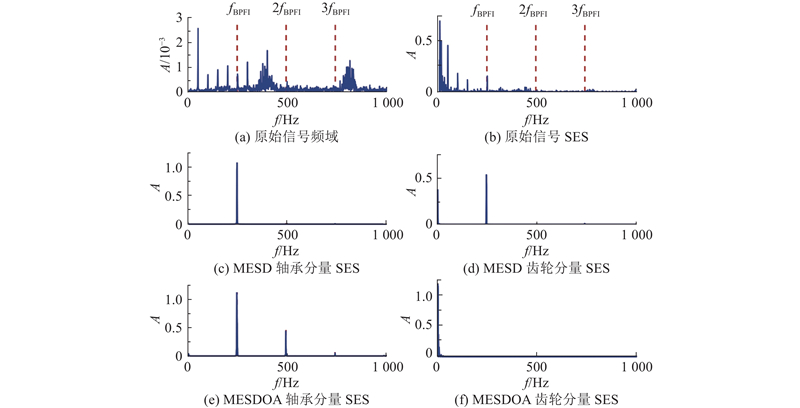
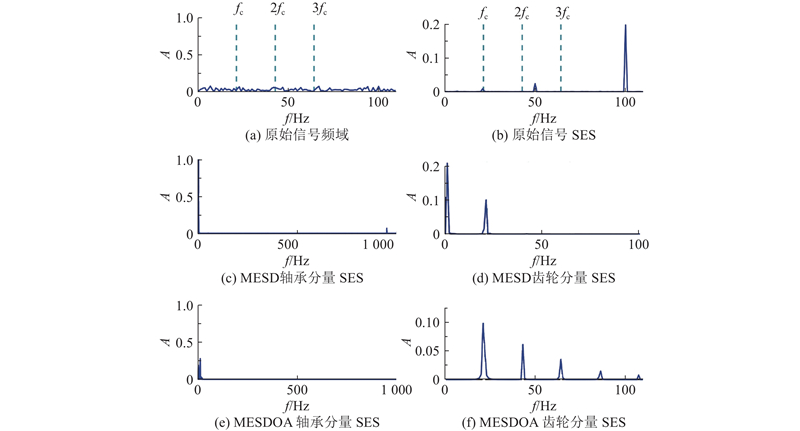
以脉冲增强后的$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $为指标，在较大的间隔下进行初次的参数取值，得到如图9（a）所示的结果. 在图9（a）虚线框的取值范围内进行较小间隔的寻优，得到如图9（b）所示的结果，确定当$ f=7\;510 $，$ \chi =44 \;360 $时，AGCM的参数最优.

如图10所示为MESDOA与MESD方法的稀疏表示结果对比. 图中，fBPFI为故障轴承的故障特征频率. 如图10（a）、（b）所示分别为原始信号的频域分析及全频带滤波后的平方包络谱. 由于滚动轴承内环故障特征频率与5倍转频高度接近，利用传统频谱分析方法，难以有效地区分二者. 如图10（c）、（d）所示为利用MESD方法分离出的滚动轴承与齿轮瞬态分量平方包络谱，如图10（e）、（f）所示为MESDOA算法的分离结果. 实验表明，利用2种方法均能够有效地提取滚动轴承瞬态分量，但MESD方法存在信号泄露问题——在齿轮瞬态分量中残留轴承故障特征频率（见图10（d）的箭头标注），利用MESDOA算法分离的齿轮分量仅在0~10 Hz频段存在微弱干扰分量.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   PHM 2009“直齿7”数据的稀疏表示结果

Fig.10   Sparse representation result of PHM 2009 spur 7 dataset


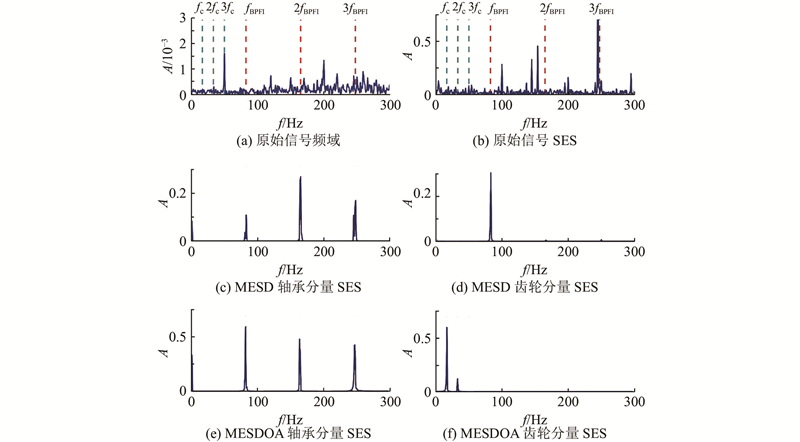
为了验证轴承和齿轮均发生故障时的结果，使用PHM 2009数据集的“斜齿5”在主动轴转速为$ 3\; 000\;\mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n} $时的数据，得到如图11所示的结果. 图中，fc为故障齿轮的故障特征频率. 图11（a）中存在齿轮的3倍故障特征频率，从图8可知，由于主动轴与中间轴的齿数比为1∶3，因此，图11（a）中齿轮的3倍故障特征频率应为主动轴的1倍转频. 在原始信号的频域和平方包络谱中都无法观察到齿轮与滚动轴承的故障特征频率. 可以发现，两者都成功地从原始信号中分离得到滚动轴承的瞬态分量，但利用MESD方法分离得到的齿轮瞬态分量不包含齿轮故障特征频率，缺失了对齿轮故障的正确诊断，利用MESDOA方法分离得到齿轮故障的瞬态分量.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   PHM 2009“斜齿5”数据的稀疏表示结果

Fig.11   Sparse representation result of PHM 2009 helical 5 dataset


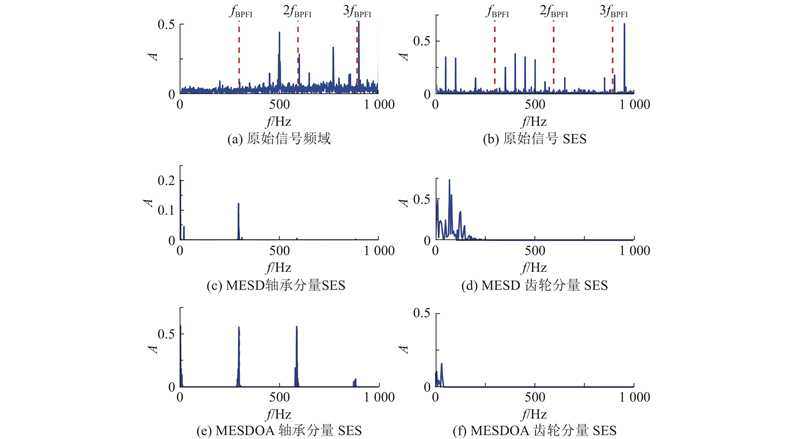
由于齿轮箱故障模拟数据集不包括齿轮与轴承的复合故障，分别以滚动轴承内环故障与斜齿齿轮从动轮断齿在主动轴转速为$ 3 \;000\;\mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n} $，负载为$ 8\;\mathrm{N}\cdot \mathrm{m} $条件下的数据为例，展示MESDOA方法在较低信噪比数据集下的效果，结果分别如图12、13所示. 从图12可知，利用MESDOA与MESD方法，均提取得到轴承的瞬态分量，但MESDOA轴承瞬态分量的2、3倍频更加明显，且两者的齿轮瞬态分量均存在无关频率，MESDOA方法的无关谱线更少. 通过对图13所示的结果进行对比可知，MESD方法存在较明显的无关频率，且2、3倍频不如MESDOA方法明显. 提出的原子寻优方法相较于使用最大化相关系数的方法在实际情况中更有效.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   齿轮箱故障模拟数据集的滚动轴承故障稀疏表示结果

Fig.12   Sparse representation result of rolling bearing fault in gearbox fault simulation data set


图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   齿轮箱故障模拟数据集的齿轮故障稀疏表示结果

Fig.13   Sparse representation result of gear fault in gearbox fault simulation dataset


4.3. 算法效果的对比

为了定量地对比MESDOA与其他方法的降噪水平与特征增强性能，引入一些量化指标[2].

使用故障特征指数（fault feature index，FFI），评价SES结果中故障特征频率谱线的明显程度：

$ {\mathrm{FFI}}=\frac{{\displaystyle \sum} _{i=1}^{3}{A}^{*}\left(i{f}_{\mathrm{m}}\right)}{{\displaystyle \sum} _{f=0}^{3.2{f}_{\mathrm{m}}}A\left(f\right)}. $
(34)

$ {A}^{*}\left(i{f}_{\mathrm{m}}\right)= \mathrm{m}\mathrm{a}\mathrm{x}\; A(f);f=if_{\mathrm{m}}-0.02f_{\mathrm{m}} \sim if_{\mathrm{m}}+0.02f_{\mathrm{m}}. $
(35)

式中：$ A\left(f\right) $为SES频谱在频率$ f $处的幅值，$ {f}_{\mathrm{m}} $为对应的故障特征频率. 与FFI的构建过程相类似的其他频域评估指标还有修正的频谱损伤指数（modified spectrum impairment indice，MSII）、修正的频谱变化指数（spectral variation index，SVI）和修正的特征频率强度系数（characteristic frequency intensity coefficient，CFIC）.

$ {\mathrm{MSII}}=\sum _{i=1}^{3}\left(\frac{{\displaystyle \sum} _{f=i{f}_{m}-\Delta f}^{i{f}_{\mathrm{m}}+\Delta f}{A}^{2}\left(f\right)}{3{\displaystyle \sum} _{f=i{f}_{\mathrm{m}}-0.3{f}_{\mathrm{m}}}^{i{f}_{m}+0.3{f}_{\mathrm{m}}}{A}^{2}\left(f\right)}\right). $
(36)

$ {\mathrm{SVI}}=\frac{{\displaystyle \sum} _{i=1}^{3}{B}^{*}\left(i{f}_{\mathrm{m}}\right)}{{\displaystyle \sum} _{f={f}_{\mathrm{m}}+1}^{{2f}_{\mathrm{m}}-1}A\left(f\right)}. $
(37)

$ {B}^{*}\left(i{f}_{{\mathrm{m}}}\right)= {\mathrm{mean}}\;A(f);f=if_{\mathrm{m}}-0.02f_{\mathrm{m}} \sim if_{\mathrm{m}}+0.02f_{\mathrm{m}}. $
(38)

$ {\mathrm{CFIC}}=\frac{K}{S}\frac{{\displaystyle \sum} _{i=1}^{S}{A}^{*}\left(i{f}_{\mathrm{m}}\right)}{{\displaystyle \sum} _{f=0}^{{f}_{\mathrm{K}}}A\left(f\right)}. $
(39)

式中：$ \Delta f=4\;\mathrm{H}\mathrm{z} $，$ S $为故障特征频率的谐波数，$ K $为频谱中所有的频率分量数. 上述指标值越大，表示特征增强效果越好，信噪比越高.

由于式(34)~(39)中的量化指标是针对含噪信号开发的，而稀疏表示的瞬态分量除故障特征频率外，大部分的频率幅值均为0. 受Hou等[19]将故障频率分量与其他频率分量通过正负符号分隔思想的启发，将平方包络谱中非故障特征频率处的幅值置为负，得到新的双边平方包络谱（double sides SES，DSS）.

通过计算双边平方包络谱的和与原平方包络谱之和的比值，得到双边平方包络谱指数（double sides SES index，DSSI），量化原始平方包络谱中故障特征频率及其谐波谱线与无关频率分量的明显程度.

$ {A}_{\mathrm{D}\mathrm{S}\mathrm{S}}=AT, $
(40)

$ {\mathrm{DSSI}}=\frac{{\displaystyle \sum} _{f=0}^{3.2{f}_{\mathrm{m}}}{A}_{\mathrm{D}\mathrm{S}\mathrm{S}}\left(f\right)}{{\displaystyle \sum} _{f=0}^{3.2{f}_{\mathrm{m}}}A\left(f\right)}. $
(41)

式中：$ A $为SES的幅值；$ {A}_{\mathrm{D}\mathrm{S}\mathrm{S}} $为DSS的幅值；$ T $为故障特征频率及其左右$ 2\mathrm{H}\mathrm{z} $处等于$ 1 $，其余位置等于$ -1 $的脉冲向量.

为了定量评估谐波成分的存在性及显著程度，提出多谐波指数（multiple harmonic index，MHI）.

$ {\mathrm{MHI}}=\sum _{i=1}^{3}\frac{{A^{*}(if_{\mathrm{m}})}}{\max A(f)};\;\;0 < f < 3.2 f_{\mathrm{m}} . $
(42)

$ {P}^{*}\left(i{f}_{\mathrm{m}}\right)=\mathrm{m}\mathrm{a}\mathrm{x}\;P\left(f\right);f=if_{\mathrm{m}} - 0.02f_{\mathrm{m}} \sim if_{\mathrm{m}} + 0.02f_{\mathrm{m}} . $

选取MESD[9]、MOMEDA[20]、FMTVD[17]、BCSM[21]、OA-TVF-EMD[22]方法与提出的MESDOA方法进行对比，利用4.2节中用于效果验证的数据集进行故障特征提取. 通过式(34)~(43)中的量化指标对故障特征提取的结果进行量化，得到如图14~17所示的结果.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

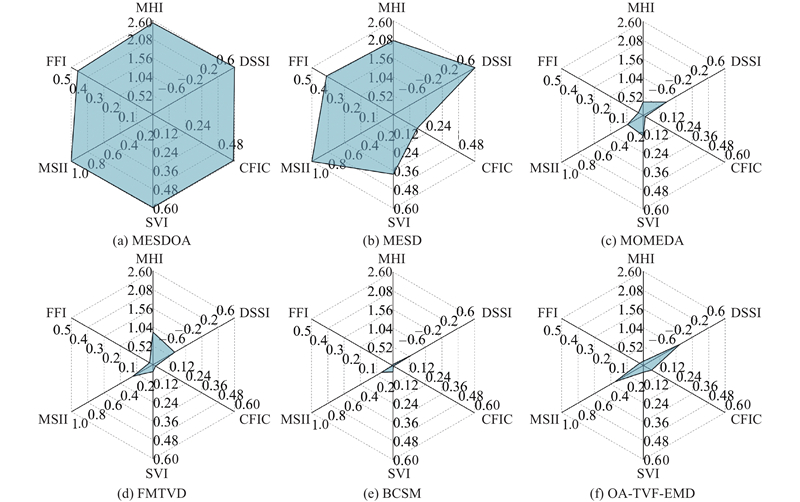
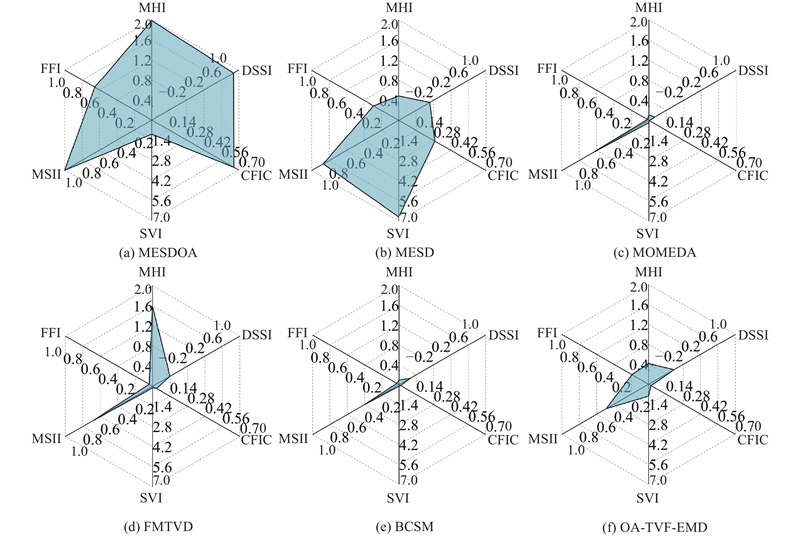
图 14   PHM 2009“斜齿5”数据各方法提取的滚动轴承内环故障特征量化雷达图

Fig.14   Radar chart of rolling bearing inner race fault characteristics extracted by various methods of PHM 2009 helical 5 data


图 15

新窗口打开| 下载原图ZIP| 生成PPT

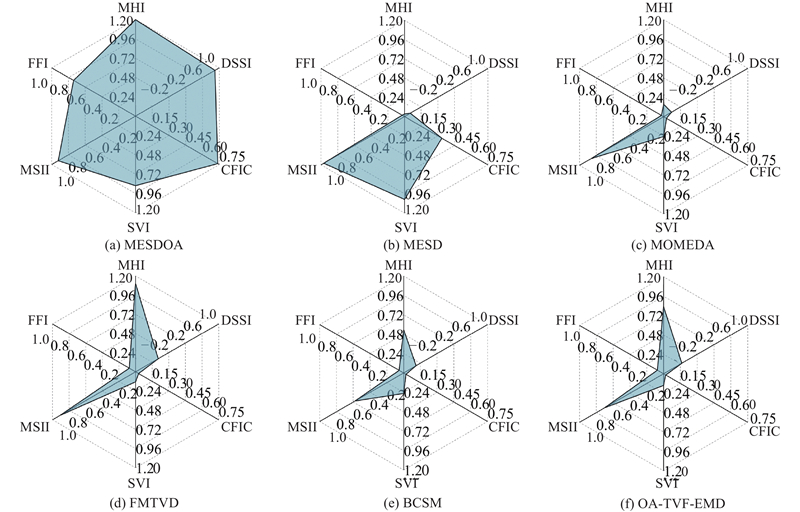
图 15   PHM 2009“斜齿5”数据各方法提取的齿轮故障特征量化雷达图

Fig.15   Radar chart of gear fault characteristics extracted by various methods of PHM 2009 helical 5 data


图 16

新窗口打开| 下载原图ZIP| 生成PPT

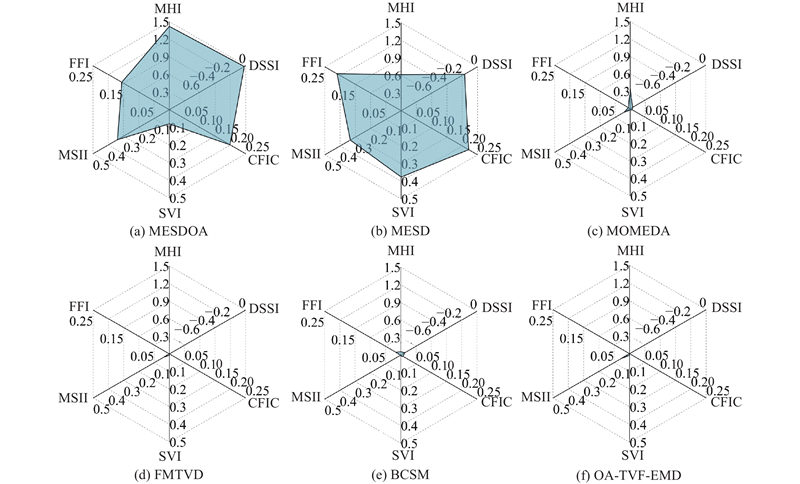
图 16   齿轮箱故障模拟数据集各方法提取的滚动轴承内环故障特征量化雷达图

Fig.16   Radar chart of rolling bearing inner race fault characteristics extracted by various methods of gearbox simulation data set


图 17

新窗口打开| 下载原图ZIP| 生成PPT

图 17   齿轮箱故障模拟数据集各方法提取的齿轮故障特征量化雷达图

Fig.17   Radar chart of gear fault characteristics extracted by various methods of gearbox simulation data set


各评价指标的最大值均出现在MESDOA或MESD方法中，这表明相较于传统的解卷积和信号分解方法，基于稀疏表示的解决方案具有更优的性能表现. FFI、MSII、SVI和CFIC这4项指标的最优结果在2种稀疏方法间呈现交替分布. 在专门针对稀疏表示特性设计的DSSI和MHI 2项评估指标中，MESDOA方法展现出显著优势，验证了基于优化算法的MESDOA方法在保持信号稀疏表征方面的理论优势.

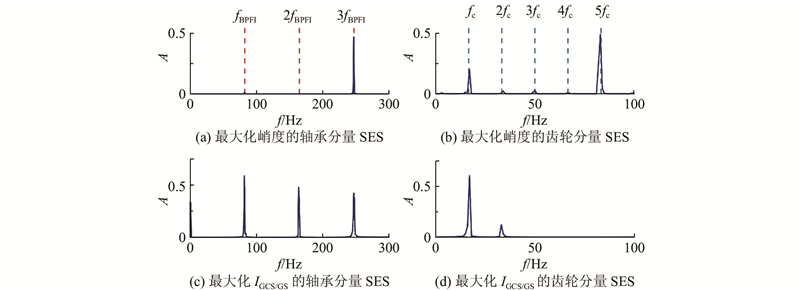
为了展现目标函数广义似然比$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $相较于峭度的优越性，以PHM 2009数据集“斜齿5”数据为例，分别以峭度和$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $为算法的目标函数，通过最大化指标寻找最优原子，得到的稀疏表示结果如图18所示. 如图18（a）、（b）所示为最大化峭度的稀疏表示结果，如图18（c）、（d）所示为最大化广义似然比$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $的稀疏表示结果. 可以看出，无论是轴承分量还是齿轮分类， $ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $的稀疏表示结果均优于最大化峭度的稀疏表示结果.

图 18

新窗口打开| 下载原图ZIP| 生成PPT

图 18   PHM 2009“斜齿5”数据通过峭度与广义似然比得到的稀疏表示结果

Fig.18   Sparse representation result of PHM 2009 helical 5 data with kurtosis and generalized likelihood ratio index


5. 结　语

本文通过非对称高斯啁啾模型（AGCM）构造出的小波对原始信号进行脉冲特征增强，计算不同参数组合的AGCM进行增强后的信号的广义似然比指标$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $. 通过最大化$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $寻找到最优的AGCM参数，构建稀疏表示的对应分量字典，实现齿轮箱滚动轴承的瞬态分量与齿轮瞬态分量从原始信号中的分离，对齿轮箱进行故障诊断. 在PHM 2009数据集与自行进行的齿轮箱故障模拟数据集上，验证了提出方法的有效性. 与其他信号处理方法进行比较，说明了本文所提方法的优越性.

通过将AGCM与脉冲特征增强方法相结合，利用AGCM与原始信号的“共振”，对原始信号进行脉冲增强，计算脉冲增强后的$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $. 通过选取不同AGCM的参数，最大化脉冲增强后的$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $，使得AGCM与故障脉冲的形状最接近，生成最优的稀疏表示字典. 相较于使用最大化相关系数的方法，由于AGCM能够对原始信号进行脉冲增强，一定程度上提高了信噪比，且$ {I}_{\mathrm{G}\mathrm{C}\mathrm{S}/\mathrm{G}\mathrm{S}} $指标在给定循环周期下的最大化即为故障特征的明显化，能够在存在较多干扰的实际环境中取得较好的效果.

参考文献

HOU Y, WU P, WU D

An operating condition information-guided iterative variational mode decomposition method based on Mahalanobis distance criterion for surge characteristic frequency extraction of the centrifugal compressor

[J]. Mechanical Systems and Signal Processing, 2023, 186 (3): 109836

[本文引用: 1]

HOU Y, ZHOU C, TIAN C, et al

Acoustic feature enhancement in rolling bearing fault diagnosis using sparsity-oriented multipoint optimal minimum entropy deconvolution adjusted method

[J]. Applied Acoustics, 2022, 201 (12): 109105

[本文引用: 1]

侯耀春, 周昶清, 武鹏, 等. 基于最大李雅普诺夫指数异常感知和CatBoost识别的机械密封失效模式层次化诊断框架[J]. 工程热物理学报, 2024, 45(1): 93-100.

[本文引用: 1]

HOU Yaochun, ZHOU Changqing, WU Peng, et al. Hierarchical diagnostic framework of mechanical seal failure modes based on maximum Lyapunov exponent anomaly sensing and CatBoost model recognition [J]. Journal of Engineering Thermophysics . 2024, 45(1): 93-100.

[本文引用: 1]

丁康, 李巍华, 朱小勇. 齿轮及齿轮箱故障诊断实用技术[M]. 北京: 机械工业出版社, 2005.

[本文引用: 1]

ERRICHELLO R, MULLER J. Gearbox reliability collaborative gearbox 1 failure analysis report: December 2010-January 2011 [R]. United States: National Renewable Energy Lab, 2012.

[本文引用: 1]

WANG W Q, ISMAIL F, GOLNARAGHI M F

Assessment of gear damage monitoring techniques using vibration measurements

[J]. Mechanical Systems and Signal Processing, 2001, 15 (5): 905- 922

DOI:10.1006/mssp.2001.1392      [本文引用: 1]

HUANG W, LI S, FU X, et al. Transient extraction based on minimax concave regularized sparse representation for gear fault diagnosis [J]. Measurement . 2020, 151(2): 107273.

[本文引用: 1]

WANG S, HUANG W, ZHU Z K

Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis

[J]. Mechanical Systems and Signal Processing, 2011, 25 (4): 1299- 1320

DOI:10.1016/j.ymssp.2010.10.013      [本文引用: 3]

LI N, HUANG W, GUO W, et al

Multiple enhanced sparse decomposition for gearbox compound fault diagnosis

[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 69 (3): 770- 781

[本文引用: 2]

WANG S, SELESNICK I, CAI G, et al

Nonconvex sparse regularization and convex optimization for bearing fault diagnosis

[J]. IEEE Transactions on Industrial Electronics, 2018, 65 (9): 7332- 7342

DOI:10.1109/TIE.2018.2793271      [本文引用: 1]

ZHOU Q, ZHANG Y, YI C, et al

Convolutional sparse coding using pathfinder algorithm-optimized orthogonal matching pursuit with asymmetric Gaussian chirplet model in bearing fault detection

[J]. IEEE Sensors Journal, 2021, 21 (16): 18132- 18145

DOI:10.1109/JSEN.2021.3086015      [本文引用: 2]

SELESNICK I

Sparse regularization via convex analysis

[J]. IEEE Transactions on Signal Processing, 2017, 65 (17): 4481- 4494

DOI:10.1109/TSP.2017.2711501      [本文引用: 3]

RAGUET H, LANDRIEU L

Preconditioning of a generalized forward-backward splitting and application to optimization on graphs

[J]. SIAM Journal on Imaging Sciences, 2015, 8 (4): 2706- 2739

DOI:10.1137/15M1018253      [本文引用: 1]

ANTONI J, BORGHESANI P

A statistical methodology for the design of condition indicators

[J]. Mechanical Systems and Signal Processing, 2019, 114 (1): 290- 327

[本文引用: 1]

EDWARDS A W F. Likelihood [M]// Time series and statistics . New York: Springer, 1972: 126-129.

[本文引用: 1]

RICE J A. Mathematical statistics and data analysis [M]. Stamford: Cengage Learning, 2006.

[本文引用: 1]

LIN H, WU F, HE G

Rolling bearing fault diagnosis using impulse feature enhancement and nonconvex regularization

[J]. Mechanical Systems and Signal Processing, 2020, 142 (8): 106790

[本文引用: 2]

PHM Society. Public Data Sets. 2009 PHM challenge competition data set [DB/OL]. (2009-08-10)[2024-05-21]. https://phmsociety.org/public-data-sets.

[本文引用: 1]

HOU B, WANG D, KONG J, et al

Understanding importance of positive and negative signs of optimized weights used in the sum of weighted normalized Fourier spectrum/envelope spectrum for machine condition monitoring

[J]. Mechanical Systems and Signal Processing, 2022, 174 (7): 109094

[本文引用: 1]

MCDONALD G L, ZHAO Q

Multipoint optimal minimum entropy deconvolution and convolution fix: application to vibration fault detection

[J]. Mechanical Systems and Signal Processing, 2017, 82 (1): 461- 477

[本文引用: 1]

LOPEZ C, WANG D, NARANJO A, et al

Box-cox-sparse-measures-based blind filtering: understanding the difference between the maximum kurtosis deconvolution and the minimum entropy deconvolution

[J]. Mechanical Systems and Signal Processing, 2022, 165 (2): 108376

[本文引用: 1]

YE X, HU Y, SHEN J, et al

An adaptive optimized TVF-EMD based on a sparsity-impact measure index for bearing incipient fault diagnosis

[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 70 (4): 1- 11

[本文引用: 1]

/

〈 〉