Mohammadi等[5]将等效磁路法(magnetic equivalent circuit, MEC)与法拉第定律和安培定则相结合,建立轴向通量涡流耦合器的分析模型,对于无对称性的复杂几何形状拥有良好的处理能力. Aberoomand等[6]通过MEC法提出双面永磁轴向涡流耦合器的稳态模型,通过遗传算法获得耦合器的最佳组件集. Arslan等[7]设计适用于航空启功机和发电机机构的同步径向磁力耦合器,采用多目标遗传算法对其进行优化,研究部分参数对磁力耦合器扭矩的影响. Alshammari等[8]通过大量的模拟研究,比较采用鼠笼式的径向场永磁涡流耦合器和采用导电片的轴向场永磁涡流耦合器在扭矩传输密度和功率传输效率方面的性能,证明鼠笼式结构更适合高效率的动力传输. 葛研军等[9]设计出新型的磁力耦合器调速机构,使用复数矢量法建立磁力耦合器调速机构的数学模型,通过Matlab和Adams软件分析位移、速度和加速度的规律. 杨超君等[10]通过基尔霍夫定律求得筒式异步磁力耦合器磁路的磁感应强度,分析得到耦合器的最终转矩,推导出调速关系式,为耦合器的实际设计与调速提供了参考方法. 杨超君等[11]针对盘式异步磁力耦合器的转速调控问题,采取等效磁路法建立磁路计算模型,通过仿真软件分析不同负载下磁力耦合器的调速特性,并进行了实验验证. 周凯凯等[12]利用法拉第电磁感应原理与安培力计算公式,得到异步磁力耦合器的电磁转矩和削弱齿槽转矩的方法. 葛研军等[13]设计锥型转子磁力耦合器,利用等效磁路法分别得到各模型的气隙磁密和电磁转矩表达式,分析锥形转子磁力耦合器的运行特性.
综上所述,虽然调速型磁力耦合器相较于传统的调速装置具有较多的优势,但传统的调速机构具有体积较大、调节精度较低的缺点. 以55 kW的磁力耦合器为例,当采用传统连杆机构作为调隙装置时,调节精度较低,定位精度为1 mm,同时需要安装额外的执行电机,安装尺寸比磁力耦合器本体增大了20%. 采用螺旋差动机构作为调隙装置,需要在轴端增加一个执行机构,使磁力耦合器的轴向长度增加70 mm,定位精度为50 μm,不适用于狭小恶劣的工作环境[14-15]. 提出新型的电磁混合式磁力耦合器,引入独特的电磁调隙装置,具有低速、大推力的优点. 电磁调隙装置基于变气隙下的电磁感应原理,通过电流控制气隙大小,从而实现精准调隙. 将机构设置于轴内部,无需额外的执行电机和附加机构,在安装尺寸不变的同时提升变转矩负载情况的精确调速性能,定位精度为10 μm[16]. 针对磁场解析模型的建立过程进行研究,推导得到推力的计算公式,通过有限元分析进行验证.
1. 新型电磁混合式磁力耦合器的结构与原理
1.1. 结构及原理
新型电磁混合式磁力耦合器主要由输入轴、轭铁、铜导体盘、连接杆、永磁体、外罩、开槽铝盘、挡块、轴承、透盖及键组成,如图1所示. 当电机旋转时,通过输入轴将动力传入,铜导体盘开始转动. 铜导体盘与开槽铝盘之间进行相对运动,铜导体盘的转速与开槽铝盘的转速存在转速差,在铜导体盘上的磁通量伴随时间的变化一直在变化,因此在铜导体盘上产生涡流,永磁体产生的磁场与涡流产生的磁场相互作用,使得开槽铝盘伴随着铜导体盘同向旋转,将动力通过输出轴传递到负载,驱动负载做功.
图 1
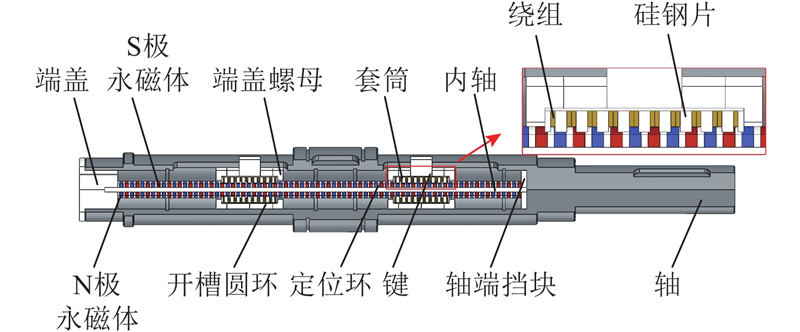
图 1 新型电磁混合式磁力耦合器的结构
Fig.1 Structure of new electromagnetic hybrid magnetic coupler
新型电磁混合式磁力耦合器调隙装置主要由内轴、套筒、硅钢片、永磁体、绕组和键等组成. 内轴通过轴端端盖固定在输入轴的内部,永磁体采用轴向分段式分布,间隔固定在内轴上并通过定位环隔开. 定位环既可以固定永磁体,又可以调整极距. 键通过2个开槽圆盘固定在套筒上,开槽圆盘通过2个端盖螺母固定在套筒上. 绕组通过硅钢片间隔分布并固定在套筒内,端盖螺母、开槽圆环、键、硅钢片、绕组和套筒构成轴向移动机构,2个轴向移动机构对称分布,如图2所示. 当轴向移动机构中的绕组工作时产生沿着直线运动的气隙磁场——行波磁场,其速度由电流的频率与极距决定. 行波磁场产生与永磁体相反的磁极,利用同极相斥、异极相吸的原理带动轴向移动机构发生相对移动,从而改变磁力耦合器的气隙.
图 2
1.2. 数学模型
图 3
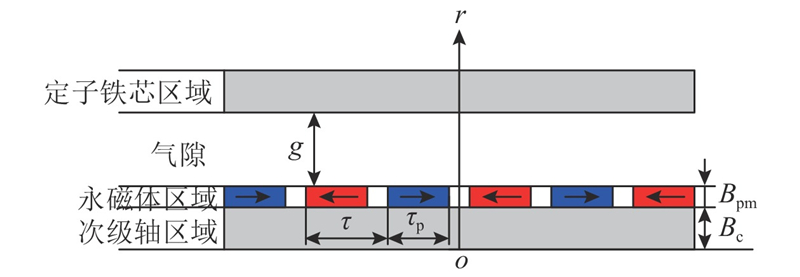
图 3 电磁调隙装置的二维磁场解析模型
Fig.3 Two-dimensional analytical model of magnetic field of electromagnetically regulated air gap device
根据上述假设,采用等效电流法,得到区域磁矢位方程.
气隙区域为
永磁体区域为
式中:A1和A2为磁矢位,μ0为真空磁导率,Jm为永磁体的等效磁化电流密度. 气隙磁感应强度分布Bg为
式中:Br和Bz分别为径向和轴向的磁感应强度,
图 4
图 5
根据安培力计算公式F = BLI,可知
式中:J为平均电流密度,J = Jc/k,其中Jc为线圈导线中的电流密度,k为占空系数.
式中:
图 6
2. 多目标优化设计
2.1. 优化设计思路
新型电磁混合式磁力耦合器的电磁调隙装置具有独特的驱动结构,设计参数有次级铁芯宽Bc、次级铁芯长Lc、永磁体宽Bpm、永磁体长Lpm、气隙g、槽宽bs、槽深hs、锷高hm、槽满率Ks、切槽深度Bs 10个参数,数量较多. 新型电磁混合式磁力耦合器是需要精密调控的装置,电磁调隙装置需要满足新型电磁混合式磁力耦合器的高精度要求. 采用多目标优化技术优化,综合考虑优化时效和优化精度的需求,根据不同结构参数对优化目标的影响程度,采取具有针对性的分级优化设计方法.
综合考虑新型电磁混合式磁力耦合器电磁调隙装置低速大推力的特性,确定优化目标,选取合适的优化参数,根据相关理论和经验确定主要尺寸参数的初始值和变化范围. 建立新型电磁混合式磁力耦合器电磁调隙装置的参数化模型,对电磁性能进行初步的评估. 由于待优化的参数众多,部分参数相互影响. 若采用单一的优化方式,则效率低下,很难得到最优尺寸[20]. 利用有限元分析得到优化目标值,合理评估优化目标对于不同优化参数的敏感度. 根据敏感度的不同,将优化参数分为强敏感度优化参数(Ⅰ)、中等敏感度参数(Ⅱ)、弱敏感度参数(Ⅲ)3组. 对于不同敏感度的优化参数,采取不同的优化方法得到最优解,通过有限元计算判断是否达到优化目标,确定最优尺寸.
2.2. 优化设计目标
新型电磁混合式磁力耦合器的电磁调隙装置基于磁场调制原理,对绕组通入三相电流产生行波磁场,与永磁体磁场相互作用产生推力,可以实现低速大推力的输出特性,适用于磁力耦合器低速调隙的场合,因此电磁调隙装置的平均推力Favg是重点衡量指标. 电磁调隙装置具有边端效应和齿槽效应,则会引起较大的推力波动,严重影响稳定运作,因此推力波动Fripple是设计过程中需要考虑的设计目标. 新型电磁混合式磁力耦合器电磁调隙装置的目标函数可以表示为
优化目标为尽可能地增大Favg,减小Fripple.
2.3. 优化参数的敏感性分析
图 7
图 7 电磁调隙装置结构参数的示意图
Fig.7 Schematic representation of structural parameter of electromagnetic gap shifter
表 1 待优化结构参数的初始值及变化范围
Tab.1
| 结构参数 | 初始值 | 优化范围 |
| Bc/mm | 3 | 2~4 |
| Bpm/mm | 4.75 | 3.5~5.5 |
| Lpm/mm | 3.2 | 2.5~3.5 |
| g/mm | 1 | 0.5~1.5 |
| hs/mm | 8 | 8~13 |
| bs/mm | 2.5 | 2.0~3.0 |
| hm/mm | 1.5 | 1.0~2.0 |
| Ks | 0.75 | 0.70~0.80 |
| Bs/mm | 2 | 2~6 |
在新型电磁混合式磁力耦合器的电磁调隙装置中,需要优化设计的参数众多,且每个参数对优化目标的影响不同. 若对每个待优化参数都使用单扫描法进行寻优,则计算成本太高,无法综合考虑各个参数对于优化目标的交叉影响. 采用Taguchi法对9个待优化参数进行敏感性分析,通过敏感度S(xi)分析将9个待优化参数进行分级[21]. 敏感度S(xi)定义为
式中:V(y/xi)为当待优化参数xi取某定值时优化目标y的方差,
建立关于9个待优化参数的L27(39)正交表,利用有限元软件对27组参数进行仿真计算,得到目标值,计算方差,开展敏感度分析. 方差结果如表2所示.
表 2 平均推力方差与推力波动方差
Tab.2
| 结构参数 | 平均推力方差 | 推力波动方差 |
| Bc/mm2 | 99.601 | |
| Bpm/mm2 | ||
| Lpm/mm2 | ||
| g/mm2 | ||
| hs/mm2 | ||
| bs/mm2 | ||
| hm/mm2 | ||
| Ks | ||
| Bs/mm2 |
图 8
2.4. 参数分级多目标优化
通过上述参数敏感度分析结果,对每一级参数采用与其相适应的优化方法,降低每级优化计算量,获得更高的优化精度. 结构参数分级优化的流程如图9所示.
图 9
2.4.1. 强敏感度参数分析
提出蜣螂优化算法,优化BP神经网络的近似代理模型和多目标金豺优化算法,优化过程如下.
1)试验设计. 对3个强敏感度设计参数采用拉丁超立方实验设计,获得均匀分布的样本空间. 利用有限元软件,分析对应的目标函数值.
2)代理模型. 为了获得高精度预测模型,提出新型的DBO-BP神经网络模型,构建函数关系.
3)金豺优化算法的优化. 以平均推力和推力波动为优化目标,在原有的金豺优化算法(golden jackal optimization, GJO)基础上,提出适用于多目标优化求解的多目标金豺优化算法(multi-objective golden jackal optimization, MOGJO).
利用Ansys软件中的实验设计模块,选取拉丁超立方试验设计,设置样本空间维度为3,样本数为1 000. 通过Ansys软件对1 000组样本点进行求解,得到每个样本点的值.
为了对比DBO-BP神经网络模型的性能,将该模型与PSO-BP神经网络[24]、BP神经网络进行比较,随机选取样本空间中30%的点作为测试集. 通过以上3种模型对测试集样本点的推力和推力波动进行预测,采用R和均方根误差(RMSE)作为评价指标. RMSE的公式如下:
式中:
3种拟合模型根据R和式(12)计算得到各指标,如表3所示. 可以看出,对于Favg的预测,3种模型的R差别不大,都大于0.99,但DBO-BP模型的RMSE较PSO-BP模型减少了8%,较BP模型减少了14%. 对于Fripple的预测,DBO-BP模型的R略高于PSO-BP模型和BP模型,DBO-BP模型的RMSE较PSO-BP模型减少了14%,较BP模型减少了19%. DBO-BP神经网络模型优于PSO-BP神经网络模型和BP神经网络模型,说明使用DBO-BP神经网络模型预测新型电磁混合式磁力耦合器电磁调隙装置的平均推力和推力波动具有可行性.
表 3 不同代理模型的拟合效果检验
Tab.3
| 代理模型 | 平均推力 | 推力波动 | |||
| RMSE | R | RMSE | R | ||
| BP | 1.285 4 | 0.994 13 | 2.291 2 | 0.924 24 | |
| PSO-BP | 1.207 6 | 0.994 82 | 2.143 3 | 0.923 | |
| DBO-BP | 1.111 3 | 0.994 71 | 1.846 7 | 0.931 | |
GJO算法具有收敛速度快、收敛精度高的特点[25]. 目前,GJO算法仅应用于单目标优化,提出基于非支配序列解的MOGJO算法,将金豺优化算法运用于多目标优化问题中.
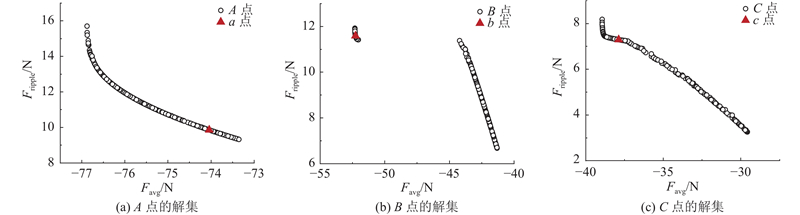
采用MOGJO算法进行迭代求解,得到pareto解集,运行结果如图10所示.
图 10
从pareto解集中选择有一定距离的典型点A、B、C作为下一级优化的初始点,选取点如表4所示.
表 4 第2级优化的初始点
Tab.4
| 点 | Bc/mm | Bpm/mm | g/mm | Favg/N | Fripple/N |
| A | 4 | 5.5 | 0.711 4 | 71.221 8 | 24.782 1 |
| B | 3.165 2 | 3.5 | 0.610 9 | 48.447 7 | 9.634 0 |
| C | 2.576 2 | 3.5 | 0.938 1 | 36.122 7 | 6.296 7 |
2.4.2. 中敏感度参数分析
中敏感度参数具有以下特点. 1)中敏感度参数共有4个结构参数,共同影响Favg和Fripple 2个优化目标. 其中Lpm和bs对Favg的影响较大, hm和Bs对Favg的影响较小,4个参数对Fripple都有影响,其中Lpm和Bs的影响最大. 2)相比于强敏感度参数,中级敏感度对优化目标的影响较弱,对代理模型的拟合精度要求低于强敏感度参数. 3)结构参数的相互作用影响2个优化目标,2个优化目标之间相互影响,因此将拟合好的代理模型导入到MOGJO算法中进行寻优,得到最优解集.
根据中敏感度参数的上述特点,选用响应面法(response surface method,RSM)构造代理模型,所需的样本点数量较少,拟合精度较高[26].
试验设计方法采用Box-Behnken试验设计,设计变量为三水平四因素,节省大量的时间成本. 通过Box-Behnken设计试验,得到以A、B、C点的取值作为初始参数值的29组试验结果,部分结果见表5.
表 5 中敏感度参数 Box-Behnken实验设计及结果
Tab.5
| 序号 | 组合 | 点A | 点B | 点C | |||||||||
| Lpm/mm | hm/mm | bs/mm | Bs/mm | Favg/N | Fripple/N | Favg/N | Fripple/N | Favg/N | Fripple/N | ||||
| 1 | 3 | 1.5 | 2.5 | 4 | |||||||||
| 2 | 3 | 2 | 3.0 | 4 | |||||||||
| 28 | 3 | 1 | 2.5 | 2 | |||||||||
| 29 | 3 | 2 | 2.5 | 6 | |||||||||
各设计参数对推力波动的影响较复杂,响应面法常用的二次多项式拟合精度较差,因此采用三次多项式和四次多项式进行拟合,提高拟合精度. 平均推力采用二次多项式拟合.
在完成计算后,A、B、C 3点的部分响应面如图11所示. 如图11(a)~(d)所示为A点的响应面图,如图11(e)~(h)所示为B点的响应面图,如图11(i)~(l)所示为C点的响应面图. 各因素对Favg和Fripple的影响程度与图8一致,证明了敏感度分析的正确性. 如图11(a)、(b)、(e)、(f)、(i)、(j)所示,Favg随着Lpm增大先增大后减小,随着bs增大而减小,随hm的变化较小,随着Bs增大而略微减小. 如图11(c)、(d)、(g)、(h)、(k)、(l)所示,Fripple的变化较复杂. 当以A点的取值为初始值时,Fripple随着Lpm的增大而减小,当Lpm较小时随着bs的增大而减小,但当Lpm较大时,bs增加使Fripple增大,而当Bs增加时,Fripple减小. 当以B点的取值为初始值时,Fripple随着Lpm增大先减小后增大,随着hm增大而减小,随着bs增大而减小. 当以C点为初始值时,Fripple随着Lpm增加而增大,随着hm增大先略微减小后增大,当Lpm较小时随着bs增加而减小,当Lpm较大时随着bs增加而增大.
图 11
图 12
表 6 第3级优化的初始点
Tab.6
| 点 | Lpm/mm | hm/mm | bs/mm | Bs/mm | Favg/N | Fripple/N |
| a | 2 | 2 | 2 | − | ||
| b | 2 | 2 | 2 | − | ||
| c | 2 | 2 | − |
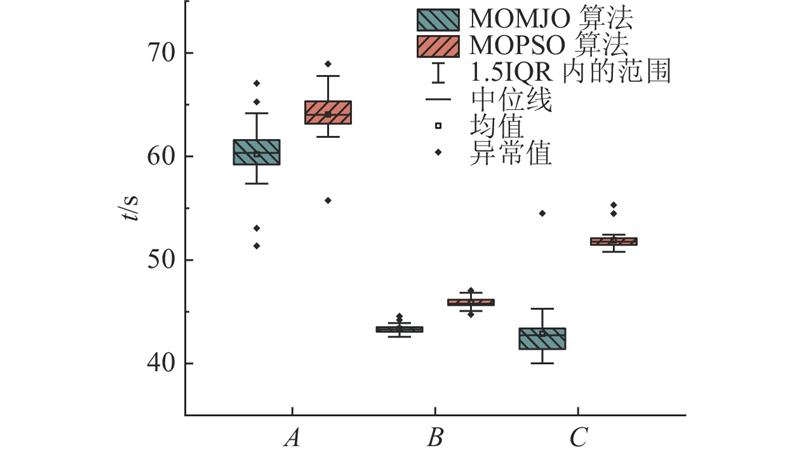
MOGJO算法除了精度高、寻优能力强外,具有较快的求解速度. 将MOGJO算法与MOPSO算法进行比较,对A、B和C 3点分别采用MOGJO算法和MOPSO算法求解50次,运行时间如图13所示. 图中,t为求解时间. 对于A点的计算模型,利用MOGJO算法求解时间的中位值为60.33 s,均值为60.21 s;利用MOPSO算法求解时间的中位值为64.03 s,均值为64.06 s;与MOPSO算法相比,MOGJO算法的求解时间中位值减少了5.8%,均值减少了6%. 对于B点的计算模型,利用MOGJO算法求解时间的中位值为43.30 s,均值为43.33 s;利用MOPSO算法求解时间的中位值为45.79 s,均值为45.91 s;与MOPSO算法相比,MOGJO算法的求解时间中位值减少了5.4%,均值减少了5.6%. 对于C点的计算模型,利用MOGJO算法求解时间的中位值为42.73 s,均值为42.88 s;利用MOPSO算法求解时间的中位值为51.76 s,均值为51.91 s;与MOPSO算法相比,利用MOGJO算法求解时间的中位值减少了17.4%,均值减少了17.4%. 在相同的计算模型下,MOGJO算法的运行时间明显少于MOPSO算法.
图 13
2.4.3. 弱敏感度参数分析
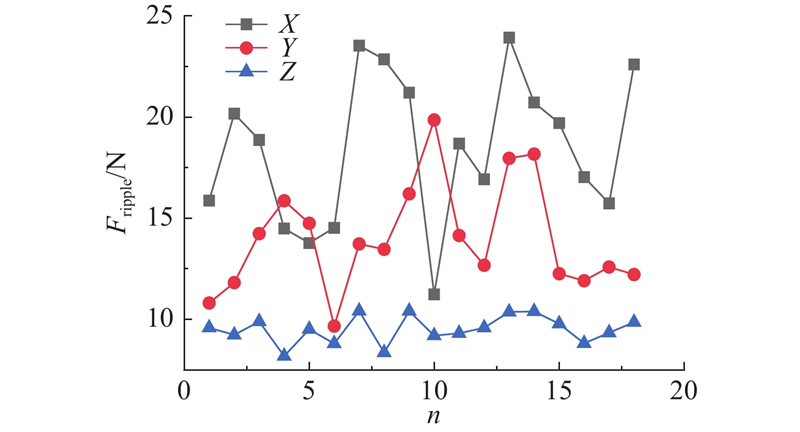
从图8可知,弱敏感参数槽深和槽满率对平均推力的影响极其微小,因此仅考虑弱敏感参数对推力波动的影响. 采用扫描法进行寻优,二者的设计初值分别为8 mm和0.75. 选取合适的参数值变化步长,取值如表7所示. 借助有限元分析,得到推力波动随槽深、槽满率的变化情况,有限元仿真结果如图14所示. 图中,n为参数序号,X是以a点为初始值点的仿真结果,Y是以b点为初始值点的仿真结果,Z是以c点为初始值点的仿真结果. 当Ks = 0.7,Bs=11 mm时,推力波动达到最小值,Fripple = 11.23 N,此时的Favg = 74.92 N. 当Ks =0.8,Bs =9 mm时,推力波动达到最小值,Fripple = 9.67 N,此时的Favg = 52.77 N. 当Ks = 0.7,Bs = 9 mm时,推力波动达到最小值,Fripple = 8.18 N,此时Favg = 37.87 N. 综合考虑设计要求,选取X的最小值点为电磁调隙装置最终设计点.
表 7 弱敏感度设计参数扫描表
Tab.7
| 序号 | 结构参数 | 序号 | 结构参数 | |||
| Ks | hs/mm | Ks | hs/mm | |||
| 1 | 0.70 | 8 | 10 | 0.70 | 11 | |
| 2 | 0.75 | 8 | 11 | 0.75 | 11 | |
| 3 | 0.80 | 8 | 12 | 0.80 | 11 | |
| 4 | 0.70 | 9 | 13 | 0.70 | 12 | |
| 5 | 0.75 | 9 | 14 | 0.75 | 12 | |
| 6 | 0.80 | 9 | 15 | 0.80 | 12 | |
| 7 | 0.70 | 10 | 16 | 0.70 | 13 | |
| 8 | 0.75 | 10 | 17 | 0.75 | 13 | |
| 9 | 0.80 | 10 | 18 | 0.80 | 13 | |
图 14
考虑实际加工,将优化后的结构参数进行取整,结果如表8所示.
表 8 参数优化前、后的对比表
Tab.8
| 结构参数 | 数值 | |
| 优化前 | 优化后 | |
| Bc/mm | 3 | 4 |
| Bpm/mm | 4.75 | 5.5 |
| Lpm/mm | 3.2 | 3.45 |
| g/mm | 1 | 0.71 |
| hs/mm | 8 | 11 |
| bs/mm | 2.5 | 2 |
| hm/mm | 1.5 | 2 |
| Ks | 0.75 | 0.7 |
| Bs/mm | 2 | 2 |
| Favg/N | ||
| Fripple/N | ||
经过结构参数的优化设计后,虽然推力波动增加了1.35 N,但平均推力提升了约57.8%,而推力波动比值降低了28.3%,电磁推力性能大幅提升.
3. 电磁性能分析
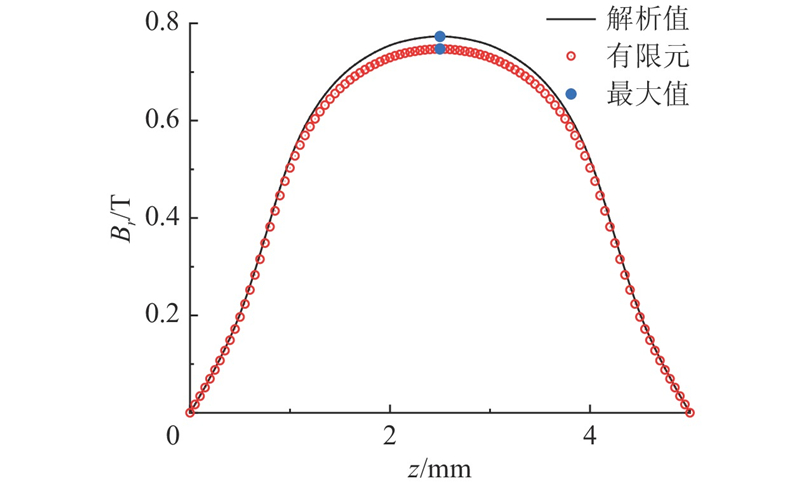
图 15
图 15 优化后径向气隙磁感应强度
Fig.15 Magnetic induction of radial air gap after optimization
图 16
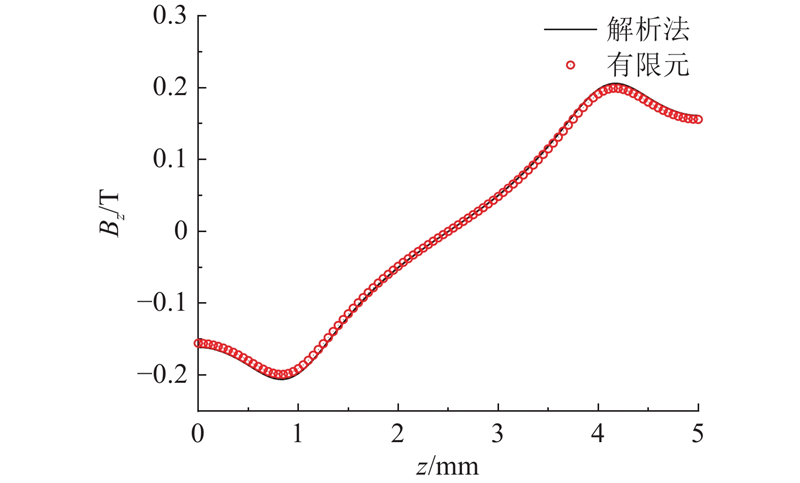
图 16 优化后轴向气隙磁感应强度
Fig.16 Magnetic induction of axial air gap after optimization
图 17
通过有限元分析,在额定移动速度下得到电磁调隙装置的3项空载感应电动势波形,如图18所示. 图中,U为感应电动势. 优化之后的三相空载感应电动势波形均匀对称,三相感应电动势幅值由优化前的322 mV提升到了优化后的537 mV,提高了66.8%.
图 18
图 18 优化前、后的感应电动势波形图
Fig.18 Waveform of induced electromotive force before and after optimization
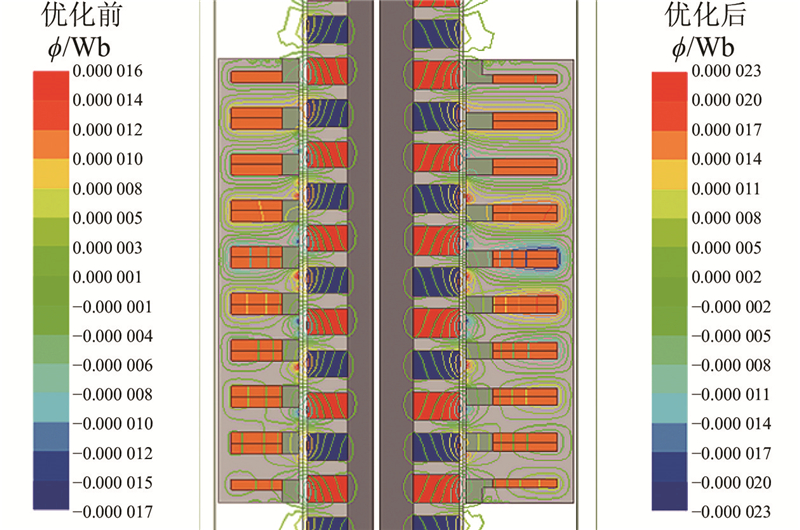
图19中,ϕ为磁通量. 从图19可以看出,电磁调隙装置的磁力线大部分由永磁体出发,穿过气隙、初级铁心,最后返回永磁体形成闭合回路,磁力线分布均匀对称,同时动子和定子通过磁力线很好地铰链在一起,证明了电磁调隙装置的电磁能量转换的合理性. 因电磁调隙装置的结构特殊,在端部存在少量漏磁的现象,优化后磁通高于优化前磁通,因此优化后的电磁调隙装置具有更大的推力和输出功率. 从图20可以看出,优化后的电磁调隙装置磁感应强度低于优化前的电磁调隙装置,在电磁调隙装置的设计中,过大的磁感应强度会导致过热和磁场饱和,而优化后的电磁调隙装置磁感应强度最大为2.59 T,集中于其齿顶部,在保证电磁调隙装置效率的同时,更好地避免了过热和磁场饱和的问题.
图 19
图 20
4. 结 论
(1)针对传统磁力耦合器体积大、精度低的缺点,基于电磁相关理论提出新型的电磁混合式磁力耦合器. 设计电磁调隙装置进行精准调隙,体积更小,精度更高,可以精确地调控磁力耦合器所传递的扭矩. 在结构设计的基础上,提出基于敏感度分析的多级多目标优化方法. 针对设计目标对于不同结构参数的敏感度,将结构参数进行分级优化,从而快速、精确地获得电磁调隙装置的最优结构参数.
(2)提出蜣螂优化算法,优化BP神经网络模型(DBO-BP). 采用DBO算法,对BP神经网络的初始权值阈值进行寻优,获得最优的网络模型. 与BP神经网络和PSO-BP神经网络模型相比,该模型具有更高的预测精度和更小的均方根误差,对于极复杂的推力波动具有更好的预测表现.
(3)提出基于非支配序列的多目标金豺优化算法,结合收敛速度快、收敛精度高的金豺优化算法与非支配序列解,实现金豺优化算法从求解单目标优化问题到多目标问题的扩展,从而实现对最优设计参数的寻优,得到平均推力和推力波动的Pareto前沿. 与DBO-BP神经网络模型和响应面法相结合,获得最优的设计参数. 采用扫描法对最后的弱敏感度参数进行寻优,得到最终的电磁调隙装置最优结构参数.
参考文献
盘式实心异步磁力耦合器的机械特性与调速特性
[J].
Mechanical properties and adjustable-speed characteristics of axial-flux-solid-type asynchronous magnetic couplers
[J].
轴向磁通调速磁力耦合器漏磁系数分析计算与试验研究
[J].
Calculation method of magnetic flux leakage coefficient and experimental study of permanent magnet coupler with axial magnetic flux
[J].
A simple method for performance prediction of permanent magnet eddy current couplings using a new magnetic equivalent circuit model
[J].
Designing high-accuracy permanent magnets for low-power magnetic resonance imaging
[J].
Analytical modeling and analysis of axial-flux interior permanent-magnet couplers
[J].DOI:10.1109/TIE.2014.2311391 [本文引用: 1]
Design optimization of double-sided permanent-magnet axial eddy-current couplers for use in dynamic applications
[J].DOI:10.1109/TEC.2018.2880679 [本文引用: 1]
Fem-based optimal design and testing of synchronous magnetic coupling for aerospace starter/generator applications
[J].
Comparison of eddy current coupling topologies for high efficiency mechanical power transmission
[J].DOI:10.1109/TEC.2022.3217347 [本文引用: 1]
磁力耦合器调速机构研究
[J].DOI:10.3969/j.issn.1673-9590.2014.03.008 [本文引用: 1]
Research on the speed regulation mechanism of magnetic coupling
[J].DOI:10.3969/j.issn.1673-9590.2014.03.008 [本文引用: 1]
筒式异步磁力耦合器的转矩与调速关系研究
[J].
Torque and adjustable-speed relation for drum-type asynchronous magnetic couplers
[J].
开槽型盘式异步磁力耦合器调速特性
[J].
Speed-control characteristics of slotted-type axial-flux asynchronous magnetic couplers
[J].
永磁式异步磁力耦合器设计及分析
[J].
Design and analysis of a permanent magnetic asynchronous coupler
[J].
锥形转子磁力耦合器调速机理研究
[J].
Study on speed-regulation mechanism of cone-rotor magnetic coupler
[J].
Analysis and performance evaluation of an efficient power-fed permanent magnet adjustable speed drive
[J].DOI:10.1109/TIE.2018.2832018 [本文引用: 1]
温度影响下的开槽盘式磁力耦合器调速特性
[J].
Speed regulation performance of slotted-type axial-flux magnetic couplers under temperature influence
[J].
基于自学习非线性PID的音圈电机精密定位系统
[J].
A voice coil motor-driven precision positioning system based on self-learning nonlinear PID
[J].
磁悬浮无轴离心泵叶轮转子动力学特性
[J].
Rotor dynamics of impeller in a magnetic suspension bearingless centrifugal pump
[J].
新型斜气隙圆筒型横向磁通切换直线电机及其建模分析
[J].
Novel oblique air-gap tubular transverse flux switching permanent magnet linear motors and its modeling analysis
[J].
永磁游标直线电机磁场解析计算
[J].
Analytical magnetic field calculation of linear permanent magnet vernier motor
[J].
可调旋转式流体阻尼器参数多目标优化设计
[J].
Multi-objective optimization design of adjustable rotary fluid damper parameter
[J].
电励磁双定子场调制电机的多目标优化设计分析
[J].
Multi-objective optimization analysis of electric-excitation double-stator field-modulated machine
[J].
基于BP神经网络的立式离心泵导叶与蜗壳优化设计
[J].DOI:10.6041/j.issn.1000-1298.2022.04.013 [本文引用: 1]
Optimization design of vane diffuser and volute in vertical centrifugal pump based on back propagation neural network
[J].DOI:10.6041/j.issn.1000-1298.2022.04.013 [本文引用: 1]
Dung beetle optimizer: a new meta-heuristic algorithm for global optimization
[J].
Optimal parameters selection for BP neural network based on particle swarm optimization: a case study of wind speed forecasting
[J].
Golden jackal optimization: a novel nature-inspired optimizer for engineering applications
[J].
Design and optimization of a flux-modulated fault-tolerant permanent magnet rim-driven machine with combined stator to improve torque density
[J].DOI:10.1109/TEC.2022.3210266 [本文引用: 1]