随着全球移动通信技术的快速发展，第5代移动通信技术^[1]（the fifth generation mobile communication technology, 5G）凭借高速传输、低延迟和大容量的特性，在车联网^[2]（vehicle to everything, V2X）和工业物联网^[3-4]（industrial internet of things, IIoT）中展现出变革性能力，推动了智能交通系统的发展^[5]. 随着智能交通需求增加和场景复杂化，5G在网络延迟、数据处理效率及高密度通信环境下的服务质量保障面临挑战. 这些挑战催生了对5G演进（5G-Advanced）和第6代移动通信技术^[6]（the sixth generation of mobile communication technology, 6G）的需求. 这类技术将提供更高的传输速率、更低的延迟和更广的连接能力. 5G-Advanced通过引入边缘计算和深层次网络切片技术，支持更复杂的智能通信场景，对未来智慧车联网和工业物联网的发展至关重要. 在此背景下，语义通信^[7-10]（semantic communication, SC）技术日益受到关注. 相较于传统通信聚焦传输效率，语义通信更重视信息的意义传达. 在智能车联网中，系统可以根据交通环境和驾驶情境的语义需求优化数据传输，优先处理关键的安全信息，提升道路安全和交通效率.

车联网中存在大量时效性强、延迟低和可靠性高的数据，均有传输截止时间（deadline, DDL）. 超出DDL的数据传输无意义，对语义通信的时间敏感性提出了更高的要求. 5G通过确定性网络^[11]（deterministic networking, DN）技术扩展以太网，提供确定性通信解决方案. 当前面向车联网的语义通信系统未考虑编码时间与低时延需求的矛盾，编码时间是否满足确定性传输要求尚不清楚^[12-14]. 针对上述问题，本文提出截止时间敏感的语义通信方案（deadline-aware semantic communication, DDA-SC）. 利用截止时间敏感的语义编码器（deadline-aware semantic encoder, DDA-SE），根据DDL控制编码深度，确保数据在有效时间内完成编码和传输. 设计基于编码深度的信噪比感知网络（coding-depth based signal-noise ratio aware network, CDSAN），通过注意力机制增强对信道噪声的鲁棒性. 实验表明，当编码截止时间<10 μs时，该系统在CIFAR-10分类任务上的准确度提升了75%以上.

本节介绍语义通信系统中典型的联合信源信道编码系统^[15]（joint source and channel coding, JSCC），指出该系统处理时间敏感数据的不足及本文所提工作的优化目标.

典型的联合信源信道编码系统由联合信源信道编码器（joint source and channel encoder, JSC Encoder）和联合信源信道解码器（joint source and channel decoder, JSC Decoder）组成. 当完成通信任务时，联合信源信道编码器和联合信源信道解码器分别被部署在发送端和接收端，完成信源信道编码和信源信道解码任务.

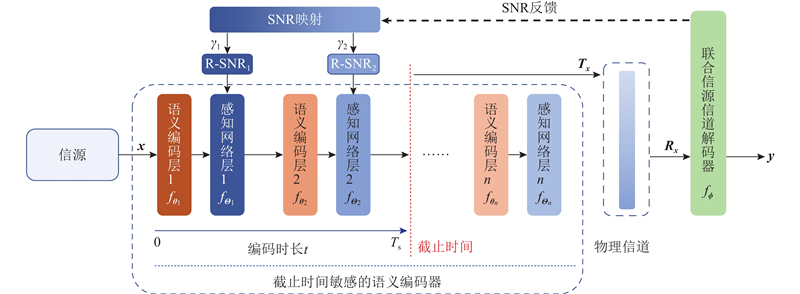
如图1所示为联合信源信道编码系统的系统结构. 在发射端，信源产生消息$ {\boldsymbol{x}} $，$ {\boldsymbol{x}} $经联合信源信道编码器${{{f}}_{\boldsymbol{\theta}} }$编码得到待传输符号${{\boldsymbol{T}}_{\boldsymbol{x}}}$，表示为$ {{\boldsymbol{T}}_{\boldsymbol{x}}} = {{{f}}_{\boldsymbol{\theta}} }({\boldsymbol{x}}) $，其中${{{f}}_{\boldsymbol{\theta}} }( \cdot )$表示参数为${\boldsymbol{\theta}} $的联合信源信道编码器. 待传输符号${{\boldsymbol{T}}_{\boldsymbol{x}}}$经信道传输后得到接收符号${{\boldsymbol{R}}_{\boldsymbol{x}}}$，表示为${{\boldsymbol{R}}_{\boldsymbol{x}}} = {\boldsymbol{H}}{{\boldsymbol{T}}_{\boldsymbol{x}}}+{\boldsymbol{N}}$. 其中${\boldsymbol{H}}$表示信道响应，${\boldsymbol{N}}$表示加性高斯白噪声（additive white Gaussian noise, AWGN），即${\boldsymbol{N}}\sim \text{N}(0,{\sigma ^2})$，其中$\text{N}(0,{\sigma ^2})$表示均值为0、方差为${\sigma ^2}$的高斯分布，此处${\sigma ^2}$为噪声功率. 传输符号${{\boldsymbol{T}}_{\boldsymbol{x}}}$经信道传输被接收端接收后，由接收端的联合信源信道解码器${{{f}}_{\boldsymbol{\theta}} }$解码得到系统输出${\boldsymbol{y}}$，表示为$ {\boldsymbol{y}} = {{{f}}_{\boldsymbol{\phi}} }({{\boldsymbol{R}}_{\boldsymbol{x}}}) $，其中${{{f}}_{\boldsymbol{\phi }}}( \cdot )$表示参数为${\boldsymbol{\phi}} $的联合信源信道解码器.

典型信源信道编码系统在节省面向任务的通信所需要的带宽资源方面非常有效. 由于典型信源信道编码系统未考虑时间敏感数据对快速编码传输的要求，且联合信源信道编码的计算复杂度较高，所需的时间较长，所以在处理时间敏感数据时易导致数据失效，无法满足5G-Advanced智能车联网中确定性网络进行确定性传输的要求. 对于联合信源信道编解码系统，以下问题亟待解决：

(1)$ \left.\begin{gathered} \mathop {\min }\limits_{{\boldsymbol{\phi}} ,{\boldsymbol{\theta}} } \;{L}\;({\boldsymbol{y}},{{\boldsymbol{y}}_{{\text{truth}}}}) ; \\ {\mathrm{s.t.}}\quad {T_{\text{e}}}+{T_{\text{t}}}+{T_{\text{d}}} \leqslant T. \\ \end{gathered} \right\}$

式中：$ {{\boldsymbol{y}}_{{\text{truth}}}} $表示任务的真实目标，${L}\;({\boldsymbol{y}},{{\boldsymbol{y}}_{{\text{truth}}}})$为衡量系统输出${\boldsymbol{y}}$和任务的真实目标$ {{\boldsymbol{y}}_{{\text{truth}}}} $间差异的误差函数，${T_{\text{e}}}$、${T_{\text{t}}}$、${T_{\text{d}}}$和$T$分别为系统编码消息$ {\boldsymbol{x}} $所需要的时间、传输符号${{\boldsymbol{T}}_{\boldsymbol{x}}}$由发送端经信道至接收端的时间、系统解码接收符号${{\boldsymbol{R}}_{\boldsymbol{x}}}$得到系统输出${\boldsymbol{y}}$的时间和自消息$ {\boldsymbol{x}} $产生至其失效的截止时间. 本文的目标是设计联合信源信道编码系统，在保证编解码时间和传输时间之和小于截止时间的情况下，系统输出尽量接近任务真实目标.

截止时间敏感的语义通信系统如图2所示，该系统主要由截止时间敏感的语义编码器和联合信源信道解码器组成. 截止时间敏感的语义编码器根据截止时间控制编码深度，以达到在车联网通信要求的截止时间内完成通信任务的目标.

考虑车联网通信中的传输时间和解码时间分别取决于物理信道和边端解码硬件，将传输时间和解码时间固定，即式(1)中${T_{\text{t}}}$和${T_{\text{d}}}$视为常数，只考虑编码时间的截止时间.

如图2所示，截止时间敏感的语义编码器由一系列同构的编码层构成，而每个编码层都包含1个语义编码层${f_{{{\boldsymbol{\theta}} _i}}}$和1个感知网络层${f_{{{\boldsymbol{\varTheta}} _i}}}$. 每个语义编码层都是一个Transformer编码块，参数为${{\boldsymbol{\theta}} _i}$，每个感知网络层都是基于自注意力机制的SNR感知网络，参数为${{\boldsymbol{\varTheta}} _i}$. 当完成通信任务时，编码器接收信源消息${\boldsymbol{x}}$作为输入，根据编码的截止时间${T_{\text{s}}}$控制从哪个编码层输出传输符号${{\boldsymbol{T}}_{\boldsymbol{x}}}$. 根据截止时间进行语义编码的算法如算法1所示. 在算法1中，首先初始化编码开始时间${t_{{\text{start}}}}$和当前时间${t_{{\text{curr}}}}$为0，然后判断在当前时间的基础上，下一编码层编码所需时间是否超出了编码截止时间${T_{\text{s}}}$，并且是否达到最大编码深度. 若上述判断条件均为真，则继续由下一层语义编码层继续编码语义特征；否则结束编码，将最后编码的语义特征作为传输符号${{\boldsymbol{T}}_{\boldsymbol{x}}}$经由信道传输. 考虑到每一层语义编码层的结构和参数量均完全相同，以提前计算的平均每层语义编码层的平均编码时间${t_{{\text{ave}}}}$作为下一层语义编码层提取语义特征的预测时间. 在截止时间敏感的语义编码器得到传输符号${{\boldsymbol{T}}_{\boldsymbol{x}}}$后，联合信源信道解码器接收到${{\boldsymbol{T}}_{\boldsymbol{x}}}$经信道传输后的接收符号${{\boldsymbol{R}}_{\boldsymbol{x}}}$，该接收符号继续由解码器解码得到最终系统输出${\boldsymbol{y}}$. 由于所设计的截止时间敏感的语义编码器能够通过算法1根据编码截止时间动态调整，整个系统可以适应数据的有效时间，完成通信任务.

提出的基于编码深度的信噪比感知网络的结构如图3所示. 以第i层感知网络层为例，该感知网络接收第i层语义编码层的输出语义特征作为输入，将语义特征经过池化和线性变换后，得到每一维语义特征对应的单个语义特征. 单个语义特征与变换后的相关信噪比（relevant signal-to-noise ratio, R-SNR）拼接经线性变换和Softmax函数映射后，得到每一维度语义特征对应的缩放因子. 这些缩放因子与信噪比感知网络的输入语义特征相乘并相加后，得到信噪比感知网络的输出语义特征. 相关信噪比R-SNR是和编码深度相关的补偿SNR，其由接收端反馈的SNR映射得到. 具体而言，第i层的R-SNR_i等于SNR乘以层补偿因子${\gamma _i}$，即

(2)$ {\text{R}}{\text{-}}{\text{SN}}{{\text{R}}_i} = {\gamma _i} s . $

浅层编码层提取的任务相关信息较深层编码层而言较少，包含的冗余信息较多. 从完成智能任务的角度而言，其包含的无用信息即噪声较多，面向完成任务的有用信息与噪声（由编码冗余信息和信道噪声2部分构成）的比值较低. 从信息论的角度考虑，较浅层语义特征${\boldsymbol{z}}_{n-1} $与任务目标的互信息小于较深层语义特征${\boldsymbol{z}}_n $与任务目标的互信息$ I({{\boldsymbol{z}}_{n - 1}};{\boldsymbol{y}}) \leqslant I({{\boldsymbol{z}}_n};{\boldsymbol{y}}) $，补偿因子${\gamma _i}$的目的为补偿这部分由编码不充分而导致的较低的有用信号功率. ${\gamma _i}$的存在使得基于编码深度的信噪比感知网络能够在实际的信道环境下，补偿编码深度较浅时与完成智能任务相关的有用信息. 从这个角度而言，${\gamma _i}$与编码深度i负相关，即编码深度越深，需要补偿的任务相关的信息量越少，${\gamma _i}$越小. 当编码深度足够大时，${\gamma _i} \approx 1$，此时$ {\text{R}}{\text{-}}{\text{SN}}{{\text{R}}_i} \approx {{s}} $.

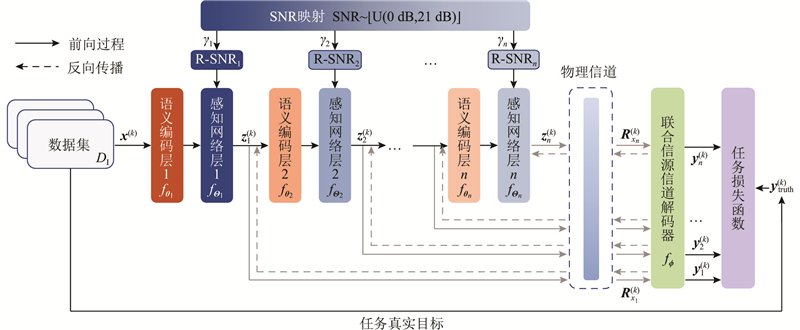
截止时间敏感的语义通信系统的训练过程如图4所示. 对于数据集${{D}_{\text{I}}}$中的第$k$个训练样本${{\boldsymbol{x}}^{(k)}}$，所有编码层$ ({f_{{{\boldsymbol{\theta}} _1}}},{f_{{{\boldsymbol{\varTheta}} _1}}}),({f_{{{\boldsymbol{\theta}} _2}}},{f_{{{\boldsymbol{\varTheta}} _2}}}), \cdots ,({f_{{{\boldsymbol{\theta}} _n}}},{f_{{{\boldsymbol{\varTheta}} _n}}}) $递进地计算编码的语义特征${\boldsymbol{z}}_1^{(k)},{\boldsymbol{z}}_2^{(k)}, \cdots ,{\boldsymbol{z}}_n^{(k)}$. 对于每一层编码层输出的语义特征，联合信源信道解码器${{{f}}_{\boldsymbol{\phi}} }$都对应地计算系统输出，系统的优化目标为尽量使所有系统输出与任务的真实目标接近，即

(3)$ \mathop {\min }\limits_{({{\boldsymbol{\theta}} _1},{{\boldsymbol{\varTheta}} _1},{\gamma _1}), \cdots ,({{\boldsymbol{\theta}} _n},{{\boldsymbol{\varTheta}} _n},{\gamma _n}),{\boldsymbol{\phi}} } \sum\limits_{i = 1}^n {{L}\;({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})} . $

式中：$ {\boldsymbol{y}}_i^{(k)} = {{{f}}_{\boldsymbol{\phi}} }(\hat {{{\boldsymbol{z}}}}_i^{(k)}) $，$ \hat {\boldsymbol{z}}_i^{(k)} = {{\mathrm{C}}}{{\mathrm{H}}}({\boldsymbol{z}}_i^{(k)},{\gamma _i} s) $， ${\mathrm{CH}}({{\boldsymbol{T}}_{\boldsymbol{x}}},{{s}}) $为模拟信号在物理信道中传输的信道函数. 在训练中只考虑加性高斯白噪声（additive Gaussian white noise, AWGN），具体算法如算法2所示.

在算法2中，同时优化截止时间敏感的语义编码器$({f_{\boldsymbol{\theta}} },{f_{\boldsymbol{\varTheta}} })$的参数集$({\boldsymbol{\theta}} ,{\boldsymbol{\varTheta}} ) = \{ ({{\boldsymbol{\theta}} _1},{{\boldsymbol{\varTheta}} _1}),({{\boldsymbol{\theta}} _2},{{\boldsymbol{\varTheta}} _2}), \cdots , ({{\boldsymbol{\theta}} _n},{{\boldsymbol{\varTheta}} _n})\} $和语义解码器${f_{\boldsymbol{\phi}} }$的参数集${\boldsymbol{\phi}} $. 在一个训练轮次中，将截止时间敏感的语义编码器的输入$ {{\boldsymbol{x}}^{(k)}} $作为最浅层语义特征${\boldsymbol{z}}_0^{(k)}$，递归地计算下一层语义特征${\boldsymbol{z}}_i^{(k)}$($i > 0$). 在每次递归计算语义特征后，将${\boldsymbol{z}}_i^{(k)}$输入到信道模拟函数${\mathrm{CH}}({{\boldsymbol{T}}_{\boldsymbol{x}}},{{s}})$，模拟在R-SNR_i下的信道环境，得到输出的接收信号$\hat {\boldsymbol{z}}_i^{(k)}$. 补偿因子初始化为如下所示的随编码深度指数衰减的形式：

(4)$ {\gamma _i} = {{\mathrm{exp}}\;{[{(n - i)}/{n}]}} . $

补偿后的R-SNR使编码层提取的任务相关信息在趋势上大致符合Transformer的“规模定律”，在编码层数较深时，${\gamma _i} \approx 1$即$ {\text{R}} {\text{-}} {\text{SN}}{{\text{R}}_i} \approx s$的条件. 为了进一步减小初始化的$\gamma = \{ {\gamma _1},{\gamma _2}, \cdots ,{\gamma _n}\} $和真实值之间的差距，训练时使用反向传播更新$\gamma = \{ {\gamma _1},{\gamma _2}, \cdots ,{\gamma _n}\} $.

在得到模拟信号函数输出的接收信号$\hat {\boldsymbol{z}}_i^{(k)}$后，计算由当前层语义特征$\hat {\boldsymbol{z}}_i^{(k)}$经语义解码器${{{f}}_{\boldsymbol{\phi}} }$解码得到的系统输出，计算该输出和样本$ {{\boldsymbol{x}}^{(k)}} $对应的真实标签$ {\boldsymbol{y}}_{{\text{truth}}}^{(k)} $之间的差异，进而计算由所有语义编码层编码的语义特征对应的系统输出和训练样本真实标签之间的总误差$L$. 计算$L$对语义编码器$({f_{\boldsymbol{\theta}} },{f_{\boldsymbol{\varTheta}} })$的参数$({\boldsymbol{\theta}} ,{\boldsymbol{\varTheta}} ) = \{ ({{\boldsymbol{\theta}} _1},{{\boldsymbol{\varTheta}} _1}),({{\boldsymbol{\theta}} _2},{{\boldsymbol{\varTheta}} _2}), \cdots ,({{\boldsymbol{\theta}} _n},{{\boldsymbol{\varTheta}} _n})\} $、补偿因子$\gamma = \{ {\gamma _1},{\gamma _2}, \cdots ,{\gamma _n}\} $和语义解码器${{{f}}_{\boldsymbol{\phi}} }$的参数${\boldsymbol{\phi}} $的梯度. 利用反向传播算法^[16]更新上述参数，直至达到保证$L$收敛到一定值的最大训练轮次${{T}}$，解决式(3)所示的优化问题.

更新第$i$个语义编码层$ {f_{{{\boldsymbol{\theta}} _i}}} $的参数${{\boldsymbol{\theta}} _i}$的具体计算方法如下所示：

(5)$ {{\boldsymbol{\theta}} _i} \leftarrow {{\boldsymbol{\theta}} _i} - \alpha \cdot \frac{{\partial {L}({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})}}{{\partial {{\boldsymbol{\theta}} _i}}} . $

因为有$ {\boldsymbol{y}}_i^{(k)} = {{{f}}_{\boldsymbol{\phi}} }({\boldsymbol{z}}_i^{(k)}) $，且中间语义编码输出的中间变量${\boldsymbol{z}}_i^{(k)} = {f_{{{\boldsymbol{\varTheta}} _i}}}({{\boldsymbol{f}}_{{{\boldsymbol{\theta}} _i}}}( \cdots {f_{{{\boldsymbol{\varTheta}} _1}}}({f_{{{\boldsymbol{\theta}} _1}}}({{\boldsymbol{x}}^{(k)}})) ) )$，根据链式法则，使用反向传播算法更新第$i$个语义编码层$ {f_{{{\boldsymbol{\theta}} _i}}} $的参数${{\boldsymbol{\theta}} _i}$的具体计算公式如下所示.

(6)$ \begin{split} {{\boldsymbol{\theta}} _i} \leftarrow & {{\boldsymbol{\theta}} _i} - \alpha \cdot \frac{{\partial {L}\;({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})}}{{\partial {\boldsymbol{y}}_i^{(k)}}} \cdot \frac{{\partial {\boldsymbol{y}}_i^{(k)}}}{{\partial {{\boldsymbol{\theta}} _i}}}= \\ & {{\boldsymbol{\theta}} _i} - \alpha \cdot \frac{{\partial {L}\;({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})}}{{\partial {\boldsymbol{y}}_i^{(k)}}} \cdot \frac{{\partial {f_{\boldsymbol{\phi}} }(\hat {\boldsymbol{z}}_i^{(k)})}}{{\partial {{\boldsymbol{\theta}} _i}}} =\\ & {{\boldsymbol{\theta}} _i} - \alpha \cdot \frac{{\partial {L}\;({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})}}{{\partial {\boldsymbol{y}}_i^{(k)}}} \cdot \frac{{\partial {f_{\boldsymbol{\phi}} }({\boldsymbol{z}}_i^{(k)}+N)}}{{\partial {{\boldsymbol{\theta}} _i}}}= \\ & {{\boldsymbol{\theta}} _i} - \alpha \cdot \frac{{\partial {L}\;({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})}}{{\partial {\boldsymbol{y}}_i^{(k)}}} \cdot \frac{{\partial {f_{\boldsymbol{\phi}} }({\boldsymbol{z}}_i^{(k)})}}{{\partial {\boldsymbol{z}}_i^{(k)}}} \cdot \frac{{\partial {\boldsymbol{z}}_i^{(k)}}}{{\partial {{\boldsymbol{\theta}} _i}}}= \\ & {{\boldsymbol{\theta}} _i} - \alpha \cdot \frac{{\partial {L}\;({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})}}{{\partial {\boldsymbol{y}}_i^{(k)}}} \cdot \frac{{\partial {f_{\boldsymbol{\phi}} }({\boldsymbol{z}}_i^{(k)})}}{{\partial {\boldsymbol{z}}_i^{(k)}}} \times\\ & \frac{{\partial {f_{{{\boldsymbol{\varTheta}} _i}}}({f_{{{\boldsymbol{\theta}} _i}}}( \cdots {f_{{{\boldsymbol{\varTheta}} _1}}}({f_{{{\boldsymbol{\theta}} _1}}}({x^{(k)}})) ))}}{{\partial {{\boldsymbol{\theta}} _i}}}.\end{split}$

第$i$个语义编码层的梯度同时受之前所有层参数的影响，反向传播时使深层和浅层的语义编码层深度耦合，以实现更有效的深层语义表征. 感知网络层${f_{{{\boldsymbol{\varTheta}} _i}}}$和${\gamma _i}$的梯度计算与式(6)类似. 给出使用反向传播算法更新语义解码器${f_{\boldsymbol{\phi}} }$的参数${\boldsymbol{\phi}} $的具体计算公式：

(7)$ \begin{split} {\boldsymbol{\phi}} \leftarrow & {\boldsymbol{\phi}} - \beta \cdot \frac{{\partial {L}\;({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})}}{{\partial {\boldsymbol{\phi}} }} \cdot \frac{{\partial {\boldsymbol{y}}_i^{(k)}}}{{\partial {{\boldsymbol{\theta}} _i}}}= \\ & {\boldsymbol{\phi}} - \beta \cdot \frac{{\partial {L}\;({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})}}{{\partial {\boldsymbol{y}}_i^{(k)}}} \cdot \frac{{\partial {\boldsymbol{y}}_i^{(k)}}}{{\partial {\boldsymbol{\phi}} }} =\\ & {\boldsymbol{\phi}} - \beta \cdot \frac{{\partial {L}\;({\boldsymbol{y}}_i^{(k)},{\boldsymbol{y}}_{{\text{truth}}}^{(k)})}}{{\partial {\boldsymbol{y}}_i^{(k)}}} \cdot \frac{{\partial {f_{\boldsymbol{\phi}} }({\boldsymbol{z}}_i^{(k)})}}{{\partial {\boldsymbol{\phi}} }}. \end{split} $

算法2的训练过程可以使所有编码层编码的语义特征尽量能由解码器解码得到正确的任务输出.

截止时间敏感的语义通信系统与一般语义通信系统最大的不同如下：所提系统可以根据通信时延的要求动态调整数据的编码时间，以满足在5G-Advanced智能车联网应用时的低时延要求. 基于当前车联网中的通信时延要求进行对应的信道补偿，以最大程度地提升系统的信道鲁棒性.

使用在MNIST数据集^[17]、CIFAR-10数据集上的图像分类任务和CARS-196数据集上的汽车识别任务，验证所设计的截止时间敏感的语义通信系统的有效性.

如表1所示为截止时间敏感的语义通信系统的模型参数. 其中截止时间敏感的语义编码器整体上为视觉Transformer（vision Transformer, ViT）结构，除第1层语义编码层进行图像块划分和图像嵌入之外，其他层均为同构的Transformer编码器. 基于编码深度的信噪比感知网络的整体结构如图3所示，基本上由线性的全连接层组成. 这些全连接层按照图3的结构组成基于自注意力机制的信噪比感知网络. 联合信源信道解码器由2个线形层组成，其中第1个线性层在所有图像块维度上进行加权，第2个线性层在图像嵌入维度上计算输出类别. 具体的参数设置如表1所示. 模型训练的超参数设置如表2所示.

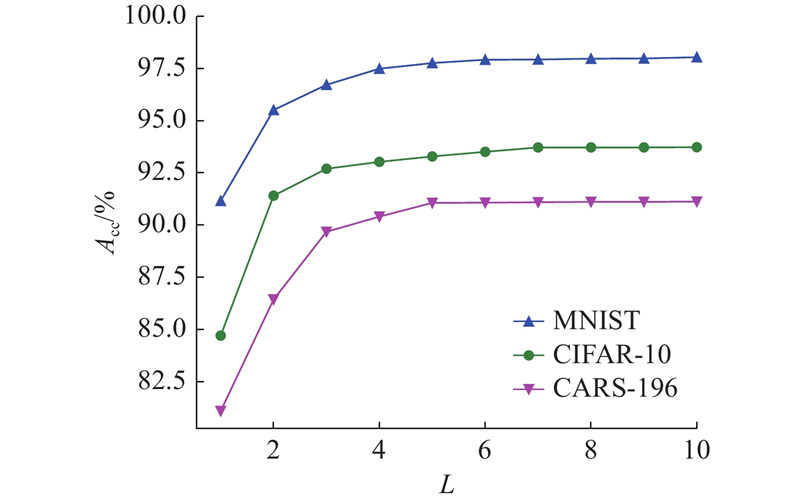
如图5所示为编码深度对提出系统性能的影响. 图中，A_cc为准确率，L为编码深度. 在MNIST数据集、CIFAR-10数据集和CARS-196数据集上，当编码层数为1时模型准确率分别为91.16%、80.71%和81.10%，当编码层数为7时模型准确率分别为98.04%、93.73%和91.13%，性能均有所提升. 这是由于编码深度越深，语义表征能力越强，对应的解码输出错误的概率越小，即编码截止时间越长，系统输出错误的概率越小.

如图6所示为不同编码截止时间下的模型性能. 选择deep JSCC^[18]作为对比系统，由于原deep JSCC系统是面向图像传输的JSCC系统，将原模型的编码器中的5个卷积层修改为4卷积层后连接多层感知机，解码器为单层的线性层. 将和本文同构的7层语义编码层、但无法感知编码截止时间的语义通信系统作为对比系统之一，即图6中的“SC”曲线.

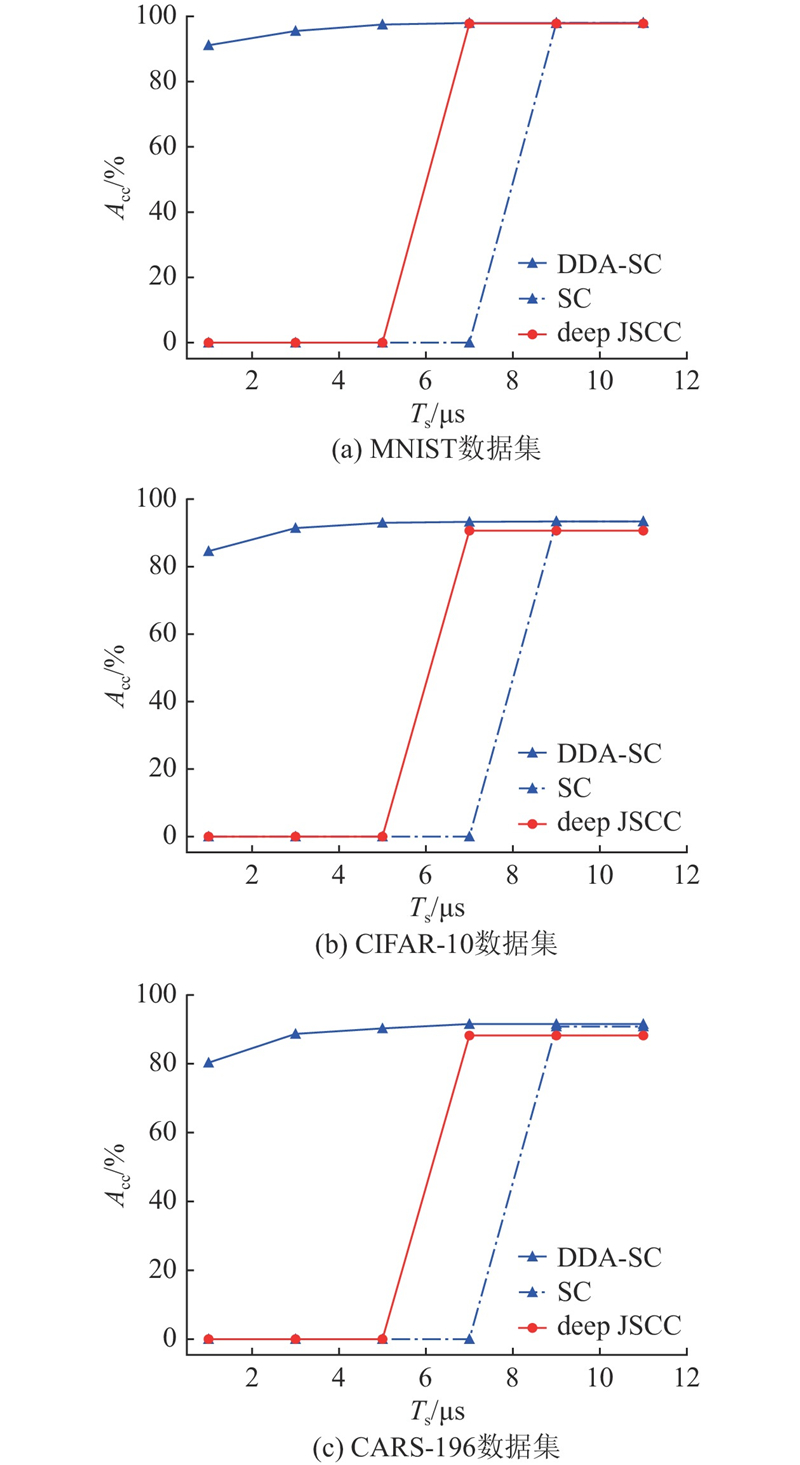
如图6 (c)所示为在CARS-196数据集上不同编码截止时间下的模型性能. 当截止时间≤5 μs时，提出的截止时间敏感的语义通信系统的准确度比deep JSCC系统和SC系统提高了80.31%以上，有显著优势. 这主要是因为提出的系统可以根据编码的截止时间动态调整编码深度，以在截止时间内完成语义编码进行传输. deep JSCC系统和SC系统无法根据编码的截止时间动态调整，当编码截止时间小于deep JSCC系统和SC系统的编码器编码对信源信息编码所需的时间时，2个系统均处于不可用状态. 当截止时间> 7 μs时，3个系统均可正常完成语义编码，此时三者性能几乎相同. 如图6 (b)、(c)所示分别为在CIFAR-10数据集和MNIST数据集上不同编码截止时间下的模型性能，整体趋势与CARS-196数据集上类似. 当截止时间≤5 μs提出的截止时间敏感的语义通信系统在2个数据集上的准确度较deep JSCC系统和SC系统提高84.58%和91%以上.

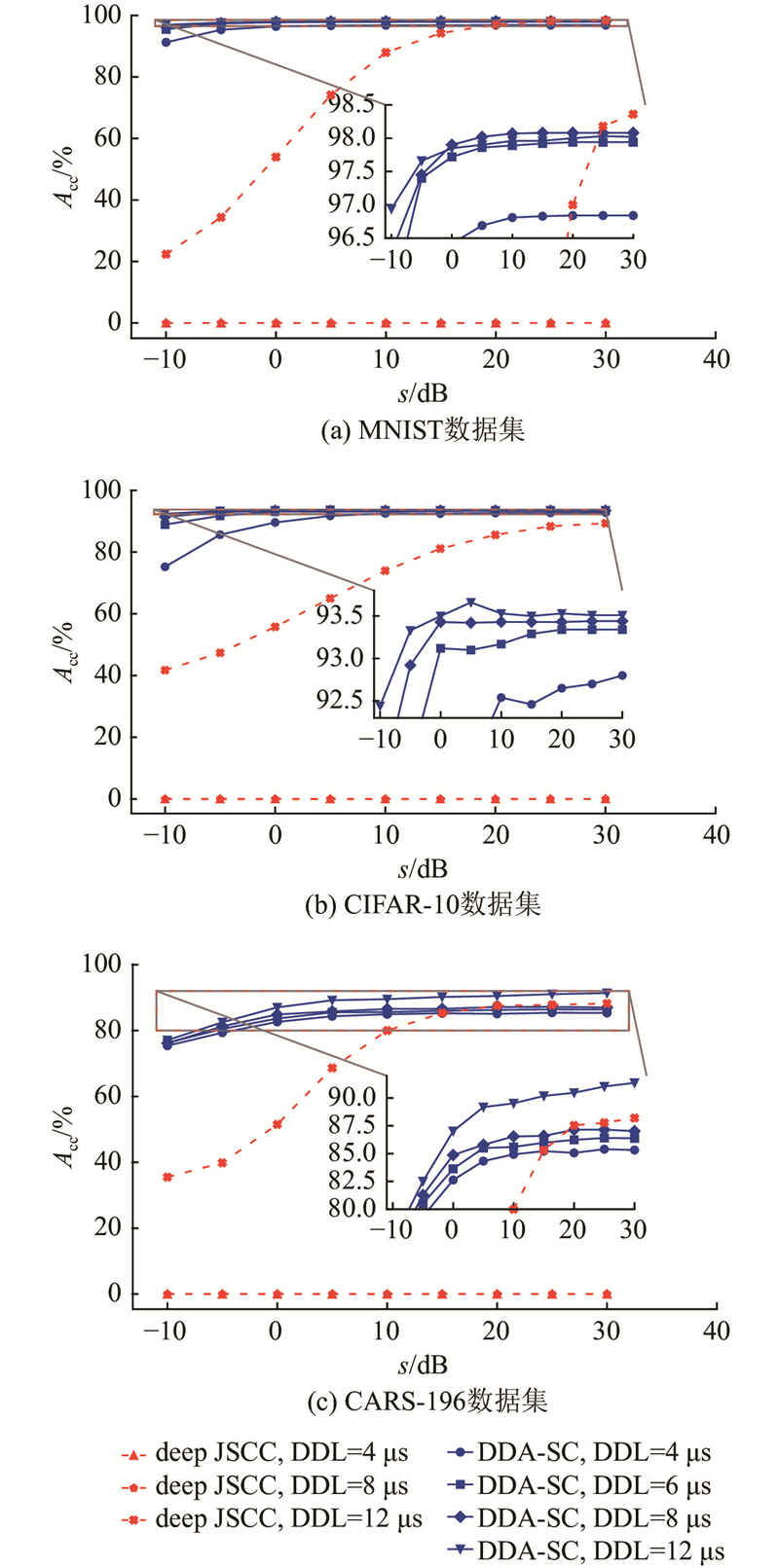
如图7所示为在不同信道条件下（即不同信噪比下），截止时间敏感的语义通信系统和deep JSCC系统分别在编码截止时间为4、6、8和12 μs时的系统性能. 如图7 (c)所示为模型在CARS-196数据集上的性能. 在编码截止时间为12 μs，信噪比为−10 dB的情况下，提出的截止时间敏感的语义通信系统的准确率较deep JSCC系统提升了41.57%. 在此条件下，DDA-SC系统和deep JSCC系统均可以正常完成语义编码，但上述结果说明DDA-SC的抗噪能力远强于deep JSCC系统，造成该结果的原因如下. 1）提出的基于编码深度的信噪比感知网络能够有效地抵御信道噪声，尤其在训练时使用补偿后相关信噪比能够使较浅的编码层充分感知信道噪声，从而有较好的信道鲁棒性. 2）DDA-SC的语义编码层采用Transformer的编码器架构，该架构在抵抗信道噪声带来的数据扰动方面较卷积层有天然优势. 3）利用算法2所示的训练方法，DDA-SC的语义编码器的每一层都能够提取最有效的语义表征，使得深层次的语义特征在完成通信任务时更有效. 当编码截止时间≤8 μs时，编码截止时间小于deep JSCC系统的编码器编码对信源信息编码所需的时间，该系统处于不可用状态，分类准确率为0.

如图7 (b)、(c)所示分别为在CIFAR-10数据集和MNIST数据集上不同编码截止时间下的模型性能，整体趋势与CARS-196数据集上类似. 在编码截止时间为12 μs，信噪比为−10 dB的情况下，提出的截止时间敏感的语义通信系统在2个数据集上的准确率分别较deep JSCC系统提升50.69%和74.68%. 当编码截止时间≤8 μs时，deep JSCC系统不可用，分类准确率为0.

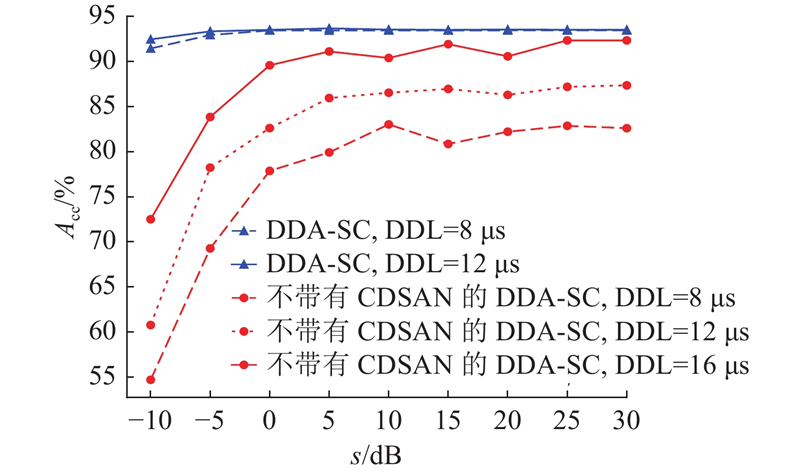
为了验证提出的基于编码深度的信噪比感知网络的有效性，设计消融实验，对比有感知网络层的DDA-SC系统和不带有感知网络层的DDA-SC系统. 如图8所示，在编码截止时间分别为8和12 μs的情况下，有感知网络层的DDA-SC系统在CIFAR-10数据集上的性能在各SNR下均优于没有感知网络层的DDA-SC系统. 当编码截止时间为8 μs时，在信噪比为−10 dB的情况下，有感知网络层的DDA-SC系统的准确率较没有感知网络层的DDA-SC系统提高了36.71%. 这证明了感知网络层在抵御信道噪声方面的有效性；在同编码截止时间下有感知网络层的DDA-SC系统的性能优势说明感知网络层带来的性能增益远超引入其而带来的额外的计算复杂度.

本文针对5G-Advanced智能车联网场景中的确定性网络，设计截止时间敏感的语义通信系统. 通过控制语义特征的编码深度，确保时间敏感数据在截止时间内完成可靠传输. 为了提升系统的抗噪能力，提出基于编码深度的信噪比感知网络（CDSAN）. 利用注意力机制感知相关信噪比（R-SNR），增强在不同截止时间下的鲁棒性. 该方法为车联网低时延语义通信提供了解决方案，为相关算法的设计提供了指导，是该领域首篇考虑了编码截止时间的工作，开拓了新视角. 未来研究将探索该方法在更多车联网具体任务中的应用，验证其广泛适用性，并研究语义通信与边缘计算的融合，以提高网络的响应速度和可靠性，为5G-Advanced及6G低时延场景提供启示.