[1]
CHEN Z, GUO W, FENG Y, et al Deep-learned regularization and proximal operator for image compressive sensing
[J]. IEEE Transactions on Image Processing , 2021 , 30 : 7112 - 7126
[本文引用: 1]
[2]
QIAO M, LIU X, YUAN X Snapshot spatial–temporal compressive imaging
[J]. Optics Letters , 2020 , 45 (7 ): 1659 - 1662
DOI:10.1364/OL.386238
[本文引用: 1]
[3]
LU R, CHEN B, LIU G, et al Dual-view snapshot compressive imaging via optical flow aided recurrent neural network
[J]. International Journal of Computer Vision , 2021 , 129 (12 ): 3279 - 3298
DOI:10.1007/s11263-021-01532-1
[本文引用: 1]
[4]
LLULL P, LIAO X, YUAN X, et al Coded aperture compressive temporal imaging
[J]. Optics Express , 2013 , 21 (9 ): 10526 - 10545
DOI:10.1364/OE.21.010526
[本文引用: 1]
[5]
YUAN X, BRADY D, KATSAGGELOS A Snapshot compressive imaging: theory, algorithms, and applications
[J]. IEEE Signal Processing Magazine , 2021 , 38 (2 ): 65 - 88
DOI:10.1109/MSP.2020.3023869
[6]
SUN Y, YUAN X, PANG S Compressive high-speed stereo imaging
[J]. Optics Express , 2017 , 25 (15 ): 18182 - 18190
DOI:10.1364/OE.25.018182
[7]
ZHANG Z, DENG C, LIU Y, et al Ten-mega-pixel snapshot compressive imaging with a hybrid coded aperture
[J]. Photonics Research , 2021 , 9 (11 ): 2277 - 2287
DOI:10.1364/PRJ.435256
[本文引用: 2]
[8]
ZHAN C, HU H, SUI X, et al Joint resource allocation and 3D aerial trajectory design for video streaming in UAV communication systems
[J]. IEEE Transactions on Circuits and Systems for Video Technology , 2020 , 31 (8 ): 3227 - 3241
[本文引用: 1]
[9]
LIN F, FU C, HE Y, et al Learning temporary block-based bidirectional incongruity-aware correlation filters for efficient UAV object tracking
[J]. IEEE Transactions on Circuits and Systems for Video Technology , 2020 , 31 (6 ): 2160 - 2174
[本文引用: 1]
[10]
LIU Y, YUAN X, SUO J, et al Rank minimization for snapshot compressive imaging
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2018 , 41 (12 ): 2990 - 3006
[本文引用: 2]
[11]
YUAN X, LIU Y, SUO J, et al. Plug-and-play algorithms for large-scale snapshot compressive imaging [C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 1447-1457.
[12]
YUAN X, LIU Y, SUO J, et al Plug-and-play algorithms for video snapshot compressive imaging
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2021 , 44 (10 ): 7093 - 7111
[本文引用: 1]
[13]
YANG J, YUAN X, LIAO X, et al Video compressive sensing using Gaussian mixture models
[J]. IEEE Transactions on Image Processing , 2014 , 23 (11 ): 4863 - 4878
DOI:10.1109/TIP.2014.2344294
[本文引用: 2]
[14]
SHI B, WANG Y, LI D Provable general bounded denoisers for snapshot compressive imaging with convergence guarantee
[J]. IEEE Transactions on Computational Imaging , 2023 , 9 (2 ): 55 - 69
[本文引用: 1]
[15]
SHI B, LI D, WANG Y, et al Provable deep video denoiser using spatial–temporal information for video snapshot compressive imaging: algorithm and convergence analysis
[J]. Signal Processing , 2024 , 214 (1 ): 109236
[本文引用: 1]
[16]
SHI B, WANG Y, LIAN Q. A trainable bounded denoiser using double tight frame network for snapshot compressive imaging [C]// IEEE International Conference on Acoustics, Speech and Signal Processing . Singapore: IEEE, 2022: 1516-1520.
[本文引用: 1]
[17]
QIAO M, MENG Z, MA J, et al Deep learning for video compressive sensing
[J]. Apl Photonics , 2020 , 5 (3 ): 030801
DOI:10.1063/1.5140721
[本文引用: 2]
[18]
CHENG Z, CHEN B, LIU G, et al. Memory-efficient network for large-scale video compressive sensing [C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition . Nashville: IEEE, 2021: 16246-16255.
[本文引用: 2]
[19]
HAN X, WU B, SHOU Z, et al. Tensor FISTA-Net for real-time snapshot compressive imaging [C]// Proceedings of the AAAI Conference on Artificial Intelligence . New York: AAAI, 2020, 34(7): 10933-10940.
[本文引用: 1]
[20]
MENG Z, YUAN X, JALALI S Deep unfolding for snapshot compressive imaging
[J]. International Journal of Computer Vision , 2023 , 131 (11 ): 2933 - 2958
DOI:10.1007/s11263-023-01844-4
[本文引用: 3]
[21]
WANG Z, ZHANG H, CHENG Z, et al. Metasci: scalable and adaptive reconstruction for video compressive sensing [C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition . Nashville: IEEE, 2021: 2083-2092.
[本文引用: 2]
[22]
NIKLAUS S, MAI L, LIU F. Video frame interpolation via adaptive convolution [C]// IEEE Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 670-679.
[本文引用: 1]
[23]
LIU Z, YEH R, TANG X, et al. Video frame synthesis using deep voxel flow [C]// IEEE International Conference on Computer Vision . Venice: IEEE, 2017: 4463-4471.
[本文引用: 1]
[24]
ZHANG Y, LIU X, WU B, et al. Video synthesis via transform-based tensor neural network [C]// Proceedings of the 28th ACM International Conference on Multimedia . Melbourne: ACM, 2020: 2454-2462.
[本文引用: 1]
[25]
KRIZHEVSKY A, SUTSKEVER I, HINTON G ImageNet classification with deep convolutional neural networks
[J]. Communications of the ACM , 2017 , 60 (6 ): 84 - 90
DOI:10.1145/3065386
[本文引用: 1]
[26]
XIE S, GIRSHICK R, DOLLÁR P, et al. Aggregated residual transformations for deep neural networks [C]// IEEE Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 1492-1500.
[27]
HUANG G, LIU S, MAATEN L, et al. Condensenet: an efficient DenseNet using learned group convolutions [C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition . Salt Lake City: IEEE, 2018: 2752-2761.
[本文引用: 1]
[28]
MIAO Y, ZHAO X, WANG J, et al Snapshot compressive imaging using domain-factorized deep video prior
[J]. IEEE Transactions on Computational Imaging , 2024 , 10 (1 ): 93 - 102
[本文引用: 1]
[29]
LI S, ZHENG Z, DAI W, et al. REV-AE: a learned frame set for image reconstruction [C]// IEEE International Conference on Acoustics, Speech and Signal Processing. Barcelona: IEEE, 2020: 1823-1827.
[本文引用: 2]
[30]
WU Z, ZHANG J, MOU C. Dense deep unfolding network with 3D-CNN prior for snapshot compressive imaging [C]// IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021: 4872-4881.
[本文引用: 1]
[31]
LI S, DAI W, ZHENG Z, et al Reversible autoencoder: a CNN-based nonlinear lifting scheme for image reconstruction
[J]. IEEE Transactions on Signal Processing , 2021 , 69 (5 ): 3117 - 3131
[本文引用: 2]
[32]
CHEN Z, LI R, LI Y, et al. Video snapshot compressive imaging via optical flow [C]// IEEE International Conference on Multimedia and Expo . Brisbane: IEEE, 2023: 2177-2182.
[本文引用: 1]
[33]
WANG L, CAO M, YUAN X. Efficientsci: densely connected network with space-time factorization for large-scale video snapshot compressive imaging [C]// IEEE/CVF Conference on Computer Vision and Pattern Recognition . Vancouver: IEEE, 2023: 18477-18486.
[本文引用: 1]
[34]
WANG P, WANG L, YUAN X. Deep optics for video snapshot compressive imaging [C]// IEEE/CVF International Conference on Computer Vision . Paris: IEEE, 2023: 10646-10656.
[本文引用: 1]
Deep-learned regularization and proximal operator for image compressive sensing
1
2021
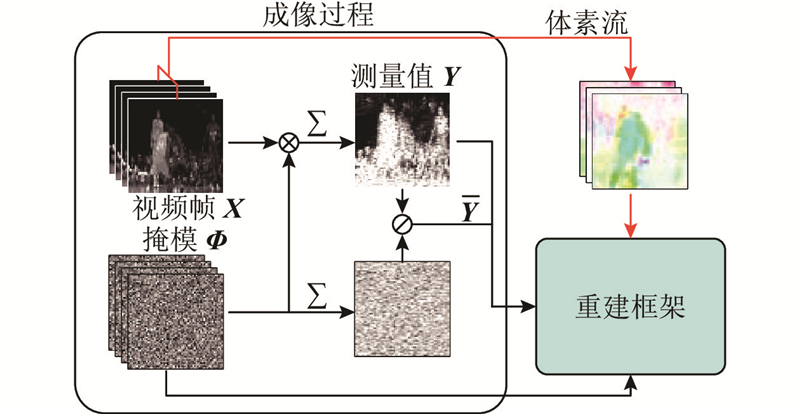
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
Snapshot spatial–temporal compressive imaging
1
2020
... 视频SCI的真实数据存在不可避免的噪声,由于光照不均,掩膜可能不准确. 此外,较小的压缩采样率意味着更多的视频帧在测量值中被压缩,重构难度增加. 对于SCI重构方法来说,真实数据的重构更具挑战性[2 ,7 ] . 在压缩采样率为$ 1/14 $ 图5 所示为不同方法在真实数据上重构的结果. 可以看出,与其他方法相比,利用本文方法得到的字母“D”和“手”的边缘更清晰. ...
Dual-view snapshot compressive imaging via optical flow aided recurrent neural network
1
2021
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
Coded aperture compressive temporal imaging
1
2013
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
Snapshot compressive imaging: theory, algorithms, and applications
0
2021
Compressive high-speed stereo imaging
0
2017
Ten-mega-pixel snapshot compressive imaging with a hybrid coded aperture
2
2021
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
... 视频SCI的真实数据存在不可避免的噪声,由于光照不均,掩膜可能不准确. 此外,较小的压缩采样率意味着更多的视频帧在测量值中被压缩,重构难度增加. 对于SCI重构方法来说,真实数据的重构更具挑战性[2 ,7 ] . 在压缩采样率为$ 1/14 $ 图5 所示为不同方法在真实数据上重构的结果. 可以看出,与其他方法相比,利用本文方法得到的字母“D”和“手”的边缘更清晰. ...
Joint resource allocation and 3D aerial trajectory design for video streaming in UAV communication systems
1
2020
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
Learning temporary block-based bidirectional incongruity-aware correlation filters for efficient UAV object tracking
1
2020
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
Rank minimization for snapshot compressive imaging
2
2018
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
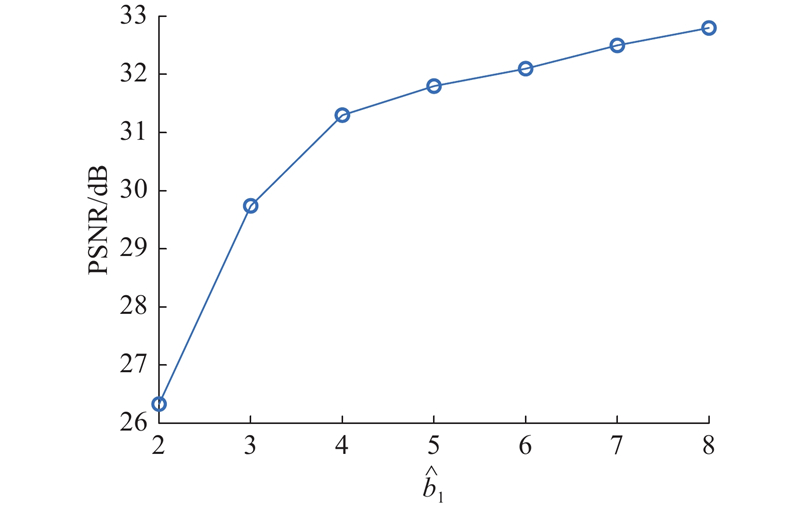
... 式中:$ {N_{\mathrm{s}}} $ $ \hat {\boldsymbol{X}} $ [28 ] ,其中包含90个不同场景的480像素和1080 像素分辨率的图像. 通过随机裁剪、缩放和水平翻转等数据增强方法,共获得26 000对灰度数据和21 000对彩色数据. 从原始图像中裁剪连续图像作为基准真实视频帧,在每段视频帧中选择奇数帧作为原始帧. 为了便于比较,使用原始尺寸为256×256×8(即$ {b_1} = {b_2} = 4 $ [10 ,13 ] . 为了进行实际验证,使用原始大小为256×256×14的真实数据集Chopper wheel和Hand lens,对所提模型进行测试. 所有方法都在相同的硬件上,使用相同的数据集和掩码进行重新训练和测试. 使用峰值信噪比(peak signal-to-noise ratio, PSNR)和结构相似性(structure similarity index measure, SSIM)作为重构质量评估指标. ...
Plug-and-play algorithms for video snapshot compressive imaging
1
2021
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
Video compressive sensing using Gaussian mixture models
2
2014
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
... 式中:$ {N_{\mathrm{s}}} $ $ \hat {\boldsymbol{X}} $ [28 ] ,其中包含90个不同场景的480像素和1080 像素分辨率的图像. 通过随机裁剪、缩放和水平翻转等数据增强方法,共获得26 000对灰度数据和21 000对彩色数据. 从原始图像中裁剪连续图像作为基准真实视频帧,在每段视频帧中选择奇数帧作为原始帧. 为了便于比较,使用原始尺寸为256×256×8(即$ {b_1} = {b_2} = 4 $ [10 ,13 ] . 为了进行实际验证,使用原始大小为256×256×14的真实数据集Chopper wheel和Hand lens,对所提模型进行测试. 所有方法都在相同的硬件上,使用相同的数据集和掩码进行重新训练和测试. 使用峰值信噪比(peak signal-to-noise ratio, PSNR)和结构相似性(structure similarity index measure, SSIM)作为重构质量评估指标. ...
Provable general bounded denoisers for snapshot compressive imaging with convergence guarantee
1
2023
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
Provable deep video denoiser using spatial–temporal information for video snapshot compressive imaging: algorithm and convergence analysis
1
2024
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
1
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
Deep learning for video compressive sensing
2
2020
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...
2
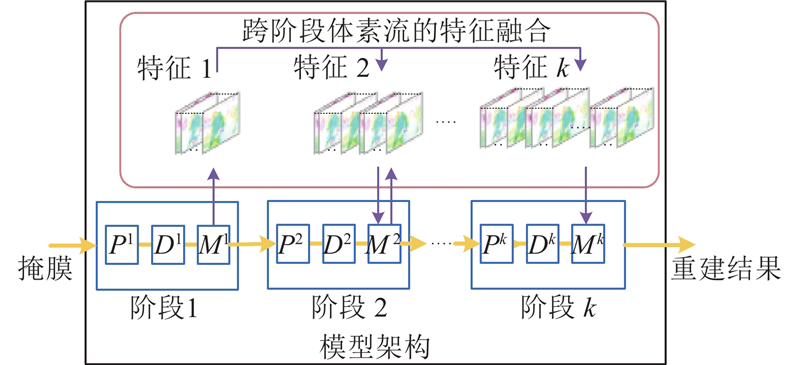
... 考虑到上述问题,本文提出新的深度展开框架. 具体来说,基于深度展开框架的基础,在重构过程中整合了基于体素流的帧合成方法,在时间维度上扩展视频数据,而不是直接降低压缩采样率,因为后者会造成大量的硬件内存和训练时间的消耗[21 ] . 本文提出的深度展开框架使用深度去噪器学习粗糙重建帧到原始帧的映射,采用运动正则化方法从去噪特征中直接提取体素流,以探索帧与帧之间的时空相关性[18 -20 ] . 为了进一步提高模型性能,本文提出跨阶段体素流特征融合策略并引入群卷积[22 -24 ] . ...
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...
1
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...
Deep unfolding for snapshot compressive imaging
3
2023
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
... 考虑到上述问题,本文提出新的深度展开框架. 具体来说,基于深度展开框架的基础,在重构过程中整合了基于体素流的帧合成方法,在时间维度上扩展视频数据,而不是直接降低压缩采样率,因为后者会造成大量的硬件内存和训练时间的消耗[21 ] . 本文提出的深度展开框架使用深度去噪器学习粗糙重建帧到原始帧的映射,采用运动正则化方法从去噪特征中直接提取体素流,以探索帧与帧之间的时空相关性[18 -20 ] . 为了进一步提高模型性能,本文提出跨阶段体素流特征融合策略并引入群卷积[22 -24 ] . ...
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...
2
... 压缩感知近年来推动了计算成像技术的发展[1 -3 ] . 快照压缩成像(snapshot compressive imaging, SCI)是基于压缩感知理论的计算成像系统的分支. 视频SCI系统使用特殊的硬件掩膜对连续高速场景进行采样,并将采样数据压缩为单个测量值[4 -7 ] . 缺乏快速准确的重建算法是限制SCI系统实际应用的因素之一[8 -9 ] . 一些算法采用各种先验知识作为正则化,将SCI重构转化为正则优化问题[10 -12 ] . 此类算法的可解释性强,但重建性能不够理想[13 ] . 此外,Shi等[14 ] 提出结合双重紧框架和空间变化阈值的可训练有界去噪器. 此外,Shi等[15 ] 为视频SCI系统设计基于双紧框架的深度视频去噪器,增强了对视频特征的处理能力. 最近,Shi等[16 ] 通过扩展双紧框架,提出可训练的高斯去噪器. 此外,一些深度神经网络被用来学习从测量值到原始帧的直接映射[17 -20 ] . 一些研究人员结合了迭代优化算法和深度学习的优势,提出各种用于SCI重建的深度展开框架,但是网络的训练需要大量的硬件内存. 除此之外,受掩膜移动速度、机械或电路故障的影响,视频SCI系统很难在每个采样瞬间都理想地采样到相应的图像[21 ] . ...
... 考虑到上述问题,本文提出新的深度展开框架. 具体来说,基于深度展开框架的基础,在重构过程中整合了基于体素流的帧合成方法,在时间维度上扩展视频数据,而不是直接降低压缩采样率,因为后者会造成大量的硬件内存和训练时间的消耗[21 ] . 本文提出的深度展开框架使用深度去噪器学习粗糙重建帧到原始帧的映射,采用运动正则化方法从去噪特征中直接提取体素流,以探索帧与帧之间的时空相关性[18 -20 ] . 为了进一步提高模型性能,本文提出跨阶段体素流特征融合策略并引入群卷积[22 -24 ] . ...
1
... 考虑到上述问题,本文提出新的深度展开框架. 具体来说,基于深度展开框架的基础,在重构过程中整合了基于体素流的帧合成方法,在时间维度上扩展视频数据,而不是直接降低压缩采样率,因为后者会造成大量的硬件内存和训练时间的消耗[21 ] . 本文提出的深度展开框架使用深度去噪器学习粗糙重建帧到原始帧的映射,采用运动正则化方法从去噪特征中直接提取体素流,以探索帧与帧之间的时空相关性[18 -20 ] . 为了进一步提高模型性能,本文提出跨阶段体素流特征融合策略并引入群卷积[22 -24 ] . ...
1
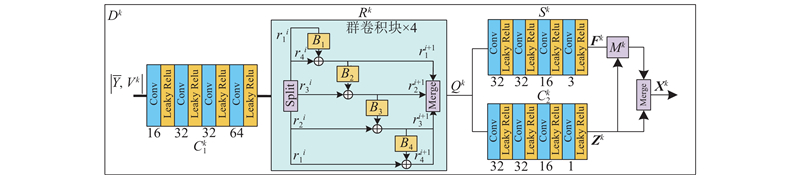
... 式中:$ {{\boldsymbol{W}}^{ijl}} $ [23 ] . 构成体素流的3个分量分别为空间和时间维度的像素偏移量. 基于这些偏移量,通过三线性插值计算得到连续2个原始帧之间的中间帧像素,原始帧和中间帧的精确度随着算法迭代和网络训练的进行而逐渐提高. ...
1
... 考虑到上述问题,本文提出新的深度展开框架. 具体来说,基于深度展开框架的基础,在重构过程中整合了基于体素流的帧合成方法,在时间维度上扩展视频数据,而不是直接降低压缩采样率,因为后者会造成大量的硬件内存和训练时间的消耗[21 ] . 本文提出的深度展开框架使用深度去噪器学习粗糙重建帧到原始帧的映射,采用运动正则化方法从去噪特征中直接提取体素流,以探索帧与帧之间的时空相关性[18 -20 ] . 为了进一步提高模型性能,本文提出跨阶段体素流特征融合策略并引入群卷积[22 -24 ] . ...
ImageNet classification with deep convolutional neural networks
1
2017
... 在一定程度上堆叠相同的结构,有利于提高非线性性能. 此外,群卷积通过限制超参数的自由选择,降低了对特定数据集过拟合的风险[25 -27 ] . ...
1
... 在一定程度上堆叠相同的结构,有利于提高非线性性能. 此外,群卷积通过限制超参数的自由选择,降低了对特定数据集过拟合的风险[25 -27 ] . ...
Snapshot compressive imaging using domain-factorized deep video prior
1
2024
... 式中:$ {N_{\mathrm{s}}} $ $ \hat {\boldsymbol{X}} $ [28 ] ,其中包含90个不同场景的480像素和1080 像素分辨率的图像. 通过随机裁剪、缩放和水平翻转等数据增强方法,共获得26 000对灰度数据和21 000对彩色数据. 从原始图像中裁剪连续图像作为基准真实视频帧,在每段视频帧中选择奇数帧作为原始帧. 为了便于比较,使用原始尺寸为256×256×8(即$ {b_1} = {b_2} = 4 $ [10 ,13 ] . 为了进行实际验证,使用原始大小为256×256×14的真实数据集Chopper wheel和Hand lens,对所提模型进行测试. 所有方法都在相同的硬件上,使用相同的数据集和掩码进行重新训练和测试. 使用峰值信噪比(peak signal-to-noise ratio, PSNR)和结构相似性(structure similarity index measure, SSIM)作为重构质量评估指标. ...
2
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...
... 为了验证群卷积块(GC)的有效性,在另一项实验中用可逆块结构[29 ,31 ] 替换GC . 本文只取了可逆结构的正向部分,因为正向可逆结构可以看作是群数较少的群卷积. 模型的其他设置和参数保持不变,实验结果如表2 所示. 可以看出,用正向可逆块替换GC后,模型的PSNR性能降低了0.32 dB,这说明增加卷积的组数可以有效地改善模型的重构性能. ...
1
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...
Reversible autoencoder: a CNN-based nonlinear lifting scheme for image reconstruction
2
2021
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...
... 为了验证群卷积块(GC)的有效性,在另一项实验中用可逆块结构[29 ,31 ] 替换GC . 本文只取了可逆结构的正向部分,因为正向可逆结构可以看作是群数较少的群卷积. 模型的其他设置和参数保持不变,实验结果如表2 所示. 可以看出,用正向可逆块替换GC后,模型的PSNR性能降低了0.32 dB,这说明增加卷积的组数可以有效地改善模型的重构性能. ...
1
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...
1
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...
1
... Comparison results and running time of simulated data reconstruction, the left data of the cell is PSNR and the right is SSIM
Tab.1 对比方法 PSNR/dB, SSIM t r /sKobe Traffic Runner Drop Aerial Crash 平均值 Tensor-FISTA[19 ] 25.02, 0.804 22.71, 0.822 30.32, 0.942 34.36, 0.971 25.95, 0.876 25.50, 0.891 27.31, 0.884 0.0166 E2E-CNN[17 ] 26.24, 0.820 24.53, 0.888 33.80, 0.974 36.66, 0.989 27.29, 0.915 26.30, 0.912 29.14, 0.917 0.0098 RevSCI[18 ] 27.51, 0.884 24.87, 0.898 34.05, 0.976 37.70, 0.990 26.97, 0.912 26.31, 0.915 29.57, 0.929 0.1412 ISTA-Rev-AE[29 ] 25.91, 0.811 24.09, 0.870 33.07, 0.977 38.05, 0.970 26.73, 0.903 26.18, 0.908 28.96, 0.909 0.0481 GAP-Unet-S12[20 ] 27.48, 0.856 25.55, 0.907 35.29, 0.980 37.18, 0.992 27.90, 0.924 26.83, 0.925 30.04, 0.931 0.0327 HQS-RevSCI[30 ] 27.59, 0.875 25.14, 0.902 34.30, 0.977 38.15, 0.990 27.27, 0.917 26.32, 0.914 29.79, 0.929 0.4136 FISTA-Rev-AE-3D[31 ] 27.58, 0.865 25.59, 0.909 35.03, 0.979 38.59, 0.991 27.58, 0.921 26.57, 0.915 30.16, 0.930 0.1281 SCI-OF[32 ] 29.03, 0.916 26.83, 0.933 35.32, 0.980 39.68, 0.992 28.07, 0.932 27.34, 0.939 31.04, 0.949 0.2476 EfficientSCI[33 ] 25.25, 0.826 22.65, 0.828 31.34, 0.962 35.51, 0.984 26.02, 0.890 25.52, 0.898 27.71, 0.898 0.0206 Res2former[34 ] 26.54, 0.858 24.32, 0.868 33.42, 0.973 37.90, 0.989 27.30, 0.916 26.58, 0.924 29.34, 0.921 0.0216 本文方法 28.87, 0.912 27.05, 0.935 36.29, 0.982 39.82, 0.993 28.29, 0.933 27.35, 0.941 31.27, 0.949 0.2509
从表1 可以看出,在大多数个场景的PSNR和SSIM方面,本文的方法都优于对比方法,尤其是平均PSNR比排名第2的SCI-OF高0.23 dB. Tensor-FISTA、E2E-CNN和ISTA-Rev-AE的运行速度较快,但重构结果相对较差. 得益于较小的网络结构和简便的GAP算法,GAP-Unet-S12在较短的运行时间内获得了与FISTA-Rev-AE-3D几乎相当的重构结果,但重构帧的视觉质量较差. 如图4 所示为本文方法与对比方法重构时间维超分辨率帧结果的可视化对比. 由于采用了基于体素流的运动正则化,本文方法重构的帧具有更清晰的细节和更锐利的边缘,对比方法重构的帧更平滑粗糙,如Kobe中的数字“24”和Aerial中的“树枝”. ...