海上弱小目标检测与跟踪一直是雷达目标跟踪领域的重要研究内容，具有一定的挑战性^[1]. 常用的检测算法主要包括恒虚警（constant false alarm rate, CFAR）检测法^[2-3]、基于分形及神经网络的方法^[4]、基于匹配滤波的检测算法^[5]、基于时频分析及小波变换的方法^[6-7]等，在复杂杂波环境下的目标检测性能会受到很大的限制.

为了在低信噪比场景中能够更好地检测弱小目标，Wang等^[8]提出基于检测前多帧跟踪（multi-frame track-before-detect, MF-TBD）的方法. 与先检测后跟踪的方法不同，检测前跟踪不仅仅是根据某一帧的数据来跟踪，而是累积多帧的数据以积累目标信息，从而进行门限处理，给出估计目标的状态与轨迹. 通过联合多帧信息，能够提高弱小目标的信噪比，但算法复杂度较高. 随后，MF-TBD被广泛应用于雷达系统^[9-12]，对雷达目标进行检测与跟踪. 这些算法仅使用峰值振幅强度作为区分目标和杂波的主要指标，无法反映不同目标更多的变化特征. Davey等^[13]比较了复杂背景下几种基于弱小目标的检测前跟踪方法: 贝叶斯估计、动态规划、粒子滤波方法和直方图概率多假设. 这些方法在研究场景中仅考虑单个目标，没有充分考虑多目标场景. Henriques等^[14]提出核相关滤波器（kernel correlation filter, KCF），将原始像素的强度作为特征，但算法大多采用固定大小的外观模板，无法在长时间跟踪中适应多个目标的不同模型变化. 为了解决该问题，Zhou等^[15]提出多核相关滤波（multiple KCF, MKCF），利用多个模板来跟踪单个雷达目标，取得了较好的效果，但在信噪比较低的跟踪场景中，仍会出现漏跟现象. Zhou等^[16]提出基于多核相关滤波的检测前跟踪算法（MKCF-based TBD, MKCF-TBD），当MKCF模板跨帧估计目标状态时，参考模板和候选模板之间的相似性得分被记录为检验统计量，作为区别目标与杂波的指标，并进行积分以增强对弱目标的检测，但在信噪比较低的情况下，由于海杂波淹没了目标信号，大大增加了检测跟踪的难度，会出现许多虚假航迹.

针对上述问题，本文提出优化多核相关滤波的弱小目标检测前跟踪算法. 引入基于分数阶傅里叶变换（fractional Fourier transform, FRFT）的滤波方法对雷达信号进行预处理，增强目标与海杂波之间的差异性，以便有效地滤除杂波. 提出KCF模板优化提取方法，结合卡尔曼滤波进行目标匹配. 根据目标类型采用不同的模板提取方法，采用最大似然方法融合预测结果，以解决MKCF算法应用多目标跟踪时由于目标之间的相互干扰导致跟踪精度下降的问题. 结合检测前跟踪算法，累积目标多帧信息，实现对雷达弱小目标的最优航迹估计，以解决低信噪比场景下弱小目标难以检测跟踪的问题.

核相关滤波算法是通过循环矩阵扩充训练样本，对目标进行快速检测及定位^[17]. 通过使用映射函数，评估新帧中的候选区域，将具有最高响应的位置作为目标中心^[18].

假设目标状态表示为$ {{\boldsymbol{x}}_k}{\text{ = [}}{a_{k{\text{,}}}}{b_k}{\text{]}} $，初始帧中目标宽度为$ {w_1} $，高度为$ {h_1} $，目标在$k$帧中生成的模板$ {{{z}}_k} $ 表示为

(1)$ \begin{split} &{{{{z}} }_k}({{\boldsymbol{x}}_k}) = \{ {{{{z}} }_k}({a_k},{b_k}):|{a_{k-{\text{ 1}}}} - {a_k}| \leqslant {w_{\text{z}}}, \\ &|{b_{k{{ - 1}}}} - {b_k}| \leqslant {h_{\text{z}}},{w_{\text{z}}} \geqslant 2{w_1},{h_{\text{z}}} \geqslant 2{h_1}\}. \end{split} $

式中：$ {a_{{k}}} $与$ {b_{{k}}} $为目标的中心坐标，$ {w_{\text{z}}} $与$ {h_{\text{z}}} $分别为KCF模板区域的宽和高.

给定初始帧中的模板$ {{{\boldsymbol{z}} }_1}({{\boldsymbol{x}}_1}) $，循环移位$ n = {w_{\text{z}}} \times {h_{\text{z}}} $次，生成$ n $个密集样本$ {{{\boldsymbol{z}} }_1}^{1},\cdots,{{{\boldsymbol{z}} }_1}^n $. 第k帧中的新模板$ {{{\boldsymbol{z}} }_k} $将产生如下响应矩阵$ {{\boldsymbol{L}}_k} $：

(2)$ {{\boldsymbol{L}}_k} = {F^{ - 1}}({F}({{\boldsymbol{K}}_{{{{{\boldsymbol{z}}}}_{\text{1}}}{{\boldsymbol{z}}_k}}}){F}({\boldsymbol{A}})) . $

式中：$ {{{\boldsymbol{z}} }_1} $为目标的初始模板；$ {F} $为傅里叶变换；$ {{\boldsymbol{A}}} $为权重；$ {{{K}}_{{{\boldsymbol{z}}_{\text{1}}}{{\boldsymbol{z}}_k}}} $为核函数，

(3)$ \begin{split} {{{K}}}_{{\boldsymbol{z}}_{\text{1}}{\boldsymbol{z}}_{k}}= \mathrm{exp}\left\{-\dfrac{1}{{\sigma }_{{\mathrm{g}}}^{2}}\left[\Vert {{\boldsymbol{z}}}_{1}{\Vert }^{2}+\Vert {{\boldsymbol{z}}}_{k}{\Vert }^{2} -2{F}^{-1}({F}^{*}({{\boldsymbol{z}}}_{1})F({{\boldsymbol{z}}}_{k}))\right]\right\}.\end{split} $

式中：${\sigma }_{{\mathrm{g}}} $为高斯函数标准差.

通常，目标外观变化是不可避免的，改变目标模板外观会导致能量扩散，因此提出利用多个KCF，以增强目标模板的多样性^[19]. MKCF利用峰值旁瓣比(peak to sidelobe ratio, PSR)来反映模板的变化，从而反映模板的可靠性.

假设在第k个时间步长中存在m个KCF模板$T_k^1,\cdots,T_k^m $，MKCF通过似然函数$ p({{T}}_k^{\text{1}},\cdots,{{T}}_k^{{m}}|{{\boldsymbol{x}}_k}) $最大化评估目标状态$ {{\boldsymbol{x}}_k} $. 由于每个KCF模板独立工作，融合似然定义为

(4)$ p\left( {{{T}}_k^{\text{1}},\cdots,{{T}}_k^{{m}}\mid {{\boldsymbol{x}}_k}} \right) \triangleq \prod\limits_{i = 1}^m p \left( {{{T}}_k^{{i}}\mid {{\boldsymbol{x}}_k}} \right) \triangleq \prod\limits_{i = 1}^m {{\boldsymbol{L}}_k^{{i}}} . \\ $

式中：$ {\boldsymbol{L}}_k^{{i}} $表示第i个KCF模板的响应，最大化融合似然函数，可以得到目标的最优位置估计$ {{\boldsymbol{\hat x}}_k} $,即

(5)$ {{\boldsymbol{\hat x}}_k} = \arg {{\mathrm{max}} _{{{{\boldsymbol{x}}}_k}}}\prod\limits_{{{i = 1}}}^{{m}} {{\boldsymbol{L}}_k^{{i}}} . $

分数阶傅里叶变换是傅里叶变换的一种扩展，它将信号从时域转换到分数阶域，分析信号的相关性和非平稳性^[20]. 分数阶傅里叶变换作为一种统一的时频变换，分数阶傅里叶变换随着阶数从0连续增长到1.0，展示出信号从时域逐步变化到频域的所有变化特征，为信号的时频分析提供更大的选择余地.

$ p $阶分数阶傅里叶变换的定义为

(6)$ \left.\begin{aligned} &{{{X}}_{{p}}}(u) = \int_{ - \infty }^{+\infty } {{{{K}}_{{p}}}} (u,\tilde t)x(t){\mathrm{d}}t,\\ &{{{K}}_{{p}}}(u,\tilde t) = {A_\alpha }{\text{exp}}\left[ {{\mathrm{j}}\text{π} ({u^2}{\text{cot}}\alpha - } {2ut\csc \alpha +{t^2}\cot \alpha )} \right] .\end{aligned}\right\}$

式中：$ {A_\alpha } = \sqrt {1 - {\mathrm{j}}\cot \alpha } ,\alpha = p\text{π} /2,p \ne 2n $，$ {{x}}{\text{(}}t{\text{)}} $为时域信号，$ {{{K}}_{{p}}}(u,\widetilde t) $为核函数.

当$ p = 4n $时，$ {{{K}}_{{p}}}(u,\tilde t) = {{\delta }}(u - t) $. 当$ p = 4n \pm 2 $时，$ {K_p}(u,\tilde t) = \delta (u+t) $. 令$ u = u/\sqrt {2\text{π} } $，$ t = t/\sqrt {2\text{π} } $，则式（6）可以表示为

(7)$ \begin{gathered} {{{X}}_{{p}}}(u) = {{{F}}^{{p}}}[x(t)] (u) = \int_{ - \infty }^{+\infty } {{{{K}}_{{p}}}} (u,t)x(t){\mathrm{d}}t = \\ \left\{ \begin{gathered} {B_\alpha }\int_{ - \infty }^{+\infty } {\exp } \left( {{\mathrm{j}}\frac{{{t^2}+{u^2}}}{2}\cot \alpha - \frac{{{\mathrm{j}}tu}}{{\sin \alpha }}} \right)x(t){\text{d}}t,\alpha \ne n\text{π} ; \\ x(t){\text{ }},\;\alpha = 2n\text{π}; \\ x( - t){\text{ }},\;\alpha = (2n \pm 1)\text{π}. \\ \end{gathered} \right. \\ \end{gathered} $

令$ p = 1 $，$ \alpha = \text{π} /2 $，$ {A_\alpha } = 1 $，则式（7）可以表示为

(8)$ {{{X}}_1}(u) = \int_{ - \infty }^{+\infty } {\exp }\left({ - {\text{j}}2\text{π} ut}\right){{x}}(t){\text{d}}t . $

可以看出，式（8）为傅里叶变换，$ {{{X}}_{ - 1}}(u) $为普通的傅里叶逆变换.

根据分数阶傅里叶变换的阶数可加性，可以用 $ - p $来替代$ p $，得到变换核函数的性质：

(9)$ \begin{split} {{{K}}_{{{-p}}}}(u,t) = {{K}}_{{p}}^{{\text{ −1}}}(u,t) = {{K}}_{{p}}^{\text{*}}(u,t) = {{K}}_{{p}}^{\text{*}}(t,u) = {{K}}_{{p}}^{\text{H}}(u,t). \end{split} $

对于分数阶傅里叶变换，仅考虑$ p $为0~1.0. 当$ p = 0 $时，分数阶傅里叶变换为原函数，当$ p = 1 $时，分数阶傅里叶变换为普通的傅里叶变换. 当$ p $从0变化到1.0时，分数阶从原函数变换到普通的傅里叶变换，分数阶傅里叶变换以连续的参数$ p $在原函数和对应的普通傅里叶变换之间变换.

通过对一维分数阶傅里叶变换的推广，可以扩展到更高维度的分数阶傅里叶变换，实现基于图像的二维分数阶傅里叶变换.

二维分数阶傅里叶变换可以用于信号增强、滤波和特征提取. 通过选择适当的分数阶参数，可以突出感兴趣的频域特性，同时抑制干扰成分. 二维连续分数阶傅里叶变换的核函数可以表示为

(10)$ {{\boldsymbol{X}}_{{{p_1,p_2}}}}(u,v) = \int_{ - \infty }^{+\infty } {\int_{ - \infty }^{+\infty } {{{\boldsymbol{x}}}} } (s,t){{{K}}_{{{p_1,p_2}}}}(s,t,u,v){{\mathrm{d}}s}{{\mathrm{d}}t} . $

式中：$ {\boldsymbol{x}}(s,t) $为原始的二维信号；$ {{{K}}_{{{p_1,p_2}}}}(s,t,u,v) $为二维的分数阶傅里叶变换的变换核，是二维可分离的核.

根据一维离散分数阶傅里叶变换的公式和二维连续分数阶傅里叶变换的核可分离性，定义基于二维的离散分数阶傅里叶变换：

(11)$ {\boldsymbol{X}}(m,n) = \sum\limits_{{{p=0}}}^{{{M-1}}} {\sum\limits_{{{q=0}}}^{{{N-1}}} {\boldsymbol{x}} } (p,q){{K}}(p,q,m,n) . $

由变换核函数的二维可分离性可知，二维的离散分数阶傅里叶变换可由分离的形式定义：

(12)$ {{{K}}_{{{p_1,p_2}}}} = {{{K}}_{{{p_1}}}} \otimes {{{K}}_{{{p_2}}}} . $

式中：$ {{{K}}_{{{p_1}}}} $和$ {{{K}}_{{{p_2}}}} $为一维离散分数阶傅里叶变换的变换核函数，单独分数阶次分别为$ {p_1} $、${p_2}$ .

提出算法引入分数阶傅里叶变换，将弱小目标从特征不明显的时域变换到幅值变化较明显的分数阶域，在分数阶域对弱小目标进行滤波降噪处理，减少杂波的干扰. 针对MKCF方法模板提取不鲁棒的问题，提出KCF模板优化提取方法，从新生目标及存活目标识别算法中得到存活目标集. 根据目标类型采用不同的模板提取方法，进行目标位置的预测融合，增强目标的跟踪精度. 此外，基于优化多核相关滤波提出检测前多帧跟踪方法，利用多帧信息累积目标航迹，提取疑似目标轨迹集合，得到目标最优航迹的估计.

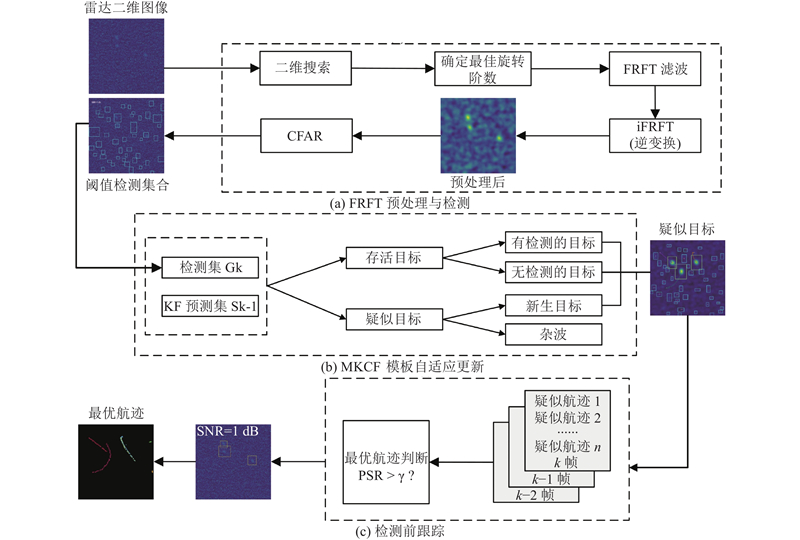
算法流程如图1所示. 对雷达二维图像进行分数阶傅里叶变换，确定最佳旋转阶数. 利用滤波进行去噪，应用恒虚警检测算法进行检测，得到目标的检测集合. 与上一帧跟踪结果的KF预测集合进行关联，以区分目标类型. 针对不同类型的目标进行相应的MKCF模板优化提取，将符合条件的目标加入疑似航迹中. 联合前3帧的航迹进行最优航迹判断.

在复杂环境下对雷达弱小运动目标进行检测与跟踪时，会出现由于信噪比过低无法检测出弱小目标的情况，对检测结果的准确度产生影响. 提出对动目标进行检测，利用二维分数阶傅里叶变换的特性对图像进行预处理，通过分数阶傅里叶变换寻找最佳旋转角度，对目标进行滤波降噪处理. 通过CFAR算法得到准确的目标信息，具体的算法流程如图1（a）所示.

基于离散的二维分数阶傅里叶变换能够保留分数阶傅里叶变换的性质. 提出算法利用分数阶傅里叶变换，对输入的雷达二维图像进行二维峰值搜索，通过图像的信噪比增益，确定相对最佳的旋转阶数. 在最佳旋转阶次下，对输入的雷达二维图像进行FRFT，同时进行低通滤波，过滤大部分噪声. 对滤波后的信号进行逆分数阶傅里叶变换，还原到时域，得到降噪后的雷达图像，达到杂波抑制的效果.

二维正向和反向的离散分数阶傅里叶变换分别表示为

(13)$ {{\boldsymbol{X}}_{(\alpha ,\,\,\beta )}}(m,n) = \sum\limits_{{{m = 0}}}^{{{M-1}}} {\sum\limits_{{{n = 0}}}^{{{N-1}}} {{{\boldsymbol{x}}}} } (p,q){{{K}}_{(\alpha ,\,\,\beta )}}(p,q,m,n), $

(14)$ {\boldsymbol{x}}(p,q) = \sum\limits_{{{m = 0}}}^{{{M-1}}} {\sum\limits_{{{n = 0}}}^{{{N-1}}} {{{\boldsymbol{X}}_{(\alpha ,\,\,\beta )}}} } (m,n){{{K}}_{( - \alpha , - \beta )}}(p,q,m,n). $

由FRFT的特性可知，在某一确定阶次，信号与噪声在分数阶傅里叶变换域不再耦合，可以通过滤波器来滤除噪声. 在实验过程中，信号与噪声可能无法通过单一的阶次实现完全解除耦合. 完全耦合信号与噪声是相对复杂的问题，可以通过调整分数阶参数及滤波操作解决. 提出算法通过分级迭代搜索方法搜索得到最佳阶数，实现对信号和噪声不同程度的调控.

利用分级迭代搜索方法搜索得到最佳旋转阶数，在多个层级上进行迭代搜索，有效地缩小搜索范围并提高搜索效率. 通过联合优化2个方向的阶次，可以考虑2个维度之间的相互作用和依赖，获得更精确的最优解.

在初始阶段，搜索在较大的范围和较粗的粒度上进行，以快速缩小可能的最优解区域. 每个后续的迭代在更细的粒度上进行探索，逐渐精确到最优解.

1）提出算法的旋转阶数的搜索范围为0~1.0，初始搜索步长为${{{k}}_1} = 0.1$，使用步长0.1在0~1.0进行FRFT，并进行二维搜索寻找峰值，得到初步的最佳阶数${\alpha _1}$、${\beta _1}$.

2）利用初次迭代的最佳阶数，计算二次迭代的搜索范围如下：

(15)$ \left. \begin{gathered} {{a}}_2^\alpha = {\alpha _1} - {{{k}}_1},\;{{b}}_2^\alpha = {\alpha _1}+{{{k}}_1} , \\ {{a}}_2^\beta = {\beta _1} - {{{k}}_1},\;{{b}}_2^\beta = {\beta _1}+{{{k}}_1}, \\ {{{k}}_2} = 0.1{{{k}}_1}. \\ \end{gathered} \right\} $

式中：$\alpha $取值为$ {{a}}_2^\alpha $~$ {{b}}_2^\alpha $，$\beta $取值为$ {{a}}_2^\beta $~$ {{b}}_2^\beta $，搜索步长$ {{{k}}_2} = 0.01 $，使用步长$ {{{k}}_2} $在搜索范围内进行FRFT，并进行二维搜索寻找峰值，得到二次迭代后的最佳旋转阶数${\alpha _2}$、${\beta _2}$.

3）重复步骤2），得到3次迭代后的最佳阶数${\alpha _3}$、${\beta _3}$. 利用最佳阶数对雷达图像进行FRFT滤波，并进行逆分数傅里叶变换，还原原始图像信息.

4）将利用FRFT处理后的雷达图像信号进行CFAR处理，得到检测出的目标集合.

针对弱小目标跟踪过程中，MKCF方法模板提取鲁棒性不强从而影响目标跟踪精度的问题，提出MKCF模板自适应更新方法，提出算法包括目标匹配与模板更新2个阶段. 提出算法将多个KCF的预测结果进行加权融合，得到MKCF的预测结果. 结合卡尔曼滤波进行目标匹配，关联目标的检测集合与预测集合，得到存活目标集合和疑似目标集合. 根据不同的目标类型，采取对应的MKCF模板，增强目标的跟踪精度，具体的算法流程如图1（b）所示.

提出算法通过目标匹配，将目标分类为存活目标、新生目标和杂波. 根据不同类型的目标，采取不同的模板更新策略，具体的目标匹配方法如下.

1）利用基于分数阶傅里叶变换的CFAR方法，对全局的目标进行检测，得到检测集$ {G_k} $. 对第$k - 1$帧的跟踪结果进行KF预测，得到预测结果$ {S_{k{{ - 1}}}} $.

2）关联检测集合$ {{{G}}_k} $和预测集合$ {{{S}}_{k{{ - 1}}}} $，利用下式判断集合中的目标类型：

(16)$ t_1 = (\Delta d({\boldsymbol{s}},{\boldsymbol{g}}) < {d_{{\text{th}}}}) \wedge (\Delta {\text{iou}}({\boldsymbol{s}},{\boldsymbol{g}}) > {\text{io}}{{\text{u}}_{{\mathrm{th}}}}).$

式中：$ {\boldsymbol{s}} $为目标的KF预测结果，$ {\boldsymbol{g}} $为目标的检测结果，$ \Delta d({\boldsymbol{s}},{\boldsymbol{g}}) $为欧氏距离，$ {d_{{\mathrm{th}}}} $为距离阈值，$ \Delta {\text{iou}}({\boldsymbol{s}},{\boldsymbol{g}}) $为交并比，$ {\text{io}}{{\text{u}}_{{\text{th}}}} $为交并比阈值.

当$ t_1 = 0 $时，判定当前目标为无检测的目标，说明当前目标周围的杂波强度较大，受到的干扰比较大. 当$ t_1 = 1 $时，判断当前目标为待检测的目标，说明当前目标周围的杂波强度较小，目标受到的干扰较小.

3）在从检测集中去除已经确认存活的目标后，剩余的目标集合被称为疑似目标集合. 这些疑似目标可能是新生目标、误检、噪声或其他非目标物体，因此需要进一步的关联和验证. 通过下式关联上一时刻与当前时刻的疑似目标：

(17)$ t_2 = (\Delta d({\boldsymbol{s}},{\boldsymbol{g}}) < {d_{{\mathrm{th}}}}) . $

当$ t_2 = 1 $时，判定当前目标为新生目标，说明该目标在之前的时刻未被检测到，但在当前时刻首次出现在检测集中. 此外，集合中剩余的目标判定为杂波. 由于新生目标可能存在误检或不确定性，提出算法不会立即将其视为可靠的目标，会采用检测前跟踪算法，通过累计多帧信息进一步确认.

提出算法根据目标匹配策略，将目标分类为无检测的存活目标、带检测的存活目标、新生目标和杂波. 分别采用不同的模板更新策略，进行有效的目标跟踪和监测. 这不仅有助于提高算法的准确性和效率，还能够为实际应用提供更加可靠和有用的信息. 具体的模板自适应更新策略如下.

1）对于无检测的存活目标，说明当前该目标周围的杂波强度较大，受到的干扰较多，可能是多种原因造成的，比如背景噪声或其他非目标物体的影响. 利用下式更新模板：

(18)$ {\boldsymbol{\hat b}} = \frac{{\displaystyle\sum\nolimits_{{{i = 1}}}^{{M}} {{{\boldsymbol{b}}_i}y_i^\prime } }}{{\displaystyle\sum\nolimits_{{{i = 1}}}^{{M}} {y_i^\prime } }} = \sum\limits_{{{i = 1}}}^{{M}} {({a_{{i}}}{{\boldsymbol{b}}_{{i}}})} . $

式中：$ {\boldsymbol{b}}{\text{ = }}[c_x,c_y,c_{\mathrm{w}},c_{\mathrm{h}}] $，其中$ c_x $和$ c_y $为目标的中心位置，$ c_{\mathrm{w}} $和$ c_{\mathrm{h}} $为目标框的长和宽；$ {y_{{i}}} $为第i个KCF的预测结果；$ M $为KCF模板的数量；$ {a_{{i}}} $为每个KCF模板的归一化权重.

2）对于已经检测到的存活目标，说明当前目标周围的杂波强度较小，目标信号受到的干扰小. 利用下式融合检测框与KCF预测框的结果，得到目标预测结果，旨在结合两者的优势，有效减少单一方法可能带来的误差，提高目标跟踪的稳定性和准确性，得到更准确的目标预测结果.

(19)$ {\boldsymbol{\theta }} = ({\boldsymbol{b}}+{\boldsymbol{g}})/2 . $

3）对于新生目标，利用下式计算新生目标预测结果：

(20)$ {\boldsymbol{\theta}} = ({\boldsymbol{b}}+{\boldsymbol{s}})/2 . $

将该目标加入目标航迹中，以便后续进行持续跟踪和监测. 提出算法不会立即将新生目标视为可靠的目标，会采用检测前跟踪算法，通过累计多帧信息，进一步验证和确认该新生目标的真实性和轨迹.

针对强海杂波使算法误将杂波认作目标，导致错误的检测和跟踪，对算法性能造成严重干扰的问题，利用目标在帧间的运动相关性，对多帧数据进行目标信号积累，对杂波进行有效地抑制，以有效地积累目标航迹能量. 具体的算法流程见图1（c）.

假设目标可能的轨迹为

(21)$ {{f}}{{{(t)}}_{{T}}}=\left\{{{\boldsymbol{l}}_{\text{1}}}{\text{,}}\;{{\boldsymbol{l}}_{\text{2}}}{\text{,}}\;\cdots{\text{,}}\;{{\boldsymbol{l}}_{{n}}}\right\} . $

式中：$ {{f}}{(t)_{{T}}} $为目标在经过T帧后的航迹估计，$ n $为疑似航迹的数目，$ {{\boldsymbol{l}}_{{i}}} $为所有疑似航迹中的一条航迹.

假设目标的位置向量为$ {\boldsymbol{h}} $，采用n个KCF模板进行预测，获得预测值. 将位置向量$ {\boldsymbol{h}} $作为目标单个模板预测位置的中心，可以似然表示为$ p({{\boldsymbol{\hat h}}_\iota }|{\boldsymbol{h}}) $. 由于每个模板的观测值是独立的，将超过阈值的预测值作为目标的一条航迹：

(22)$ {{f}}{({\boldsymbol{h}})_{{T}}} = \{ {{\boldsymbol{\hat h}}_\iota }\} _{{{t = 1}}}^{{n}} = \left\{{{\boldsymbol{l}}_1},{{\boldsymbol{l}}_2},\cdots,{{\boldsymbol{l}}_{{n}}}\right\} . $

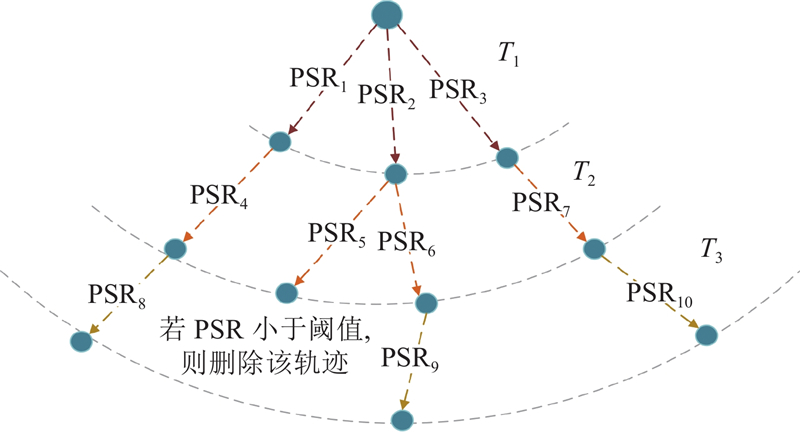
跟踪目标的每条疑似航迹的得分为

(23)$ \begin{split} \Delta {{\boldsymbol{s}}_{{t}}} = &g({{f}}{({\boldsymbol{h}})_{{T}}}) = g({{\boldsymbol{l}}_1},{{\boldsymbol{l}}_2},\cdots,{{\boldsymbol{l}}_{{n}}}) = \\ &[{\text{PS}}{{\text{R}}_1},{\text{PS}}{{\text{R}}_2},\cdots,{\text{PS}}{{\text{R}}_{{n}}}] .\end{split}$

式中：$ \Delta {{\boldsymbol{s}}_{{t}}} $为每条航迹的分数，$ g({{f}}{({\boldsymbol{h}})_{{T}}}) $为对每条航迹计算分数的函数，$ {{\mathrm{PSR}}_{{i}}} $为其中一条航迹的分数.

将高PSR值与高IOU值的检测框初始化为新的KCF模板，同时将该PSR值加入该航迹的总PSR值中.

如图2所示，$ T_1 $、$ T_2 $、$ T_3 $表示时间间隔，设定为1帧. 目标在上一时刻拥有3个KCF模板，在$ T_1 $时刻，目标拥有3个满足PSR条件的预测结果. 在$ T_2 $时刻，目标存在4个满足PSR条件的预测结果. 在 $ T_3 $时刻，目标存在3个满足PSR条件的预测结果，若有一个预测结果不满足阈值条件，则删除该航迹. 选取最大PSR值的航迹作为最优航迹估计.

为了验证提出算法的有效性，对提出算法的性能进行研究，在模拟海杂波数据中与几种相关算法进行详细的比较.

1）有效轨迹的均方根误差（root mean square error, RMSE）：有效轨迹与真实轨迹的平均差.

2）交并集精度（intersection-over-union, IOU）：$ {\mathrm{IOU}} = ({\boldsymbol{E}} \cap {\boldsymbol{G}})/({\boldsymbol{E}} \cup {\boldsymbol{G}}) $，IOU越大，效果越好，其中$ {\boldsymbol{E}} $和$ {\boldsymbol{G}} $分别为目标的预测框与真实框.

3）轨迹命中率（rate of hit, ROH）：所有轨迹中正确轨迹所占的百分比.

4）轨迹碎片数量（number of trajectory fragments, NTF）：组成一条真实轨迹的子轨迹数量. NTF=1为最好的结果. NTF越大，结果越差.

5）检测概率（probability of detection, PD）：目标检测框与目标真实框的重叠部分和目标真实框的比值.

6）跟踪精度（precision rate, PR）：目标跟踪轨迹中正样本和真实轨迹的比值.

实验在k分布^[21-22]的海杂波仿真场景中进行，采取与文献[16]相同的信噪比模型和目标能量模型. 名为Victor、Amelia和Urich的3种波动目标根据不同的运行模型，分别进行匀速运动、匀加速运动和匀转弯运动.

如图3所示为不同信噪比的仿真场景及目标的真实运动轨迹，如表1所示为3种目标的具体运动参数. 实验在$\alpha = 0.15$，$\beta = 0.20$，${\text{PSR}} = 8$的条件下进行，仿真场景的SNR为1~12 dB. 仿真场景中杂波的显著增加导致目标信号逐渐淹没，使得在背景噪声中有效地识别和跟踪目标变得异常困难. 在这种环境下，目标轨迹的清晰性逐渐丧失，在目标跟踪过程中容易产生误差.

针对分数阶傅里叶变换的阈值检测算法进行实验，与基于CFAR的优化多核相关滤波检测前跟踪算法、基于傅里叶变换的优化多核相关滤波检测前跟踪算法进行对比，跟踪结果如表2所示. 表中，MIOU为平均交并比.

基于FRFT的算法的整体跟踪性能优于其他算法. 由于提出算法引入FRFT滤波，有效增强了目标与海杂波的差异，有利于抑制杂波信号. 基于CFAR的算法对杂波的抑制作用较低，会出现大量的虚假轨迹. 基于FFT的预处理方法采用二维傅里叶转换的阈值检测法，可以降低部分杂波干扰，虽然有一定的杂波抑制效果，但是最终的跟踪性能不如提出算法使用的基于分数阶傅里叶变换的杂波抑制方法.

为了验证提出算法在低信噪比环境下的有效性，与基于多核相关滤波的检测前跟踪算法（MKCF-TBD）^[16]、基于卡尔曼滤波的检测前跟踪算法（KF-TBD）^[23]进行对比，结果如表3、4所示. 表3给出跟踪目标的平均交并比、轨迹命中率、轨迹碎片数量的对比结果. 表4给出优化算法与其他算法的均方根误差RMSE的跟踪结果. 采用MKCF-TBD和KF-TBD的方法在针对杂波干扰强的场景下，预测结果偏差较大. 采用优化的MKCF模板预测方法，融合目标KCF预测框和检测框作为最终的跟踪结果，这种融合策略有效提高了跟踪的准确性. 尤其是在存在杂波干扰的复杂环境中，这种融合方法使得跟踪算法能够有效区分目标与干扰杂波，维持跟踪. 在目标被杂波干扰的情况下，能够稳定地跟踪目标，实现动态变化环境下的稳定跟踪.

为了验证在不同的杂波干扰强度下提出算法的有效性，分别在SNR=1、3、5 dB的仿真数据上进行实验. 可以看出，随着SNR的逐渐降低，杂波和噪声的干扰相对增强，使得目标的运动轨迹变得越来越模糊. 图4给出提出算法的跟踪轨迹结果对比. 表5给出在不同信噪比场景下的RMSE对比结果.

从表5可以看出，杂波干扰越来越强，基于分数阶傅里叶变换的检测算法能够抑制杂波，有效跟踪目标. 提出的模板自适应更新方法由于融合目标KCF预测框和检测框作为最终的跟踪结果，使得跟踪算法能够有效区分目标与周围环境中的干扰，维持对目标的持续跟踪. 实验结果表明，提出算法在复杂环境中具有较强的鲁棒性和稳定性. 它能够在强杂波干扰下实现对目标的精确跟踪. 该算法在不同SNR场景下的表现证明其具有广泛的适用性和灵活性.

为了验证在不同的PSR下提出算法的有效性，在SNR=3 dB的仿真数据上进行实验，表6给出提出算法的跟踪结果. 可以看出，当PSR = 8时，提出算法表现出较其他算法更加准确的跟踪能力，这表明提出算法在该条件下对目标的估计与实际情况的偏差最小. 当PSR降至6时，算法性能表现有所下降，这是由于较低的PSR意味着更多的虚假轨迹，影响了算法对目标信号的识别与跟踪准确性. 此外，当PSR = 10时，过高的PSR导致算法在一定程度上可能过滤掉目标部分的真实轨迹，造成跟踪性能的降低.

针对提出算法，对提出算法与其他方法的跟踪性能进行评估，对比方法如下.

MM-PF-TBD^[24]: 基于多模型的弱机动目标联合检测和跟踪方法，使用贝叶斯理论推导提出基于MM的方法.

SiamMT^[25]：基于孪生网络的多目标跟踪方法. SiamMT将单独的视觉跟踪技术以高效的方式应用于多个对象.

RNNMOT^[26]：基于循环神经网络和目标外观模型的算法.

MSAR-TBD^[11]：两阶段的检测前多帧跟踪算法，对帧上的平方振幅积分进行检测.

WTSA-TBD^[27]：将加权平方振幅作为区别目标与杂波的主要指标，进行弱小目标的检测.

MKCF-TBD^[16]：基于多核相关滤波的检测前跟踪算法，用于海洋环境中的弱小目标跟踪.

如表7所示为提出算法与其他方法在3个跟踪目标上的均方根误差对比结果. 表中，加粗的字体表示最优结果. 如表7所示，提出算法的RMSE显著低于其他方法，验证了其在雷达弱小目标位置估计方面具有更高的精度.

表8给出7种算法的虚警率PFA、检测概率、跟踪精度、平均交并比、轨迹命中率、轨迹碎片率对比结果. 可以看出，提出算法的检测概率为0.55，跟踪精度为0.97，优于其他方法，且交并比高于其他算法，轨迹碎片数量有所降低，虚警率低于其他方法. 这是由于引入的分数阶傅里叶变换增强了目标与杂波的差异，对杂波的抑制效果显著，能够提升检测概率，降低虚警率与最终的目标轨迹碎片率. 此外，改进的模板自适应更新策略与检测前跟踪结合的算法对目标干扰和运动变化的适应性较强，减少了目标漏跟的情况，因此在目标跟踪精度和轨道命中率上有明显提升.

SiamMT和RNN-MOT分别是基于卷积神经网络和循环神经网络的目标跟踪方法，二者在均方根误差对比和性能对比上表现相对不佳. 这主要是由于虽然深度学习方法在雷达弱小目标跟踪领域已经得到了广泛的应用，但深度学习模型的效果很大程度上依赖于训练数据的覆盖范围和质量. 雷达数据通常包含与距离、速度、角度相关的信息. SiamMT和RNN-MOT侧重于视觉特征，这种差异导致模型在雷达数据上的表现不佳.

MSAR-TBD 和 WTSA-TBD 专注于检测前跟踪的方法，将振幅强度作为区别目标与杂波的指标，无法反映目标的变化特征，在后续的跟踪精度上不如提出算法. MKCF-TBD没有对强杂波进行抑制，且模板提取方法单一，无法适应复杂的跟踪场景，因此各方面的性能比提出算法差.

提出算法利用FRFT进行降噪处理，使用MKCF模板自适应更新方法，并结合检测前跟踪算法，相较于其他算法，准确性和稳健性更高. 这种综合性的跟踪策略不仅能够提高目标跟踪的精确度，而且能够增强在各种复杂场景中的适应能力，确保更可靠的跟踪结果.