[1]
KALOGERAKIS E, HERTZMANN A, SINGH K Learning 3D mesh segmentation and labeling
[J]. ACM Transactions on Graphics , 2010 , 29 (4 ): 102
[本文引用: 3]
[4]
WANG Y, GONG M, WANG T, et al Projective analysis for 3D shape segmentation
[J]. ACM Transactions on Graphics , 2013 , 32 (6 ): 192
[本文引用: 1]
[5]
GUO K, ZOU D, CHEN X 3D mesh labeling via deep convolutional neural networks
[J]. ACM Transactions on Graphics , 2015 , 35 (1 ): 3
[本文引用: 4]
[6]
GEORGE D, XIE X, TAM G K 3D mesh segmentation via multi-branch 1D convolutional neural networks
[J]. Graphical Models , 2018 , 96 : 1 - 10
DOI:10.1016/j.gmod.2018.01.001
[本文引用: 4]
[7]
XIE Z, XU K, SHAN W, et al Projective feature learning for 3D shapes with multi-view depth images
[J]. Computer Graphics Forum , 2015 , 34 (7 ): 1 - 11
DOI:10.1111/cgf.12740
[本文引用: 1]
[8]
KALOGERAKIS E, AVERKIOU M, MAJI S, et al. 3D shape segmentation with projective convolutional networks [C]// Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 6630-6639.
[本文引用: 3]
[9]
KUNDU A, YIN X, FATHI A, et al. Virtual multi-view fusion for 3D semantic segmentation [C]// Proceedings of the European Conference on Computer Vision . Glasgow: Springer, 2020: 518-535.
[本文引用: 1]
[10]
WANG P, LIU Y, GUO Y, et al O-CNN: octree-based convolutional neural networks for 3D shape analysis
[J]. ACM Transactions on Graphics , 2017 , 36 (4 ): 72
[本文引用: 1]
[11]
WANG Z, LU F VoxSegNet: volumetric CNNs for semantic part segmentation of 3D shapes
[J]. IEEE Transactions on Visualization and Computer Graphics , 2020 , 26 (9 ): 2919 - 2930
DOI:10.1109/TVCG.2019.2896310
[本文引用: 1]
[12]
HU Z, BAI X, SHANG J, et al. VMNet: voxel-mesh network for geodesic-aware 3D semantic segmentation [C]// Proceedings of the IEEE International Conference on Computer Vision . Venice: IEEE, 2021: 15468-15478.
[本文引用: 1]
[13]
XU H, DONG M, ZHONG Z. Directionally convolutional networks for 3D shape segmentation [C]// Proceedings of the IEEE International Conference on Computer Vision . Venice: IEEE, 2017: 2717-2726.
[本文引用: 1]
[14]
HUANG J, ZHANG H, YI L, et al. TextureNet: consistent local parametrizations for learning from high-resolution signals on meshes [C]// Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition . Long Beach: IEEE, 2019: 4440-4449.
[本文引用: 1]
[15]
FENG Y, FENG Y, YOU H, et al. MeshNet: mesh neural network for 3D shape representation [C]// Proceedings of the AAAI Conference on Artificial Intelligence . Palo Alto: AAAI Press, 2019: 8279-8286.
[本文引用: 1]
[16]
HANOCKA R, HERTZ A, FISH N, et al MeshCNN: a network with edge
[J]. ACM Transactions on Graphics , 2019 , 38 (4 ): 90
[本文引用: 1]
[17]
HU S, LIU Z, GUO M, et al Subdivision-based mesh convolution networks
[J]. ACM Transactions on Graphics , 2022 , 41 (3 ): 25
[本文引用: 1]
[18]
PÉREZ D, SHEN Y, LI J Mesh convolutional networks with face and vertex feature operators
[J]. IEEE Transactions on Visualization and Computer Graphics , 2023 , 29 (3 ): 1678 - 1690
DOI:10.1109/TVCG.2021.3129156
[本文引用: 1]
[19]
LAHAV A, TAL A MeshWalker: deep mesh understanding by random walks
[J]. ACM Transactions on Graphics , 2020 , 39 (6 ): 263
[本文引用: 1]
[20]
SHARP N, ATTAIKI S, CRANE K, et al DiffusionNet: discretization agnostic learning on surfaces
[J]. ACM Transactions on Graphics , 2022 , 41 (3 ): 27
[本文引用: 1]
[21]
QIAO Y, GAO L, YANG J, et al Learning on 3D meshes with Laplacian encoding and pooling
[J]. IEEE Transactions on Visualization and Computer Graphics , 2022 , 28 (2 ): 1317 - 1327
DOI:10.1109/TVCG.2020.3014449
[本文引用: 1]
[22]
DONG Q, WANG Z, LI M, et al Laplacian2Mesh: Laplacian-based mesh understanding
[J]. IEEE Transactions on Visualization and Computer Graphics , 2023 , 30 (7 ): 4349 - 4361
[本文引用: 1]
[23]
WONG C. Heat diffusion based multi-scale and geometric structure-aware transformer for mesh segmentation [C]// Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition . Vancouver: IEEE, 2023: 4413-4422.
[本文引用: 1]
[24]
YI L, SU H, GUO X, et al. SyncSpecCNN: synchronized spectral CNN for 3D shape segmentation [C]// Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition . Honolulu: IEEE, 2017: 6584-6592.
[本文引用: 1]
[25]
SCHULT J, ENGELMANN F, KONTOGIANNI T, et al. DualConvMesh-net: joint geodesic and Euclidean convolutions on 3D meshes [C]// Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition . Seattle: IEEE, 2020: 8609-8619.
[本文引用: 1]
[26]
LI X, YANG J, ZHANG F. Laplacian mesh transformer: dual attention and topology aware network for 3D mesh classification and segmentation [C]// Proceedings of the European Conference on Computer Vision . Tel Aviv: Springer, 2022: 541-560.
[本文引用: 1]
[27]
ROY B. Neural shape diameter function for efficient mesh segmentation [C]// Proceedings of ACM SIGGRAPH Annual Conference Posters . Los Angeles: ACM, 2023.
[本文引用: 1]
[28]
XU X, LIU C, ZHENG Y 3D tooth segmentation and labeling using deep convolutional neural networks
[J]. IEEE Transactions on Visualization and Computer Graphics , 2019 , 25 (7 ): 2336 - 2348
DOI:10.1109/TVCG.2018.2839685
[本文引用: 2]
[29]
LI Y, HE X, JIANG Y, et al MeshFormer: high-resolution mesh segmentation with graph transformer
[J]. Computer Graphics Forum , 2022 , 41 (7 ): 38 - 49
[本文引用: 2]
[31]
SHU Z, SHEN X, XIN S, et al Scribble-based 3D shape segmentation via weakly-supervised learning
[J]. IEEE Transactions on Visualization and Computer Graphics , 2020 , 26 (8 ): 2671 - 2682
DOI:10.1109/TVCG.2019.2892076
[本文引用: 1]
[32]
SHU Z, YANG S, WU H, et al 3D shape segmentation using soft density peak clustering and semi-supervised learning
[J]. Computer-Aided Design , 2022 , 145 : 103181
DOI:10.1016/j.cad.2021.103181
[本文引用: 1]
[33]
SHU Z, QI C, XIN S, et al Unsupervised 3D shape segmentation and co-segmentation via deep learning
[J]. Computer-Aided Geometric Design , 2016 , 43 : 39 - 52
DOI:10.1016/j.cagd.2016.02.015
[本文引用: 1]
[34]
LIANG Y, ZHAO S, YU B, et al. MeshMAE: masked autoencoders for 3D mesh data analysis [C]// Proceedings of the European Conference on Computer Vision . Tel Aviv: Springer, 2022: 37-54.
[本文引用: 1]
[35]
JIAO X, CHEN Y, YANG X SCMS-Net: self-supervised clustering-based 3D meshes segmentation network
[J]. Computer-Aided Design , 2023 , 160 : 103512
DOI:10.1016/j.cad.2023.103512
[本文引用: 1]
[36]
LOUKAS A Graph reduction with spectral and cut guarantees
[J]. Journal of Machine Learning Research , 2019 , 20 (116 ): 1 - 42
[本文引用: 4]
[37]
ZHANG Z, LIU Q, HU Q, et al. Hierarchical graph transformer with adaptive node sampling [C]// Proceedings of the Conference on Neural Information Proceeding Systems . New Orleans: MIT Press, 2022, 35: 21171-21183.
[本文引用: 1]
[38]
WU L, HOU Y, XU J, et al Robust mesh segmentation using feature-aware region fusion
[J]. Sensor , 2023 , 23 (1 ): 416
[本文引用: 1]
[39]
SHAPIRA L, SHAMIR A, COHEN-OR D Consistent mesh partitioning and skeletonisation using the shape diameter function
[J]. The Visual Computer , 2008 , 24 (4 ): 249 - 259
DOI:10.1007/s00371-007-0197-5
[本文引用: 1]
[40]
BEN-CHEN M, GOTSMAN C. Characterizing shape using conformal factors [C]// Proceedings of the Eurographics Conference on 3D Object Retrieval . Crete: Springer, 2008: 1-8.
[本文引用: 1]
[41]
SUN J, OVSJANIKOV M, GUIBAS L A concise and provably informative multi-scale signature based on heat diffusion
[J]. Computer Graphics Forum , 2009 , 28 (5 ): 1383 - 1392
DOI:10.1111/j.1467-8659.2009.01515.x
[本文引用: 1]
[42]
CHEN X, GOLOVINSKIY A, FUNKHOUSER T A benchmark for 3D mesh segmentation
[J]. ACM Transactions on Graphics , 2009 , 28 (3 ): 73
[本文引用: 1]
[43]
GEORGE D, XIE X, LAI Y, et al A deep learning driven active framework for segmentation of large 3D shape collections
[J]. Computer-Aided Design , 2022 , 144 : 103179
DOI:10.1016/j.cad.2021.103179
[本文引用: 3]
Learning 3D mesh segmentation and labeling
3
2010
... 随着机器学习的发展,越来越多的工作将数据驱动的方法引入三维网格分割问题. Kalogerakis等[1 ] 通过条件随机场进行建模,以衡量面片和标签的一致性. Benhabiles等[2 ] 利用Adaboost分类器获取分割边界. Hu等[3 ] 提出共分割方法,将网格分割转换为聚类问题来实现. Wang等[4 ] 将网格模型进行多视角投影,在已标记的图像中检索并实现标签转化,将标签映射回网格表面. ...
... 除了视觉效果,还通过定量实验将本文算法与经典算法[1 , 5 -6 , 8 , 43 ] 进行分割准确率的比较. 不同算法在PSB数据集上各个类别的分割准确率P seg 和平均准确率如表1 所示. 可以看出,在大多数类别上,本文所取得的准确率高于其他算法,平均准确率比文献[5 , 43 ]的结果高3.3%. 对于一些较难学习的类别,比如Bird、Fourleg、Vase,由于这些模型的形态差异很大且分割边界不显著,除了1DCNN[6 ] 在Bird上的准确率为91.0%,其他算法在这3个类别上的准确率都低于90%. 本文算法分别取得了97.8%、90.9%和97.4%的准确率,远远超过其他算法. ...
... Comparison of segmentation accuracy on PSB dataset
% Tab.1 模型 P seg Shape[1 ] TOG[5 ] Shape [8 ] 1D[6 ] DL [43 ] 本文 Human 86.8 91.2 94.5 90.6 90.7 94.7 Cup 94.0 99.7 93.8 94.5 98.1 99.6 Glasses 96.9 97.6 96.6 96.3 98.1 98.9 Airplane 96.1 96.7 93.0 95.9 95.2 97.6 Ant 98.7 98.8 98.6 98.7 98.8 99.0 Chair 98.1 98.7 98.5 97.7 97.6 99.0 Octopus 98.2 98.8 98.3 98.5 98.7 99.1 Table 99.4 99.6 99.5 99.6 99.0 99.4 Teddy 98.7 98.2 97.7 88.3 98.6 98.1 Plier 95.2 96.2 95.5 95.8 95.3 97.3 Fish 95.7 95.6 96.0 96.5 96.4 98.3 Bird 89.6 88.3 88.5 91.0 88.6 97.8 Armadillo 92.6 92.3 92.8 93.3 95.0 93.8 Fourleg 83.3 87.0 85.0 87.7 84.6 90.9 Vase 81.7 77.8 86.8 81.9 82.9 97.4 平均值 93.7 94.1 93.7 93.6 94.1 97.4
3.3. 消融实验 组成本文分割框架的关键之处主要有2个:边缘保持的粗化算法、结合Graph Transformer和GCN的GTG模块. 为了证明它们的有效性,在6类网格模型上开展4组消融实验. 消融实验的结果如表2 所示. 其中GTra指神经网络中只使用Graph Transformer模块,没有引入GCN模块;GTG指本文提出的GTG模块. 第2列是基础的分割框架,利用原粗化算法生成多尺度特征,且只使用Graph Transformer模块. 第3列在基础分割框架上,探究GTG模块对结果的影响,即利用原粗化算法生成多尺度特征,且使用本文提出的GTG模块. 第4列在基础分割的框架上,探究边缘保持的粗化算法对结果的影响,即利用本文边缘保持的粗化算法生成多尺度特征,且使用Graph Transformer模块. 第5列是本文最终的分割框架,同时使用边缘保持的粗化算法和GTG模块. ...
Learning boundary edges for 3D-mesh segmentation
1
2011
... 随着机器学习的发展,越来越多的工作将数据驱动的方法引入三维网格分割问题. Kalogerakis等[1 ] 通过条件随机场进行建模,以衡量面片和标签的一致性. Benhabiles等[2 ] 利用Adaboost分类器获取分割边界. Hu等[3 ] 提出共分割方法,将网格分割转换为聚类问题来实现. Wang等[4 ] 将网格模型进行多视角投影,在已标记的图像中检索并实现标签转化,将标签映射回网格表面. ...
Co-segmentation of 3D shapes via subspace clustering
1
2012
... 随着机器学习的发展,越来越多的工作将数据驱动的方法引入三维网格分割问题. Kalogerakis等[1 ] 通过条件随机场进行建模,以衡量面片和标签的一致性. Benhabiles等[2 ] 利用Adaboost分类器获取分割边界. Hu等[3 ] 提出共分割方法,将网格分割转换为聚类问题来实现. Wang等[4 ] 将网格模型进行多视角投影,在已标记的图像中检索并实现标签转化,将标签映射回网格表面. ...
Projective analysis for 3D shape segmentation
1
2013
... 随着机器学习的发展,越来越多的工作将数据驱动的方法引入三维网格分割问题. Kalogerakis等[1 ] 通过条件随机场进行建模,以衡量面片和标签的一致性. Benhabiles等[2 ] 利用Adaboost分类器获取分割边界. Hu等[3 ] 提出共分割方法,将网格分割转换为聚类问题来实现. Wang等[4 ] 将网格模型进行多视角投影,在已标记的图像中检索并实现标签转化,将标签映射回网格表面. ...
3D mesh labeling via deep convolutional neural networks
4
2015
... 由于硬件的提升和数据规模的增长,神经网络被广泛地应用在三维网格分割问题中. 相较于传统的机器学习方法,神经网络具有更强的表征能力. 鉴于网格模型不规则采样的特性,有些方法采用重采样策略进行分割. Guo等[5 ] 将网格模型的特征重组成二维矩阵,再输入卷积神经网络,建立面片特征和标签之间的关系. George等[6 ] 认为将卷积作用在二维矩阵上,可能会在不相关特征之间产生关联,所以将网格模型的特征重组成一维向量. Xie等[7 ] 对网格模型进行多视角投影,通过多视角的深度极限学习机在不同视角的深度图之间共享权值,为面片赋标签. Kalogerakis等[8 ] 提出端到端的分割框架,先将网格模型的多视角渲染图和深度图输入全卷积神经网络,再将获得的置信度映射回网格表面,实现分割. Kundu等[9 ] 将从多视角虚拟图中提取的特征融合到三维网格,实现网格模型的分割. 此外,可以利用体素化的方法进行重采样. Wang等[10 ] 利用八叉树将网格模型转换为体素形式,将叶子节点的平均法向量输入3D卷积神经网络,实现分割. Wang等[11 ] 设计体素卷积神经网络,通过构造特征提取模块和注意力特征聚合模块来提取网格特征. Hu等[12 ] 指出仅依赖体素的方法会忽略网格模型的测地线信息,提出结合体素和网格模型的自编码器框架.将体素中提取的欧几里得信息输入编码器以提取长距离特征,在解码器中将它和网格中提取的测地线信息进行自适应地融合,提高了神经网络对网格模型的几何信息的利用. ...
... 除了视觉效果,还通过定量实验将本文算法与经典算法[1 , 5 -6 , 8 , 43 ] 进行分割准确率的比较. 不同算法在PSB数据集上各个类别的分割准确率P seg 和平均准确率如表1 所示. 可以看出,在大多数类别上,本文所取得的准确率高于其他算法,平均准确率比文献[5 , 43 ]的结果高3.3%. 对于一些较难学习的类别,比如Bird、Fourleg、Vase,由于这些模型的形态差异很大且分割边界不显著,除了1DCNN[6 ] 在Bird上的准确率为91.0%,其他算法在这3个类别上的准确率都低于90%. 本文算法分别取得了97.8%、90.9%和97.4%的准确率,远远超过其他算法. ...
... 所示. 可以看出,在大多数类别上,本文所取得的准确率高于其他算法,平均准确率比文献[5 , 43 ]的结果高3.3%. 对于一些较难学习的类别,比如Bird、Fourleg、Vase,由于这些模型的形态差异很大且分割边界不显著,除了1DCNN[6 ] 在Bird上的准确率为91.0%,其他算法在这3个类别上的准确率都低于90%. 本文算法分别取得了97.8%、90.9%和97.4%的准确率,远远超过其他算法. ...
... Comparison of segmentation accuracy on PSB dataset
% Tab.1 模型 P seg Shape[1 ] TOG[5 ] Shape [8 ] 1D[6 ] DL [43 ] 本文 Human 86.8 91.2 94.5 90.6 90.7 94.7 Cup 94.0 99.7 93.8 94.5 98.1 99.6 Glasses 96.9 97.6 96.6 96.3 98.1 98.9 Airplane 96.1 96.7 93.0 95.9 95.2 97.6 Ant 98.7 98.8 98.6 98.7 98.8 99.0 Chair 98.1 98.7 98.5 97.7 97.6 99.0 Octopus 98.2 98.8 98.3 98.5 98.7 99.1 Table 99.4 99.6 99.5 99.6 99.0 99.4 Teddy 98.7 98.2 97.7 88.3 98.6 98.1 Plier 95.2 96.2 95.5 95.8 95.3 97.3 Fish 95.7 95.6 96.0 96.5 96.4 98.3 Bird 89.6 88.3 88.5 91.0 88.6 97.8 Armadillo 92.6 92.3 92.8 93.3 95.0 93.8 Fourleg 83.3 87.0 85.0 87.7 84.6 90.9 Vase 81.7 77.8 86.8 81.9 82.9 97.4 平均值 93.7 94.1 93.7 93.6 94.1 97.4
3.3. 消融实验 组成本文分割框架的关键之处主要有2个:边缘保持的粗化算法、结合Graph Transformer和GCN的GTG模块. 为了证明它们的有效性,在6类网格模型上开展4组消融实验. 消融实验的结果如表2 所示. 其中GTra指神经网络中只使用Graph Transformer模块,没有引入GCN模块;GTG指本文提出的GTG模块. 第2列是基础的分割框架,利用原粗化算法生成多尺度特征,且只使用Graph Transformer模块. 第3列在基础分割框架上,探究GTG模块对结果的影响,即利用原粗化算法生成多尺度特征,且使用本文提出的GTG模块. 第4列在基础分割的框架上,探究边缘保持的粗化算法对结果的影响,即利用本文边缘保持的粗化算法生成多尺度特征,且使用Graph Transformer模块. 第5列是本文最终的分割框架,同时使用边缘保持的粗化算法和GTG模块. ...
3D mesh segmentation via multi-branch 1D convolutional neural networks
4
2018
... 由于硬件的提升和数据规模的增长,神经网络被广泛地应用在三维网格分割问题中. 相较于传统的机器学习方法,神经网络具有更强的表征能力. 鉴于网格模型不规则采样的特性,有些方法采用重采样策略进行分割. Guo等[5 ] 将网格模型的特征重组成二维矩阵,再输入卷积神经网络,建立面片特征和标签之间的关系. George等[6 ] 认为将卷积作用在二维矩阵上,可能会在不相关特征之间产生关联,所以将网格模型的特征重组成一维向量. Xie等[7 ] 对网格模型进行多视角投影,通过多视角的深度极限学习机在不同视角的深度图之间共享权值,为面片赋标签. Kalogerakis等[8 ] 提出端到端的分割框架,先将网格模型的多视角渲染图和深度图输入全卷积神经网络,再将获得的置信度映射回网格表面,实现分割. Kundu等[9 ] 将从多视角虚拟图中提取的特征融合到三维网格,实现网格模型的分割. 此外,可以利用体素化的方法进行重采样. Wang等[10 ] 利用八叉树将网格模型转换为体素形式,将叶子节点的平均法向量输入3D卷积神经网络,实现分割. Wang等[11 ] 设计体素卷积神经网络,通过构造特征提取模块和注意力特征聚合模块来提取网格特征. Hu等[12 ] 指出仅依赖体素的方法会忽略网格模型的测地线信息,提出结合体素和网格模型的自编码器框架.将体素中提取的欧几里得信息输入编码器以提取长距离特征,在解码器中将它和网格中提取的测地线信息进行自适应地融合,提高了神经网络对网格模型的几何信息的利用. ...
... 除了视觉效果,还通过定量实验将本文算法与经典算法[1 , 5 -6 , 8 , 43 ] 进行分割准确率的比较. 不同算法在PSB数据集上各个类别的分割准确率P seg 和平均准确率如表1 所示. 可以看出,在大多数类别上,本文所取得的准确率高于其他算法,平均准确率比文献[5 , 43 ]的结果高3.3%. 对于一些较难学习的类别,比如Bird、Fourleg、Vase,由于这些模型的形态差异很大且分割边界不显著,除了1DCNN[6 ] 在Bird上的准确率为91.0%,其他算法在这3个类别上的准确率都低于90%. 本文算法分别取得了97.8%、90.9%和97.4%的准确率,远远超过其他算法. ...
... [6 ]在Bird上的准确率为91.0%,其他算法在这3个类别上的准确率都低于90%. 本文算法分别取得了97.8%、90.9%和97.4%的准确率,远远超过其他算法. ...
... Comparison of segmentation accuracy on PSB dataset
% Tab.1 模型 P seg Shape[1 ] TOG[5 ] Shape [8 ] 1D[6 ] DL [43 ] 本文 Human 86.8 91.2 94.5 90.6 90.7 94.7 Cup 94.0 99.7 93.8 94.5 98.1 99.6 Glasses 96.9 97.6 96.6 96.3 98.1 98.9 Airplane 96.1 96.7 93.0 95.9 95.2 97.6 Ant 98.7 98.8 98.6 98.7 98.8 99.0 Chair 98.1 98.7 98.5 97.7 97.6 99.0 Octopus 98.2 98.8 98.3 98.5 98.7 99.1 Table 99.4 99.6 99.5 99.6 99.0 99.4 Teddy 98.7 98.2 97.7 88.3 98.6 98.1 Plier 95.2 96.2 95.5 95.8 95.3 97.3 Fish 95.7 95.6 96.0 96.5 96.4 98.3 Bird 89.6 88.3 88.5 91.0 88.6 97.8 Armadillo 92.6 92.3 92.8 93.3 95.0 93.8 Fourleg 83.3 87.0 85.0 87.7 84.6 90.9 Vase 81.7 77.8 86.8 81.9 82.9 97.4 平均值 93.7 94.1 93.7 93.6 94.1 97.4
3.3. 消融实验 组成本文分割框架的关键之处主要有2个:边缘保持的粗化算法、结合Graph Transformer和GCN的GTG模块. 为了证明它们的有效性,在6类网格模型上开展4组消融实验. 消融实验的结果如表2 所示. 其中GTra指神经网络中只使用Graph Transformer模块,没有引入GCN模块;GTG指本文提出的GTG模块. 第2列是基础的分割框架,利用原粗化算法生成多尺度特征,且只使用Graph Transformer模块. 第3列在基础分割框架上,探究GTG模块对结果的影响,即利用原粗化算法生成多尺度特征,且使用本文提出的GTG模块. 第4列在基础分割的框架上,探究边缘保持的粗化算法对结果的影响,即利用本文边缘保持的粗化算法生成多尺度特征,且使用Graph Transformer模块. 第5列是本文最终的分割框架,同时使用边缘保持的粗化算法和GTG模块. ...
Projective feature learning for 3D shapes with multi-view depth images
1
2015
... 由于硬件的提升和数据规模的增长,神经网络被广泛地应用在三维网格分割问题中. 相较于传统的机器学习方法,神经网络具有更强的表征能力. 鉴于网格模型不规则采样的特性,有些方法采用重采样策略进行分割. Guo等[5 ] 将网格模型的特征重组成二维矩阵,再输入卷积神经网络,建立面片特征和标签之间的关系. George等[6 ] 认为将卷积作用在二维矩阵上,可能会在不相关特征之间产生关联,所以将网格模型的特征重组成一维向量. Xie等[7 ] 对网格模型进行多视角投影,通过多视角的深度极限学习机在不同视角的深度图之间共享权值,为面片赋标签. Kalogerakis等[8 ] 提出端到端的分割框架,先将网格模型的多视角渲染图和深度图输入全卷积神经网络,再将获得的置信度映射回网格表面,实现分割. Kundu等[9 ] 将从多视角虚拟图中提取的特征融合到三维网格,实现网格模型的分割. 此外,可以利用体素化的方法进行重采样. Wang等[10 ] 利用八叉树将网格模型转换为体素形式,将叶子节点的平均法向量输入3D卷积神经网络,实现分割. Wang等[11 ] 设计体素卷积神经网络,通过构造特征提取模块和注意力特征聚合模块来提取网格特征. Hu等[12 ] 指出仅依赖体素的方法会忽略网格模型的测地线信息,提出结合体素和网格模型的自编码器框架.将体素中提取的欧几里得信息输入编码器以提取长距离特征,在解码器中将它和网格中提取的测地线信息进行自适应地融合,提高了神经网络对网格模型的几何信息的利用. ...
3
... 由于硬件的提升和数据规模的增长,神经网络被广泛地应用在三维网格分割问题中. 相较于传统的机器学习方法,神经网络具有更强的表征能力. 鉴于网格模型不规则采样的特性,有些方法采用重采样策略进行分割. Guo等[5 ] 将网格模型的特征重组成二维矩阵,再输入卷积神经网络,建立面片特征和标签之间的关系. George等[6 ] 认为将卷积作用在二维矩阵上,可能会在不相关特征之间产生关联,所以将网格模型的特征重组成一维向量. Xie等[7 ] 对网格模型进行多视角投影,通过多视角的深度极限学习机在不同视角的深度图之间共享权值,为面片赋标签. Kalogerakis等[8 ] 提出端到端的分割框架,先将网格模型的多视角渲染图和深度图输入全卷积神经网络,再将获得的置信度映射回网格表面,实现分割. Kundu等[9 ] 将从多视角虚拟图中提取的特征融合到三维网格,实现网格模型的分割. 此外,可以利用体素化的方法进行重采样. Wang等[10 ] 利用八叉树将网格模型转换为体素形式,将叶子节点的平均法向量输入3D卷积神经网络,实现分割. Wang等[11 ] 设计体素卷积神经网络,通过构造特征提取模块和注意力特征聚合模块来提取网格特征. Hu等[12 ] 指出仅依赖体素的方法会忽略网格模型的测地线信息,提出结合体素和网格模型的自编码器框架.将体素中提取的欧几里得信息输入编码器以提取长距离特征,在解码器中将它和网格中提取的测地线信息进行自适应地融合,提高了神经网络对网格模型的几何信息的利用. ...
... 除了视觉效果,还通过定量实验将本文算法与经典算法[1 , 5 -6 , 8 , 43 ] 进行分割准确率的比较. 不同算法在PSB数据集上各个类别的分割准确率P seg 和平均准确率如表1 所示. 可以看出,在大多数类别上,本文所取得的准确率高于其他算法,平均准确率比文献[5 , 43 ]的结果高3.3%. 对于一些较难学习的类别,比如Bird、Fourleg、Vase,由于这些模型的形态差异很大且分割边界不显著,除了1DCNN[6 ] 在Bird上的准确率为91.0%,其他算法在这3个类别上的准确率都低于90%. 本文算法分别取得了97.8%、90.9%和97.4%的准确率,远远超过其他算法. ...
... Comparison of segmentation accuracy on PSB dataset
% Tab.1 模型 P seg Shape[1 ] TOG[5 ] Shape [8 ] 1D[6 ] DL [43 ] 本文 Human 86.8 91.2 94.5 90.6 90.7 94.7 Cup 94.0 99.7 93.8 94.5 98.1 99.6 Glasses 96.9 97.6 96.6 96.3 98.1 98.9 Airplane 96.1 96.7 93.0 95.9 95.2 97.6 Ant 98.7 98.8 98.6 98.7 98.8 99.0 Chair 98.1 98.7 98.5 97.7 97.6 99.0 Octopus 98.2 98.8 98.3 98.5 98.7 99.1 Table 99.4 99.6 99.5 99.6 99.0 99.4 Teddy 98.7 98.2 97.7 88.3 98.6 98.1 Plier 95.2 96.2 95.5 95.8 95.3 97.3 Fish 95.7 95.6 96.0 96.5 96.4 98.3 Bird 89.6 88.3 88.5 91.0 88.6 97.8 Armadillo 92.6 92.3 92.8 93.3 95.0 93.8 Fourleg 83.3 87.0 85.0 87.7 84.6 90.9 Vase 81.7 77.8 86.8 81.9 82.9 97.4 平均值 93.7 94.1 93.7 93.6 94.1 97.4
3.3. 消融实验 组成本文分割框架的关键之处主要有2个:边缘保持的粗化算法、结合Graph Transformer和GCN的GTG模块. 为了证明它们的有效性,在6类网格模型上开展4组消融实验. 消融实验的结果如表2 所示. 其中GTra指神经网络中只使用Graph Transformer模块,没有引入GCN模块;GTG指本文提出的GTG模块. 第2列是基础的分割框架,利用原粗化算法生成多尺度特征,且只使用Graph Transformer模块. 第3列在基础分割框架上,探究GTG模块对结果的影响,即利用原粗化算法生成多尺度特征,且使用本文提出的GTG模块. 第4列在基础分割的框架上,探究边缘保持的粗化算法对结果的影响,即利用本文边缘保持的粗化算法生成多尺度特征,且使用Graph Transformer模块. 第5列是本文最终的分割框架,同时使用边缘保持的粗化算法和GTG模块. ...
1
... 由于硬件的提升和数据规模的增长,神经网络被广泛地应用在三维网格分割问题中. 相较于传统的机器学习方法,神经网络具有更强的表征能力. 鉴于网格模型不规则采样的特性,有些方法采用重采样策略进行分割. Guo等[5 ] 将网格模型的特征重组成二维矩阵,再输入卷积神经网络,建立面片特征和标签之间的关系. George等[6 ] 认为将卷积作用在二维矩阵上,可能会在不相关特征之间产生关联,所以将网格模型的特征重组成一维向量. Xie等[7 ] 对网格模型进行多视角投影,通过多视角的深度极限学习机在不同视角的深度图之间共享权值,为面片赋标签. Kalogerakis等[8 ] 提出端到端的分割框架,先将网格模型的多视角渲染图和深度图输入全卷积神经网络,再将获得的置信度映射回网格表面,实现分割. Kundu等[9 ] 将从多视角虚拟图中提取的特征融合到三维网格,实现网格模型的分割. 此外,可以利用体素化的方法进行重采样. Wang等[10 ] 利用八叉树将网格模型转换为体素形式,将叶子节点的平均法向量输入3D卷积神经网络,实现分割. Wang等[11 ] 设计体素卷积神经网络,通过构造特征提取模块和注意力特征聚合模块来提取网格特征. Hu等[12 ] 指出仅依赖体素的方法会忽略网格模型的测地线信息,提出结合体素和网格模型的自编码器框架.将体素中提取的欧几里得信息输入编码器以提取长距离特征,在解码器中将它和网格中提取的测地线信息进行自适应地融合,提高了神经网络对网格模型的几何信息的利用. ...
O-CNN: octree-based convolutional neural networks for 3D shape analysis
1
2017
... 由于硬件的提升和数据规模的增长,神经网络被广泛地应用在三维网格分割问题中. 相较于传统的机器学习方法,神经网络具有更强的表征能力. 鉴于网格模型不规则采样的特性,有些方法采用重采样策略进行分割. Guo等[5 ] 将网格模型的特征重组成二维矩阵,再输入卷积神经网络,建立面片特征和标签之间的关系. George等[6 ] 认为将卷积作用在二维矩阵上,可能会在不相关特征之间产生关联,所以将网格模型的特征重组成一维向量. Xie等[7 ] 对网格模型进行多视角投影,通过多视角的深度极限学习机在不同视角的深度图之间共享权值,为面片赋标签. Kalogerakis等[8 ] 提出端到端的分割框架,先将网格模型的多视角渲染图和深度图输入全卷积神经网络,再将获得的置信度映射回网格表面,实现分割. Kundu等[9 ] 将从多视角虚拟图中提取的特征融合到三维网格,实现网格模型的分割. 此外,可以利用体素化的方法进行重采样. Wang等[10 ] 利用八叉树将网格模型转换为体素形式,将叶子节点的平均法向量输入3D卷积神经网络,实现分割. Wang等[11 ] 设计体素卷积神经网络,通过构造特征提取模块和注意力特征聚合模块来提取网格特征. Hu等[12 ] 指出仅依赖体素的方法会忽略网格模型的测地线信息,提出结合体素和网格模型的自编码器框架.将体素中提取的欧几里得信息输入编码器以提取长距离特征,在解码器中将它和网格中提取的测地线信息进行自适应地融合,提高了神经网络对网格模型的几何信息的利用. ...
VoxSegNet: volumetric CNNs for semantic part segmentation of 3D shapes
1
2020
... 由于硬件的提升和数据规模的增长,神经网络被广泛地应用在三维网格分割问题中. 相较于传统的机器学习方法,神经网络具有更强的表征能力. 鉴于网格模型不规则采样的特性,有些方法采用重采样策略进行分割. Guo等[5 ] 将网格模型的特征重组成二维矩阵,再输入卷积神经网络,建立面片特征和标签之间的关系. George等[6 ] 认为将卷积作用在二维矩阵上,可能会在不相关特征之间产生关联,所以将网格模型的特征重组成一维向量. Xie等[7 ] 对网格模型进行多视角投影,通过多视角的深度极限学习机在不同视角的深度图之间共享权值,为面片赋标签. Kalogerakis等[8 ] 提出端到端的分割框架,先将网格模型的多视角渲染图和深度图输入全卷积神经网络,再将获得的置信度映射回网格表面,实现分割. Kundu等[9 ] 将从多视角虚拟图中提取的特征融合到三维网格,实现网格模型的分割. 此外,可以利用体素化的方法进行重采样. Wang等[10 ] 利用八叉树将网格模型转换为体素形式,将叶子节点的平均法向量输入3D卷积神经网络,实现分割. Wang等[11 ] 设计体素卷积神经网络,通过构造特征提取模块和注意力特征聚合模块来提取网格特征. Hu等[12 ] 指出仅依赖体素的方法会忽略网格模型的测地线信息,提出结合体素和网格模型的自编码器框架.将体素中提取的欧几里得信息输入编码器以提取长距离特征,在解码器中将它和网格中提取的测地线信息进行自适应地融合,提高了神经网络对网格模型的几何信息的利用. ...
1
... 由于硬件的提升和数据规模的增长,神经网络被广泛地应用在三维网格分割问题中. 相较于传统的机器学习方法,神经网络具有更强的表征能力. 鉴于网格模型不规则采样的特性,有些方法采用重采样策略进行分割. Guo等[5 ] 将网格模型的特征重组成二维矩阵,再输入卷积神经网络,建立面片特征和标签之间的关系. George等[6 ] 认为将卷积作用在二维矩阵上,可能会在不相关特征之间产生关联,所以将网格模型的特征重组成一维向量. Xie等[7 ] 对网格模型进行多视角投影,通过多视角的深度极限学习机在不同视角的深度图之间共享权值,为面片赋标签. Kalogerakis等[8 ] 提出端到端的分割框架,先将网格模型的多视角渲染图和深度图输入全卷积神经网络,再将获得的置信度映射回网格表面,实现分割. Kundu等[9 ] 将从多视角虚拟图中提取的特征融合到三维网格,实现网格模型的分割. 此外,可以利用体素化的方法进行重采样. Wang等[10 ] 利用八叉树将网格模型转换为体素形式,将叶子节点的平均法向量输入3D卷积神经网络,实现分割. Wang等[11 ] 设计体素卷积神经网络,通过构造特征提取模块和注意力特征聚合模块来提取网格特征. Hu等[12 ] 指出仅依赖体素的方法会忽略网格模型的测地线信息,提出结合体素和网格模型的自编码器框架.将体素中提取的欧几里得信息输入编码器以提取长距离特征,在解码器中将它和网格中提取的测地线信息进行自适应地融合,提高了神经网络对网格模型的几何信息的利用. ...
1
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
1
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
1
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
MeshCNN: a network with edge
1
2019
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
Subdivision-based mesh convolution networks
1
2022
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
Mesh convolutional networks with face and vertex feature operators
1
2023
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
MeshWalker: deep mesh understanding by random walks
1
2020
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
DiffusionNet: discretization agnostic learning on surfaces
1
2022
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
Learning on 3D meshes with Laplacian encoding and pooling
1
2022
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
Laplacian2Mesh: Laplacian-based mesh understanding
1
2023
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
1
... 与重采样的方法相比,直接处理网格曲面,能够更好地利用网格模型的结构信息. 有些工作致力于研究适用网格曲面的卷积和池化操作. Xu等[13 ] 基于面片曲率设计有向卷积,实现网格模型的鲁棒分割. Huang等[14 ] 利用四旋转对称场定义关于面片的卷积域,使卷积操作可以直接从网格表面提取特征. Feng等[15 ] 设计网格卷积来聚合面片的邻域信息,处理网格模型的复杂性和不规则性. 有部分工作假设网格模型是流形结构. Hanocka等[16 ] 利用一条边属于2个面片的性质,定义了关于边的卷积和池化操作. Hu等[17 ] 依据每个面片与3个面片共边的特性,设计卷积和池化操作. Pérez等[18 ] 提出关于面片和顶点的2种卷积网络算子. 此外,Lahav等[19 ] 结合随机游走和循环神经网络,获得网格表面的几何信息和拓扑信息. Sharp等[20 ] 利用扩散网络,直接学习网格表面的几何信息. Qiao等[21 ] 采用谱分析方法编码网格的连接关系,提出特征聚集块,实现采样操作. Dong等[22 ] 将网格模型映射到多维Laplacian-Beltrami空间中,可以消除不规则采样的影响,更好地学习全局特征. 受热扩散机制的启发,Wong[23 ] 将热核特征相关的结构编码与顶点特征一同输入到由测地线距离引导的多层次的Transformer中,自适应地提取从局部到全局的信息. ...
1
... 除此之外,还可以利用图方法实现分割. Yi等[24 ] 将图卷积神经网络作用在谱空间上,利用参数化卷积核实现权值共享,以解决跨域问题. Schult等[25 ] 提出结合测地线图卷积和欧几里得图卷积的神经网络,利用顶点聚类和二次误差度量定义池化操作. Li等[26 ] 将顶点位置和拉普拉斯矩阵的特征向量分别输入Graph Transformer中,学习网格模型的几何信息和拓扑信息,采用自注意力机制融合. Roy[27 ] 将全分辨率和稀疏分辨率的网格模型输入神经网络,利用生成的形状直径函数值进行图切割,获得分割结果. 为了降低计算成本,Xu等[28 -29 ] 开始研究感知边缘的粗化算法. Xu等[28 ] 通过给边界区域的能量项赋更大的权重来实现粗化,应用改进的模糊聚类方法进一步细化边界. Li等[29 ] 利用网格模型的形状描述符训练分类器,获得顶点属于边界的概率,采用二次误差度量移除低概率顶点所在的边. ...
1
... 除此之外,还可以利用图方法实现分割. Yi等[24 ] 将图卷积神经网络作用在谱空间上,利用参数化卷积核实现权值共享,以解决跨域问题. Schult等[25 ] 提出结合测地线图卷积和欧几里得图卷积的神经网络,利用顶点聚类和二次误差度量定义池化操作. Li等[26 ] 将顶点位置和拉普拉斯矩阵的特征向量分别输入Graph Transformer中,学习网格模型的几何信息和拓扑信息,采用自注意力机制融合. Roy[27 ] 将全分辨率和稀疏分辨率的网格模型输入神经网络,利用生成的形状直径函数值进行图切割,获得分割结果. 为了降低计算成本,Xu等[28 -29 ] 开始研究感知边缘的粗化算法. Xu等[28 ] 通过给边界区域的能量项赋更大的权重来实现粗化,应用改进的模糊聚类方法进一步细化边界. Li等[29 ] 利用网格模型的形状描述符训练分类器,获得顶点属于边界的概率,采用二次误差度量移除低概率顶点所在的边. ...
1
... 除此之外,还可以利用图方法实现分割. Yi等[24 ] 将图卷积神经网络作用在谱空间上,利用参数化卷积核实现权值共享,以解决跨域问题. Schult等[25 ] 提出结合测地线图卷积和欧几里得图卷积的神经网络,利用顶点聚类和二次误差度量定义池化操作. Li等[26 ] 将顶点位置和拉普拉斯矩阵的特征向量分别输入Graph Transformer中,学习网格模型的几何信息和拓扑信息,采用自注意力机制融合. Roy[27 ] 将全分辨率和稀疏分辨率的网格模型输入神经网络,利用生成的形状直径函数值进行图切割,获得分割结果. 为了降低计算成本,Xu等[28 -29 ] 开始研究感知边缘的粗化算法. Xu等[28 ] 通过给边界区域的能量项赋更大的权重来实现粗化,应用改进的模糊聚类方法进一步细化边界. Li等[29 ] 利用网格模型的形状描述符训练分类器,获得顶点属于边界的概率,采用二次误差度量移除低概率顶点所在的边. ...
1
... 除此之外,还可以利用图方法实现分割. Yi等[24 ] 将图卷积神经网络作用在谱空间上,利用参数化卷积核实现权值共享,以解决跨域问题. Schult等[25 ] 提出结合测地线图卷积和欧几里得图卷积的神经网络,利用顶点聚类和二次误差度量定义池化操作. Li等[26 ] 将顶点位置和拉普拉斯矩阵的特征向量分别输入Graph Transformer中,学习网格模型的几何信息和拓扑信息,采用自注意力机制融合. Roy[27 ] 将全分辨率和稀疏分辨率的网格模型输入神经网络,利用生成的形状直径函数值进行图切割,获得分割结果. 为了降低计算成本,Xu等[28 -29 ] 开始研究感知边缘的粗化算法. Xu等[28 ] 通过给边界区域的能量项赋更大的权重来实现粗化,应用改进的模糊聚类方法进一步细化边界. Li等[29 ] 利用网格模型的形状描述符训练分类器,获得顶点属于边界的概率,采用二次误差度量移除低概率顶点所在的边. ...
3D tooth segmentation and labeling using deep convolutional neural networks
2
2019
... 除此之外,还可以利用图方法实现分割. Yi等[24 ] 将图卷积神经网络作用在谱空间上,利用参数化卷积核实现权值共享,以解决跨域问题. Schult等[25 ] 提出结合测地线图卷积和欧几里得图卷积的神经网络,利用顶点聚类和二次误差度量定义池化操作. Li等[26 ] 将顶点位置和拉普拉斯矩阵的特征向量分别输入Graph Transformer中,学习网格模型的几何信息和拓扑信息,采用自注意力机制融合. Roy[27 ] 将全分辨率和稀疏分辨率的网格模型输入神经网络,利用生成的形状直径函数值进行图切割,获得分割结果. 为了降低计算成本,Xu等[28 -29 ] 开始研究感知边缘的粗化算法. Xu等[28 ] 通过给边界区域的能量项赋更大的权重来实现粗化,应用改进的模糊聚类方法进一步细化边界. Li等[29 ] 利用网格模型的形状描述符训练分类器,获得顶点属于边界的概率,采用二次误差度量移除低概率顶点所在的边. ...
... [28 ]通过给边界区域的能量项赋更大的权重来实现粗化,应用改进的模糊聚类方法进一步细化边界. Li等[29 ] 利用网格模型的形状描述符训练分类器,获得顶点属于边界的概率,采用二次误差度量移除低概率顶点所在的边. ...
MeshFormer: high-resolution mesh segmentation with graph transformer
2
2022
... 除此之外,还可以利用图方法实现分割. Yi等[24 ] 将图卷积神经网络作用在谱空间上,利用参数化卷积核实现权值共享,以解决跨域问题. Schult等[25 ] 提出结合测地线图卷积和欧几里得图卷积的神经网络,利用顶点聚类和二次误差度量定义池化操作. Li等[26 ] 将顶点位置和拉普拉斯矩阵的特征向量分别输入Graph Transformer中,学习网格模型的几何信息和拓扑信息,采用自注意力机制融合. Roy[27 ] 将全分辨率和稀疏分辨率的网格模型输入神经网络,利用生成的形状直径函数值进行图切割,获得分割结果. 为了降低计算成本,Xu等[28 -29 ] 开始研究感知边缘的粗化算法. Xu等[28 ] 通过给边界区域的能量项赋更大的权重来实现粗化,应用改进的模糊聚类方法进一步细化边界. Li等[29 ] 利用网格模型的形状描述符训练分类器,获得顶点属于边界的概率,采用二次误差度量移除低概率顶点所在的边. ...
... [29 ]利用网格模型的形状描述符训练分类器,获得顶点属于边界的概率,采用二次误差度量移除低概率顶点所在的边. ...
Semi-supervised mesh segmentation and labeling
1
2012
... 上述都是监督式的三维网格分割算法,但在实际应用中,网格模型的标签需要人工标记,这极大地增加了人工成本. 半监督的分割算法越来越受到关注,它只要求部分面片具有标签,而不是所有面片. 针对标签不全的问题,Lv等[30 ] 利用条件随机场定义目标函数,实现了半监督的网格分割. Shu等[31 ] 通过交互式的方法对不同的部分进行标记,利用神经网络进行标签传播,得到未标记面片的标签. Shu等[32 ] 通过密度峰值聚类的方法定位种子点,基于概率分布矩阵优化能量项,充分利用未标记数据. ...
Scribble-based 3D shape segmentation via weakly-supervised learning
1
2020
... 上述都是监督式的三维网格分割算法,但在实际应用中,网格模型的标签需要人工标记,这极大地增加了人工成本. 半监督的分割算法越来越受到关注,它只要求部分面片具有标签,而不是所有面片. 针对标签不全的问题,Lv等[30 ] 利用条件随机场定义目标函数,实现了半监督的网格分割. Shu等[31 ] 通过交互式的方法对不同的部分进行标记,利用神经网络进行标签传播,得到未标记面片的标签. Shu等[32 ] 通过密度峰值聚类的方法定位种子点,基于概率分布矩阵优化能量项,充分利用未标记数据. ...
3D shape segmentation using soft density peak clustering and semi-supervised learning
1
2022
... 上述都是监督式的三维网格分割算法,但在实际应用中,网格模型的标签需要人工标记,这极大地增加了人工成本. 半监督的分割算法越来越受到关注,它只要求部分面片具有标签,而不是所有面片. 针对标签不全的问题,Lv等[30 ] 利用条件随机场定义目标函数,实现了半监督的网格分割. Shu等[31 ] 通过交互式的方法对不同的部分进行标记,利用神经网络进行标签传播,得到未标记面片的标签. Shu等[32 ] 通过密度峰值聚类的方法定位种子点,基于概率分布矩阵优化能量项,充分利用未标记数据. ...
Unsupervised 3D shape segmentation and co-segmentation via deep learning
1
2016
... 无监督的网格分割需要在完全没有标签信息的情况下实现. Shu等[33 ] 训练自动编码器来提取特征,通过高斯混合模型来实现聚类. Liang等[34 ] 通过重建掩码特征的方法训练自动编码器,将面片的编码特征和嵌入特征一起输入到多层感知机进行预测. Jiao等[35 ] 获得网格模型的K近邻图和形状描述符,并输入到不同的分支进行训练,利用聚类获得面片标签. ...
1
... 无监督的网格分割需要在完全没有标签信息的情况下实现. Shu等[33 ] 训练自动编码器来提取特征,通过高斯混合模型来实现聚类. Liang等[34 ] 通过重建掩码特征的方法训练自动编码器,将面片的编码特征和嵌入特征一起输入到多层感知机进行预测. Jiao等[35 ] 获得网格模型的K近邻图和形状描述符,并输入到不同的分支进行训练,利用聚类获得面片标签. ...
SCMS-Net: self-supervised clustering-based 3D meshes segmentation network
1
2023
... 无监督的网格分割需要在完全没有标签信息的情况下实现. Shu等[33 ] 训练自动编码器来提取特征,通过高斯混合模型来实现聚类. Liang等[34 ] 通过重建掩码特征的方法训练自动编码器,将面片的编码特征和嵌入特征一起输入到多层感知机进行预测. Jiao等[35 ] 获得网格模型的K近邻图和形状描述符,并输入到不同的分支进行训练,利用聚类获得面片标签. ...
Graph reduction with spectral and cut guarantees
4
2019
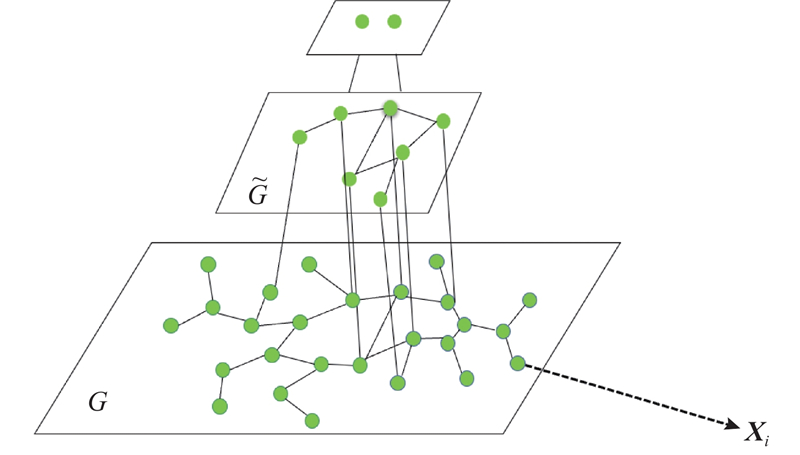
... 文献[36 ]的粗化算法在尽可能保持全局信息的基础上,通过移除边,将图节点划分为互不相交的簇. 每一个簇用一个节点表示,得到粗化图$ \tilde G $
... 对文献[36 ]的算法进行改进,得到适合分割任务的边缘保持的粗化算法. 由于边界区域的重要性,定义了图$ G $ $ v $ $ v $ 36 ],本文分3步实现粗化算法. 1)利用$ G $
... 为边界点. 基于文献[36 ],本文分3步实现粗化算法. 1)利用$ G $
... Segmentation accuracy of ablation experiment
% Tab.2 模型 粗化算法[36 ] 边缘保持的粗化算法 GTra GTG GTra GTG Human 91.04 91.94 92.25 94.69 Ant 96.34 97.24 98.88 98.96 Teddy 97.45 97.66 97.67 98.05 Bird 97.19 97.51 97.47 97.84 Fourleg 87.03 88.64 89.42 90.92 Vase 93.67 96.20 95.68 97.44 平均值 93.79 94.87 95.23 96.32
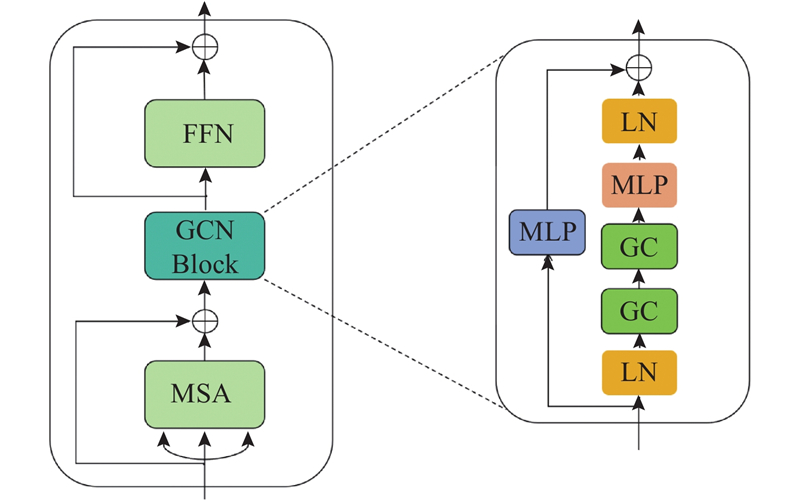
GTG模块结合了Graph Transformer模块和GCN模块,与Graph Transformer模块相比,加强了神经网络对局部精细信息的提取,有效地提高了网络的学习能力. 如表2 所示分别为利用原粗化算法和边缘保持的粗化算法,通过Graph Transformer模块和GTG模块得到的准确率. 可以看出,无论利用哪种粗化算法,GTG模块都能够使准确率平均上升约1.10%. ...
1
... 根据文献[37 ]进行多尺度特征的构造. 对于图$ G $ $ i $ $ G $ $ \tilde G $ $ {n_1} $ $ {n_2} $ $ {n_3} $ $ d $ $ {{\boldsymbol{X}}_i} \in {\mathbf{R}^{(1+{n_1}+{n_2}+{n_3})d}} $ . ...
Robust mesh segmentation using feature-aware region fusion
1
2023
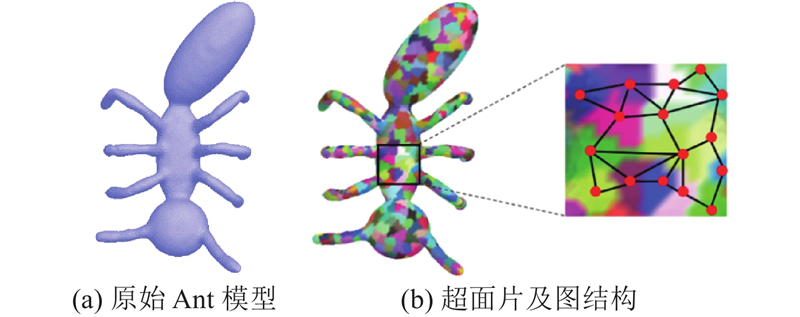
... 利用GTG模块,构造三维网格模型的分割网络. 因为网格模型由大量的三角面片组成,计算成本非常高. 利用过分割算法[38 ] ,将它分解成一系列的超面片. 如图5 (b)所示为图5 (a)中Ant模型的过分割结果,每个区域表示一个超面片. 以每个超面片为一个节点,相邻的超面片之间用边相连,生成超面片的图结构$ G $ . 如图5 (b)的局部放大图所示为过分割结果的部分图结构. ...
Consistent mesh partitioning and skeletonisation using the shape diameter function
1
2008
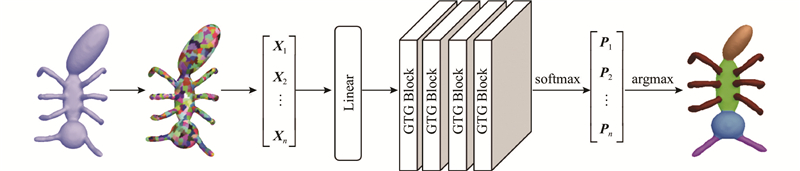
... 假设网格模型过分割后生成n 个超面片,对于每一个超面片,由法向、形状直径函数[39 ] 、保角因子[40 ] 和热核描述符[41 ] 等组成它的特征,即对应节点的特征. 按照2.1节的方式,得到图$ G $ $ {\boldsymbol{X}} $ $ {{\boldsymbol{X}}_i} $ $ i $ $ {\boldsymbol{X}} $ $ {\boldsymbol{P}} = [{{\boldsymbol{P}}_1},{{\boldsymbol{P}}_2}, \cdots ,{{\boldsymbol{P}}_n}]^{\mathrm{T}} \in {{\bf{R}}^{n \times C}} $ $ {{\boldsymbol{P}}_i} $ $ i $ $ C $ 图6 所示,以Ant模型为例,展示了本文算法的网络架构. ...
1
... 假设网格模型过分割后生成n 个超面片,对于每一个超面片,由法向、形状直径函数[39 ] 、保角因子[40 ] 和热核描述符[41 ] 等组成它的特征,即对应节点的特征. 按照2.1节的方式,得到图$ G $ $ {\boldsymbol{X}} $ $ {{\boldsymbol{X}}_i} $ $ i $ $ {\boldsymbol{X}} $ $ {\boldsymbol{P}} = [{{\boldsymbol{P}}_1},{{\boldsymbol{P}}_2}, \cdots ,{{\boldsymbol{P}}_n}]^{\mathrm{T}} \in {{\bf{R}}^{n \times C}} $ $ {{\boldsymbol{P}}_i} $ $ i $ $ C $ 图6 所示,以Ant模型为例,展示了本文算法的网络架构. ...
A concise and provably informative multi-scale signature based on heat diffusion
1
2009
... 假设网格模型过分割后生成n 个超面片,对于每一个超面片,由法向、形状直径函数[39 ] 、保角因子[40 ] 和热核描述符[41 ] 等组成它的特征,即对应节点的特征. 按照2.1节的方式,得到图$ G $ $ {\boldsymbol{X}} $ $ {{\boldsymbol{X}}_i} $ $ i $ $ {\boldsymbol{X}} $ $ {\boldsymbol{P}} = [{{\boldsymbol{P}}_1},{{\boldsymbol{P}}_2}, \cdots ,{{\boldsymbol{P}}_n}]^{\mathrm{T}} \in {{\bf{R}}^{n \times C}} $ $ {{\boldsymbol{P}}_i} $ $ i $ $ C $ 图6 所示,以Ant模型为例,展示了本文算法的网络架构. ...
A benchmark for 3D mesh segmentation
1
2009
... 实验使用Python和C++编程实现,配置分别是NVIDIA Tesla T4 GPU和Intel Core i7-8750H CPU. 对普林斯顿数据集PSB[42 ] 进行实验,通过视觉效果、对比实验和消融实验,证明算法的有效性. PSB数据集的种类丰富,包含Human、Cup、Airplane、Ant等多个类别的网格模型. ...
A deep learning driven active framework for segmentation of large 3D shape collections
3
2022
... 除了视觉效果,还通过定量实验将本文算法与经典算法[1 , 5 -6 , 8 , 43 ] 进行分割准确率的比较. 不同算法在PSB数据集上各个类别的分割准确率P seg 和平均准确率如表1 所示. 可以看出,在大多数类别上,本文所取得的准确率高于其他算法,平均准确率比文献[5 , 43 ]的结果高3.3%. 对于一些较难学习的类别,比如Bird、Fourleg、Vase,由于这些模型的形态差异很大且分割边界不显著,除了1DCNN[6 ] 在Bird上的准确率为91.0%,其他算法在这3个类别上的准确率都低于90%. 本文算法分别取得了97.8%、90.9%和97.4%的准确率,远远超过其他算法. ...
... , 43 ]的结果高3.3%. 对于一些较难学习的类别,比如Bird、Fourleg、Vase,由于这些模型的形态差异很大且分割边界不显著,除了1DCNN[6 ] 在Bird上的准确率为91.0%,其他算法在这3个类别上的准确率都低于90%. 本文算法分别取得了97.8%、90.9%和97.4%的准确率,远远超过其他算法. ...
... Comparison of segmentation accuracy on PSB dataset
% Tab.1 模型 P seg Shape[1 ] TOG[5 ] Shape [8 ] 1D[6 ] DL [43 ] 本文 Human 86.8 91.2 94.5 90.6 90.7 94.7 Cup 94.0 99.7 93.8 94.5 98.1 99.6 Glasses 96.9 97.6 96.6 96.3 98.1 98.9 Airplane 96.1 96.7 93.0 95.9 95.2 97.6 Ant 98.7 98.8 98.6 98.7 98.8 99.0 Chair 98.1 98.7 98.5 97.7 97.6 99.0 Octopus 98.2 98.8 98.3 98.5 98.7 99.1 Table 99.4 99.6 99.5 99.6 99.0 99.4 Teddy 98.7 98.2 97.7 88.3 98.6 98.1 Plier 95.2 96.2 95.5 95.8 95.3 97.3 Fish 95.7 95.6 96.0 96.5 96.4 98.3 Bird 89.6 88.3 88.5 91.0 88.6 97.8 Armadillo 92.6 92.3 92.8 93.3 95.0 93.8 Fourleg 83.3 87.0 85.0 87.7 84.6 90.9 Vase 81.7 77.8 86.8 81.9 82.9 97.4 平均值 93.7 94.1 93.7 93.6 94.1 97.4
3.3. 消融实验 组成本文分割框架的关键之处主要有2个:边缘保持的粗化算法、结合Graph Transformer和GCN的GTG模块. 为了证明它们的有效性,在6类网格模型上开展4组消融实验. 消融实验的结果如表2 所示. 其中GTra指神经网络中只使用Graph Transformer模块,没有引入GCN模块;GTG指本文提出的GTG模块. 第2列是基础的分割框架,利用原粗化算法生成多尺度特征,且只使用Graph Transformer模块. 第3列在基础分割框架上,探究GTG模块对结果的影响,即利用原粗化算法生成多尺度特征,且使用本文提出的GTG模块. 第4列在基础分割的框架上,探究边缘保持的粗化算法对结果的影响,即利用本文边缘保持的粗化算法生成多尺度特征,且使用Graph Transformer模块. 第5列是本文最终的分割框架,同时使用边缘保持的粗化算法和GTG模块. ...