数控机床是重要的工业母机,电主轴作为高档数控机床的核心部件, 其回转精度直接影响机床的加工精度、性能稳定性. 径向回转误差是指主轴转动过程中轴线相对于理想回转轴线的偏离程度,即主轴轴线的径向偏移量[1],是测量和分析电主轴回转误差的重要指标. 与径向回转误差相对应的是轴向回转误差,指主轴轴线的轴向偏移量. 径向回转误差是影响加工工件精度的关键因素[2]. 在精密加工和高精度加工中,特别是涉及旋转刀具加工工件时,主轴径向方向的误差对加工精度的影响更显著,它会直接影响切削力、表面质量和尺寸精度. 为了检测高速电主轴在工作中的回转误差,了解加工中的误差来源,采取相应的技术手段提高电主轴在加工过程中的精度,在线实时监测高速电主轴的回转误差具有重要的理论和实际应用价值.
现有径向回转误差测量方法主要包括传统测量方法和新型光学法. 传统的测量方法主要包括转位测量法和多测头法. 转位测量法通过位置调整和重复测量主轴获得回转误差的信息. 按照测量原理,转位测量法主要分为反向法[3]和多步法[4]. Grejda等[5]改进反向法,通过设计运动装置和消除低频噪声干扰,实现三维显示主轴同步运动误差的测量. 蓝河等[6]设计非接触式回转误差测量系统,通过反向法获得回转轴系的回转误差. Denis等[7]在多步法的基础上提出适用于高速主轴的回转误差测量方法,利用谐波分析进行数据分析,实现主轴回转误差的测量和评定. 马平等[8]采用多步法逐步消除单一误差,获得主轴回转误差测量结果. 多测头法利用多个传感器测头同时测量主轴的运动,实现对回转误差的测量. 三点法是常用的回转误差测量方法[9]. Lee等[10]基于三点法研究倾角误差与回转误差,搭建实时测量系统来验证方法的准确性和可行性. 张根明[11]通过调偏装置和三点法误差分离原理来提高回转误差的测量精度. 光学法使用透镜、激光发射仪并应用激光干涉原理测量主轴的回转误差. Kavitha等[12]提出基于机器视觉的径向误差测量法,该方法简单易行且测量精度高,是解决现代主轴回转误差测量的典型方案. 娄志峰等[13]提出非接触式的测量方法,结合圆光栅、环形平面镜和激光自准仪,实现精密主轴的回转误差在线测量. 上述介绍的现有的回转误差测量方法中,转位测量法须多次调整线位移传感器和被测轴系的角位置,无法满足在线测量的要求;多测头法的测量分辨力受限于圆标准器轮廓精度和位移传感器的测量分辨力,无法适用于高转速的电主轴;光学法的光信号响应与轴系径向位移变化间非线性关系强,无法保证测量精度;这些方法均须在主轴非加工状态下测量,且须安装响应的仪器,受到成本和空间限制. 有学者提出使用动力学建模方法预测回转精度,郑烽[14]使用动力学建模的方法建立拾振点和主轴之间的振动传递模型,从而预测回转进度;康婷等[15]基于动力学模型提出的回转精度预测方法考虑了切削力的影响. 动力学建模方法预测回转精度的共同点是考虑主轴和机壳由轴承进行刚性连接,并使用轴承的振动情况代表主轴的振动情况. 在实际中,高速旋转中的主轴刚性会下降,也就是说,主轴的轴线不再是一条直线,各个部位的振动情况不相同,从轴承处的振动到切削位置的振动存在差异.
实现误差补偿并提高工件回转精度亟须适应高转速、具备较高精度、考虑到实际旋转中轴刚度变化且能在实际加工过程中采用的回转误差测量方法. 本研究将深入分析机床主轴振动响应与径向回转误差的内在机理,揭示主轴振动重构在线测量径向回转误差的机制,提出电主轴在高速转动下通过振动信号获取径向回转误差的新方法,开展电主轴径向回转误差在线测量实验,探索数控机床在加工过程中电主轴径向回转误差在线测量的技术新路径.
1. 电主轴振动响应重构方法
1.1. 振动响应模态扩展方法
对于结构可离散化、多自由度的机械结构,物理坐标的动力学方程为
式中:
式中:
式中:
通过模型位移模态振型矩阵,将机械结构有限测点的振动响应扩展为全场振动响应:
式中:
式中:
1.2. 基于有限元的电主轴模态振型提取
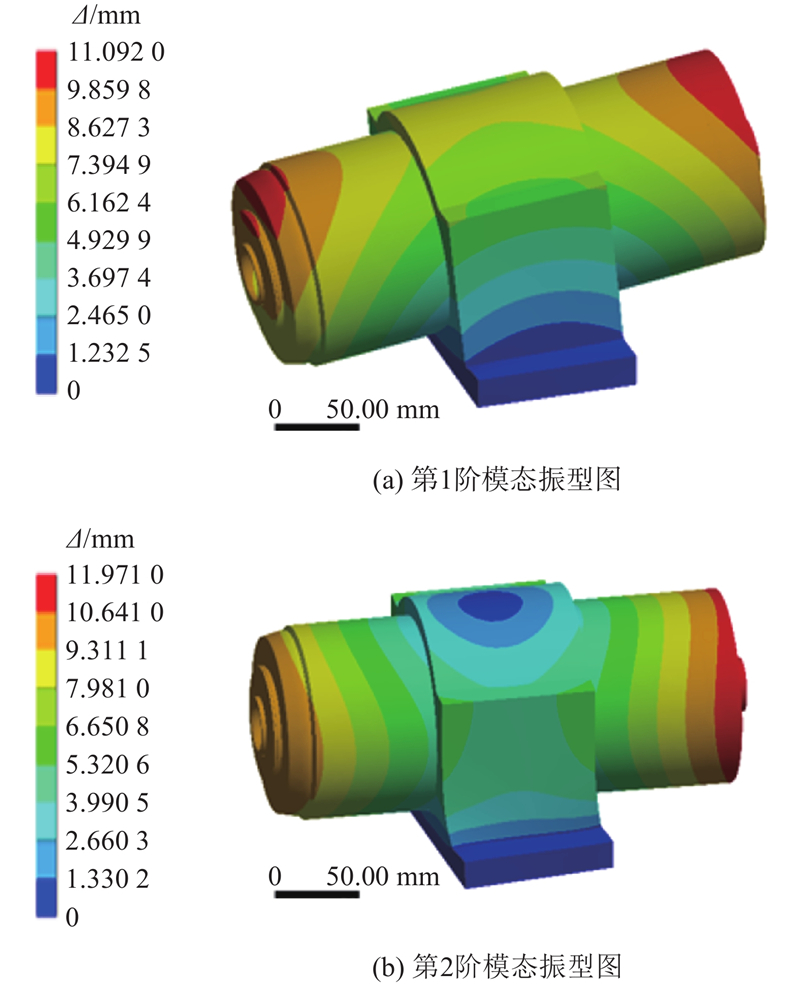
电主轴整机长512 mm,最大外径为125 mm. 利用自适应网格对电主轴有限元模型进行网格划分,自适应网格划分会出现网格大小划分过大或者过小问题,导致较小结构处网格表达不清楚. 此外,电主轴的各个组成部分的材料属性与标准的材料属性不完全相同,会影响最终分析结果. 为了提高有限元获取的电主轴各阶模态振型的精度,有限元分析之前对电主轴模型进行修正. 通过修正有限元模型的局部参数来减小模型与实际实验结果之间的偏差. 本实验主要进行各关键部件的材料属性修正和网格尺寸的适当调整,部件尺寸修正后的材料性能参数如表1所示. 表中,ρ为密度,E为弹性模量,μ为泊松比. 依据电主轴实验台的设计情况固定电主轴的基座底部,将电主轴和基座之间的连接关系设置为无分离连接,进行前20阶的模态分析,有限元模型修正后得到的前2阶位移模态振型如图1所示,其中Δ为总变形.
表 1 电主轴关键部件材料力学特性参数
Tab.1
| 结构 | 材料 | ρ/(kg·m−3) | E/GPa | μ |
| 芯轴 | 45# | 210 | 0.31 | |
| 基座 | 铸铝 | 70 | 0.30 | |
| 轴承内圈 | 轴承钢 | 208 | 0.30 | |
| 轴承外圈 | 轴承钢 | 208 | 0.30 |
图 1
图 1 电主轴前2阶模态振型图
Fig.1 First two orders of modal vibration pattern of electric spindle
图 2
图 3
表 2 电主轴有限元模型修正前后各阶固有频率
Tab.2
| 模态阶数 | f/Hz | ε/% | ||
| 修正前 | 修正后 | 实验结果 | ||
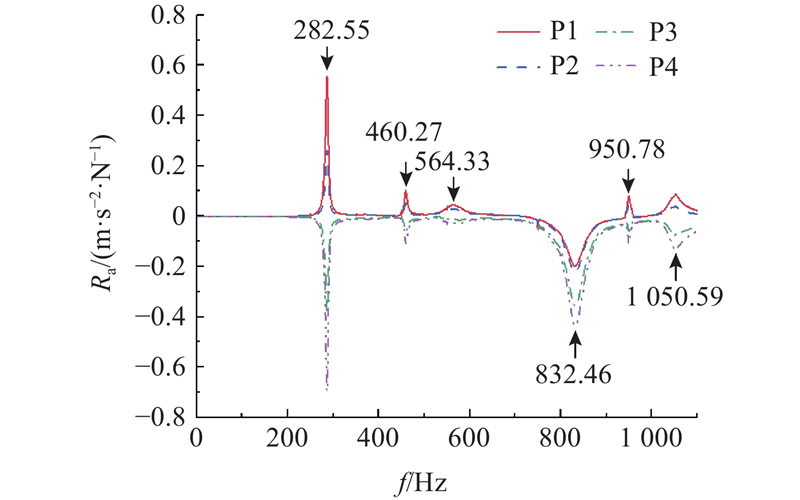
| 1 | 270.53 | 275.92 | 282.55 | 0.93 |
| 2 | 445.54 | 452.21 | 460.27 | 1.98 |
| 3 | 538.54 | 554.38 | 564.33 | 1.76 |
| 4 | 820.58 | 826.15 | 832.46 | 0.76 |
| 5 | 924.59 | 947.24 | 950.78 | 0.37 |
| 6 | 1 042.61 | 1 048.75 | 1 050.59 | 0.18 |
1.3. 基于费舍尔信息矩阵的模态分析阶数确定
在电主轴基于多振动传感器开展的振动场重构中,合理的选取模态分析阶数有助于减少计算时间,通常采用费舍尔(Fisher)矩阵选取合适的分析阶数,以Fisher信息矩阵的2-范数变化率(rate of change,ROC)作为判别函数[18],根据模态振型求解Fisher矩阵,计算式为
ROC计算式为
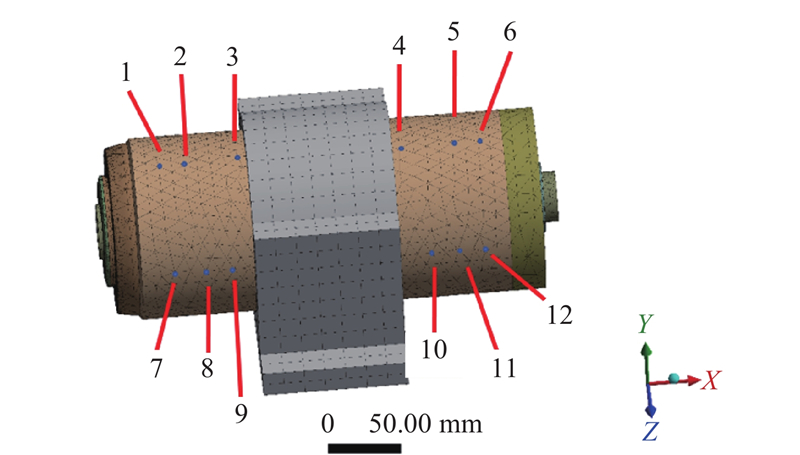
根据判别准则确定目标阶数:当第k阶ROC趋于0时,表示前k阶模态已经可以准确反映前k+1阶的信息,由此确定目标模态阶数为前k阶. 振动传感器布置在电主轴机壳上,因此只提取机壳外表面的节点. AD100T ICP加速度传感器只能测量垂直于吸附位置方向的振动信号,实验主要分析电主轴的水平(Z)和垂直(Y)方向的振动,为此将加速度传感器布置的位置选择在电主轴的顶部和侧面. 传感器磁吸底座的面积较大,电主轴在铸铝基座外可布置的空间有限,因此可选的加速度传感器布置位置不多,本实验选择在电主轴的顶部和侧面分别安装6个加速度传感器,同时避免使这些测点成为振动节点而影响后续的数据处理. 具体的加速度传感器布置位置的网格位置如图4所示.
图 4
图 4 电主轴传感器测点布置图
Fig.4 Arrangement of measurement points of electric spindle sensor
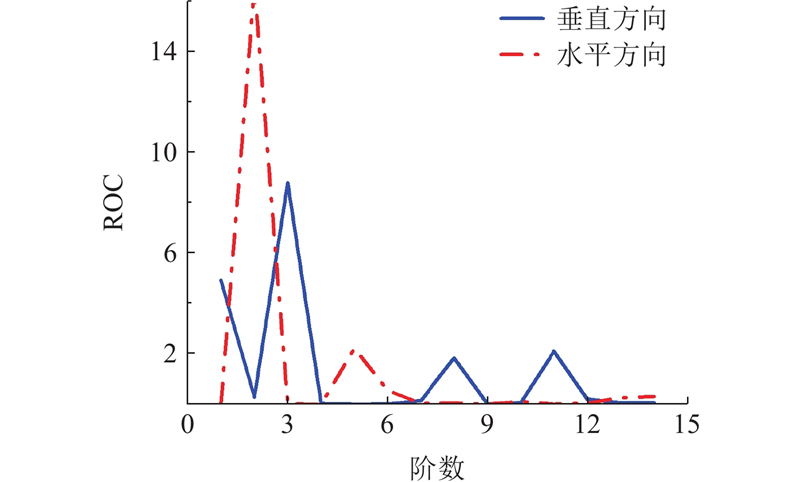
提取电主轴有限元模态分析时12个选择测点位置的各阶模态信息,将这些数据代入求解电主轴的Fisher信息矩阵,由顶部6个测点的模态振型求解得到垂直方向的2-范数变化率,由侧面6个测点的模态振型求解得到水平方向的2-范数变化率,具体结果如图5所示. 由图可知,在模态阶数为5时,水平方向的ROC趋近于0,若选取阶数大于5,计算量将增加但所含信息未得到有效提升,竖直方向的ROC在模态阶数为4时趋近于0,但考虑到在2个方向使用的振动传感器数量为6个,并且常用的模态分析阶数为6阶,因此,针对电主轴的振动场重构采用其前6阶模态进行分析.
图 5
图 5 不同电主轴振动方向的费舍尔信息矩阵的2-范数变化率随模态分析阶数的变化
Fig.5 Variation of rate of change of Fisher information matrix 2-norm with modal analysis order for different spindle vibration directions
1.4. 基于振动场重构结果的电主轴回转误差求解
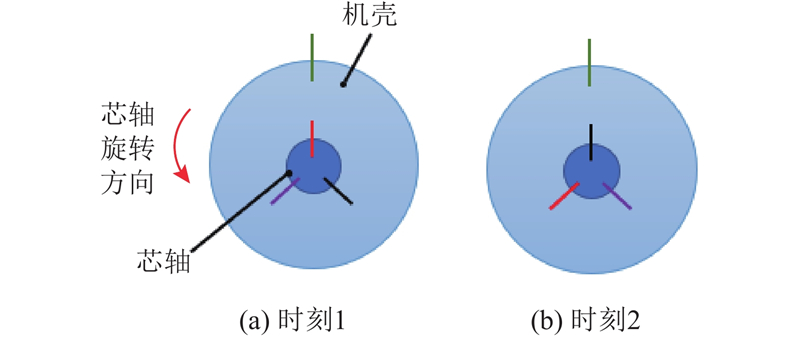
电主轴出厂前须矫正动平衡,这对各零件的加工质量有极高要求,其中芯轴的周向尺寸稳定性、力学性能均匀性和质量分布均匀性等性质都受到严格把控,转速对主轴的模态振型的影响很小. 如图6所示,在电主轴运行时,不同时刻,机壳的同一位置与芯轴的确定空间坐标对应的位置间的振动传递性质应该是相同的. 具体来说,在转速和温度不变的情况下,时刻1的机壳标记位置与芯轴的红线标注位置间的振动传递关系与时刻2机壳标记位置与芯轴黑线标注位置间的振动传递关系应当基本一致. 根据黄伟迪等[19]的研究,当高速电主轴在不超过10 000 r/min转速下工作时,轴承刚度的变化极小,可以忽略. 结合主轴回转误差的定义,在电主轴稳定运转的前提下,可以认为任何时刻,不超过10 000 r/min转速的电主轴机壳与芯轴确定空间坐标位置振动传递关系都是固定的.
图 6
图 6 转速对模态振型影响的合理性示意图
Fig.6 Schematic rationalization of effect of rotational speed on modal vibration pattern
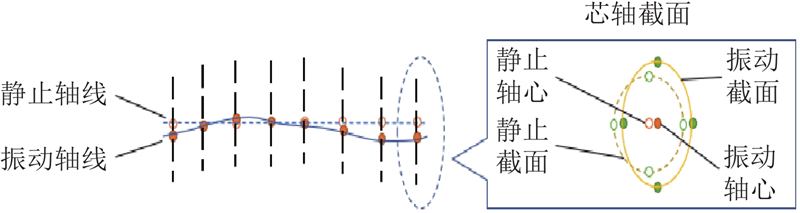
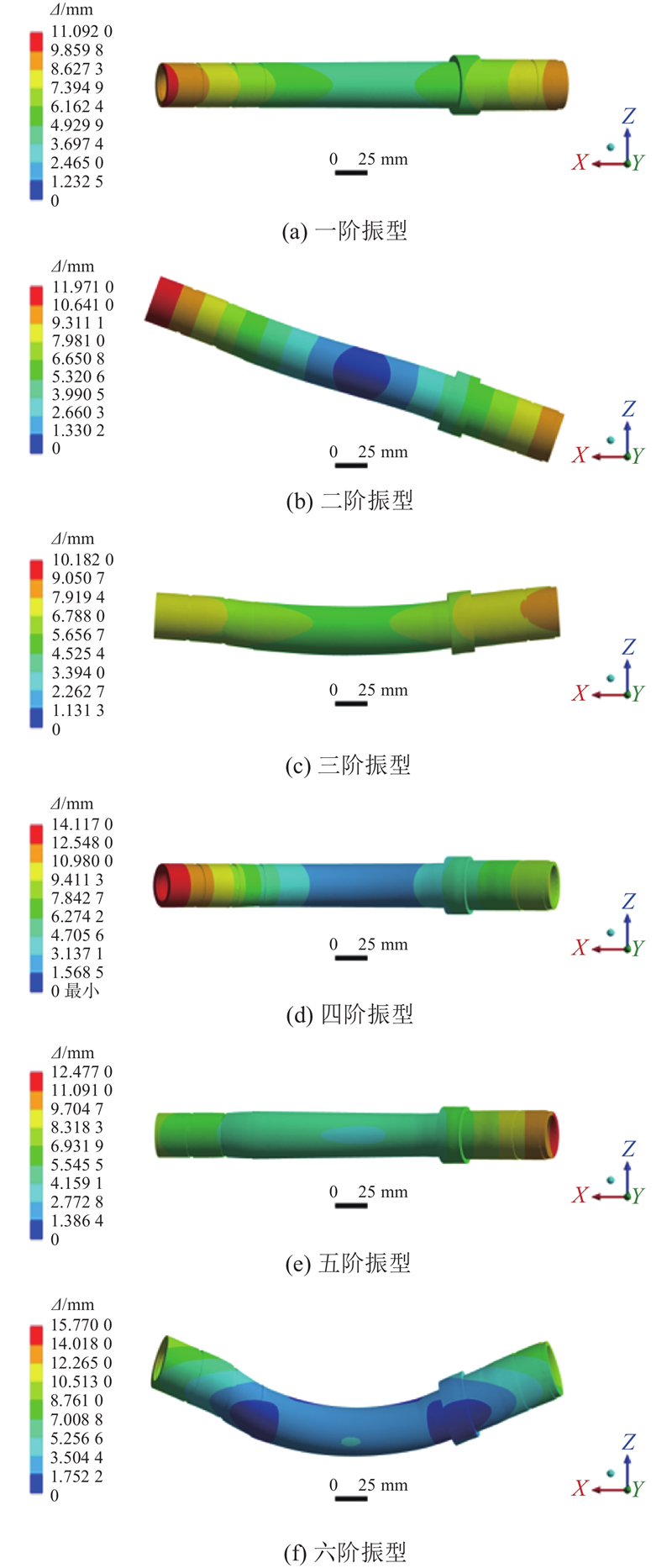
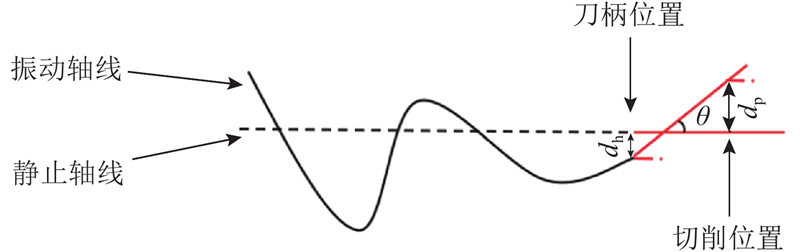
将提取的各阶模态振型和各加速度传感器测得的振动信号代入加速度响应模态扩展方程式(6),重构出芯轴的振动响应,主轴上沿轴向分布14个重构位置,如图7所示. 选取的14个重构位置不是均匀分布的,位置为模态振型分析时振动特征明显的14个节点. 常用的电主轴芯轴采用的是空心轴结构,无法直接求解轴线上各点的振动情况,只能通过各重构位置截面上周向分布的各点振动情况间接拟合出轴心的振动情况. 在芯轴的每个重构位置,通过周向节点的振动情况拟合出其中心位置的振动情况,再将14个重构位置的轴心位置的振动情况进行拟合,得到如图8所示的芯轴轴线拟合曲线,以此得到电主轴的回转误差. 具体地,在每个振动重构位置选取4个节点,节点选取的原则与重构位置的选取相同,通过模态扩展公式求得芯轴截面周向分布的4个振动特性最明显的节点,获取这4个节点的振动情况. 通过将这些点拟合成圆(椭圆),得到的圆心(中心)位置即为主轴在该截面位置的轴心. 再用拟合曲线连接各重构位置的轴心,得到所求的主轴振动轴线,与静止轴线相比较得到电主轴的回转误差. 根据如图9所示的电主轴芯轴前6阶振型图可知,芯轴的轴线变化情况基本可以通过不超过4次的多项式近似拟合. 本实验统一采用4次多项式曲线对芯轴轴线进行曲线拟合,开展回转误差的计算. 振动响应重构方法中回转误差计算方法的原理图如图10所示. 在刀柄位置处,振动轴线与静止轴线的垂直距离为电主轴在刀柄处的径向跳动
图 7
图 8
图 9
图 9 电主轴芯轴前6阶振型
Fig.9 First six orders of vibration pattern of electric spindle mandrel
图 10
2. 电主轴模态振型修正实验
得到准确的电主轴芯轴的振动响应,须先获得可靠的加速度模态贡献量矩阵
图 11
2.1. 电主轴机壳振动响应重构实验
根据构建的Fisher信息矩阵可以得到,模态分析阶数超过5阶就能保证振动响应重构的有效性. 将顶部的6个加速度传感器从刀柄位置至末端位置编为1~6号,侧面的6个加速度传感器从刀柄位置至末端位置编为7~12号. 通过顶部或侧面其中5个位置的振动传感器的加速度信号来重构剩余位置的振动响应,比较对应位置的振动传感器的信号来验证振动响应重构的准确性. 传感器1~6号互为重构对象,7~12号互为重构对象. 为了增加实验的数据点和样本量,设置如图12所示的敲击点,使用LC-1激振锤分别敲击,经测试LC-1激振锤敲击激发的振动信号的持续时间为0.6 s,设定振动信号采集时间为5 s,采样频率设置为10 000 Hz,重构实验只选用包含力锤激振信号在内的1 s开展,即每次实验重构10 000个时间点的振动信号. 经过测试,在重复实验过程中,每个位置敲击后的重构情况基本一致,后续只展示某次的重构结果.
图 12
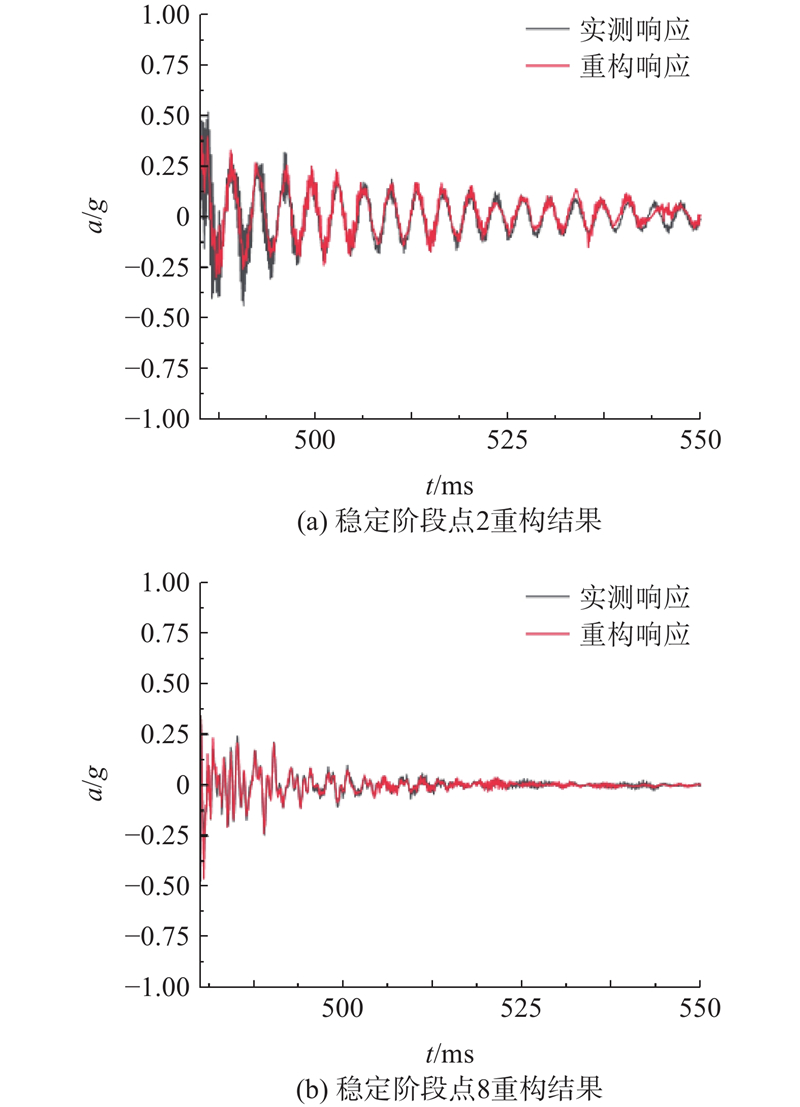
2号和8号传感器位置分别在电主轴前轴承投影到外壳的位置,电主轴前轴承的振动对电主轴的回转精度的影响最大,为此重点分析这2个点的重构情况. 实验时观测到当敲击位置为点G时,重构误差普遍最大,对振动响应重构的准确性的表征效果最为显著,因此对该敲击点进行分析. 在通常情况下,激振起始阶段的振动情况较为复杂,不具有重构意义,振动稳定阶段的加速度只有最大加速度的几十分之一甚至更小,实验中将电主轴的稳定阶段定义为加速度幅值在最大幅值的1%~10%的振动阶段,并且着重考虑稳定阶段的重构误差,2号和8号传感器位置的重构结果如图13所示. 整合各个敲击点的振动响应重构实验结果,得到的重构误差ei对比结果如图14所示,除了点G以外,其余敲击点对振动响应重构的精度影响不大. 主要原因是该点引发的是轴向激励,安装的AD100T ICP加速度传感器只能测量径向振动,此时激励形成的径向振动和噪声数量级接近,无法很好分离,因而重构效果不佳. 由图14可知,除了1号和2号传感器位置外,其余各位置的重构误差均为得到控制,须修正模态振型.
图 13
图 14
图 14 不同重构点振动响应重构误差对比(模态振型修正前)
Fig.14 Comparison of reconstruction errors of vibration response at different reconstruction points (before modal vibration pattern correction)
2.2. 电主轴机壳模态振型修正方法
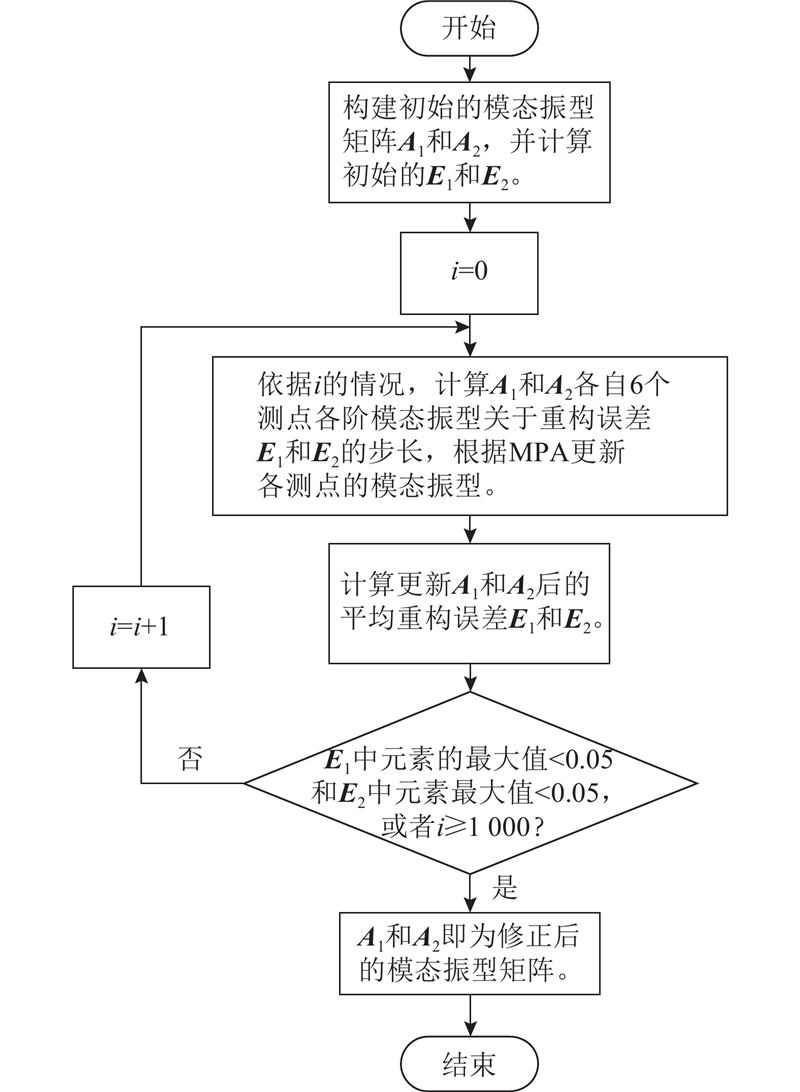
Farmarzi等[20]提出的海洋捕食者算法(marine predators algorithm, MPA)具备自适应性和可调节性,能够适应不同类型的优化问题. 将重构误差设为优化目标,可以把电主轴模态振型修正问题转化为优化问题,因此MPA可用于电主轴模态振型修正. 此外,MPA的基本原理和操作具有直观性和易理解性,无需繁琐的数学推导和复杂的参数设置. 本研究采用基于MPA的优化算法修正电主轴机壳模态振型. 考虑不同的速度比,同时模拟捕食者和猎物的整个生命周期,MPA优化过程主要分为3个阶段:1)高速度比或猎物移动速度快于捕食者,2)单位速度比或捕食者和猎物以几乎相同的速度移动,3)低速度比且当捕食者的移动速度比猎物快. 算法流程如图15所示,其中
图 15
图 15 电主轴机壳模态振型修正算法的流程图
Fig.15 Flowchart of modal vibration pattern correction algorithm for electric spindle housing
图 16
图 16 不同重构点振动响应重构误差对比(模态振型修正后)
Fig.16 Comparison of reconstruction errors of vibration response at different reconstruction points (after modal vibration pattern correction)
2.3. 电主轴芯轴模态振型修正方法
图 17
图 17 电主轴芯轴模态振型修正实验方案
Fig.17 Test program for modal vibration pattern correction of electric spindle mandrel
图 18
3. 电主轴径向回转误差测量实验
3.1. 振动响应重构法的重复性实验
图 19
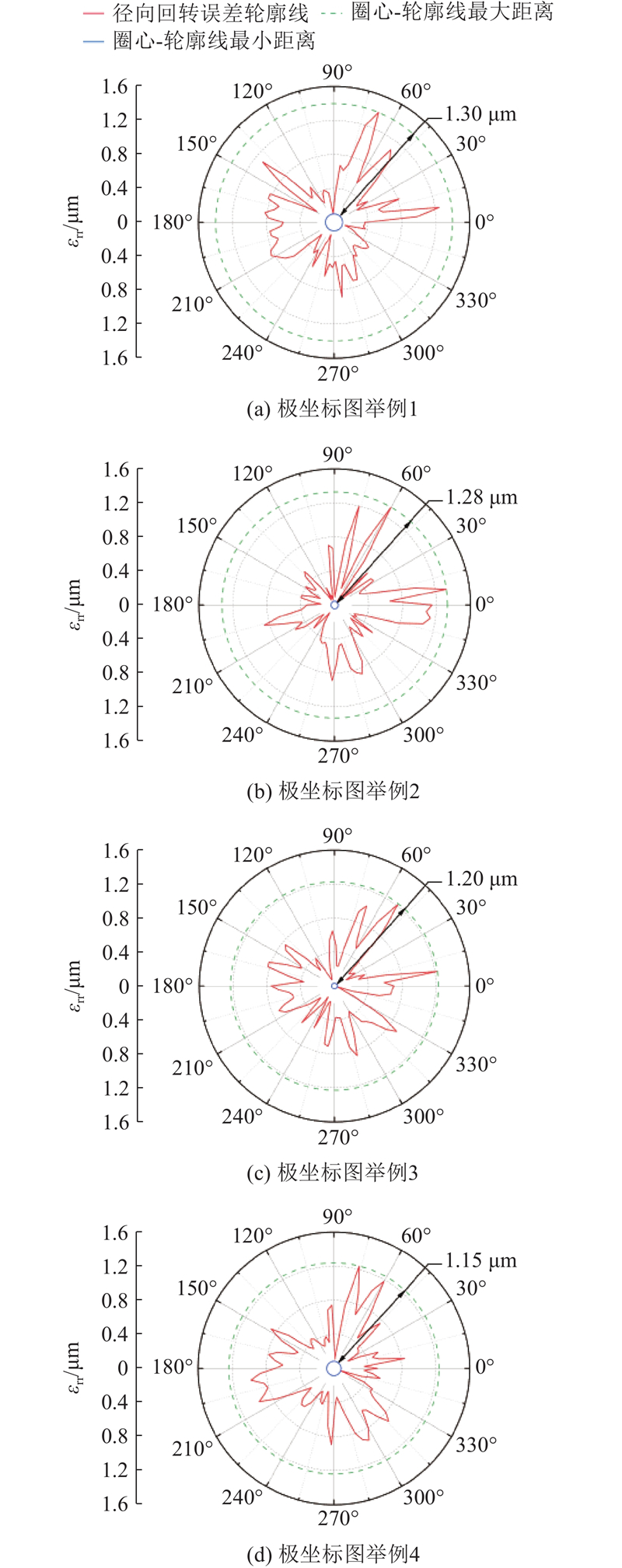
图 19 振动响应重构法重复测量部分极坐标图
Fig.19 Polar coordinates of repeated measurement part of vibration response reconstruction method
表 3 被测电主轴振动场重构法径向回转误差测量值
Tab.3
| 序号 | 序号 | 序号 | |||||
| 1 | 1.30 | 8 | 1.11 | 15 | 1.39 | ||
| 2 | 1.29 | 9 | 1.35 | 16 | 1.26 | ||
| 3 | 1.28 | 10 | 1.31 | 17 | 1.29 | ||
| 4 | 1.20 | 11 | 1.35 | 18 | 1.38 | ||
| 5 | 1.23 | 12 | 1.22 | 19 | 1.28 | ||
| 6 | 1.15 | 13 | 1.21 | 20 | 1.12 | ||
| 7 | 1.26 | 14 | 1.36 | 21 | 1.32 |
图 20
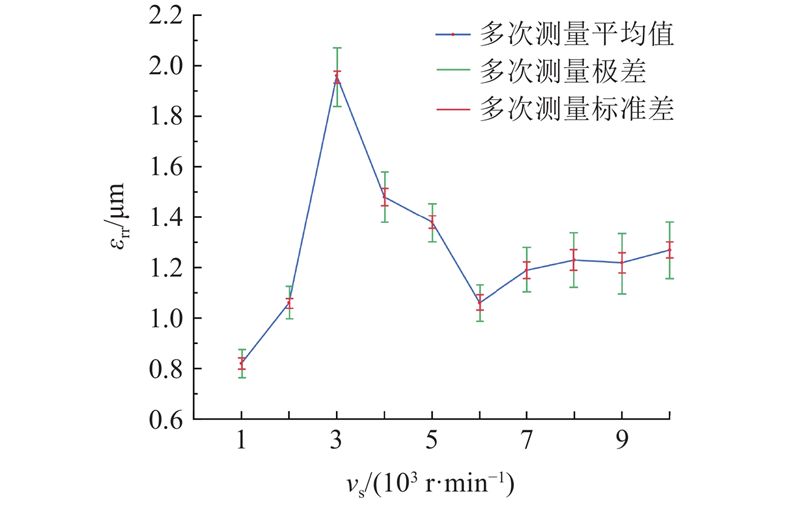
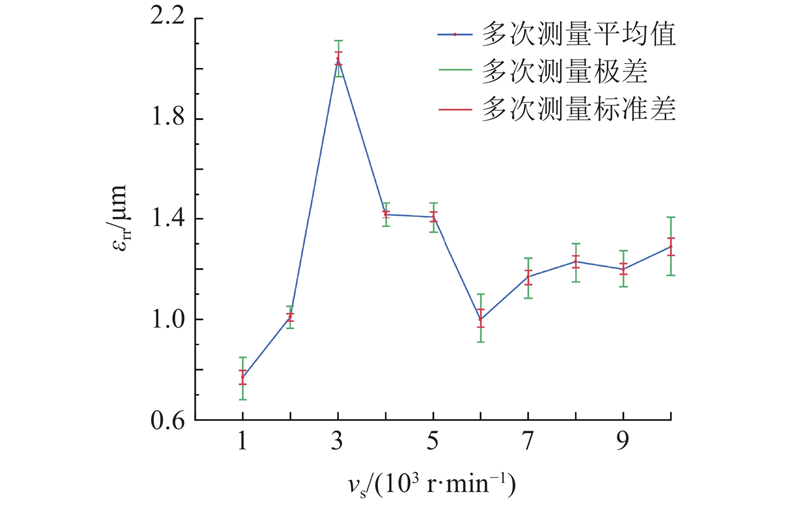
图 20 电主轴不同转速下振动响应重构法测量结果分布图
Fig.20 Distribution of measurement results of vibration response reconstruction method at different rotational speeds of electric spindle
表 4 电主轴振动响应重构法径向回转误差测量结果
Tab.4
| vs/(103 r·min−1) | R/μm | ||
| 1 | 0.82 | 0.14 | 0.056 |
| 2 | 1.06 | 0.16 | 0.048 |
| 3 | 1.96 | 0.29 | 0.059 |
| 4 | 1.48 | 0.25 | 0.085 |
| 5 | 1.38 | 0.19 | 0.063 |
| 6 | 1.06 | 0.18 | 0.076 |
| 7 | 1.19 | 0.22 | 0.082 |
| 8 | 1.23 | 0.27 | 0.103 |
| 9 | 1.22 | 0.30 | 0.099 |
| 10 | 1.27 | 0.28 | 0.080 |
3.2. 振动响应重构法的准确性实验
三点法是现有主轴回转精度测量方法中使用广泛、相对精度高的测量方法. 为了验证振动响应重构法的准确性,在相同的条件下采用三点法和振动响应重构法测量主轴回转精度. 三点法的传感器装置为高采样频率的Keyence LK-H020激光位移传感器头与Keyence LK-G5001控制器,它们能够实现高频采样. 在电主轴转速为1 000~10 000 r/min条件下测量径向回转误差,将测量结果与振动响应重构法进行比较,相应的实验装置如图21所示,在同一转速的测量中随机采集21次数据. 不同转速下测得的径向回转误差结果如图22所示. 结果表明,三点法对被测电主轴在不同转速下的测量重复性几乎保持一致,测量结果最大极差为0.29 μm,出现在vs=10 000 r/min的条件下,最大标准差为0.090 μm,出现在vs=6 000 r/min条件下. 说明使用高采样频率的激光传感器后的三点法作为验证实验具备可靠性. 以三点法结果为基准,本研究提出的振动响应重构法在各转速下的误差情况如表5所示. 表中,Ea为绝对误差,
图 21
图 22
图 22 电主轴不同转速下三点法测量结果分布图
Fig.22 Distribution of measurement results of three-point method at different rotational speeds of electric spindle
表 5 不同转速下被测电主轴振动响应重构法测量误差结果
Tab.5
| vs/(103 r·min−1) | Ea/μm | |
| 1 | 0.05 | 6.49 |
| 2 | 0.05 | 4.95 |
| 3 | 0.08 | 3.92 |
| 4 | 0.06 | 4.23 |
| 5 | 0.03 | 2.13 |
| 6 | 0.06 | 6.00 |
| 7 | 0.05 | 1.71 |
| 8 | 0 | 0 |
| 9 | 0.02 | 1.67 |
| 10 | 0.02 | 1.55 |
4. 结 语
针对电主轴径向回转误差在线测量的需求,本研究提出基于振动响应重构的在线测量径向回转误差方法,建立主轴振动响应与回转误差间的数学模型. 所提方法具有在线测量和精度可靠的优点,为实际加工过程中实现在线测量径向回转误差提供了新的思路和方法. 针对基于有限元提取的电主轴模态振型与实际情况存在偏差的问题,开发基于海洋捕食者算法的模态振型修正技术,大幅度减少了基于电主轴模态振型得到的振动响应重构误差. 本研究为数控机床电主轴径向回转误差的在线测量和监控提供了新方法,实现了电主轴转速不超过10 000 r/min情况下的在线测量,具有工程应用价值. 基于振动响应重构的径向回转误差虽然能保证较高的测量精度,但是引入模态振型修正实验延长了测量时间,还存在较大改进空间. 此外在测量其他型号电主轴时须重新进行前期的准备工作(包括模态振型的提取、模态振型的修正),前期准备工作只进行一次. 在未来研究中,计划1)更换与实验适配的更高采样频率的振动传感器,开展更高转速下的电主轴径向回转误差测量;2)开展随转速变化的电主轴模态振型研究,虽然转速对模态振型的影响不大,但当转速超过一定阈值后电主轴的轴承刚度会快速下降,这时电主轴的模态振型会发生较大的变化;3)设计集成模态振型修正与径向回转误差测量功能的基于振动响应重构的软件,简化测量流程并减少测试时间,实现加工条件下的电主轴径向回转误差实时在线测量. 由于实际加工中的复杂情况(如负载、噪声等)会使主轴的动力学特征更加复杂,对测量的准确性和稳定性会有一定影响,对此将进行深入研究.
参考文献
关于主轴回转运动精度及其动态测量方法的分析
[J].
Analysis of rotary motion accuracy of spindle and its dynamic measurement method
[J].
Dynamics of high-speed milling
[J].DOI:10.1115/1.3187052 [本文引用: 1]
A simple method for separating spindle error from test ball roundness error
[J].
Techniques for calibrating spindles with nanometer error motion
[J].DOI:10.1016/j.precisioneng.2004.05.003 [本文引用: 1]
基于光谱共焦位移传感器的非接触式回转误差测量系统
[J].
A non contact system for measurement of rotating error based on confocal chromatic displacement sensor
[J].
Harmonic-analysis-based method for separation of form error during evaluation of high-speed spindle radial errors
[J].DOI:10.1177/0954405411434868 [本文引用: 1]
主轴回转精度多步误差分离研究
[J].
Study on multi-step error separation of spindle rotation precision
[J].
Easy measuring instrument for analyzing the radial and tilt error motions of a rotating shaft
[J].DOI:10.1177/1475090216680891 [本文引用: 1]
A new approach to spindle radial error evaluation using a machine vision system
[J].DOI:10.1515/mms-2017-0018 [本文引用: 1]
圆光栅配合自准直仪测量主轴径向运动误差
[J].DOI:10.3788/OPE.20192709.2053 [本文引用: 1]
Spindle radial motion error measurement using a circular grating and a autocollimator
[J].DOI:10.3788/OPE.20192709.2053 [本文引用: 1]
切削工况下机床主轴回转精度动态预测方法
[J].
Dynamic prediction method for machine tool spindle rotational accuracy under cutting condition
[J].
一类高速电主轴的动力学建模及振动响应分析
[J].
Dynamic modeling and vibration response analysis of high speed motorized spindle
[J].
基于模态参数验证的机床结构件优化设计
[J].
Optimization design to machine tool structures using experimental verification of modal parameters
[J].
高速电主轴角接触球轴承刚度及其对电主轴临界转速的影响分析
[J].
Analysis on the stiffness of angular contact ball bearings and its effect on the critical speed of a high speed motorized spindle
[J].
Marine predators algorithm: a nature-inspired metaheuristic
[J].DOI:10.1016/j.eswa.2020.113377 [本文引用: 3]
基于测点优化与模态扩展的机械结构振动响应全场重构
[J].
Full field reconstruction of mechanical structure vibration responses based on measurement point optimization and modal expansion
[J].