[1]
WEAVER W Recent contributions to the mathematical theory of communication
[J]. ETC: A Review of General Semantics , 1953 , 10 (4 ): 261 - 281
[本文引用: 1]
[3]
张平, 戴金晟, 张育铭, 等 面向语义通信的非线性变换编码
[J]. 通信学报 , 2023 , 44 (4 ): 1 - 14
DOI:10.11959/j.issn.1000-436x.2023087
[本文引用: 1]
ZHANG Ping, DAI Jincheng, ZHANG Yuming, et al Nonlinear transform coding for semantic communications
[J]. Journal on Communications , 2023 , 44 (4 ): 1 - 14
DOI:10.11959/j.issn.1000-436x.2023087
[本文引用: 1]
[4]
XIE H, QIN Z, LI G Y, et al Deep learning enabled semantic communication systems
[J]. IEEE Transactions on Signal Processing , 2021 , 69 : 2663 - 2675
DOI:10.1109/TSP.2021.3071210
[本文引用: 2]
[5]
TONG H, YANG Z, WANG S, et al. Federated learning based audio semantic communication over wireless networks [C]// Proceedings of the IEEE Global Communications Conference . Madrid: IEEE, 2021: 1–6.
[本文引用: 1]
[6]
HUANG D, TAO X, GAO F, et al. Deep learning-based image semantic coding for semantic communications [C]// Proceedings of the IEEE Global Communications Conference . Madrid: IEEE, 2021: 1–6.
[本文引用: 1]
[7]
PATWA N, AHUJA N, SOMAYAZULU S, et al. Semantic-preserving image compression [C]// Proceedings of the IEEE International Conference on Image Processing . Abu Dhabi: IEEE, 2020: 1281–1285.
[本文引用: 1]
[8]
SUN Q, GUO C, YANG Y, et al. Deep joint source-channel coding for wireless image transmission with semantic importance [C]// Proceedings of the IEEE 96th Vehicular Technology Conference . London: IEEE, 2022: 1–7.
[本文引用: 5]
[9]
WANG J, WANG S, DAI J, et al. Perceptual learned source-channel coding for high-fidelity image semantic transmission [C]// Proceedings of the GLOBECOM 2022-2022 IEEE Global Communications Conference . Rio de Janeiro: IEEE, 2022: 3959–3964.
[本文引用: 1]
[10]
WANG Q, SHEN L, SHI Y Recognition-driven compressed image generation using semantic-prior information
[J]. IEEE Signal Processing Letters , 2020 , 27 : 1150 - 1154
DOI:10.1109/LSP.2020.3004967
[本文引用: 1]
[11]
HU Q, ZHANG G, QIN Z, et al. Robust semantic communications against semantic noise [C]// Proceedings of the IEEE 96th Vehicular Technology Conference . London: IEEE, 2022: 1–6.
[本文引用: 1]
[12]
牛冠冲, 刘飞翔, 杨雯, 等 面向多任务的语义通信架构设计与实现
[J]. 移动通信 , 2024 , 48 (2 ): 47 - 55
DOI:10.3969/j.issn.1006-1010.20240109-0001
[本文引用: 1]
NIU Guanchong, LIU Feixiang, YANG Wen, et al Design and implementation of semantic communication for goal-oriented multi-tasking
[J]. Mobile Communications , 2024 , 48 (2 ): 47 - 55
DOI:10.3969/j.issn.1006-1010.20240109-0001
[本文引用: 1]
[14]
KUTAY E, YENER A. Classification-oriented semantic wireless communications [C]// 2024 IEEE International Conference on Acoustics, Speech and Signal Processing . Seoul: IEEE, 2024: 9096–9100.
[本文引用: 1]
[15]
GRASSUCCI E, PARK J, BARBAROSSA S, et al. Generative AI meets semantic communication: evolution and revolution of communication tasks [EB/OL]. (2024−01−10)[2024−07−15]. https://arxiv.org/pdf/2401.06803.
[本文引用: 1]
[16]
LI N, IOSIFIDIS A, ZHANG Q. Dynamic semantic compression for CNN inference in multi-access edge computing: a graph reinforcement learning-based autoencoder [EB/OL]. (2024−01−19)[2024−07−15]. https://arxiv.org/pdf/2401.12167.
[本文引用: 1]
[17]
WANG C, HAN Y, WANG W An end-to-end deep learning image compression framework based on semantic analysis
[J]. Applied Sciences , 2019 , 9 (17 ): 3580
DOI:10.3390/app9173580
[本文引用: 1]
[18]
SEBAI D. Multi-rate deep semantic image compression with quantized modulated autoencoder [C]// Proceedings of the IEEE 23rd International Workshop on Multimedia Signal Processing . Tampere: IEEE, 2021: 1–6.
[本文引用: 1]
[19]
DONG C, LIANG H, XU X, et al Semantic communication system based on semantic slice models propagation
[J]. IEEE Journal on Selected Areas in Communications , 2023 , 41 (1 ): 202 - 213
DOI:10.1109/JSAC.2022.3221948
[本文引用: 2]
[20]
何晨光, 黄声显, 陈舒怡, 等 基于语义通信的低比特率图像语义编码方法
[J]. 信号处理 , 2023 , 39 (3 ): 410 - 418
[本文引用: 1]
HE Chenguang, HUANG Shengxian, CHEN Shuyi, et al A low bitrates image semantic coding method based on semantic communication
[J]. Journal of Signal Processing , 2023 , 39 (3 ): 410 - 418
[本文引用: 1]
[21]
LUO S H, YANG Y Z, YIN Y L, et al. DeepSIC: deep semantic image compression [C]// Neural Information Processing . [S. l.]: Springer, 2018: 96–106.
[本文引用: 1]
[22]
PARK S, SIMEONE O, KANG J. End-to-end fast training of communication links without a channel model via online meta-learning [C]// Proceedings of the IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications . Atlanta: IEEE, 2020: 1–5.
[本文引用: 1]
[23]
JIANG S, LIU Y, ZHANG Y, et al Reliable semantic communication system enabled by knowledge graph
[J]. Entropy , 2022 , 24 (6 ): 846
DOI:10.3390/e24060846
[本文引用: 2]
[24]
WANG Y, CHEN M, SAAD W, et al. Performance optimization for semantic communications: an attention-based learning approach [C]// Proceedings of the IEEE Global Communications Conference . Madrid: IEEE, 2021: 1–6.
[本文引用: 2]
[25]
刘传宏, 郭彩丽, 杨洋, 等 人工智能物联网中面向智能任务的语义通信方法
[J]. 通信学报 , 2021 , 42 (11 ): 97 - 108
DOI:10.11959/j.issn.1000-436x.2021214
[本文引用: 6]
LIU Chuanhong, GUO Caili, YANG Yang, et al Intelligent task-oriented semantic communication method in artificial intelligence of things
[J]. Journal on Communications , 2021 , 42 (11 ): 97 - 108
DOI:10.11959/j.issn.1000-436x.2021214
[本文引用: 6]
[26]
ZITNICK C L, VEDANTAM R, PARIKH D Adopting abstract images for semantic scene understanding
[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence , 2016 , 38 (4 ): 627 - 638
DOI:10.1109/TPAMI.2014.2366143
[本文引用: 5]
[27]
KANG B Y. A novel approach to semantic indexing based on concept [C]// Proceedings of the 41st Annual Meeting on Association for Computational Linguistics . Sapporo: ACL, 2003: 44–49.
[本文引用: 3]
[28]
LIU C, GUO C, YANG Y, et al. Adaptable semantic compression and resource allocation for task-oriented communications [EB/OL]. (2022−04−19)[2024−07−15]. https://arxiv.org/pdf/2204.08910.
[本文引用: 3]
Recent contributions to the mathematical theory of communication
1
1953
... 香农(Claude Elwood Shannon)和韦弗(Warren Weaver)都深入探讨了通信的本质[1 ] ,他们将通信问题细分为技术层(语法层)、语义层和效用层(语用层),传统的基于统计概率的通信技术主要涉及最基础的语法层面. 自香农提出信息论以来[2 ] ,这种经典的通信方式在信息压缩、传输和处理等多个领域迅速发展,也逐渐出现发展瓶颈. 特别是在信息压缩领域,目前的语音、图像和视频压缩编码技术几乎达到信息熵理论和率失真函数的极限,进一步提高压缩效率的成本非常高,收益却有限. 在信息传输领域,现有的信道传输能力几乎触及信道容量极限,通过增加频谱、天线数量或提升功率来扩充容量不仅代价昂贵,而且难以持续. 在信息处理领域,随着摩尔定律的减缓,芯片的计算能力提升已近极限. 经典通信技术亟须开拓新的理论和技术创新路径[3 ] . ...
A mathematical theory of communication
1
1948
... 香农(Claude Elwood Shannon)和韦弗(Warren Weaver)都深入探讨了通信的本质[1 ] ,他们将通信问题细分为技术层(语法层)、语义层和效用层(语用层),传统的基于统计概率的通信技术主要涉及最基础的语法层面. 自香农提出信息论以来[2 ] ,这种经典的通信方式在信息压缩、传输和处理等多个领域迅速发展,也逐渐出现发展瓶颈. 特别是在信息压缩领域,目前的语音、图像和视频压缩编码技术几乎达到信息熵理论和率失真函数的极限,进一步提高压缩效率的成本非常高,收益却有限. 在信息传输领域,现有的信道传输能力几乎触及信道容量极限,通过增加频谱、天线数量或提升功率来扩充容量不仅代价昂贵,而且难以持续. 在信息处理领域,随着摩尔定律的减缓,芯片的计算能力提升已近极限. 经典通信技术亟须开拓新的理论和技术创新路径[3 ] . ...
面向语义通信的非线性变换编码
1
2023
... 香农(Claude Elwood Shannon)和韦弗(Warren Weaver)都深入探讨了通信的本质[1 ] ,他们将通信问题细分为技术层(语法层)、语义层和效用层(语用层),传统的基于统计概率的通信技术主要涉及最基础的语法层面. 自香农提出信息论以来[2 ] ,这种经典的通信方式在信息压缩、传输和处理等多个领域迅速发展,也逐渐出现发展瓶颈. 特别是在信息压缩领域,目前的语音、图像和视频压缩编码技术几乎达到信息熵理论和率失真函数的极限,进一步提高压缩效率的成本非常高,收益却有限. 在信息传输领域,现有的信道传输能力几乎触及信道容量极限,通过增加频谱、天线数量或提升功率来扩充容量不仅代价昂贵,而且难以持续. 在信息处理领域,随着摩尔定律的减缓,芯片的计算能力提升已近极限. 经典通信技术亟须开拓新的理论和技术创新路径[3 ] . ...
面向语义通信的非线性变换编码
1
2023
... 香农(Claude Elwood Shannon)和韦弗(Warren Weaver)都深入探讨了通信的本质[1 ] ,他们将通信问题细分为技术层(语法层)、语义层和效用层(语用层),传统的基于统计概率的通信技术主要涉及最基础的语法层面. 自香农提出信息论以来[2 ] ,这种经典的通信方式在信息压缩、传输和处理等多个领域迅速发展,也逐渐出现发展瓶颈. 特别是在信息压缩领域,目前的语音、图像和视频压缩编码技术几乎达到信息熵理论和率失真函数的极限,进一步提高压缩效率的成本非常高,收益却有限. 在信息传输领域,现有的信道传输能力几乎触及信道容量极限,通过增加频谱、天线数量或提升功率来扩充容量不仅代价昂贵,而且难以持续. 在信息处理领域,随着摩尔定律的减缓,芯片的计算能力提升已近极限. 经典通信技术亟须开拓新的理论和技术创新路径[3 ] . ...
Deep learning enabled semantic communication systems
2
2021
... 在深度学习和智能硬件的推动下,6G语义通信领域受到学术界的广泛关注. 研究者正致力于探索基于深度学习的通信技术,设计出基于文本、图像和音频的语义通信系统,极大降低了传输成本,保障了任务性能,提升了系统稳健性. Xie等[4 ] 开发了深度学习驱动的语义通信系统,Tong等[5 ] 在无线网络中针对音频数据设计了基于CNN的高效传输系统. 在图像语义通信方面,Huang等[6 ] 使用生成对抗网络(generative adversarial networks, GAN)开发分阶段的编码过程,Patwa等[7 ] 提出提高视觉数据分析性能的压缩方法,Sun等[8 ] 研发图像传输的联合源通道编码技术. Wang等[9 -10 ] 采用对抗性损失优化编码方法,研究语义先验信息在图像压缩中的应用. Hu等[11 ] 设计的端到端系统框架能够显著提升系统稳健性,降低传输成本. ...
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
1
... 在深度学习和智能硬件的推动下,6G语义通信领域受到学术界的广泛关注. 研究者正致力于探索基于深度学习的通信技术,设计出基于文本、图像和音频的语义通信系统,极大降低了传输成本,保障了任务性能,提升了系统稳健性. Xie等[4 ] 开发了深度学习驱动的语义通信系统,Tong等[5 ] 在无线网络中针对音频数据设计了基于CNN的高效传输系统. 在图像语义通信方面,Huang等[6 ] 使用生成对抗网络(generative adversarial networks, GAN)开发分阶段的编码过程,Patwa等[7 ] 提出提高视觉数据分析性能的压缩方法,Sun等[8 ] 研发图像传输的联合源通道编码技术. Wang等[9 -10 ] 采用对抗性损失优化编码方法,研究语义先验信息在图像压缩中的应用. Hu等[11 ] 设计的端到端系统框架能够显著提升系统稳健性,降低传输成本. ...
1
... 在深度学习和智能硬件的推动下,6G语义通信领域受到学术界的广泛关注. 研究者正致力于探索基于深度学习的通信技术,设计出基于文本、图像和音频的语义通信系统,极大降低了传输成本,保障了任务性能,提升了系统稳健性. Xie等[4 ] 开发了深度学习驱动的语义通信系统,Tong等[5 ] 在无线网络中针对音频数据设计了基于CNN的高效传输系统. 在图像语义通信方面,Huang等[6 ] 使用生成对抗网络(generative adversarial networks, GAN)开发分阶段的编码过程,Patwa等[7 ] 提出提高视觉数据分析性能的压缩方法,Sun等[8 ] 研发图像传输的联合源通道编码技术. Wang等[9 -10 ] 采用对抗性损失优化编码方法,研究语义先验信息在图像压缩中的应用. Hu等[11 ] 设计的端到端系统框架能够显著提升系统稳健性,降低传输成本. ...
1
... 在深度学习和智能硬件的推动下,6G语义通信领域受到学术界的广泛关注. 研究者正致力于探索基于深度学习的通信技术,设计出基于文本、图像和音频的语义通信系统,极大降低了传输成本,保障了任务性能,提升了系统稳健性. Xie等[4 ] 开发了深度学习驱动的语义通信系统,Tong等[5 ] 在无线网络中针对音频数据设计了基于CNN的高效传输系统. 在图像语义通信方面,Huang等[6 ] 使用生成对抗网络(generative adversarial networks, GAN)开发分阶段的编码过程,Patwa等[7 ] 提出提高视觉数据分析性能的压缩方法,Sun等[8 ] 研发图像传输的联合源通道编码技术. Wang等[9 -10 ] 采用对抗性损失优化编码方法,研究语义先验信息在图像压缩中的应用. Hu等[11 ] 设计的端到端系统框架能够显著提升系统稳健性,降低传输成本. ...
5
... 在深度学习和智能硬件的推动下,6G语义通信领域受到学术界的广泛关注. 研究者正致力于探索基于深度学习的通信技术,设计出基于文本、图像和音频的语义通信系统,极大降低了传输成本,保障了任务性能,提升了系统稳健性. Xie等[4 ] 开发了深度学习驱动的语义通信系统,Tong等[5 ] 在无线网络中针对音频数据设计了基于CNN的高效传输系统. 在图像语义通信方面,Huang等[6 ] 使用生成对抗网络(generative adversarial networks, GAN)开发分阶段的编码过程,Patwa等[7 ] 提出提高视觉数据分析性能的压缩方法,Sun等[8 ] 研发图像传输的联合源通道编码技术. Wang等[9 -10 ] 采用对抗性损失优化编码方法,研究语义先验信息在图像压缩中的应用. Hu等[11 ] 设计的端到端系统框架能够显著提升系统稳健性,降低传输成本. ...
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
... 现有语义压缩方法从语义与任务相关性的角度训练编解码器实现压缩,缺乏有效的语义重要性度量标准,未充分考虑语义重要性对压缩效果的影响程度. 为了最大程度压缩冗余信息,有必要基于现有方案提出更全面的语义重要性评估方法进行语义信息衡量. 语义重要性的度量方法多用于文字或图像的恢复、传输和处理任务[22 ] ,分为以下3类. 1)基于语义相似度的语义重要性度量[23 -24 ] ,指通过计算不同语义信息在语义空间中的距离或相似度来衡量语义重要性. 在基于知识图谱的语义通信系统中,传输的句子通过知识图谱转换为三元组,三元组被视为基本的语义符号,通过计算三元组与句子的余弦相似度来表征三元组的语义重要性,根据信道质量自适应地调整传输内容,将更多的传输资源分配给重要的三元组,可以增强通信的可靠性[23 -24 ] . 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
... [8 ,26 ]. 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
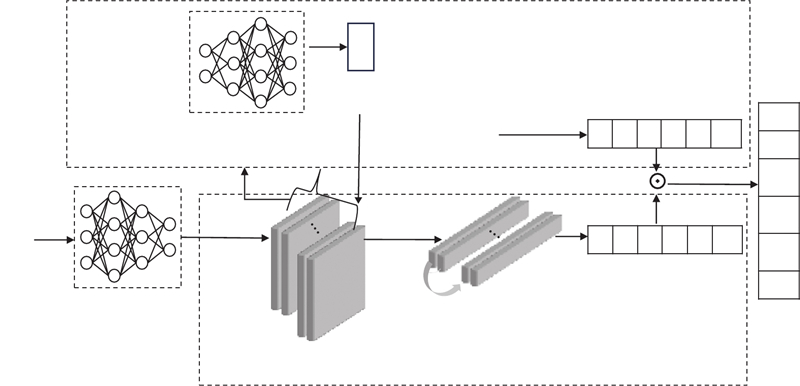
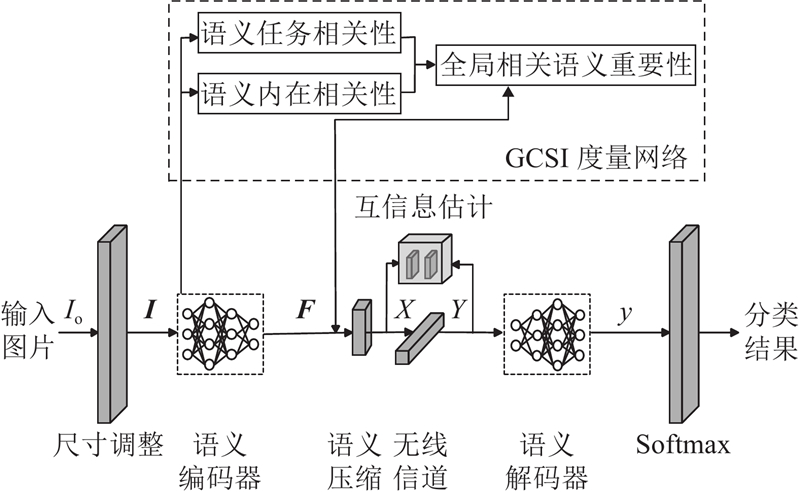
... 如图2 所示,基于GCSI的语义压缩算法网络结构以面向任务的语义通信框架为基础,由语义编码器、语义重要性度量模块、语义压缩和语义解码器等部分组成. 语义编码器基于CNN提取图片的语义特征,主要由卷积层和池化层构成. 语义重要性度量模块通过语义任务相关性和语义内在相关性衡量GCSI. 语义压缩模块根据GCSI自适应地保留少数重要的语义特征,语义解码器基于全连接层处理保留的语义特征,完成智能任务. 为了对编码器和解码器进行端到端(end-to-end,E2E)的训练,信道必须支持反向传播. 使用神经网络来定义物理信道模型. 例如,使用简单的神经网络来构建加性白高斯噪声(additive white Gaussian noise,AWGN)信道、乘性高斯噪声信道和擦除信道等[8 ,26 ] . 由于衰落信道的复杂特性,处理衰落信号通常使用更复杂的神经网络模型,以更准确地捕捉信道状态信息并提高信号恢复能力. 本研究关注语义编解码和语义压缩过程,选择简单的AWGN信道作为主要研究对象. ...
1
... 在深度学习和智能硬件的推动下,6G语义通信领域受到学术界的广泛关注. 研究者正致力于探索基于深度学习的通信技术,设计出基于文本、图像和音频的语义通信系统,极大降低了传输成本,保障了任务性能,提升了系统稳健性. Xie等[4 ] 开发了深度学习驱动的语义通信系统,Tong等[5 ] 在无线网络中针对音频数据设计了基于CNN的高效传输系统. 在图像语义通信方面,Huang等[6 ] 使用生成对抗网络(generative adversarial networks, GAN)开发分阶段的编码过程,Patwa等[7 ] 提出提高视觉数据分析性能的压缩方法,Sun等[8 ] 研发图像传输的联合源通道编码技术. Wang等[9 -10 ] 采用对抗性损失优化编码方法,研究语义先验信息在图像压缩中的应用. Hu等[11 ] 设计的端到端系统框架能够显著提升系统稳健性,降低传输成本. ...
Recognition-driven compressed image generation using semantic-prior information
1
2020
... 在深度学习和智能硬件的推动下,6G语义通信领域受到学术界的广泛关注. 研究者正致力于探索基于深度学习的通信技术,设计出基于文本、图像和音频的语义通信系统,极大降低了传输成本,保障了任务性能,提升了系统稳健性. Xie等[4 ] 开发了深度学习驱动的语义通信系统,Tong等[5 ] 在无线网络中针对音频数据设计了基于CNN的高效传输系统. 在图像语义通信方面,Huang等[6 ] 使用生成对抗网络(generative adversarial networks, GAN)开发分阶段的编码过程,Patwa等[7 ] 提出提高视觉数据分析性能的压缩方法,Sun等[8 ] 研发图像传输的联合源通道编码技术. Wang等[9 -10 ] 采用对抗性损失优化编码方法,研究语义先验信息在图像压缩中的应用. Hu等[11 ] 设计的端到端系统框架能够显著提升系统稳健性,降低传输成本. ...
1
... 在深度学习和智能硬件的推动下,6G语义通信领域受到学术界的广泛关注. 研究者正致力于探索基于深度学习的通信技术,设计出基于文本、图像和音频的语义通信系统,极大降低了传输成本,保障了任务性能,提升了系统稳健性. Xie等[4 ] 开发了深度学习驱动的语义通信系统,Tong等[5 ] 在无线网络中针对音频数据设计了基于CNN的高效传输系统. 在图像语义通信方面,Huang等[6 ] 使用生成对抗网络(generative adversarial networks, GAN)开发分阶段的编码过程,Patwa等[7 ] 提出提高视觉数据分析性能的压缩方法,Sun等[8 ] 研发图像传输的联合源通道编码技术. Wang等[9 -10 ] 采用对抗性损失优化编码方法,研究语义先验信息在图像压缩中的应用. Hu等[11 ] 设计的端到端系统框架能够显著提升系统稳健性,降低传输成本. ...
面向多任务的语义通信架构设计与实现
1
2024
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
面向多任务的语义通信架构设计与实现
1
2024
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
基于上下文语义相似度的软压缩方法
1
2024
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
基于上下文语义相似度的软压缩方法
1
2024
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
1
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
1
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
1
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
An end-to-end deep learning image compression framework based on semantic analysis
1
2019
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
1
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
Semantic communication system based on semantic slice models propagation
2
2023
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
... 已知信道的先验信息(AWGN 信道),因此设定$w$ $b$ $X$ ${R_{{\mathrm{SN}}}} $ $P $ [19 ] : ...
基于语义通信的低比特率图像语义编码方法
1
2023
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
基于语义通信的低比特率图像语义编码方法
1
2023
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
1
... 语义通信旨在传递数据中与语义相关的关键内容,它通过分析和提取数据的主要语义特征,在维持信息本质意义的同时对数据进行有效压缩,不但能够减少使用频谱资源,还能够在信道条件恶劣,尤其是在低信噪比(signal-to-noise ratio, SNR)的情况下,保持较高的稳定性和可靠性[4 ] . 语义通信方法强调理解发送者信息的重要性,实现有效的语义传达. 如联合图像专家小组(joint photographic experts group, JPEG)压缩的传统压缩方法在语义压缩过程中常忽视数据的深层含义和重要性,专注于提取并表达数据的核心语义信息,以便在节约存储空间的同时保持信息的完整性和准确性. 牛冠冲等[12 ] 将WebRTC-SVC技术与基于语义的运动检测及压缩(semantic motion detection and compression,SMDC)方法结合,采用分层编码技术优化视频数据的传输和处理效率. 莫肇豪等[13 ] 开发基于上下文语义相似度的图像压缩技术,利用LDPC码进行编码传输,该技术在噪声环境下展现出优于传统无损压缩方法的性能. Kutay等[14 ] 预训练神经网络,采用记忆和学习的策略实现对分类任务的数据压缩,Grassucci等[15 ] 探讨生成模型在语义通信中的作用和在减少数据流量、开启新任务方面的潜力. Li等[16 ] 提出的动态语义压缩方法适用于CNN推理任务,通过语义压缩和部分卸载提升了任务处理的准确性和效率. 这些研究凸显了语义压缩技术在减少数据冗余和维持信息完整性方面的重要性,关注神经网络架构在实现数据有效压缩方面的应用,Wang 等[17 -18 ] 评估图像像素与其语义内容的相关性,提出针对图像重要区域的特定编解码方法,强调语义任务相关性在决定编解码策略中的核心作用,有效改善了人眼的感知效果. Sun等[8 ] 采用基于语义任务相关性的方法,对特征进行语义信息与任务相关性加权,利用这种加权的均方误差(MSE)来训练通信模型,确保语义压缩的同时优先传输最重要的特征. Dong 等[19 ] 利用GAN构建包含基础模型和增强模型的语义压缩系统,特别设计的增强模型增强了语义任务的准确性和控制能力. 何晨光等[20 -21 ] 基于语义信息的任务重要性对语义特征进行语义压缩,强化了语义任务相关性在传输关键特征中的应用. ...
1
... 现有语义压缩方法从语义与任务相关性的角度训练编解码器实现压缩,缺乏有效的语义重要性度量标准,未充分考虑语义重要性对压缩效果的影响程度. 为了最大程度压缩冗余信息,有必要基于现有方案提出更全面的语义重要性评估方法进行语义信息衡量. 语义重要性的度量方法多用于文字或图像的恢复、传输和处理任务[22 ] ,分为以下3类. 1)基于语义相似度的语义重要性度量[23 -24 ] ,指通过计算不同语义信息在语义空间中的距离或相似度来衡量语义重要性. 在基于知识图谱的语义通信系统中,传输的句子通过知识图谱转换为三元组,三元组被视为基本的语义符号,通过计算三元组与句子的余弦相似度来表征三元组的语义重要性,根据信道质量自适应地调整传输内容,将更多的传输资源分配给重要的三元组,可以增强通信的可靠性[23 -24 ] . 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
Reliable semantic communication system enabled by knowledge graph
2
2022
... 现有语义压缩方法从语义与任务相关性的角度训练编解码器实现压缩,缺乏有效的语义重要性度量标准,未充分考虑语义重要性对压缩效果的影响程度. 为了最大程度压缩冗余信息,有必要基于现有方案提出更全面的语义重要性评估方法进行语义信息衡量. 语义重要性的度量方法多用于文字或图像的恢复、传输和处理任务[22 ] ,分为以下3类. 1)基于语义相似度的语义重要性度量[23 -24 ] ,指通过计算不同语义信息在语义空间中的距离或相似度来衡量语义重要性. 在基于知识图谱的语义通信系统中,传输的句子通过知识图谱转换为三元组,三元组被视为基本的语义符号,通过计算三元组与句子的余弦相似度来表征三元组的语义重要性,根据信道质量自适应地调整传输内容,将更多的传输资源分配给重要的三元组,可以增强通信的可靠性[23 -24 ] . 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
... [23 -24 ]. 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
2
... 现有语义压缩方法从语义与任务相关性的角度训练编解码器实现压缩,缺乏有效的语义重要性度量标准,未充分考虑语义重要性对压缩效果的影响程度. 为了最大程度压缩冗余信息,有必要基于现有方案提出更全面的语义重要性评估方法进行语义信息衡量. 语义重要性的度量方法多用于文字或图像的恢复、传输和处理任务[22 ] ,分为以下3类. 1)基于语义相似度的语义重要性度量[23 -24 ] ,指通过计算不同语义信息在语义空间中的距离或相似度来衡量语义重要性. 在基于知识图谱的语义通信系统中,传输的句子通过知识图谱转换为三元组,三元组被视为基本的语义符号,通过计算三元组与句子的余弦相似度来表征三元组的语义重要性,根据信道质量自适应地调整传输内容,将更多的传输资源分配给重要的三元组,可以增强通信的可靠性[23 -24 ] . 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
... -24 ]. 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
人工智能物联网中面向智能任务的语义通信方法
6
2021
... 现有语义压缩方法从语义与任务相关性的角度训练编解码器实现压缩,缺乏有效的语义重要性度量标准,未充分考虑语义重要性对压缩效果的影响程度. 为了最大程度压缩冗余信息,有必要基于现有方案提出更全面的语义重要性评估方法进行语义信息衡量. 语义重要性的度量方法多用于文字或图像的恢复、传输和处理任务[22 ] ,分为以下3类. 1)基于语义相似度的语义重要性度量[23 -24 ] ,指通过计算不同语义信息在语义空间中的距离或相似度来衡量语义重要性. 在基于知识图谱的语义通信系统中,传输的句子通过知识图谱转换为三元组,三元组被视为基本的语义符号,通过计算三元组与句子的余弦相似度来表征三元组的语义重要性,根据信道质量自适应地调整传输内容,将更多的传输资源分配给重要的三元组,可以增强通信的可靠性[23 -24 ] . 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
... 语义重要性的度量方法没有统一的衡量标准,且现有方法存在片面性,未从语义对智能任务影响和语义在语义空间中重要性的双重维度进行全面考虑. 本研究提出基于全局相关语义重要性(global correlated semantic importance, GCSI)的语义压缩算法,从语义对智能任务影响程度和语义特征在语义空间的相关性全面度量语义特征的重要性,将智能任务结果对语义特征的梯度定义为语义任务相关性[25 ] ,将语义特征在语义空间的相关性定义为语义内在相关性. ...
... 实验使用Ubuntu 20.04操作系统,采用Pytorch深度学习库,编程采用Python语言. 在图像识别领域,ResNet结构已被证实能够在提高分类精度和模型泛化能力方面发挥显著效用[25 ] . 在分类实验中,选用ResNet结构作为特征提取的网络结构,完成精确且高效的图像分类. 本研究的特征提取网络架构为ResNet18,它在处理速度和资源消耗方面具有显著优势,适合在资源受限的环境中运行,能够满足实时处理的应用需求;该网络结构被广泛应用于有节约资源需求的各种任务中,并且处理图像分类和特征提取的性能良好. ResNet18模型的训练参数:50轮迭代,批次大小为12,优化器采用随机梯度下降,学习率为0.01. 系统仿真参数方面,待分类图片为8 000张,无线信道类型为高斯信道,压缩比例分别为0.65、0.80、0.85和0.90. 在进行对比实验时,为了确保公平和一致性,各个对比实验均采用统一的实验设置和模型生成方法:所有算法均使用相同的硬件配置、软件环境和神经网络基础架构,即采用ResNet18作为特征提取的主体结构,确保所有数据都经过相同的预处理步骤,包括图像的大小调整和归一化处理. 实验中使用的训练和测试数据集完全一致,以排除数据变异对实验结果的影响. 对比的关键在于语义重要性的度量和语义压缩算法的实现方式. 在测试过程中,对不同的语义压缩方法进行实验,每种方法都采用独特的策略来评估语义特征的重要性,并据此进行数据压缩. 不同的语义重要性评估方法直接影响压缩算法的选择和性能,决定哪些数据须保留,哪些数据可以被压缩或丢弃. ...
... 将所提算法与基于随机压缩算法和基于语义任务相关性的语义压缩算法[25 ,28 ] 进行对比. 设置信噪比为20 dB,如表1 所示为不同压缩方法在各个压缩率设置下的性能测试结果. 表中,p 、r 、F1分别为精确率、召回率和F1分数. 可以看出,所提算法在各个评价指标上均优于对比算法. 特别是在较低的压缩率(如$\tau $
... Performance testing results of different compression algorithms in STL-10 dataset
Tab.1 算法 $\tau = 0.98 $ $\tau = 0.90 $ $\tau = 0.80 $ $\tau = 0.60 $ Acc p r F1 Acc p r F1 Acc p r F1 Acc p r F1 本研究 0.81 0.82 0.81 0.81 0.94 0.94 0.94 0.94 0.95 0.95 0.95 0.95 0.96 0.96 0.96 0.96 文献[25 ]、[28 ] 0.70 0.84 0.70 0.70 0.90 0.92 0.90 0.91 0.93 0.93 0.93 0.93 0.94 0.95 0.94 0.94 随机压缩 0.54 0.60 0.54 0.48 0.63 0.79 0.63 0.61 0.79 0.86 0.79 0.77 0.91 0.92 0.91 0.91
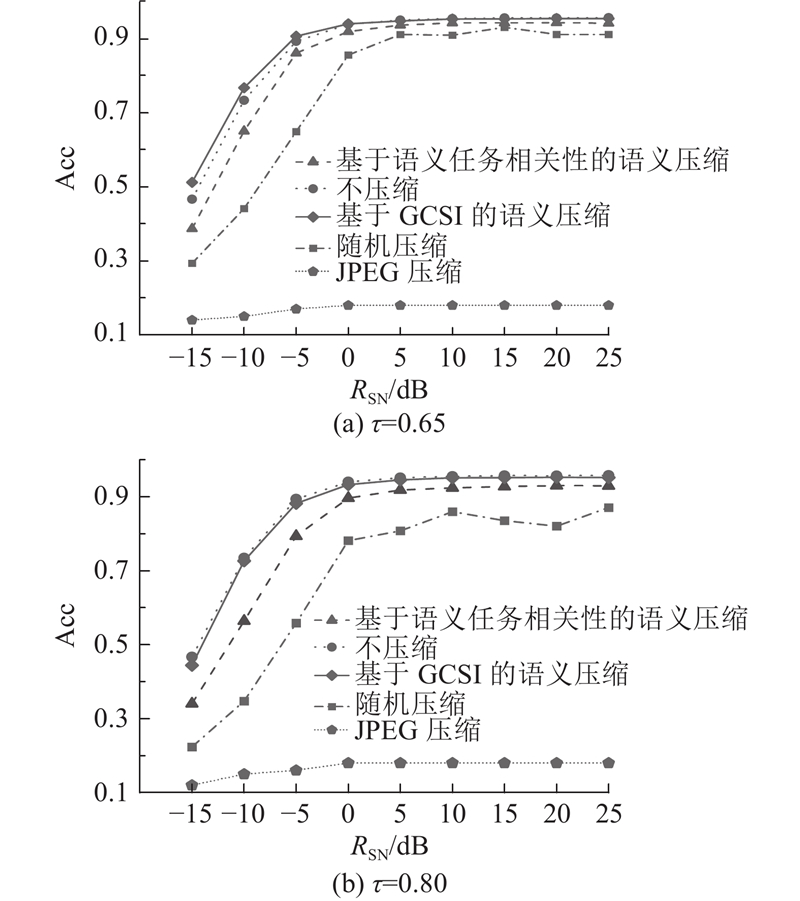
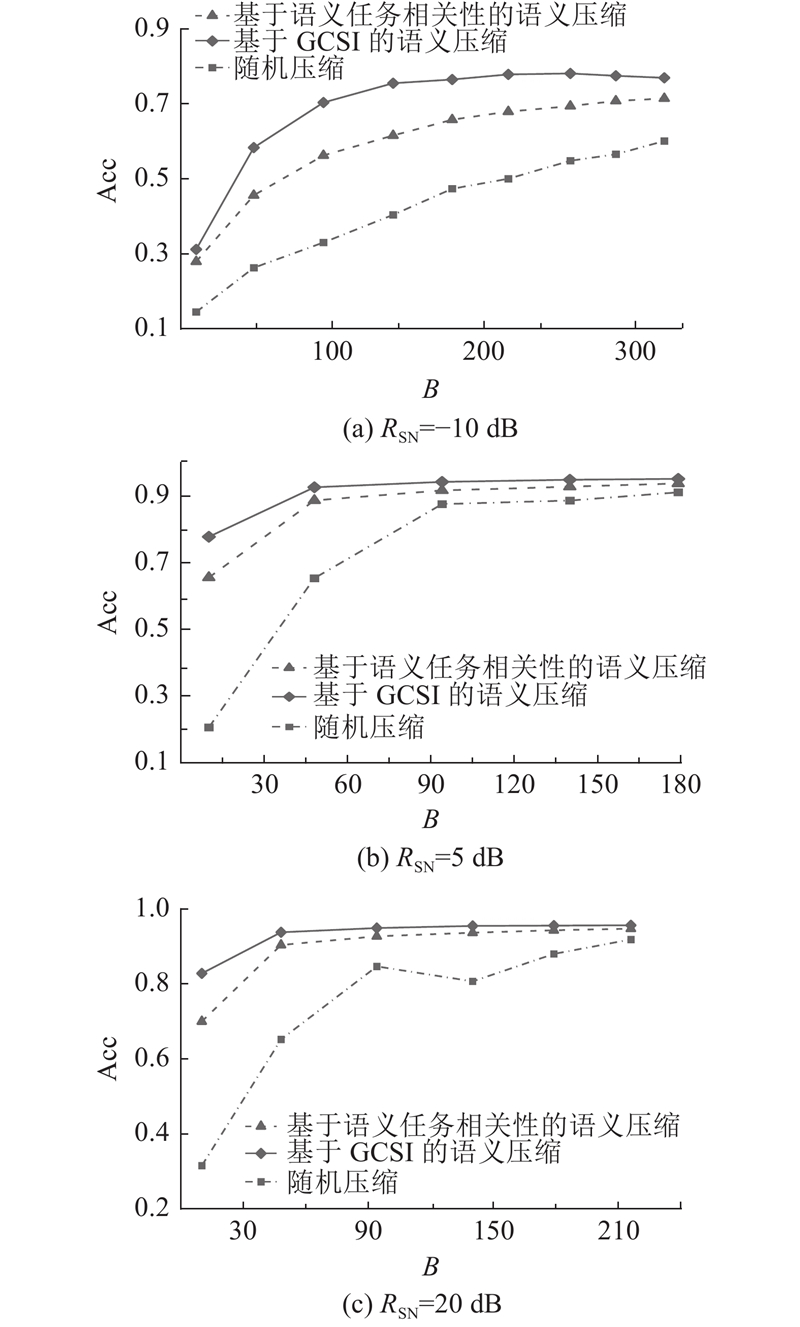
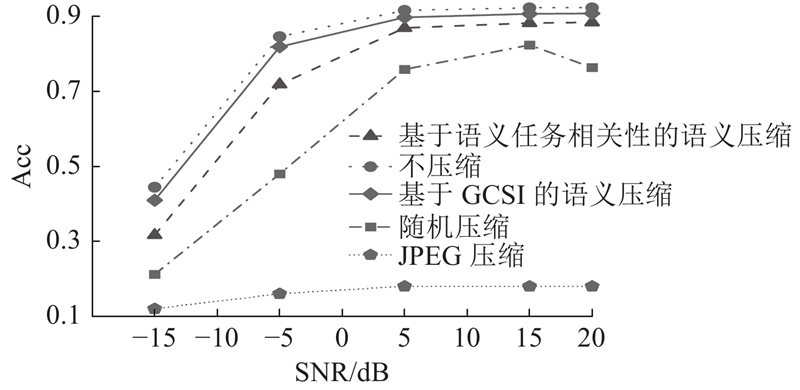
3.4.1. 不同信噪比条件下任务性能分析 如图4 所示为2种压缩率条件下,不同压缩方式的性能对比分析. 当$\tau $ 图4 (a)中,在较低信噪比的情况下,基于GCSI的语义压缩性能略优于不压缩,图4 (b)中没有这种现象,这主要是由信噪比、压缩率和特征的选择相互影响决定的. 一方面,在低信噪比的环境中,由于噪声比例较高,传统的包含大量冗余信息的完整数据容易受到噪声的干扰. GCSI通过有选择地压缩数据,减少了可能受噪声影响的数据量. 这种策略不仅降低了数据的复杂度,还保留了数据的核心语义,在功能性任务(如分类)中,相对于未压缩的数据,压缩后的数据能够展示更优的性能. 另一方面,随着压缩率的进一步提高,更多的关键信息被丢弃,导致即使是高性能的GCSI算法也无法完全克服信息丢失带来的影响. 这表明虽然GCSI算法在一定程度上能够优化信息的保留,但在非常高的压缩率下有局限性. 传统的压缩方法如JPEG压缩在所有信噪比条件下性能提升有限,基于GCSI的压缩方法在信噪比提升时能够更有效地增强任务性能. 相比之下,基于GCSI的语义压缩方法能更好地保持数据的语义信息,这对于在复杂通信环境中传输信息至关重要. 图4 表明,在实际应用中基于GCSI的语义压缩方法适应各种信道条件,特别是在信噪比低的情况下,该算法仍然能够保证高效且可靠的信息传输. ...
... Performance testing results of different compression algorithms in CIFAR-10 dataset
Tab.2 算法 $\tau = 0.98 $ $\tau = 0.90$ $\tau = 0.80 $ $\tau = 0.60 $ Acc p r F1 Acc p r F1 Acc p r F1 Acc p r F1 本研究 0.79 0.79 0.79 0.79 0.90 0.90 0.90 0.89 0.91 0.91 0.91 0.91 0.92 0.92 0.92 0.92 文献[25 ]、[28 ] 0.68 0.73 0.68 0.68 0.85 0.86 0.85 0.85 0.88 0.89 0.88 0.88 0.91 0.91 0.91 0.91 随机压缩 0.17 0.30 0.17 0.11 0.65 0.78 0.65 0.62 0.76 0.80 0.76 0.73 0.86 0.88 0.86 0.85
图 6 不同压缩算法在不同信噪比下的分类准确度(CIFAR-10数据集) ...
人工智能物联网中面向智能任务的语义通信方法
6
2021
... 现有语义压缩方法从语义与任务相关性的角度训练编解码器实现压缩,缺乏有效的语义重要性度量标准,未充分考虑语义重要性对压缩效果的影响程度. 为了最大程度压缩冗余信息,有必要基于现有方案提出更全面的语义重要性评估方法进行语义信息衡量. 语义重要性的度量方法多用于文字或图像的恢复、传输和处理任务[22 ] ,分为以下3类. 1)基于语义相似度的语义重要性度量[23 -24 ] ,指通过计算不同语义信息在语义空间中的距离或相似度来衡量语义重要性. 在基于知识图谱的语义通信系统中,传输的句子通过知识图谱转换为三元组,三元组被视为基本的语义符号,通过计算三元组与句子的余弦相似度来表征三元组的语义重要性,根据信道质量自适应地调整传输内容,将更多的传输资源分配给重要的三元组,可以增强通信的可靠性[23 -24 ] . 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
... 语义重要性的度量方法没有统一的衡量标准,且现有方法存在片面性,未从语义对智能任务影响和语义在语义空间中重要性的双重维度进行全面考虑. 本研究提出基于全局相关语义重要性(global correlated semantic importance, GCSI)的语义压缩算法,从语义对智能任务影响程度和语义特征在语义空间的相关性全面度量语义特征的重要性,将智能任务结果对语义特征的梯度定义为语义任务相关性[25 ] ,将语义特征在语义空间的相关性定义为语义内在相关性. ...
... 实验使用Ubuntu 20.04操作系统,采用Pytorch深度学习库,编程采用Python语言. 在图像识别领域,ResNet结构已被证实能够在提高分类精度和模型泛化能力方面发挥显著效用[25 ] . 在分类实验中,选用ResNet结构作为特征提取的网络结构,完成精确且高效的图像分类. 本研究的特征提取网络架构为ResNet18,它在处理速度和资源消耗方面具有显著优势,适合在资源受限的环境中运行,能够满足实时处理的应用需求;该网络结构被广泛应用于有节约资源需求的各种任务中,并且处理图像分类和特征提取的性能良好. ResNet18模型的训练参数:50轮迭代,批次大小为12,优化器采用随机梯度下降,学习率为0.01. 系统仿真参数方面,待分类图片为8 000张,无线信道类型为高斯信道,压缩比例分别为0.65、0.80、0.85和0.90. 在进行对比实验时,为了确保公平和一致性,各个对比实验均采用统一的实验设置和模型生成方法:所有算法均使用相同的硬件配置、软件环境和神经网络基础架构,即采用ResNet18作为特征提取的主体结构,确保所有数据都经过相同的预处理步骤,包括图像的大小调整和归一化处理. 实验中使用的训练和测试数据集完全一致,以排除数据变异对实验结果的影响. 对比的关键在于语义重要性的度量和语义压缩算法的实现方式. 在测试过程中,对不同的语义压缩方法进行实验,每种方法都采用独特的策略来评估语义特征的重要性,并据此进行数据压缩. 不同的语义重要性评估方法直接影响压缩算法的选择和性能,决定哪些数据须保留,哪些数据可以被压缩或丢弃. ...
... 将所提算法与基于随机压缩算法和基于语义任务相关性的语义压缩算法[25 ,28 ] 进行对比. 设置信噪比为20 dB,如表1 所示为不同压缩方法在各个压缩率设置下的性能测试结果. 表中,p 、r 、F1分别为精确率、召回率和F1分数. 可以看出,所提算法在各个评价指标上均优于对比算法. 特别是在较低的压缩率(如$\tau $
... Performance testing results of different compression algorithms in STL-10 dataset
Tab.1 算法 $\tau = 0.98 $ $\tau = 0.90 $ $\tau = 0.80 $ $\tau = 0.60 $ Acc p r F1 Acc p r F1 Acc p r F1 Acc p r F1 本研究 0.81 0.82 0.81 0.81 0.94 0.94 0.94 0.94 0.95 0.95 0.95 0.95 0.96 0.96 0.96 0.96 文献[25 ]、[28 ] 0.70 0.84 0.70 0.70 0.90 0.92 0.90 0.91 0.93 0.93 0.93 0.93 0.94 0.95 0.94 0.94 随机压缩 0.54 0.60 0.54 0.48 0.63 0.79 0.63 0.61 0.79 0.86 0.79 0.77 0.91 0.92 0.91 0.91
3.4.1. 不同信噪比条件下任务性能分析 如图4 所示为2种压缩率条件下,不同压缩方式的性能对比分析. 当$\tau $ 图4 (a)中,在较低信噪比的情况下,基于GCSI的语义压缩性能略优于不压缩,图4 (b)中没有这种现象,这主要是由信噪比、压缩率和特征的选择相互影响决定的. 一方面,在低信噪比的环境中,由于噪声比例较高,传统的包含大量冗余信息的完整数据容易受到噪声的干扰. GCSI通过有选择地压缩数据,减少了可能受噪声影响的数据量. 这种策略不仅降低了数据的复杂度,还保留了数据的核心语义,在功能性任务(如分类)中,相对于未压缩的数据,压缩后的数据能够展示更优的性能. 另一方面,随着压缩率的进一步提高,更多的关键信息被丢弃,导致即使是高性能的GCSI算法也无法完全克服信息丢失带来的影响. 这表明虽然GCSI算法在一定程度上能够优化信息的保留,但在非常高的压缩率下有局限性. 传统的压缩方法如JPEG压缩在所有信噪比条件下性能提升有限,基于GCSI的压缩方法在信噪比提升时能够更有效地增强任务性能. 相比之下,基于GCSI的语义压缩方法能更好地保持数据的语义信息,这对于在复杂通信环境中传输信息至关重要. 图4 表明,在实际应用中基于GCSI的语义压缩方法适应各种信道条件,特别是在信噪比低的情况下,该算法仍然能够保证高效且可靠的信息传输. ...
... Performance testing results of different compression algorithms in CIFAR-10 dataset
Tab.2 算法 $\tau = 0.98 $ $\tau = 0.90$ $\tau = 0.80 $ $\tau = 0.60 $ Acc p r F1 Acc p r F1 Acc p r F1 Acc p r F1 本研究 0.79 0.79 0.79 0.79 0.90 0.90 0.90 0.89 0.91 0.91 0.91 0.91 0.92 0.92 0.92 0.92 文献[25 ]、[28 ] 0.68 0.73 0.68 0.68 0.85 0.86 0.85 0.85 0.88 0.89 0.88 0.88 0.91 0.91 0.91 0.91 随机压缩 0.17 0.30 0.17 0.11 0.65 0.78 0.65 0.62 0.76 0.80 0.76 0.73 0.86 0.88 0.86 0.85
图 6 不同压缩算法在不同信噪比下的分类准确度(CIFAR-10数据集) ...
Adopting abstract images for semantic scene understanding
5
2016
... 现有语义压缩方法从语义与任务相关性的角度训练编解码器实现压缩,缺乏有效的语义重要性度量标准,未充分考虑语义重要性对压缩效果的影响程度. 为了最大程度压缩冗余信息,有必要基于现有方案提出更全面的语义重要性评估方法进行语义信息衡量. 语义重要性的度量方法多用于文字或图像的恢复、传输和处理任务[22 ] ,分为以下3类. 1)基于语义相似度的语义重要性度量[23 -24 ] ,指通过计算不同语义信息在语义空间中的距离或相似度来衡量语义重要性. 在基于知识图谱的语义通信系统中,传输的句子通过知识图谱转换为三元组,三元组被视为基本的语义符号,通过计算三元组与句子的余弦相似度来表征三元组的语义重要性,根据信道质量自适应地调整传输内容,将更多的传输资源分配给重要的三元组,可以增强通信的可靠性[23 -24 ] . 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
... [26 -27 ],指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
... [26 ],这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
... 如图2 所示,基于GCSI的语义压缩算法网络结构以面向任务的语义通信框架为基础,由语义编码器、语义重要性度量模块、语义压缩和语义解码器等部分组成. 语义编码器基于CNN提取图片的语义特征,主要由卷积层和池化层构成. 语义重要性度量模块通过语义任务相关性和语义内在相关性衡量GCSI. 语义压缩模块根据GCSI自适应地保留少数重要的语义特征,语义解码器基于全连接层处理保留的语义特征,完成智能任务. 为了对编码器和解码器进行端到端(end-to-end,E2E)的训练,信道必须支持反向传播. 使用神经网络来定义物理信道模型. 例如,使用简单的神经网络来构建加性白高斯噪声(additive white Gaussian noise,AWGN)信道、乘性高斯噪声信道和擦除信道等[8 ,26 ] . 由于衰落信道的复杂特性,处理衰落信号通常使用更复杂的神经网络模型,以更准确地捕捉信道状态信息并提高信号恢复能力. 本研究关注语义编解码和语义压缩过程,选择简单的AWGN信道作为主要研究对象. ...
... 将信道带宽$B$ [26 ] . 如图5 所示为固定信噪比条件下,不同信道带宽对不同压缩方法性能的影响. 结果表明,在不同的信噪比水平下,随着带宽的减小,3种压缩方法的性能均受到影响且差异明显. 随机压缩方法对带宽的依赖性最强,其任务性能随带宽的减小而大幅下降. 基于语义任务相关性的语义压缩虽然也表现出对带宽的依赖性,但其性能衰减速度较慢. 基于GCSI的语义压缩表现出对带宽变化的最小敏感性,即使在极低的带宽条件下,也能保持超过80%的任务处理性能,证明它具有出色的带宽适应性. 基于GCSI的方法不仅在低带宽条件下表现出色,在带宽充裕的环境中也能有效利用可用资源,保持高效的性能,能够在未来的大数据量智能物联网环境中发挥关键作用,减轻信道带宽的负担,提高数据传输的效率与可靠性. 面对日益增长的数据传输量,该方法可以为物联网设备提供更加稳定和高效的通信解决方案,支撑起智能物联网环境下的高速数据交换和处理需求. ...
3
... 现有语义压缩方法从语义与任务相关性的角度训练编解码器实现压缩,缺乏有效的语义重要性度量标准,未充分考虑语义重要性对压缩效果的影响程度. 为了最大程度压缩冗余信息,有必要基于现有方案提出更全面的语义重要性评估方法进行语义信息衡量. 语义重要性的度量方法多用于文字或图像的恢复、传输和处理任务[22 ] ,分为以下3类. 1)基于语义相似度的语义重要性度量[23 -24 ] ,指通过计算不同语义信息在语义空间中的距离或相似度来衡量语义重要性. 在基于知识图谱的语义通信系统中,传输的句子通过知识图谱转换为三元组,三元组被视为基本的语义符号,通过计算三元组与句子的余弦相似度来表征三元组的语义重要性,根据信道质量自适应地调整传输内容,将更多的传输资源分配给重要的三元组,可以增强通信的可靠性[23 -24 ] . 2)基于梯度的重要性度量[8 ,25 ] ,指基于智能任务感知结果相对于语义特征的梯度来度量语义重要性. 在面向智能任务的语义通信系统中,神经网络从原始数据中提取语义特征,当信道资源比较紧张和时延敏感时,语义特征通常被压缩以减轻信道负担,语义特征对智能任务处理结果的影响程度不同,为了度量语义特征的重要性程度,提出基于梯度处理的重要性度量,从而在有限的信道资源下保证任务的处理性能[8 ,26 ] . 3)基于信息量的语义重要性度量[26 -27 ] ,指通过分析语义特征与对应语义类别的互信息来衡量语义通信中的重要信息. 在语义场景理解中,不仅要考虑信息的频率和普遍性[27 ] ,还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
... [27 ],还要评估其在构建场景意义中的独特作用. 分析抽象图像的高层次特征可以量化每个特征对整体语义理解的贡献[26 ] ,这在资源有限的通信系统中尤为有效,能够在带宽和处理能力有限的情况下,传输最重要的语义信息. ...
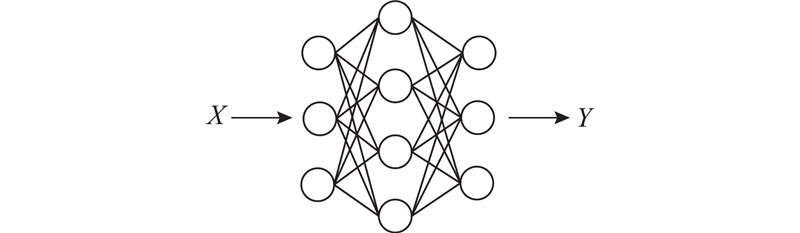
... 其中噪声$b$ ${\sigma ^2}$ [27 ] ,构建由2层全连接网络组成互信息估计网络,核心思想是通过最大化输入和输出之间的互信息$I$
3
... 将所提算法与基于随机压缩算法和基于语义任务相关性的语义压缩算法[25 ,28 ] 进行对比. 设置信噪比为20 dB,如表1 所示为不同压缩方法在各个压缩率设置下的性能测试结果. 表中,p 、r 、F1分别为精确率、召回率和F1分数. 可以看出,所提算法在各个评价指标上均优于对比算法. 特别是在较低的压缩率(如$\tau $
... Performance testing results of different compression algorithms in STL-10 dataset
Tab.1 算法 $\tau = 0.98 $ $\tau = 0.90 $ $\tau = 0.80 $ $\tau = 0.60 $ Acc p r F1 Acc p r F1 Acc p r F1 Acc p r F1 本研究 0.81 0.82 0.81 0.81 0.94 0.94 0.94 0.94 0.95 0.95 0.95 0.95 0.96 0.96 0.96 0.96 文献[25 ]、[28 ] 0.70 0.84 0.70 0.70 0.90 0.92 0.90 0.91 0.93 0.93 0.93 0.93 0.94 0.95 0.94 0.94 随机压缩 0.54 0.60 0.54 0.48 0.63 0.79 0.63 0.61 0.79 0.86 0.79 0.77 0.91 0.92 0.91 0.91
3.4.1. 不同信噪比条件下任务性能分析 如图4 所示为2种压缩率条件下,不同压缩方式的性能对比分析. 当$\tau $ 图4 (a)中,在较低信噪比的情况下,基于GCSI的语义压缩性能略优于不压缩,图4 (b)中没有这种现象,这主要是由信噪比、压缩率和特征的选择相互影响决定的. 一方面,在低信噪比的环境中,由于噪声比例较高,传统的包含大量冗余信息的完整数据容易受到噪声的干扰. GCSI通过有选择地压缩数据,减少了可能受噪声影响的数据量. 这种策略不仅降低了数据的复杂度,还保留了数据的核心语义,在功能性任务(如分类)中,相对于未压缩的数据,压缩后的数据能够展示更优的性能. 另一方面,随着压缩率的进一步提高,更多的关键信息被丢弃,导致即使是高性能的GCSI算法也无法完全克服信息丢失带来的影响. 这表明虽然GCSI算法在一定程度上能够优化信息的保留,但在非常高的压缩率下有局限性. 传统的压缩方法如JPEG压缩在所有信噪比条件下性能提升有限,基于GCSI的压缩方法在信噪比提升时能够更有效地增强任务性能. 相比之下,基于GCSI的语义压缩方法能更好地保持数据的语义信息,这对于在复杂通信环境中传输信息至关重要. 图4 表明,在实际应用中基于GCSI的语义压缩方法适应各种信道条件,特别是在信噪比低的情况下,该算法仍然能够保证高效且可靠的信息传输. ...
... Performance testing results of different compression algorithms in CIFAR-10 dataset
Tab.2 算法 $\tau = 0.98 $ $\tau = 0.90$ $\tau = 0.80 $ $\tau = 0.60 $ Acc p r F1 Acc p r F1 Acc p r F1 Acc p r F1 本研究 0.79 0.79 0.79 0.79 0.90 0.90 0.90 0.89 0.91 0.91 0.91 0.91 0.92 0.92 0.92 0.92 文献[25 ]、[28 ] 0.68 0.73 0.68 0.68 0.85 0.86 0.85 0.85 0.88 0.89 0.88 0.88 0.91 0.91 0.91 0.91 随机压缩 0.17 0.30 0.17 0.11 0.65 0.78 0.65 0.62 0.76 0.80 0.76 0.73 0.86 0.88 0.86 0.85
图 6 不同压缩算法在不同信噪比下的分类准确度(CIFAR-10数据集) ...