基于多模型Stacking融合的基坑测斜时序预测

doi:10.3785/j.issn.1008-973X.2025.04.006

基于多模型Stacking融合的基坑测斜时序预测

胡比澜^,, 王洋洋, 张永强^,

1. 浙江大学建筑工程学院，浙江杭州 310058

2. 国家电投集团云南国际电力投资有限公司，云南昆明 650228

Time series prediction of horizontal displacement in foundation pits based on Stacking multi-model

HU Bilan^,, WANG Yangyang, ZHANG Yongqiang^,

1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

2. SPIC Yunnan International Power Investment Limited Company, Kunming 650228, China

通讯作者: 张永强，男，教授. orcid.org/0000-0002-8956-5985. E-mail：cyqzhang@zju.edu.cn

收稿日期: 2024-02-6

Received: 2024-02-6

作者简介 About authors

胡比澜（1997—），女，硕士生，从事基坑变形预测研究.orcid.org/0009-0006-7060-2965.E-mail：hubilan@zju.edu.cn , E-mail：hubilan@zju.edu.cn

摘要

为了准确预测基坑倾斜变形，提出基于极致梯度提升(XGBoost)、长短期记忆（LSTM）和线性回归（LR）的堆叠多变量预测模型. 利用XGBoost集成学习的优越性和双层LSTM算法预测传统基坑变形的准确度，提升模型的预测精度和泛化能力. 在数据预处理阶段，引入K最近邻（KNN）插补算法增加可有效利用的数据总量，使用深度学习模型Informer的时间信息处理方式，改善传统算法中有监督学习忽略时间序列数据不同时间间隔的问题. 以杭州某在建基坑为工程案例，插补616条缺失数据，将时间信息转为3列时间点特征信息，使用所提模型进行基坑变形预测分析. 已有实测数据验证表明，所提模型在预测基坑最大测斜位移及该位移点处深度时的训练精度和泛化能力相比双层LSTM模型及XGBoost模型均有较大提升，使用时间点特征的XGBoost模型比LSTM模型更适合预测对时间因素敏感的指标.

关键词： 时间序列分析 ; 基坑测斜 ; 双层LSTM ; 极致梯度提升（XGBoost） ; 堆叠算法

Abstract

In order to accurately predict the lateral deformation of a foundation pit, a multivariable stacking prediction model based on extreme gradient boosting (XGBoost), long short-term memory (LSTM) and linear regression (LR) was proposed. By using the XGBoost’s advantage of ensemble learning and the accuracy of the two-layer LSTM algorithm in the traditional foundation pit deformation prediction, the prediction accuracy and the generalization ability of the model were improved. In the data pre-processing stage, the K-nearest neighbors (KNN) interpolation algorithm was introduced to increase the total amount of data that can be effectively utilized, and the processing method of time information in the deep learning model Informer was used to deal with the problem of ignoring the different time intervals of time series data by supervised learning in the traditional algorithm. Taking a foundation pit under construction in Hangzhou as a practical engineering case, 616 missing data were interpolated, the time information was converted into three columns of time point feature information, and the proposed model was used for foundation pit deformation analysis. Existing measured data verified that the training accuracy and the generalization ability of the proposed model were greatly improved compared with both the two-layer LSTM model and the XGBoost model when predicting the maximum slope displacement of the foundation pit and the depth of the displacement point. The XGBoost model, which used time-point features, was more suitable for predicting time-sensitive indicators than the LSTM model.

Keywords： time series analysis ; foundation pits lateral deformation ; two-layer LSTM ; extreme gradient boosting (XGBoost) ; Stacking algorithm

PDF (2018KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

胡比澜, 王洋洋, 张永强. 基于多模型Stacking融合的基坑测斜时序预测. 浙江大学学报(工学版)[J], 2025, 59(4): 706-716 doi:10.3785/j.issn.1008-973X.2025.04.006

HU Bilan, WANG Yangyang, ZHANG Yongqiang. Time series prediction of horizontal displacement in foundation pits based on Stacking multi-model. Journal of Zhejiang University(Engineering Science)[J], 2025, 59(4): 706-716 doi:10.3785/j.issn.1008-973X.2025.04.006

开发和完善城市地下空间是社会发展的必然趋势^[1-2]. 中国的地下空间开发利用历经多个阶段的发展，逐步从轨道交通过渡到地下综合体以及人防工程^[3-4]. 由于地基开挖是卸荷过程，会导致基坑周围土体应力场的变化和地表沉降. 支护结构（如地下连续墙）在基坑内外的压力差之下会产生水平向的位移，使支护结构后方的土体产生水平位移. 在地下空间施工中，必须做好基坑的应力及位移监测，保障基坑安全.

除实测及数值分析外，机器学习方法被广泛应用于基坑变形预测问题上. 李尚明等^[5]使用计算机视觉方法预测基坑变形位移图像. 曹净等^[6]使用小波变换实现基坑深层水平位移的滚动预测. 程龙飞等^[7]使用前馈神经网络预测测斜管堵塞段位移和基坑壁的变形趋势. 王雨等^[8]使用遗传算法和广义回归神经网络优化围护结构的变形预测结果. 考虑到不同监测点的空间特征，洪宇超等^[9]将CNN与长短期记忆神经网络(long short-term memory, LSTM)结合进行地表沉降预测，沉降预测结果优于仅考虑时间关联性的单一LSTM模型. 陈艳茹^[10]利用遗传算法优化极限学习机的权值和阈值，改善了基坑变形预测精度. 李彦杰等^[11]使用遗传算法优化BP神经网络中的权重和阈值，提高了围护结构水平位移的预测准确性. 刘锦等^[12]优化了GA-BP神经网络的预测结果. 徐长节等^[13]采用考虑时序性输入的循环神经网络（RNN）模型预测不同基坑支护结构的最大侧移. Li等^[14]将双向LSTM与自注意力机制结合，实现动态预测深基坑相邻建筑物的竖向位移. Ding等^[15]采用粒子群算法及神经网络理解岩质边坡的变形演化和失稳机制. 秦胜伍等^[16]采用堆叠（Stacking）集成学习对地面沉降进行预测，发现集成学习在基坑预测上的优越性. Xu等^[17]基于多保真深度算子网络，实现隧道掘进中的实时地面沉降预测.

在上述预测方法中，仅袁金荣等^[18]（使用多项式插值）、曹净等^[6]（使用分段线性插值）考虑数据等时间间隔收集问题，Li等^[14]（使用线性插值）考虑缺失数据. 本研究提出基于K最近邻算法(K-nearest neighbors, KNN)进行数据插补、极致梯度提升(extreme gradient boosting, XGBoost)和双层LSTM的堆叠多变量预测模型，利用深度学习模型Informer^[19]的时间信息处理方式对时间特征进行数据转换，在杭州某基坑中进行实例变形预测研究.

1. 算法原理

1.1. 基于堆叠算法的多模型融合预测

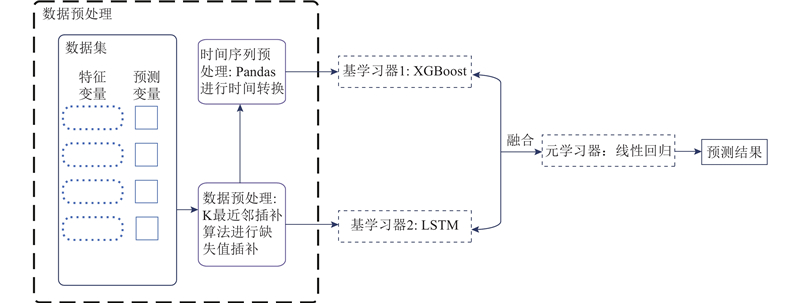
集成学习一般分为提升算法（Boosting）、装袋算法（Bagging）和堆叠算法（Stacking）. Stacking是集成了2个及以上不同种类的基学习器，被称为异质集成方法. Stacking可以降低模型的方差，但对模型本身的偏差影响不大，高偏差低方差的计算方式能够提升模型的计算精度. Stacking有2类学习器：基学习器与元学习器，先构建多种不同类别的基学习器，分别得到不同的预测结果，再基于这些基学习器的学习结果构建元学习器，得到最终的预测结果. 在实际预测中，若某个基学习器在预测过程中产生错误，Stacking可以通过元学习器采用其他类别基学习器产生的预测结果，适度纠正该类错误. 陈振宇等^[20]在电力负荷预测中使用XGBoost和LSTM组合模型，成功提升了超短期电力负荷预测精度，通过对比实验发现，不是所有的模型单一组合都能有效提高精度，正确选择参与组合的单一模型是降低预测误差的前提. XGBoost在保证预测精度情况下，运行速度高于同类树模型，使用也较为方便，用户可以通过Python的机器学习库scikit-learn实现模型的训练与评估. LSTM为传统处理时间序列相关问题的循环神经网络，能够有效解决长期依赖问题，适合处理本研究的长时间序列问题. 如图1所示为本研究所提Stacking的计算流程，其中元学习器拟使用线性回归算法.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1 堆叠算法计算流程图

Fig.1 Flow chart of Stacking algorithm

1.2. K最近邻插补算法

KNN^[21]是经典的机器学习算法. K最近邻插补算法（KNNImputer）是基于KNN的缺失值插补方法，可以通过欧几里得距离矩阵找寻最近邻点，从而估算数据中的缺失值. 相比使用均值、中位数的方法，KNNImputer可以借助现有数据集与未知数据集的其他特征分布对目标特征进行缺失值插补，使用方便、易于实现，能够较好适配本研究中的基坑小型数据集插补需求.

1.3. 极致梯度提升算法

XGboost是基于梯度提升决策树（gradient boosting decision tree，GBDT）同时拥有集成树（Boosting）思想的算法^[22]，在各类工程中有广泛应用^[20,23-24].

(1)$ {\text{Ob}}{{\text{j}}^t} = \sum\limits_{i = 1}^{{n}} {L\left( {{y_i},\hat y_i^t} \right)} +\sum\limits_{k = 1}^{{t}} {{\varOmega }\left( {{f_t}} \right)} , $

(2)$ {\varOmega }\left( {{f_t}} \right) = \gamma {{T}}+\frac{1}{2}\lambda {\left\| {\boldsymbol{w}} \right\|^2}. $

式中：$ {\text{Ob}}{{\text{j}}^t} $为算法的优化目标函数；$ L\left( {{y_i},\hat y_i^t} \right) $为损失函数；$ {\varOmega }\left( {{f_t}} \right) $为添加的正则化项，包含L1正则项和L2正则项，用于控制决策树分裂次数防止模型过拟合；$ \gamma $、$\lambda $均为正则化参数；T为叶子结点数；w为叶子节点分数. 通过优化损失函数，将式(1)中的$ L(\theta ) $改为二阶泰勒公式，提高计算精度；通过添加的正则化项控制模型的复杂度，防止模型出现过拟合. 对式(1)进行泰勒公式二次展开、化简，得到

(3)$ {\text{Ob}}{{\text{j}}^t} = \sum\limits_{j = 1}^{{T}} {\left[ {{G_j}{w_j}+\frac{1}{2}({H_j}+\lambda )w_j^2} \right]} +\gamma {{T}}{\text{.}} $

集成树中第j个叶子结点的误差函数为

(4)$ f({w_j}) = {G_j}{w_j}+\frac{1}{2}({H_j}+\lambda )w_j^2. $

当$ w_j^* = - {{{G_j}}}/({{H_j}+\lambda }) $时，$ f({w_j}) $取最小值，此时

(5)$ {\text{Ob}}{{\text{j}}^*} = - \frac{1}{2}\sum\limits_{j = 1}^{{T}} {\frac{{G_j^2}}{{{H_j}+\lambda }}} +\gamma {{T}}. $

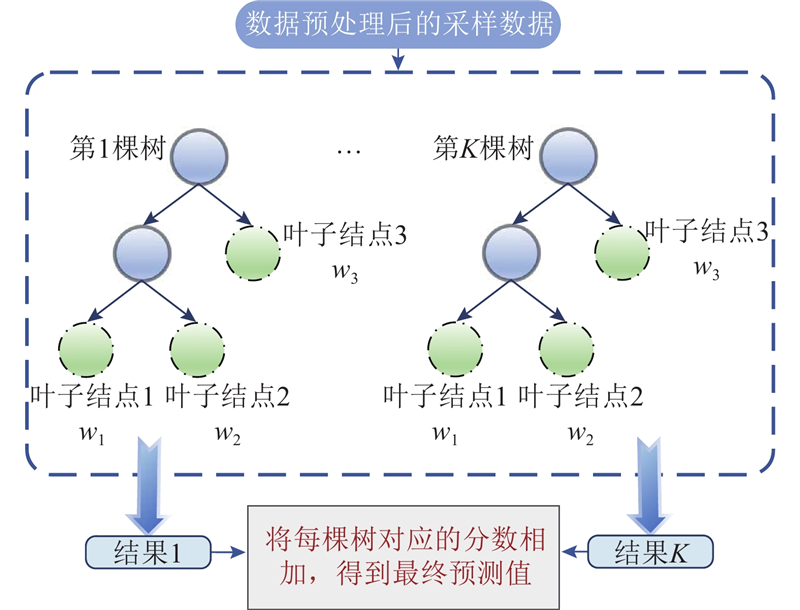
在该点处整个树结构获得最优解. XGBoost的结构示意图如图2所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2 极致梯度提升算法的结构示意图

Fig.2 Structure diagram of extreme gradient boosting algorithm

1.4. 长短期记忆算法

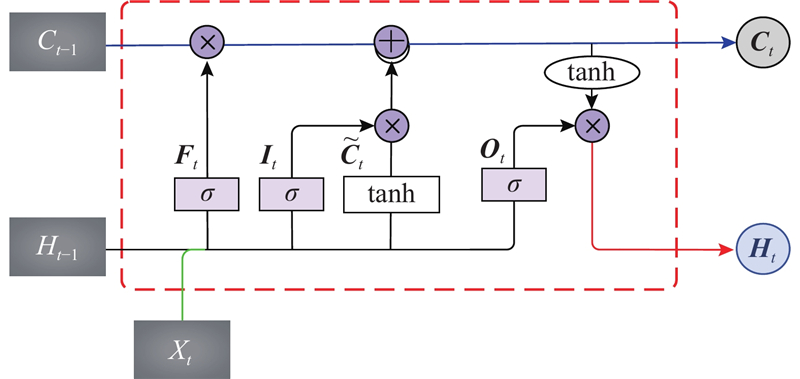
LSTM通过将RNN中单一的神经网络层改进为4个网络层（1个用于保存当前状态信息的隐状态${\boldsymbol{H}}_{t-1} $，3个门结构：遗忘门${\boldsymbol{F}}_t $、记忆门和输出门${\boldsymbol{O}}_t $），实现把时刻t−1的记忆元${\boldsymbol{C}}_{t-1} $与隐状态传递给当前时刻，改变原有的前馈神经网络时刻t−1与时刻t无关的处理方式. 这种特殊结构能够有效解决RNN的长期依赖、梯度消失和梯度爆炸等问题，可以更好地处理长时间序列中的信息，使较长时间前的有用信息不被遗忘. LSTM的结构如图3所示. 图中，$\sigma $为Sigmoid激活函数，${\boldsymbol{I}}_t $为输入门，$\tilde{\boldsymbol{C}}_t $为候选记忆，${\boldsymbol{X}}_t $为输入.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3 长短期记忆算法的结构示意图

Fig.3 Structure diagram of long short-term memory algorithm

2. 预测算法

2.1. 基坑变形影响因素分析

未来的人工智能计算是知识与数据相结合的双驱动模型^[25-26]. 在选取基坑水平位移的影响因素时，既要采取数据为导向的相关性分析^[27]，又要考虑具体特征值的物理意义^[28]. 钟国强等^[29]采用RS-MIV-ELM模型对基坑水平位移的影响因素进行量化分析，将各影响因素按照物理意义分为地质因素（包括工程地质因素与水文地质因素）、施工因素、设计因素及环境因素.

基坑位移产生变化的过程较为复杂且涵盖时空效应，单一影响因素（如各土层厚度、重度）作为预测特征是不切实际的. 此外，现有的基坑数据通常为每日一测，单个项目通常工期仅为2~3 a，即便每天按时定点观测，相比计算机大预测模型所需的数据量，获得的基坑数据量仍然十分稀少. 上述原因导致基坑位移变化预测不理想，难以达到计算机领域的当前最优效果模型（state-of-the-art，SOTA）. 本研究采用地连墙后面已开挖部分主动土压力与地连墙后被动区被动土压力取代单一影响因素，以土力学的基本理论知识为基础，减少特征数量，同时将理论与预测模型相结合，增强所提模型的可解释性和预测精度. 坑外水位也对基坑位移变化有重大影响. 基坑内、外有明显的水位差会产生巨大的静水压力，导致基坑测斜位移变化，在这股压力差之下还会出现管涌现象，土体会伴随水的渗流由高水位流向低水位，造成坑外的水土流失甚至土体塌陷. 某些区域还会出现沉降回升现象，主要是由于地下水位恢复上升以及土体发生回弹效应所致^[30]. 当土方开挖时，基坑围护结构的位移变化最为明显. 原因是坑内土体卸载使得外侧土压力与内侧土压力失去平衡，围护结构整体向内偏转. 在开始支撑系统安装前，围护结构变形类同悬臂梁，水平位移呈现上大下小的三角形分布. 支撑系统整体安装完成后，墙体侧移呈鼓腹型变形形态. 钟国强等^[29]的影响因素相关性分析显示，支撑轴力的总相关性权重达到0.465，充分说明支撑轴力在土体变形预测中的重要性，该研究团队将3个支撑轴力的取值分别作为3列特征列. 在大型的地下空间结构中，支撑轴力的观测点可多达数十个，在实际监测中很难将单个的支撑轴力测点与基坑深层水平位移测点一一对应. 本研究综合考虑各个基坑内部支撑轴力的变化，采用各个基坑当日支撑轴力观测值的平均值，减少了不必要的特征数量，进一步提高了预测的准确度和泛化能力.

2.2. 数据预处理

2.2.1. 主动土压力及被动土压力计算

根据文献[31]：当坑外地面为水平面，基坑围护墙背为竖直面时，主动土压力强度标准值和被动土压力强度标准值的计算式分别为

(6)$ {p_{{\mathrm{a}},k}} = \left(\sum {{\gamma _i}{h_i}+{q_k}} \right){K_{\mathrm{a}}} - 2{c_k}\sqrt {{K_{\mathrm{a}}}} , $

(7)$ {p_{{\mathrm{p}},k}} = \sum {{\gamma _i}{h_i}{K_{\mathrm{p}}}+2{c_k}\sqrt {{K_{\mathrm{p}}}} } . $

式中：$ {p_{{\mathrm{a}},k}} $为该点主动土压力的强度标准值，$ {p_{{\mathrm{a}},k}} \leqslant 0 $时，取$ {p_{{\mathrm{a}},k}} = 0 $；$ {p_{{\mathrm{p}},k}} $为该点被动土压力强度标准值；$q_k $为基坑坑边地面超载；$ {K_{\mathrm{a}}} $为计算点处的主动土压力系数，$ {K_{\mathrm{a}}} = {\tan ^2}({45^ \circ } - {{{\varphi _k}} / 2}) $；$ {K_{\mathrm{p}}} $为计算点处的被动土压力系数，$ {K_{\mathrm{p}}} = {\tan ^2} ({45^ \circ }+ {{{\varphi _k}} / 2}) $；$ {\gamma _i} $为第i层土的重度；$ {h_i} $为第i层土的厚度；$ {c_k} $为计算点处土的黏聚力标准值；$ {\varphi _k} $为计算点处土的内摩擦角标准值，计算时应考虑各土层差别.

2.2.2. 基于最近邻插补算法的缺失值插补

在实际工程中，各种突发状况（如设备问题）常常会导致个别数据点的遗漏，直接忽略或删除这些含有缺失值部分的数据会让本就不充分的监测数据进一步减少. KNNImputer能够选取和缺失值相似度（出现频率）最高的数据进行插补，使数据得到充分利用.

2.2.3. 支撑轴力数据预处理

将完成缺失值插补的支撑轴力数据按照时间顺序分测点汇总成CSV逗号分隔值文件，之后传入Python文件. 重新创建新列，用于存储各个基坑支撑轴力数据的平均值，使用mean函数在‘axis=1’，即在列的方向水平求得平均值. 例如项目中共有3个基坑，编号为1#、2#、3#，每个基坑该日的支撑轴力分别计算平均值，得到最终特征量.

2.2.4. 测斜孔号位置信息处理

在现实的基坑项目中，监测点位通常多达几个甚至数百个，现有的数据无法满足将监测点一一作为特征量. 为此将这部分监测点的位置信息转为分类信息，再按照独热编码的思想将各个监测点的分类信息转化为数字. 在数据处理时，记录下各个测斜孔号，将孔号位置进行分类信息编码.

2.2.5. 时间信息预处理

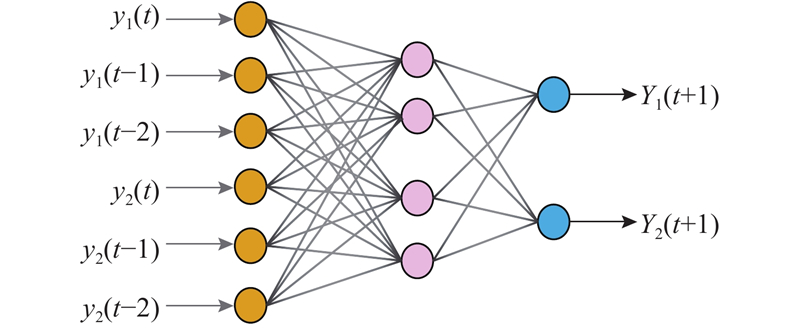
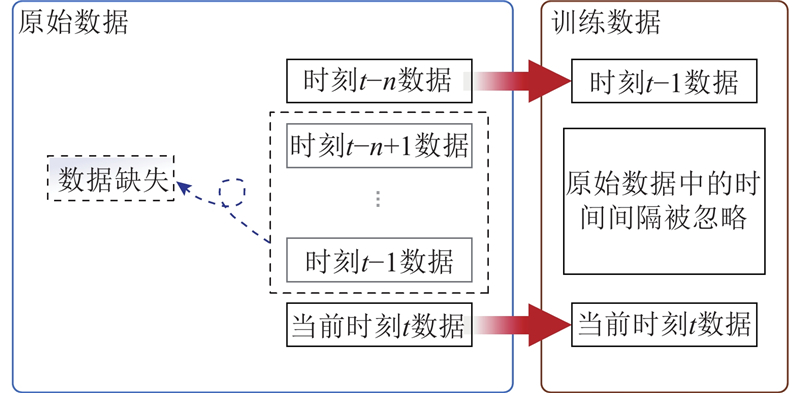
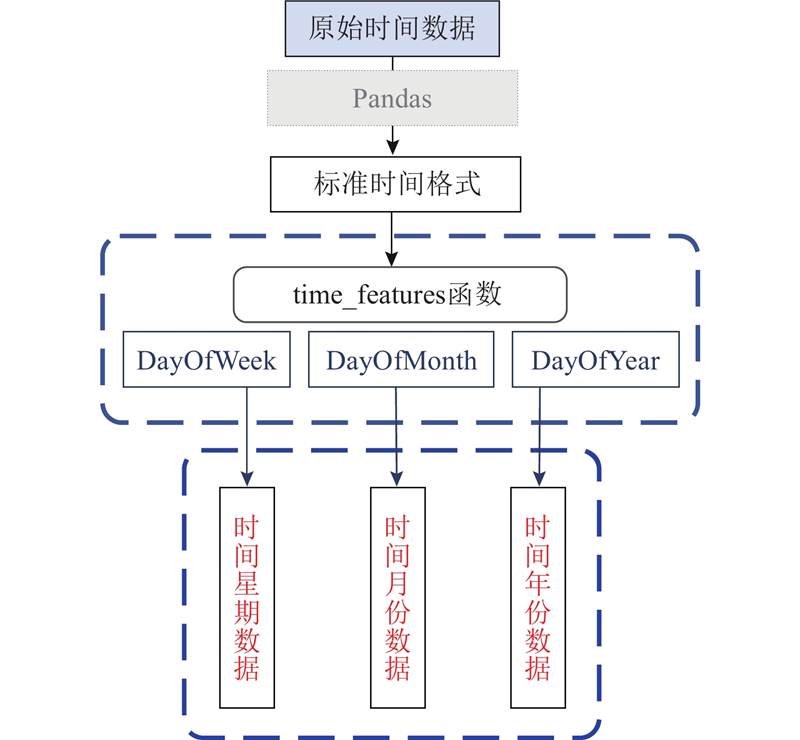
在深度学习模型出现之前，研究基坑变形预测时通常将时间序列分析转化为有监督学习进行处理，即时间列作为索引不参与后续特征训练，只是用于划分训练集与测试集^[16]. 有监督学习使用Pandas中的shift函数将每列的特征变量进行平移：向前平移1个步长得到时刻t−1的特征量，向前平移2个步长得到时刻t−2的特征量. 如图4所示，BP神经网络通过学习时刻t−1、t−2和t的数据得到最终的训练结果. 使用shift函数进行特征变量平移的方法没有考虑基坑监测数据采集中的实际问题：监测数据不都是按照相同的时间间隔采集得到的. 如图5所示，由于某些天的监测数据完全缺失，模型在进行训练时会错误地将时刻t−n的数据当做是时刻t−1的数据，忽略了缺失的时间间隔. 本研究的时间数据预处理采用深度学习模型Informer^[19]的时间处理方式，处理流程如图6所示：使用Pandas中的to_datatime函数将数据中的时间列数字格式转化为标准的时间格式即年月日信息，再使用time_features函数转化时间信息. time_features函数有多种频率，每种频率代表不同种类的时间处理方式. 通过在该函数中选择合适的频率，将原始数据中的时间戳转化为多个时间数据列.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4 基坑变形时间序列预测的反向传播网络模型

Fig.4 Back propagation network model for time series prediction of foundation pit deformation

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5 时间列作为索引时的数据处理方式

Fig.5 Data processing when time column as index

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6 时间数据预处理流程图

Fig.6 Flow chart for time data preprocessing

3. 工程案例应用及模型验证

3.1. 工程背景

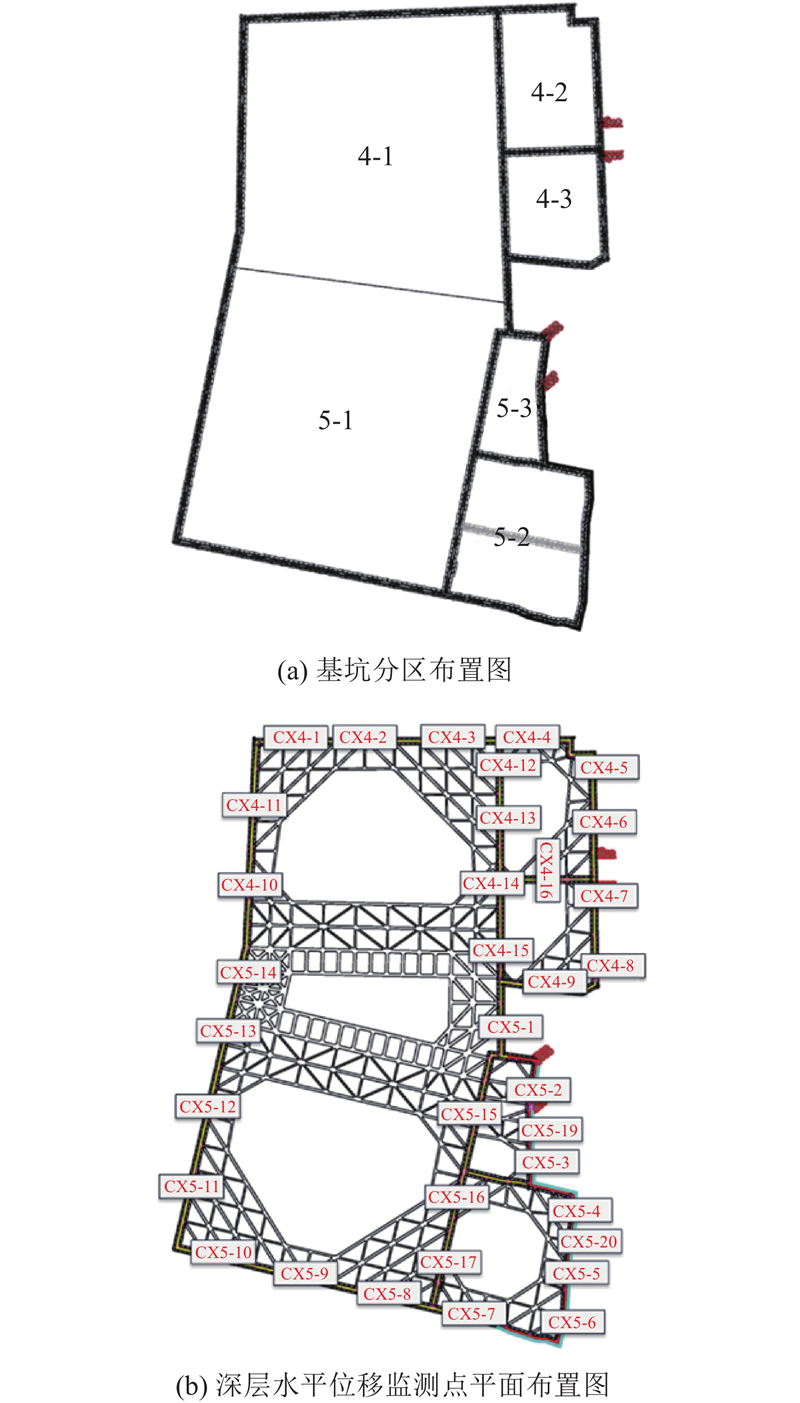
选取杭州某软土基坑，利用2022年3月至5月的监测数据进行基坑测斜水平最大位移的预测. 该项目分为地块4#和5#，平面布置如图7所示，占地共29 000 m²，其中基坑总面积为27 280 m²，周长为770 m，基坑顶标高−1.00 m，地下4层，基坑底标高−20.45 m，基坑开挖深度19.95 m，土方开挖量约为5.5×10⁵ m³. 本项目属于深基坑工程，对侧墙渗漏、降水平衡、变形等控制要求较高. 收集基坑4-1和5-1共20个测斜孔的817条数据. 选择的时间段为基坑4-1和5-1的主体结构已完成，基坑4-2、4-3、5-2、5-3尚未进行开挖. 相较其余时间段，所选时段的基坑位移变化稳定，未见明显的不明情况影响. 在817条采集数据中，616条数据有不同程度的缺失. 其中缺失严重的数据占总数据的48.5%，主要缺失是各测点的支撑轴力. 采用KNNImputer，选取和缺失值相似度（出现频率）最高的数据进行插补. 将基坑4#、5#的支撑轴力按照基坑类别分类，通过学习各基坑各测点未缺失支撑轴力的关系，选择与该测点缺失值支撑轴力最相似的数据进行插补，得到基坑插补后的完整数据集.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7 基坑平面布置图及测孔位置

Fig.7 Foundation pit layout plan and location of monitoring holes

为了方便模型评估，将完成插补的数据作为完整数据集，随机抽取75%的数据作为训练集，余下的25%的数据作为测试集. 如表1所示，综合考虑各个影响因素及现有基坑监测数据，选取8个特征变量，包括3列处理好的时间特征列，5个具体特征：位置信息（测斜孔号）、坑外水位、支撑轴力、主动土压力和被动土压力；时间预测类型为多变量预测多变量. 实验平台为装有NVIDIA MX450 GPU的笔记本电脑. 所有代码均使用Python语言，LSTM模型和XGBoost使用的是Pytorch框架.

表 1 模型性能验证参数

Tab.1 Model performance validation parameters

类别	参数	类型	取值范围
预测变量	基坑最大测斜位移点处的深度$H_{u,{\mathrm{max}}} $	连续	具体量测、预测值
预测变量	基坑最大测斜位移$u_{\mathrm{max}} $	连续	具体量测、预测值
预测变量	基坑最大测斜变化点处的深度$H_{v,{\mathrm{max}}} $	连续	具体量测、预测值
预测变量	基坑最大测斜变化率$v_{\mathrm{max}} $	连续	具体量测、预测值
特征变量	测斜孔号	分类	0~19等20个测斜孔
特征变量	坑外水位	连续	具体量测值
特征变量	支撑轴力	连续	具体量测值
特征变量	主动土压力	连续	具体计算值
特征变量	被动土压力	连续	具体计算值
特征变量	时间(月份)	连续	[−0.5,0.5]
特征变量	时间(星期)	连续	[−0.5,0.5]
特征变量	时间(年)	连续	[−0.5,0.5]

新窗口打开| 下载CSV

3.2. 模型训练与评价指标

3.2.1. 基于极致梯度提升的模型构造

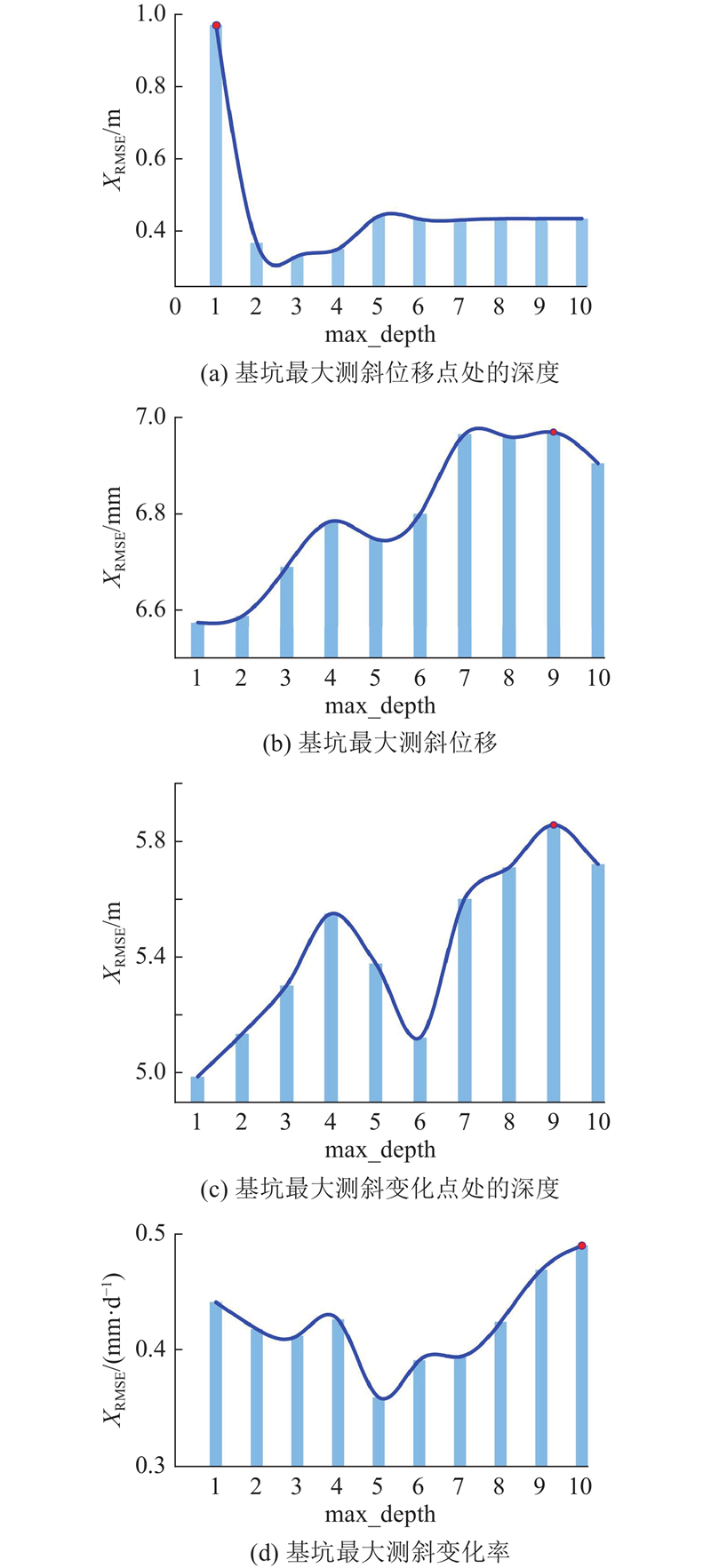
所用树模型为CART树模型. XGBoost通过不断迭代，每次生成的新树都会拟合前一棵树的残差，随着迭代次数不断增加，预测误差显著下降. 使用网格搜索^[32]调整基础超参数，得到最优初始化值如下：n_estimators迭代次数为100；Gamma函数为0.3；Subsample下采样为0.9；colsample_bytree为0.7；learning_rate为0.5. max_depth树的最大高度直接影响后续模型复杂度与准确性，进行该参数调优：将其他参数设置成网格搜索得到的最优初始化参数值，改变模型中树的最大高度，分别计算测试数据的误差大小. 如图8所示为各预测目标中不同的树最大高度与对应的测试数据误差，评价指标采用均方根误差. 图中，树的最大高度取值为1~10的整数. 竖坐标分别代表横坐标取值不同情况下，各预测变量的测试误差.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8 树的最大高度和测试误差

Fig.8 Maximal depth and test error of tree

3.2.2. 基于长短期记忆算法的模型构造

如图9所示为本实验构造的LSTM网络结构. 为了满足训练要求，在模型训练前对输入的基坑测量数据进行统一的初步处理. 具体方法为将特征数据进行归一化处理：

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9 基坑位移预测的长短期记忆网络结构

Fig.9 Long short-term memory network structure for foundation pit displacement prediction

(8)$ x_i^* = \frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}. $

式中，$ {x_{\min }} $为各基坑特征数据中的最小值，$ {x_{\max }} $为各基坑特征数据中的最大值，$ {x_i} $为待标准化处理的基坑特征数据. 将除时间特征外的其他特征数据线性映射到0~1.0. 本实验中丢弃率（dropout）为0.2，代表每个神经元在每次训练迭代中有20%的概率被丢弃，此操作能够有效增强模型的泛化能力，防止过拟合. 输出层使用线性回归全连接层对结果进行降维. 前述处理并未对基坑预测目标数据进行归一化，无须对预测数据进行反归一化. 模型实验使用Adam优化算法^[33]，损失函数为均方误差的计算式为

(9)$ {X_{{\text{MSE}}}} = \sum\limits_{t = 1}^{n} {{{({y_t} - {{\hat y}_t})}^2}} . $

式中：$ {y_t} $为基坑各因变量实际测量值，$ {\hat y_t} $为基坑各因变量预测值，n为因变量数据数量.

3.2.3. 实验评价

选取均方根误差作为各变量模型预测性能的评价指标，选取平均绝对误差MAE和平均绝对百分比误差作为补充评价指标，计算式分别为

(10)$ {X_{{\text{RMSE}}}} = \sqrt {\frac{1}{{{n}}}\sum\limits_{t = 1}^{{n}} {{{({y_t} - {{\hat y}_t})}^2}} } , $

(11)$ {X_{{\mathrm{MAE}}}} = \frac{1}{{n} }\sum\limits_{t = 1}^{n} {\left| {{y_t} - {{\hat y}_t}} \right|} , $

(12)$ {X_{{\mathrm{MAPE}}}} = \frac{100{\text{%}}}{{n} }\sum\limits_{t = 1}^{n} {\left| {\frac{{{y_t} - {{\hat y}_t}}}{{{y_t}}}} \right|} . $

3.3. 结果分析

使用前31d共613条数据来预测后18 d共204条数据，其中616条数据有不同程度的缺失，缺失严重的数据占总数据的48.5%. 案例涵盖2个基坑共20个测点，工程情况复杂，测点变形多样，前期设计文件分析结果与实际结果偏差较大，具有预测难、预测不及时的特点，须构建全面有效的基坑变形预测模型. LSTM是特殊的循环神经网络，须通过接收时间序列信息进行长序列的训练及学习. 尽管LSTM是时间序列分析中经典的算法，但是训练过程没有时间点的参与，数据按照时间排列之后，由上个时间段的记忆元和隐状态训练得到当前时刻的记忆元和隐状态. 本研究将时间信息转为3列具体的时间点特征，直接使用时间特征进行时间序列学习，避免了文献[6]、[18]中使用多项式插值将各数据进行等时间分隔. 双层LSTM的训练效果不理想，原因可能是LSTM不适用于多时间点特征的长序列学习，无法达到应有的效果. 因此LSTM基学习器使用未经Pandas处理的数据.

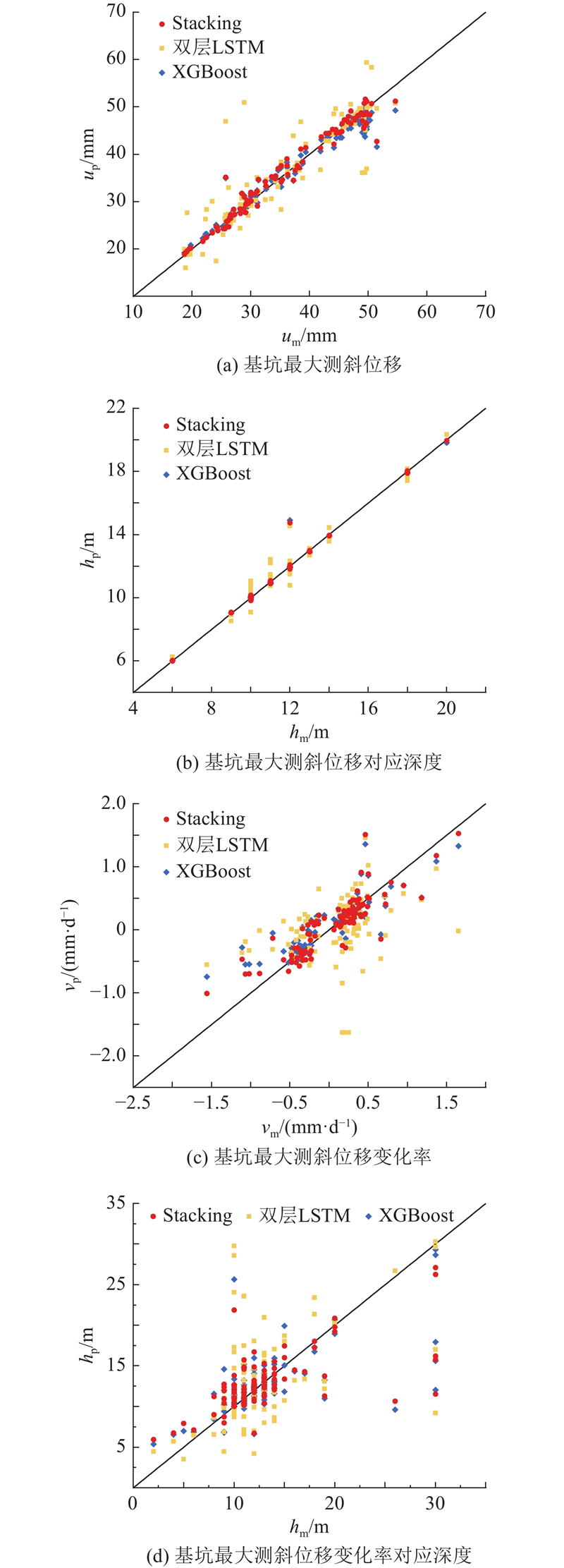
各变量预测值的均方根误差及平均绝对误差如图10所示，Stacking的预测结果均方根误差均优于单一的XGBoost预测结果与双层LSTM模型，在长时间序列预测中表现优秀. Stacking在预测基坑最大测斜位移时误差不超过2.3 mm，预测该最大测斜位移的对应深度不超过0.17 m，从侧面反映出各个基坑的最大测斜深度具有一定的空间性与时序性. 如图11所示，Stacking的平均绝对百分比误差不总是优于2种单一方法. 在缺失值近50%情况下，使用Stacking对基坑位移变化率预测精度为82%，XGBoost的预测精度近95%. 原因1）可能在前期选取特征值时，主要围绕引起基坑位移变化的影响因素进行相关性分析，忽略了引起基坑位移变化率改变的特征量. 2）对于数值型的输出类型，集成学习一般使用平均法，由于LSTM在预测位移变化率时的精度过低，拉低了XGBoost在预测该指标时的精度值. 由此可知，使用时间点特征的XGBoost相较于LSTM更适合如预测位移变化率的对于某特定时刻的周围环境因素更敏感的指标.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10 不同算法的多变量误差对比

Fig.10 Multivariable error comparison of different algorithms

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11 不同算法4个预测变量的平均绝对百分比误差

Fig.11 Mean absolute percentage errors of four predictor variables for different algorithms

不同变量的各单一模型预测值与组合模型预测值的对比如图12所示. 图中，$ {u_{\text{m}}} $、$ {h_{\text{m}}} $、$ {v_{\text{m}}} $为各变量的现场实测数据，$ {u_{\text{p}}} $、$ {h_{\text{p}}} $、$ {v_{\text{p}}} $为各变量的预测值. 可以看出，Stacking在预测基坑最大测斜位移、基坑最大测斜位移对应深度与基坑最大测斜位移变化率时与最终实测值的拟合程度明显优于XGBoost和双层LSTM. 在预测基坑最大测斜位移变化率对应深度时，尽管Stacking的预测结果优于双层LSTM与XGBoost，但是与实测值仍有较大偏差.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12 不同算法的多变量预测结果

Fig.12 Multivariable prediction results of different algorithms

如图13所示为使用测试集进行预测分析得到的逐点相对均方根误差图，其中i为测试集的样本序号. 可以看出，XGBoost对基坑最大测斜位移、基坑最大测斜位移对应深度与基坑最大测斜位移变化率的预测结果一般小于实测值，其预测结果较实测值更为保守，双层LSTM的预测结果一般大于实测值. 对于数值型的输出类型，集成学习一般使用平均法，在这3类预测目标上，Stacking可以有效参考XGBoost和双层LSTM的预测结果，使得最终结果更加贴近实测值，进一步提高预测精度. 在预测基坑最大测斜位移变化率对应深度时，XGBoost和双层LSTM的预测结果要么都小于实测值，要么都大于实测值，Stacking在预测基坑最大测斜位移变化率对应深度时偏差较大. 这与陈振宇等^[20]提出的正确选择参与组合的单一模型是降低模型误差的前提的概念相一致.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13 不同算法的逐点相对均方根误差对比

Fig.13 Comparison of point-by-point relative root-mean-square errors of different algorithms

4. 结　语

本研究采用集成学习思想，提出基于XGBoost和LSTM的数据融合多变量预测方法，用以预测基坑的测斜变形. 引入time_features函数处理方法，提高时间数据特征的利用效率，使用KNN进行数据插补，在有限的数据下实现长序列多变量的成功预测. 1）引入多个时间点的数据特征和KNN数据插补方法，无须使用多项式插值使得所有数据序列为等时间间隔，完善了基坑位移预测体系. 2）XGBoost在处理将时间点作为特征列的数据时，效果明显优于双层LSTM. 可能的原因是LSTM为RNN，在学习时已经考虑时间序列信息. 3）相较单一的XGBoost与LSTM，所提方法得到的均方根误差显著小于XGBoost与LSTM得到的均方根误差，实现了预测精度的进一步优化. 4）使用堆叠模型对各预测变量预测分析后发现，基坑最大测斜位移变化率对应深度的预测均方根误差偏大. 原因是本研究使用的2类基学习器不适用于该预测目标，且本研究选取的特征变量不总是利于预测基坑最大测斜位移变化率. 在使用所提方法进行预测时，可以重点关注基坑最大测斜位移及基坑最大测斜位移对应深度，从而达到基坑安全评价的目的.

本研究通过系统分析揭示了传统基坑变形预测方法在时间维度建模上的局限性，具体表现为对监测数据时间间隔非均匀性特征的量化表征不足. 尽管通过时间点数据预处理方法解决了数据异构性问题，但受限于当前预处理模块与预测模块的离散化架构，仍存在以下待改进方向. 1）数据预处理阶段的多源数据时空对齐及特征工程流程依赖人工经验干预，尚未实现全流程自动化建模；2）动态施工参数与复杂地质条件的耦合效应对预测精度的定量影响机制仍有待深化研究.

后续研究拟从以下维度展开深入探索. 1）构建融合数据治理的端到端预测框架：通过引入自动化特征提取（automated feature engineering, AFE）技术，开发涵盖数据清洗、缺失值插补、时空特征融合的智能预处理模块，并与预测模型进行参数协同优化，提升系统整体鲁棒性；2）推动工程知识嵌入的混合建模：将如岩土本构方程的机理模型与混合神经网络进行分层耦合，通过物理信息约束提升小样本工况下的外推预测能力，为基坑工程数字化管控提供更完备的技术支撑.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

钱七虎

迎接我国城市地下空间开发高潮

[J]. 岩土工程学报, 1998, 20 (1): 112- 113