自21世纪初以来，风电机组在可再生能源生产中发挥着日益关键的作用，提供清洁可持续的电力资源^[1]. 然而，风电机组经常面临恶劣的工作条件和复杂的天气状况，由此带来的安全隐患^[2-3]显著增加了风电场的运营和维护成本. 已有研究表明叶片故障主要源于应力疲劳载荷导致叶片变形和结构松动，最终导致叶片断裂^[4-5]. 近年来，越来越多的风机部署在山区、高原和近海等偏远地区，以更好地利用风资源. 这些地区均具有典型的复杂风况与恶劣的自然环境，使得风机叶片结冰、扫塔、断桨等事故愈加频繁^[6-7]. 因此，实时智能监测风电机组叶片状态，并及时发出异常警报，在减少运营停机时间、降低风电场运营成本方面具有重要价值.

风电机组叶片智能状态监测方向现存在部分成熟的研究^[8]. 从方法论的角度来看，信号处理和数据驱动方法是监测的主要方法. 信号处理研究利用适当的传感器捕获各种类型的信息，包括振动信号、应变测量、声波测量^[9-11]. 目前存在一些基于直接振动监测识别叶片异常的体系结构^[12-13]，但它们并不广泛符合众多在役风电机组的叶片故障诊断需求，因为众多在役风机缺乏直接监测的复杂传感器且停机、装卸安装的维护成本高昂. 深度学习作为数据驱动方法中的主要方法，近年来在使用监控和数据采集（supervisory control and data acquisition， SCADA）数据进行风机故障检测方面变得越来越受欢迎^[14-16]. Wang等^[16]开发了基于深度自动编码器的框架，用于预测性地检测风电机组叶片断裂. 此外，随着Transformer的流行^[17]，研究人员一直在提出基于注意机制的各种变种模型，用于检测风电机组的故障^[18-19]. 但是这些方法抛开了风力机组叶片故障的振动学特性，缺乏可解释性，难以工程落地.

本研究建立用于风电机组叶片自监督正常-异常二分类的模型. 提出变分模态分解-核主成分分析（variational mode decomposition-kernel principal component analysis, VMD-kPCA）方法，以实现对机舱多通道振动数据的特征自适应提取；融合机舱振动数据与SCADA系统运行数据，设计自适应双向时序卷积网络（adaptive bidirectional temporal convolution neural network, ABT）作为骨干特征提取器，从而实现振动主成分特征的自监督回归表征；基于其他SCADA运行变量，构建风电机组正常行为模型，以排除其他因素对机舱振动特征的干扰；最后，采用基于马氏距离的残差序列检测策略，旨在实现高精度的叶片正常-异常二分类.

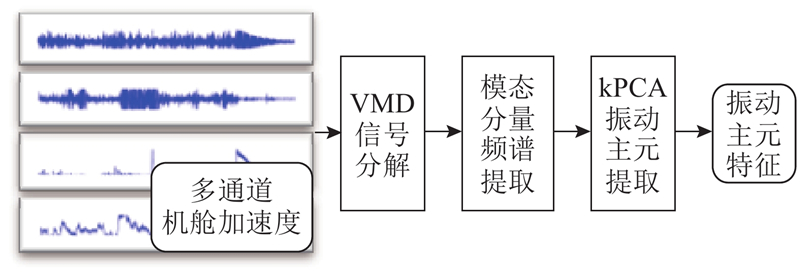
提出的叶片异常检测框架分为4个模块，分别为VMD-kPCA机舱振动主元特征提取模块、基于ABT神经网络的振动主元回归器、风电机组正常行为模型以及异常检出策略模块.

1） VMD-kPCA机舱振动主元特征提取模块.采用SCADA数据中记录的多通道机舱前后、左右加速度多通道数据作为输入，提取与叶片运行相关的降维频域特征. 这里假设一个长度为w的输入窗口中，多通道振动信号为${\boldsymbol{y}} $，$ {\boldsymbol{y}} \in {{\bf{R}}^{C \times w}} $，其中C为振动信号通道数. 经过本研究提出的VMD-kPCA机舱振动主元特征提取模块${f_{{\text{vk}}}}$处理后，模块输出K个从y中提取出的主元特征$\boldsymbol{y}_{\mathrm{f}} $，${{\boldsymbol{y}}_{\text{f}}} \in {{\bf{R}}^K}$，数学映射关系表达式如下：

式中：$ {{\boldsymbol{\alpha}} _{{\text{vk}}}} $为VMD-kPCA函数预设超参数.

2） 基于ABT神经网络的振动主元回归器. 使用与振动主元高相关性的SCADA时序变量$ {{{\boldsymbol{x}}}} \in {{{\bf{R}}}^{n \times w}} $作为输入，其中n为SCADA相关变量维度，采用基于自适应双向时序卷积网络(ABT)的特征提取器${f_{{\text{ABT}}}}$，回归振动主元特征$ \hat{\boldsymbol{y}}_{\text{f}} $. 数学映射关系如下：

式中：${{\boldsymbol{W}}_{{\text{ABT}}}}$为ABT深度学习网络待训练参数.

3）风电机组正常行为模型. 使用与叶片不直接相关的SCADA变量${\boldsymbol{z}} $，（${\boldsymbol{z}} \in {{\bf{R}}^{m \times w}}$，m为与叶片不直接相关的SCADA变量参数）作为目标对象，建立自编码器模型${f_{{\text{nm-e}}}}$与${f_{{\text{nm-d}}}}$. 数学映射关系如下：

式中：$\boldsymbol{W}_{\mathrm{e}} $、$\boldsymbol{W}_{\mathrm{d}} $为编码器的待训练参数和解码器的待训练参数，$\hat{\boldsymbol{z}} $为重构后的与叶片不直接相关的SCADA变量.

4）异常检出策略模块. 结合训练集中主元特征真值与回归值序列$ \{ {\boldsymbol{y}}_{\text{f}}^i,\hat {\boldsymbol{y}}_{\text{f}}^i\} (i = 1, \cdots ,N) $和风电机组正常行为模型残差序列$ \{ {{\boldsymbol{z}}^i} - {\hat {\boldsymbol{z}}^i}\} (i = 1, \cdots ,N) $，构建振动主元异常阈值以及风机运行异常阈值，判断实时数据样本${{\boldsymbol{x}}_{\mathrm{r}}} \in {{\bf{R}}^{n \times w}}、{{\boldsymbol{y}}_{\mathrm{r}}} \in {{\bf{R}}^{C \times w}}、{{\boldsymbol{z}}_{\mathrm{r}}} \in {{\bf{R}}^{m \times w}}$是否存在叶片异常，从而输出正常-异常的二分类0-1标签.

本模块通过变分模态分解（VMD）^[20]与核主成分分析（kPCA）^[21]相结合的方法，自适应提取多通道机舱加速度振动信号的主元特征，用作自监督模型的回归目标. VMD方法能够将原始振动信号分解为围绕特定中心频率的模态分量，从而实现对振动信号的初步解调. 在此基础上，kPCA方法对VMD输出的模态分量进行频域特征降维，提取关键主元特征，最终生成用于回归的目标变量. 整体振动主元特征提取流程如图1所示.

在VMD分解方法中，将原始的单通道振动信号${{\boldsymbol{y}}_c},c \in \{ 1, \cdots ,C\} $分解为待定的$K$个模态分量$ {\boldsymbol{u}}_k^c $. 在分解中，假定所有模态分量都是集中在各自中心频率${\omega ^c_k}$附近的窄带信号，因此VMD根据分量窄带条件建立约束优化问题，表达式如下：

而后，通过增广拉格朗函数$\lambda $将上述等式约束优化问题等效为无约束优化问题，并通过ADMM交替方向乘子法^[22]对$ {\boldsymbol{u}}_k^c $和$\omega _k^c$迭代求解：

式中：$ {\boldsymbol{u}}_k^{c,n+1} $和$ \omega _k^{c,n+1} $分别表示第n+1次迭代时，第c通道信号的第k个模态的模态分量和中心频率，r表示学习步长. 在这里，最终收敛的模态分解结果表示为$ \left\{ {\left. {{\boldsymbol{u}}_k^{c*} } \right|} c \in \{ 1,2, \cdots ,C\} ,\;k \in \{ 1,2, \cdots ,K\} \right\} $.

在提取$C$个通道的$C \times K$个模态分量后，对每个模态分量进行傅里叶变换，得到每个模态分量的频谱$\left\{ \left.{{\boldsymbol{U}}_k^{c*}}\right| c \in \{ 1,2, \cdots ,C\} ,k \in \{ 1,2, \cdots ,K\} \right\} $，并采用kPCA方法进行主元提取. 以分量${{\boldsymbol{U}}_k^{c*}}$为例，介绍所使用的kPCA主元提取算法.

首先，根据所选用核函数构建核矩阵S，矩阵元素表示为${{{S}}_{i,j}} $，${{{S}}_{i,j}} = s({\boldsymbol{U}}_k^c(i),{\boldsymbol{U}}_k^c(j))$为核函数$s( \cdot , \cdot )$对第i和j个样本的计算结果.

其次，对核矩阵进行中心化处理，得到标准化核矩阵：

式中：$ {{\boldsymbol{1}}_w} $为维数为$w \times w$的矩阵，其中所有元素均为${1 \mathord{\left/ {\vphantom {1 w}} \right. } w}$.

接着，对于标准化核矩阵$ \widetilde {\boldsymbol{S}} $进行特征值分解，并选取最大的特征值及对应的特征向量，构建降维后的主元特征. 第i个样本的第c个振动通道的第k个模态的主元特征的$ \hat {\boldsymbol{y}}_c^k(i) $可以表示为

式中：$ {\lambda _{\max }}、{{\boldsymbol{v}}_{{\mathrm{max}}}} $分别为特征值分解得到的最大特征值和对应的特征向量；$\phi ( \cdot )$表示核函数中的高维映射函数，本模型中使用的是高斯核函数.

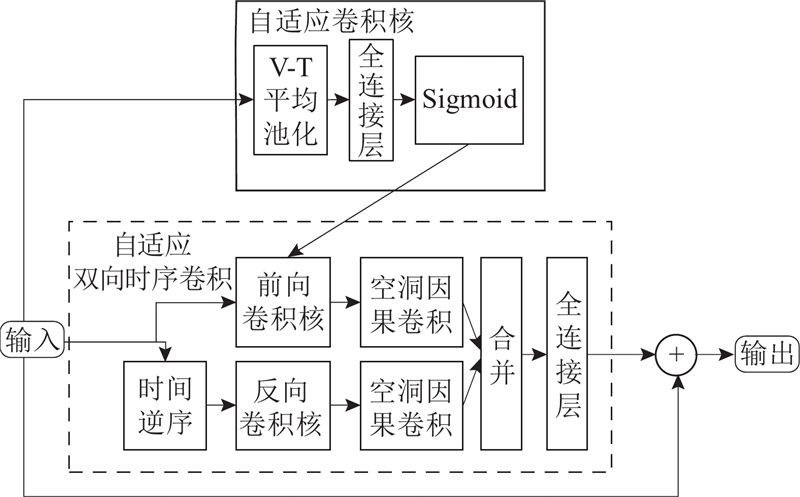
本模块采用自适应卷积的双向深度网络结构，将主元特征相关的SCADA数据作为输入，提取与融合SCADA数据中的双向多时间尺度的多变量时序特征，从而建立SCADA数据与1.2节中得到的多通道振动主元特征之间的复杂非线性关系.

为了应对SCADA时序数据中多变的时序-变量相关性与克服传统时序卷积神经网络(temporal convolutional neural network，TCN)无法双向提取时序特征的局限性，基于原始TCN结构，进行2个主要修改并提出自适应双向时序卷积网络(ABT). 详细的内部结构如图2所示.

面向SCADA数据复杂的时变特性，提出自适应卷积核来替代空洞因果卷积中的常值卷积核，对输入${{\boldsymbol{S}}_{{\text{in}}}}$进行2次特征维度和时间维度的平均池化，获得拼接后的一维特征向量. 此特征向量涵盖了输入样本整体的时序信息和特征维信息. 接着，将其送入前向网络与sigmoid激活函数组成的非线性变换后，构建出最终在卷积计算采用的卷积核参数. 采用这样非线性变换的好处在于将卷积核参数限制在（−1.0，1.0），限制了网络中参数的剧烈变化，从而抑制梯度消失问题. 上述卷积核构建过程的数学表达如下：

式中：$ {{\boldsymbol{S}}_{{\text{in}}}} \in {{{\bf{R}}}^{w \times n}} $为网络的输入，$ {{\boldsymbol{W}}_{\text{k}}} $为得到的卷积核参数，$ {{\boldsymbol{W}}_{\text{d}}} $和$ {{\boldsymbol{b}}_{\text{d}}} $为待优化权重及偏置.

通过以上方法构建出的卷积核参数是随着输入样本$ {{\boldsymbol{S}}_{{\text{in}}}} $的变化而变化的，其中参数动态自适应地跟随输入而改变，故而可以更加有效地提取复杂时序特征.

本模型的目的在于整合输入样本完整的时序信息并回归全局的振动主元特征. 因此，本模型采用了时间正向和反向卷积的双向卷积模式以提取双向时序特征. 随后，模型使用全连接网络融合来自2个方向的时序特征以维持网络的总体维度. 以上模型结构的数学表达如下：

式中：$ {\boldsymbol{W}}_{\text{k}}^{\text{f}} $和$ {\boldsymbol{W}}_{\text{k}}^{\text{b}} $分别为前向与后向动态卷积核参数，$ {{\boldsymbol{S}}_{{\text{out}}}} $为网络输出的时序特征，W_out和b_out分别为输出层的待训练权重参数和偏置参数.

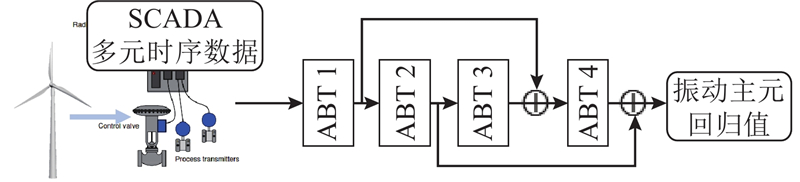
整体自监督回归框架如图3所示. 整体框架应用提出的ABT网络作为单元特征提取器，对SCADA原始多元时序数据进行特征提取. 本模型使用4个连续的ABT网络，网络中的空洞长度逐层递增，使得网络由浅入深逐步提取局部与全局多时间尺度的时序特征. 特别地，在多尺度时序特征融合中，模型使用“跨层”连接的方式融合局部和全局特征，以加快模型收敛速度，解决深度网络的梯度消失问题. 在训练过程中，训练残差由ABT构成的特征提取器输出目标估计值与真实目标变量构成，采用平均平方误差作为损失函数.

风电机组正常行为模型整体结构如图4所示. 本模块对风电机组中与叶片行为无直接关联的其他SCADA变量进行自编码正常行为建模，以排除叶片以外的其他部件在机舱加速度上面产生的影响.

在风电机组正常行为模型中，采用多层门控循环单元(gated recurrent unit，GRU)对其他相关SCADA运行变量进行编码. 对于输入的数据样本$ {\boldsymbol{z}} \in {{{\bf{R}}}^{m \times w}} $，在每一个时间t，GRU可以生成隐藏状态${{{\boldsymbol{\tilde h}}}_t}$，由更新门$ {{\boldsymbol{u}}_t} $和重置门${{\boldsymbol{r}}_t}$控制，其表达式如下：

式中：${{\boldsymbol{W}}_{\text{z}}},{{\boldsymbol{W}}_{\text{r}}},{{\boldsymbol{W}}_{\text{h}}} \in {{\bf{R}}^{h_{{\mathrm{s}}} \times m}}$，${{\boldsymbol{U}}_{\text{z}}},{{\boldsymbol{U}}_{\text{r}}},{{\boldsymbol{U}}_{\text{h}}} \in {{\bf{R}}^{h_{{\mathrm{s}}} \times h_{{\mathrm{s}}}}}$，${{\boldsymbol{b}}_{\text{z}}},{{\boldsymbol{b}}_{\text{r}}}, {{\boldsymbol{b}}_{\text{h}}} \in {{\bf{R}}^{h_{{\mathrm{s}}}}}$，均为须学习的参数，其中，h_s为隐藏状态的大小， m为SCADA变量的数量.

每一个GRU的输入都来自前一个GRU的隐藏特征h，最后一个GRU输出的隐藏特征$ {{\boldsymbol{h}}^3} $被送入全连接层构成的解码器，从而得到对于原始输入SCADA相关变量的重构值，即

式中：$ {{\boldsymbol{W}}_{{\text{fc}}}} $为全连接解码器中须学习的参数. 自编码器训练使用重构值与原始输入样本的MSE平均平方误差作为残差进行训练.

假设，在训练集中振动主元回归得到的残差序列为$ {{\boldsymbol{E}}^{\mathrm{y}}} \in {{\bf{R}}^{N \times (C K)}} $，表示训练集中N个样本的$C \times K$个主元特征的回归残差，其中，N个样本的残差序列符合时间顺序排列. 同理，记风电机组正常行为模型在训练集中获得的重构残差序列为$ {{\boldsymbol{E}}^{{\text{norm}}}} \in {{\bf{R}}^{N \times m}} $，其中，样本顺序符合时间顺序排列.

由于残差序列具有多维特征，每个维度残差尺度并不统一，为了标准化每个维度残差在最终阈值构建中的权重，通过构建马氏距离空间^[23]量化残差偏离正常阈值的程度. 计算方法如下，记含有${N_{\mathrm{e}}}$个$ {n_{\mathrm{e}}} $维特征样本的残差序列${\boldsymbol{E}} ({\boldsymbol{E}}\in {{\bf{R}}^{{N_{\mathrm{e}}} \times {n_{\mathrm{e}}}}})$中第k个训练样本的残差为${{\boldsymbol{e}}_k}$，其马氏距离${d_k}$可以定义为

式中：$\bar {\boldsymbol{e}} $、${\boldsymbol{M}} $分别为训练集残差序列的均值与协方差矩阵，$ \bar {\boldsymbol{e}} \in {{\bf{R}}^{{n_{\mathrm{e}}}}} $，$ {\boldsymbol{M}} \in {{\bf{R}}^{{n_{\mathrm{e}}} \times {n_{\mathrm{e}}}}} $. 应用以上马氏距离计算方法，可以获得由$ {{\boldsymbol{E}}^{\mathrm{y}}} $和$ {{\boldsymbol{E}}^{{\text{norm}}}} $构建出的振动主元残差距离序列${{\boldsymbol{D}}^{\mathrm{y}}} \in {{\bf{R}}^N}$和重构残差距离序列${{\boldsymbol{D}}^{{\text{norm}}}} \in {{\bf{R}}^N}$.

根据马氏距离的定义，构建出的距离序列是完全的正数序列，由序列构成的分布属于单边单峰分布. 于是，计算2类距离序列的99分位数$d_{99}^{\mathrm{y}}$和$ d_{99}^{{\mathrm{norm}}} $，并将他们作为超限阈值. 这意味着，当振动主元残差距离大于$d_{99}^{\mathrm{y}}$时，当前样本属于机舱振动“可疑”状态；当重构残差距离大于$ d_{99}^{{\mathrm{norm}}} $时，当前样本属于运行“可疑”状态.

由于风电机组SCADA数据存在噪声干扰，为了减少实际应用中的误报，不能直接将每一个“可疑”状态都作为异常报出. 故而，统计在训练集中主元特征残差距离序列${{\boldsymbol{D}}^{\mathrm{y}}}$，将训练集中主元特征残差距离序列按照时间顺序排列，并统计连续超过阈值$d_{99}^{\mathrm{y}}$的次数，并记为$c_{{\mathrm{max}}}^{\mathrm{y}}$. 在实际应用阶段，对于一个实时的同一时间长度w内的振动相关SCADA变量样本${{\boldsymbol{x}}_{\mathrm{r}}} \in {{\bf{R}}^{n \times w}}$，多通道机舱加速度数据样本${{\boldsymbol{y}}_{\mathrm{r}}} \in {{\bf{R}}^{C \times w}}$和其他SCADA相关变量样本${{\boldsymbol{z}}_{\mathrm{r}}} \in {{\bf{R}}^{m \times w}}$，通过训练完成的主元回归模型与振动主元提取模块获取实时振动主元估计值和真实值，并计算误差${\boldsymbol{e}}_{\mathrm{r}}^{\mathrm{y}}$，并根据式(16)将其转化为马氏距离$d_{\mathrm{r}}^{\mathrm{y}}$；通过训练完成的正常行为模型获取重构误差${\boldsymbol{e}}_{\mathrm{r}}^{{\mathrm{norm}}}$，并根据式(16)将其转化为马氏距离$d_{\mathrm{r}}^{{\mathrm{norm}}}$.

基于以上条件，当连续$c_{{\mathrm{max}}}^{\mathrm{y}}$个实时数据样本满足$d_{\mathrm{r}}^{\mathrm{y}} > d_{99}^{\mathrm{{\mathrm{y}}}}$并且$d_{\mathrm{r}}^{{\mathrm{norm}}} < d_{99}^{{\mathrm{norm}}}$时，本策略报出叶片异常警告. 此时样本所代表的风机状态处于机舱振动异常，且其余与叶片不相关部分处于正常状态，故而可以认为机舱振动的异常是由叶片单方面引起的，即给出报警.

使用山西省某商用风电场收集的SCADA数据. 该风电场由20台同型号风电机组组成，SCADA数据采样间隔为1 s. 数据集的时间跨度从2021年1月—2023年1月. 在此期间，共发生了16起叶片相关故障，包括4起叶片结冰、6起叶片扫塔、4起叶片震荡、1起叶片断桨和1起叶片螺栓断裂. 在数据训练集和测试集划分方面，针对每一起故障事件，选取故障发生前2个月之前的所有机组的数据进行训练，故障时及故障前2个月之内的数据进行测试. 首先根据模型的输入需求，将连续时间数据集分割成输入样本，取时间窗口为600 s，即连续600个时间点为一个输入样本. 在划分过程中，滑窗步长采用300 s，即相邻样本间存在300个时间点重叠. 如表1所示显示了所使用的SCADA点位的详细信息，对于1.2节中振动主元构建部分，所使用的是左右加速度1和2与前后加速度1和2，共四通道振动数据；对于1.4节中风电机组正常行为模型部分，使用点位实时风速、发电机转速、3 s平均测量功率、对风误差、风向、机舱位置等与叶片没有直接关系的变量进行自编码训练；对于1.3节中自监督振动主元回归器，采用表1中除了机舱加速度之外的所有点位作为输入.

2021年1月—2024年5月，现场已有记录13起叶片扫塔事故. 通过前期对于振动特征的研究，初步发现低频振动特征可以一定程度反映叶片扫塔的发生，以20号机组于2021年4月7日12：29的一支叶片扫塔断裂为例进行说明. 根据机组相对准确的故障发生时间，如图5、6所示，发现该机组在扫塔前后，振动模块有效值通道上出现了显著的约0.05 Hz的振荡特征. 图中，d为能量密度，f为频率. 根据以上分析观察，可以总结出叶片异常确实可以表现在振动信号与SCADA秒级特征层面上. 但是由于人工识别机舱振动特征具有不确定性，且叶片所引发的振动特征异常各异，无法人工确定精确标准衡量. 故而在本研究中，采用深度学习与频域特征构建结合的方式，建立SCADA相关变量与机舱振动特征的正常行为模型，并结合残差超限报警策略进行叶片异常识别.

在实验过程中，对提出的框架下的三部分模块的参数进行网格搜索，以最优的主元回归残差和自编码重构残差为评判标准，找到针对本风电数据集最优的模型参数. 搜索的参数包括：振动主元特征提取模块的VMD分解模态数量K，ABT网络隐藏层大小h，卷积核尺寸k_s，以及正常行为模型的隐藏层大小h_s. 根据网格搜索的结果，后续部分采用的参数设置为K=4, h=32, k_s=5, h_s=32. 模型使用均方误差(MSE)、均方根误差(RMSE)以及平均绝对误差(MAE)作为评估预测性能的指标，表达式如下：

式中：${N}$为测试样本数，$ \hat {{y}}_c^k(i) $和$ \hat y{_c^{k*}}(i) $分别表示第i个样本时间窗口的第c通道的第k个真实振动主元特征真实值和估计值.

对于叶片异常识别指标，将样本的二分类准确度作为标准：

式中：$ {\boldsymbol{1}}( \cdot ) $为指示函数，$ c(i) $和$ {c^*}(i) $分别为第i个样本类别的真实值和本模型算法策略输出的类别.

使用对比模型与提出的ABT模型共同对1.2节提出的振动主元特征进行回归，并比较模型的回归效果. 在对比模型方面，选取以下4种成熟机器学习以及深度学习算法.

1） SVR回归方法： SVR中的核函数选择为径向基函数（radial basis function，RBF），参数松弛因子为1，gamma为0.05.

2） MLP多层感知器：多层感知器设置为一个5层神经网络，隐藏层大小设置为32，每层之间的激活函数使用LeakyReLU.

3） 多层GRU^[24]：GRU中隐藏层大小为32，层数为3，最后采用线性层输出最终结果.

4） Transformer^[17]：隐藏层大小为32，多头注意力机制设置为4.

所有方法的性能对比如表2所示，其中ABT-AK与ABT-BD为ABT模型分别省去了动态卷积核构建以及“时间逆序”技巧.

通过以上对比可以发现，作为振动主元特征的回归器，所提出的ABT自适应双向时序卷积网络具有更好的回归效果. 与此同时，通过对动态卷积核构建和双向卷积的消融对比，也可以看出动态卷积核，以及时序信息双向提取在提升模型估计精准度方面具有重要作用，进一步说明了本模型架构的合理性和高效性.

使用传统叶片异常识别框架与提出的自回归模型框架进行对比. 在对比框架方面，选取以下5种框架与算法.

1） 自编码器. 使用振动通道数据，进行自编码训练，并根据重构误差的均值与标准差^[25]判别样本是否发生异常.

2） 振动有效值预测. 使用SCADA相关变量作为输入，使用GRU实时预测振动通道的有效值. 根据训练集残差序列，应用$3\sigma $准则获得残差上下阈值. 若测试集中样本的误差判别样本超过上下阈值，则报出异常.

3） 二分类器. 将正常数据与异常数据混合，分割训练集和测试集，比例为9∶1. 使用训练集样本的加速度通道数据训练正常-异常SVM二分类器. 而后，在测试集上进行分类测试.

4） 采用USAD^[26]模型作为对比框架，基于对抗自编码的训练策略，将正常样本和异常样本全部用于训练. 而后根据自编码重构误差以及利用$3\sigma $准则检出异常样本.

5） 将本框架中主元特征提取模块，降级为先进行加速度通道快速傅里叶变换（fast Fourier transform, FFT）提取频谱，而后使用PCA提取单一主元. 在后续文中，使用FFT-PCA代表此策略.

所有异常识别框架下的叶片异常识别准确率Acc结果如表3所示. 可以看出，在叶片结冰、叶片震荡、叶片扫塔3种典型叶片异常的情形下，本研究所提出的算法框架都优于其他现有对比框架，并且对3种不同叶片异常具有更加均衡的兼容性. 同时FFT-PCA框架在其余所有对比模型中平均性能最为优异，这也进一步说明了本研究提出的框架的合理性，在即使采用了降级的主元特征提取算法后，依旧保持较高的异常检出准确率.

通过消融实验逐个验证提出的叶片异常识别框架中子模块的作用. 消融实验设置如下：1）取消振动主元提取模块，直接使用振动通道原始值作为自监督目标值；2）替换ABT网络结构为传统TCN结构，模型参数如下，隐藏层为32，空洞卷积基准设置为2，层数设置为3；3）取消正常行为模型模块，单独使用主元残差距离进行故障检出；4）取消异常检出策略中马氏距离计算部分，直接使用欧氏距离作为判据.

在每一种消融方式下，都按照相应的技术路线进行模型训练以及在测试集上进行异常检出，进而从主元特征回归残差与异常检出准确率2个方面与完整的技术路线进行比较. 性能结果如表4所示.

根据消融实验的结果，有如下分析.

1） 取消振动主元提取模块. 回归MAE从0.0523增加到0.4760，叶片结冰的检出准确率从91.29%下降到45.77%，叶片震荡和叶片扫塔的准确率也有显著下降. 这表明振动主元提取模块对于突出关键振动特征至关重要. 没有这一步骤，模型将难以从原始振动数据中学习到有效的特征，导致整体性能显著下降.

2） 替换ABT网络结构为传统TCN结构. 虽然回归MAE仍然保持在0.104的较低水平，但叶片结冰、震荡和扫塔的检出准确率相比本模型分别下降了10.67、11.3和6.47个百分点. 这说明ABT网络在捕捉时间序列数据的特征方面更为有效，能更好地处理风电叶片的振动数据.

3） 取消正常行为模型模块. 虽然回归MAE保持不变，但在叶片结冰、震荡和扫塔的检出准确率上，相比本模型分别下降了3.84、2.44和2.49个百分点. 这表明正常行为模型对于排除非故障因素的干扰、提高故障检出的准确性有重要作用.

4） 取消异常检出策略中马氏距离计算部分. 使用欧氏距离后，叶片结冰、震荡和扫塔的检出准确率相比本模型分别下降了5.15、3.71和7.53个百分点. 这说明马氏距离在考虑数据特征分布的基础上提供了更为精确的相似度测量，从而提高了异常检出的准确率.

提出VMD-kPCA方法实现对机舱多通道振动数据的主元特征自适应提取；融合机舱振动与SCADA机组运行数据，以ABT网络作为骨干特征提取器，实现主元特征自监督回归模型构建；采用基于马氏距离的残差序列判别方法实现高精度叶片异常识别. 在实验验证方面，采用真实风电场实际数据集进行算法性能测试，结果表明本研究所提方法显著优于其他对比模型以及算法框架，并在叶片结冰、叶片震荡、叶片扫塔3种异常检测方面准确率超过90%. 然而，当前方法在复杂环境噪声及多种异常类型同时发生的情况下仍存在一定局限性，对算法的鲁棒性有进一步提升的空间. 未来研究将聚焦于复杂工况下的特征提取优化以及多异常类型的联合检测方法开发，以提升模型的实用性与泛化性能.