球铰作为精密机构中的关键基础零部件,其磨损直接影响机构的运动精度及可靠性[3-5]. 通过分析球铰许用磨损量与机构运动精度的定量关系,预测球铰的磨损寿命,进而保障机构服役期间的精度要求. 由于球铰间隙变化与机构的终端运动精度存在映射关系,大多数研究工作是建立考虑间隙影响的动力学模型[6-8]. Flores等[9]以空间四连杆机构为对象,构建间隙球铰的数学模型并研究间隙对机构动力学响应的影响. 王庚祥等[10]提出具有非线性刚度系数的接触力模型,分析单个球铰间隙对4-SPS/CU并联机构动态性能的影响. 李研彪等[11]以5-PSS/UPU并联机构为例,考虑所有球铰间隙的作用,探讨其动力学特性受球铰间隙深度变化的影响. 精度失效是一个连续渐进过程,具有模糊性和随机性的双重不确定性. 近些年来,针对模糊随机可靠性的研究已取得一定进展[12-13]. 国志刚等[14]以Archard 模型为基础,建立单个铰链与多个铰链的磨损可靠性模型,并以曲柄滑块机构为例进行验证. Yun等[15]为了有效计算模糊失效概率,提出新的阶跃AK-MCS方法. 陈紫起等[16]将模糊理论与T-S故障树相结合,对柴油机缸套异常磨损进行可靠性分析. 黄晓宇等[17-18]研究模糊理论结合其他方法的综合应用问题.
通过量化机构精度特性进行逆向设计,基于精度要求确定球铰最大允许磨损间隙. 再根据模糊可靠性理论,考虑固体润滑(MoS2)工况下球铰的磨损率特性,构建MoS2润滑球铰的磨损模糊可靠性模型. 以3-RPS并联机构为例,计及系统中所有球铰的影响,采用基于精度要求的球铰磨损寿命评估方法,对球铰的工作寿命进行评估.
1. 球铰磨损寿命评估方法
新方法首先采用最大误差影响指标和均方根误差影响指标,及其无量纲精度指标定量地评价机构精度特性. 其次构建间隙球铰模型,并将间隙球铰模型嵌入理想多体系统动力学模型,采用回归分析方法确定磨损间隙尺寸和机构精度指标间的函数关系. 根据机构运动精度阈值确定球铰的最大允许磨损间隙,从而得到最大允许磨损量. 最后采用模糊可靠性理论,并考虑固体润滑工况,建立球铰的磨损模糊可靠性模型,预测基于精度要求的固体润滑球铰的磨损寿命.
1.1. 量化机构精度特性
通过精度指标进行定量分析,较全面地表征机构的精度特性,为建立磨损量与机构精度之间的映射关系提供条件.
1)无量纲最大误差影响指标.
最大误差影响指标
2)无量纲均方根误差影响指标.
均方根误差影响指标
式中:RMS(x0i)为理想机构输出端位置信息的均方根,
1.2. 磨损间隙与机构精度量化指标的函数关系
1.2.1. 球副间隙确定
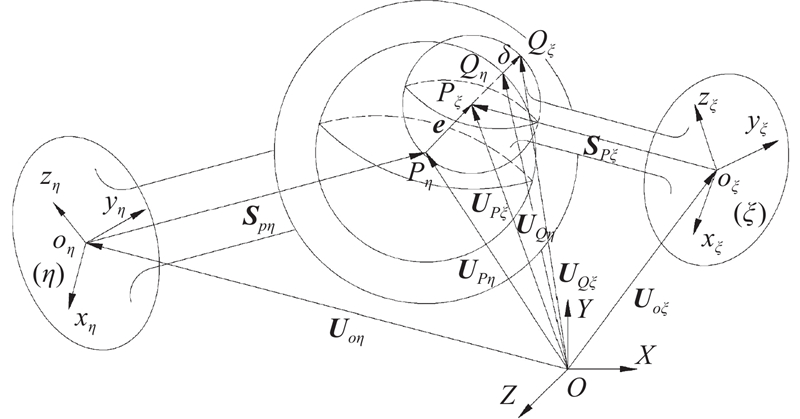
采用数学建模方式,通过构建考虑间隙影响的动力学模型[6-7],分析球铰磨损间隙尺寸对机构输出精度的影响规律. 间隙球铰模型如图1所示. 图中,η表示球窝连接刚体,ξ表示球体连接刚体,局部坐标系oη-xηyηzη和oξ-xξyξzξ分别与刚体η、ξ的质心固连;Uoη和Uoξ分别表示局部坐标系oη-xηyηzη和oξ-xξyξzξ的坐标原点在全局坐标系中的位置向量;点Pη和Pξ分别为球窝和球体的中心,点Qη和Qξ分别为球窝和球体的碰撞接触点;SPη表示点Pη在局部坐标系oη-xηyηzη中的位置向量,SPξ表示点Pξ在局部坐标系oξ-xξyξzξ中的位置向量;UPη和UPξ分别表示点Pη和Pξ在全局坐标系下的位置向量;UQη和UQξ分别表示点Qη和Qξ在全局坐标系下的位置向量. 球体与球窝的偏心向量e可以表示为
图 1
偏心量的大小可以表示为
UPi可以表示为
式中:Ti表示局部坐标系oi-xiyizi相对定坐标系的转换矩阵. 间隙球铰中球体和球窝接触点的法向单位向量n可以表示为
球窝和球体发生碰撞时的穿透深度δ(即接触变形量)可以表示为
式中:c表示球窝和球体的间隙,
式(6)可以用来判断间隙球铰中球体和球窝的接触情况,当
1.2.2. 碰撞力模型
当球铰的球窝和球体发生碰撞时,其接触点在固定坐标系下的位置矢量UQi可以表示为
式(7)两边分别对时间求导,可得接触点在固定坐标系下的速度:
接触点相对速度的法向和切向碰撞速度分别为
式中:τ表示接触面的切向单位向量,
根据文献[9],采用改进的Flores接触力模型来表示球体对球窝的法向接触力Fn,表达式如下:
式中:nf为设定指数,取1.5;ce为恢复系数;
式中:E*为球铰副的综合弹性模量;
基于Ambrósio所提出的修正的Coulomb力法则求解切向接触力,则球体对球窝的切向接触力表达式为
式中:μ为摩擦因数,cd为动态修正系数.
球体对球窝的碰撞力可以表示为
式中:Fxη、Fyη、Fzη分别为球体对球窝的碰撞力在固定坐标系下X、Y、Z方向上的分量.
根据作用力和反作用原理,可知球窝对球体的碰撞力为
将上述间隙球铰模型嵌入理想多体系统动力学模型中,建立磨损间隙尺寸和机构精度指标之间的函数关系.
1.3. 球铰磨损模糊可靠性模型
由最大允许磨损间隙,可得到最大允许磨损量,进而计算其磨损寿命. 考虑球铰初始配合间隙、磨损率和最大允许磨损量均具有随机特性,建立球铰磨损概率可靠性模型. 摩擦副的实际磨损量和耐磨寿命均可被视为正态分布[19],则磨损深度w的概率密度函数为
式中:
式中:wmax为最大允许磨损量,其不仅具有随机性,还具有模糊性. 采用模糊可靠性理论,得到球铰的磨损模糊可靠度:
式中:
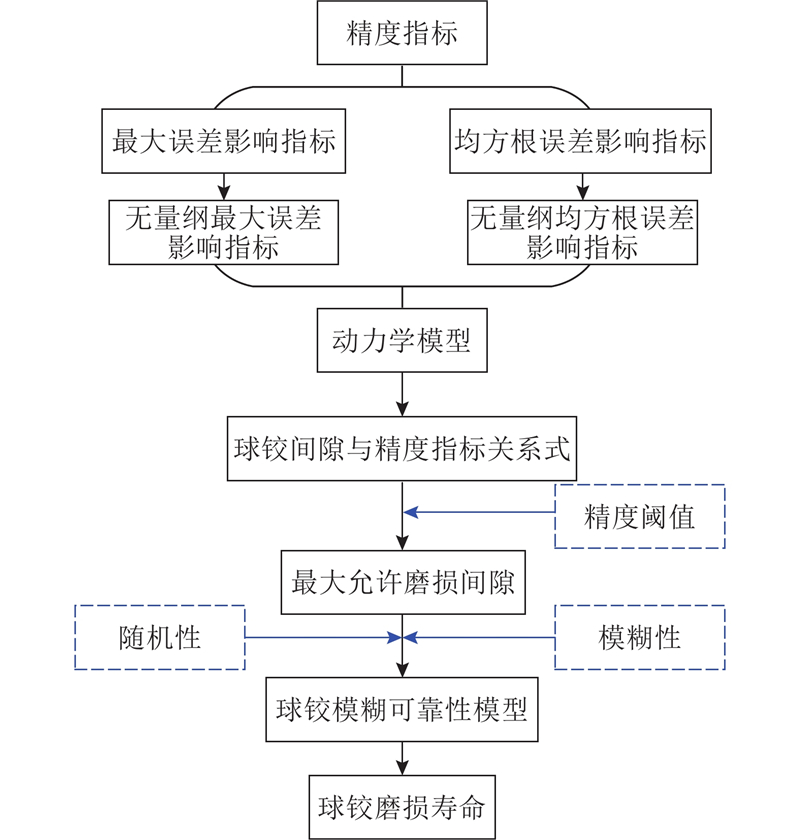
基于精度要求的球铰磨损寿命评估体系建立方法如图2所示.
图 2
图 2 基于精度要求的球铰磨损寿命评估体系
Fig.2 Wear life evaluation system of spherical hinges based on accuracy requirements
2. 固体润滑球铰磨损寿命的评估
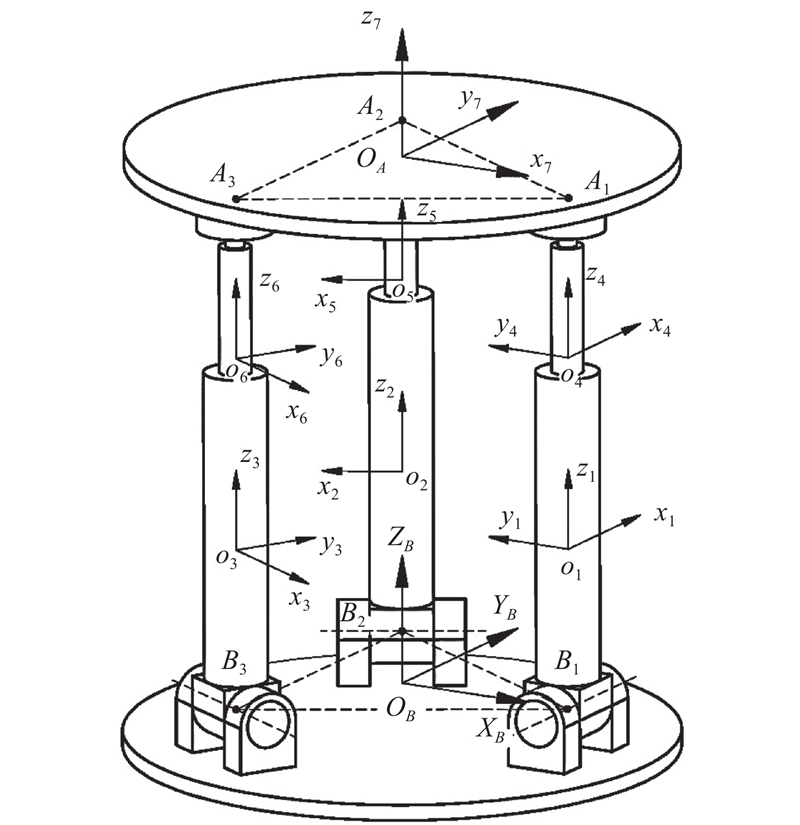
以3-RPS并联机构为例(其模型如图3所示),采用新的球铰磨损寿命评估方法,基于机构精度对固体润滑球铰不同可靠度下的磨损寿命进行预测.
图 3
2.1. 磨损间隙与机构精度指标的函数关系
通过间隙动力学方程,可得到不同间隙尺寸下,机构输出端的位移,从而建立间隙尺寸与机构精度之间的函数关系.
2.1.1. 含间隙动力学模型
如图3所示,A1、A2、A3连线构成的三角形与B1、B2、B3连线构成的三角形为大小相等的等边三角形. 在定平台上建立定坐标系OB-XBYBZB,在动平台上建立动坐标系o7-x7y7z7,分别在3条支链的移动副缸体与活塞的质心处建立随体坐标系oj-xjyjzj(j=1,2,···,6). 动坐标系o7-x7y7z7和随体坐标系oj-xjyjzj在定坐标系下的位姿可以采用ZYX欧拉角来表达,转换矩阵为
3-RPS空间并联机构共有7个活动构件,各个活动构件由其质心坐标[xi, yi, zi]T和欧拉角[αi, βi, γi]T来定义,进而得到整个机构的广义坐标:
式中:
选取系统构件的位置及姿态角,建立系统的运动学约束方程:
式中:
3-RPS并联机构中转动副的约束方程为
式中:oj为局部坐标系oj-xjyjzj原点在固定坐标系下的位置向量;jBj为点Bj在局部坐标系oj-xjyjzj下的位置向量;0Bj为点Bj在定坐标系下的位置向量;αj0为局部坐标系oj-xjyjzj相对于定系Z轴的初始欧拉角,
采用移动副作为驱动,因此在已知驱动函数时,将移动副约束与驱动约束合并后,活塞杆相对于缸体为全约束. 约束方程可以表示为
式中:jok为点
球铰的约束方程可以表示为
式中:7Aj为点Aj在动坐标系o7-x7y7z7下的位置向量,kAj为点Aj在局部坐标系ok-xkykzk下的位置向量.
对于含间隙运动副的多体系统,须用力约束来替换间隙运动副中的几何约束. 将与动平台相连的3个球铰均考虑为间隙运动副,建立3-RPS机构的运动学约束方程:
式(25)对时间求一、二阶导数可以得到速度、加速度约束方程:
式中:
对于含有3个间隙球铰的3-RPS机构,3根驱动杆与动平台所受接触力和接触力矩共同构成接触力矩阵Fmc,并与广义外力矩阵Q相加,得到3-RPS机构所受的广义力矩阵Qmc.
由Lagrange乘子法得到含有3个间隙球铰的3-RPS机构动力学方程:
式中:M为3-RPS并联机构的广义质量矩阵;
2.1.2. 含间隙动力学模型计算方法
3-RPS并联机构动力学方程采用MATLAB进行求解,过程如下:1)定义初始条件,
假设动平台质心运动轨迹如下:
3-RPS机构动平台的运动学输出具有耦合特性,通过机构约束方程可以求得其他3个运动学参数. 3-RPS并联机构的结构参数和动力学参数如表1所示.
表 1 3-RPS并联机构结构参数和动力学参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| 动平台质量mA/kg | 8.509 1 | 动平台转动惯量矩阵J7/(kg·mm2) | ||
| 活塞杆质量m4~m6/kg | 0.521 8 | |||
| 缸体质量m1~m3/kg | 1.841 2 | |||
| 活塞杆质心到球副中心距离la/mm | 100.5 | 活塞杆转动惯量矩阵J4~J6/(kg·mm2) | ||
| 缸体质心到转动副中心距离lb/mm | 94.5 | |||
| 球副与转动副初始中心距离L0/mm | 320.0 | |||
| 动系原点与定系的初始距离H0/mm | 341.2 | 缸体转动惯量矩阵J1~J3/(kg·mm2) | ||
| 动、定平台半径(r、R)/mm | 120.0 | |||
| 修正参数α | 50 | |||
| 修正参数β | 50 |
2.1.3. 含间隙动力学模型计算结果与分析
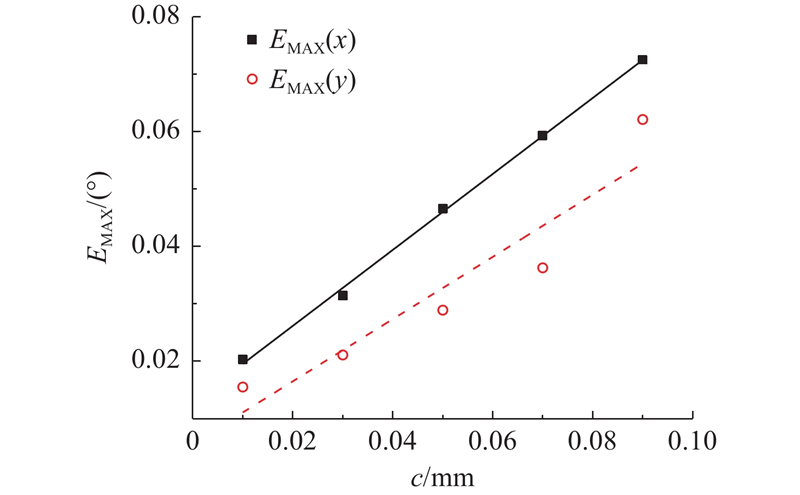
图 4
图 4 3-RPS机构位置最大误差影响指标
Fig.4 Influence index of maximum error on position of 3-RPS mechanism
图 5
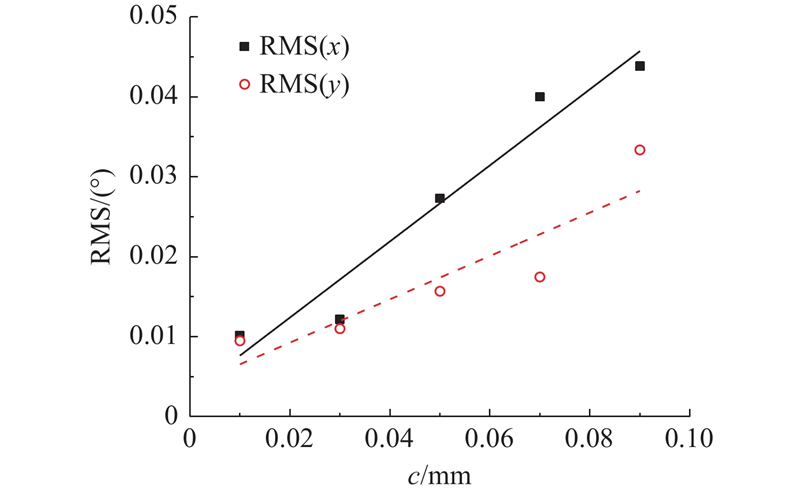
图 5 3-RPS机构位置均方根误差影响指标
Fig.5 Influence index of root mean square error on position of 3-RPS mechanism
图 6
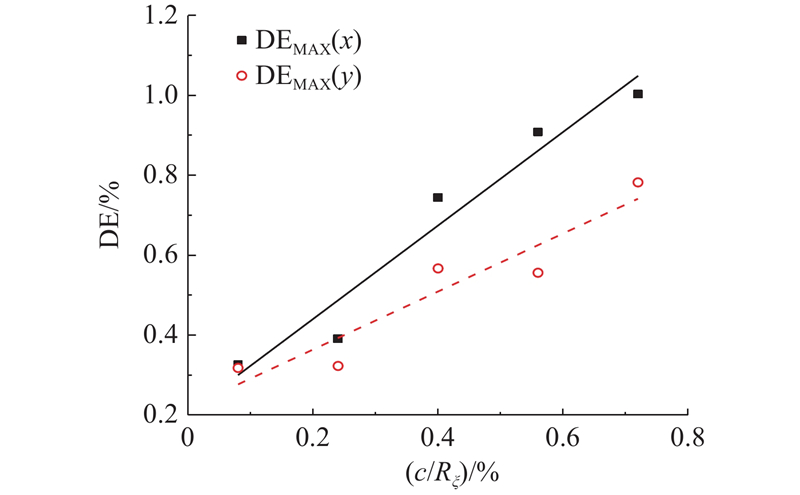
图 6 3-RPS机构位置无量纲最大误差影响指标
Fig.6 Influence index of dimensionless maximum error on position of 3-RPS mechanism
图 7
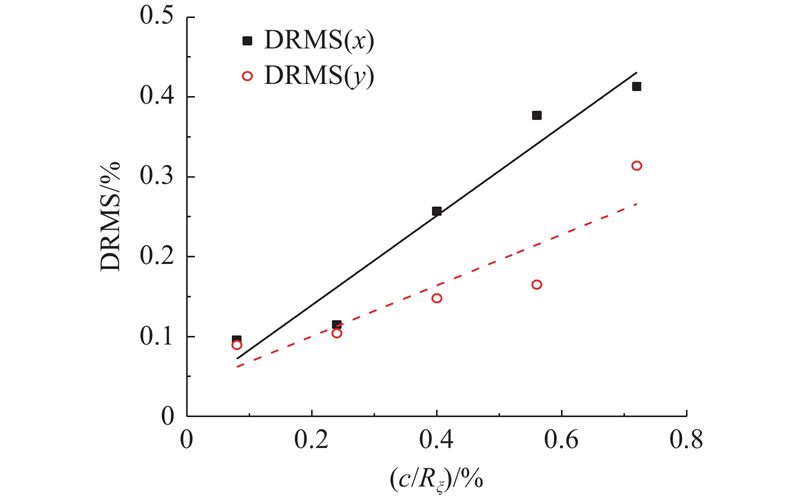
图 7 3-RPS机构位置无量纲均方根误差影响指标
Fig.7 Influence index of dimensionless root mean square error on position of 3-RPS mechanism
通过最小二乘法拟合,可以得到无量纲间隙与机构DRMS(x)的关系式为
无量纲间隙与机构DRMS(y)的关系式为
无量纲间隙与机构DEMAX(x)的关系式为
无量纲间隙与机构DEMAX(y)的关系式为
文献[22]通过研究含多个转动副间隙3-PRR并联机构的运动动态特性,认为可以将间隙大小作为指标直接衡量动平台位移误差最大值. 本研究发现在3-RPS并联机构中,球铰间隙大小与动平台的运动精度之间存在正比例关系,可根据精度指标要求确定最大允许间隙.
2.2. 固体润滑球铰磨损模糊可靠性寿命预测
由于球铰的间隙和磨损均具有随机性,磨损失效是一个渐进过程,因此,基于模糊可靠性理论,由球铰的最大允许间隙得到最大允许磨损量,对固体润滑球铰的磨损寿命进行评估.
2.2.1. 最大允许磨损量的确定
将机构的精度失效阈值定为0.05°,根据2.1 节中磨损间隙与机构精度指标的函数关系,球铰的最大允许磨损间隙为0.047 mm,最大允许磨损量wmax为0.037 mm. 采用传统最大允许磨损量的确定方法,选取其中的下限值,得到wmax为0.150 mm(本研究中球铰直径为25 mm). 传统经验方法确定的wmax显著大于新方法确定的值,且随着机构精度要求越高,两者的差别越大.
图 8
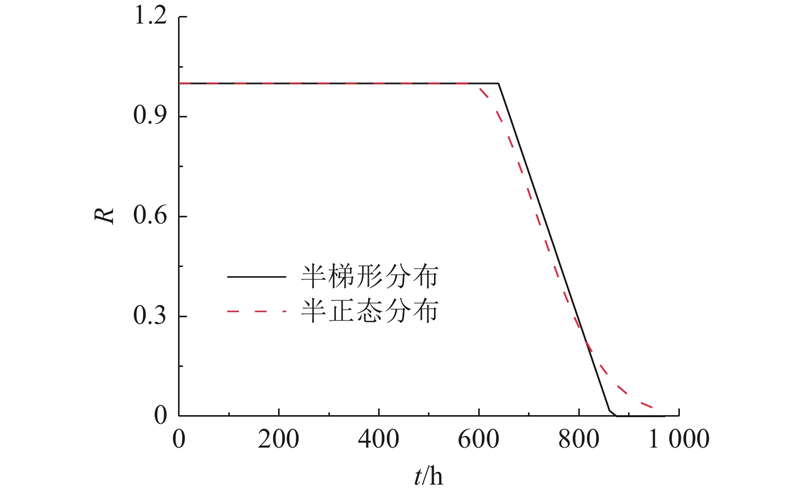
图 8 球铰磨损中半梯形和半正态隶属函数分布曲线
Fig.8 Distribution curves of semi-trapezoidal and semi-normal membership functions in wear of spherical hinge
2.2.2. 固体润滑球铰的磨损模糊可靠性寿命模型
1)采用偏小型半梯形隶属函数.
将偏小型半梯形隶属函数及磨损量的概率密度函数的表达(式(16))代入式(18),整理得到球铰磨损模糊可靠度:
式中:
2)采用偏小型正态分布隶属函数.
将偏小型正态分布隶属函数及磨损量的概率密度函数的式(16)代入式(18)进行推导. 将式(18)分2段积分,并利用超越函数的积分公式,得到球铰磨损模糊可靠度:
式中:
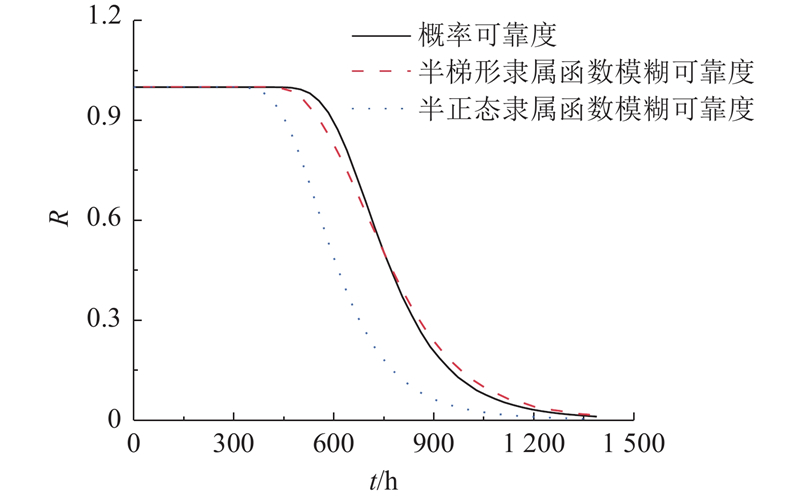
采用MoS2润滑的球铰可有效提高其服役寿命,而MoS2润滑膜的磨损是球铰最主要的失效形式. 根据所建立的球铰磨损模糊可靠性模型,基于笔者建立的MoS2润滑膜磨损模型[25],对MoS2润滑球铰磨损寿命进行预测. 球铰初始装配间隙均值为0.010 mm,标准差为0.003 mm. 球铰初始配合间隙和磨损率标准差根据变差系数法求出[26]. 根据球铰的磨损概率可靠性(式17)和磨损模糊可靠性寿命模型(式18),得到MoS2润滑球铰的可靠度随时间演化曲线如图9所示.可以看出,在MoS2润滑球铰实际磨损量未到达临界失效状态前,磨损概率可靠性模型和磨损模糊可靠性模型的可靠度曲线完全吻合. 当实际磨损量接近临界失效状态时,采用半正态隶属函数的模糊可靠度
图 9
图 9 球铰磨损的概率可靠性和模糊可靠性曲线
Fig.9 Probability reliability and fuzzy reliability curves of wear of spherical hinge
2.2.3. 大气和真空环境中MoS2润滑球铰的磨损模糊可靠性寿命
设机构系统中n个球铰各自的可靠度为Ri (i = 1,2,···,n),则系统磨损可靠度的表达式为
在实际情况中,并联机构中各个球铰的磨损情况非常复杂且难以预测,因此,假设各个球铰寿命分布相同.
根据构建的基于精度要求的球铰磨损寿命评估方法,采用偏小型半梯形隶属函数,预测在大气环境中MoS2润滑球铰的磨损寿命. 当系统可靠度R(t) = 0.90时,每个球铰各自的可靠度为R1 = R2 = R3 = 0.536,则3-RPS并联系统的模糊可靠性寿命Tf = 232 h. 并联机构中各个球铰之间存在复杂的耦合作用,各个球铰的失效模式之间存在一定的相关性,因此,计算的机构系统可靠度为上限,但同样具有一定的参考价值[14].
MoS2薄膜在真空环境中拥有更加优异的摩擦磨损性能,因此,当R(t) = 0.90时,航天机构中MoS2润滑球铰模糊可靠性寿命Tf = 42 408 h,按一年365天计算,服役年限约为4.8 a. 在相同可靠度下,真空环境中MoS2润滑球铰的寿命比在大气环境中的寿命高约2个数量级.
3. 结 论
(1)提出基于精度要求的球铰磨损寿命评估方法,通过机构精度失效阈值判定球铰磨损失效寿命,结果更加准确. 该方法同样适用于向心关节轴承和转动副,具有可推广性和普适性.
(2)以3-RPS并联机构为研究对象,发现球铰磨损间隙与精度指标之间呈线性关系,可通过球铰间隙衡量机构精度.
(3)采用偏小型半梯形隶属函数可以较准确地预测固体润滑球铰磨损的安全状态和失效状态.
(4)当R(t) = 0.90时,轻载工况下3-RPS并联机构中,MoS2润滑球铰在大气和真空环境下的磨损模糊可靠性寿命分别为232 、42 408 h.
(5)考虑多个球铰间隙的影响,各间隙之间存在复杂的耦合关系,多间隙的耦合作用有待进一步定量研究.
参考文献
Analysis of planar multibody systems with revolute joint wear
[J].DOI:10.1016/j.wear.2009.10.014 [本文引用: 1]
Fretting fatigue and wear damage of structural components in nuclear power stations-fitness for service and life management perspective
[J].DOI:10.1016/j.triboint.2006.02.052 [本文引用: 1]
Wear simulation of a spherical hinge joint with a thin composite coating
[J].DOI:10.1007/s11029-021-09993-8 [本文引用: 1]
医疗辅助机械臂关节处的球铰结构设计
[J].DOI:10.3969/j.issn.1673-3142.2020.12.024
Design of ball joint structure based on joint of medical auxiliary mechanical arm
[J].DOI:10.3969/j.issn.1673-3142.2020.12.024
A study on wear and friction of passenger vehicles control arm ball joints
[J].DOI:10.3390/en14113238 [本文引用: 1]
Dynamic analysis of a spatial mechanism including frictionless spherical clearance joint with flexible socket
[J].DOI:10.1115/1.4038508 [本文引用: 2]
Wear analysis of spatial parallel mechanisms with multiple three-dimensional spherical clearance joints
[J].DOI:10.1115/1.4044295 [本文引用: 1]
考虑运动副间隙的机构动态特性研究
[J].DOI:10.3969/j.issn.1000-3835.2011.11.005 [本文引用: 1]
Dynamic characteristics of mechanisms with joint clearance
[J].DOI:10.3969/j.issn.1000-3835.2011.11.005 [本文引用: 1]
Dynamics of multibody systems with spherical clearance joints
[J].DOI:10.1115/1.2198877 [本文引用: 2]
考虑球面副间隙的4-SPS/CU并联机构动力学分析
[J].DOI:10.3901/JME.2015.01.043 [本文引用: 1]
Dynamics analysis of 4-SPS/CU parallel mechanism with spherical joint clearance
[J].DOI:10.3901/JME.2015.01.043 [本文引用: 1]
含球面副间隙的空间并联机构动态特性
[J].
Dynamic characteristics of spatial parallel mechanism with spherical joint clearance
[J].
基于模糊理论的机械零部件磨损可靠性设计
[J].DOI:10.3969/j.issn.1000-1212.2021.12.014 [本文引用: 1]
Reliability design of machinery parts wear based on fuzzy theory
[J].DOI:10.3969/j.issn.1000-1212.2021.12.014 [本文引用: 1]
机构磨损可靠性高精度算法
[J].
The computation of wear reliability of mechanism with high accuracy
[J].
铰链磨损可靠性分析及计算方法
[J].DOI:10.3969/j.issn.1000-2758.2006.05.024 [本文引用: 2]
Wear reliability of linkage under periodic loading
[J].DOI:10.3969/j.issn.1000-2758.2006.05.024 [本文引用: 2]
A novel step-wise AK-MCS method for efficient estimation of fuzzy failure probability under probability inputs and fuzzy state assumption
[J].DOI:10.1016/j.engstruct.2019.01.020 [本文引用: 1]
基于T-S模糊故障树的某柴油机缸套可靠性分析
[J].
Reliability analysis of a diesel engine cylinder liner based on T-S fuzzy fault tree
[J].
具有模糊失效状态的涡轮盘疲劳可靠性及灵敏度分析
[J].DOI:10.3969/j.issn.1000-2758.2021.06.018 [本文引用: 1]
Fatigue reliability and sensitivity analysis of turbine disk with fuzzy failure status
[J].DOI:10.3969/j.issn.1000-2758.2021.06.018 [本文引用: 1]
Wear parameter optimization of ceramic coating using the fuzzy integrated PSI-CODAS decision-making framework
[J].DOI:10.1007/s13369-022-07212-7 [本文引用: 1]
Distribution of wear rate data and a statistical approach to sliding wear theory
[J].DOI:10.1016/0043-1648(87)90037-8 [本文引用: 1]
重叠可展开天线双轴指向机构的设计及应用
[J].DOI:10.3969/j.issn.1674-7135.2020.06.015 [本文引用: 1]
Design of a new satellite antennas deployment pointing mechanism
[J].DOI:10.3969/j.issn.1674-7135.2020.06.015 [本文引用: 1]
The research about radiometric technology of two-dimensional rotary table based on image gray level
[J].
Dynamic analysis of a 3-PRR parallel mechanism by considering joint clearances
[J].DOI:10.1007/s11071-017-3672-1 [本文引用: 1]
多因素耦合下机构运动精度可靠性仿真试验及寿命评估
[J].
Reliability simulative trial of kinematic accuracy and life evaluation for planar mechanism with multi-factor coupling
[J].
综合传动铸铁密封环磨损模糊可靠性分析与计算
[J].DOI:10.3969/j.issn.1001-0645.2005.02.005 [本文引用: 1]
Analysis and calculation of fuzzy reliability on the cast iron sealing ring in composite transmissions
[J].DOI:10.3969/j.issn.1001-0645.2005.02.005 [本文引用: 1]
MoS2薄膜摩擦因数和磨损量的数学模型
[J].
Mathematical model of friction coefficient and wear of MoS2 Film
[J].