Laniado-Jácome等[11]建立滚子轴承的有限元仿真模型,并分析滚子与内外套圈间的相对滑动问题. Kim[12-13]利用简化的动力学模型分析径向游隙及几何偏差对轴承内部保持架打滑的影响. Gupta[14-15]对Walters[16]所建立的动力学模型进行改进,在考虑弹流润滑的条件下,建立圆柱滚子轴承的完全动力学模型,以实现对轴承内部滚子及保持架运动及受力状态的全面分析. Liu等[17-18]建立弹流润滑条件下的滚动轴承打滑动力学模型,提出用于轴承打滑行为改善的结构参数优化设计准则. 贾永川等[19-20]、李猛等[21]分别建立启停阶段及非稳态工况下的圆柱滚子轴承动力学模型,分析径向载荷、工作温度对滚子及保持架打滑率的影响. 韩勤锴等[22]研究径向力、弯矩之类的工况参数对轴承打滑特性的影响. Tu等[23]建立圆柱滚子轴承的非线性动力学模型,研究滚子的局部打滑行为,分析径向载荷、主轴转速及保持架兜孔间隙对于滚子局部打滑情况的影响. 目前,在圆柱滚子轴承打滑的动力学分析方面,研究主要关注的是高速轻载之类工况下的轴承保持架宏观打滑现象,对于滚动体随其位置变化的局域打滑现象还有待深入研究[24]. 保持架打滑对应于轴承整体打滑行为,是轴承内部各滚动体局域打滑行为的“平均化”表征,无法真实反映轴承内部滚动体的实际运行状态. 因此,须进一步针对不同载荷工况下的圆柱滚子轴承内部滚动体的局域打滑特性与机理开展研究.
本研究基于圆柱滚子轴承完全动力学模型,针对其内部滚子的局域打滑特性进行系统性研究,讨论载荷工况(径向载荷、转速)对圆柱滚子轴承内部滚子局域打滑行为的影响,并探究中低速中等载荷条件下圆柱滚子轴承内部滚子局部打滑的影响因素及变化规律,同时分析滚子打滑(局域打滑)与保持架打滑(整体打滑)特性间的差异与内在联系.
1. 圆柱滚子轴承动力学分析模型
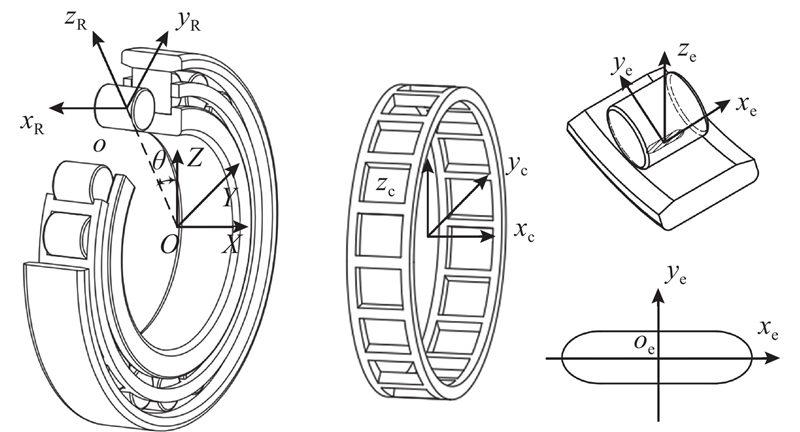
为了对轴承各组件的受力及运动进行描述,建立用于圆柱滚子轴承理论分析的多坐标系统,包括惯性坐标系及若干局部零件坐标系. 如图1所示,建立全局惯性坐标系
图 1
图 1 圆柱滚子轴承坐标系定义
Fig.1 Definition of coordinate system for cylindrical roller bearing
圆柱滚子轴承的惯性坐标系为固定坐标系,其坐标原点位于轴承质心,其空间位置不随时间及轴承零件的运动发生改变. 而轴承内各零件的局域坐标系则为运动坐标系,其空间位置随着零件的运动而持续发生变化,零件坐标系的坐标原点固定于各零件质心. 为了建立轴承的运动微分方程,在各零件坐标系下对各零件自身的运动和受力情况进行描述. 为了简化计算,在构建滚动轴承内部各组件的运动方程的过程中,首先在局部坐标系下对各零件自身的运动和受力情况进行描述,然后再通过坐标变换将上述关系统一转换到惯性系下进行求解计算. 通过三维坐标转换矩阵,可以将任意两坐标系下的位置坐标或空间向量进行坐标变换. 其中,惯性系与任意零件坐标系间的转换关系如下:
式中:
轴承内各零件的受力情况由其相对位置及运动关系所决定,本研究模型主要考虑滚子与套圈、滚子端面与套圈挡边、滚子与保持架、套圈与保持架等零件间相互作用,确定各零件的受力状态,以实现对圆柱滚子轴承动力学模型的求解.
1.1. 滚子与套圈间的相互作用
滚子所受到的作用力主要包括滚子与套圈间的法向接触力和切向拖动力. 首先须确定滚子与滚道间的接触变形量,进而再计算滚子与套圈间的接触载荷. 滚子与套圈间的接触变形量可以根据Lundberg[25]提出的经验公式给出:
式中:
图 2
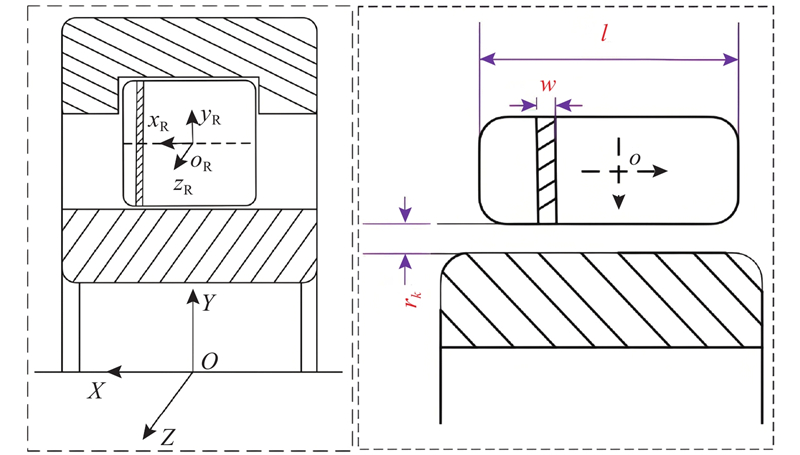
图 2 滚子与套圈相互作用示意图
Fig.2 Schematic diagram of interaction between roller and ring
式中:
式中:
滚子和套圈滚道间的法向作用力[27]为
式中:N表示切片的数量.
假设滚子与套圈接触变形量一致. 基于五参数流变模型[28],滚子与套圈间的润滑拖动系数可根据滚子局域滑动速度及润滑剂类型进行选取,进而可计算出滚子的拖动力. 由此,将作用于滚子的法向力与拖动力合成为
式中:
滚子及套圈的外力矩分别为
式中:
1.2. 滚子与挡边间的相互作用
由于滚子端面与套圈挡边间的相互作用较为复杂,为了进行简化,针对两者间的接触关系提出以下2个假设:1)当滚子端面与套圈挡边不发生接触时,两者间不存在接触力,即忽略油膜拖动作用;2)当套圈挡边与滚子在其圆角处接触时,可用Hertz点接触模型近似计算两者间的接触载荷,并计算拖动力.
基于上述2条假设,根据滚子端面与挡边间的几何相互作用关系,其弹性变形量为
式中:
滚子和套圈挡边间的接触载荷可根据Hertz接触理论得出,而润滑剂的拖动力可以表示为
式中:
式中:
式中:
因此,滚子端面所受作用力的合力为
式中:
1.3. 保持架与滚子以及保持架与套圈间的相互作用
在圆柱滚子轴承运行过程中,滚子与保持架、套圈与保持架间可能存在频繁的碰撞,且单次作用时间较短,使得两者间的接触作用十分复杂. 为了简化接触模型,提出以下3点假设:1)假设保持架为刚性,忽略其柔性变形;2)假设滚子-保持架、套圈-保持架间相互作用不存在流体动压效应造成的弹性变形;3)假设滚子-保持架、套圈-保持架间的局域接触变形为弹性变形.
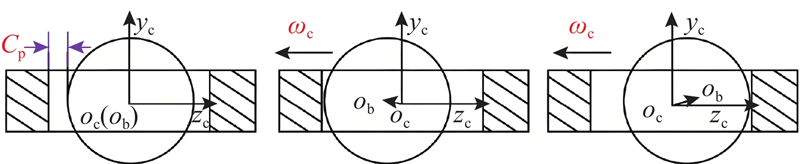
滚子与保持架的位置关系示意图如图3所示. 图中,CP表示滚子与保持架兜孔间的距离,
图 3
图 3 滚子与保持架位置关系示意图
Fig.3 Schematic diagram of position relationship between roller and cage
滚子与保持架横梁的接触变形[24]与碰撞力分别如下:
式中:
滚子与保持架之间的摩擦力为
式中:
滚子与保持架之间由于碰撞力而产生的附加力矩[26]为
式中:
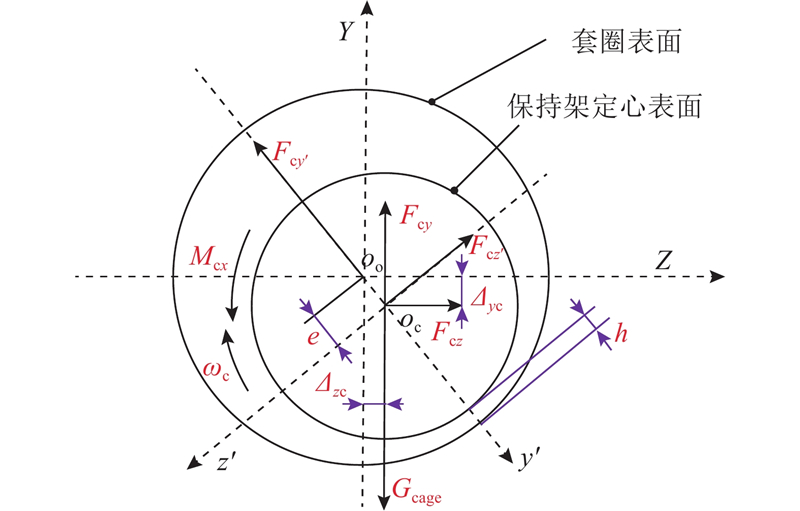
由于保持架不直接承受载荷,须通过其他部件引导来带动其运动. 保持架常见的引导方式有3种:滚子引导、内圈引导以及外圈引导. 以外圈引导为例,保持架与套圈的相互作用如图4所示.
图 4
图 4 保持架与套圈相互作用示意图
Fig.4 Schematic diagram of interaction between cage and ring
在径向平面上,假定保持架质心坐标为
式中:
用
保持架与引导面的摩擦力矩可表示为
式中:
当
式中:
保持架和引导套圈间的摩擦力矩为
1.4. 涡动与阻力损失
在阻力估计方面,可以根据圆柱体在流体中平移时所受阻力的表达式[29]来确定. 其中,阻力系数
式中:
在涡动力矩的计算方面,由于滚子在其柱面和端面上均会发生涡动,涡动力矩可以利用Rumbarge[30]提出的圆柱体涡动模型进行计算. 其中,滚子在其柱面上的涡动力矩
式中:
滚子端面上的涡动力矩可以表示为
式中:
1.5. 动力学微分方程
根据轴承各零件间的相互作用力和运动状态,分别建立圆柱滚子轴承内部各零件的动力学微分方程组.
滚子的动力学微分方程为
式中:
内圈的动力学微分方程为
式中:
保持架的动力学微分方程为
式中:
针对上述动力学微分方法,采用Hilber-Hughes-Taylor变步长积分算法进行计算.
2. 圆柱滚子轴承的打滑机制分析
2.1. 滚动轴承的打滑评价指标
在圆柱滚子轴承发生打滑时,其滚子及保持架的实际转速降低,低于其无滑移条件下的理论转速,因此可以利用基于实际转速计算得到的保持架打滑率及滚子打滑率对轴承的打滑程度进行描述. 保持架打滑率是目前圆柱滚子轴承打滑分析所采用的主流评价指标,可以反映轴承的宏观打滑现象. 保持架打滑率的表达式为
式中:
保持架的理论转速为
式中:
当轴承外圈不发生转动时,保持架理论转速可以表示为
滚子打滑率可以更加直观地描述轴承的局域打滑现象. 与保持架打滑率表达式类似,滚子打滑率可以表示为
式中:
2.2. 圆柱滚子轴承打滑特性分析
图 5
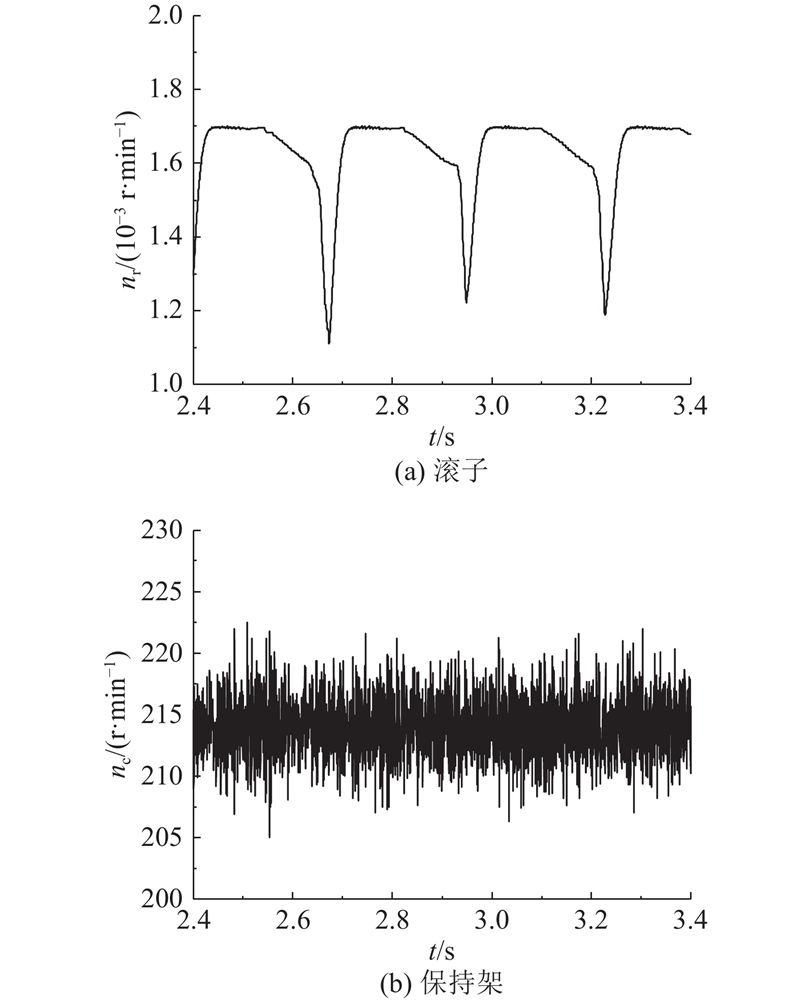
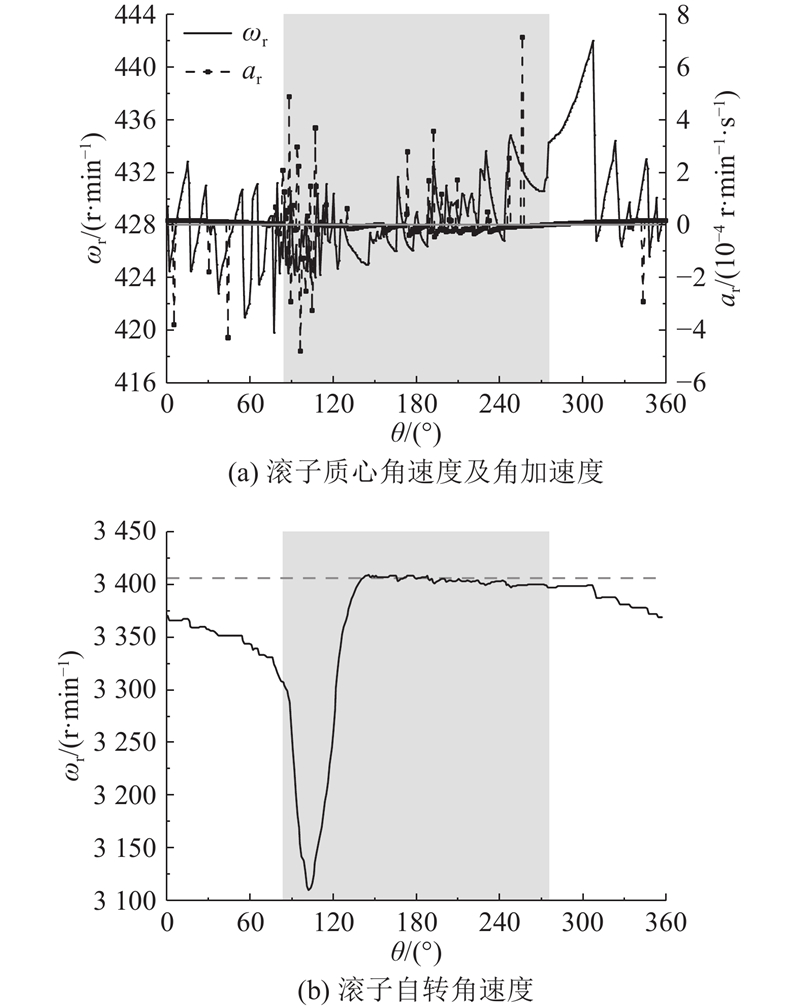
图 5 轴承转速和打滑率随时间的变化规律
Fig.5 Variation of rotational speed and skidding rate of bearing rollers with time
在后续分析中,统一选用N216 型圆柱滚子轴承,其主要结构参数如表1所示,轴承保持架材料为尼龙. 轴承内圈与主轴间采用过盈配合,过盈量为10 μm;轴承外圈与轴承座间采用间隙配合,过盈量为5 μm,原始径向游隙为1 μm,轴承的径向工作游隙为−4 μm. 选择润滑剂为美孚DTE型润滑油,其密度为0.85 kg/L,40℃时的运动黏度为31.0 mm2/s,100 ℃时的运动黏度为5.5 mm2/s,黏度指数为102. 相比于文献中设置的径向载荷为300 N、转速为4 500 r/min的高速轻载工况,本研究主要针对中低速工况条件展开研究,此时轴承保持架的宏观打滑现象并不明显,在传统研究过程中往往被忽略. 基于文献[16-19]的载荷工况,选择径向载荷为1 000 N、转速为1 000 r/min的工况条件,作为本研究的中低速工况条件,转速在4 500 r/min及以上时,视为高速工况,并开展此条件下的圆柱滚子轴承内部滚子局部打滑的影响因素及变化规律研究.
表 1 N216型圆柱滚子轴承主要参数
Tab.1
| 尺寸参数 | 数值 | 性能参数 | 数值 | |
| 滚子直径d /mm | 16 | 轴承宽度B /mm | 26 | |
| 滚子长度L /mm | 17 | 保持架内径dri /mm | 108.5 | |
| 滚子数n | 18 | 保持架外径dro /mm | 118.5 | |
| 质量m /kg | 80 | 轴承节圆直径dm /mm | 80 | |
| 轴承内径di /mm | 80 | 参考转速ni / (r·min−1) | ||
| 轴承外径do /mm | 140 | 基本额定动载荷C /kN | 160 | |
| 轴承宽度B /mm | 26 | 基本额定静载荷Co /kN | 166 | |
| 滚子直径d /mm | 16 | 极限转速n /( r·min−1) |
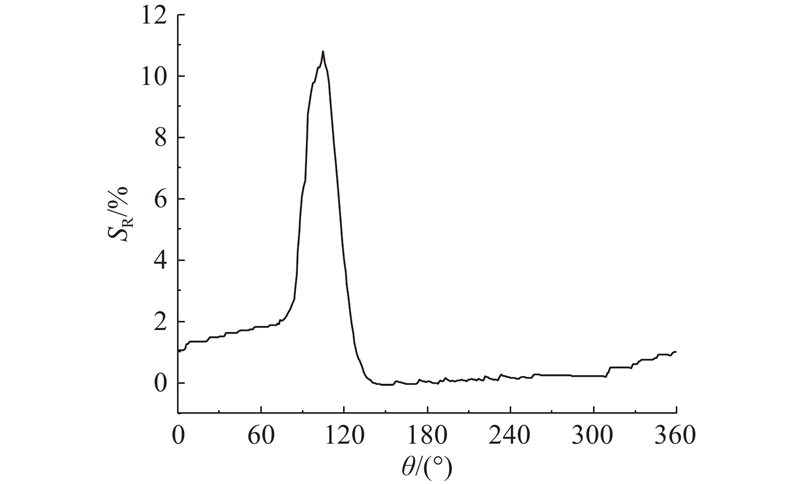
2.2.1. 滚子打滑沿圆周方向分布计算
对主轴转速为
图 6
图 7
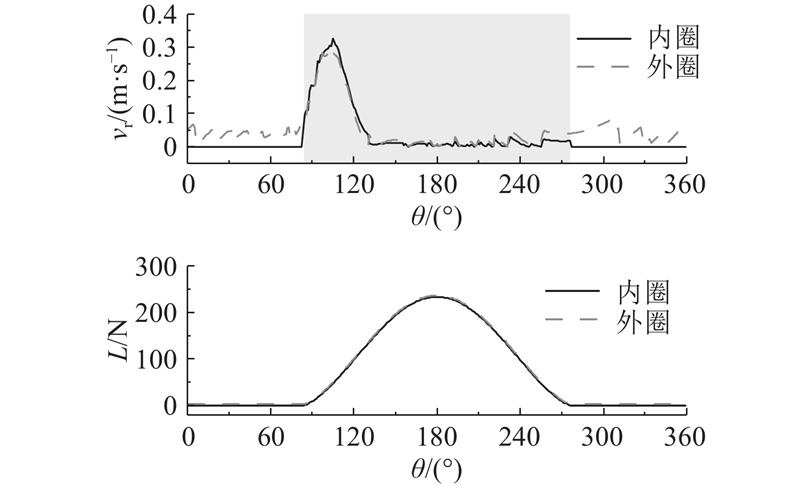
图 7 滚子-内外圈相对滑动速度、接触载荷与相位角的关系
Fig.7 Relationship of relative sliding speed, contact load, and phase angle between roller and inner or outer ring
2.2.2. 滚子与保持架间的作用
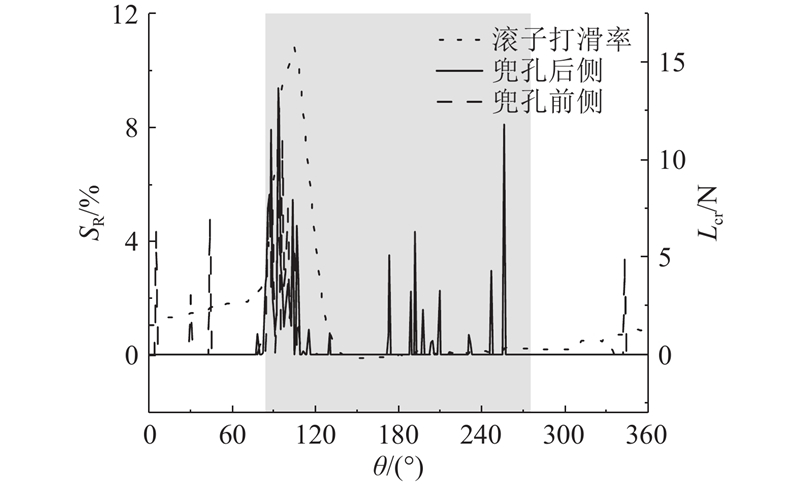
滚子在进入承载区时,所受的载荷和转速具有更加显著的时变特性,这使得打滑机理较为复杂. 为了对滚子及保持架的打滑机理进行更深入的研究,对滚子与保持架兜孔间接触力Lcr进行分析,如图8所示.
图 8
图 8 滚子与保持架间相互作用对打滑的影响
Fig.8 Effect of interaction between roller and cage on skidding
图 9
3. 工况参数对圆柱滚子轴承打滑的影响
3.1. 径向载荷对圆柱滚子轴承打滑的影响
滚动轴承的承载区位置和范围与轴承所受径向载荷的方向和大小有关,因此,轴承内部打滑的位置及剧烈程度应与轴承所受的径向载荷大小有关. 设置分析的工况条件如下:主轴转速为
图 10
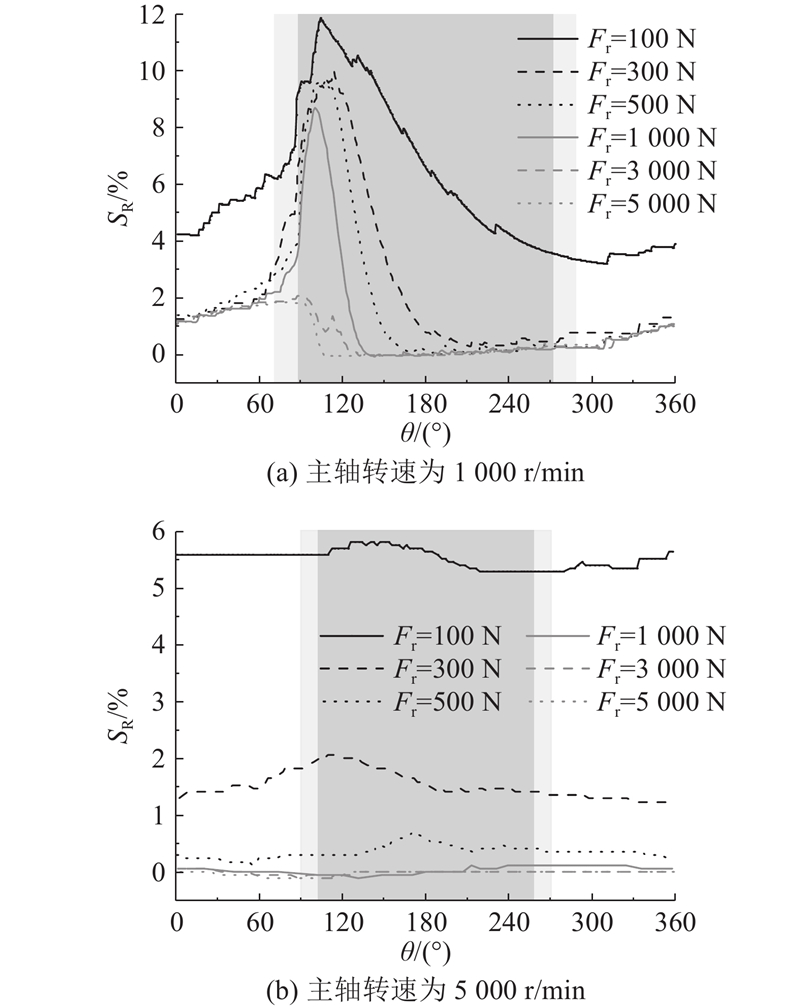
图 10 滚子打滑率与径向载荷的关系
Fig.10 Relationship between roller skidding rate and radial load
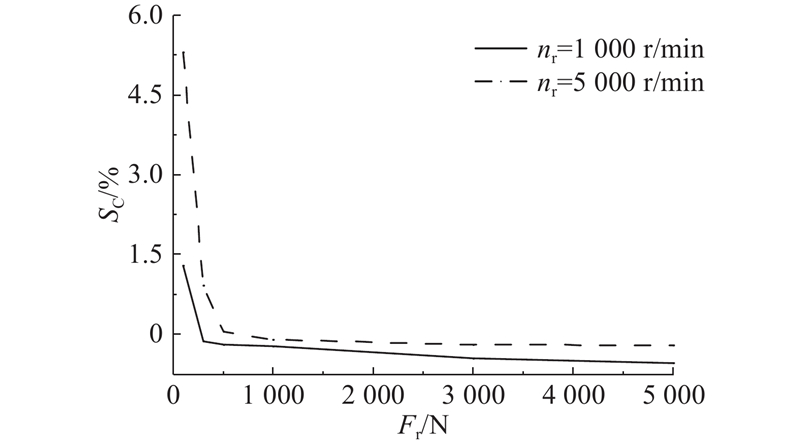
当轴承承受的径向载荷小于500 N时,滚子在轴承整个周期内均存在打滑现象,滚子打滑率在进入承载区后减小,在离开承载区前达到最小值,并在离开承载区后逐渐增大. 当径向载荷大于500 N(即临界载荷)时,滚子在非承载区存在打滑现象,而在完全进入承载区后几乎不发生打滑. 此时轴承不存在整体打滑,即保持架打滑率SC几乎为0,如图11所示.
图 11
当径向载荷为500~3 000 N时,滚子在跨区过程中出现打滑波动,滚子打滑率在进入承载区前迅速增大,在承载区入口达到峰值,并在进入承载区后迅速减小,打滑率波动范围均随径向载荷的增大而减小;当轴承受到的径向载荷大于3 000 N时,滚子在非承载区打滑率缓慢增大,随着滚子进入承载区,滚子打滑率迅速降低至0,滚子打滑率的波动范围较小,滚子的局部打滑现象不显著. 以往工作并没有聚焦于低速工况下轴承打滑特性的研究,然而对于圆柱滚子轴承而言,其多服役于较低转速区间的工况条件下. 因此,研究重载低速条件下的轴承打滑特性具有重要意义.
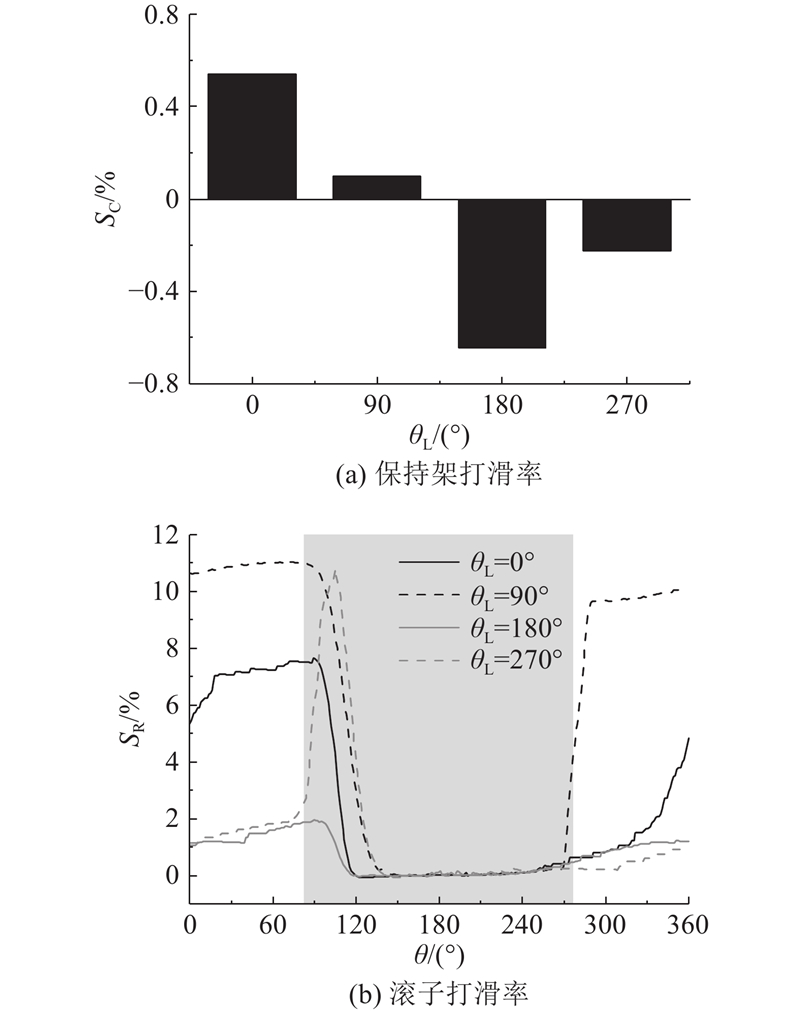
如图12所示为轴承打滑情况随径向载荷加载方向的变化. 图中,
图 12
图 12 轴承打滑情况随径向载荷加载方向的变化
Fig.12 Variation of bearing skidding with direction of radial load
3.2. 主轴转速对圆柱滚子轴承打滑的影响
对于外圈静止,且内圈与主轴过盈配合的圆柱滚子轴承而言,滚子及保持架打滑率的大小均与主轴转速大小相关. 由于受离心力作用,在高速轻载工况下,随着转速的增大,滚子在非承载区与外圈的相对滑动速度增大,在所有滚子的共同作用下,保持架的打滑率随主轴转速增大而增大. 而在中低速工况下,保持架几乎不存在整体打滑,鲜有研究涉及主轴转速对滚子局部打滑情况的研究. 为了探究滚子打滑率随主轴转速的变化规律,设置分析的工况条件如下:径向载荷为300 、
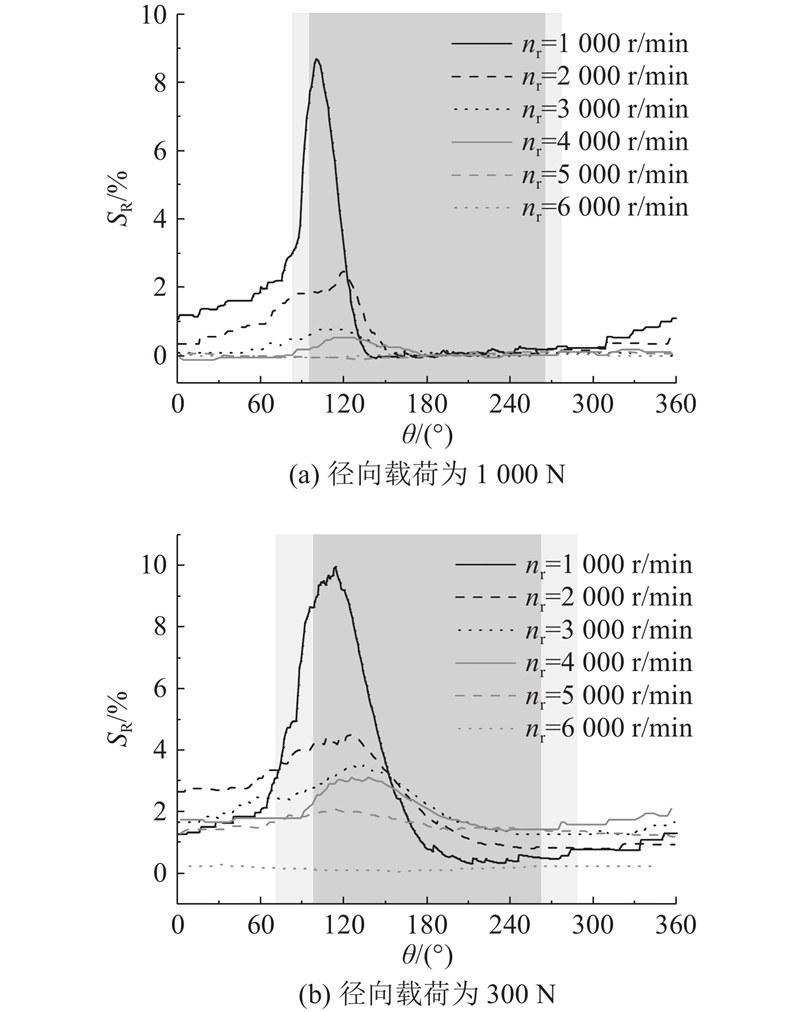
圆柱滚子轴承内部滚子打滑率在其圆周方向上随主轴转速变化的规律如图13所示. 对于中等载荷(
图 13
图 13 滚子打滑率与主轴转速关系
Fig.13 Relationship between roller skidding rate and spindle rotational speed
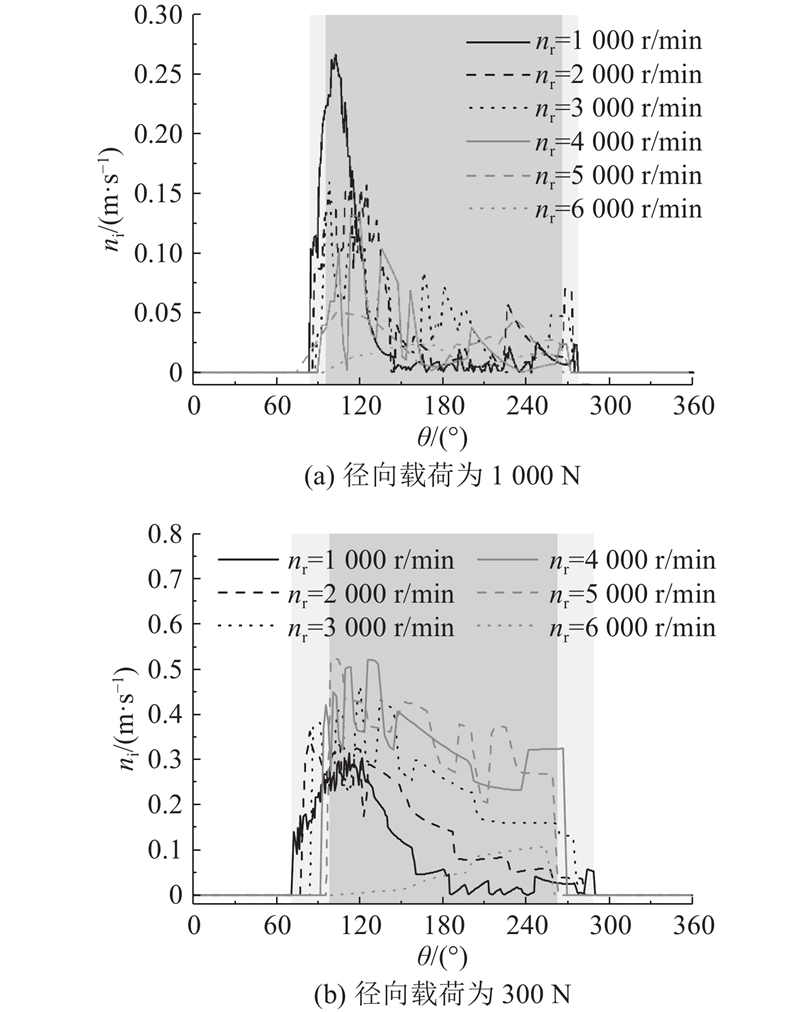
分析滚子与内圈间的相对滑动速度ni,如图14所示,当轴承处于轻载条件时,在整个承载区内滚子与内圈间均发生了较大的相对滑动;在中等载荷条件下时,滚子与内圈间仅在承载区的边缘位置具有较大的相对滑动速度.
图 14
图 14 滚子与内圈间相对滑动速度与主轴转速关系
Fig.14 Relationship between relative skidding speed on roller and inner ring and spindle rotational speed
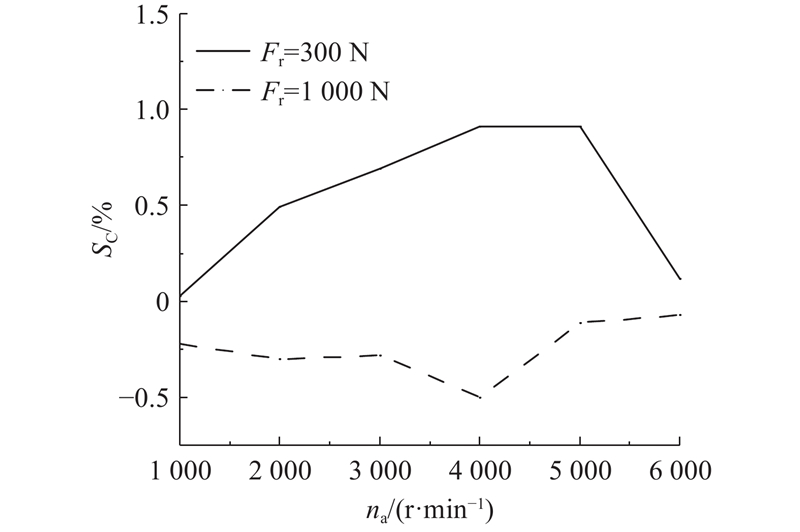
保持架打滑率与主轴转速na关系如图15所示. 当轴承承受的径向载荷小于临界载荷时,保持架打滑率随着主轴转速增大而增大;当主轴转速较小或径向载荷大于临界载荷时,保持架几乎不发生打滑. 因此,为了能够综合反映出圆柱滚子轴承的打滑特性,须选用滚子打滑率和保持架打滑率同时作为评价指标. 但对于不同主轴转速下的圆柱滚子轴承,应该优先选用不同的评价指标对轴承打滑情况进行描述. 对于应用于中低速工况下的圆柱滚子轴承,由于其保持架不表现出宏观打滑现象,优先选用滚子打滑率作为轴承打滑评价指标;对于高速圆柱滚子轴承,其滚子在圆周上的打滑情况波动较小,则应优先选用保持架打滑率作为评价指标.
图 15
图 15 保持架打滑率随主轴转速的变化规律
Fig.15 Variation of cage skidding rate with spindle rotational speed
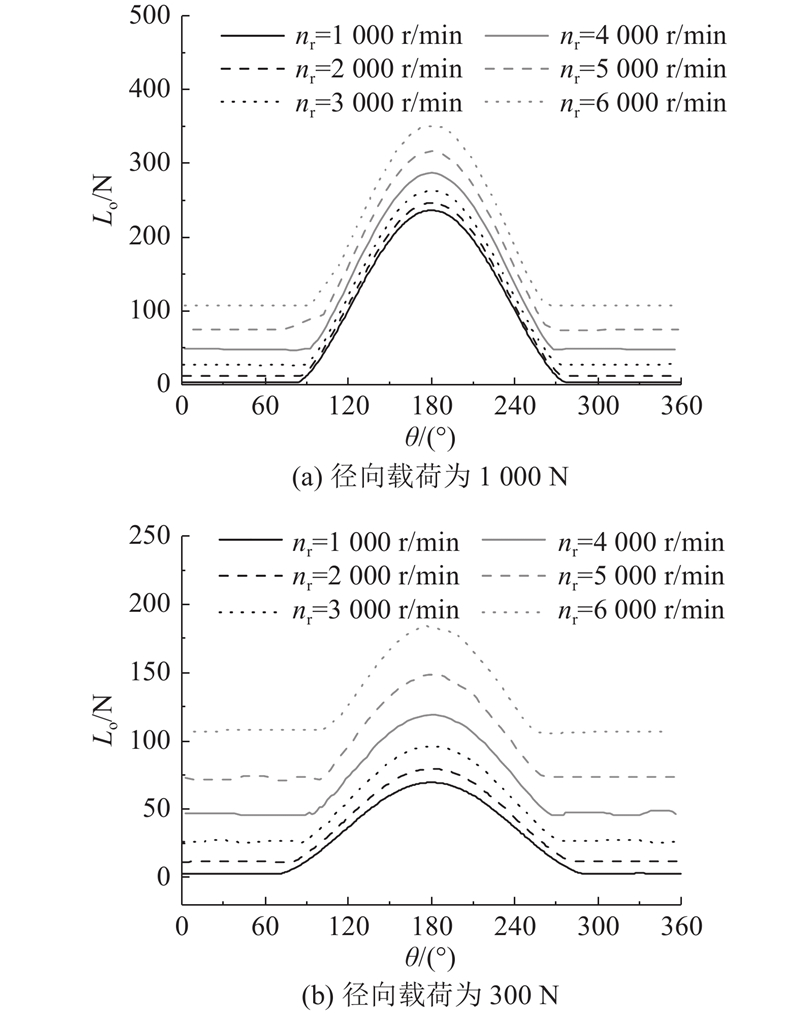
无论圆柱滚子轴承处于轻载条件还是中等载荷条件,滚子打滑率波动范围随主轴转速的增大而减小. 当转速大于
图 16
图 16 滚子与外圈间接触载荷随转速的变化规律
Fig.16 Variation of contact load between roller and outer ring with rotational speed
滚子所受载荷大小受到内外滚道接触载荷的综合作用,随着主轴转速的增大,滚子在承载区及非承载区间的载荷波动减小. 当转速大于
4. 结 论
通过对圆柱滚子轴承进行动力学建模及计算,分析轴承内部滚子的局部打滑现象,讨论滚子打滑与保持架打滑的关系,并揭示滚子打滑的产生原因与变化规律,分析滚子打滑率作为圆柱滚子轴承打滑评价标准的适用范围及必要性,以及保持架运动对于滚子打滑的影响. 结论如下:
(1) 滚子由于其承受的接触载荷的变化产生周期性的波动,其在承载区内打滑率较小,离开承载区后打滑率增大,在重新进入承载区过程中迅速增大,完全进入承载区后又迅速降低,形成打滑率峰值现象.
(2) 滚子打滑率在整个圆周上均随径向载荷的增大而减小;滚子打滑率在其非承载区及跨区过程中随主轴转速的增大而减小,当轴承处于高速工况下时,滚子在承载区内打滑率均随主轴转速的增大而增大.
(3) 对于应用于中低速工况下的圆柱滚子轴承,由于其保持架不表现出宏观打滑现象,优先选用滚子打滑率作为轴承打滑评价指标;对于高速圆柱滚子轴承,其滚子在圆周上的打滑情况波动较小,应优先选用保持架打滑率作为评价指标.
(4)本研究暂未详细介绍实验验证工作,本研究对应的实验验证工作主要是基于电磁感应原理,通过在轴承上安装径向充磁磁铁,切割环形线圈,进而测量感应电压并计算滚子打滑率,后续将对这部分内容进一步展开.
参考文献
Slip characteristics in cylindrical roller bearings. part i: influence of cage type on rolling set slip
[J].DOI:10.1115/1.4055555 [本文引用: 1]
Bearing skidding detection for high-speed and aero-engine applications
[J].
Investigation on skidding behavior of a lubricated rolling bearing with fluid–solid-heat coupling effect
[J].DOI:10.1016/j.ymssp.2023.110922
Dynamic investigation and alleviative measures for the skidding phenomenon of lubricated rolling bearing under light load
[J].DOI:10.1016/j.ymssp.2022.109685 [本文引用: 1]
滚动轴承打滑试验研究进展
[J].DOI:10.3969/j.issn.1001-3881.2019.22.037 [本文引用: 1]
Research progress on skidding experimental analysis of rolling bearings
[J].DOI:10.3969/j.issn.1001-3881.2019.22.037 [本文引用: 1]
Skidding behavior of lubricated rolling element bearings under the influence of oil film and radial clearances
[J].DOI:10.1016/j.triboint.2024.109500 [本文引用: 1]
Slip and cage forces in a high-speed roller bearing
[J].DOI:10.1115/1.3451660 [本文引用: 1]
An analytical method to predict skidding in high speed roller bearings
[J].DOI:10.1080/05698196608972139 [本文引用: 1]
An analytical method to predict skidding in thrust-loaded, angular-contact ball bearings
[J].
Validation of combined analytical methods to predict slip in cylindrical roller bearings
[J].
A study of sliding between rollers and races in a roller bearing with a numerical model for mechanical event simulations
[J].DOI:10.1016/j.triboint.2010.06.014 [本文引用: 1]
Analytical consideration of the radial clearance to reduce cage slip of the turbo engine roller bearing
[J].DOI:10.1007/s12206-021-0606-0 [本文引用: 1]
Micro-geometry deviation to reduce the cage slip of high-speed cylindrical roller bearings
[J].DOI:10.1007/s12206-023-0105-6 [本文引用: 1]
Dynamics of rolling-element bearings part I: cylindical roller bearing analysis
[J].DOI:10.1115/1.3453357 [本文引用: 1]
Dynamics of rolling-element bearings part II: cylindical roller bearing results
[J].DOI:10.1115/1.3453360 [本文引用: 1]
The dynamics of ball bearings
[J].DOI:10.1115/1.3451516 [本文引用: 2]
Dynamic investigation and alleviative measures for the skidding phenomenon of lubricated rolling bearing under light load
[J].DOI:10.1016/j.ymssp.2022.109685 [本文引用: 1]
Skidding dynamic performance of rolling bearing with cage flexibility under accelerating conditions
[J].DOI:10.1016/j.ymssp.2020.107257 [本文引用: 1]
圆柱滚子轴承启动阶段滚动体打滑特性分析
[J].
Analysis of slippage characteristic of roller in cylindrical roller bearing during the start up
[J].
非稳态工况下弹支SFD圆柱滚子轴承动态特性分析
[J].
Dynamic characteristic analysis of elastic support and squeeze film damper cylindrical roller bearing under unsteady condition
[J].
高速圆柱滚子轴承停止阶段打滑特性
[J].
Slip characteristics of high-speed cylindrical roller bearing at stop stage
[J].
变载偏斜圆柱滚子轴承打滑动力学分析
[J].DOI:10.3901/JME.2017.09.058 [本文引用: 1]
Dynamic skidding behavior of skew cylindrical roller bearings under time-variable loads
[J].DOI:10.3901/JME.2017.09.058 [本文引用: 1]
Investigation of the dynamic local skidding behaviour of rollers in cylindrical roller bearings
[J].DOI:10.1177/1464419319861616 [本文引用: 1]
Adaptive time-domain sliding average method for spall size estimation of roller bearing with skidding
[J].DOI:10.1016/j.jsv.2023.117937 [本文引用: 2]
Elastische Berührung zweier Halbräume
[J].
高速圆柱滚子轴承保持架运行稳定性分析
[J].
Operational stability analysis for cage of high-speed cylindrical roller bearings
[J].
高速圆柱滚子轴承保持架振动特性分析
[J].
Cage vibration behaviors of high - speed cylindrical roller bearings
[J].
Gas turbine engine mainshaft roller bearing-system analysis
[J].
Investigation on skidding of rolling element bearing in loaded zone
[J].
滚动轴承稳定工况下的滚动体打滑动力学分析
[J].
Dynamic skidding behavior of rolling elements under bearing steady working conditions
[J].