在空域设计中，扇区指的是具有确定空间体积的空中区域，是空域管制的基本单元. 扇区的合理规划不仅能够减轻管制员的工作量，而且能够提升空域的利用效率，对优化空域资源具有重要意义. 随着新机场的建设及现有机场的扩建工程不断增加，对扇区进行战略性的预先规划，以适应因航线结构改变而带来的空域流量的变化，变得尤为关键.

近年来，为了提升空域的使用效率并减轻空中交通的压力，许多国内外的学者对空域扇区划分展开研究，通过不同的空域建模方法，实现更合理的扇区规划. 具体而言，根据建模方法的差异，可以将现有研究归纳为以下4个主要类别. 1）基于网格模型的研究. 这类研究通常将空域划分为凸多边形网格，采用聚类算法或启发式算法进行扇区的组合划分. Yousefi等^[1]通过将空域划分成六边形网格，评估管制员的工作负荷，提出基于工作负荷和空域复杂度的扇区优化方法. 戴福青等^[2]建立带有流量特征的正方形栅格矩阵，通过环形生长的区域生长算法，对厦门终端区进行有效的划分. Tang等^[3]使用立方网格的元胞划分方法，结合遗传算法和基于Agent的建模，实现了简单三维空域的划分. 2）基于飞行航迹模型的研究. 通过充分挖掘4D飞行航迹的信息，围绕航迹的分组形成扇区边界. Brinton等^[4]提出航空器轨迹聚类算法，通过相似性矩阵辅助扇区划分. 高伟等^[5]通过对航空器航迹进行检测，建立带有权重的空域图论模型，利用谱聚类算法生成扇区边界. 3）基于Voronoi图模型的研究. 该方法利用Voronoi图的凸性保证扇区非凹性的需求. 其中，林福根等^[6-7]结合算法优化生成Voronoi图所需的生成点位置，进行空域Voronoi图扇区划分，生成的Voronoi图边界是划分的扇区边界. 王莉莉等^[8-9]利用空域中的航路点、航线交叉点作为生成点，构建初始Voronoi图，利用算法将得到的Voronoi图组合成扇区. 4）基于图分割模型的研究. 通过建立空域内航路航线的拓扑结构，采用图分割理论将空域图划分为扇区子图. 叶志坚等^[10]构建Voronoi图自顶向下切割空域模型，设计动态步长蚁群搜索算法以划分扇区. Chen等^[11]结合最优动态负载平衡算法和K-L算法，进行扇区的初步划分.

根据模型中优化目标的数量，可以将扇区划分的多目标优化问题划分为加权单目标优化和多目标优化. 在加权单目标优化的研究中，Chen等^[12-13]通过加权法，将多个优化目标合并为一个综合优化目标，解决多目标扇区划分问题. 加权单目标优化的局限性如下：每个目标的权重必须由依赖专家决策者给出，不利于多主体决策情景，在使用上受到一定的限制. 与之相比，基于Pareto最优解的算法可以同时优化多个目标，避免多主体决策者间的主观差异^[14-15]. 该算法通过一次解算得到一组Pareto最优解，这些解之间不存在绝对的优劣关系，而是考虑了对不同优化目标的侧重. 现有研究主要集中在二维扇区划分的问题上，对于三维扇区划分的研究相对较少.

本文主要针对多目标扇区划设问题进行以下2个方面的改进. 1）现有的终端区的扇区划分的多目标优化研究未能充分利用高空的高度资源进行纵向扇区划分，即三维扇区划分. 2）为了充分利用空域资源实现高效的空域管理，须建立综合三维扇区划分与多目标优化问题的模型和算法. 本文的主要工作如下. 1）将网格模型和Voronoi图模型融合，构建网格化-区域块化-扇区化的三维航路空域扇区划分模型. 2）以均衡扇区内管制员监视和解决冲突负荷以及减小扇区间管制员移交负荷为目标，以扇区连续性、扇区边界处冲突、航空器短暂穿越、航空器再入为主要约束条件，建立三维扇区划分的多目标优化数学模型. 3）对NSGA-II算法进行改进，使其能够从扇区水平形状和高度间隔2个方面对扇区进行组合优化. 4）通过西安高空空域扇区划分的仿真实验，验证本文模型和算法的有效性.

三维航路扇区划分问题可以定义为在一定的优化原则和约束条件下，将三维空域A划分为N_s个管制扇区. 明确每个扇区的几何形状及边界，是典型的有约束多目标优化问题. 优化目标和约束条件在设置时通常考虑以下7个评价标准.

1）不同扇区间管制员的工作负荷均衡性.

2）飞行器穿越不同扇区而发生的管制移交频次.

3）单个扇区的最大管制工作负荷.

4）飞行器发生冲突位置点与扇区边界的距离.

5）飞行器发生短暂穿越扇区事件的频次.

6）飞行器发生再次进入扇区事件的频次.

7）扇区划分后的连续性保障.

扇区划分的评价标准与管制员工作负荷直接相关，将空域内管制员的工作负荷分为以下2类. 一类是发生在扇区内的工作负荷${\text{w}}{{\text{l}}^1}$，包括检查飞行器是否按照飞行计划飞行的监视负荷，${\text{w}}{{\text{l}}^2}$以及调配因其他原因造成飞行器间发生潜在冲突的冲突解决负荷${\text{w}}{{\text{l}}^3}$. 另一类是发生在扇区之间的工作负荷${\text{w}}{{\text{l}}^4}$，主要包括飞机穿越不同扇区所需要进行的协调工作负荷${\text{w}}{{\text{l}}^5}$.

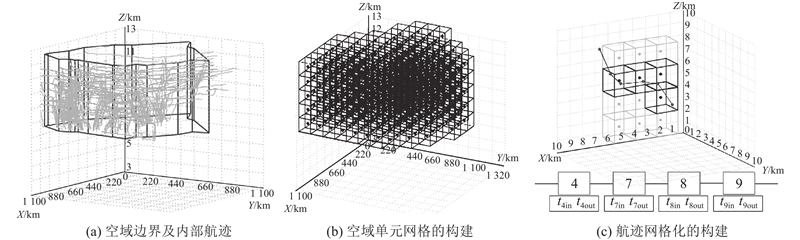
网格层级建模过程. 为了挖掘空域内四维航迹的局部交通流信息，将空域离散为网格单元. 以区域管制的推荐雷达间隔10 km为依据，将空域$ A $（见图1(a)） 离散为如图1(b)所示的系列尺寸为10 km×10 km×0.15 km的长方体网格块单元$ {c_i} $，此时空域$ A $可以表示为$ A = \{ {c_i}\} _{i = 1}^{{N_{\text{c}}}} $. 对于四维航迹集合$ T $中的每一条航迹${t_i} = {\text{\{ (}}{x_{ij}},{\mathrm{sp}}{{\mathrm{d}}_{ij}}, {t_{ij}}{\text{)\} }}_{j = 1}^M$（其中spd_ij为飞机经过第j个位置点的速度），依次计算第$ j $个位置点$ {x_{ij}} $和第$ j+1 $个位置点${x_{i(j+1)}}$之间所经过的网格块集合$ \{ {C_{j1}},{C_{j2}},\cdots ,{C_{jd}}\} $，$ {C_{ij}} $表示第$ i $行第$ j $列的网格块的编号，结合2个点的速度和时间信息，确定穿越网格块$ \{ {C_{j1}}, {C_{j2}}, \cdots ,{C_{jd}}\} $的对应进出时间$ \{ ({t_{j1{\text{in}}}},{t_{j1{\text{out}}}}),({t_{j2{\text{in}}}},{t_{j2{\text{out}}}}), \cdots , ({t_{jd{\text{in}}}},{t_{jd{\text{out}}}})\} $. 此时，航迹$ t_{i} $可以由一系列如图1(c)所示的网格序号及对应的进出时间表示，$ {t_i} = \left( {{C_{id}},{t_{d{\text{in}}}},{t_{d{\text{out}}}}} \right)_{d = 1}^D $.

网格层级指标的计算. 管制员扇区内监视负荷与航空器飞行时间成正比，扇区内冲突解决负荷与航空器发生的潜在飞行冲突成正比，建立网格内的飞行时间数组$ {M_1} $和网格内的飞行冲突数组$ {C_1} $.

网格内飞行时间数组$ {M_1} $：数组元素$ {m_1}\left( i \right) $表示所有航空器在网格i内的飞行时间之和. 初始化数组$ {M_1} $的各元素为零，遍历每一条航迹$ {t_i} = \left( {{C_{id}},{t_{d{\text{in}}}},{t_{d{\text{out}}}}} \right)_{d = 1}^D $. 若该航迹经过网格$ {C_{id}} $，则在相应的数组元素$ {m_1}\left( {id} \right) $增加穿越此网格的飞行时间$ \left( {{t_{{\text{out}}}} - {t_{{\text{in}}}}} \right) $.

网格内的飞行冲突数组$ {C_1} $：数组元素$ {c_1}\left( i \right) $表示航空器之间可能在网格$ i $内发生冲突的个数. 初始化数组$ {C_1} $各元素为零，如果2条航迹$ {t_1} $和$ {t_2} $通过网格$ i $的穿越时间分别为$ \left( {t_{1{\text{in}}}^i,t_{1{\text{out}}}^i} \right),\left( {t_{2i{\text{in}}}^i,t_{2{\text{out}}}^i} \right) $，则可设$ t_{1{\text{in}}}^i < t_{2{\text{in}}}^i $，若$ {t_{1{\text{out}}}^i+{t_{{\text{disturb}}}}} > {t_{2{\text{in}}}^i - {t_{{\text{disturb}}}}} $，则认为这2条航迹在网格$ i $内可能产生冲突，对应的$ {c_1}\left( i \right) $自增1，$ {t_{{\text{disturb}}}} $为因其他原因带来的航迹经过该网格的时间扰动值.

$ {\text{WL}}_{{\text{cell}}}^1 $为表征网格内管制员工作负荷的数组，数组元素$ {\text{wl}}_{{\text{cell}}}^1\left( i \right) $计算如下：

(1)$ {\text{wl}}_{\text{cell}}^{1}\left(i\right)={\alpha }_{1} \frac{{m}_{1}\left(i\right)}{600}+{\alpha }_{2} {c}_{1}\left(i\right) . $

式中：$ {\alpha _1} $为每架次航空器在扇区内飞行10 min需要的监视时间，$ {\alpha _2} $为管制员解决一个飞行冲突所需要的冲突解决时间.

区域块层级建模过程. 为了保证网格组合后产生的扇区满足凸多边形约束，在生成最终扇区之前，将网格单元组合成Voronoi区域块. 具体步骤如下.

1）在纵向维度上，将空域分为$ \left\{ {{L_1},{L_{2}}, \cdots ,{L_{{N_z}}}} \right\} $共$ {N_z} $层，每一层的高度标记$ \left( {L_z^{{\text{low}}},L_z^{{\text{high}}}} \right) $作为该层Voronoi块的高度信息.

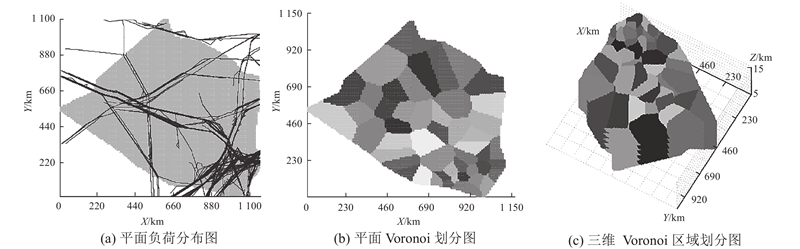
2）在水平维度上，将空间中每一个网格内的工作负荷叠加到对应的平面网格上，如图2(a)所示，采用K-mean聚类对平面网格进行聚类分析. 通过迭代优化聚类中心位置，使工作负荷高的网格不断向各聚类中心靠拢.

3）以最终聚类的中心点数据作为生成Voronoi图的生成点集，构造如图2(b)所示的平面Voronoi图，在保证凸性的同时，使主要交通流和航迹交叉点处于Voronoi区域块的中心位置，远离扇区边界.

4）保持水平形状不变，根据高度信息在每一层上划分Voronoi区域块，获得如图2(c)所示的布满整个空域的三维Voronoi区域块集合. 此时空域A可以表示为$ A = \left\{ {{V_{zb}}} \right\}_{z = 1,b = 1}^{{N_z},{N_b}} $,其中$ {V_{zb}} $为第$ z $层的第$ b $个Voronoi区域块.

区域块层级指标计算. 管制员扇区间协调工作负荷与航空器穿越扇区边界的次数成正比，扇区边界处的冲突会对飞行安全带来挑战，因此，在区域块层级需要先计算区域块间的航空器移交次数和航空器冲突次数. 建立如下2个矩阵：航空器移交架数矩阵$ {{\boldsymbol{P}}_0} $和边界冲突矩阵$ {{\boldsymbol{C}}_0} $，矩阵元素${p_0}({z_1}{b_1},{z_2}{b_2})$为从区域块${V_{{z_1}{b_1}}}$移交到区域块${V_{{z_2}{b_2}}}$的航空器架数，矩阵元素${c_0}({z_1}{b_1},{z_2}{b_2})$为2个区域块边界处可能发生冲突事件的次数. 已知航迹${t_i}$依次经过的网格序号和进出时间，若${t_i}$依次经过网格${c_1}$和网格${c_2}$，而${c_1}$在区域块${V_{{z_1}{b_1}}}$内，${c_2}$在区域块${V_{{z_2}{b_2}}}$内，则航空器在这2个区域块之间进行了一次移交，相应的${p_0}({z_1}{b_1},{z_2}{b_2})$自增1. 此外，由于网格${c_1}$和网格${c_2}$是2个区域块边界处的网格，若2个网格内存在冲突，则在这2个区域块边界处存在冲突，相应的${c_0}({z_1}{b_1},{z_2}{b_2})$自增1.

根据划设的Voronoi区域块，可以建立区域块内的工作负荷矩阵$ {\mathbf{WL}}_{{\text{blo}}}^1 $，矩阵元素$ {\text{wl}}_{{\text{blo}}}^1\left( {z,b} \right) $表示该区域块内管制员的工作负荷，则有

(2)$ {\text{wl}}_{{\text{blo}}}^1\left( {z,b} \right) = \sum\limits_{i|{c_i} \in {V_{zb}}} {{\text{wl}}_{{\text{cell}}}^1\left( i \right)} . $

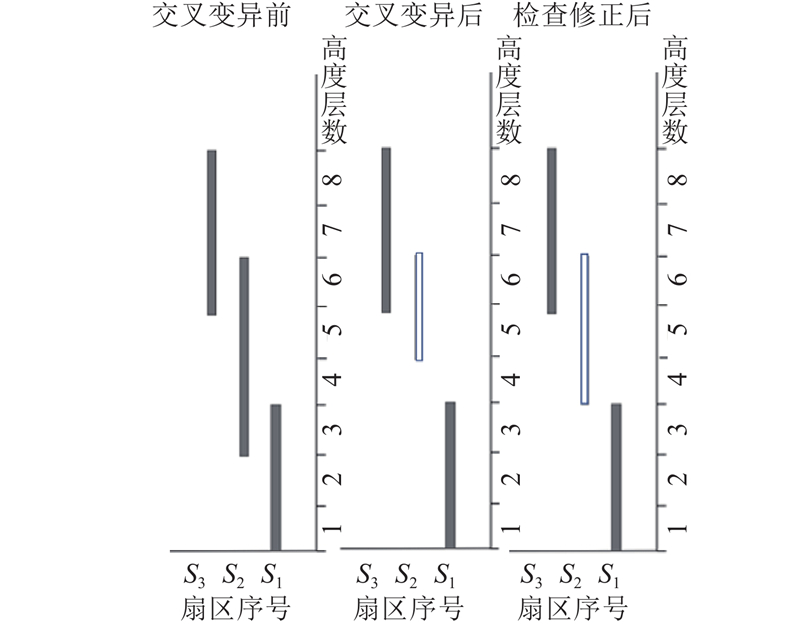
扇区层级建模过程. 在将Voronoi区域块组合成最终的扇区过程中，为了保证扇区的连续性约束，组成同一个扇区的Voronoi区域块应在纵向维度上连续，在横向维度上相近. 通过定义扇区的2个特征量——扇区的中心点位置和扇区连续跨越的高度层，指导最终扇区的形成. 以图3为例，假设将每一层空域分为8个Voronoi区域块，叉号表示Voronoi块中心点所在的位置，将该空域划分为3个扇区，黑色、白色、灰色3个实心圆点分别表示3个扇区的中心点位置，其上方3条竖线表示对应扇区所跨越的高度层，分别是1~5层、3~7层、6~10层. 图3中，由虚线组成的平行四边形所在的第3个高度层由黑色实心点扇区和灰色实心点扇区负责，白色实心点扇区未参与该层Voronoi区域块的分配过程. 根据各Voronoi区域块中心点到2个扇区中心点的距离远近，将每一个Voronoi区域块分配给离其中心点最近的扇区，将左边的4个Voronoi区域块划分给黑色实心圆点扇区，右边的4个Voronoi块划分给灰色实心圆点扇区，至此本层的Voronoi区域块分配组合完成.

扇区层级指标的计算. 随着最终扇区的生成，一部分原属区域块之间的管制移交和边界冲突随着区域块的组合变为扇区内部统计量，但扇区间的统计量更能反映扇区工作负荷. 须依次检查2个相邻Voronoi区域块是否属于同一扇区，更新$ {{\boldsymbol{P}}_0} $和$ {{\boldsymbol{C}}_0} $. 若两区域块${V_{{z_1}{b_1}}}$和${V_{{z_2}{b_2}}}$属于同一扇区，则穿越2个区域块的航空器没有发生管制移交工作，将$ {{\boldsymbol{P}}_0} $中的${p_0}({z_1}{b_1},{z_2}{b_2})$置为零. 同理，若2个区域块边界间的冲突属于同一个扇区内的冲突，没有发生在扇区边界处，则将$ {{\boldsymbol{C}}_0} $中的${c_0}({z_1}{b_1},{z_2}{b_2})$置为零.

经过网格层级-区域块层级2层工作负荷的计算更新，得到各个扇区的扇区内工作负荷数组$ {\text{WL}}_{{\mathrm{s}}} ^1 $和各个扇区的扇区间工作负荷数组$ {\text{WL}}_{{\mathrm{s}}} ^4 $. 数组元素$ {\text{wl}}_{\sec }^1\left( i \right) $表示第$ i $个扇区的扇区内监视负荷和解决冲突负荷的总负荷，数组元素$ {\text{wl}}_{\sec }^4\left( i \right) $为在第$ i $个扇区和其他所有扇区之间协调工作负荷的总负荷，计算方法如下：

(3)${\rm{wl}}_{\sec }^1\left( i \right) = \sum\limits_{\left( {z,b} \right)|{V_{zb}} \in {S_i}} {{\rm{wl}}_{{\rm{blo}}}^1\left( {z,b} \right)} .$

(4)$ {\text{wl}}_{\mathrm{sec}}^{4}\left(i\right)={\displaystyle \sum _{\scriptstyle{{{z}}_{1}{b}_{1},\;{z}_{2}{b}_{2}|{V}_{z_1b_1}\in}\atop\scriptstyle{ {S}_{1},{V}_{z_2b_2}\notin {S}_{1}}} {\alpha }_{3} {p}_{0}\left({z}_{1}{b}_{1},{z}_{2}{b}_{2}\right)}. $

式中：$ {\alpha _3} $为管制员与飞机协调一次所用的时间.

目标函数. 为了均衡化空域内工作总负荷（即最小化扇区内工作负荷标准差SD）和最小化扇区间工作负荷TWL，以均衡各个扇区内工作负荷$ {\text{w}}{{\text{l}}^1} $和减少整个空域的扇区间工作负荷$ {\text{w}}{{\text{l}}^4} $为双目标，数学表达式如下：

(5)$ {F_1} = \min \left( {\left[N^{-1} {{{\displaystyle \sum\limits_{i = 1}^N {\left( {{\text{wl}}_{\sec }^1\left( i \right) - \mu } \right)} }}} \right]^{1/2}} \right) , $

(6)$ {F_2} = \min \left( {\sum\limits_{i = 1}^N {{\text{wl}}_{\sec }^4\left( i \right)} } \right) . $

式中：N为空域内扇区的数目；μ为空域内的平均扇区内工作负荷，$ \mu = {{N^{-1}\displaystyle \sum\nolimits_{i = 1}^N {{\text{wl}}_{\sec }^1\left( i \right)} }} $.

约束条件. 为了保证空域划分的合理性，以连续性、边界处冲突、最大可接受短暂穿越事件和再入事件为约束条件. 检查组合后的扇区是否连续，避免可能发生航迹冲突的扇区边界过近，尽可能减少空域内航空器发生再入事件和短暂穿越事件的次数.

(7)$ N_b^6 = 0 . $

(8)$ N_b^{{\text{BC}}} = \sum\limits_{i = 0,j = 0}^{{N_b},{N_b}} {{c_0}\left( {i,j} \right) = 0} . $

(9)$ N_b^{\text{R}} = \sum\limits_{t = 1}^T {n_{{\text{br}}}^t} < N_{\max }^{\text{R}} . $

(10)$ N_b^{\text{S}} = \sum\limits_{t = 1}^T {n_{{\text{bs}}}^t} < N_{\max }^{\text{S}} . $

式中：$ N_{{b}}^6 $为整个空域中属于同一个扇区的Voronoi块之间不连续的总次数，$ N_{{b}}^{{\text{BC}}} $为根据边界冲突矩阵$ {{\boldsymbol{C}}_0} $得到的边界处冲突总次数，$ N_{{b}}^{\text{R}} $为空域内航空器发生再入事件的总次数，$ n_{{\text{br}}}^t $为空域内第$ t $条航迹发生再入事件的次数，$ N_{\max }^{\text{R}} $为空域内可以接受的最大再入事件次数，$ N_b^{\text{S}} $为空域内航空器发生短暂穿越事件的次数，$ n_{{\text{bs}}}^t $为空域内第t条航迹发生短暂穿越的次数，$ N_{\max }^{\text{S}} $为空域内可接受的最大短暂穿越事件次数.

构建的模型属于典型的有约束多目标优化模型，由于2个目标函数相互冲突，在实际寻优的过程中，很难存在一个最优解可以使2个目标同时达到最优. 通常只能求得系列Pareto互不占优的最优解集，为决策者提供参考. 选用带有精英策略的非支配排序的遗传算法（NSGA-II），求解扇区划分多目标优化模型. 种群中的每一个个体表示一种扇区划分方案，在遗传算子的指导下，种群不断朝着适应度高的个体方向进化，直至找到满意的最优扇区划分方案.

将染色体编码分为2个部分：各扇区中心点位置和各扇区跨越高度层. 扇区的中心点采用浮点数编码，跨越高度层标记采用整数编码，具体的编码结构如图4所示.图中，N为空域内扇区的数目，$ \left( {{x_i},{y_i}} \right) $为第$ i $个扇区的中心点坐标，$ \left( {h_i^{\min },h_i^{\max }} \right) $为第$ i $个扇区跨越的最低高度层标记和最高高度层标记.

本文的初代解有以下2种类型. 为了保证在进化开始的解空间中有数量可观的可行解存在，一些解的2个特征信息参考实际空域的实际划分构型设置，并增加微小扰动和变化. 一些解的特征信息完全通过随机生成，以增加初始解的多样性，提高算法向全局探索的能力.

适应度评估算子. 由于多种扇区划分约束的存在，可行解空间比搜索空间小得多. 每一代种群解码生成的扇区划分方案中会存在一定比例的不可行解，但这些不可行解可能包含一些有用的信息. 一些当前代中的不可行解通过交叉和变异，对扇区进行微小变动后极有可能变成优质可行解. 引入适应度评估算子$ {F_i}\left( x \right) $，结合目标函数和约束条件，充分挖掘个体信息，依据可行解在种群中的比例，灵活指导搜索方向，向可行解方向或最优解方向移动.

(11)$ {F}_{i}\left(x\right)=\left\{\begin{array}{*{20}{l}}v\left(x\right),\qquad\qquad\qquad {r}_{{\mathrm{f}}}=0;\\{\tilde{f}}_{i}\left(x\right),\qquad\qquad\qquad {r}_{{\mathrm{f}}}\ne 0,\;x是可行解;\\ \sqrt{{\tilde{f}}_{i}{\left(x\right)}^{2}+v{\left(x\right)}^{2}}+\left(1-{r}_{{\mathrm{f}}}\right) v\left(x\right)+{r}_{{\mathrm{f}}} {\tilde{f}}_{i}\left(x\right),\\\qquad\qquad\qquad\qquad\;{r}_{{\mathrm{f}}}\ne 0,\;x不是可行解.\end{array} \right. $

式中：$ {r_{\mathrm{f}}} $为当前代中可行解在种群中所占的比例，$ v\left( x \right) $为衡量个体超出各个约束条件的加权值，$ {\tilde f _i}\left( x \right) $为种群中每个个体$ x $的第$ i $个目标函数的归一化值.

环境选择算子. 在适应度评估算子的基础上，采用锦标赛选择法，每次从种群中选择2个个体，对每个个体进行适应度评估，选出适应度高的个体. 根据新种群需要保留的个体数，反复进行个体挑选.

变概率组合交叉算子. 为了有效组合采用浮点数编码的扇区中心点和采用整数编码的跨越高度层，须设计2种不同的交叉方式. 考虑中心点坐标之间的距离会随着空域范围的扩大而增加，选择模拟二进制交叉算子处理扇区中心点坐标，以避免出现多目标优化过程中个体空间稀疏性大的问题，选择简单的均匀交叉算子对高度层标记. 在变异操作中，将个体以$ {{{P}}_1} $的概率对扇区中心点进行SBX交叉，高度层信息保持不变. 以$ {{{P}}_{\text{2}}} $的概率对高度层信息进行均匀交叉，扇区中心点信息保持不变. 以$(1 - {{{P}}_1} - {{{P}}_2})$的概率对扇区中心点进行组合交叉. 在进化前期，为了加大个体的组合交叉，设定较小的$ {{{P}}_1} $、$ {{{P}}_{\text{2}}} $，随着进化代数的增加，$ {{{P}}_1} $、$ {{{P}}_{\text{2}}} $逐渐增大.

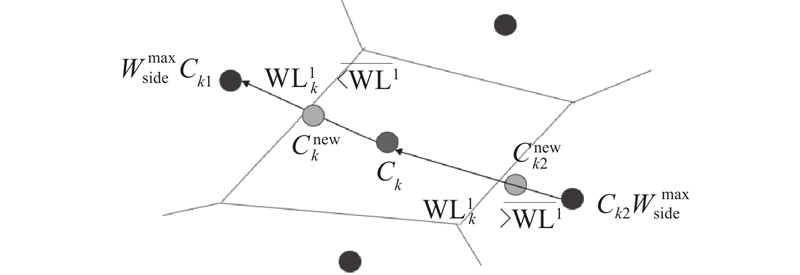
基于工作负荷的动态变异算子. 随机挑选划分方案中的一个扇区$ {S_k} $，将扇区中心点位置变异或高度层变异.

如图5所示，若进行中心点位置变异，则计算该扇区中心点对应的扇区内工作负荷$ {\text{WL}}_k^1 $，将其与平均扇区内工作负荷$ \overline {{\text{W}}{{\text{L}}^1}} $比较. 若$ {\text{WL}}_k^1 > \overline {{\text{W}}{{\text{L}}^1}} $，则该扇区工作负荷较大，应将一部分工作负荷分给相邻扇区. 确定该扇区相邻扇区集合中工作负荷最小的扇区$ S_k^{{\text{side}}} $，将$ S_k^{{\text{side}}} $对应的扇区中心点位置沿着直线向$ {S_k} $对应的扇区中心点位置移动，移动的距离与两者的工作负荷差值$ \left( {{\text{WL}}_k^1 - {\text{WL}}_{{\text{side}}}^1} \right) $成正比. 若$ {\text{WL}}_k^1 < \overline {{\text{W}}{{\text{L}}^1}} $，则$ {S_k} $对应的中心点向着周围扇区工作负荷最大的扇区对应的中心点位置移动.

若进行高度层变异，则计算该扇区的工作负荷$ {\text{WL}}_k^1 $. 若$ {\text{WL}}_k^1 > \overline {{\text{W}}{{\text{L}}^1}} $，则更新$ h_k^{\max } = h_k^{\max } - 1 $或者$ h_k^{\min } = h_k^{\min }+1 $；若$ {\text{WL}}_k^1 < \overline {{\text{W}}{{\text{L}}^1}} $，则更新$ h_k^{\max } = h_k^{\max }+ 1 $或者$ h_k^{\min } = h_k^{\min } - 1 $.

检查修正算子. 对进行交叉变异后的个体高度层标记进行合规性检查. 如图6所示，通过交叉变异算组操作后，第2个扇区高度从3~6层变为5~6层，这导致空域内第4层没有扇区负责. 这样的划分方案明显不合理，需要对该方案进行检查修正. 为了与实际扇区的划分要求相符，可将高度改为4~6层.

当利用传统NSGA-II算法解决多目标问题时，不同类型的约束条件往往导致需要设计复杂的非支配排序的策略，增加了计算量. 将约束条件对算法搜索方向的影响融入适应度评估算子的设计中，因此，当进行个体非支配排序时，避免重复考虑约束条件的冲突，直接采用原始非支配排序策略. 具体来说，如果一个个体$ m $在2个目标维度上的适应度评估算子$ {F_1}\left( m \right) $和$ {F_2}\left( m \right) $分别小于另一个个体$ n $对应的$ {F_1}\left( n \right) $和$ {F_2}\left( n \right) $，则定义个体$ m $支配个体$ n $. 遍历种群所有个体，可以得到两个体之间的支配关系，进而得到每层的非支配集合. 处于第一层非支配集合中的个体为多目标优化问题所寻找的Pareto前沿.

为了尽可能地保留含有优秀基因的个体，将父代和经过选择交叉变异后的中间一代合并，形成规模为2×10⁶的新种群. 利用非支配排序对新种群进行排序，生成非支配集，计算集合中每个个体的拥挤度距离. 按照非支配等级从低到高的顺序挑选个体，直至形成规模为10⁶的子代种群.

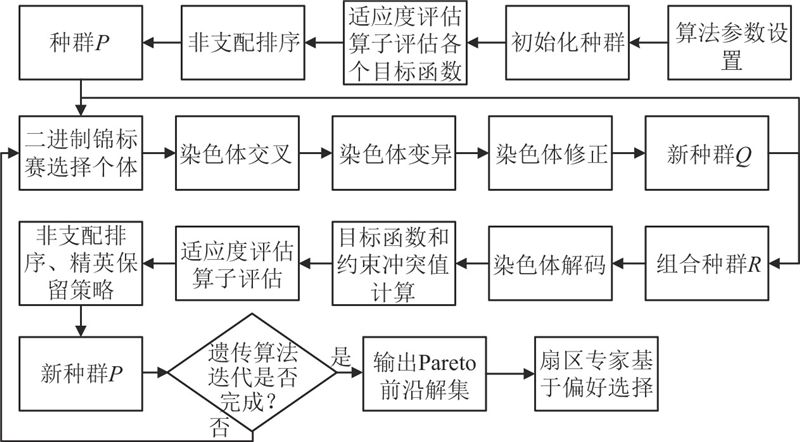
采用IntelliJ IDEA2020对上述算法进行编程，基于改进的NSGA-II的扇区划分优化算法的流程如图7所示.

以西安地区6 000 m以上的高空空域为例进行扇区划分(E105.49~E110.52, N31.54~N39.06). 空域内航班包括从西安咸阳机场起飞爬升到航路段的航班或即将要进近到西安终端区的涉及飞行高度变化的航班，以及经过西安地区的水平穿越航班2类. 为了保证划分的扇区能够满足最繁忙时刻空域内交通流的管制需求，选取航班数量最多的10点—11点时间段内的航班作为交通流输入数据，该时段内共有203个航班.

NSGA-II的参数设置如下：种群规模为500，进化代数为500，交叉概率为0.9，变异概率为0.1. 设划分扇区数为10，最大可接受再入事件次数为10，最大可接受短暂穿越次数为3.

基于上述模型和约束条件，保持实验数据不变，开展10次仿真实验. 每次改进的NSGA-II算法都会找到一组具有多样性的Pareto最优划分方案，仿真结果的统计数据见表1. 表中，N_op为Pareto最优解个数，t_s为仿真时间. 其中第4次试验得到的Pareto最优解的个数为35，与10次仿真最优解的平均值一致，结果具有较好的代表性. 选择第4次仿真实验结果，测试扇区间工作负荷的不平衡程度和所有扇区间的协调工作负荷，评估解决方案的质量. 2个值越小，解的质量越高.

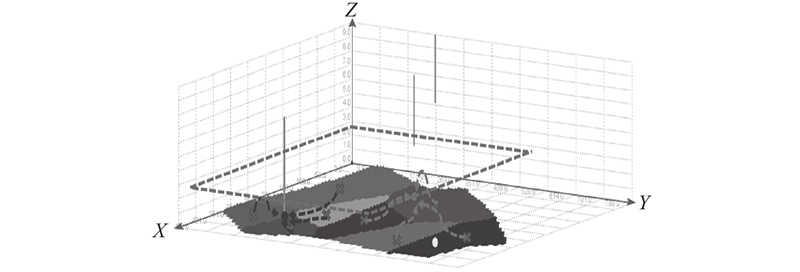
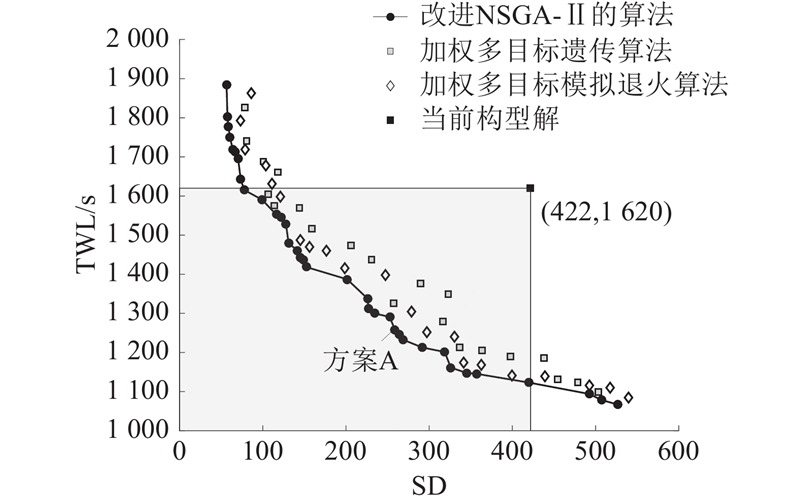
选取第4次实验中的Pareto最优解，记为方案A（位置如图10所示）. 对比实际西安空域扇区划分构型和方案A，表2、3分别给出两者扇区内工作负荷和扇区间工作负荷的结果. 如图8、9所示分别为2种划分方案的三维示意图. 在该空域中，实际构型下共划分有10个扇区，其中高扇、低扇各5个，且在水平维度上相应的高、低扇区形状保持一致. 从工作负荷角度分析，可得如下结论. 1）实际构型扇区4和扇区9的扇区内工作负荷较小. 因两扇区相邻，在新的扇区划分方案中，2个扇区被合并成1个跨越全部高度层的新扇区4. 2）实际构型扇区7的工作负荷最大，在方案A中，该扇区所在的空域位置被划分成2个新的扇区，扇区7和9共同承担这一区域的管制工作. 3）相较于实际构型，方案A将扇区内工作负荷的标准差由422减小到262，扇区的均衡性提高了37%. 扇区间工作负荷由1 620 s降低到1233 s，减小了24%的工作量，2个优化目标函数值都有较大的提升.

为了验证改进NSGA-II算法的有效性和可行性，选择传统加权遗传算法与加权模拟退火算法与其进行对比. 加权后的目标函数如下所示：

(12)$ {g_{{\text{AOF}}}} = w{g_1}+\left( {1 - w} \right){g_2} . $

式中： $ w $为权重系数，$ 0 \leqslant w \leqslant 1.0 $，在仿真实验中$ w $以$ 0.05 $的步长趋向$ 1 $变化. 对于每一个$ w $都运行一次遗传算法（模拟退火算法），得到Pareto最优点. 将所有得到的Pareto点绘制在一起，可以近似得到Pareto前沿. 3种算法的优化效果见图10. 这里以SD和TWL分别衡量优化目标函数F₁和F₂. 算法的运行时间（running time, RT）如表4所示.

对比传统加权遗传算法、加权模拟退火算法和改进NSGA-II算法的结果，可得如下结论. 1）3种算法都可以获得优于实际构型2个目标函数的解（图10中灰色矩形内部的解），说明通过算法得到的划分方案可以在2个目标维度上优化实际西安空域的管制工作. 2）在3种算法中，基于遗传算法的平均耗时最短，模拟退火算法次之，但是这2种算法通过一次运行仅能获得一种划分方案，且代表不同权重的最优解都可以从NSGA-II求得的Pareto 最优面上找到相对应的支配它的解，即NSGA-II算法有更高的计算精度和搜索能力. 3）从图10可知，NSGA-II求得的最优解集分布空间广且密度大，说明该算法可以提供更多不同偏好角度的划分方案，在同一个偏好下，可以为决策者提供不同的扇区划分方案.

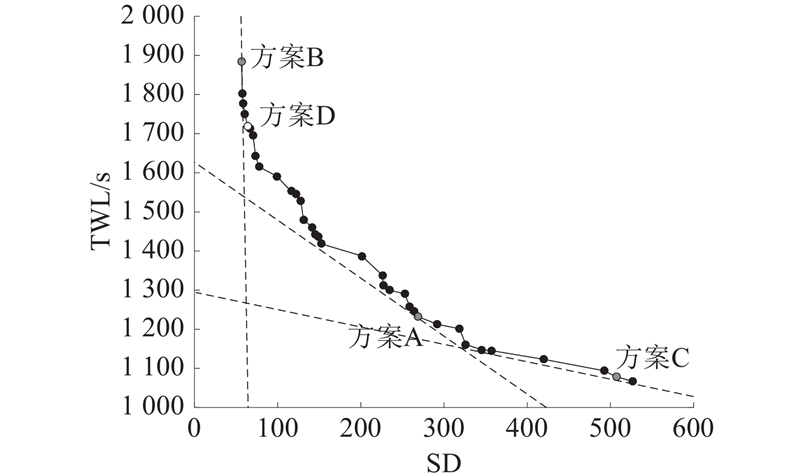
扇区划分智能优化算法只是辅助工具，只有满足不同偏好的决策者的需求，扇区划分方案才能显示其实际价值. 专家决策者可以只向模型提供偏好系数$\alpha $，表示专家决策者愿为提高1单位标准差的扇区内工作负荷平衡性而增加的扇区间工作负荷. 在目标空间中，将一条斜率为${{ - }}\alpha $的直线从左下方朝着右上方向Pareto最优面出发，当这条探索直线触碰到Pareto最优前沿时，该切点对应的扇区划分方案是对该决策者来说最优的选择. 如图11所示，考虑不同需求的决策者可以选取不同的扇区划分方案. 追求扇区内工作负荷极致平衡的决策者倾向于选择方案B，但该方案总的扇区间工作负荷较高. 不愿增加扇区间协调工作负荷的决策者倾向于选择方案C. 对2种工作负荷接受程度一致的决策者倾向于选择方案A. 通过分析NSGA-II算法生成的较完整的Pareto最优面，方案D与方案B在划分扇区内工作负荷的均衡性方面表现相近，但方案D的总扇区间工作负荷比方案B减少将近150个单位. 与方案B相比，方案D在实际应用中的价值更高. 考虑多个目标因素的影响，提供多种扇区规划方案从而满足具有不同偏好的决策者的需求，这是多目标规划的意义.

本文综合考虑了空域扇区划分的多重约束条件，构建网格化-区域块化-扇区化的空域划分三维模型. 通过定义扇区中心点位置和扇区跨越高度层2个表征扇区划分构型的决策变量，利用改进NSGA-II算法对扇区形状划分进行优化，有效均衡并降低了管制员的工作负荷. 基于西安高空空域的仿真实验结果表明，利用NSGA-II算法，能够有效找到一组在解空间中分布广、密度大的Pareto最优扇区划分方案，求解效果明显优于传统的加权多目标遗传算法和加权多目标模拟退火算法. 在可接受的运行时间内，该算法可以通过一次运行得到多个反映不同偏好的解，大大提高了问题解算效率，满足了扇区划分方案多样性的需求.

从实际的应用需求出发，根据实时交通流量而动态调整扇区划分及管制人员分配是未来空中交通管理的重要突破方向. 在以后的工作中，结合4D航迹数据与航迹预测模型，更进一步地拓展模型和算法的实时性和可适应性.