在不可避撞场景下,车辆无法完全避免碰撞. Vangi等[7]研究车辆速度变化和碰撞位置对乘员损伤的影响,提出自适应调整纵向制动和转向的方法减小碰撞损伤,研究相关的碰撞模型[8-9]. Parseh等[10]结合车辆运动规划、车辆动力学和事故重建模型,讨论如何将车辆碰撞后运动纳入碰撞损伤最小化的研究中. 为了减小车辆在不可避撞场景下的碰撞损伤,Wang等[11]提出自动驾驶车辆在不可避撞场景下的路径规划算法,以减小车辆碰撞损伤. 该算法采用模型预测控制,在代价函数中考虑碰撞损伤,碰撞损伤取决于碰撞角度、车辆速度和碰撞车辆的质量比. Parseh等[12]提出以控制车辆极限的转向角率和制动率为基础创建离线轨迹库,利用基于事故数据的碰撞损伤评估模型,从轨迹库中选择最优轨迹并进行跟踪. Li等[13]采用神经网络建立非线性碰撞损伤评估模型,在轨迹库对每一条轨迹进行潜在碰撞损伤的估计,得到碰撞损伤最小的轨迹.
以上研究对不可避撞场景车辆碰撞损伤最小化作出了积极探索,但仍具有一定的局限性. 1)仅考虑碰撞时或碰撞后的单一情况,未利用预测的碰后状态来优化碰撞前的车辆运动,以减小车辆碰撞损伤. 2)车辆碰撞模型由于碰撞位置的不同,建模公式有所差异,采用矢量方式将各种碰撞情形统一为一种建模方式. 3)轨迹库的生成仅基于前轮极限转向角和制动率,不能充分发挥轮胎纵向的力学性能,通过引入附加横摆力矩以提供车辆更大的潜力和灵活性. 4)在不可避撞场景下车辆易失稳,缺乏轨迹跟踪和横摆稳定性的协同控制.
参考Zhou等[14]对车辆碰撞模型的研究,本文采用矢量方式将各种碰撞情形统一为一种建模方式,建立四自由度碰撞模型,提出分层结构的碰撞损伤最小化策略. 在决策层考虑车辆动力学约束,通过求解最优控制问题生成离线轨迹库,利用四自由度碰撞模型和碰撞前的车辆状态来估计碰后自车失稳风险,在线选择得到最优轨迹. 在运动控制层,基于模型预测控制建立轨迹跟踪与横摆稳定性协同控制器,保证轨迹的跟踪精度和车辆的稳定性.
1. 车辆动力学模型
1.1. 七自由度车辆动力学模型
1.1.1. 整车动力学模型
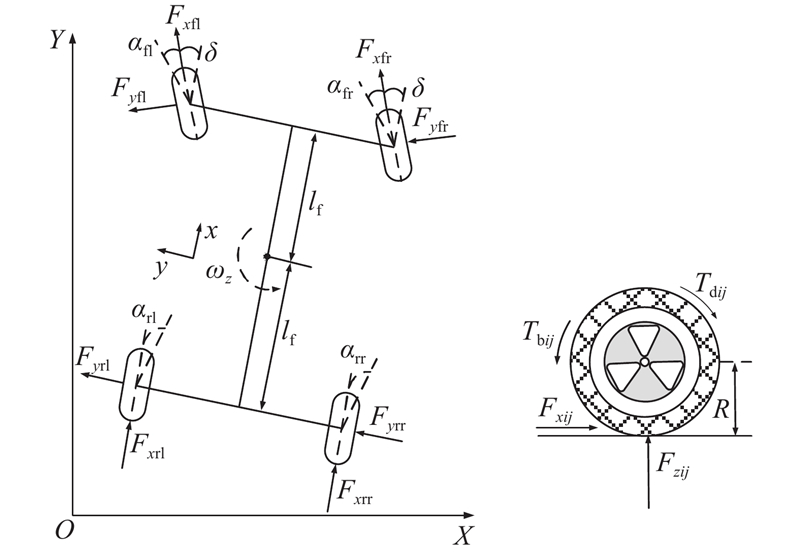
考虑模型精度和计算量,在Simulink中建立包括车身和轮胎在内的非线性车辆模型. 如图1所示,忽略车辆悬架系统垂直运动、车身俯仰运动及侧倾运动,建立包括车辆纵向、侧向、横摆和4个车轮旋转的七自由度非线性车辆模型. 整车的动力学方程如下.
图 1
4个车轮的旋转动力学方程可以表示为
式中:
1.1.2. 轮胎模型
车辆在高速行驶时,轮胎容易进入非线性区域,因此本研究的轮胎模型选用魔术公式. 在单一工况下,轮胎纵向力
式中:
刚度因子、形状因子、峰值因子、曲率因子的表达式分别为
式中:
表 1 魔术公式轮胎模型的参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 | ||
| 1.3 | 0 | 49.6 | |||||
| −22.1 | −0.354 | 226 | |||||
| 0.707 | 0.069 | ||||||
| 1.65 | −0.069 | ||||||
| 1.82 | −21.5 | 0.056 | |||||
| 0.208 | 0.486 |
式中:
当轮胎处于转向加制动联合工况时,轮胎的纵向力和侧向力应限制在附着椭圆上,考虑滑移率和侧偏角的轮胎模型表达式为
1.2. 四自由度车辆碰撞模型
1.2.1. 四自由度车辆动力学模型
图 2
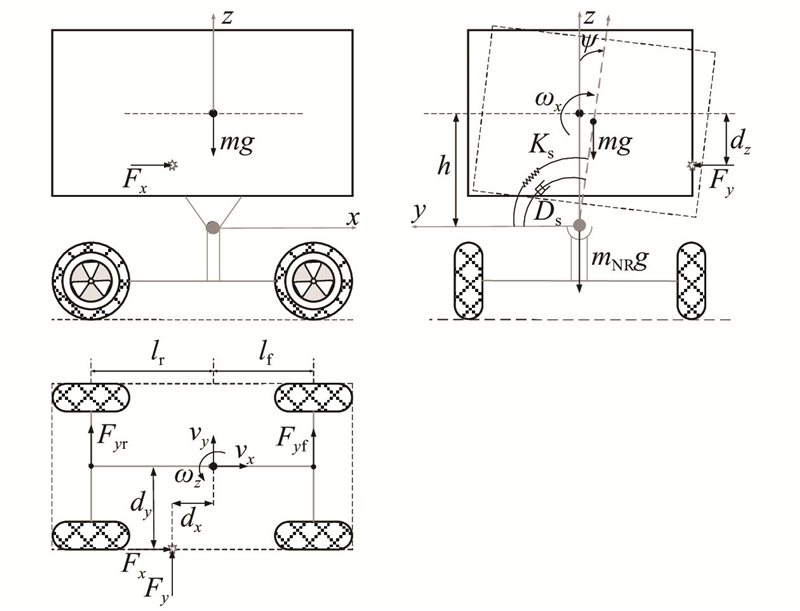
图 2 施加碰撞力的车辆模型示意图
Fig.2 Schematic diagram of vehicle model with impact forces applied
式中:
其中
1.2.2. 车辆碰撞模型
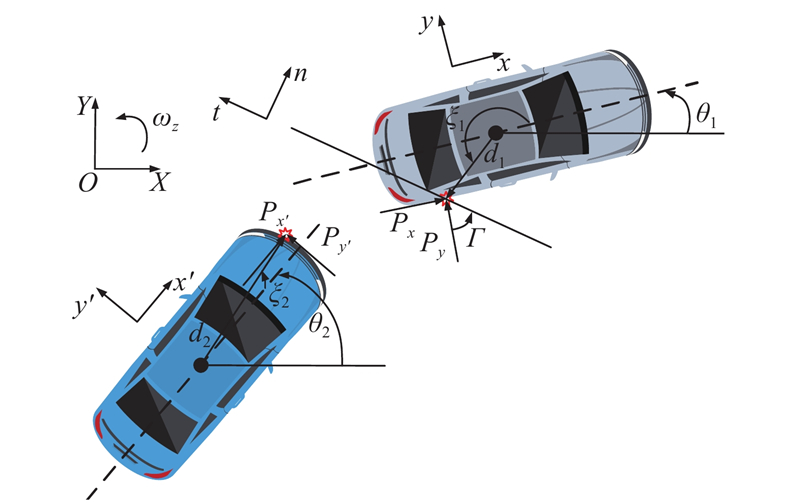
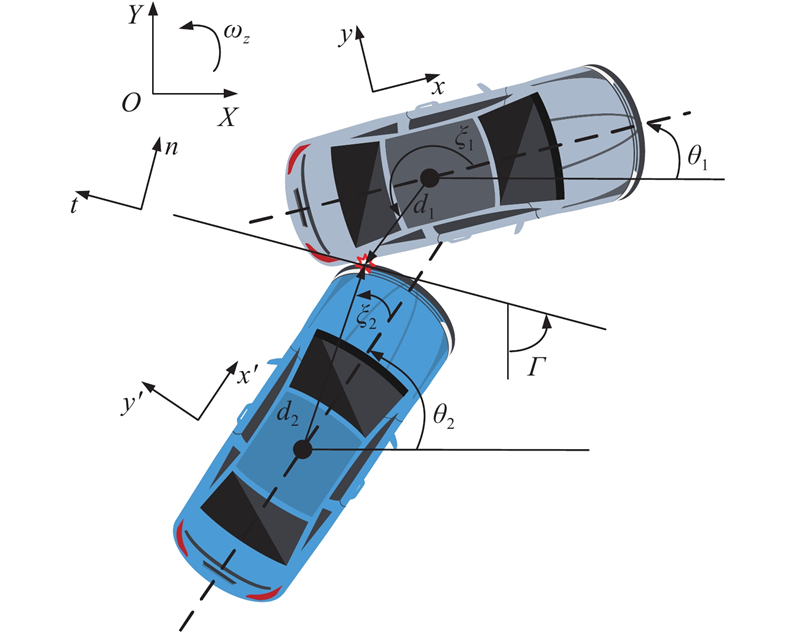
根据碰撞场景定义了另外2个局部坐标系,如图3所示,坐标系
图 3
式中:
仅由式(17)~(20)不足以求解得到碰撞瞬间车辆所受的冲量,需要引入恢复系数
式中:
式中:
切向相互作用系数
式中:
碰撞冲量从车身坐标系投影到大地坐标系,如下所示:
根据式(17)~(29),可得
式(30)将碰撞后的车辆状态与碰撞前的车辆状态联系起来,通过碰撞前的车辆状态
1.2.3. 模型验证
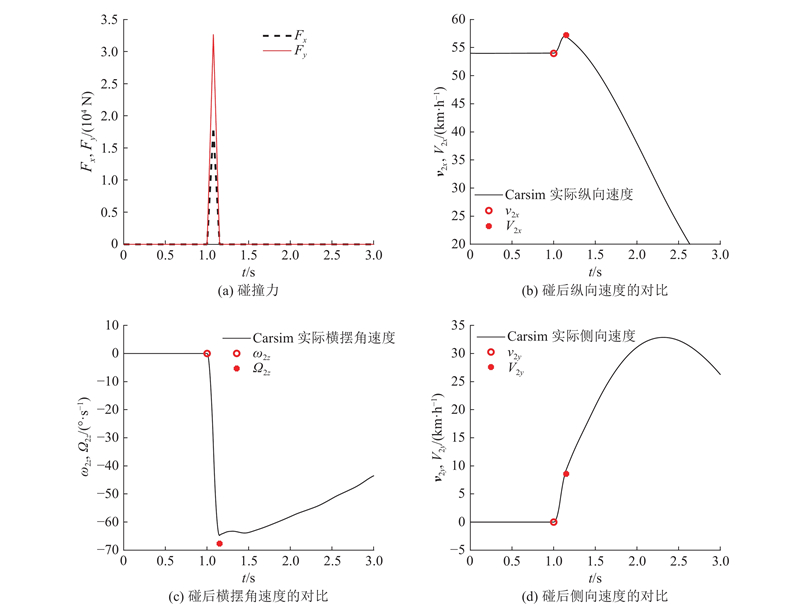
Carsim的计算结果为验证四自由度碰撞模型的精度提供了基准. 为了验证本文中碰撞模型的准确性,将基于Matlab/Simulink平台搭建的四自由度碰撞模型与Carsim的计算结果进行对比. 仿真中,施撞车辆和被撞车辆为相同型号的车辆,车辆参数来自于Carsim B-Class车辆模型,如表2所示.
表 2 车辆模型的部分参数
Tab.2
| 参数 | 数值 |
| 整车质量 m/kg | 1 230 |
| 簧上质量 mR/kg | 1 110 |
| 簧下质量 mNR/kg | 120 |
| 簧上质量惯量积 Ixz/(kg∙m2) | 40 |
| 簧上质量绕 | 440.6 |
| 总悬架侧倾刚度 Ks/(N∙m·rad−1) | 61 000 |
| 总悬架侧倾阻尼 Ds/(N∙m∙s·rad−1) | 4 120 |
图 4
图 5
从验证结果可知,采用四自由度碰撞模型计算得到的碰后状态与Carsim计算的结果吻合较好,预测的横摆角速度存在一定的偏差,但在误差允许范围内.
2. 上层决策层
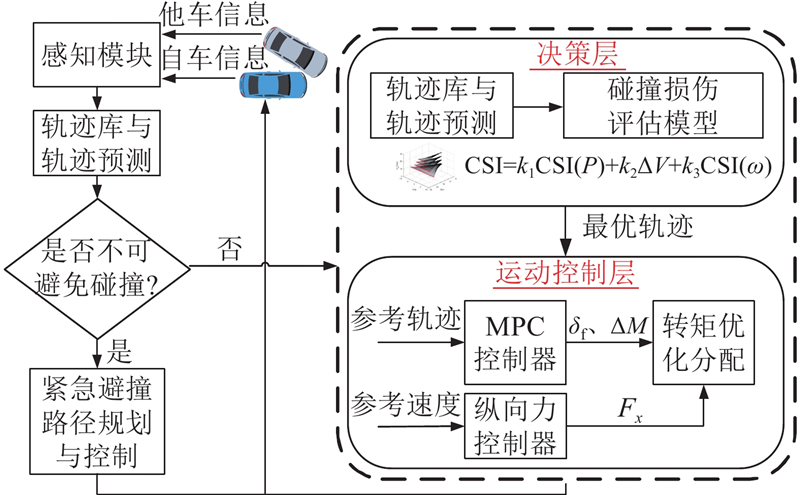
上层决策层由轨迹库、轨迹预测和碰撞损伤评估模型组成. 其中轨迹库基于数值优化,在考虑车辆动力学约束的情况下,离线生成车辆特定速度下的可行驶轨迹库. 轨迹预测用来预测对方车辆未来短时间内的行驶轨迹. 碰撞损伤评估模型在线评估轨迹库中轨迹的碰撞时风险和碰后自车失稳风险,在决策时以极短时间从轨迹库中确定出最优轨迹,并将其传给下层运动控制层,碰撞损伤最小化策略的结构图如图6所示.
图 6
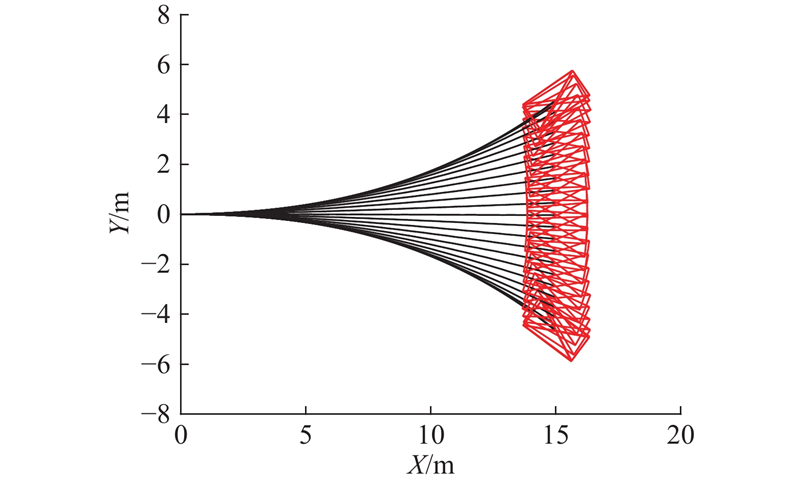
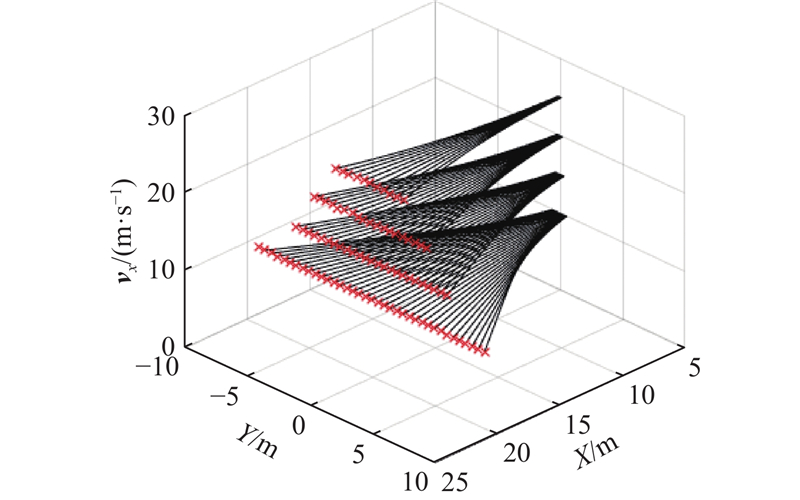
2.1. 轨迹库
轨迹库是离线生成的,在碰撞损伤最小化系统运行前就已创建好. 当碰撞损伤最小化系统运行时,根据碰撞损伤评估模型在轨迹库中选取最优的一条轨迹,并传至下层控制器. 轨迹库中的轨迹均是通过数值求解最优控制问题生成的[12]. 最优控制问题可以描述为
式中:
轨迹库的生成采用三自由度车辆模型来描述车辆运动,整车的动力学模型描述如下:
式中:
结合式(32),整理可得
图 7
图 8
2.2. 轨迹预测
为了估计两车的碰撞损伤,对对方车辆进行轨迹预测. 自身车辆检测到即将发生碰撞到碰撞这一段时间常为1.0~2.0 s,针对这种短时间的轨迹预测,可以采用运动学模型. 常见的汽车运动学模型有恒速度模型、恒加速度模型、恒角速度模型、恒转向角速度模型和恒角速度加速度模型(constant turn rate and acceleration, CTRA)等. 根据本文的研究场景,在交叉路口选择恒角速度加速度模型进行轨迹预测[15]. 车辆的位置、速度、加速度和航向角数学模型如下所示:
式中:
其中
2.3. 碰撞损伤评估模型
车辆碰撞损伤主要取决于碰撞位置、碰撞时两车相对速度及碰后自车失稳风险,碰撞损伤评估模型综合考虑这三方面,以实现碰撞损伤的最小化.
图 9
图 10
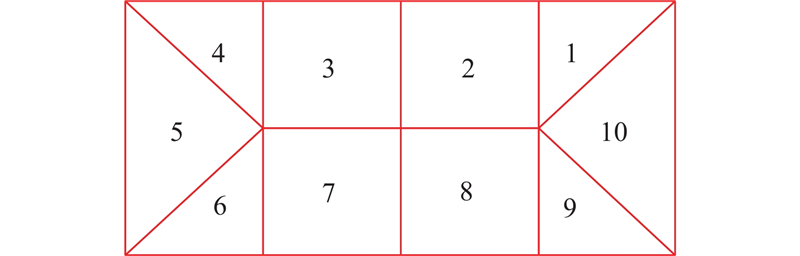
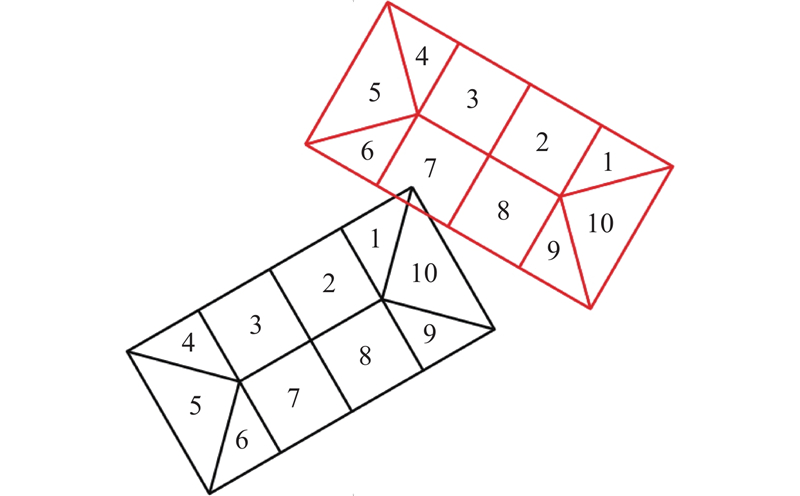
表 3 与碰撞位置相关的碰撞损伤
Tab.3
| 碰撞位置 | 碰撞损伤CSI(P) |
| 5(F1) | 1 |
| 10(F2) | 2 |
| 3或7(P2) | 3 |
| 2或8(P1) | 4 |
| 4或6(B0) | 5 |
| 1、2或8、9(Y1) | 6 |
| 1或9(F0) | 7 |
| 3、4或6、7(Z1) | 8 |
| 2、3、4或6、7、8(Z0) | 9 |
| 1、2、3、4或6、7、8、9(D0) | 10 |
| 2、3或7、8(P0) | 11 |
| 1、2、3或7、8、9(Y0) | 12 |
速度相关的指标常被用于评估碰撞损伤. 根据相关的碰撞数据分析[17]可知,碰撞时刻两车相对速度
式中:
车辆在遭受碰撞后往往会同时产生横摆运动,较大的横摆角速度极易影响碰后车辆的稳定性[10],导致二次碰撞甚至多次碰撞. 将影响碰后车辆稳定性的潜在风险定义为
式中:
总碰撞损伤为
式中:
3. 下层轨迹跟踪与稳定性协同控制器
从上层决策层基于碰撞损伤评估模型得到最优轨迹,输出给下层运动控制层. 为了保证车辆在极限工况下轨迹跟踪的精度和稳定性,控制器采用基于分层控制架构的轨迹跟踪与横摆稳定性协同控制方法[18].
3.1. 轨迹跟踪控制器
基于模型预测控制算法,设计轨迹跟踪控制器. 根据式(16)、(39),将车辆模型写为状态空间方程的形式:
式中:
使用欧拉方法,对上述状态空间方程进行离散化处理,忽略高阶项,得到离散状态空间方程:
式中:
输出向量
定义模型预测控制的目标函数为
式中:状态向量的权重
3.2. 转矩优化分配控制器
转矩优化分配控制器是在多约束条件下求解最优轮胎纵向力分配,以满足附加横摆力矩
考虑到
由于优化问题的有效解要满足车辆纵向车速与直接横摆力矩的需求,可得
式中:
驱动电机的最大输出转矩和路面附着条件决定了车轮的最大纵向力,有
综合式(43)~(45),得到下层转矩优化分配控制器:
式中:
4. 仿真分析
为了验证提出的碰撞损伤最小化算法,基于Matlab/Simulink平台搭建车辆模型和控制器模型,参考文献[16]模拟和分析2个场景. 第1个场景是T型路口,涉及2辆车. 随着车辆数的增加,碰撞损伤评估模型将变得更加复杂,所以第2个场景涉及多辆汽车.
4.1. 两车场景
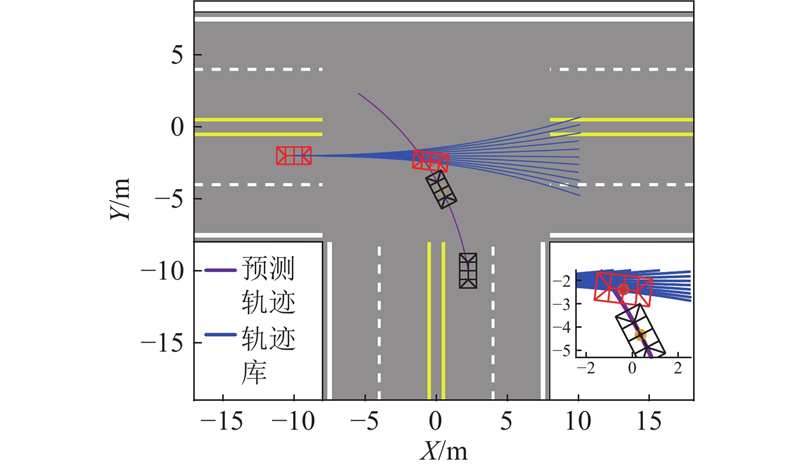
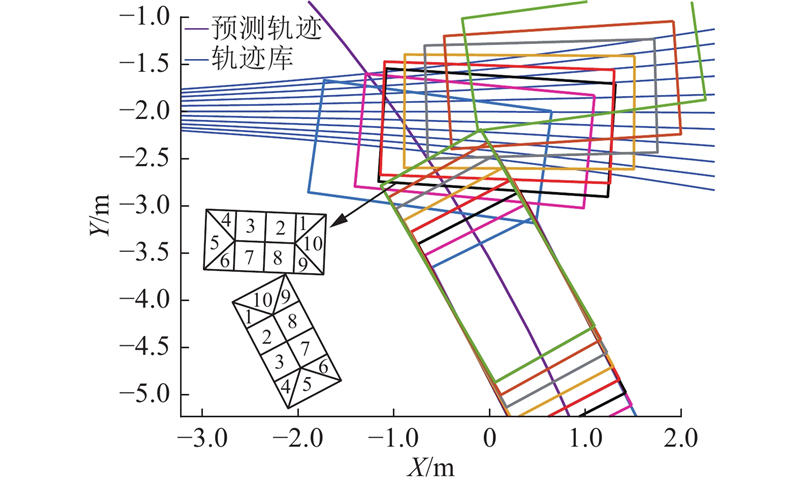
该场景具体如图11所示,场景中自车以20 m/s的速度直行通过路口,它车以20 m/s的速度行驶进入T型路口. 自车通过CTRA模型预测出它车即将左转进入内侧车道的轨迹. 当自车检测到20 m/s对应的轨迹库均与所预测的它车轨迹发生碰撞,自车触发碰撞损伤最小化系统.
图 11
图 12
表 4 两车场景下的碰撞损伤结果
Tab.4
| 轨迹编号 | 碰撞位置 | ||||
| 5 | 6(B0) | 200 | 156.6 | 113.1 | 469.7 |
| 44 | 7(P2) | 120 | 147.2 | 93.3 | 360.5 |
| 89 | 7、8(P0) | 440 | 126.4 | 73.6 | 640 |
| 136 | 8(P1) | 160 | 103.7 | 79.8 | 343.5 |
| 196 | 9(F0) | 280 | 98.3 | 94.5 | 472.8 |
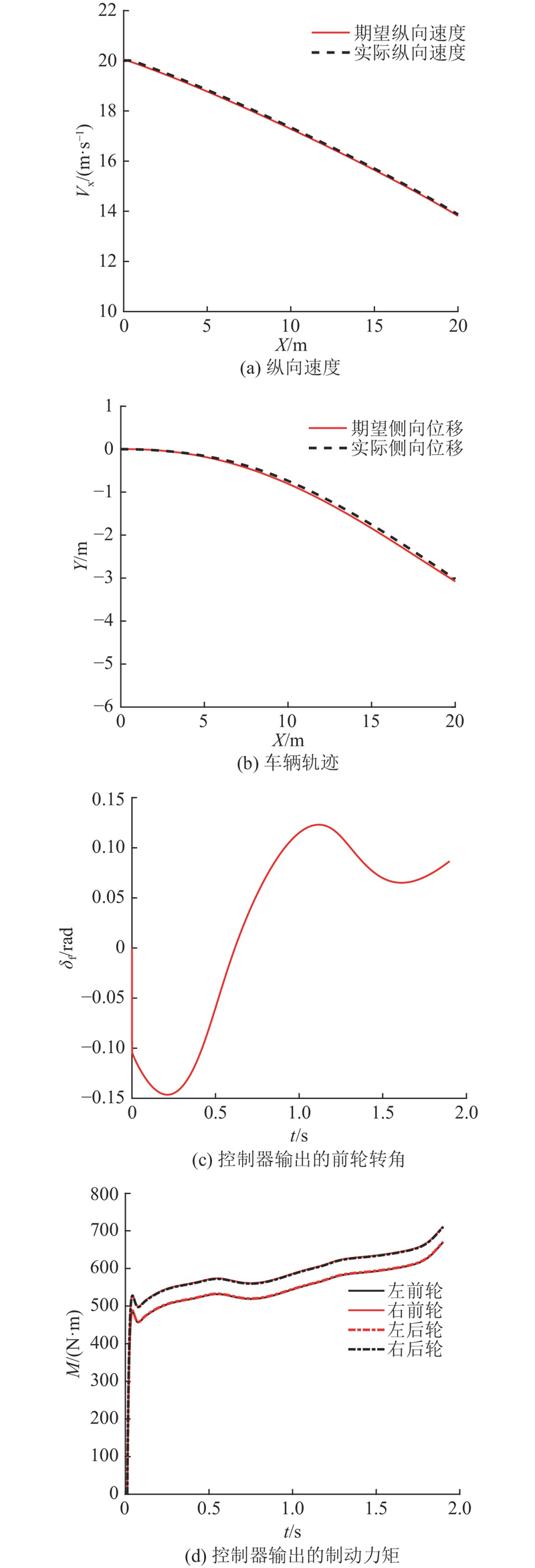
图 13
4.2. 多车场景
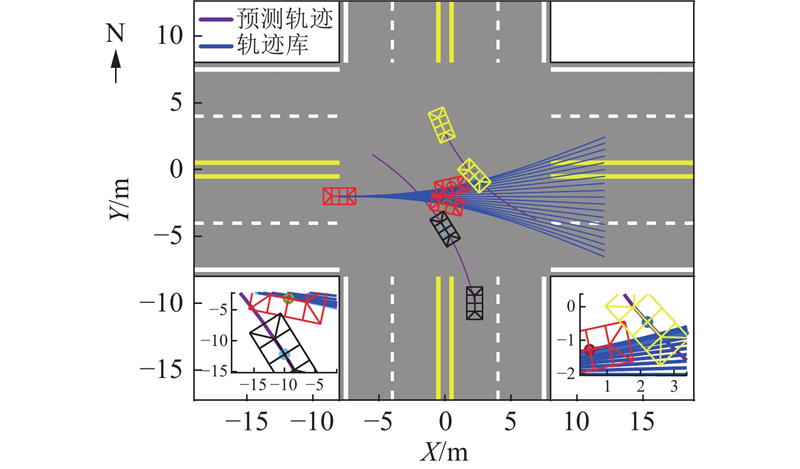
多车场景具体如图14所示,场景中自车以15 m/s的速度直行通过路口,自南向北左转的它车1以15 m/s的速度行驶进入十字交叉路口,自北向南左转的它车2以15 m/s的速度行驶进入十字交叉路口. 自车通过CTRA模型预测出它车1、2的未来行驶轨迹. 当自车检测到15 m/s对应的离线轨迹库均与所预测的它车轨迹发生碰撞时,自车触发碰撞损伤最小化系统.
图 14
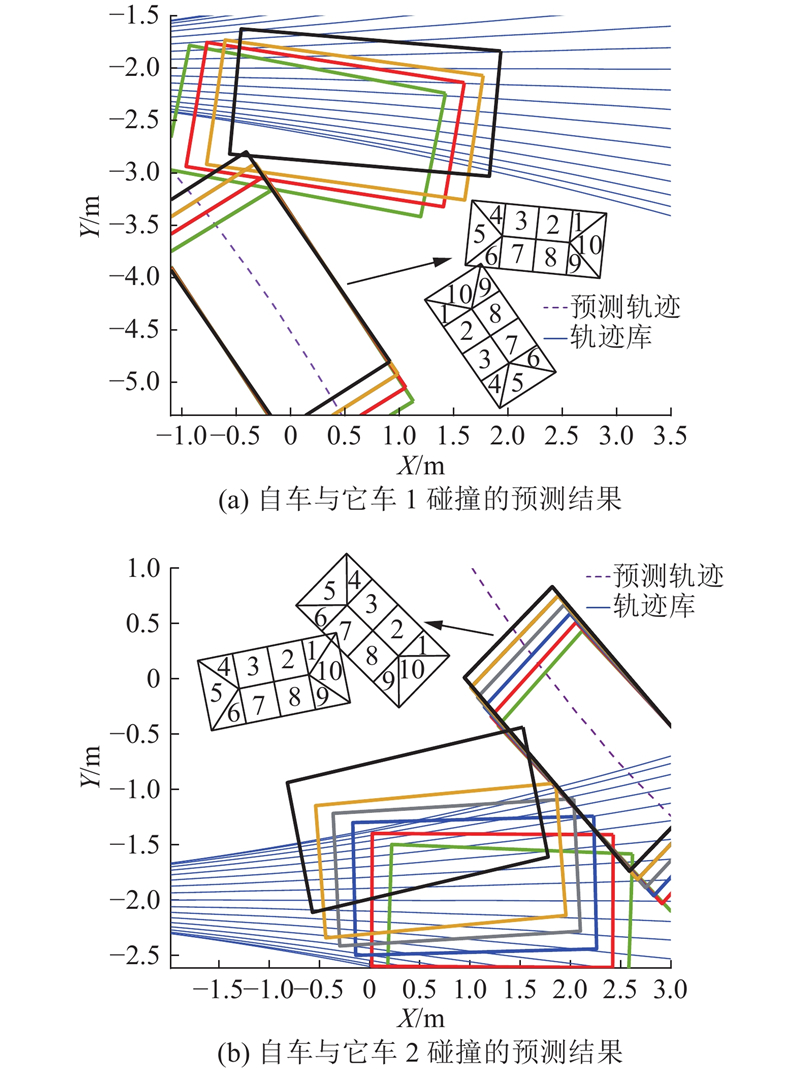
图 15
图 15 多车场景下的碰撞预测结果
Fig.15 Result of collision prediction in multi-vehicle scenario
表 5 多车场景下的碰撞损伤结果
Tab.5
| 轨迹编号 | 碰撞位置 | ||||
| 78 | 7(P2) | 120 | 78.3 | 61.7 | 260.0 |
| 96 | 8(P1) | 160 | 84 | 63.1 | 307.1 |
| 123 | 9(F0) | 280 | 91 | 73.2 | 444.2 |
| 187 | 6(B0) | 200 | 109.5 | 68.5 | 378.0 |
| 230 | 7(P2) | 120 | 113.2 | 58.4 | 291.6 |
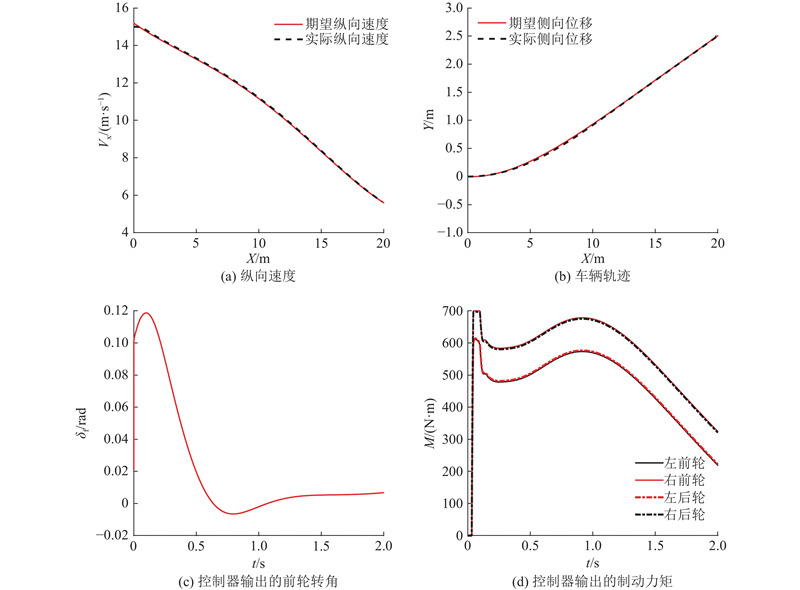
图 16
5. 结 论
(1)采用矢量方式,将各种碰撞情形统一为一种建模方式,建立四自由度碰撞模型. 通过四自由度碰撞模型和碰撞前的车辆状态,估计碰后自车失稳风险. 碰撞损伤评估模型综合考虑碰撞位置、碰撞时两车相对速度和碰后自车失稳风险,以尽可能减小车辆碰撞损伤.
(2)利用附加横摆力矩能够改变车辆横摆角速度和航向角的特点,在轨迹库的生成中引入附加横摆力矩以提供更大的潜力和灵活性,充分发挥出轮胎纵向的力学性能,而不仅仅基于前轮极限转向角和制动率.
(3)为了保证最终的轨迹跟踪精度和车辆稳定性,基于模型预测控制建立轨迹跟踪与横摆稳定性协同控制器,实现多目标综合控制.
参考文献
交叉口车车碰撞事故车损程度的影响要素
[J].DOI:10.3969/j.issn.1674-8484.2023.01.003 [本文引用: 1]
Influencing factors of vehicle damage degree in vehicle-vehicle collision accident at intersection
[J].DOI:10.3969/j.issn.1674-8484.2023.01.003 [本文引用: 1]
中国城市道路交通安全特点解析
[J].
Characteristics of urban road traffic safety in China
[J].
汽车安全技术的研究现状和展望
[J].DOI:10.3969/j.issn.1676-8484.2010.02.002 [本文引用: 1]
Research status and prospects of automotive safety technology
[J].DOI:10.3969/j.issn.1676-8484.2010.02.002 [本文引用: 1]
A new strategy for rear-end collision avoidance via autonomous steering and differential braking in highway driving
[J].
Emergency steering collision avoidance control based on distributed driving intelligent vehicles
[J].DOI:10.1002/cpe.7486 [本文引用: 1]
A high-speed human-like collision avoidance controller based on a neural network under different road adhesion coefficients
[J].
Combined activation of braking and steering for automated driving systems: adaptive intervention by injury risk-based criteria
[J].DOI:10.1016/j.prostr.2020.02.039 [本文引用: 1]
A simplified model for analysis of the post-impact motion of vehicles
[J].DOI:10.1177/0954407012470353 [本文引用: 1]
A vehicle model for crash stage simulation
[J].
Motion planning for autonomous vehicles with the inclusion of post-impact motions for minimising collision risk
[J].DOI:10.1080/00423114.2022.2088396 [本文引用: 2]
Vehicle crash mitigation strategy in unavoidable collision scenarios: focusing on motion planning by considering a generalized crash severity model
[J].
Collision model for vehicle motion prediction after light impacts
[J].
A data-driven method towards minimizing collision severity for highly automated vehicles
[J].DOI:10.1109/TIV.2021.3061907 [本文引用: 2]
Identification and validation of a logistic regression model for predicting serious injuries associated with motor vehicle crashes
[J].DOI:10.1016/j.aap.2010.07.018 [本文引用: 1]