数据驱动的进化算法(data-driven evolutionary algorithm， DDEA)^[1]是对使用历史数据建立代理模型，并以其辅助进化算法(evolutionary algorithm， EA)中的真实目标函数对个体进行适应度评估的算法的统称，有时也被称为代理辅助的进化算法(surrogate assisted evolutionary algorithm， SAEA)^[2]. 通常，传统的EA需要多次迭代， 且每次迭代时都要对种群中的所有个体进行适应度评估.在真实环境中， 频繁评估的高昂代价可能难以承受^[3]， 这制约了EA在实际问题中的应用. 近年来， 为了节省计算资源， 学者们提出了一些DDEA， 它们在部分评价昂贵的优化问题上取得了不错的效果， 如创伤系统设计^[4]、熔镁炉性能优化^[5]、飞行器翼型优化^[6]等.

在DDEA中， 常用的代理模型包括径向基函数网络(radial basis function network， RBFN)^[7]、克里金模型(kriging)^[8]、岭回归(ridge regression， RR)^[9]、多项式回归(polynomial regression， PR)^[10]等. DDEA的性能在很大程度上受到离线数据集规模的影响^[1，6]. 一般而言，用于训练的数据越多， 代理模型越准确，从而能够更好地指导EA搜索最优解^[11]. 由于DDEA常被用来解决昂贵优化问题，在这些问题中数据的获取可能是昂贵的^[12]，因此DDEA能够利用的数据通常很少. 例如用于预测蛋白质结构的AlphaFold2， 其参数优化需要128个TPUv3核运行数周的时间， 这使得研究者很难通过实验得到充足的数据^[13].

DDEA有在线^[14]和离线^[6]2种形式. 离线的DDEA完全不进行真实评估，算法可依赖的只有数量有限的离线数据，因此更容易受到小数据的影响. 小数据难以建立准确的代理模型，这是离线的DDEA面临的主要挑战. 现有算法已为解决这一问题做出了许多尝试，主要包括引入集成学习^[15]、半监督学习^[16]、多核学习^[17]、协同进化^[18]等方法.Wang等^[19]提出的DDEA-SE通过Bagging训练大量代理模型，在迭代时自适应地选择部分模型进行集成. Huang等^{[7， 11]}分别提出TT-DDEA和SRK-DDEA. 前者使用三体训练^[20]将无标签数据转化为伪标签数据，以优化每次迭代中训练的3个代理模型；后者使用离线数据训练4个不同核函数的RBFN， 利用随机排序^[21]平衡模型之间的误差.Gong等^[22]提出的CC-DDEA同时构建局部与全局代理模型，通过协同进化实现从局部并行到全局的搜索. 除了常见的回归模型外，一些其他类型的网络被应用到DDEA中. Huang等^[23]提出的CL-DDEA使用孪生对比学习网络与拓扑排序辅助选择操作，减弱算法对离线数据质量的依赖.相关文献的实验结果表明，上述算法在数据量充足的情况下能够取得良好的效果. 当数据量大幅降低时，这些算法的性能会显著变差.

针对离线的DDEA在数据量极低的情况下表现差的问题，本文结合RBFN隐含层节点数寻优与多核学习生成伪标签数据的策略，提出基于多核数据合成的离线数据驱动的进化算法(offline data-driven evolutionary algorithm based on multi-kernel data synthesis， DDEA-MKDS). 实验表明， 利用所提算法，能够有效增强离线的DDEA对小数据的适应能力，大幅减少算法的运行时间.

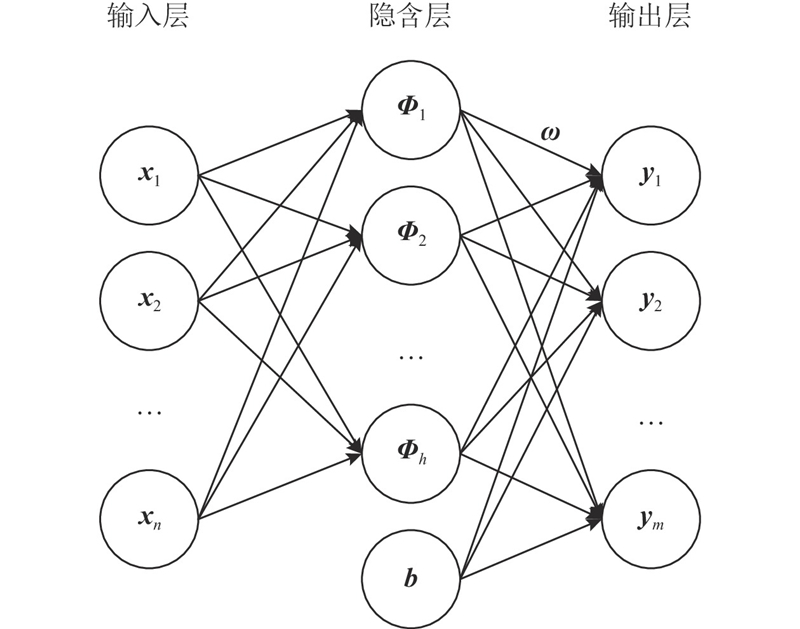
RBFN训练速度快，逼近能力强，是离线的DDEA中常用的代理模型之一. 从结构上看， RBFN属于3层前向式的神经网络， 包括输入层、隐含层、输出层， 如图1所示.

根据网络的结构， RBFN的输出可以描述为

(1)$ {{\boldsymbol{y}}_j} = \sum\limits_{i = 1}^h {{{\boldsymbol{\varPhi}} _i}{{\boldsymbol{\omega}} _{ij}}} +{\boldsymbol{b}}{\text{.}} $

式中：y_j为第j个输出层节点的输出，h为隐含层节点数，Φ_i为第i个隐含层节点的核函数输出，ω_ij为第i个隐含层节点到第j个输出层节点之间的权值，b为网络中设置的偏置单元.

当训练RBFN时，一个非常重要的问题是如何选择隐含层节点数. 从式(1)可以看出，隐含层节点数越多，则训练RBFN所需要的计算次数越多，所消耗的时间越长. 模型的复杂度会随着隐含层节点数的增多而提高， 当训练数据较少时， 高复杂度的网络更容易产生过拟合现象^[24-25]. 反之， 若隐含层节点数太少， 则RBFN可能会无法学习.

Rastegar等^[26]的研究表明， 对于某个特定的数据集而言，一定存在最佳的隐含层节点数，使得模型的训练效果最好. 目前还不存在通用的确定最佳隐含层节点数的方法. 一些尝试性的方法包括经验公式法^[27]、进化优化^[28]、引入神经网络^[29]等. 由于DDEA是强调搜索效率的算法， 其中使用的策略不应太复杂.

与其他3层神经网络相比， RBFN的主要区别是使用了径向基函数(radial basis function， RBF)作为核函数. RBF是一类实值函数， 其取值只依赖于数据点到某个特定点的距离， 该特定点一般被称为中心点. RBF的通式如下:

(2)$ \varPhi ({\text{dist}}) = \varPhi (\left\| {{\boldsymbol{x}} - {\boldsymbol{c}}} \right\|). $

式中：dist为数据点到中心点之间的欧氏距离，dist = ||x−c||.

在RBFN中，可使用的核函数有很多， 其中较常见的是gaussian函数、逆多二次函数和逆sigmoid函数， 它们的形式如下所示:

(3)$ \varPhi ({\text{dist}}) = \exp \left( - \frac{{{\text{dis}}{{\text{t}}^2}}}{{{\sigma ^2}}}\right), $

(4)$ \varPhi ({\text{dist}}) = \frac{1}{{\sqrt {{\sigma ^2}+{\text{dis}}{{\text{t}}^2}} }}, $

(5)$ \varPhi ({\text{dist}}) = \frac{1}{{1+\exp \left({{{\text{dis}}{{\text{t}}^2}}}/{{{\sigma ^2}}}\right)}}. $

式中：σ为RBF的拓展常数，有时被称为宽度， σ越大表示每个隐含层节点可控制的范围越大.

在同一个训练集上，使用不同核函数的RBFN的效果存在微小的差异^[7]，具体情况取决于训练数据的分布特性. 对于如何选择核函数，目前仍缺乏理论指导， 比较流行的做法是根据经验选择单个固定的核函数. 一些学者通过组合多个不同核函数来训练通用性更强的模型，这种方法在许多基于多核学习的研究中被证实是有效的^[30-31].

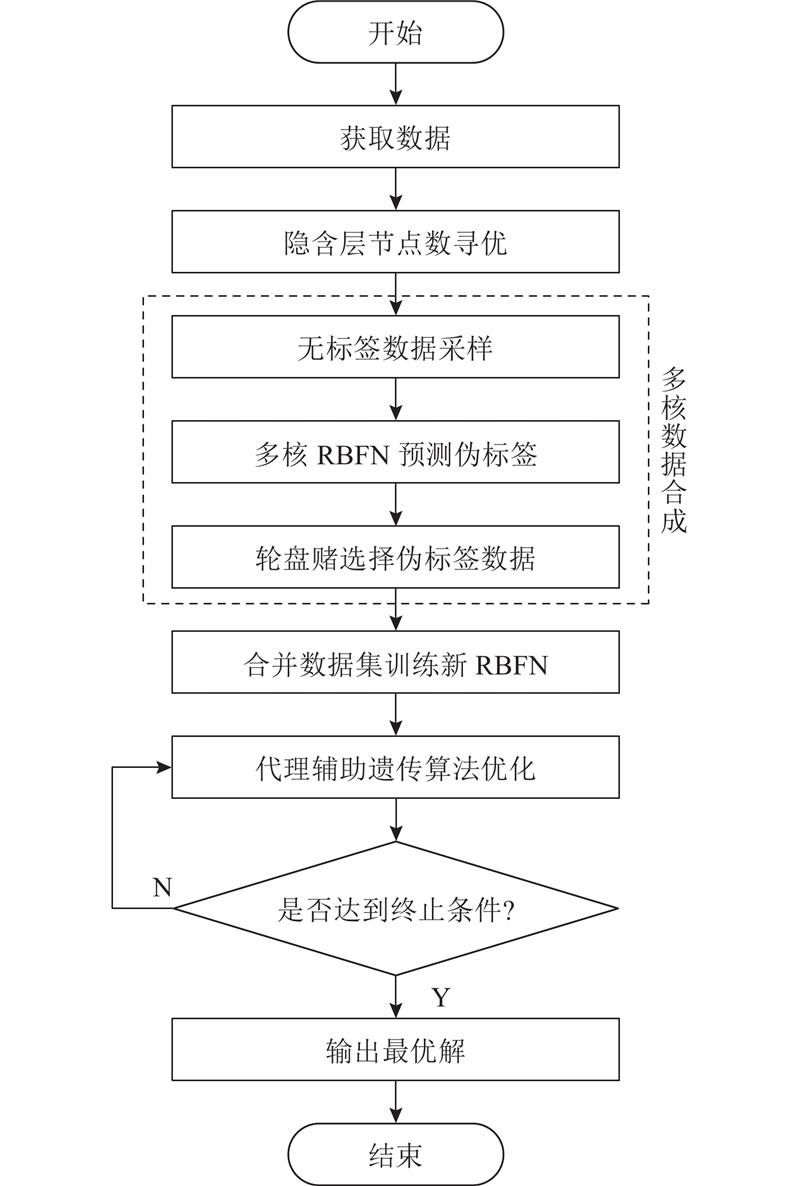
DDEA-MKDS的算法流程如图2所示.

DDEA-MKDS分为以下3个阶段.

1）算法结合经验公式与遍历搜索，找出针对离线数据集的最佳隐含层节点数，在后续训练RBFN时，参数按照该阶段的寻优结果进行设置.

2）算法采样决策空间中的大量无标签数据， 使用基于离线数据集训练的3个不同核函数的RBFN模型预测它们的伪标签. 通过轮盘赌法按不确定度规则选择其中的部分数据，将选择的伪标签数据加入原数据集，形成合成数据集.

3）算法使用合成数据集，训练单个RBFN作为代理模型来代替遗传算法中的目标函数，开展个体评估.

与大多数离线的DDEA相同， 该算法选择遗传算法作为优化器. 由于离线的DDEA中代理模型的作用仅是代替进化优化过程中的真实评估，算法可以根据实际问题的特性选择不同的EA， 代理模型的构建方法是可以移植的.

DDEA-MKDS的伪代码如下所示.

DDEA-MKDS是针对数据量极小的情况设计的. 为了避免代理模型因小数据陷入过拟合， 加快训练速度， 通过隐含层节点数寻优的策略来简化RBFN的结构.

具体而言， 该策略结合了经验公式与遍历搜索的思想. 当隐含层节点只有1个时， RBFN会失效，因此算法设置寻优区间为[2，h_T]， 上限h_T由下面的经验公式^[27]计算得出：

(6)$ {h_{\text{T}}} = \sqrt {n+m} +1. $

式中：h_T为隐含层节点数的计算结果，n为输入层节点数，m为输出层节点数.

算法重复训练拥有不同隐含层节点数的RBFN，在验证数据上比较这些模型的误差， 找出该参数的最佳设置.在小数据的条件下，每个数据对模型训练的影响都较大. 为了减少数据分割带来的干扰， 算法每次训练前都从离线数据集中随机抽取仅1个数据作为验证数据. 模型误差按照下式计算：

(7)$ {e_i} = \left| {\frac{{{p_{{\text{pre}}}} - {p_{{\text{real}}}}}}{{{p_{{\text{real}}}}}}} \right|. $

式中：e_i为隐含层节点数为i时的预测误差; p_real为所抽取的验证数据的真实值; p_pre为模型对所抽取的验证数据的预测值; 特别地， 若p_real = 0， 则重新抽取验证数据. 算法最终会输出e_i最小时的i作为隐含层节点数寻优的结果.

本部分的伪代码如下所示.

小数据条件下代理模型难以获得理想的精度. 提出基于多核RBFN的伪标签数据合成策略， 以达到补充数据量的目的.算法中无标签数据的采样量以相对于离线数据量的倍数d_m表示.

由于单个RBFN无法提供预测值的不确定度，为了在选择数据时有可靠的参考，DDEA-MKDS训练了3个RBFN模型来预测无标签数据的伪标签，将不确定度定义为预测值的标准差，如下所示：

(8)$ {\sigma _a} = \sqrt {\frac{1}{3}\sum\limits_{i = 1}^3 {{{(p_a^r - {y_a})}^2}} } ;\;r = 1,2,3. $

式中：σ_a为数据a预测值的标准差；p_a^r为模型r对数据a的预测值；y_a为3个模型预测值的均值，作为数据a的伪标签.

要使式(8)有效，3个模型的预测值在尽量准确的同时具有一定的差异，因此算法在训练这3个RBFN时使用了不同的核函数，分别为gaussian函数、逆多二次函数和逆sigmoid函数.

不确定度越低，即3个RBFN对该数据的预测值越接近，可以认为该伪标签是更可信的，所以应选择更多不确定度低的数据. 不确定度高的数据对模型训练有积极作用，这是由于RBFN的预测能力与距离相关，一般离真实数据越远，模型的预测能力越低，所以不确定度低的数据会紧密分布在真实数据的周围. 若只选择这部分数据， 则模型的泛化能力会下降. 本算法使用轮盘赌选择法， 根据下式对所有数据的不确定度进行归一化处理， 将归一化后的值作为数据被选中的概率：

(9)$ {q_a} = 1 - \frac{{{\sigma _a} - {\sigma _{\min }}}}{{{\sigma _{\max }} - {\sigma _{\min }}+\varepsilon }}. $

式中：q_a为归一化值; σ_a为数据a的不确定度; σ_min与σ_max分别为所有数据的不确定度的最小值与最大值; ε设为10⁻⁵. 每一个数据都有机会被选中， 不确定度越低，被选中的概率越大.

本部分的伪代码如算法3所示. 其中rand为随机生成的0~1.0的浮点数.

将DDEA-MKDS与流行的离线DDEA在6个经典单目标测试问题^[6，32]上进行对比，分别为Ellipsoid、Rosenbrock、Ackley、Levy、Griewank与Rastrigin. 离线数据集由拉丁超立方在决策空间中采样得到，为了观察各算法在数据量极小时的表现， 设置数据量为15. 问题的维度为10、30、50、100，在所有维度的问题上各算法都独立运行20次.

在DDEA-MKDS中，代理模型RBFN利用K-均值算法获取中心点，权重由伪逆法计算，拓展常数为中心点间平均距离的2倍，除多核数据合成阶段外，使用的核函数为gaussian函数，d_m设置为60.

对比算法为TT-DDEA^[11]、SRK-DDEA^[7]、CC-DDEA^[22]、CL-DDEA^[23]与DDEA-SE^[19]. 为了使算法在小数据时正常运行，DDEA-SE的模型隐含层节点数设置为离线数据量的算术平方根向下取整. 其余各算法的参数均按照原文献设置.

所有算法都使用遗传算法进行优化，种群大小为100，迭代次数为100，交叉与变异的概率各为1与1/d，其中d为问题的维度.

与其他同类研究中使用的方法相似， 实验中最优个体的适应度是通过真实函数计算得到的， 但真实函数仅用于算法的性能评估， 不会对优化过程产生任何影响.

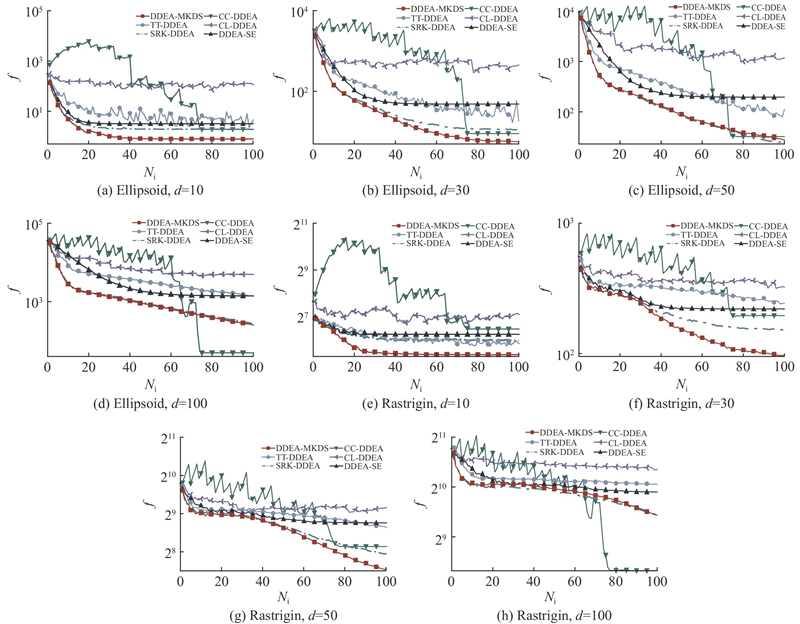
如表1所示为DDEA-MKDS与各对比算法在数据量为15时的优化结果， 形式为均值±标准差， 每个测试实例中的最优结果加粗显示. 可以看出， 综合表现最好的是DDEA-MKDS， 平均排名是最高的. 此外， 所有实验结果均经过Wilcoxon匹配对符号秩检验， 其中+/≈/−分别表示DDEA-MKDS显著优于/无显著差异于/显著差于对比算法. 在几乎所有的实例上， DDEA-MKDS都显著优于TT-DDEA、CL-DDEA和DDEA-SE. DDEA-MKDS中使用的隐含层节点数寻优能够有效地避免代理模型产生过拟合， 通过多核数据合成的策略弥补了数据量不足的问题，算法在面对小数据时的表现较优秀. DDEA-SE通过数据抽样构建大量代理模型，当数据量本身很少时，每一个模型的精度都较差，这会导致算法的性能显著降低. TT-DDEA具有同样的问题， 由于算法需要将数据集分割为3等份， 这会使单个模型可依赖的数据量进一步减少， 在这种情况下不准确的模型无法提供可信的伪标签数据. CL-DDEA中设计的孪生式对比网络需要依赖成对数据训练， 当数据量匮乏时， 对比网络无法达到理想的精度， 这会使其在拓扑排序的过程中产生严重的误差，算法很难进行正常的选择操作，其在所有问题上的表现都很差. 从结果上来看， 除DDEA-MKDS外， 对比算法中表现较好的是SRK-DDEA和CC-DDEA， 二者的平均排名相当. SRK-DDEA中使用基于多核学习训练的径向基函数网络作为代理模型，虽然当离线数据很少时模型精度不足，但随机排序的策略能够较好地平衡模型之间的误差. CC-DDEA中的全局模型是由多个局部模型集成形成的， 这在一定程度上减小了数据量匮乏带来的影响， 能够加强算法在高维度问题上的表现， 算法在所有100维的问题上都是表现最好的. 除了Levy与Griewank外， CC-DDEA在其他多数10维、30维与50维的问题上都显著差于DDEA-MKDS， 这意味着协同进化不适用于一些较低维度的问题的求解.

Ellipsoid和Rastrigin分别为单峰问题与多峰问题中的代表， 如图3所示为各算法在这2个问题上的收敛曲线. 图中，N_i为迭代次数. 从图3可以看出，DDEA-MKDS有比较优秀的收敛速度.与性能最接近的SRK-DDEA和CC-DDEA相比， DDEA-MKDS的优势随着问题维度的增大有减小的趋势， 这说明DDEA-MKDS在较低维问题中的表现更好.

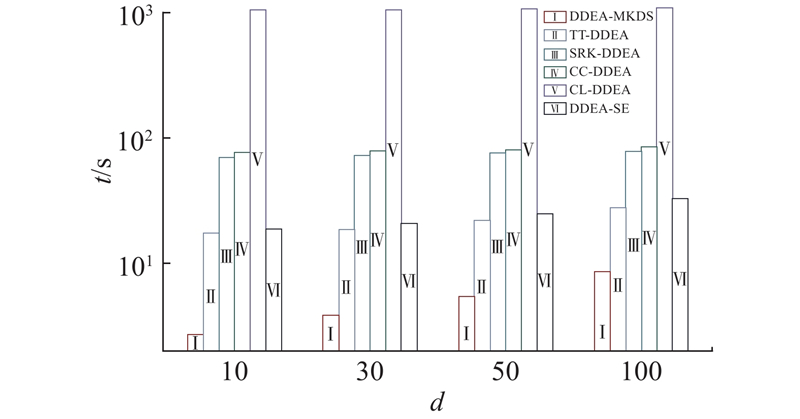
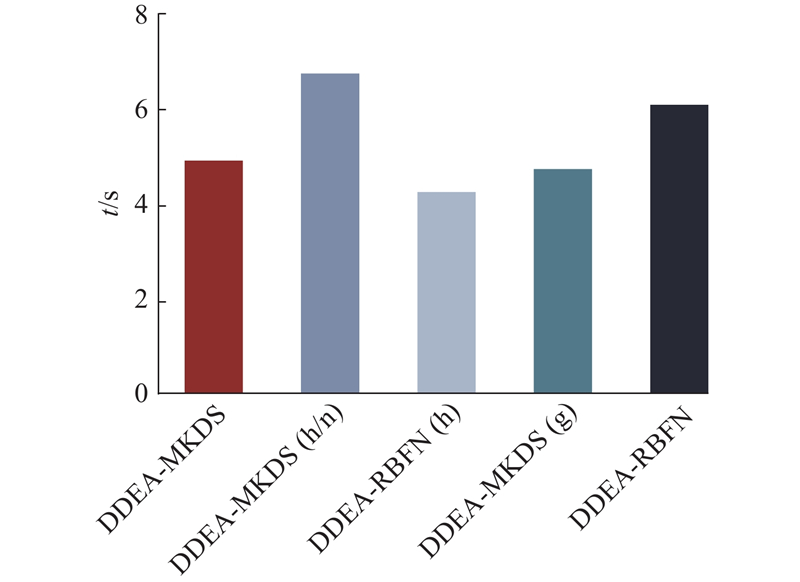
离线DDEA常被用来求解昂贵优化问题， 需要尽量减少时间成本， 因此算法的效率是很重要的. 如图4所示为各算法在所有问题上的平均运行时间，测试使用的计算机CPU为Intel(R) Core i5-10400，算法运行环境为Python 3.9.13. 可以看出，由于离线数据数量较少，且是固定规模，不随维度而变化，各算法的运行时间因维度升高而增加的幅度均不明显. DDEA-MKDS在各维度的问题上均显著快于其他所有对比算法， 差距是数量级级别的. 这主要得益于算法中的隐含层节点数寻优策略，通过减少模型隐含层节点数来简化RBFN的结构，能够显著加快训练速度. DDEA-MKDS最终用于指导进化过程的代理模型数量只有一个，不像其他算法需要训练多个模型，这进一步提升了算法的效率.速度最慢的是CL-DDEA，该算法训练对比网络时需要成对数据，实际上其训练数据量会增加到原始数据集的平方，因此对比网络的训练比传统的回归模型消耗更多的时间. 综合优化结果和运行时间来看， DDEA-MKDS是表现最好的算法.

为了验证DDEA-MKDS中使用的策略的有效性， 设计4种变体算法，与原算法进行实验对比. 变体算法的描述如下， 除有说明外，算法的其余策略和参数与DDEA-MKDS保持一致.

DDEA-MKDS(h/n):不进行隐含层节点数寻优，节点数等于离线数据量.

DDEA-RBFN(h):不添加合成数据.

DDEA-MKDS(g):不使用轮盘赌法，选择合成数据时只选择不确定度最低的一半数据.

DDEA-RBFN:无任何特殊策略，仅用离线数据训练RBFN作为代理模型，节点数等于离线数据量.

如表2所示为DDEA-MKDS与各变体算法在Ellipsoid与Rastrigin 2个问题上的优化结果.实验中，所有算法均独立运行20次， 离线数据量为15个，问题维度为10、30、50、100. 实验结果为均值±标准差的形式，且经过Wilcoxon匹配对符号秩检验，+/≈/−分别表示DDEA-MKDS在该实例上显著优于/无显著差异于/显著差于变体算法.

从表2可以看出，DDEA-MKDS在全部8个实例上都大幅优于所有的变体算法.由于DDEA-MKDS(h/n)没有使用隐含层节点数寻优的策略，代理模型容易因小数据陷入过拟合， 性能较差，这证明了隐含层节点数寻优是有效的. DDEA-RBFN(h)与DDEA-RBFN因为数据量匮乏的问题，无法训练更准确的代理模型，尤其是后者， 当不进行任何处理时， 仅依靠单个RBFN完全无法应对小数据的情况，表现最差， 说明DDEA-MKDS中设计的数据合成策略能够显著增强算法的表现. 与原算法相比， DDEA-MKDS(g)仅选择了不确定度较低的数据加入离线数据集，这会导致代理模型的泛化能力变差， 因此表现不佳， 证明原算法中进行轮盘赌选择使所有伪标签数据均有机会被选择的策略是有效的.

如图5所示为DDEA-MKDS与变体算法在所有问题上的平均运行时间. 其中DDEA-MKDS、DDEA-RBFN(h)与DDEA-MKDS(g)使用隐含层节点数寻优的策略，代理模型的结构被简化，节省的训练时间多于进行隐含层节点数寻优的时间，因此这3种算法的运行时间短于其他算法. 与不进行数据合成及不使用轮盘赌选择法的DDEA-RBFN(h)和DDEA-MKDS(g)相比，DDEA-MKDS的运行时间没有明显差异，说明这2种策略不会消耗太多时间，策略的设计是合理的.

DDEA-MKDS中用于数据合成的RBFN使用了3个不同的核函数， 对于具体该如何进行核函数的选择，目前尚无系统的研究. 设计相关实验，分析核函数的选择对算法性能的影响.

由于在DDEA-MKDS中， 算法根据不同模型预测值的标准差选择合成数据， 一般认为若数据少于2个，其标准差无统计学意义，因此核函数的数量应至少为3. 采用最常见的4种径向基核函数的不同组合，具体设置如下.

DDEA-MKDS: gaussian函数、逆多二次函数和逆sigmoid函数.

DDEA-MKDS(k3b): gaussian函数、逆多二次函数和多二次函数.

DDEA-MKDS(k3c): gaussian函数、多二次函数和逆sigmoid函数.

DDEA-MKDS(k3d): 多二次函数、逆多二次函数和逆sigmoid函数.

DDEA-MKDS(k4): gaussian函数、多二次函数、逆多二次函数和逆sigmoid函数.

多二次函数的形式如下：

(10)$ \varPhi ({\text{dist}}) = \sqrt {{\sigma ^2}+{\text{dis}}{{\text{t}}^2}} . $

如表3所示为使用不同核函数时DDEA-MKDS在Ellipsoid与Rastrigin 2个问题上的优化结果， 实验中离线数据量为15个， 在所有情况下算法均独立运行20次，问题维度为10、50、100， 结果以均值±标准差的形式呈现. 从结果来看，表现最好的是原算法中的组合，但优势不明显，总体上不同的核函数组合之间的差距不显著，p为0.050.

如表4所示为使用3个与4个核函数时算法在Ellipsoid与Rastrigin问题上的平均运行时间，在所有测试实例上使用3个核函数时的运行时间均较短.使用4个核函数意味着要多训练一个RBFN，且算法须花费更多的时间来计算标准差和选择数据.综合而言，原算法中的3个核函数组合是最优设置.

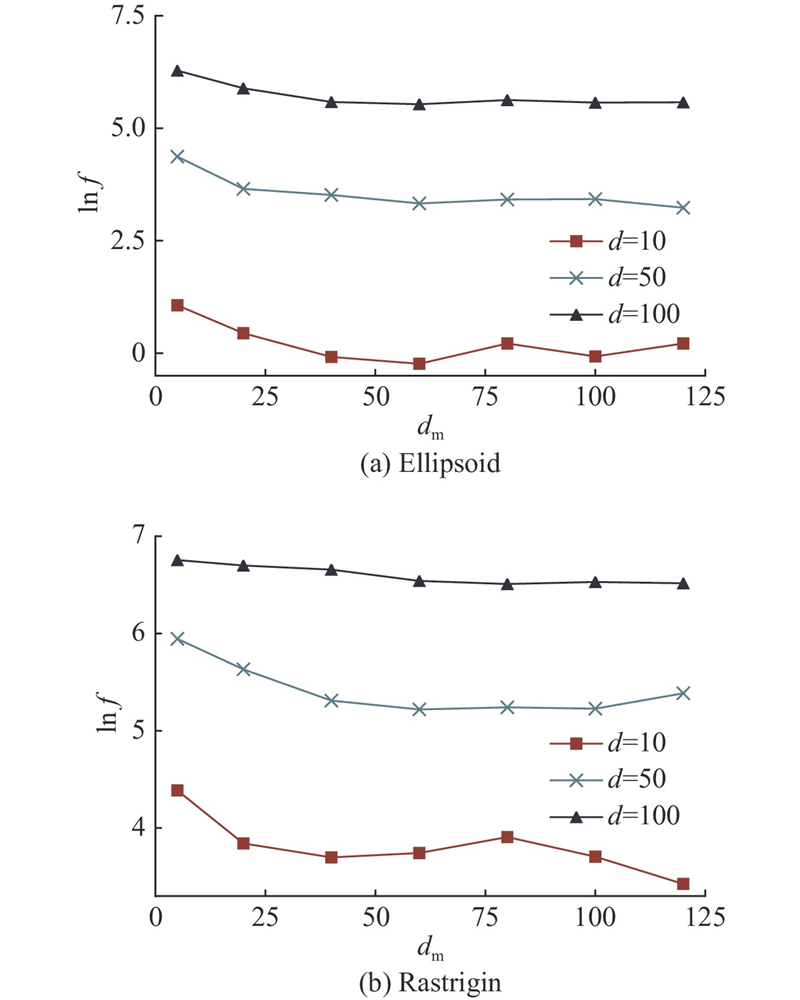
针对DDEA-MKDS中的特有参数d_m进行相应的敏感性分析. 如表5所示为当d_m分别取5、20、40、60、80、100与120时，DDEA-MKDS在10维、50维及100维的Ellipsoid与Rastrigin 2个问题上的优化结果. 如图6所示为优化结果的变化趋势. 在实验中，离线数据量为15个，所有情况下算法均独立运行20次.

从结果来看，当d_m = 60时，DDEA-MKDS的表现最好. d_m越大， 采样得到的无标签数据量越多，最终加入原数据集的伪标签数据也越多. 当d_m较小时，DDEA-MKDS的性能随着d_m的增大而提升，原因是在一定范围内合成数据量的增多会使代理模型的准确率更高. 在d_m超过60后，算法的表现变差，性能的变化不再有趋势性.这是因为伪标签数据的标签是由模型预测得到的，与真实值之间存在一定的差异，过多地加入伪标签数据会对进化过程及代理模型的训练产生误导， 因此d_m的取值要在合理范围内进行选择.

针对离线的DDEA在数据量极少时表现差的问题， 本文提出基于多核数据合成的离线小数据驱动的进化算法DDEA-MKDS. 该算法使用结合经验公式与遍历法的隐含层节点数寻优策略，简化算法中使用的RBFN的结构， 以避免模型因小数据产生过拟合，大幅加快训练速度. 该算法提出基于多核学习的数据合成策略和使用轮盘赌的数据选择方法， 弥补离线数据量的不足. 将DDEA-MKDS与5种代表性的离线DDEA在6个基准测试问题上进行对比，结果表明，本文算法在小数据条件下的优化能力和效率显著优于对比算法.实验部分通过DDEA-MKDS与变体算法的对比，证明了原算法中所提策略的有效性，讨论了核函数的选择对算法性能的影响，对算法中的特有参数进行敏感性分析.未来将针对算法在高维小数据问题中的表现进行改善，提出更有效的数据合成策略， 并将算法用于实际的昂贵优化问题的求解.