[23]
SONG D, TU Y, WANG L, et al Coordinated optimization on energy capture and torque fluctuation of wind turbines via variable weight NMPC with fuzzy regulator
[J]. Applied Energy , 2022 , 312 : 118821
DOI:10.1016/j.apenergy.2022.118821
[本文引用: 1]
[24]
SONG D, LI Z, WANG L, et al Energy capture efficiency enhancement of wind turbines via stochastic model predictive yaw control based on intelligent scenarios generation
[J]. Applied Energy , 2022 , 312 : 118773
DOI:10.1016/j.apenergy.2022.118773
[本文引用: 1]
[26]
DAHLBERG J A, MEDICI D. Potential improvement of wind turbine array efficiency by active wake control (AWC) [C]// European Wind Energy Conference and Exhibition . Madrid: [s.n.], 2003: 65−84.
[本文引用: 1]
[27]
GEBRAAD P M O, TEEUWISSE F W, VAN WINGERDEN J W, et al Wind plant power optimization through yaw control using a parametric model for wake effects: a CFD simulation study
[J]. Wind Energy , 2016 , 19 : 95 - 114
DOI:10.1002/we.1822
[本文引用: 1]
[28]
BARTHELMIE R J, LARSEN G C, FRANDSEN S T, et al Comparison of wake model simulations with offshore wind turbine wake profiles measured by sodar
[J]. Journal of Atmospheric and Oceanic Technology , 2006 , 23 (7 ): 888 - 901
DOI:10.1175/JTECH1886.1
[本文引用: 1]
[29]
BARTHELMIE R J, FRANDSEN S T, NIELSEN M N, et al Modelling and measurements of power losses and turbulence intensity in wind turbine wakes at Middelgrunden offshore wind farm
[J]. Wind Energy , 2007 , 10 : 517 - 528
DOI:10.1002/we.238
[本文引用: 1]
[30]
BLONDEL F, CATHELAIN M An alternative form of the super-Gaussian wind turbine wake model
[J]. Wind Energy Science , 2020 , 5 (3 ): 1225 - 1236
DOI:10.5194/wes-5-1225-2020
[本文引用: 1]
[31]
ZHU X, CHEN Y, XU S, et al Three-dimensional non-uniform full wake characteristics for yawed wind turbine with LiDAR-based experimental verification
[J]. Energy , 2023 , 270 : 126907
DOI:10.1016/j.energy.2023.126907
[本文引用: 2]
[32]
JIMÉNEZ A, CRESPO A, MIGOYA E Application of a LES technique to characterize the wake deflection of a wind turbine in yaw
[J]. Wind Energy , 2009 , 13 : 559 - 572
[本文引用: 1]
[33]
LING Z, ZHAO Z, LIU Y, et al A three-dimensional wave model for wind turbines based on a polynomial distribution of wake velocity
[J]. Ocean Engineering , 2023 , 282 : 115064
DOI:10.1016/j.oceaneng.2023.115064
[本文引用: 1]
[34]
WU Y T, PORTÉ-AGEL F Large-eddy simulation of wind-turbine wakes: evaluation of turbine parametrisations
[J]. Boundary-Layer Meteorology , 2011 , 138 : 345 - 366
DOI:10.1007/s10546-010-9569-x
[本文引用: 1]
[1]
国家能源局. 2023年全国电力工业统计数据[EB/OL]. (2024−01−26) [2024−03−01] . https://www.nea.gov.cn/2024-01/26/c_1310762246.htm.
[本文引用: 1]
[2]
JENSEN N O. A note on wind generator interaction [R]. Roskilde: Risø National Laboratory, 1983.
[本文引用: 2]
[3]
KATIC I, HØJSTRUP J, JENSEN N O. A simple model for cluster efficiency [C]// European Wind Energy Association Conference and Exhibition . Rome: [s.n.], 1986: 407−410.
[本文引用: 1]
[4]
FRANDSEN S, BARTHELMIE R, PRYOR S, et al Analytical modelling of wind speed deficit in large offshore wind farms
[J]. Wind Energy , 2006 , 9 (1/2 ): 39 - 53
[本文引用: 1]
[6]
TIAN L, ZHU W, SHEN W, et al Development and validation of a new two-dimensional wake model for wind turbine wakes
[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2015 , 137 : 90 - 99
DOI:10.1016/j.jweia.2014.12.001
[本文引用: 1]
[7]
GAO X, YANG H, LU L Optimization of wind turbine layout position in a wind farm using a newly-developed two-dimensional wake model
[J]. Applied Energy , 2016 , 174 : 192 - 200
DOI:10.1016/j.apenergy.2016.04.098
[本文引用: 1]
[9]
XIE S, ARCHER C Self-similarity and turbulence characteristics of wind turbine wakes via large-eddy simulation
[J]. Wind Energy , 2015 , 18 : 1815 - 1838
DOI:10.1002/we.1792
[本文引用: 1]
[10]
ABKAR M, PORTÉ-AGEL F Influence of atmospheric stability on wind-turbine wakes: a large-eddy simulation study
[J]. Physics of Fluids , 2015 , 27 : 035104
DOI:10.1063/1.4913695
[本文引用: 1]
[11]
HE R, YANG H, SUN H, et al A novel three-dimensional wake model based on anisotropic Gaussian distribution for wind turbine wakes
[J]. Applied Energy , 2021 , 296 : 117059
DOI:10.1016/j.apenergy.2021.117059
[本文引用: 4]
[12]
WANG T, CAI C, WANG X, et al A new Gaussian analytical wake model validated by wind tunnel experiment and LiDAR field measurements under different turbulent flow
[J]. Energy , 2023 , 271 : 127089
DOI:10.1016/j.energy.2023.127089
[本文引用: 1]
[13]
DHIMAN H S, DEB D, FOLEY A M Bilateral Gaussian wake model formulation for wind farms: a forecasting based approach
[J]. Renewable and Sustainable Energy Reviews , 2020 , 127 : 109873
DOI:10.1016/j.rser.2020.109873
[14]
PARADA L, HERRERA C, FLORES P, et al Wind farm layout optimization using a Gaussian-based wake model
[J]. Renewable Energy , 2017 , 107 : 531 - 541
DOI:10.1016/j.renene.2017.02.017
[15]
GUO N, ZHANG M, LI B, et al Influence of atmospheric stability on wind farm layout optimization based on an improved Gaussian wake model
[J]. Journal of Wind Engineering and Industrial Aerodynamics , 2021 , 211 : 104548
DOI:10.1016/j.jweia.2021.104548
[本文引用: 1]
[16]
田琳琳. 风力机尾流数值模拟及风电场机组布局优化研究[D]. 南京: 南京航空航天大学, 2014: 1–153.
[本文引用: 1]
TIAN Linlin. Numerical simulation of wind turbine wakes and the study of wind farm layout optimization [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014: 1–153.
[本文引用: 1]
[17]
杨祥生, 赵宁, 田琳琳 两种新修正工程模型对多台风力机尾流数值模拟分析
[J]. 太阳能学报 , 2018 , 39 (4 ): 1127 - 1134
[本文引用: 1]
YANG Xiangsheng, ZHAO Ning, TIAN Linlin Numerical simulation analysis of multiple wind turbine wake based on two new modified engineering models
[J]. Acta Energiae Solaris Sinica , 2018 , 39 (4 ): 1127 - 1134
[本文引用: 1]
[18]
SCHREIBER J, BALBAA A, BOTTASSO C L Brief communication: a double-Gaussian wake model
[J]. Wind Energy Science , 2020 , 5 (1 ): 237 - 244
DOI:10.5194/wes-5-237-2020
[本文引用: 1]
[20]
AINSLIE J F. Development of an eddy viscosity model for wind turbine wakes [C]// 7th BWEA Wind Energy Conference . Oxford: [s.n.], 1985: 61−66.
[本文引用: 1]
[21]
MAKRIDIS A. Modelling of wind turbine wakes in complex terrain using computational fluid dynamics [D]. Edinburgh: The University of Edinburgh, 2012: 1−328.
[22]
夏露. 基于二维尾流模型的风电场布局优化研究[D]. 保定: 华北电力大学, 2018: 1−45.
[本文引用: 1]
XIA Lu. Research on wind farm layout optimization based on 2D wake models [D]. Baoding: North China Electric Power University, 2018: 1−45.
[本文引用: 1]
[35]
BASTANKHAH M, PORTÉ-AGEL F Experimental and theoretical study of wind turbine wakes in yawed conditions
[J]. Journal of Fluid Mechanics , 2016 , 806 : 506 - 541
DOI:10.1017/jfm.2016.595
[本文引用: 1]
[36]
QIAN G W, ISHIHARA T A new analytical wake model for yawed wind turbines
[J]. Energies , 2018 , 11 (3 ): 665
DOI:10.3390/en11030665
[本文引用: 1]
[37]
HE R, DENG X, LI Y, et al Three-dimensional yaw wake model development with validation from wind tunnel experiments
[J]. Energy , 2023 , 282 : 128402
DOI:10.1016/j.energy.2023.128402
[本文引用: 1]
Coordinated optimization on energy capture and torque fluctuation of wind turbines via variable weight NMPC with fuzzy regulator
1
2022
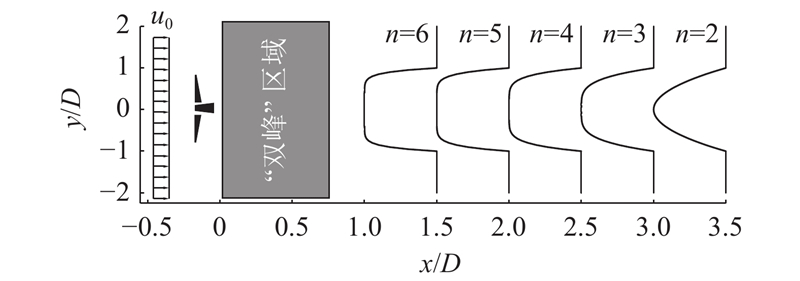
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Energy capture efficiency enhancement of wind turbines via stochastic model predictive yaw control based on intelligent scenarios generation
1
2022
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Effect investigation of yaw on wind turbine performance based on SCADA data
1
2018
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
1
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Wind plant power optimization through yaw control using a parametric model for wake effects: a CFD simulation study
1
2016
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Comparison of wake model simulations with offshore wind turbine wake profiles measured by sodar
1
2006
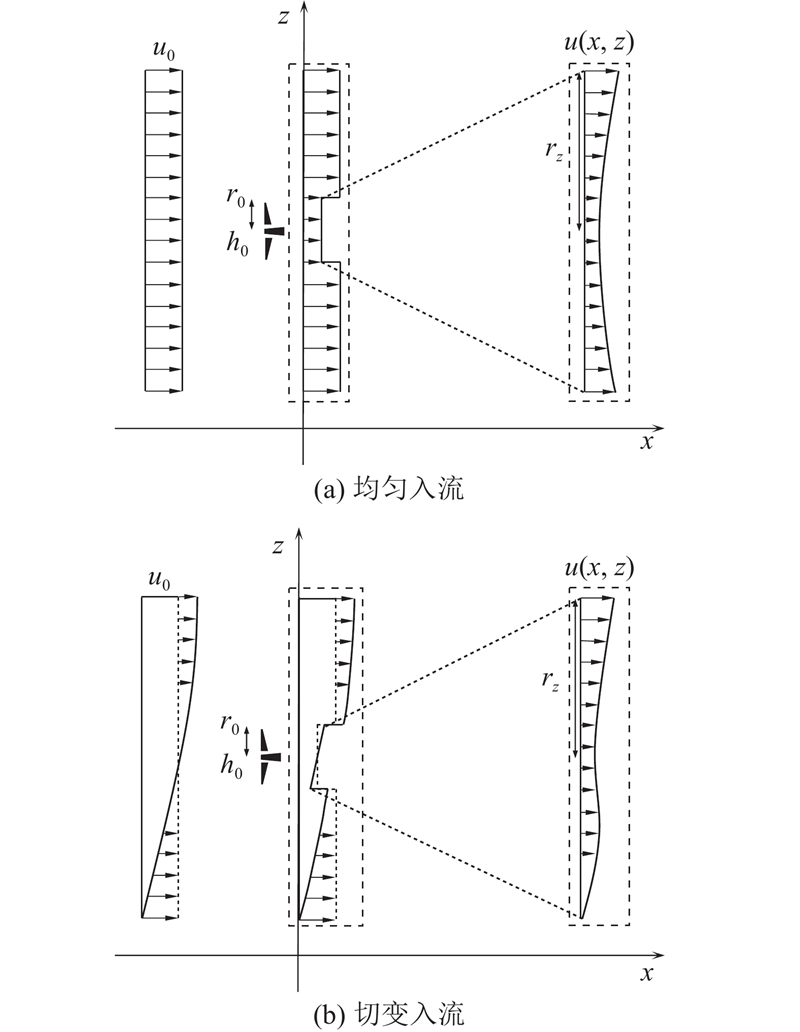
... 式中:u* 为Jensen模型计算得到的坐标(x , z )处的风速. u 0 k 为尾流半径增长率,当地表粗糙度已知时,k =0.5/ln (h 0 /z 0 );也可以参照经验,陆上风机取k =0.075[28 ] ,海上风机取k =0.04或0.05[29 ] . r 0 C T 为风力机推力系数. a 为风机轴向诱导因子,可由推力系数计算得到a =[1−(1−C T cosβ )1/2 ]/2;其中β 为偏航角,当来流方向与风轮平面垂直时,cosβ =1. x 为计算位置的相对坐标,Jensen模型为一维尾流模型,故只需要提供x 的值. r z z 方向的尾流影响半径. 联立式(2)~式(4),求解得到 ...
Modelling and measurements of power losses and turbulence intensity in wind turbine wakes at Middelgrunden offshore wind farm
1
2007
... 式中:u* 为Jensen模型计算得到的坐标(x , z )处的风速. u 0 k 为尾流半径增长率,当地表粗糙度已知时,k =0.5/ln (h 0 /z 0 );也可以参照经验,陆上风机取k =0.075[28 ] ,海上风机取k =0.04或0.05[29 ] . r 0 C T 为风力机推力系数. a 为风机轴向诱导因子,可由推力系数计算得到a =[1−(1−C T cosβ )1/2 ]/2;其中β 为偏航角,当来流方向与风轮平面垂直时,cosβ =1. x 为计算位置的相对坐标,Jensen模型为一维尾流模型,故只需要提供x 的值. r z z 方向的尾流影响半径. 联立式(2)~式(4),求解得到 ...
An alternative form of the super-Gaussian wind turbine wake model
1
2020
... 式中:ky 、kz 分别为y 方向、z 方向尾流膨胀系数. 除尾流膨胀系数外,幂指数n 也须标定. 如果在归一化的尾流影响半径上将超高斯函数进行泰勒展开并保留其最大项,可以得到与式(1)相似的表达式,为此令n 与超高斯阶表达式[30 ] 相同:n =C 1 exp(C 2 x )+2,其中C 1 、C 2 分别为尾迹变化系数参数、指数参数. 再令y =0、z =h 0 ,得到轮毂中心下游的风速表达式: ...
Three-dimensional non-uniform full wake characteristics for yawed wind turbine with LiDAR-based experimental verification
2
2023
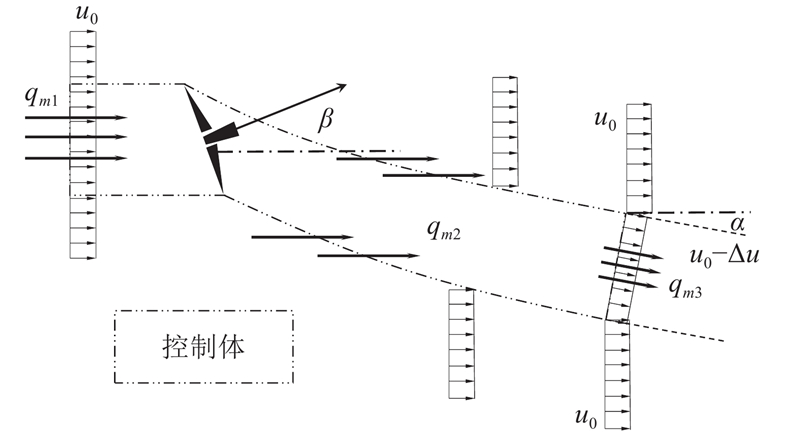
... Jiménez根据偏航工况下风力机尾流控制体的动量、质量守恒方程,推导了风力机偏航时的尾流迹线挠度方程[31 -32 ] ,如图3 所示. 在x ,y 方向对风力机推力进行分解,可以得到 ...
... 式中:k w =(W (k z 2 +k y 2 ))1/2 ,其中W 为经验系数[31 ] . 结合式(14)与式(20),得到考虑偏航的三维风机下游风速表达式: ...
Application of a LES technique to characterize the wake deflection of a wind turbine in yaw
1
2009
... Jiménez根据偏航工况下风力机尾流控制体的动量、质量守恒方程,推导了风力机偏航时的尾流迹线挠度方程[31 -32 ] ,如图3 所示. 在x ,y 方向对风力机推力进行分解,可以得到 ...
A three-dimensional wave model for wind turbines based on a polynomial distribution of wake velocity
1
2023
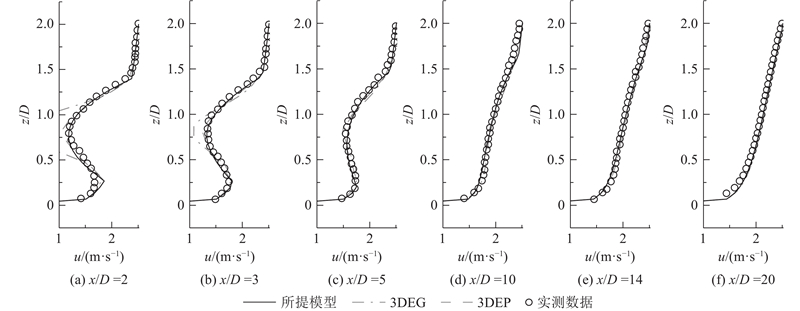
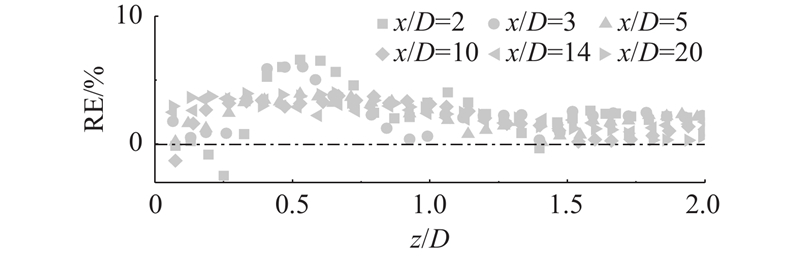
... 采用风洞试验实测数据对所提模型进行垂直入流验证,将三维各向异性多项式函数模型(3DEP)[33 ] 、三维各向异性高斯模型(3DEG)[11 ] 与所提模型进行对比分析. 本研究使用的水平尾流剖面验证数据来自Marchwood工程实验室. Hassan于1989年在Marchwood大气边界层风洞中对水平轴风力发电机尾流速度进行了测量 [8 ] ,该风力机尾流风洞试验将水平轴风力机进行缩尺,几何缩尺比为1∶160,记录单个和多个风力机尾流区域的湍流和平均流速的综合数据. 风洞场地平整,表面粗糙度均匀,粗糙度长度为0.075 m. 真实风力机的直径为43.2 m,轮毂高度为50 m,自由来流风速为5.3 m/s,对应的模型尺寸转子半径为0.27 m,轮毂高度为0.313 m. 本次验证选择转子转速为6.78 r/min,叶尖风速比为2.9的工况. ...
Large-eddy simulation of wind-turbine wakes: evaluation of turbine parametrisations
1
2011
... 垂直尾流剖面验证数据[34 ] 来源于St. Anthony Falls实验室,该试验利用热线法采集微型风力机尾流区域的高分辨率测量数据. 将三叶片的GWS/EP-6030×3转子固定在风力机模型上,与小型直流发电机相连,电机为圆柱状,长0.03 m,直径为0.015 m. 风机下部连接长0.011 8 m,直径为0.005 m的塔筒. 自由来流风速为2.8 m/s,边界层深度为0.46 m. 风机轮毂高度为0.125 m,轮毂高度处的风速为2.2 m/s,风切变幂定律指数为0.15. ...
1
... 截至2023年12月底,中国风电装机容量约为4.4×108 kW,同比增长20.7%[1 ] ,位于世界前列. 风机的布局优劣直接影响风能的利用效率,其中构建高效、准确的风机尾流模型是优化风机布局的关键. 随着计算机技术的发展,计算流体力学(CFD)方法逐渐代替风洞试验成为研究风力机尾流的重要手段,但风力机组的布局优化过程须考虑风机距离和排列方式的变化,CFD和风洞试验难以实现,工业界通常采用简化计算的风机尾流数学模型. ...
2
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
... Jensen模型的表达式[2 ] 为 ...
1
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Analytical modelling of wind speed deficit in large offshore wind farms
1
2006
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
A new analytical model for wind-turbine wakes
1
2014
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Development and validation of a new two-dimensional wake model for wind turbine wakes
1
2015
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Optimization of wind turbine layout position in a wind farm using a newly-developed two-dimensional wake model
1
2016
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Study on an innovative three-dimensional wind turbine wake model
2
2018
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
... 采用风洞试验实测数据对所提模型进行垂直入流验证,将三维各向异性多项式函数模型(3DEP)[33 ] 、三维各向异性高斯模型(3DEG)[11 ] 与所提模型进行对比分析. 本研究使用的水平尾流剖面验证数据来自Marchwood工程实验室. Hassan于1989年在Marchwood大气边界层风洞中对水平轴风力发电机尾流速度进行了测量 [8 ] ,该风力机尾流风洞试验将水平轴风力机进行缩尺,几何缩尺比为1∶160,记录单个和多个风力机尾流区域的湍流和平均流速的综合数据. 风洞场地平整,表面粗糙度均匀,粗糙度长度为0.075 m. 真实风力机的直径为43.2 m,轮毂高度为50 m,自由来流风速为5.3 m/s,对应的模型尺寸转子半径为0.27 m,轮毂高度为0.313 m. 本次验证选择转子转速为6.78 r/min,叶尖风速比为2.9的工况. ...
Self-similarity and turbulence characteristics of wind turbine wakes via large-eddy simulation
1
2015
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Influence of atmospheric stability on wind-turbine wakes: a large-eddy simulation study
1
2015
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
A novel three-dimensional wake model based on anisotropic Gaussian distribution for wind turbine wakes
4
2021
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
... 在风机尾流影响区域内,影响半径在yz 平面存在各向异性,原因是水平方向的环境湍流度大于垂直方向,加速了尾流与自由流动的混合过程,促进了尾流的恢复[11 ] . 参考各向异性尾流膨胀系数经验表达式[11 ] : ...
... [11 ]: ...
... 采用风洞试验实测数据对所提模型进行垂直入流验证,将三维各向异性多项式函数模型(3DEP)[33 ] 、三维各向异性高斯模型(3DEG)[11 ] 与所提模型进行对比分析. 本研究使用的水平尾流剖面验证数据来自Marchwood工程实验室. Hassan于1989年在Marchwood大气边界层风洞中对水平轴风力发电机尾流速度进行了测量 [8 ] ,该风力机尾流风洞试验将水平轴风力机进行缩尺,几何缩尺比为1∶160,记录单个和多个风力机尾流区域的湍流和平均流速的综合数据. 风洞场地平整,表面粗糙度均匀,粗糙度长度为0.075 m. 真实风力机的直径为43.2 m,轮毂高度为50 m,自由来流风速为5.3 m/s,对应的模型尺寸转子半径为0.27 m,轮毂高度为0.313 m. 本次验证选择转子转速为6.78 r/min,叶尖风速比为2.9的工况. ...
A new Gaussian analytical wake model validated by wind tunnel experiment and LiDAR field measurements under different turbulent flow
1
2023
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Bilateral Gaussian wake model formulation for wind farms: a forecasting based approach
0
2020
Wind farm layout optimization using a Gaussian-based wake model
0
2017
Influence of atmospheric stability on wind farm layout optimization based on an improved Gaussian wake model
1
2021
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
1
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
1
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
两种新修正工程模型对多台风力机尾流数值模拟分析
1
2018
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
两种新修正工程模型对多台风力机尾流数值模拟分析
1
2018
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Brief communication: a double-Gaussian wake model
1
2020
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Advancement of an analytical double-Gaussian full wind turbine wake model
1
2021
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
1
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
1
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
1
... Jensen模型[2 ] 是被广泛使用的一维尾流模型,该模型假定风速亏损在水平方向上保持恒定,仅与纵向垂直距离相关,质量守恒定律用于求解具体的风速亏损值;在尾流半径扩张方面,Jensen认为扩张率是线性的,尾流膨胀系数仅与来流的环境湍流相关. Jensen模型高效的计算效率和广泛的适用性为后续的二维、三维尾流模型研究打下了基础. Jensen模型的目的不是精确模拟风力机的尾流风速分布,而是借对风机下游能量的描述辅助工作人员开展风电场的微观选址工作[3 ] . 在尾流影响半径方面,Frandsen等[4 ] 假定尾流扩展为非线性,但Bastankhah等[5 ] 指出,Frandsen模型与大涡模拟(large eddy simulation, LES)测得的尾流扩张曲线不符. Tian等[6 -7 ] 分别根据实验数据和CFD模拟提出依赖湍流强度计算尾流扩张率的经验公式,在二维尾流模型中这种经验算法被广泛使用. Sun等[8 ] 将Jensen-Gaussian模型推广到三维,但假定风机后的尾流区域为一圆域,即在垂直于尾流迹线的平面上尾流影响半径各向同性,这与Xie等[9 -10 ] 的LES模拟结果不符. He等[11 ] 将各向异性的尾流影响半径引入三维尾流模型,与实测数据进行对比后证实,模型在远尾流垂向和水平向同时取得了较好的模拟效果. 在风亏分布的拟合方面,Gaussian模型由Jensen模型发展而来,将风速亏损修正为高斯函数分布[12 -15 ] ,这一结论与实测结果更为契合. 不少学者利用不同的函数修正Jensen的风速亏损形式,如田琳琳[16 ] 提出基于余弦函数的尾流模型,杨祥生等[17 ] 利用二次多项式进行风机尾流建模. 如果在归一化的尾流影响半径上将余弦函数与高斯函数进行泰勒展开,它们的基函数相同,仅系数矩阵不同. 从这一角度来说,高斯函数、余弦函数以及二次多项式函数没有本质区别. Schreiber等[18 -19 ] 分别提出区别于高斯函数、二次多项式的风速亏损函数,利用双高斯函数的偏移完成风速亏损函数从双峰到单峰的过渡. 在极近尾流区域(不超过风轮平面2倍直径),叶尖涡清晰而集中,双高斯函数在近场尾流区域具有很好的适用性,但是叶尖涡结构往往会迅速被湍流运动耗散,且在湍流混合发生之前迅速变为平滑的顶帽形式[20 -22 ] ,对于风机布局问题,不必考虑如此近距离的尾流风速亏损. 在远尾流区域,高斯函数、二次多项式函数具有比较好的拟合效果(大于风轮平面5倍直径),但在实际的风电场项目中,风机之间的距离可能较小,许多风机间距小于5倍风机直径,将使以高斯函数、二次多项式为风亏函数的尾流模型失效. 真实流场的来流风向不断变化,风机会根据实测风向进行转向以获得最大的捕风面积[23 -24 ] . 与常见尾流模型假设的垂直入流情况不同,由于实测数据和风机转向的滞后,在实际风电场运行中的风机常处于偏航工作状态[25 ] . 除了主动寻求最大的捕风面积外,偏航控制被认为是很有前景的风电场功率优化方法[26 -27 ] ,主要通过上游风机主动偏航来诱导尾流侧动量,使得尾流区域偏移,下游风机避开上游风机的尾流影响区域. ...
Experimental and theoretical study of wind turbine wakes in yawed conditions
1
2016
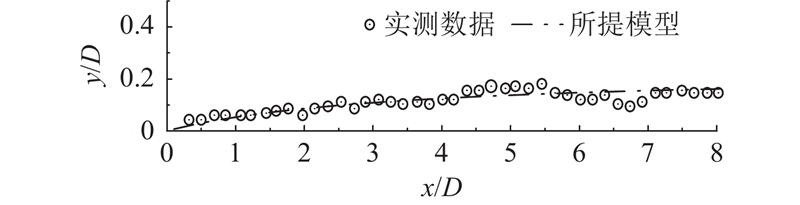
... 选择Bastankhah等[35 ] 由偏航尾迹实验获得的数据集开展所提模型的泛化能力与准确性验证实验,该数据集利用高分辨率立体粒子图像测速系统精确测量风机下游的详细流场信息. 本实验在EPFL WIRE大气边界层风洞中进行,试验段高2 m,宽2.6 m,长28 m;微型风机直径为0.15 m,放置高度为0.125 m;来流风切变指数为0.178,湍流强度7.5%,轮毂高度处的来流风为4.88 m/s. ...
A new analytical wake model for yawed wind turbines
1
2018
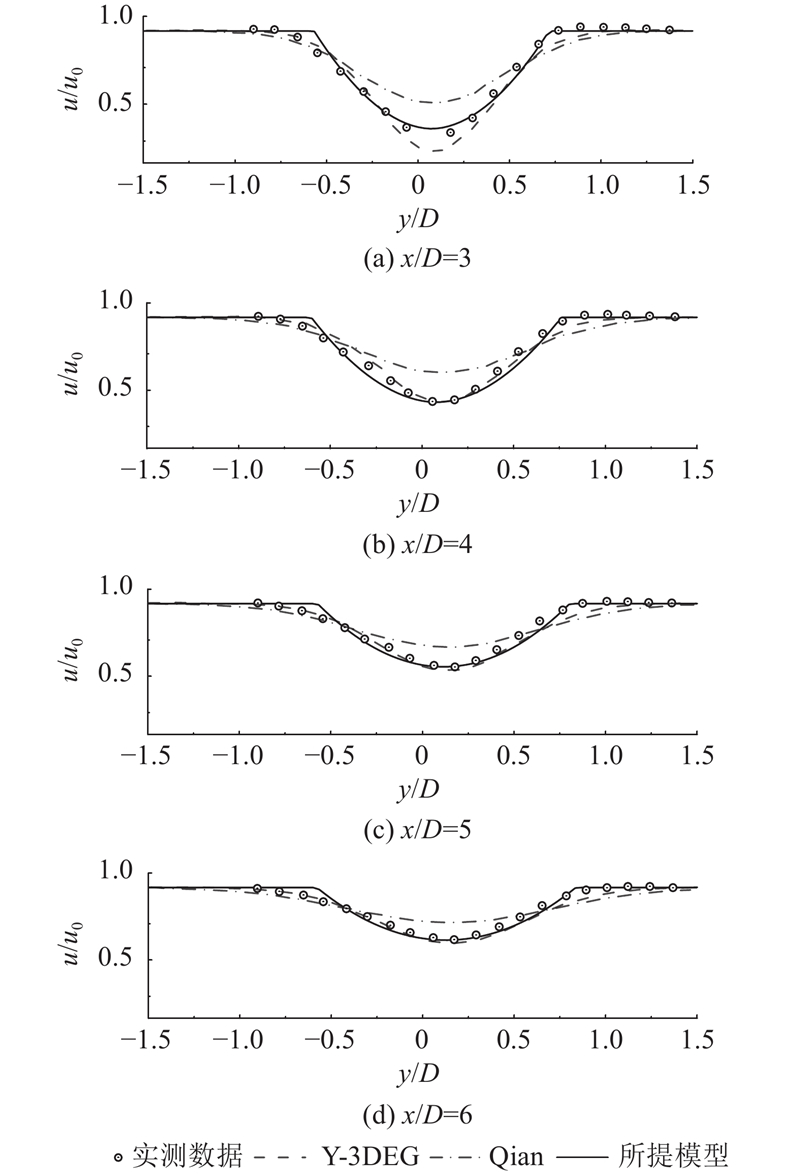
... 选择如图10 所示的剖面进行风速分布验证,由于3DEP和3DEG没有考虑偏航的影响,验证实验中由2种著名的偏航尾流模型:Qian模型[36 ] 与Y-3DEG模型[37 ] 替代. 可以看出,3种模型对尾迹中心的预测效果均较好,但尾迹形状和数值的拟合结果存在差异. Qian模型没有考虑尾流影响区域的各向异性,不准确的尾流影响半径将影响风亏分布函数最大值的计算,Qian模型在尾迹中心位置显著高估了风速大小,但低估了其他区域的风速大小,随着与风力机距离的增加,这种误差在逐渐减小. Y-3DEG模型对风速分布的描述相对准确,但在x =3D 剖面仍然存在高斯分布函数拟合近尾流时的误差,这与3DEG模型在近尾流区域拟合的效果类似. 此外,Qian模型、Y-3DEG模型都将高斯函数作为风亏分布函数,在高斯函数的边界处,其导数趋向零,故在尾流影响区域的边界处不会出现突变情况. 由于利用幂函数的指数变化,所提模型仍然具有近尾流拟合的优势,在x =3D 剖面的描述效果显著优于其他2种模型,但在尾流影响区域的左侧边界,所提模型仍然存在边界拟合不准的问题,不能实现与Qian模型、Y-3DEG模型这2种基于高斯函数的模型类似的平滑过渡. 在尾流影响区域的右侧边界,所提模型比这2种基于高斯函数的模型描述得更好. 从实测数据的分布可以观察到,当风机存在偏航角时,偏转角的对侧边界风速亏损发生更加突然,这与所提模型的幂函数假定类似. ...
Three-dimensional yaw wake model development with validation from wind tunnel experiments
1
2023
... 选择如图10 所示的剖面进行风速分布验证,由于3DEP和3DEG没有考虑偏航的影响,验证实验中由2种著名的偏航尾流模型:Qian模型[36 ] 与Y-3DEG模型[37 ] 替代. 可以看出,3种模型对尾迹中心的预测效果均较好,但尾迹形状和数值的拟合结果存在差异. Qian模型没有考虑尾流影响区域的各向异性,不准确的尾流影响半径将影响风亏分布函数最大值的计算,Qian模型在尾迹中心位置显著高估了风速大小,但低估了其他区域的风速大小,随着与风力机距离的增加,这种误差在逐渐减小. Y-3DEG模型对风速分布的描述相对准确,但在x =3D 剖面仍然存在高斯分布函数拟合近尾流时的误差,这与3DEG模型在近尾流区域拟合的效果类似. 此外,Qian模型、Y-3DEG模型都将高斯函数作为风亏分布函数,在高斯函数的边界处,其导数趋向零,故在尾流影响区域的边界处不会出现突变情况. 由于利用幂函数的指数变化,所提模型仍然具有近尾流拟合的优势,在x =3D 剖面的描述效果显著优于其他2种模型,但在尾流影响区域的左侧边界,所提模型仍然存在边界拟合不准的问题,不能实现与Qian模型、Y-3DEG模型这2种基于高斯函数的模型类似的平滑过渡. 在尾流影响区域的右侧边界,所提模型比这2种基于高斯函数的模型描述得更好. 从实测数据的分布可以观察到,当风机存在偏航角时,偏转角的对侧边界风速亏损发生更加突然,这与所提模型的幂函数假定类似. ...