新能源汽车爆发式增长使电动汽车的充电问题成为研究热点，无线电能传输（wireless power transfer, WPT）技术作为安全的充电方式受到广泛关注^[1-2]. 磁耦合谐振WPT技术以能量谐振耦合原理通过高频电磁场进行能量传递，实现将能量由一次侧无线传输至二次侧^[3-4]. 该技术传输距离较远、灵活性较高，能够实现同谐振频率设备间能量高效传输，适用于电动汽车的无线充电. 双向无线电能传输（bidirectional wireless power transfer, BD-WPT）系统将电动汽车与电网相结合，实现能量交互，有利于电网的“削峰填谷”，改善电能质量，促进能量的灵活流动和能源高效利用^[5-6]. 有关磁耦合谐振WPT技术的研究集中在基于整数阶的数学模型上，采用整数阶微积分分析电路存在不精确性，基于分数阶微积分的建模方法能够准确地分析分数阶电路系统的特性^[7]. 实际生活中的电感和电容均是分数阶的，相比整数阶元件增加了电感阶数和电容阶数，因此分数阶元件构成的电路具有与传统整数阶电路不同的特性. 将阶数大于1的电容应用到BD-WPT系统中，分数阶电容负电阻分量可以抵消耦合线圈的内阻，提高系统的传输功率和传输效率^[8-9].

磁耦合谐振线圈和谐振补偿网络是BD-WPT系统的关键组成部分，直接影响系统输出功率和传输效率. 谢文燕等^[10-11]提出一系列磁耦合线圈类型，其中平面圆形线圈便于封装且电能传输效果较好^[12]. 增加线圈间的传输距离会降低耦合系数，导致传输效率下降，须进行线圈参数和谐振补偿网络的优化设计^[13]. 马涛等^[14-16]将圆形线圈的半径、匝数、距离等参数作为设计变量，优化了系统的输出功率、传输效率和线圈功率密度. 刘旭等^[17-18]通过改变谐振补偿网络中补偿电容和电感的参数，在系统输出功率范围内有效提升了传输效率. 由于分数阶磁耦合谐振BD-WPT系统中参数多，各个参数对系统影响程度不同，须进行参数评估. 常用的指标评价方法有层次分析法、加权因素比较法、灰色关联度分析（grey relation analysis, GRA）等^[19-20]. 靳夏^[21]采用GRA建立移动式感应耦合电能传输（inductively coupled power transmission, ICPT）系统综合指标评价体系，对系统运行影响大的参数进行优化. 向利娟等^[22]针对感应电能传输（IPT）系统电磁耦合机构设计的非全局性问题，提出电磁耦合机构的综合性能评判指标体系，得到具体、直观的数值评价结果，为耦合机构类型的确定提供了参考.

分数阶磁耦合谐振BD-WPT系统运行须同时考虑电动汽车的额定充电功率、系统传输效率和线圈功率密度等因素，系统部分参数存在冲突，系统综合性能最佳可利用多目标优化算法实现^[23-24]. 杨云虎等^[25-26]采用遗传算法和约束型粒子群算法实现对系统效率与输出功率的优化. 针对动态WPT中互感波动问题，李阳等^[27]采用多目标粒子群优化（multi-objective particle swarm optimization，MOPSO）算法调整频率和谐振补偿电容，实现了传输功率和线圈传输效率优化. 在优化分数阶磁耦合谐振BD-WPT系统参数过程中，须考虑多个系统参数对传输功率、传输效率和线圈功率密度的影响，多参数的全局优化须基于合适的指标评价体系. 已有研究多基于低阶谐振补偿拓扑来优化系统传输功率和效率，对于高阶谐振拓扑的传输效率和线圈功率密度的优化研究鲜少. 针对上述问题，本研究以提升系统传输效率和线圈功率密度为优化目标，基于GRA对系统各个参数的影响大小进行评估，选出对系统运行影响大的参数，采用MOPSO算法实现多个参数的优化设计，通过Matlab/Simulink仿真验证优化方法的可行性.

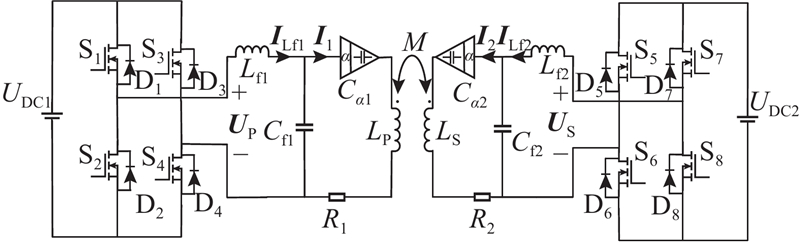
分数阶磁耦合谐振BD-WPT系统结构如图1所示. 图中，U_DC1、U_DC2分别为系统原、副边侧的直流电压源；开关管S₁~S₄、S₅~S₈分别组成系统原、副边的单相全桥逆变/整流电路；D₁~D₈分别为S₁~S₈的反向并联二极管；U_P、U_S分别为原、副边单相全桥变换电路输出电压的基波分量；原、副边采用相同的LCC型谐振补偿电路. 2种系统工况分别为正向电能传输工况和反向电能传输工况. 电能从原边侧传输到副边侧为正向电能传输工况，原边侧电源充当“源”，副边侧电源充当“荷”，此时原边侧单相全桥电路工作在高频逆变状态，副边侧单相全桥电路工作在高频可控整流状态. 电能从副边侧传输到原边侧为反向电能传输工况，副边侧电源作为“源”，原边侧电源作为“荷”，此时副边侧单相全桥电路工作在高频逆变状态，原边侧单相全桥电路工作在高频可控整流状态.

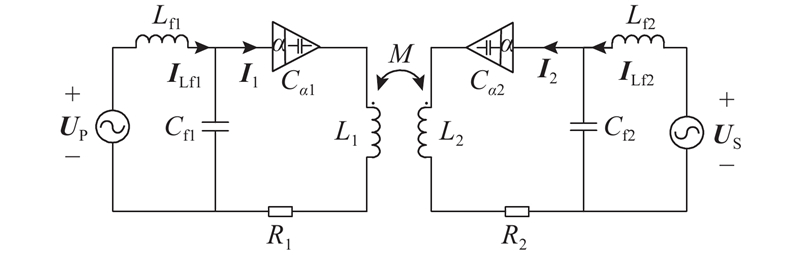
LCC型谐振补偿电路具有带通滤波特性，因此忽略系统的高次谐波成分，采用基波近似等效对系统进行分析. 分数阶磁耦合谐振BD-WPT系统的等效电路如图2所示. 图中，I_Lf1、I_Lf2分别为原、副边单相全桥变换电路输出电流的基波分量；L_f1、C_f1为原边补偿电感和补偿电容，L_f2、C_f2为副边补偿电感和补偿电容，C_α1、C_α2分别为原、副边谐振补偿电路的分数阶电容，α为分数阶电容的阶数；L₁、L₂分别为原、副边耦合线圈的自感，R₁、R₂分别为原、副边耦合线圈的等效内阻，M为原、副边耦合线圈之间的互感. 根据基尔霍夫电压定律，分析分数阶磁耦合谐振BD-WPT系统正向电能传输工况，得到系统等效电路的基本方程：

(1)$ \left. {\begin{array}{*{20}{l}} {{{{\boldsymbol{U}}}_{\text{P}}} = {\text{j}}\omega {L_{{\text{f}}1}}{{{\boldsymbol{I}}}_{{\text{Lf}}1}}+\left( {{R_1}+{\text{j}}\omega {L_1}+\dfrac{1}{{{{({\text{j}}\omega )}^\alpha }{C_{\alpha 1}}}}} \right){{{\boldsymbol{I}}}_1}+{\text{j}}\omega M{{{\boldsymbol{I}}}_2},} \\ {\left( {{R_1}+{\text{j}}\omega {L_1} + \dfrac{1}{{{{({\text{j}}\omega )}^\alpha }{C_{\alpha 1}}}}} \right){{{\boldsymbol{I}}}_1}+{\text{j}}\omega M{{{\boldsymbol{I}}}_2} = \dfrac{1}{{{\text{j}}\omega {C_{{\text{f}}1}}}}\left( {{{{\boldsymbol{I}}}_{{\text{Lf}}1}} - {{{\boldsymbol{I}}}_1}} \right),} \\ {{{{\boldsymbol{U}}}_{\text{S}}} = {\text{j}}\omega {L_{{\text{f}}2}}{{{\boldsymbol{I}}}_{{\text{Lf}}2}}+\left( {{R_2}+{\text{j}}\omega {L_2}+\dfrac{1}{{{{({\text{j}}\omega )}^\alpha }{C_{\alpha 2}}}}} \right){{{\boldsymbol{I}}}_2}+{\text{j}}\omega M{{{\boldsymbol{I}}}_1},} \\ {\left( {{R_2}+{\text{j}}\omega {L_2} + \dfrac{1}{{{{({\text{j}}\omega )}^\alpha }{C_{\alpha 2}}}}} \right){{{\boldsymbol{I}}}_2}+{\text{j}}\omega M{{{\boldsymbol{I}}}_1} = \dfrac{1}{{{\text{j}}\omega {C_{{\text{f}}2}}}}\left( {{{{\boldsymbol{I}}}_{{\text{Lf}}2}} - {{{\boldsymbol{I}}}_2}} \right).} \end{array}} \right\} $

分数阶电容的阻抗表达式为

(2)$ \begin{split} {Z_C}({\text{j}}\omega ) =& \frac{1}{{{{({\text{j}}\omega )}^\alpha }{C_\alpha }}} = \\& \frac{1}{{{\omega ^\alpha }{C_\alpha }}}\cos \left( {\frac{{\text{π}}}{2}\alpha } \right) - {\text{j}}\frac{1}{{{\omega ^\alpha }{C_\alpha }}}\sin \left( {\frac{{\text{π}}}{{\text{2}}}\alpha } \right). \end{split} $

将分数阶电容等效为整数阶电容C_eq和电阻R_Ceq的串联. 当α<1时，R_Ceq>0，分数阶电容吸收能量；当α>1时，R_Ceq<0，分数阶电容发出能量^[9]. 当分数阶电容的负电阻分量与耦合线圈内阻抵消时，使原、副边侧谐振电路相当于无损电路：

(3)$ {R_1}+\frac{1}{{{\omega ^\alpha }{C_{\alpha 1}}}}\cos \left(\frac{{\text{π}}}{2}\alpha \right) = {R_2}+\frac{1}{{{\omega ^\alpha }{C_{\alpha 2}}}}\cos \left(\frac{{\text{π}}}{2}\alpha \right) = 0. $

其中ω为系统谐振角频率. 系统工作在谐振状态的条件为

(4)$ \left. {\begin{array}{*{20}{c}} \begin{gathered} \omega = {\left[ {\frac{{\sin \;(0.5{\text{π }}\alpha )}}{{\left( {{L_1} - {L_{{\text{f}}1}}} \right){C_{\alpha 1}}}}} \right]^{\frac{1}{{\alpha +1}}}} = \frac{1}{{\sqrt {{C_{{\text{f}}1}}{L_{{\text{f}}1}}} }}, \\ \omega {L_1} - \dfrac{1}{{{\omega ^\alpha }{C_{\alpha 1}}}}\sin \left(\dfrac{{\text{π}}}{2}\alpha \right) = \dfrac{1}{{\omega {C_{{\text{f}}1}}}} = \omega {L_{{\text{f}}1}}, \\ \end{gathered} \\ {\omega {L_2} - \dfrac{1}{{{\omega ^\alpha }{C_{\alpha 2}}}}\sin \left(\dfrac{{\text{π}}}{2}\alpha \right) = \dfrac{1}{{\omega {C_{{\text{f2}}}}}} = \omega {L_{{\text{f2}}}}.} \end{array}} \right\} $

将式(2)~式(4)代入式(1)，求解得到

(5)$ \left. {\begin{array}{*{20}{l}} {{{{\boldsymbol{I}}}_1} = \dfrac{{{{{\boldsymbol{U}}}_{\text{P}}}}}{{{\text{j}}\omega {L_{{\text{f}}1}}}},} \; {{{\boldsymbol{I}}}_2} = \dfrac{{{{{\boldsymbol{U}}}_{\text{S}}}}}{{{\text{j}}\omega {L_{{\text{f}}2}}}}, \\ {{{{\boldsymbol{I}}}_{{\text{Lf1}}}} = {\text{j}}\dfrac{M}{{\omega {L_{{\text{f}}1}}{L_{{\text{f}}2}}}}{{{\boldsymbol{U}}}_{\text{S}}},} \\ {{{{\boldsymbol{I}}}_{{\text{Lf2}}}} = {\text{j}}\dfrac{M}{{\omega {L_{{\text{f}}1}}{L_{{\text{f}}2}}}}{{{\boldsymbol{U}}}_{\text{P}}}.} \end{array}} \right\} $

系统传输功率和效率的表达式为

(6)$ {P_{\text{S}}} = {{\mathrm{Re}}} \left( {{{{\boldsymbol{U}}}_{\text{S}}}{{\boldsymbol{I}}}_{{\text{Lf2}}}^{\text{*}}} \right) = \frac{M}{{\omega {L_{{\text{f}}1}}{L_{{\text{f}}2}}}}{U_{\text{P}}}{U_{\text{S}}}\sin \theta . $

式中：I_Lf2^*为电流I_Lf2的共轭，θ为系统原、副边侧H桥控制信号的外移相角.

(7)$ \begin{split}& \eta = \frac{{{P_{\text{S}}}}}{{{P_{\text{S}}}+{P_{{\text{R1}}}}+{P_{{\text{R2}}}}}} = \frac{{{P_{\text{S}}}}}{{{P_{\text{S}}}+I_1^2{R_1}+I_2^2{R_2}}} = \\&\qquad \dfrac{{\dfrac{M}{{\omega {L_{{\text{f}}1}}{L_{{\text{f}}2}}}}{U_{\text{P}}}{U_{\text{S}}}\sin \theta }}{{\dfrac{M}{{\omega {L_{{\text{f}}1}}{L_{{\text{f}}2}}}}{U_{\text{P}}}{U_{\text{S}}}\sin \theta +\dfrac{{U_{\text{P}}^2}}{{{\omega ^2}L_{{\text{f1}}}^2}}{R_1}+\dfrac{{U_{\text{S}}^2}}{{{\omega ^2}L_{{\text{f2}}}^2}}{R_2}}}. \end{split} $

可以看出，系统的传输特性受ω、L_f1、L_f2、M、R₁、R₂的影响. 优化系统传输特性须求解耦合线圈自感、互感、等效内阻等解析表达式，为后续优化模型的建立提供参考.

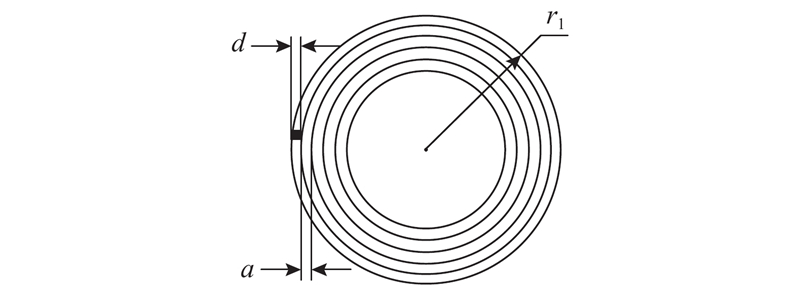
平面圆形螺线圈易于封装且电能传输效果好，是构建磁耦合谐振WPT系统的首选形状. 如图3所示为非紧密缠绕的平面圆形螺线圈，其中d为导线直径，r₁为线圈外径，N为匝数，a为匝间间隙. 为了方便计算推导，将平面圆形螺线圈等效为N个半径不同且各匝数具有一定间隙的同心圆形线圈.

将非紧密缠绕的平面圆形螺线圈的自感看作是线圈内部各单匝圆形线圈的自感与其内部任意两匝线圈之间的互感之和. 设N匝线圈中第i匝线圈的自感为

(8)$ {L_i} = {\mu _0}{r_i}\left[\ln \left({{16{r_i}}}/{d}\right) - 1.75\right]. $

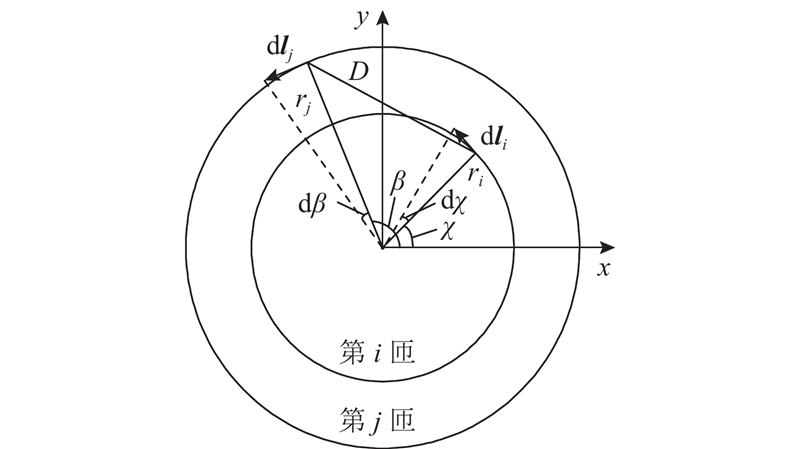
如图4所示，令N匝线圈中第i匝线圈和第j匝线圈之间的互感为M_ij，r_i、r_j为第i匝和第j匝线圈的半径，dI_il_i、dI_jl_j分别为2匝线圈上的电流源矢量. 2匝线圈的互感与线圈中的电流无关，因此忽略电流的影响，将内外圈圆环中的电流矢量元简化成矢量元dl_i、dl_j；2个矢量元之间的距离为D，2个矢量元和圆心的连线与x轴的夹角分别为χ、β；矢量元对应的圆弧夹角分别为dχ、dβ.

(9)$ {\text{d}}{{{\boldsymbol{l}}}_i} = {r_i} \cdot {\text{d}}\chi \cdot {{{\boldsymbol{l}}}_i}, $

(10)$ {\text{d}}{{{\boldsymbol{l}}}_j} = {r_j} \cdot {\text{d}}\beta \cdot {{{\boldsymbol{l}}}_j}. $

(11)$ D = \sqrt {r_i^2+r_j^2 - 2{r_i}{r_j} {\mathrm{cos}}\; (\beta - \chi )} . $

式中：l_i、l_j为矢量元dl_i、dl_j的单位向量，l_i· l_j= cos (β−χ). 根据诺依曼公式得到平面同心圆环载流线圈的互感为

(12)$ {M_{ij}} = \frac{{{\mu _0}}}{{{{4{\text{π}} }}}}\mathop \int \nolimits_0^{{{2{\text{π}} }}} \mathop \int \nolimits_0^{{{2{\text{π}} }}} \frac{{{\text{d}}{{\boldsymbol{l}}_i} \cdot {\text{d}}{{\boldsymbol{l}}_j}}}{D}. $

非紧密绕制平面圆形螺线圈的自感为

(13)$ L=\underset{i}{\overset{N}{\mathop \sum }}\,{{L}_{i}}+\underset{i}{\overset{N}{\mathop \sum }}\,\underset{\begin{smallmatrix} j \end{smallmatrix}}{\overset{N}{\mathop \sum }}\,{{M}_{ij}},\quad i\ne j. $

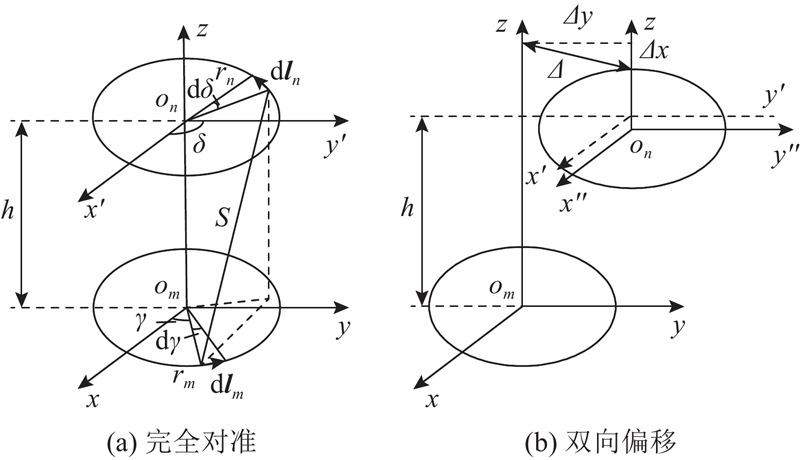
发射线圈与接收线圈的耦合互感等效为同心圆形线圈的互感叠加进行计算. 首先计算发射线圈第m匝与接收线圈第n匝的单匝线圈互感，互感计算几何模型如图5所示. 图中，h为两线圈之间的垂直高度差，dl_m、dl_n为线圈m、n中的矢量元，γ为dl_m与坐标原点O_m的连线与O_mx方向的夹角，δ为dl_n与坐标原点O_n的连线与O_nx'方向的夹角，dγ和dδ分别为对应的圆弧夹角，S为dl_m，dl_n之间的距离，μ₀为真空磁导率，r_m、r_n为发射线圈和接收线圈中的单匝线圈半径，Δ为发射线圈与接收线圈产生相对于Z轴的横向偏移量. 当两线圈完全对准时，dl_m与dl_n的间距为

(14)$ {S_{mn}} = \sqrt {r_m^2+r_n^2 - 2{r_m}{r_n}\cos\; (\delta - \gamma )+{h^2}} . $

当2匝线圈发生双向偏移时，dl_m与dl_n的间距为

(15)$ \begin{split} {S_{\Delta mn}} = & \left( {{({r_m}\cos \gamma - {r_n}\cos \delta )}^2}+\right. \\&\left.{{(\varDelta - {r_m}\sin \gamma +{r_n}\sin \delta )}^2}+{h^2}\right)^{1/2} . \end{split} $

由诺依曼公式得到两单匝线圈的互感为

(16)$ {M_{mn}} = \frac{{{\mu _0}}}{{{{4{\text{π}} }}}}\mathop \int \nolimits_0^{{{2{\text{π}} }}} \mathop \int \nolimits_0^{{{2{\text{π}} }}} \frac{1}{S}{{{\text{d}}{{\boldsymbol{l}}_m} \cdot {\text{d}}{{\boldsymbol{l}}_n}}}. $

发射线圈与接收线圈之间的耦合互感M为2匝线圈内部各单匝线圈的互感之和：

(17)$ M = \sum\limits_{m = 1}^{{N_1}} {\sum\limits_{n = 1}^{{N_2}} {{M_{mn}}} } . $

在低频情况下，磁耦合线圈的内阻R只有欧姆损耗R_s；在高频的情况下，线圈内部除了欧姆损耗之外，还存在辐射损耗R_r.

(18)$ {R_{\text{s}}} = \sqrt {\frac{{\omega {\mu _0}}}{{2\sigma }}} \cdot \frac{l}{{2{\text{π}}r_{\mathrm{a}}}}. $

其中σ为电导率，r_a为单股线圈的横截半径，l为平面圆形螺线圈绕线的总长度.

(19)$ {R_{\text{r}}} = \sqrt {\frac{{{\mu _0}}}{{{\varepsilon _0}}}} \left[\frac{{\text{π}}}{{12}}{N^2}{\left(\frac{{\omega r}}{c}\right)^4}+\frac{2}{{3{{\text{π}}^3}}}{\left(\frac{{\omega h}}{c}\right)^2}\right]. $

其中真空介电常数ε₀=8.854×10⁻¹² F/m，c为光速. 在实际测量中的线圈欧姆损耗与理论计算值存在误差，因此根据文献[15]中实际测量数据，引入补偿系数k=12.9来匹配实际数据，线圈内阻的表达式为

(20)$ R = k{R_{\text{s}}}+{R_{\text{r}}}. $

为了实现系统多个参数的全局优化，进行系统中各个参数的影响评估，选择对系统运行影响程度大的参数进行优化，以提高系统的传输效率和线圈功率密度. 本研究采用GRA进行系统参数评估，得到各参数对系统传输效率影响的排序.

GRA是多因素统计分析方法，用来分析系统中母因素与子因素的密切程度，进行系统动态发展态势的量化比较分析，判断引起系统变化的主要决定因素和次要决定因素. GRA计算过程简单，所需的信息少、数据量小，不需要样本信息有明显的分布特征，量化结果与定量分析结果符合. GRA的分析步骤如下. 1）从系统中选择待判断关联度的变量，其中母因素（参考序列）X₀=（x_01, x₀₂, x₀₃···, x_0n），其余量子因素（比较序列）X_i=（x_i1，x_i2, x_i3···, x_in），i=1, 2, 3, ···, n. 2）对系统中变量的数据进行归一化处理. 系统中各个影响因素数据的量纲不同，须进行数据的归一化处理. 常用的处理方法有初值化、区间化和均值化等，本研究采用初值化方法，得到$X'_i=X_i/x_{i1}=(x'_{i1},x'_{i2},x'_{i3},\cdots,x'_{in}) $, i=0, 1, 2, ···, m. 3）求出差序列、最大差和最小差. 差序列为Δ_0i(k)=|$x'_0 $(k)-$x'_i $(k)|，其中k=1, 2, ···,n；最大差为M₁=max_imax_kΔ_i(k)；最小差为M₂=min_imin_kΔ_i(k). 4）计算灰色关联度系数. ξ(x₀(k), x_i(k))=(M₂+ζM₁)/(Δ_0i(k)+ζM₁)，其中ζ=0.5为分辨系数，取值范围为0~1.0. 5）计算关联度. 关联度系数反应子序列与母序列的关联程度，但关联度系数的信息过于分散，不方便对系统整体进行比较. 因此将关联度系数集中为平均值，作为子序列与母序列的关联度：

(21)$ \xi ({x}_{0}\text{，}{x}_{i})=\frac{1}{n}{\displaystyle \sum _{ki=1}^{n}r({x}_{0}(k),{x}_{i}(k))};\quad i=0,1,2,\cdots,m. $

6）关联度排序. 若关联度ξ(x₀，x_i)> ξ(x₀，x_j)，则x_i优于x_j，即x_i对参考序列x₀的灰色关联度大于x_j，其余因子的灰色关联度大小以此类推. 关联度越大，表明该因素与母因素的密切程度越强.

根据分数阶磁耦合谐振BD-WPT系统的传输特性分析和磁耦合线圈参数计算模型，采用不同的参数对系统进行仿真计算，得到系统数据如表1所示. 表中，系统 1 为《电动汽车无线充电系统 第7部分：互操作性要求及测试 车辆端：GB/T 38775.7—2021》（以下简称国标）参数对称系统，系统 2 至系统 5 是基于系统 1 附近随机系统参数的仿真计算数据. 令分数阶磁耦合谐振BD-WPT系统原、副边补偿电路的参数相等；L_f、C_f为原、副边补偿电感和补偿电容；L_t为原、副边线圈电感值；原、副边串联谐振补偿的分数阶电容C_α，由式(4)计算得出，r₁为线圈外径；N为线圈匝数；h为两线圈间的垂直距离. 将各种影响因素与系统传输效率进行比较，计算关联程度，以传输效率为参考序列，其他参数作为比较序列，采用GRA分析系统影响因素. 采用初值化方法归一化处理表1中数据，结果如表2所示. 由步骤3）得到最大差M₁=1.55，最小差M₂=0，分辨系数ζ=0.5，灰色关联系数和灰色关联度如表3所示. 由表3可知，对分数阶磁耦合谐振BD-WPT系统传输效率影响最大的因素是谐振频率f，之后依次是N、h、r₁、L_f、C_f、R、L_t、M. 这些参数包含与功率密度相关性强的参数N和r₁.

当系统设计参数发生变化时，系统的传输特性会受到影响，系统性能参数往往存在相互冲突，不能同时达到最优值. 系统的参数优化是多参数多目标优化问题. 为了提高系统的传输效率和线圈功率密度，须进行参数优化. 在待优化变量f、L_f、C_f、L_t、R、M、r₁、h、N中，有的是非独立变量，可以利用等式关系简化减少变量个数，同时降低约束数目，最终选择f、L_f、r₁、h、N为待优化的变量.

在分数阶磁耦合谐振BD-WPT系统的传输特性中，系统传输功率和效率是2个最基本最重要的性能指标. 系统传输功率不是越大越好，而是要满足电动汽车双向充放电需求. 系统传输效率越高，系统的性能越好，因此将系统传输效率作为优化设计的目标之一，如式(7)所示. 对于电动汽车无线充电系统，电动汽车底盘的接收线圈须轻量化、小型化，在满足电动汽车充放电功率要求的前提下，减少线圈用量，因此将线圈的功率密度作为另一个优化目标. 线圈单位面积的传输功率为耦合线圈的功率密度:

(22)$ \rho = {{{P_{{\text{req}}}}}}/{S}. $

综上所述，分数阶磁耦合谐振BD-WPT系统的优化目标是最大化传输效率和最大化线圈功率密度.

在分数阶磁耦合谐振BD-WPT系统的参数优化设计过程中，系统传输效率与线圈功率密度受多个因素的影响和约束，系统约束条件如下.

1）传输功率：分数阶磁耦合谐振BD-WPT系统的输出功率P_out应该大于电动汽车无线充电要求的功率P_req=3.7 kW，即P_out>P_req.

2）器件的实际条件约束：在参数设计过程中，按照实际工程应用需求设置电容和电感的最大值和最小值；开关管器件及其他硬件电路承受范围有最大频率和最小频率的限制.

(23)$ \left. \begin{gathered} {C_{{\text{fmin}} }} < {C_{\mathrm{f}}} < {C_{{\text{fmax}} }}, \; {C_{\alpha{\mathrm{min}} }} < {C_\alpha } < {C_{\alpha{\mathrm{max}} }}, \\ {L_{{\text{fmin}} }} < {L_{\text{f}}} < {L_{{\text{fmax}} }}, \; {L_{ \min }} < L < {L_{\max }}, \\ {f_{\min }} < f < {f_{\max }}. \\ \end{gathered} \right\} $

3）电气参数范围约束：考虑线圈的耐流值I_L和补偿电容的耐压值V_C，谐振线圈中的电流应该小于线圈的耐流值，补偿电容两端的电压应小于电容的耐压值. 系统的变换器输入电流I_f、线圈最大电流I_L、变换器输入电压U、设备离地间隙h等模块的电气参数满足国际中的约束范围.

(24)$ \left. \begin{gathered} {I_L} \leqslant {I_{L{\mathrm{max}} }}, \; {V_C} \leqslant {V_{C{\mathrm{max}} }}, \; {I_{\text{f}}} \leqslant 15.0{\text{ A,}} \\ {I_L} \leqslant 35.0{\text{ A,}} \; U \leqslant 415.0{\text{ V,}} \; \;h \in [100, 150]{\text{ mm}}. \end{gathered} \right\} $

4）谐振条件约束：分数阶磁耦合谐振BD-WPT系统必须工作在完全谐振状态下，谐振条件如式(4)所示；分数阶电容的电阻分量与耦合线圈的内阻抵消，如式(3)所示.

根据优化目标和约束条件分析，将分数阶磁耦合谐振BD-WPT系统的参数优化设计问题描述如下：在满足系统传输功率、器件实际条件、谐振条件和电气设备参数范围约束的前提下，以系统传输效率和线圈功率密度最优为目标，确定系统频率、补偿电感、线圈外径、线圈垂直距离和线圈匝数. 多目标优化算法均为极小化目标函数，因此取传输效率和线圈功率密度的负数作为目标函数，系统参数优化设计的多目标优化数学模型为

(25)$ \left.\begin{gathered} \mathrm{min}\Big\{{{f}_{1}=-\eta \;(f,{L}_{\text{f}},{r}_{1},h,N),\;{f}_{2}=-\rho \;({r}_{1},N)}\Big\}. \\ {\text{s}}{\text{.t}}{\text{.}}\; {g_1} = {P_{{\text{req}}}} - \frac{M}{{\omega L_{\text{f}}^2}}{U^2} \leqslant 0, \\\quad\;\;{g_2}{{ = 1 - 4}}{{\text{π }}^2}{C_{{\text{fmax}}}}{f^2}{L_{\text{f}}} \leqslant 0, \\\quad\;\;{g_3}{\text{ = 4}}{{\text{π }}^2}{C_{{\text{fmin}}}}{f^2}{L_{\text{f}}} - 1 \leqslant 0, \\\quad\;\;{g_4}{\text{ = }}{I_L} - {I_{L{\mathrm{max}} }} \leqslant 0, \\\quad\;\;{g_5}{\text{ = }}{I_{\text{t}}} - {I_{{\text{t}}\max }} \leqslant 0, \\\quad\;\;{g_6}{\text{ = }}{V_C} - {V_{C{\mathrm{max}} }} \leqslant 0, \\\quad\;\;{g_7}{\text{ = }}0.85 - {f_1} \leqslant 0, \\\quad\;\;{g_8}{\text{ = }}\omega {L_{\text{t}}} - \frac{1}{{{\omega ^\alpha }{C_\alpha }}}\sin \left(\frac{{\text{π}}}{2}\alpha \right) - \frac{1}{{\omega {C_{\text{f}}}}}{\text{ = 0,}} \\\quad\;\;{g_9}{\text{ = }}R - \frac{1}{{{\omega ^\alpha }{C_\alpha }}}\cos \left(\frac{{\text{π}}}{2}\alpha \right) = 0. \\\end{gathered}\right\} $

优化变量的解空间为

(26)$ \begin{split} \Big\{&{f}_{{\mathrm{min}}} < {x}_{1} < {f}_{{\mathrm{max}}}\text{，}{L}_{\text{f}{\mathrm{min}}} < {x}_{2} < {L}_{\text{f}{\mathrm{max}}}\text{，}\\ &{r}_{{\mathrm{1min}}} < {x}_{3} < {r}_{{\mathrm{1max}}},\;{h}_{{\mathrm{min}}} < {x}_{4} < {h}_{{\mathrm{max}}},\\ &{N}_{{\mathrm{min}}} < {x}_{5} < {N}_{{\mathrm{max}}}.\Big\}\end{split} $

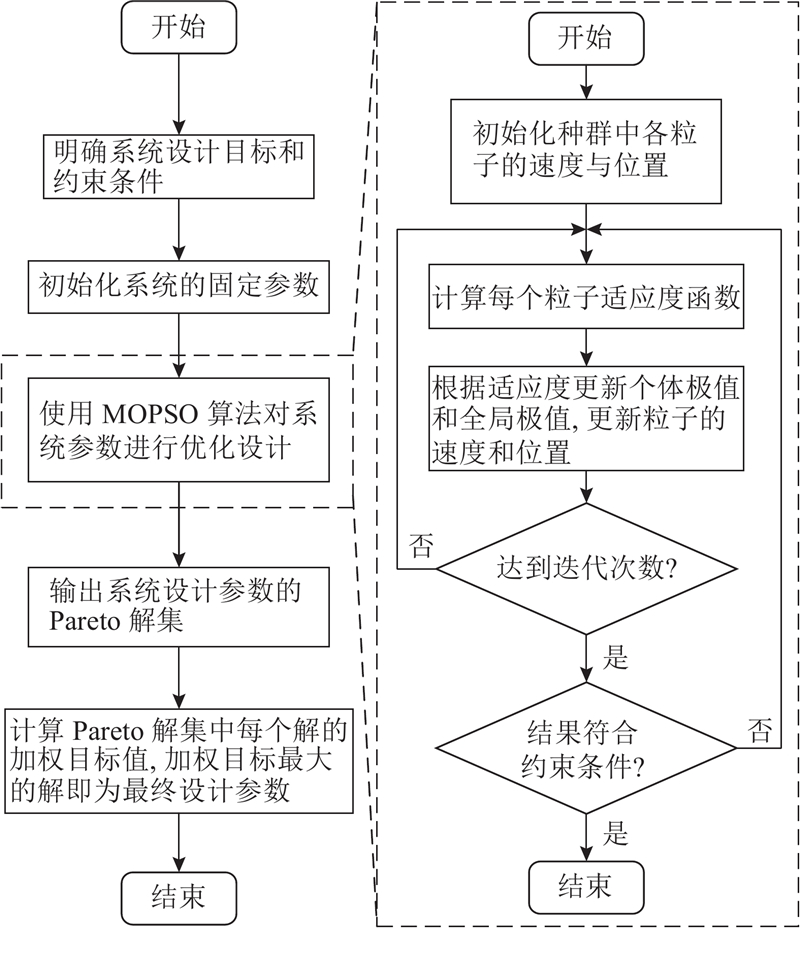
分数阶磁耦合谐振BD-WPT系统是多约束非线性系统，须采用算法对系统多参数进行优化设计. MOPSO算法基于群体智能，用于在多个目标函数的情况下寻找最优解，其核心思想是通过粒子之间的协作和竞争来搜索最优解. 该算法模拟了鸟群或鱼群的行为，将每个粒子视为个体，它们通过不断地更新速度和位置来搜索最优解；每个粒子也可以看作是某个群体的成员，它们通过交流信息和竞争资源来协作搜索最优解. 该算法具有较好的全局搜索能力和收敛性，算法流程图如图6所示.

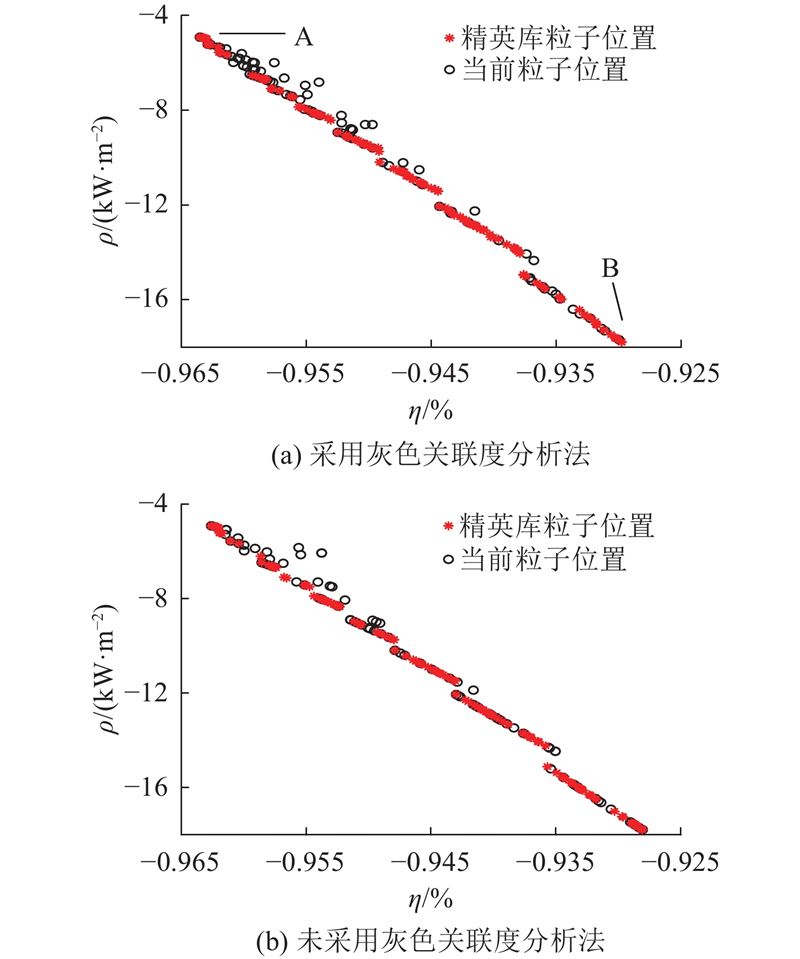
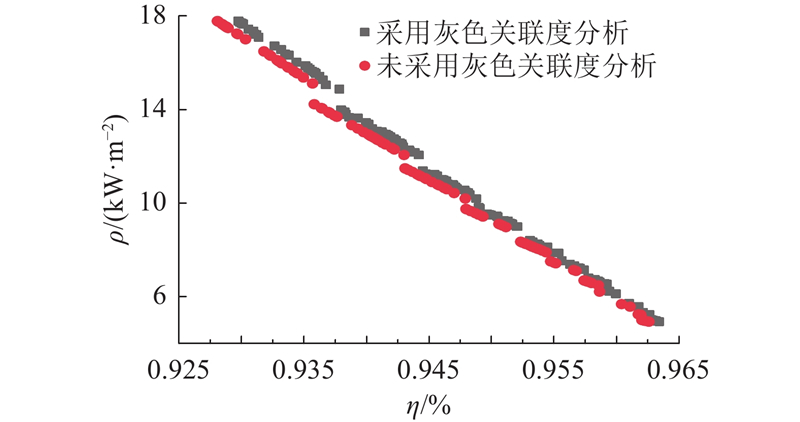
为了对整个系统的参数进行优化设计，根据实际工程应用需求及国家标准确定优化变量和相关的参数取值范围，线圈线径为5 mm，由单股直径0.1 mm的多股利兹线绕制而成，线圈绕线间距6.66 mm. 优化变量f、L_f、r₁、N、h的解空间分别为[82,90] kHz、[20,40] μF、[0.20,0.45] m、[2,15]、[0.10,0.15] m. 其余系统参数根据电动汽车无线充电系统实际情况，设置U_DC1、U_DC2=300 V，需求功率P_req=3.7 kW，变流器最大输入电流I_fmax=15 A，线圈最大电流I_max=35 A，补偿电容的最大耐压值V_Cmax=200 V，补偿电容C的取值范围为[0.01,5.00] μF. 采用MOPSO算法在Matlab中对系统参数进行优化，设置种群大小为100，迭代次数为100. 2个优化目标的最优Pareto前沿解，如图7所示. 图中，点A为传输效率最优，线圈功率密度最劣的点，传输效率为96.35%，功率密度为4.91 kW/m²；点B为线圈功率密度最优，传输效率最劣的点，传输效率92.98%，功率密度为17.78 kW/m². 为了对比分析，在不采用GRA时未选取系统工作频率作为设计变量，而是根据国标中设定设备额定工作频率为85.5 kHz，采用MOPSO算法对谐振补偿结构和线圈参数进行优化，优化变量为L_f、r₁、N、h，得到传输效率和线圈功率密度的最优Pareto前沿解. 对图中的Pareto前沿解取负值后整合，得到2组系统传输效率和线圈功率密度的关系图，如图8所示. 可以看出，系统效率和线圈的功率密度呈负相关，无法同时达到最优值，随着系统传输效率提升，线圈的功率密度减小. 采用GRA得到的系统传输效率和线圈功率密度都优于未采用GRA的结果. 在系统传输效率相同的情况下，采用GRA得到的线圈功率密度更大. 由此可见，通过GRA对分数阶磁耦合谐振BD-WPT系统参数的评估，有选择性地进行参数优化，可使系统运行更稳定、可靠.

采用GRA后通过MOPSO算法得到的部分Pareto前沿最优解和对应的目标函数值如表4所示. 由表可知，MOPSO算法得到的Pareto前沿最优解对应的谐振频率、传输距离基本保持不变，随着线圈匝数和线圈外径同时增大，系统传输效率增加，线圈功率密度减小. 在实际工程应用中，优化得到的Pareto前沿最优解集须根据电动汽车充放电效率和车辆底部线圈功率密度的不同要求，选择一组最优解用于设计参考. 对Pareto前沿最优解集中的解进行规范化排序，再将最优解集中最大加权目标值对应的解作为最优设计参数，

(27)$ {f_t} = \sum\limits_{n = 1}^{{n_{{\mathrm{obj}}}}} {\frac{{{f_t}(n) - {f_{ {\mathrm{min}} }}(n)}}{{{f_{ {\mathrm{max}} }}(n) - {f_{ {\mathrm{min}} }}(n)}}} {\alpha _t}. $

式中：f_t为最优解集中的第t个解对应的加权目标值，n_obj为优化目标的个数，f_t(n)为第t个解对应的第n个优化目标的目标函数值，f_max(n)、f_min(n)分别为所有Pareto解中第n个优化目标函数值的最大、最小值，α_t为不同目标函数的权重. 权衡实际应用中优化目标的权重，选择传输效率的权重为0.6，线圈的功率密度的权重为0.4. 由权重计算式得到最大加权目标值对应的最优结果，设计参数如表5所示. 此时系统的传输效率为94.32%，线圈功率密度为12.35 kW/m²，均高于优化前采用国标系统参数的89.86%与11.44 kW/m²，因此本研究所提优化方法可行.

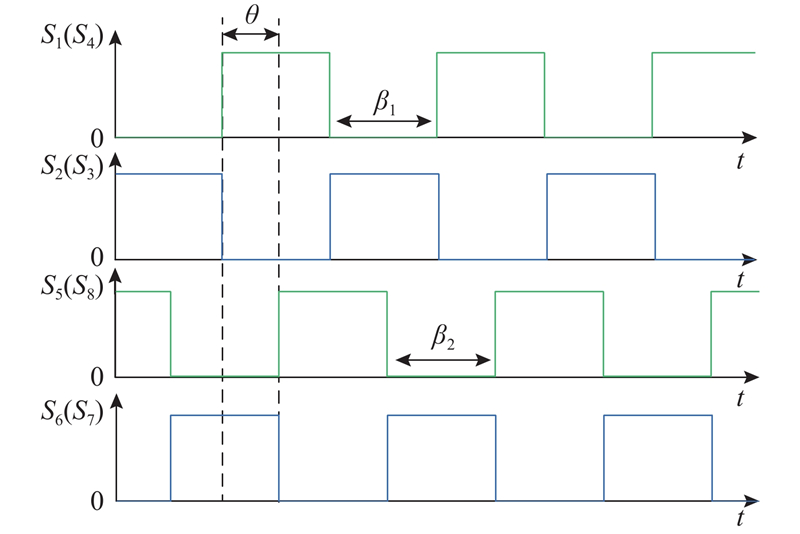
为了验证MOPSO算法结果的有效性，在Matlab/Simulink中搭建分数阶磁耦合谐振BD-WPT系统，对比分析采用MOPSO算法优化后系统和国标参数对称系统的传输效率和线圈功率密度. 系统结构对称，因此正向能量传输工况与反向能量传输工况的工作原理相似. 本研究以反向能量传输工况为例，忽略系统一、二次侧变换器的开关损耗和死区时间的影响，设系统能量从一次侧传输到二次侧为正向能量传输模式；二次侧传向一次侧为反向能量传输模式. 如图9所示为BD-WPT系统能量反向传输时的开关信号S₁~S₈的工作波形图，设置一、二次侧变换器的内移相角β₁=β₂=π，外移相角θ=−π/2；当仿真时间到达0.05s时，系统能量传输模式切换到正向能量传输模式，此时一、二次侧变换器的内移相角β₁=β₂=π，外移相角θ=π/2.

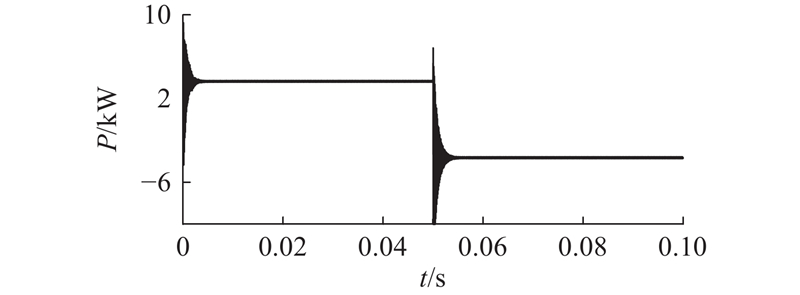
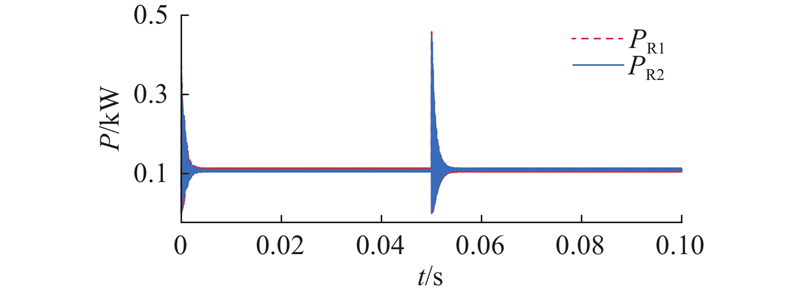
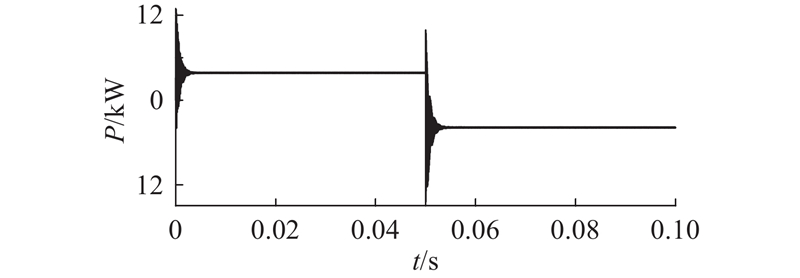
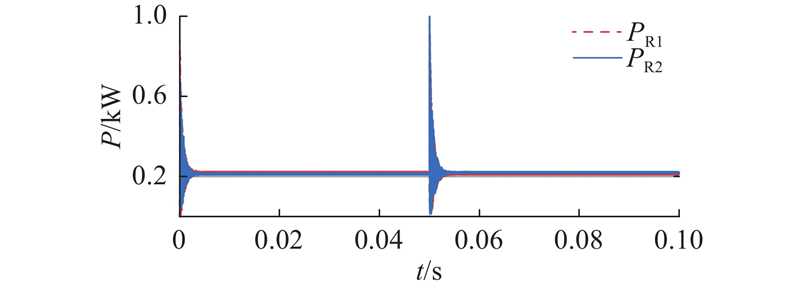
如图10所示为MOPSO算法优化后的BD-WPT系统反向能量传输模式向正向能量传输模式切换的二次侧输出功率仿真波形图. 当仿真时间在0.05 s时，系统由反向能量传输工况切换到正向能量传输工况，并快速达到稳定. 当系统工作在反向能量传输工况时，系统输出功率P_S=3 709.0 W，由表5和式(22)得到此时的线圈功率密度ρ=12.38 kW/m². 如图11所示为系统线圈损耗功率. 此时系统一次侧线圈内阻R₁损耗的功率P_R1=113.1 W，二次侧线圈内阻R₂损耗的功率P_R2=105.8 W，计算得到系统的传输效率为η=94.43%. 如图12所示为采用国标参数对称的BD-WPT系统反向能量传输模式向正向能量传输模式切换的二次侧输出功率仿真波形图. 当系统工作在反向能量传输工况时，系统输出功率为P_S=3 870.6 W，由表1和式(22)得到此时ρ=11.96 kW/m². 如图13所示为系统线圈损耗功率. 此时P_R1=219.0 W、P_R2=214.5 W，计算得到η=89.93%. 对比分析2个系统的仿真结果可知，优化后系统的传输效率比国标参数对称系统的传输效率提高了4.5个百分点，线圈功率密度提高了0.42 kW/m².

以分数阶磁耦合谐振BD-WPT系统为研究对象，基于GRA和MOPSO算法提出系统参数多目标优化设计方法. 分析含分数阶电容的双LCC型BD-WPT系统的传输特性，建立面圆形螺线圈的数学模型来替代传统有限元仿真计算模型，缩短了线圈参数的计算时间. 采用GRA选取对系统影响较大的参数进行优化设计，在含有非线性约束条件下，以传输效率和线圈功率密度为优化目标，采用MOPSO算法对系统参数进行优化，结果表明通过GRA有选择性地优化参数能够有效提高系统的传输效率. 结合电动汽车实际充放电需求，对2个目标函数赋予不同权重，对MOPSO算法结果中的Pareto前沿最优解进行规范化处理，选择最优解用于系统设计. 仿真实验结果验证了所提方法的可行性，表明所提方法能够实现BD-WPT系统多参数多目标优化，适用于其他补偿拓扑，对磁耦合谐振BD-WPT系统的参数设计有参考意义. 本研究在车辆固定状态下进行，后续将开展车辆在移动状态下的动态优化研究.