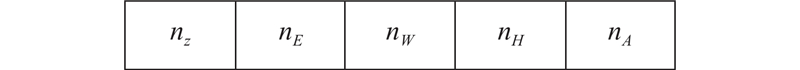以飞机总装为背景研究物流资源配置问题的文献较少,物流资源投入量常作为总装车间配送车辆调度[2-3]和设施布局优化[4-5]的已知条件或约束. 在飞机装配场景的资源配置方面,学者多关注装配作业资源,特别是人力资源配置对生产调度的影响[6-7]. 以离散制造车间生产场景下物流资源配置为参考,研究方法主要包括仿真优化与集中式建模优化. 仿真优化通过对生产过程进行模拟和多维度评价,完成关键参数优化. 周韶武等[8]采用Petri网和Witness软件对某电装车间生产物流系统进行建模仿真,通过调整瓶颈设备的数量,实现生产线的平衡. Li等[9]基于工厂仿真软件Plant Simulation提出物流系统资源配置方案,通过识别瓶颈资源和实施正交试验,得到包括自动引导车(automatic guided vehicle, AGV)投入数量、暂存区容量在内的物流资源最优决策. Wu等[10]利用数字孪生技术建立虚拟仿真物流系统,确定不同工况下的AGV投入数量,有效提升了资源利用率. 在以上文献中,仿真优化大多着眼于瓶颈资源的识别与调整,难以对多类资源进行联合优化. 此外,由于仿真环境搭建和实验耗时的限制,仿真优化更多应用于有限数量候选方案的择优和现有方案的调整,不适用于飞机总装这类可行方案数量较多、配送周期长的复杂场景. 在集中式建模优化方面,陈炫锐等[11]研究多层车间中自动存取系统的AGV配置优化问题,基于排队网络模型建立含吞吐率和空闲AGV数量2个性能指标的函数,利用启发式迭代算法求解得到最优AGV配置方案. 刘雪梅等[12]考虑装配线平衡与配置的集成优化问题,建立多目标数学规划模型,基于改进遗传算法得到任务分配和缓冲区容量配置的最优结果. 为了提高AGV无人仓储系统的物流效率,Tang等[13]建立任务分配和资源配置的两阶段数学模型,设计双层遗传算法进行求解,得到最优AGV数量和取货站布局方案. 集中式建模优化方法在优化选定的系统运行指标的同时,一定程度上忽视了系统内各子系统的交互和自身运行指标的优化,导致资源配置不均衡和部分子系统运行效率低下.
飞机总装物流配送系统是多级仓储和多阶段配送的复杂系统. 在系统规划层面,各仓储和配送子系统的资源投入数量是确定车间设施布局中各仓储区域面积和车道设置的重要依据. 各子系统资源的均衡配置有助于车间各功能区域的合理划分,避免物料积压和配送效率低下. 在生产管理层面,物料在各仓储区域的存储时长和各配送阶段的时间窗长度是评价各仓储和配送子系统运行效率的重要指标. 作为研究多主体间理性决策及行为交互的理论,博弈论已被广泛应用于云计算[14]、网络通信[15]、雷达搜索[16]等资源配置场景中. 在生产物流配送系统资源配置领域,博弈论的应用鲜少. 王金凤等[17]将煤炭生产物流系统中的安全和效率水平抽象为博弈主体,基于合作博弈框架和纳什讨价还价法,寻求总资源投入确定下的资源配置方案. 已投入使用的飞机总装物流配送系统主要借鉴前代支线客机和同类型客机总装车间资源配置的经验. 由于产品尺寸、装配工艺的差异,现有车间存在部分仓储区域物料积压和部分物料配送延迟送达的情况. 本研究在飞机总装生产场景中引入博弈论,将配送系统内各类仓储和配送子系统抽象成独立的博弈主体,以成本和效率对各主体的资源投入决策进行评价,建立基于非合作博弈框架的物流配送系统资源配置模型;将纳什均衡条件转化为博弈目标函数,提出改进粒子群算法求解博弈模型,获得兼具经济性和纳什均衡性的物流配送系统资源配置方案,使各子系统运行效率保持在相对均衡的状态.
1. 背景描述
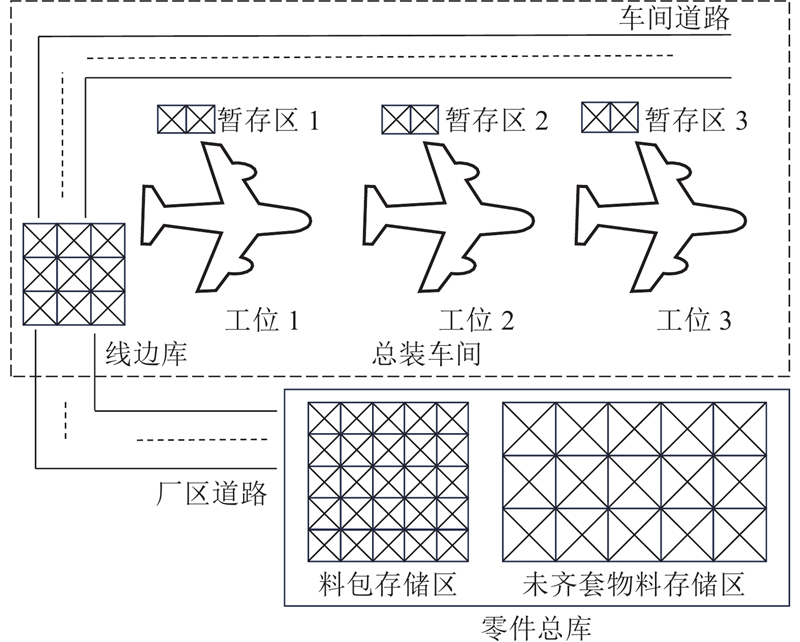
某民用客机总装车间共有3个装配工位,分别负责客机功能系统安装、系统总装与分系统测试以及最终功能试验. 每个工位旁设有工位暂存区,存放待上线装配的物料. 车间西南角设有线边库,作为零件总库料包存储区和工位暂存区之间的缓存区. 厂区内零件总库负责接收采购的物料并打包,是物流配送系统的起点. 总装车间和零件总库的布局如图1所示. 如图2所示为总装车间三级仓储、两阶段配送的流程示意图. 物料一般在上线装配前数日内,根据物料清单(bill of material, BOM)拣选齐套,形成以标准化料箱存储和配送的料包,存储于零件总库内的料包存储区. 料包从零件总库料包存储区至线边库的配送由货车完成,从线边库至目标工位暂存区的配送由AGV完成.
图 1
图 2
图 2 飞机总装物流配送系统的配送流程
Fig.2 Distribution process of aircraft final assembly logistics distribution system
本研究的物流配送系统资源配置问题:确定给定生产节拍下零件总库料包存储区、线边库、工位暂存区的容量,以及货车、AGV的数量,为总装车间物流系统规划提供决策依据. 为了简化问题建模和考虑生产实际,进行如下假设:1)物流配送系统仅考虑能够使用标准化料箱进行存储的标准件、中小型构件及成品件物料,使用专用牵引设备直接上线装配的物料(如扰流板)不在研究范围中;2)飞机装配工艺稳定,装配严格按照计划时间执行,料包的最晚送达时刻等于该料包在工位用于装配的时刻;3)车间为各工位预留的暂存区面积相同,因此将3个工位暂存区的容量视为1个决策变量;4)车辆配送使用车间专用道路,不考虑车间人员和其余物料移动对车辆配送耗时的影响;5)配送过程所用车辆相同,同一车辆可以进行多次配送.
2. 飞机总装物流配送系统资源配置博弈模型
2.1. 博弈关系分析
飞机总装物流配送系统各类仓储和配送在合作响应物料配送需求的同时,在提高自身运行效率和降低资源投入成本上存在竞争. 非合作博弈框架常用来对系统内各主体的策略和收益进行单独建模,并分析主体的联合决策行为[18],以便较好地描述配送系统中各类仓储和配送间的竞争合作关系.
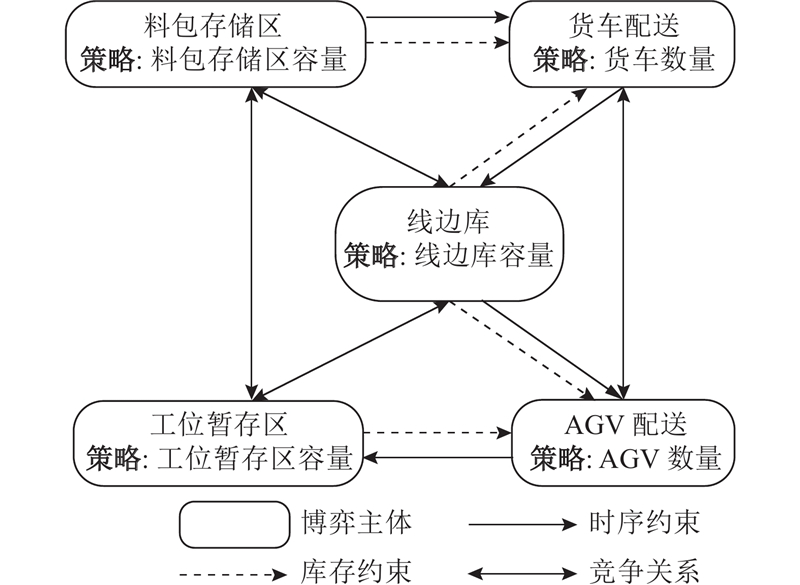
将各类仓储和配送抽象为独立的博弈主体,以各主体的资源投入量(仓储容量和配送车辆数量)为博弈策略,得到主体间的博弈关系如图3所示. 图中,时序约束是指料包在各仓储和配送主体间流转的先后顺序约束,库存约束是指仓储主体在任意时刻存储的料包数量不应超过其容量. 各主体在满足库存约束和料包最晚送达时刻约束的基础上,展开博弈,包括不同类主体间的博弈和同类主体内部的博弈. 仓储类主体与配送类主体的博弈体现在:配送主体通过时序约束对仓储主体的资源投入提出要求;仓储主体通过库存约束对配送主体的资源投入进行制约. 以线边库仓储主体和货车配送主体为例,线边库仓储主体的资源投入应当满足货车配送主体将料包送达时的入库需求;线边库仓储主体的资源投入对货车配送主体的资源投入及配送速率进行制约. 此外,同类主体间也存在博弈,各仓储主体均希望减少料包在自身的存储时长以降低仓储管理成本,避免料包在自身出现积压现象,各配送主体均希望争夺更长的配送时间窗口以换取进一步减少资源投入的可能.
图 3
2.2. 博弈主体及策略空间
博弈模型包含仓储和配送2个类别的主体;仓储主体有3个,分别是料包存储区
2.3. 效用值函数
效用值函数是衡量博弈主体在不同策略组合下自身收益的函数,用来分析主体的最优策略选择及博弈的均衡状态. 将所有博弈主体选择的策略组成的集合记作
成本效用值
式中:
式中:
式中:
此时,各主体均以最小化自身成本效用值和效率效用值为优化目标:
2.4. 基于纳什均衡的博弈目标函数
为了优化成本效用值和效率效用值,博弈主体不断调整资源投入
其中
为了统一量纲,对
记方案
式中:
式中:
3. 资源配置博弈模型求解
粒子群优化算法(particle swarm optimization algorithm, PSO)具有设计简单、收敛速度快的特点,被广泛应用于纳什均衡求解中[20]. 本研究提出融合策略空间动态调整的粒子群优化算法(particle swarm optimization algorithm with dynamic adjustment of strategy space, PSODASS)求解博弈模型. 粒子与博弈策略组合一一对应,粒子的每个维度取值对应1个博弈主体的策略选择,搜索空间为该主体的策略空间. 如图4所示为粒子示意图,其中方格表示粒子的维度,
图 4
3.1. 算法流程
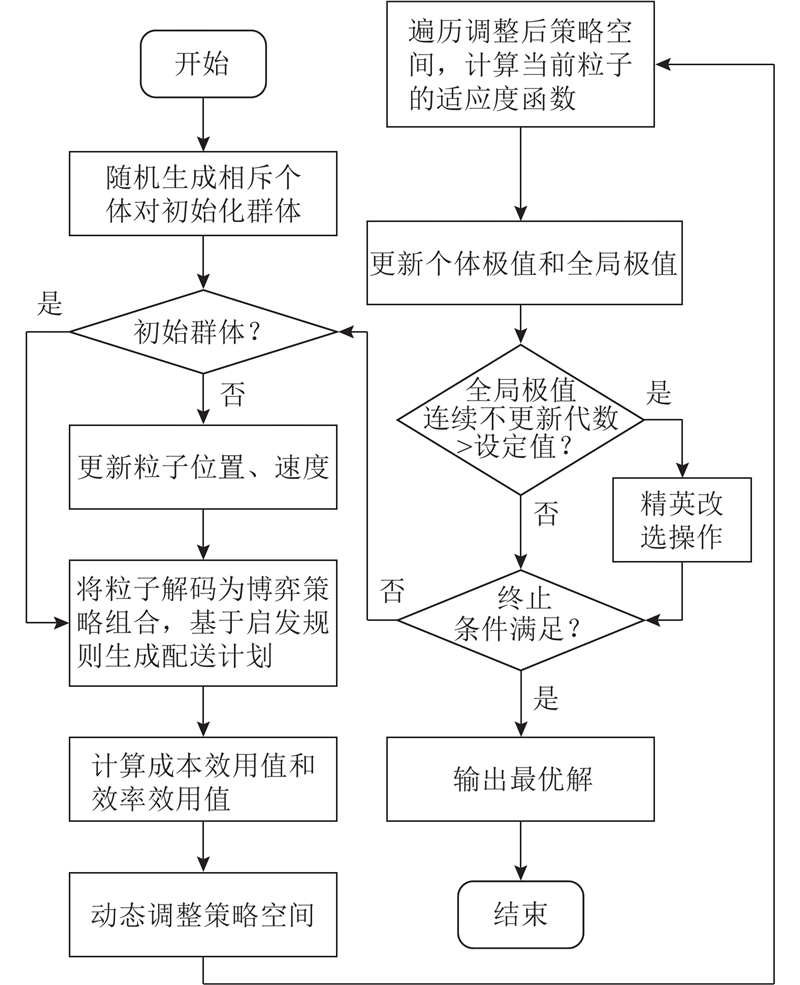
基于粒子对应的博弈策略组合(资源配置方案),利用启发式规则实现当前方案下物流配送计划的快速生成,进而对各主体效用值进行评价;为了减少无效搜索,加快效用值计算,提出策略空间动态调整策略. 为了避免算法陷入局部最优解,在初始化种群时引入相斥个体对的概念;在迭代过程中引入精英改选操作,即当全局极值连续不更新代数超过设定值后,对群体中后20%的个体进行变异操作,并将变异个体和原群体一起进行当次迭代全局极值的选取. 算法流程如图5所示.
图 5
图 5 所提粒子群优化算法的流程图
Fig.5 Flow chart of proposed particle swarm optimization algorithm
3.2. 物流配送计划生成
本研究设计基于以下规则的启发式物流配送计划生成方法. 1)以车辆容量为组合大小,按照最晚送达时刻(料包上线装配时刻)和目标暂存区一致性进行料包分组. 2)优先为平均最晚送达时刻较小的料包组合安排配送. 3)优先选择可使用时刻最早的车辆进行配送,当车辆被安排配送任务,更新该车辆可使用时刻为完成当次配送任务的返回时刻. 4)当前车辆配送批次的开始配送时刻为该车辆可使用时刻、批次所含料包进入待配送状态时刻(对于货车配送,该时刻等于料包进入零件总库料包存储区域的时刻;对于AGV配送,该时刻等于料包进入线边库的时刻)和目标仓储区域基于库存约束允许该批次开始配送的最早时刻这3个时刻的最大值. 计算每个粒子表征的资源配置方案各博弈主体的成本效用值;基于上述规则快速生成当前方案下的配送计划,计算得到各主体的效率效用值;基于效率效用值、成本效用值和配送计划,完成粒子适应度的评价.
3.3. 策略空间动态调整策略
为了评估粒子的纳什均衡状态,算法须遍历每个博弈主体的策略空间,并计算效用值. 为了提高算法效率,通过分析效用值函数和粒子不可行性信息动态调整策略空间,减少无效计算. 基于以下策略,在历次迭代中动态调整各博弈主体的策略空间,加快适应度函数计算和算法求解.
策略1 在保证粒子可行的前提下,仓储主体和货车配送主体均存在降低自身资源投入量以进一步优化自身效用值的倾向. 设定策略空间的上界为当前资源投入量.
策略2 当仓储主体存在库存溢出时,策略空间搜索起点调整为当前容量与溢出库存容量之和.
策略3 当出现延迟送达时,各主体不应减少自身资源投入量.
3.4. 适应度函数
粒子群优化算法以博弈目标函数为适应度函数,基于策略空间动态调整策略,实现对博弈主体单方面改变自身策略能够获得的最大效用值优化量的快速计算,利用式(15)实现对粒子纳什均衡性的评价. 考虑到非合作博弈框架仍以各主体合作完成物料配送为前提,因此对于可能出现的不可行状况:物料延迟送达和库存溢出,引入惩罚因子
式中:
式中:
4. 实例验证
开展计算实验,验证所提博弈模型与求解算法. 算例源于某民用客机制造企业总装车间. 计算程序代码语言为Python 3.8.2,电脑配置为Intel Pentium G4600 CPU 4.60 GHZ 8.0 GB RAM.
4.1. 算例描述
当前飞机总装生产节拍为14 d,单架次飞机装配要求完成812个料包的存储及配送. 综合考虑采购成本、变动成本、使用年限、维修成本等因素,确定料包存储区、线边库、工位暂存区的单位成本分别为3、6、9千元/料包,货车和AGV的单位成本分别为120、12千元/辆. 结合访谈调研中决策者对系统建设成本和运行效率的重视程度,
4.2. 算法性能分析
基于实际生产数据生成8个不同规模的算例. 针对每个算例,每种算法运行10次,选取最优结果进行对比. 算法求解结果如表1所示.
表 1 所提粒子群优化算法的最优性和求解速度分析
Tab.1
| 算法 | ||||||||||||
| 100 | PSO | {80,24,12,1,7} | 0.10 | 912 | 23 | 1.24 | 0.05 | 0.00 | 0.00 | 17.39 | −8.06 | −20.00 |
| BreedPSO | {80,24,12,1,7} | 0.10 | 912 | 25 | 1.15 | 0.05 | 0.00 | 0.00 | 8.00 | −0.87 | −20.00 | |
| SimuAPSO | {80,24,12,1,7} | 0.10 | 912 | 25 | 1.17 | 0.05 | 0.00 | 0.00 | 8.00 | −2.56 | −20.00 | |
| 本研究 | {80,24,12,1,7} | 0.10 | 912 | 27 | 1.14 | 0.04 | — | — | — | — | — | |
| 200 | PSO | {180,20,20,1,3} | 0.10 | 24 | 9.50 | 0.40 | −100.00 | 3.54 | 62.50 | −6.21 | −42.50 | |
| BreedPSO | {180,28,20,1,3} | 0.00 | 26 | 7.13 | 0.27 | 0.00 | 0.00 | 50.00 | 24.96 | −14.81 | ||
| SimuAPSO | {180,20,20,1,3} | 0.10 | 31 | 7.88 | 0.25 | −100.00 | 3.54 | 25.81 | 13.07 | −8.00 | ||
| 本研究 | {180,28,20,1,3} | 0.00 | 39 | 8.91 | 0.23 | — | — | — | — | — | ||
| 300 | PSO | {280,36,32,1,3} | 0.10 | 48 | 27.29 | 0.57 | −100.00 | −19.08 | 10.42 | −29.83 | −36.85 | |
| BreedPSO | {280,20,20,1,8} | 0.10 | 31 | 21.00 | 0.68 | −100.00 | −2.10 | 70.97 | −8.81 | −47.06 | ||
| SimuAPSO | {280.20,20,1,5} | 0.00 | 45 | 25.37 | 0.56 | 0.00 | 0.00 | 17.78 | −24.52 | −35.71 | ||
| 本研究 | {280,20,20,1,5} | 0.00 | 53 | 19.15 | 0.36 | — | — | — | — | — | ||
| 400 | PSO | {298,60,24,1,1} | 0.10 | 2034 | 30 | 70.44 | 2.35 | −100.00 | −3.83 | 63.33 | −72.25 | −82.98 |
| BreedPSO | {281,72,20,1,10} | 0.11 | 30 | 43.82 | 1.46 | −100.00 | −4.82 | 63.33 | −55.39 | −72.60 | ||
| SimuAPSO | {292,64,20,1,3} | 0.00 | 1956 | 32 | 59.81 | 1.87 | 0.00 | 0.00 | 53.13 | −67.32 | −78.61 | |
| 本研究 | {292,64,20,1,3} | 0.00 | 1956 | 49 | 19.55 | 0.40 | — | — | — | — | — | |
| 500 | PSO | {252,104,68,1,3} | 0.22 | 33 | 133.66 | 4.05 | −54.55 | −21.62 | 54.55 | −66.74 | −78.52 | |
| BreedPSO | {292,68,40,3,10} | 0.13 | 39 | 103.96 | 2.67 | −23.08 | −7.07 | 30.77 | −57.23 | −67.42 | ||
| SimuAPSO | {296,68,44,1,5} | 0.10 | 44 | 129.69 | 2.95 | 0.00 | −0.79 | 15.91 | −65.72 | −70.51 | ||
| 本研究 | {281,72,44,1,5} | 0.10 | 51 | 44.46 | 0.87 | — | — | — | — | — | ||
| 600 | PSO | {299,72,64,2,10} | 0.11 | 34 | 229.27 | 6.74 | −9.09 | −14.93 | 41.18 | −69.96 | −78.78 | |
| BreedPSO | {294,76,52,1,7} | 0.10 | 40 | 160.49 | 4.01 | 0.00 | −1.32 | 20.00 | −57.09 | −64.34 | ||
| SimuAPSO | {294,92,48,1,10} | 0.10 | 45 | 226.84 | 5.04 | 11.11 | −2.12 | 6.67 | −69.64 | −71.63 | ||
| 本研究 | {285,108,44,1,8} | 0.10 | 48 | 68.87 | 1.43 | — | — | — | — | — | ||
| 700 | PSO | {339,32,64,2,10} | 0.11 | 33 | 330.45 | 10.01 | −100.00 | −23.93 | 78.79 | −46.92 | −70.33 | |
| BreedPSO | {347,76,32,1,10} | 0.10 | 36 | 262.04 | 7.28 | −100.00 | −3.58 | 63.89 | −33.06 | −59.20 | ||
| SimuAPSO | {347,100,20,1,6} | 0.11 | 39 | 356.77 | 9.15 | −100.00 | 5.69 | 51.28 | −50.83 | −67.54 | ||
| 本研究 | {348,76,32,1,2} | 0.00 | 59 | 175.42 | 2.97 | — | — | — | — | — | ||
| 812 | PSO | {352,32,52,2,4} | 0.13 | 38 | 365.65 | 9.62 | −100.00 | −25.82 | 36.84 | −19.73 | −41.37 | |
| BreedPSO | {396,20,32,1,10} | 0.10 | 37 | 302.97 | 8.19 | −100.00 | −9.58 | 40.54 | −3.13 | −31.14 | ||
| SimuAPSO | {399,44,20,1,5} | 0.00 | 44 | 382.62 | 8.70 | 0.00 | 0.00 | 18.18 | −23.29 | −35.17 | ||
| 本研究 | {399,44,20,1,5} | 0.00 | 52 | 293.50 | 5.64 | — | — | — | — | — |
若
4.3. 实际场景求解及纳什均衡解验证
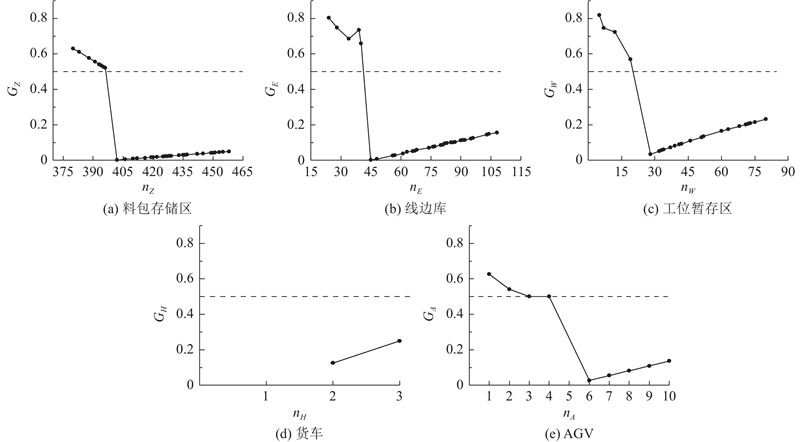
验证算法所得资源配置方案的纳什均衡性. 以料包数量为812的实际场景为例,对应最优解为
随机改变
若
所有邻域解的
图 6
图 6 博弈主体单方面改变策略得到的效用值变化
Fig.6 Variation of utility value obtained by unilateral change of strategy of game players
4.4. 资源配置方案的适应性评价
物流配送系统资源配置属于中长期决策,应具有一定柔性,能够应对产能变化,为此对物流配送系统资源配置方案进行适应性评估. 将求解得到的生产节拍为14 d的物流配送系统资源配置方案应用于节拍为10~13 d的生产场景中. 如表2所示为不同生产节拍
表 2 不同生产节拍下的仓储资源利用率
Tab.2
| TP/d | U% | ||
| 料包存储区 | 线边库 | 工位暂存区 | |
| 14 | 51.72 | 76.07 | 51.45 |
| 13 | 54.30 | 79.88 | 54.02 |
| 12 | 57.15 | 84.08 | 56.86 |
| 11 | 60.33 | 88.75 | 60.02 |
| 10 | 63.88 | 93.98 | 63.55 |
5. 结 语
本文研究某民用客机总装车间物流配送系统的资源配置优化,构造博弈决策模型,建立博弈策略集合和粒子维度变量空间的映射,提出融合策略空间动态调整的改进粒子群算法,求解各仓储区域容量和配送车辆数量. 算例求解结果表明,所提算法在纳什均衡性、总成本和求解速度上均优于对比算法,验证了策略空间动态调整策略和精英改选机制能够改善求解质量,提高优化效率. 针对实际生产场景,所提算法能够快速得到最优的资源配置方案. 对所得结果的纳什均衡性验证结果证明,各子系统的资源配置达到均衡状态. 基于数值实验,对所得资源配置方案对生产节拍加快的适应性进行评估,结果表明基于博弈模型求解的物流配送系统资源配置方案能够较好地响应车间的产能提升需求. 随着中国民用飞机的产能提升,总装生产节拍将不断加快. 如何在节拍不断加快的生产场景下,建立资源配置方案的适应性评价体系和设计动态调整策略将是未来可延伸的研究方向.
参考文献
Research and application of bottom-up route-based product data conformity inspection approach for civil aircraft
[J].DOI:10.1080/0951192X.2013.834464 [本文引用: 1]
物料配送与线边存储集成决策模型与算法
[J].
Integrated modeling and algorithm of material delivery and line-side storage problem
[J].
基于正态模糊时间窗约束的飞机装配物料配送路径规划
[J].
Aircraft assembly material delivery path planning based on normal fuzzy time window constraints
[J].
飞机移动装配线资源水平问题的建模研究
[J].
Modeling resource leveling problem for aircraft moving assembly line
[J].
考虑工时可变的飞机总装资源配置与作业调度
[J].
Resource allocation and process scheduling problem of aircraft final assembly considering variable processing time
[J].
基于Petri网和Witness的SMT生产物流系统仿真及优化
[J].
Modeling and simulation optimization of SMT production logistics system based on Petri net and Witness
[J].
Resource allocation methodology based on object-oriented discrete event simulation: a production logistics system case study
[J].DOI:10.1016/j.cirpj.2020.07.001 [本文引用: 1]
Dynamic scheduling and optimization of AGV in factory logistics systems based on digital twin
[J].DOI:10.3390/app13031762 [本文引用: 1]
多层车间中自动存取系统的AGV配置优化
[J].
AGV configuration optimization of autonomous vehicle storage and retrieval system in multi-floor workshop
[J].
随机型装配线平衡与缓冲区配置集成优化
[J].
Simultaneous balancing and buffer allocation for assembly line with stochastic task times
[J].
Research on equipment configuration optimization of AGV unmanned warehouse
[J].DOI:10.1109/ACCESS.2021.3066622 [本文引用: 1]
基于非合作博弈论的CoMP-JP资源分配算法
[J].
Resource allocation algorithm for CoMP-JP based on non-cooperative game theory
[J].
相控阵雷达搜索和跟踪资源博弈分配策略
[J].
Game strategy of resource allocation for phased array radar search and tracking
[J].
基于合作博弈的煤矿生产物流系统资源配置研究
[J].
Research of resource allocation of coal mine production logistics system based on cooperative game
[J].
Non-cooperative games
[J].
An improved predator-prey particle swarm optimization algorithm for Nash equilibrium solution
[J].DOI:10.1371/journal.pone.0260231 [本文引用: 1]
自动导引车调度优化研究综述
[J].
Review on AGV scheduling optimization
[J].
基于BreedPSO算法及交叠法的紧凑型大角度双自由曲面透镜设计
[J].
Optimization of double freeform-surface lens with large view angle based on BreedPSO algorithm and overlapping method
[J].